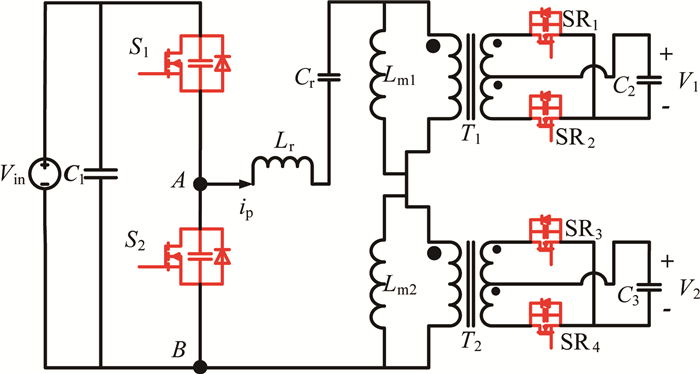
近年来,随着相控阵雷达、导弹以及飞机等现代武器装备的快速发展,对输入高压/宽范围、输出低压/大电流的高功率密度/大功率DC-DC模块电源的需求越来越迫切[1-3];目前,国内外该类电源产品普遍存在功率密度不高和效率低下等问题,例如,美国著名模块电源公司SYNQOR生产的输入240~425 V转28 V输出的全砖DC-DC模块电源,最大输出功率为800 W,最高效率为91%.显然,高功率密度与高功率等级是模块电源研制的主要重点和难点.目前,高功率密度DC-DC模块电源采用的功率电路拓扑大致可以分为单级结构和两级结构2种拓扑方式[4-12].
单级隔离型DC-DC功率电路拓扑主要有:反激、半桥、正激、移相全桥以及LLC半桥和全桥谐振变换器等几种拓扑形式.反激变换器虽然结构最简单,广泛适用于功率较小的电能变换场合,但效率很难超过90%;半桥和全桥变换器的输出功率相对较大,但存在功率开关管硬开关工作以及输出占空比丢失等问题;正激变换器不仅工作在硬开关状态,而且存在开关管电压应力较大等问题;移向全桥变换器虽然可以实现开关管的零电压开关(zero voltage switching,ZVS),但存在工作在轻载时滞后桥臂不能实现ZVS和二次侧占空比丢失等问题.LLC电路可以在宽输入电压范围以及全负载范围内实现一次侧开关管的ZVS和二次侧整流管的零电流开关(zero voltage switching,ZCS),且无需输出电感[13-14],但单级LLC变换器须采用变频控制,在宽输入电压范围或负载变化较大的情况下,开关频率变化范围大,主电路和控制参数均难以优化设计.综上所述,对于高功率密度与高功率等级的应用场合,上述的单级DC-DC拓扑均不是最优的选择.
两级结构的DC-DC功率主电路拓扑主要有:前级隔离型+后级非隔离型和前级非隔离型+后级隔离型2种结构类型.任小永等[15]提出半桥+Buck级联的结构;其中,半桥电路采用开环控制方式,为后级Buck电路提供合理的输入电压范围;后级电路采用闭环控制方式,输出恒定的直流电压.在该方案中,前级和后级电路均工作在硬开关状态,制约了整机效率的进一步提升.Kim等[16-17]提出Boost+LLC级联的结构;其中,后级LLC开环工作在谐振频率点附近,前级Boost电路闭环工作.在该方案中,后级LLC电路可以在宽输入和全负载范围内实现软开关,具有较高的效率;在高电压输入应用场合,因前级Boost电路进一步抬高输入电压,制约了后级LLC功率开关器件的选择.闭环Buck+开环LLC级联变换器系统虽然可以克服上述缺点,但后级开环LLC的增益往往会随负载的波动而变化较大,因而该拓扑难以获得较好的负载调整率.开环LLC+闭环Buck级联拓扑结构具有更多的优点:前级开环LLC在宽输入电压范围和全负载范围内均可以实现软开关;后级闭环Buck的增益与负载无关,可以实现较好的负载调整率;此外,经过前级LLC降压后,后级Buck的输入电压和输入电压范围均变小,这有利于后级Buck电路功率开关器件的选择,进一步提高整个级联系统的性能[18].
针对上述并联变换器存在的问题,石健将等[19]提出高频变压器串-并联LLC+Buck级联电路拓扑:前级高频变压器串-并联LLC定频工作,可以同时实现输入宽电压范围和输出全负载范围内的软开关;后级交错并联Buck电路采用相同占空比/闭环交错控制工作方式,既减小了输出电压纹波,又提高了输出电压的稳压精度;此外,该拓扑结构具有良好的自动均流特性,无需额外的均流控制器,可以实现串-并联变压器均衡传输功率及并联Buck电路均衡输出功率.石健将等[19]对该拓扑均流特性的理论分析仅仅建立在两个串-并联变压器的工作状态完全一致的基础上;实际上,由于后级2个Buck变换器间的参数差异,会使2个高频变压器的励磁电流的变化速率不同,从而导致2个串-并联变压器处于不同的工作状态.
在石健将等[19]的研究基础上,根据2个串-并联变压器励磁电流变化速率的不同,本文将变压器串-并联LLC+Buck级联变换器划分为3种不同的工作模式,分析在不同的工作模式下变换器的均流特性;同时,分别研究均流精度随占空比、匝比及励磁电感差异变化的规律,可得该级联电路拓扑具有良好的自动均流特性.本文通过PSIM仿真验证了理论分析的正确性,研制了一台240~425 V输入转28 V/1 kW输出的实验样机,功率密度为166 W/inch3,满载输出最高效率为94.3%,这进一步验证了该级联拓扑结构具有良好的自动均流特性,适合应用于高功率密度/大功率DC-DC电能变换场合.
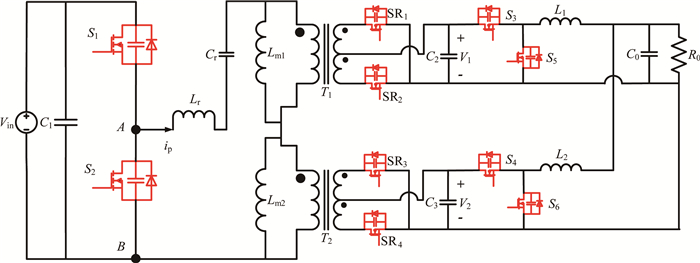
1 电路工作模式分析如图 1所示为前级变压器串-并联LLC+后级交错并联Buck级联功率电路拓扑.其中,开关管S1与S2互补导通,占空比为0.5(忽略死区时间),其与谐振电感Lr、谐振电容Cr、变压器励磁电感Lm1和Lm2以及副边的全波整流电路一起构成高频变压器串-并联的半桥LLC变换器;S3、S5、L1以及S4、S6、L2分别组成两个交错并联工作的Buck电路,采用相同占空比/闭环交错控制工作方式,即开关管S3与S4的占空比D1和D2相等,相位差为180°,并且通过实时调节D1和D2,使级联变换器在不同输入电压和负载条件下均保证输出电压恒定.
|
图 1 前级变压器串-并联LLC+后级交错Buck级联变换器拓扑 Fig. 1 Topology of transformer series connected LLC at primary side and interleaved Buck converter at secondary side |
由图 1可得,对应的2个Buck输入端电压V1和V2分别为
| $ {V_1} = {V_{\rm{o}}}/{D_1}, $ | (1) |
| $ {V_2} = {V_{\rm{o}}}/{D_2}. $ | (2) |
设计变压器T1、T2的匝比分别为n1:1:1和n2:1:1.由图 2可知,当Lr和Cr一起谐振时,两个变压器原边电压VLm1和VLm2分别为
| $ {V_{{\rm{Lm1}}}} = {n_1}{V_1}, $ | (3) |
| $ {V_{{\rm{Lm2}}}} = {n_2}{V_2}, $ | (4) |
由于实际参数的差异,会使VLm1/ Lm1与VLm2/ Lm2不同,即变压器T1、T2励磁电流变化速率不同,这将导致电路工作在3种不同的工作模式,并可能影响该级联变换器的均流特性.
为了便于分析,特进行如下假设. 1)除考虑两个变压器T1、T2的励磁电感、匝比以及开关管S1和S2的结电容外,其他所有的元件都是理想的;2)电路运行在稳定状态;3)谐振电感Lr存储的能量足够大,能够实现原边开关管的ZVS;4)励磁电感Lm1和Lm2均远大于谐振电感Lr;5)变压器T1励磁电流的变化速率总是大于等于变压器T2的励磁电流变化速率,即满足:VLm1/Lm1≥ VLm2/Lm2;6) LLC输出电压V1和V2均大于Buck输出电压Vo.
1.1 模式1在该模式下,两个变压器的励磁电流变化速率相等,满足下式:
| $ {n_1}{V_1}/{L_{{\rm{m1}}}} = {n_2}{V_2}/{L_{{\rm{m2}}}}. $ | (5) |
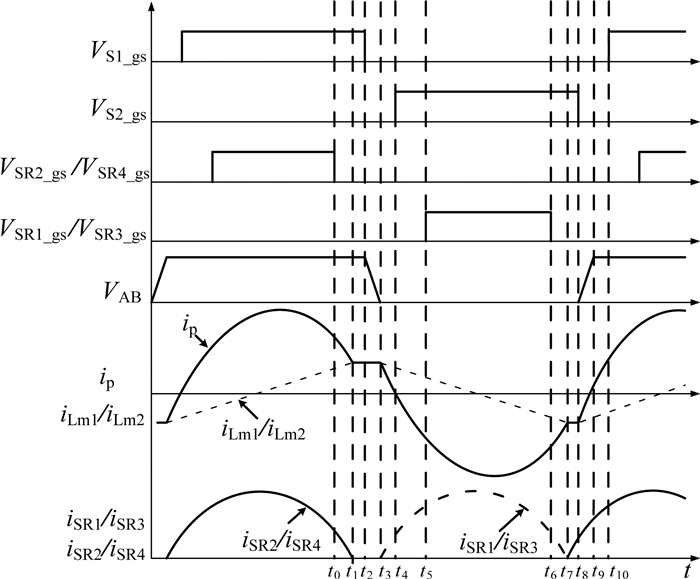
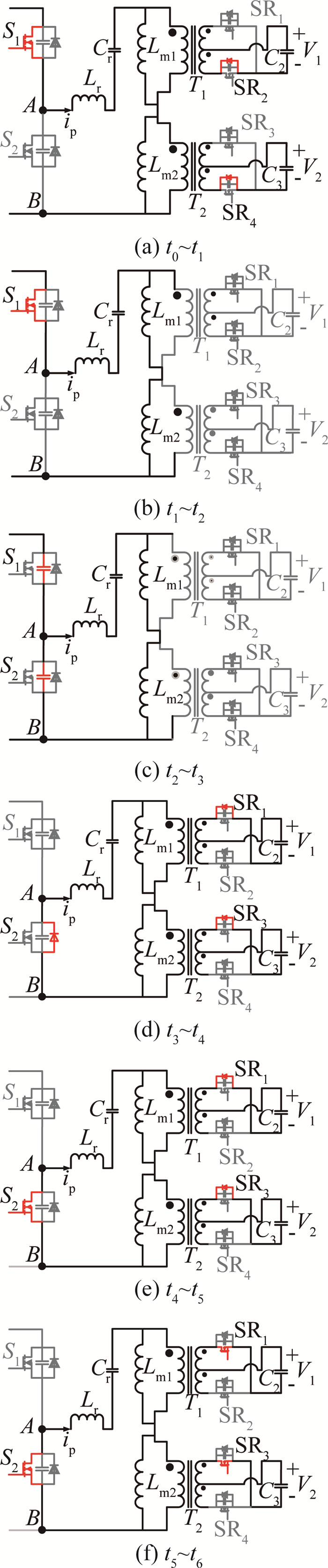
LLC电路工作在模式1下的主要波形如图 3所示.在半个开关周期内,该级联变换器共有6个工作阶段,它们的等效电路分别如图 4(a)~(f)所示.
|
图 3 模式1下的LLC电路工作波形 Fig. 3 Waveforms of LLC circuit in mode 1 |
|
图 4 模式1下不同阶段的等效电路 Fig. 4 Equivalent circuit for different stage in mode 1 |
模态1(t0~t1):t0时刻,同步整流管SR2、SR4关断,LLC副边电流iSR2、iSR4从整流管SR2、SR4转移到相应的体内二极管,变压器原边电压VLm1和VLm2分别被钳位在n1V1和n2V2;此后,Lr和Cr一起谐振至t1时刻.
模态2(t1~t2):t1时刻,谐振电流ip与励磁电流iLm1(或者iLm2)相等,变压器T1、T2不再向副边传输能量,副边关断;励磁电感Lm1+Lm2和谐振电感Lr、谐振电容Cr一起谐振至t2时刻.
模态3(t2~t3):t2时刻,开关管S1关断,同时开关管S1、S2的结电容进行充放电至t3时刻,为开关管S2的ZVS开通创造条件.
模态4(t3~t4):t3时刻,开关管S2的体内二极管自然导通续流,同时副边同步整流管SR1、SR3的体内二极管自然导通,变压器T1、T2重新开始向副边传输能量;变压器原边电压VLm1、VLm2分别被钳位在-n1V1和-n2V2;此后,Lr和Cr一起谐振至t4时刻.
模态5(t4~t5):t4时刻,开关管S2导通,谐振电流从S2的体内二极管转移到S2,实现了ZVS开通;此后,Lr和Cr一起谐振至t5时刻.
模态6(t5~t6):t5时刻,同步整流管SR1、SR3导通,变压器副边电流由体内二极管转移到相应的同步整流管;此后,Lr和Cr一起谐振至t6时刻.
在t6时刻以后,电路进入下一个半周期工作模态,该电路工作模态类似于上述半个周期工作模态.
1.2 模式2在该模式下,2个变压器的励磁电流变化速率虽然不相等,但当Lm1、Lr和Cr共同谐振时,变压器T2的励磁电流能够达到该谐振电流,故满足下式:
| $ \left. \begin{array}{l} \left( {{n_1}{V_1}/{L_{{\rm{m1}}}}} \right) \times \left( {{T_{\rm{r}}}/2} \right) = \left( {{n_2}{V_2}/{L_{{\rm{m2}}}}} \right) \times \left( {{T_{\rm{p}}}/2} \right);\\ {T_{\rm{r}}} < {T_{\rm{p}}} < {T_{\rm{s}}}. \end{array} \right\} $ | (6) |
式中:Tr为谐振周期,Ts为开关周期,Tp为开关周期内变压器T2的励磁电流与谐振电流相等的时刻.
LLC电路工作在模式2下的主要波形如图 5所示;在半个开关周期内,该级联变换器共有7个工作阶段,它们的等效电路分别如图 6(a)~(g)所示.

|
图 5 模式2下的LLC电路工作波形 Fig. 5 Waveforms of LLC circuit in mode 2 |

|
图 6 模式2下不同阶段的等效电路 Fig. 6 Equivalent circuit for different stage in mode 2 |
该模式下t0~t1和t3~t7期间电路的工作模态分别与模式1下t0~t1和t2~t6期间的类似,不再重述;t1~t3期间的电路工作模态分析如下.
模态2(t1~t2):t1时刻,谐振电流ip与励磁电流iLm1相等,副边电流iSR2为零,变压器T1停止向副边传输能量;此时,SR4有电流流过,变压器T2在向副边传输能量;此后,励磁电感Lm1、谐振电感Lr和谐振电容Cr一起谐振至t2时刻.
模态3(t2~t3):t2时刻,谐振电流ip与励磁电流iLm2相等,此时副边电流iSR4为零,变压器T2停止向副边传输能量,励磁电感Lm1和Lm2、谐振电感Lr和谐振电容Cr一起谐振至t3时刻.
在t7时刻以后,电路进入下一个半周期工作过程,其工作过程类似于上述半个周期工作过程.
1.3 模式3在该模式下,2个变压器的励磁电流变化速率不相等;当Lm1、Lr和Cr共同谐振时,变压器T2的励磁电流达不到该谐振电流,即满足:
| $ \left( {{n_1}{V_1}/{L_{{\rm{m1}}}}} \right) \times \left( {{T_{\rm{r}}}/2} \right) > \left( {{n_2}{V_2}/{L_{{\rm{m2}}}}} \right) \times \left( {{T_{\rm{p}}}/2} \right). $ | (7) |
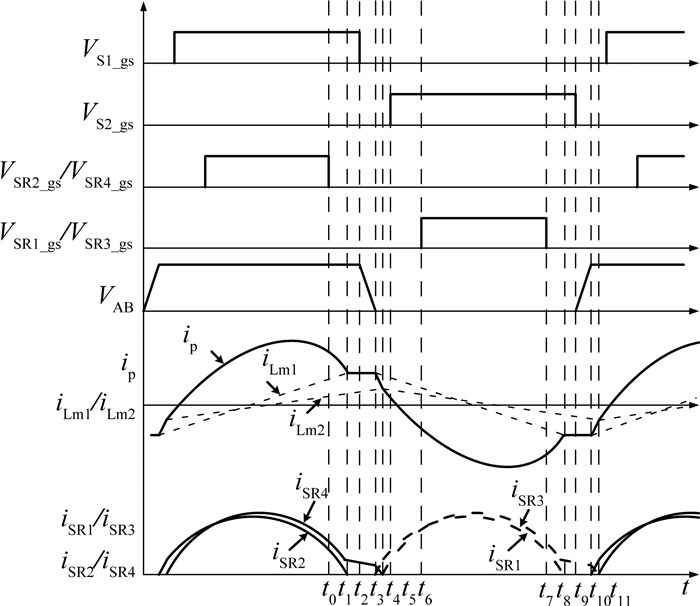
LLC电路工作在模式3下的主要波形如图 7所示;在半个开关周期内,该级联变换器共有7个工作阶段,它们的等效电路分别如图 8(a)~(g)所示.
|
图 7 模式3下的LLC电路工作波形 Fig. 7 Waveforms of LLC circuit in mode 3 |

|
图 8 模式3下的不同阶段等效电路 Fig. 8 Equivalent circuit for different stage in mode 3 |
该模式下t0~t2和t4~t7期间电路的工作模态分别与模式2下t0~t2和t4~t7期间的相类似,不再重述;t3~t4期间的电路工作模态分析如下.
模态4(t3~t4):t3时刻,原边电流ip完成对开关管S1、S2结电容的充放电,开关管S2的体内二极管自然续流,同步整流管SR1的体内二极管导通,变压器T1开始向副边传输能量;同时,由于励磁电流iLm2小于谐振电流ip,同步整流管SR4的体内二极管仍导通,变压器原边电压VLm1和VLm2分别被钳位在-n1V1和n2V2;此后,谐振电感Lr和谐振电容Cr一起谐振至t4时刻.
在t7时刻以后,电路进入下一个半周期工作过程,其工作过程类似于上述半个周期工作过程.
2 均流分析 2.1 不同工作模式下的均流特性分析 2.1.1 模式1下的均流性能分析由图 1的电路拓扑结构可知,前级LLC副边电流的平均值等于后级Buck电路输入电流的平均值,可得两个Buck电路的输入电流平均值I1、I2分别为
| $ {I_1} = \frac{{{n_1}}}{{{T_{\rm{s}}}/2}}\int_0^{{T_{\rm{s}}}/2} {\left( {{i_{\rm{p}}}\left( t \right) - {i_{{\rm{Lm1}}}}\left( t \right)} \right){\rm{d}}t} , $ | (8) |
| $ {I_2} = \frac{{{n_2}}}{{{T_{\rm{s}}}/2}}\int_0^{{T_{\rm{s}}}/2} {\left( {{i_{\rm{p}}}\left( t \right) - {i_{{\rm{Lm2}}}}\left( t \right)} \right){\rm{d}}t} . $ | (9) |
分析图 3可知,在模式1下,iLm1(t)=iLm2(t).结合式(8)、(9),可得
| $ \frac{{{I_1}}}{{{I_2}}} = \frac{{{n_1}}}{{{n_2}}}. $ | (10) |
由于两路Buck电路的占空比分别为D1和D2,可知相应的Buck电路输出电流平均值分别为
| $ {I_{{\rm{o1}}}} = {I_1}/{D_1}, $ | (11) |
| $ {I_{{\rm{o2}}}} = {I_2}/{D_2}. $ | (12) |
为了便于分析,分别定义级联变换器的均流精度ΔI、占空比差异ΔD、匝比差异Δn及励磁电感差异ΔLm如下:
| $ \Delta I = \frac{{{I_{{\rm{o1}}}} - {I_{{\rm{o2}}}}}}{{{I_{{\rm{o1}}}} + {I_{{\rm{o2}}}}}} \times 100\% , $ | (13) |
| $ \Delta D = \frac{{{D_2} - {D_1}}}{{{D_1}}} \times 100\% , $ | (14) |
| $ \Delta n = \frac{{{n_2} - {n_1}}}{{{n_1}}} \times 100\% , $ | (15) |
| $ \Delta {L_{\rm{m}}} = \frac{{{L_{{\rm{m2}}}} - {L_{{\rm{m1}}}}}}{{{L_{{\rm{m1}}}}}} \times 100\% . $ | (16) |
由式(10)~(16)可得,均流精度随占空比和匝比差异变化的关系式为
| $ \Delta I = \frac{{\Delta D - \Delta n}}{{2 + \Delta D + \Delta n}}. $ | (17) |
式(17)表明:级联变换器工作在模式1下,当ΔD=Δn时,均流误差ΔI=0,可以实现完全均流;当ΔD=-Δn时,ΔI=ΔD,此时的均流精度最差.
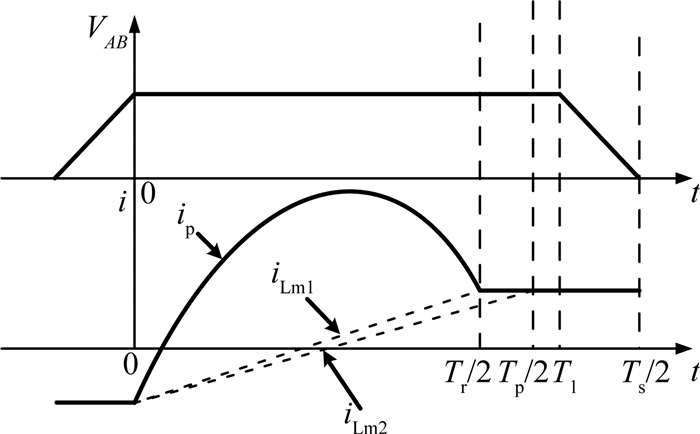
2.1.2 模式2下的均流性能分析工作在模式2下,级联变换器在半个开关周期内简化的工作波形如图 9所示.iLm1和iLm2在开关周期内分别正、负对称,且平均值为0,可得iLm1和iLm2分别满足下式:
| $ {i_{{\rm{Lm1}}}}\left( 0 \right) = - {i_{{\rm{Lm1}}}}\left( {{T_{\rm{r}}}/2} \right), $ | (18) |
| $ {i_{{\rm{Lm2}}}}\left( 0 \right) = - {i_{{\rm{Lm2}}}}\left( {{T_{\rm{p}}}/2} \right). $ | (19) |
|
图 9 模式2下LLC电路的电流波形 Fig. 9 Current waveforms of LLC circuit in mode 2 |
由式(18)、(19)可知,iLm1在0~Tr/2期间和iLm2在0~Tp/2期间的平均值均为0;结合式(8)、(9),可得Buck输入电流I1、I2分别为
| $ \begin{array}{l} {I_1} = \frac{{{n_1}}}{{{T_{\rm{s}}}/2}}\int_0^{{T_{\rm{s}}}/2} {\left( {{i_{\rm{p}}}\left( t \right) - {i_{{\rm{Lm1}}}}\left( t \right)} \right){\rm{d}}t} = \\ \;\;\;\;\;\frac{{2{n_1}}}{{{T_{\rm{s}}}}}\int_0^{{T_{\rm{r}}}/2} {{i_{\rm{p}}}\left( t \right){\rm{d}}t} , \end{array} $ | (20) |
| $ \begin{array}{l} {I_2} = \frac{{{n_2}}}{{{T_{\rm{s}}}/2}}\int_0^{{T_{\rm{s}}}/2} {\left( {{i_{\rm{p}}}\left( t \right) - {i_{{\rm{Lm2}}}}\left( t \right)} \right){\rm{d}}t} = \\ \;\;\;\;\;\frac{{2{n_2}}}{{{T_{\rm{s}}}}}\left[ {\int_0^{{T_{\rm{r}}}/2} {{i_{\rm{p}}}\left( t \right){\rm{d}}t} + \int_{{T_{\rm{r}}}/2}^{{T_{\rm{p}}}/2} {{i_{\rm{p}}}\left( t \right){\rm{d}}t} } \right]. \end{array} $ | (21) |
假设级联变换器输出电流为Io,可得
| $ {I_{{\rm{o1}}}} + {I_{{\rm{o2}}}} = {I_{\rm{o}}}, $ | (22) |
由于级联变换器前级LLC电路开环工作,且开关频率设置在谐振频率点附近,LLC电路的电压增益近似为1,可得
| $ \frac{{{V_{\rm{o}}}}}{{{D_1}}}{n_1} + \frac{{{V_{\rm{o}}}}}{{{D_2}}}{n_2} = \frac{1}{2}{V_{{\rm{in}}}}, $ | (23) |
由式(14)、(15)和(24),可得D1满足:
| $ {D_1} = \frac{{2 + \Delta D + \Delta n}}{{1 + \Delta D}} \cdot \frac{{2{n_1}{V_{\rm{o}}}}}{{{V_{{\rm{in}}}}}}. $ | (24) |
结合式(6)、(20)~(24),可得级联变换器的均流精度:
| $ \begin{array}{l} \Delta I = \frac{{\Delta D - \Delta n}}{{2 + \Delta D + \Delta n}} + N{\left( {1 + \Delta D} \right)^2} \times \\ \;\;\;\;\;\;\frac{{\left( {\Delta n - \Delta D - \Delta {L_{\rm{m}}} - \Delta D \cdot \Delta {L_{\rm{m}}}} \right)}}{{{{\left( {2 + \Delta D + \Delta n} \right)}^3}}}. \end{array} $ | (25) |
式中:
| $ N = \frac{{V_{{\rm{in}}}^2T_{\rm{r}}^2}}{{8{V_{\rm{o}}}{I_{\rm{o}}}{L_{{\rm{m1}}}}{T_{\rm{s}}}}}. $ | (26) |
式(25)、(26)表明:工作在模式2下,级联变换器的均流精度不仅与ΔD、Δn及ΔLm有关,还受到开关频率、输入电压、输出电压、匝比、占空比、励磁电感、负载大小等参数的影响.
当单独考虑ΔI随ΔD变化的影响时,由式(6)、(25),可得
| $ \left. {\begin{array}{*{20}{c}} {\Delta I = \frac{{\Delta D}}{{2 + \Delta D}} - N\frac{{\Delta D{{\left( {1 + \Delta D} \right)}^2}}}{{{{\left( {2 + \Delta D} \right)}^3}}},}\\ {0 \le \Delta D \le {f_{\rm{r}}}/{f_{\rm{s}}} - 1.} \end{array}} \right\} $ | (27) |
类似地,可得ΔI分别单独随Δn和ΔLm变化时的关系式:
| $ \left. {\begin{array}{*{20}{c}} {\Delta I = - \frac{{\Delta n}}{{2 + \Delta n}} + N\frac{{\Delta n}}{{{{\left( {2 + \Delta n} \right)}^3}}},}\\ {{f_{\rm{s}}}/{f_{\rm{r}}} - 1 \le \Delta n \le 0.} \end{array}} \right\} $ | (28) |
| $ \left. {\begin{array}{*{20}{c}} {\Delta I = - N\Delta {L_{\rm{m}}}/8,}\\ {0 \le \Delta {L_{\rm{m}}} \le {f_{\rm{r}}}/{f_{\rm{s}}} - 1.} \end{array}} \right\} $ | (29) |
式中:N=2.196,fr/fs=1.105,可以分别由仿真和实验电路参数计算得到.
由式(27)~(29),可得级联变换器的均流精度ΔI分别随ΔD、Δn和ΔLm变化的曲线,如图 10所示.可知,当单独考虑ΔD对均流精度的影响时,均流精度仅近似为ΔD的0.2倍;当分别单独考虑Δn和ΔLm对均流精度的影响时,均流精度分别近似为Δn绝对值的0.2倍和ΔLm的0.3倍.
|
图 10 模式2下参数差异对均流误差的影响 Fig. 10 Influence of parameter difference on current-sharing accuracy in mode 2 |
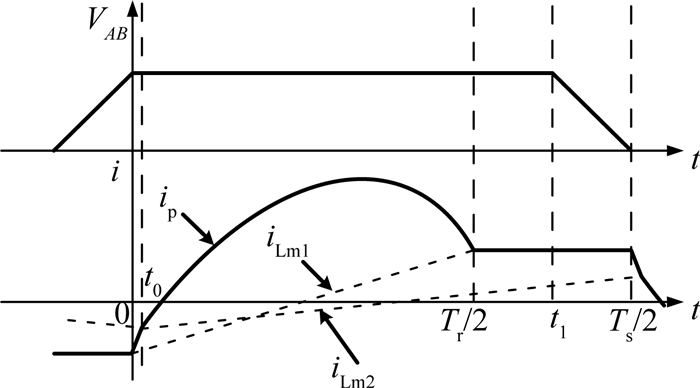
工作在模式3下,级联变换器在半个开关周期内的简化电压、电流工作波形如图 11所示.电路工作在模式3下,类似于模式2下的分析,可得
| $ \Delta I = \frac{{\Delta D - \Delta n}}{{2 + \Delta D + \Delta n}} - M\frac{{\left( {1 + \Delta n} \right){{\left( {1 + \Delta D} \right)}^2}}}{{{{\left( {2 + \Delta D + \Delta n} \right)}^3}}}. $ | (30) |
|
图 11 模式3下LLC电路的电流运行波形 Fig. 11 Current waveforms of LLC circuit in mode 3 |
式中:
| $ M = \frac{{V_{{\rm{in}}}^2{T_{\rm{r}}}\left( {{T_{\rm{s}}} - {T_{\rm{r}}}} \right)}}{{8{V_{\rm{o}}}{I_{\rm{o}}}{L_{{\rm{m1}}}}{T_{\rm{s}}}}}. $ | (31) |
从式(30)、(31)可知,当工作在模式3下时,级联变换器的均流精度不仅与ΔD和Δn有关,还受到开关频率、输入电压、输出电压、匝比、占空比、励磁电感、负载大小等的影响,但是与ΔLm无关.
当单独考虑ΔI随ΔD变化的影响时,由式(7)、(30)可得
| $ \left. {\begin{array}{*{20}{c}} {\Delta I = \frac{{\Delta D}}{{2 + \Delta D}} - M\frac{{{{\left( {1 + \Delta D} \right)}^2}}}{{{{\left( {2 + \Delta D} \right)}^3}}},}\\ {\Delta D \ge {f_{\rm{r}}}/{f_{\rm{s}}} - 1.} \end{array}} \right\} $ | (32) |
类似地,可得ΔI分别单独随Δn和ΔLm变化时的关系式:
| $ \left. {\begin{array}{*{20}{c}} {\Delta I = - \frac{{\Delta n}}{{2 + \Delta n}} - M\frac{{1 + \Delta n}}{{{{\left( {2 + \Delta n} \right)}^3}}},}\\ {\Delta n \le {f_{\rm{s}}}/{f_{\rm{r}}} - 1.} \end{array}} \right\} $ | (33) |
| $ \left. {\begin{array}{*{20}{c}} {\Delta I = - M/8,}\\ {\Delta {L_m} \ge {f_{\rm{r}}}/{f_{\rm{s}}} - 1.} \end{array}} \right\} $ | (34) |
式中:M=0.23, fr/fs=1.105,可以分别由仿真和实验电路参数计算得到.
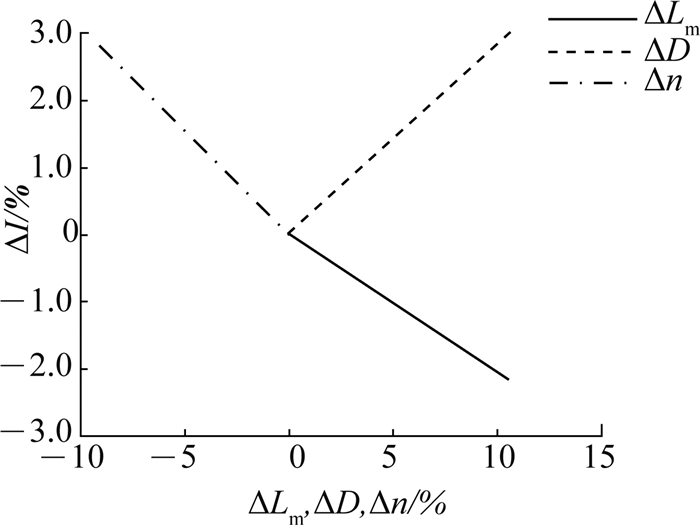
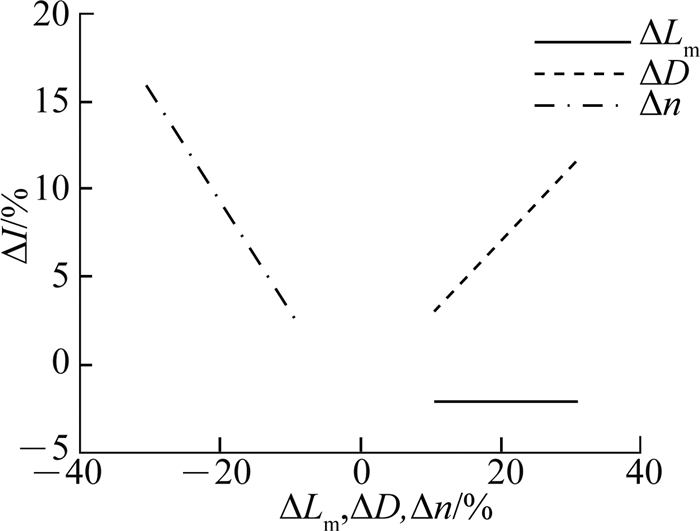
从式(32)~(34)可得级联变换器的均流精度分别随ΔD、Δn及ΔLm变化的曲线,如图 12所示.可知,当单独考虑ΔD对均流精度的影响时,均流精度仅近似为ΔD的0.3倍;当单独考虑Δn对均流精度的影响时,均流精度近似为Δn绝对值的0.3倍;当单独考虑ΔLm对均流精度的影响时可知,不论ΔLm如何变化,均流精度始终为-2.875%.
|
图 12 模式3下参数差异对均流误差的影响 Fig. 12 Influence of parameter difference on current-sharing accuracy in mode 3 |
综合上述3种工作模式的分析可得,当ΔD、Δn和ΔLm单独影响时ΔI的变化规律.
由式(27)、(32)可得如下结论:当0≤ΔD≤10.5%时,ΔI随ΔD的增大而变大,当ΔD=10.5%时,ΔI=1.97%达到最大值;当ΔD≥10.5%时,ΔI变化曲线的斜率随ΔD的增大而逐渐减小;当ΔD=10.5%时,曲线斜率ΔI/ΔD=0.44达到最大值;当仅考虑ΔD对ΔI的影响时,可得
| $ \left. {\begin{array}{*{20}{c}} {\Delta I \le 1.97\% ,\;\;\;0 \le \Delta D \le 10.5\% ;}\\ {\Delta I/\Delta D \le 0.44,\;\;\;\Delta D \ge 10.5\% .} \end{array}} \right\} $ | (35) |
由式(28)、(33)可得如下结论.当-9.09%≤Δn≤0时,均流精度ΔI随Δn的增大而减小;当Δn=-9.09%时,ΔI=1.89%达到最大值;当Δn≤-9.09%时,ΔI曲线斜率的绝对值随Δn的增大而变大;当Δn=-9.09%时,曲线斜率的绝对值|ΔI/Δn|=0.57达到最大值;当仅考虑Δn对ΔI的影响时,可得
| $ \left. {\begin{array}{*{20}{c}} {\Delta I \le 1.89\% ,\;\;\; - 9.09\% \le \Delta D \le 0;}\\ {\left| {\Delta I/\Delta n} \right| \le 0.57,\;\;\;\Delta D \le - 9.09\% .} \end{array}} \right\} $ | (36) |
由式(29)、(34)可得如下结论:当0≤ΔLm≤10.5%时,|ΔI|随ΔLm的增加而线性增加;当ΔLm=10.5%时,|ΔI|=2.875%达到最大值;当ΔLm≥10.5%时,均流精度的绝对值等于2.875%;当仅考虑ΔLm对ΔI的影响时,可得
| $ \left| {\Delta I} \right| \le 2.875\% ;\;\;\;\;\Delta {L_{\rm{m}}} \ge 0. $ | (37) |
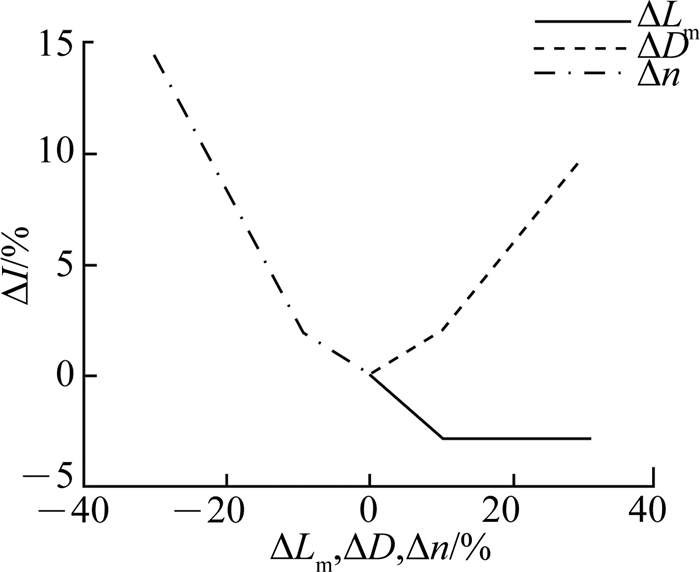
ΔI分别随ΔD、Δn和ΔLm单独变化时的曲线如图 13所示.综上分析可得结论:变压器励磁电感、匝比以及Buck电路占空比差异变化会影响该级联变换器的均流精度,但均流精度的变化均是在可控范围内的.
|
图 13 ΔD、Δn以及ΔLm对于均流精度的影响 Fig. 13 Influence of duty cycle, turns ratio and magnetizing inductance difference on current-sharing accuracy |
为了验证该级联变换器的均流特性,有必要开展电路仿真和实验验证.
3.1 PSIM仿真研究仿真电路的系统参数如表 1所示.
| 表 1 变压器串并联LLC+BUCK级联电路仿真参数 Table 1 Circuit parameters of simulation in converter composed of LLC with series-parallel transformer and interleaved Buck |
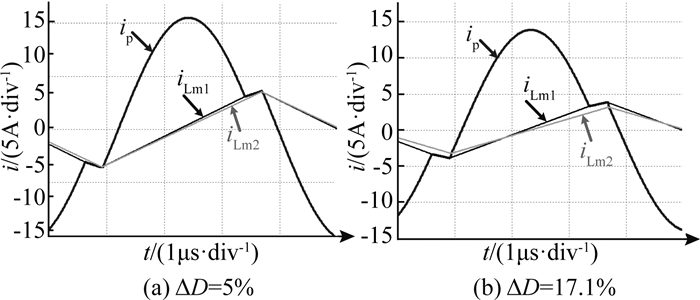
根据表 1的参数,在额定300 V输入、1 kW满载输出以及不同的Buck电路占空比条件下,通过PSIM仿真得到前级LLC电路的电流波形,分别如图 14(a)、(b)所示.可以看出,当ΔD=5%时,级联变换器工作于模式2;当ΔD=17.1%时,级联变换器工作于模式3.
|
图 14 不同占空比下LLC的电流波形 Fig. 14 Current waveforms of LLC converter with different duty cycle |
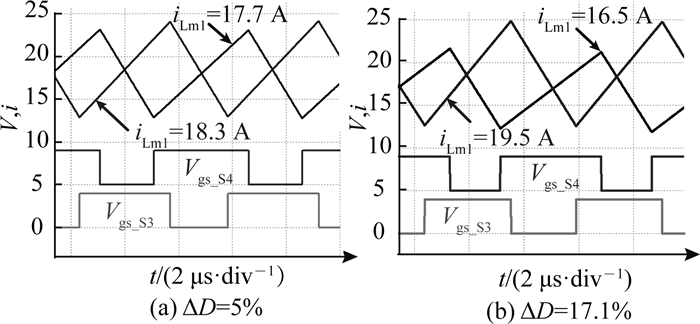
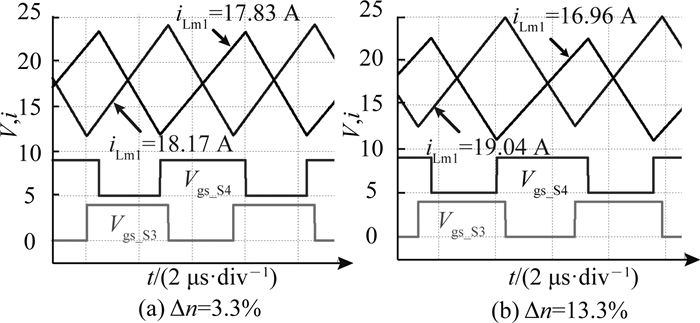
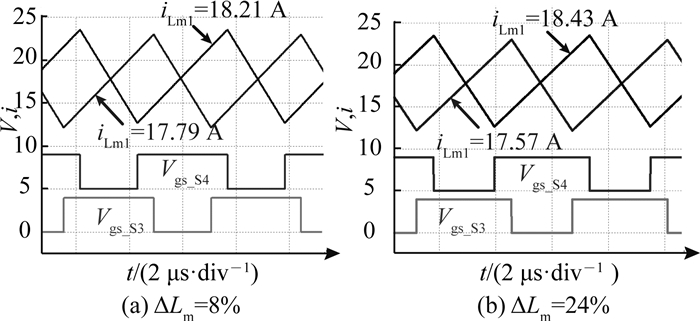
当额定300 V输入、1 kW满载输出时,在不同的占空比、匝比及励磁电感条件下,通过PSIM仿真得到的后级Buck电路的电压和电流波形分别如图 15~17所示.可以看出,ΔI均会随占空比、匝比及励磁电感差异的增大而变大.
|
图 15 不同占空比下Buck电路的电压和电流波形 Fig. 15 Voltage and current waveforms of Buck converter with different duty cycle |
|
图 16 不同匝比下Buck电路的电压和电流波形 Fig. 16 Voltage and current waveforms of Buck converter with different turns ratio |
|
图 17 不同励磁电感下Buck电路的电压和电流波形 Fig. 17 Voltage and current waveforms of Buck converter with different magnetizing inductance |
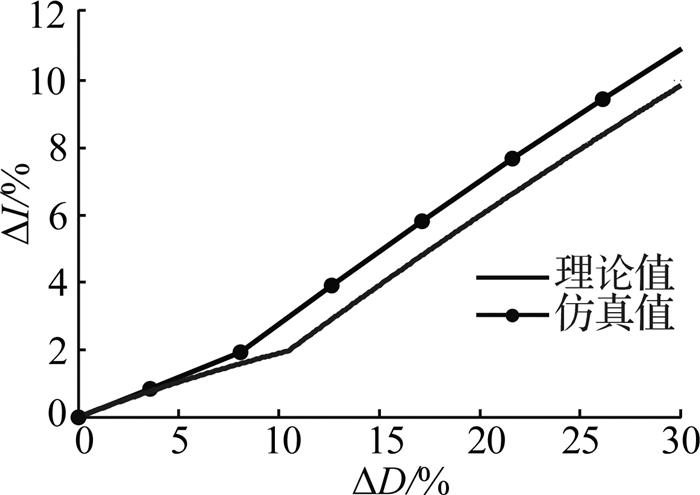
在单独考虑占空比参数差异影响的条件之下,通过理论分析和仿真结果所得的均流精度变化曲线对比,如图 18所示.可以看出,在占空比差异单独影响下,通过理论分析和仿真结果所得的均流精度变化曲线的变化基本一致,故均流精度的变化在可控范围内.由于本文假设当Lm1(或Lm2或Lm1+Lm2)、Lr、Cr共同参与谐振时,谐振电流恒定不变,而实际上,此时的谐振电流是逐渐增大的,使图 5的t1~t2阶段和图 7的t1~t3阶段持续时间减小,从而导致理论分析和仿真结果之间存在1%左右的误差.
|
图 18 占空比差异对电路均流特性的影响 Fig. 18 Influence of duty cycle difference on current-sharing accuracy |
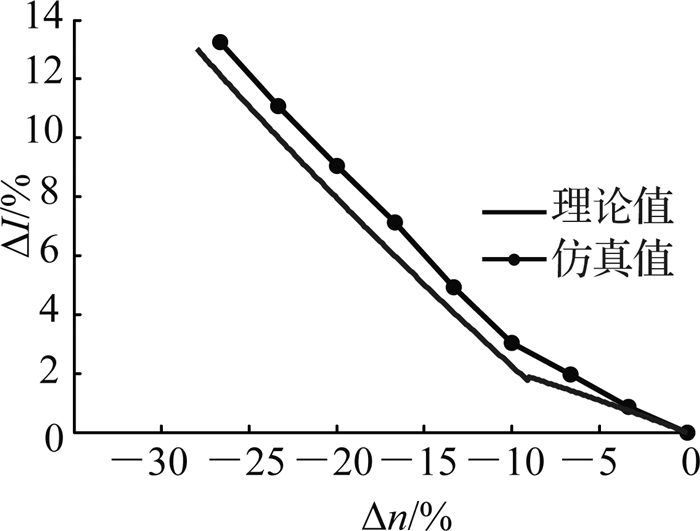
在匝比和励磁电感差异单独的影响下,仿真结果和理论分析所得的均流精度变化曲线对比,分别如图 19、20所示.类似地,可得如下结论:在匝比和励磁电感差异单独的影响下,仿真结果和理论分析所得的均流精度变化曲线的变化基本一致,故均流精度的变化均在可控范围内.
|
图 19 匝比差异对电路均流特性的影响 Fig. 19 Influence of turns ratio difference on current-sharing accuracy |
|
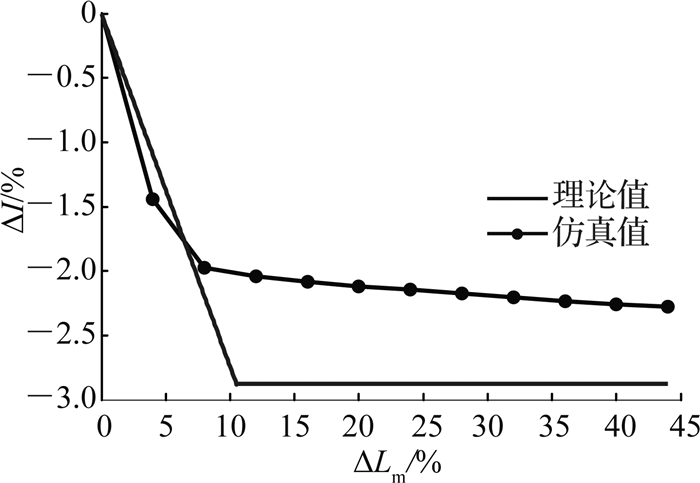
图 20 励磁电感差异对电路均流特性的影响 Fig. 20 Influence of magnetizing inductance difference on current-sharing accuracy |
综上分析可知,该级联变换器具有良好的自动均流特性.
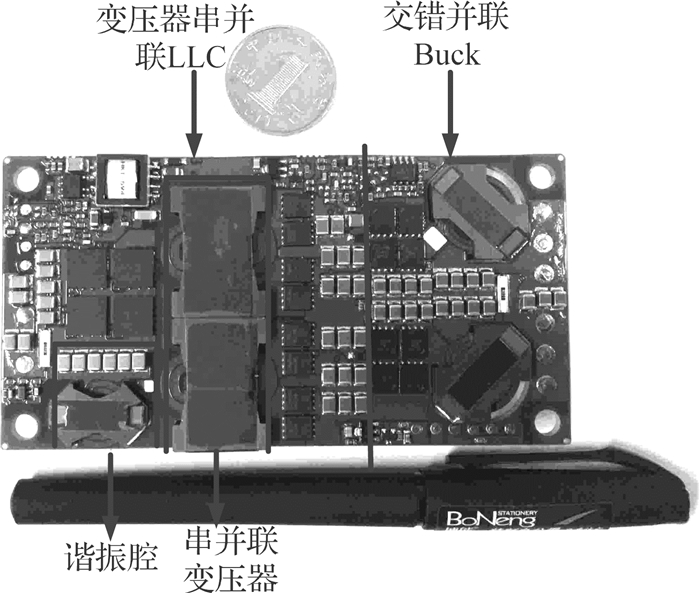
3.2 实验验证为了验证理论分析和仿真结果的正确性,搭建基于前级变压器串-并联LLC+后级交错Buck电路拓扑的1 kW全砖电源模块,实验样机图片如图 21所示,实验样机的主要参数与表 1一致,器件的选择如表 2所示.
|
图 21 变压器串并联LLC+BUCK级联实验样机照片 Fig. 21 Experimental prototype of converter composed of LLC with series-parallel transformer and interleaved Buck |
| 表 2 变压器串并联LLC+BUCK级联电路器件型号 Table 2 Device type of converter composed of LLC with series-parallel transformer and interleaved Buck |
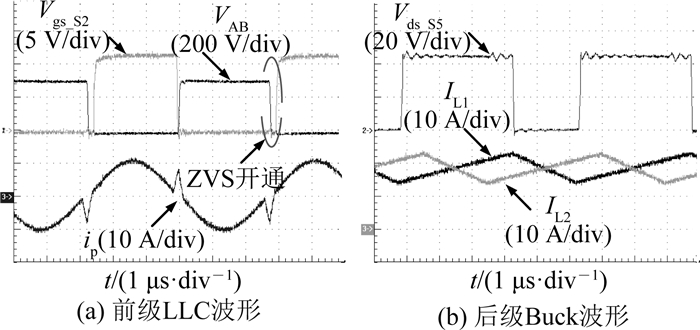
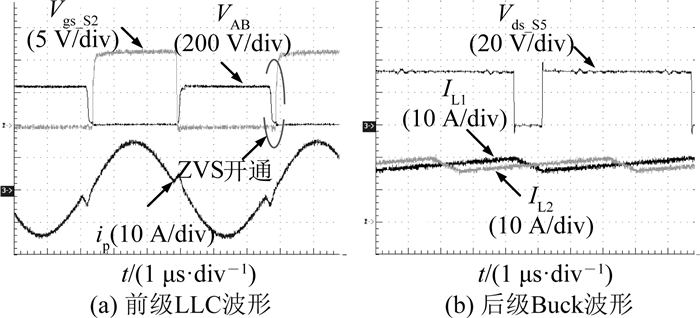
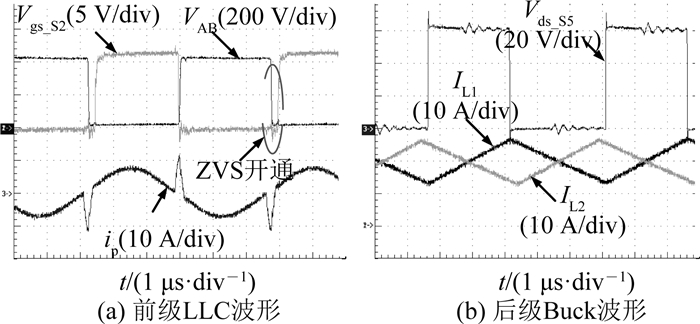
在240、300和425 V输入条件下,级联变换器在1 kW满载输出时,前级LLC和后级Buck电路的电压和电流波形分别如图 22~24所示.可以看出,在240~425 V的输入电压下,LLC均可以实现ZVS.
|
图 22 300 V输入时电路的电压和电流波形 Fig. 22 Voltage and current waveforms when input voltage is 300 V |
|
图 23 V输入时电路的电压和电流波形 Fig. 23 Voltage and current waveforms when input voltage is 240 V |
|
图 24 425 V输入时电路的电压和电流波形 Fig. 24 Voltage and current waveforms when input voltage is 425 V |
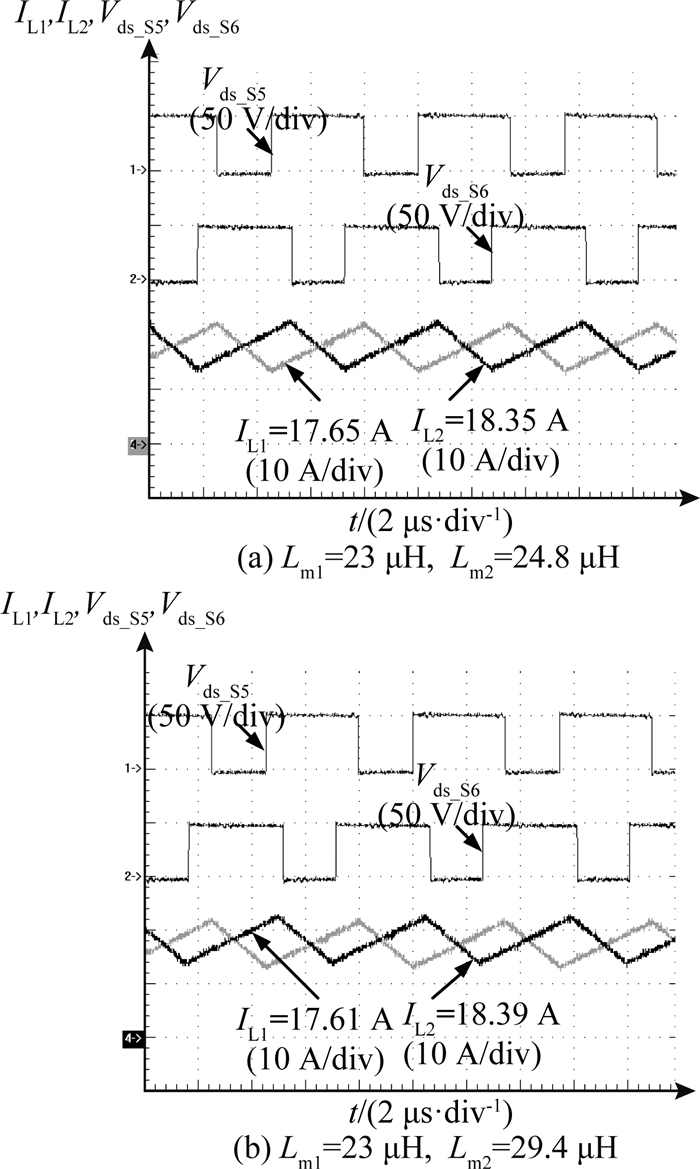
在不同的励磁电感和占空比情况下,交错Buck电路的输出电流和同步整流管的电压波形分别如图 25、26所示.可以看出,ΔI均会随占空比、励磁电感差异的增大而变大.其中,励磁电感差异的变化对均流精度的影响较小,占空比差异的变化对均流精度的影响相对较大.
|
图 25 不同励磁电感时Buck的电压和电流波形 Fig. 25 Voltage and current waveforms in Buck converter due to different magnetizing inductance |

|
图 26 不同占空比时Buck的电压和电流波形 Fig. 26 Voltage and current waveforms in Buck converter with different duty cycle |
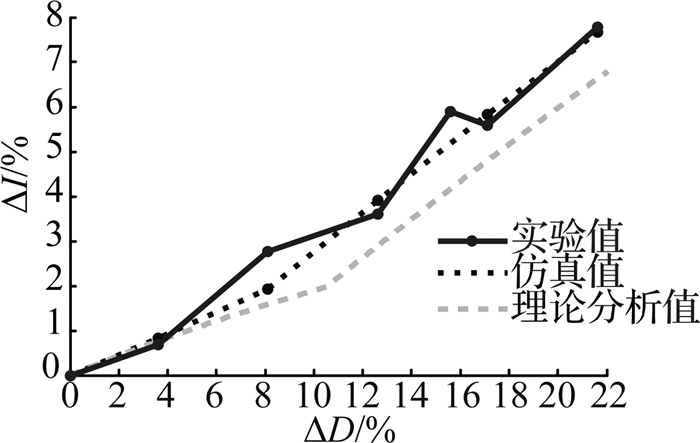
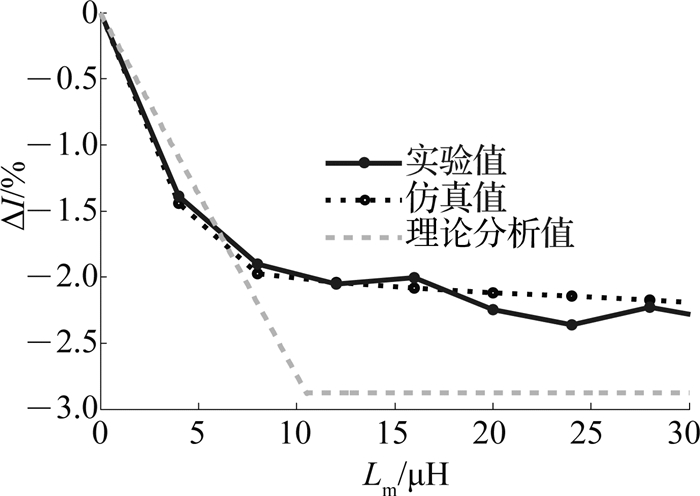
在额定300 V输入、1 kW满载输出的条件下,通过实验、仿真和理论分析所得的均流精度分别随占空比和励磁电感差异变化的曲线分别如图 27、28所示.可以看出,由于实际参数的差异以及测量误差的存在,导致实验结果与仿真和理论分析之间虽然存在一些差异,但该差异值对实际均流精度的影响在可控范围内,故实验与仿真结果一致,该级联变换器具有自动均流功能.
|
图 27 实验、仿真和理论分析所得的均流精度随占空比差异变化的关系 Fig. 27 Influence of duty cycle difference on current-sharing accuracy, analyzed by experiment, simulation and theoretical analysis |
|
图 28 实验、仿真和理论分析所得的均流精度随励磁电感差异变化关系 Fig. 28 Influence of magnetizing inductance difference on current-sharing accuracy, analyzed by experiment, simulation and theoretical analysis |
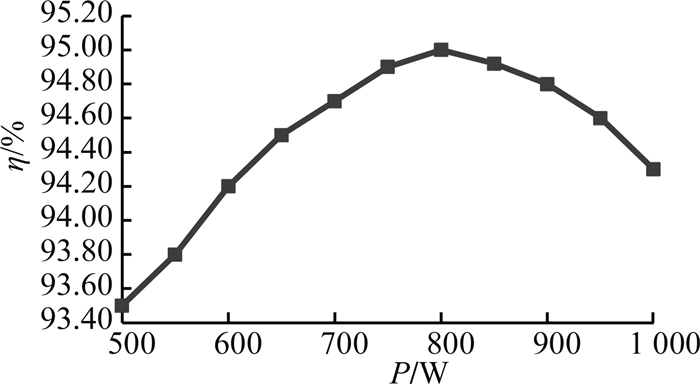
在额定300 V输入、不同负载输出的条件下,级联变换器的效率η曲线如图 29所示.图中,P为输出功率.可以看出,在800 W左右输出时,级联变换器达到最高效率95%;在1 kW满载输出时,效率为94.3%.
|
图 29 300 V额定输入、不同负载时的效率曲线 Fig. 29 Efficiency of circuit in different load and 300 V rated input voltage condition |
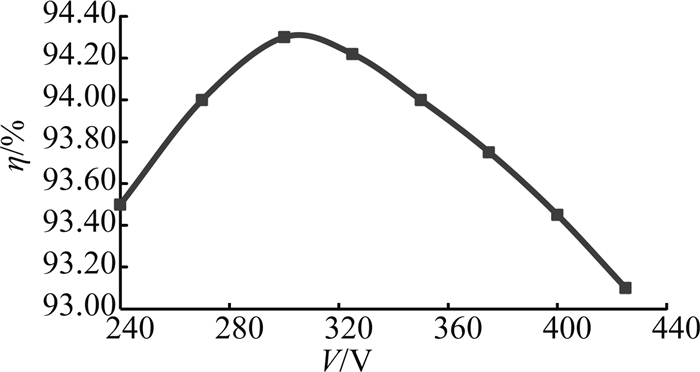
在240~425 V输入、1 kW满载输出的条件下,级联变换器的效率曲线如图 30所示.图中,V为输入电压.可以看出,级联变换器在额定300 V输入时近似达到最高效率94.3%;当输入电压为425 V时,级联变换器的效率最低,为93.1%.
|
图 30 不同输入电压、1 kW满载输出下的效率曲线 Fig. 30 Efficiency of the circuit in 1 kW full load and different input voltage condition |
本文针对高频变压器串-并联LLC+Buck级联DC-DC变换器,分析研究在前级LLC变压器励磁电感与匝比以及后级Buck占空比等参数不一致的情况下,该级联DC-DC变换器具有良好的自动均流特性;通过仿真和1 kW实验样机,进一步验证了该级联变换器拓扑具有较好的自动均流特性,适合应用于高压/宽电压范围输入、低压/大电流输出及高功率密度/大功率DC-DC电能变换场合.
| [1] |
许正平, 李俊. 双向全桥DC-DC变换器高效能控制研究与实现[J]. 电力系统保护与控制, 2016, 44(2): 140-146. XU Zheng-ping, LI Jun. Research and implementation of bidirectional full bridge DC-DC converter with high-efficiency control[J]. Power System Protection and Control, 2016, 44(2): 140-146. DOI:10.7667/j.issn.1674-3415.2016.02.020 |
| [2] |
荣德生, 代雨晴, 赵君君, 等. 基于R-S-T控制的复合电源双向DC/DC变换器设计[J]. 电力系统保护与控制, 2015, 43(7): 132-137. RONG De-sheng, DAI Yu-qing, ZHAO Jun-jun, et al. Design of hybrid power bi-directional DC/DC converters based on R-S-T control strategy[J]. Power System Protection and Control, 2015, 43(7): 132-137. DOI:10.7667/j.issn.1674-3415.2015.07.021 |
| [3] |
施林涵, 林国庆, 徐质彬, 等. Buck-Boost型双半桥DC/DC变换器研究[J]. 电气技术, 2016, 17(6): 1-4. SHI Lin-han, LIN Guo-qing, XU Zhi-bin, et al. Research on Buck-Boost double half bridge DC/DC converter[J]. Electrical Engineering, 2016, 17(6): 1-4. |
| [4] |
陈申, 吕征宇, 姚玮. LLC谐振型软开关直流变压器的研究与实现[J]. 电工技术学报, 2012, 27(10): 163-169. CHEN Shen, LV Zheng-yu, YAO Wei. Research and verification on LLC resonant soft switching DC-DC transformer[J]. Transactions of China Electrotechnical Society, 2012, 27(10): 163-169. |
| [5] |
任小永, 唐钊, 阮新波, 等. 一种新颖的四开关Buck-Boost变换器[J]. 中国电机工程学报, 2008, 28(21): 15-19. REN Xiao-yong, TANG Zhao, RUAN Xin-bo, et al. A novel four-switch Buck-Boost converter[J]. Proceedings of The Chinese Society for Electrical Engineering, 2008, 28(21): 15-19. |
| [6] |
梁小国, 危建, 阮新波. 一种新颖的交错并联正激三电平变换器[J]. 中国电机工程学报, 2004, 24(11): 139-143. LIANG Xiao-guo, WEI Jian, RUAN Xin-bo. A novel interleaved three-level forward converter[J]. Proceedings of the Chinese Society for Electrical Engineering, 2004, 24(11): 139-143. DOI:10.3321/j.issn:0258-8013.2004.11.028 |
| [7] |
胡海兵, 王万宝, 孙文进, 等. LLC谐振变换器效率优化设计[J]. 中国电机工程学报, 2013, 33(18): 48-56. HU Hai-bing, WANG Wan-bao, SUN Wen-jin, et al. Optimal efficiency design of LLC resonant converters[J]. Proceedings of the Chinese Society for Electrical Engineering, 2013, 33(18): 48-56. |
| [8] |
洪小圆, 陈威, 吕征宇. 软开关谐振复位双管正激DC/DC变流器[J]. 电工技术学报, 2009, 24(10): 65-70. HONG Xiao-yuan, CHEN Wei, LV Zheng-yu. Soft-switching resonant reset dual switch forward DC/DC converter[J]. Transactions of China Electrotechnical Society, 2009, 24(10): 65-70. DOI:10.3321/j.issn:1000-6753.2009.10.011 |
| [9] |
CHIEN C H, WANG Y H, LIN B R. Zero-voltage switching DC/DC converter with two half-bridge legs and series-parallel transformers[J]. IET Power Electronics, 2012, 5(4): 419-427. |
| [10] |
HU H, FANG X, CHEN F, et al. A modified high-efficiency LLC converter with two transformers for wide input-voltage range applications[J]. IEEE Transactions on Power Electronics, 2013, 28(4): 1946-1960. |
| [11] |
王泽景, 王颖, 龚春英. 高降压比LLC谐振型直流变压器[J]. 电工技术学报, 2015, 30(14): 193-200. WANG Ze-jing, WANG Ying, GONG Chun-ying. High step-down LLC resonant DC-DC transformer[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 193-200. DOI:10.3969/j.issn.1000-6753.2015.14.026 |
| [12] |
陈仲, 汪洋, 李梦南. 一种低环流损耗的宽范围ZVS移相全桥变换器[J]. 电工技术学报, 2015, 30(22): 71-79. CHEN Zhong, WANG Yang, LI Meng-nan. Wide-range zero voltage switching phase-shifted full-bridge converter with low circulation loss[J]. Transactions of China Electrotechnical Society, 2015, 30(22): 71-79. DOI:10.3969/j.issn.1000-6753.2015.22.010 |
| [13] |
KATO H, KARASUYAMA S, ISHIZUKA Y, et al. Optimization of a transformer used for LLC resonant DC-DC converters for photovoltaic cells[C]//2015 IEEE International Telecommunications Energy Conference (INTELEC). Osaka: IEEE, 2015: 1-6. http://ieeexplore.ieee.org/abstract/document/7572326/
|
| [14] |
MUSAVI F, CRACIUN M, GAUTAM D S, et al. An LLC resonant DC-DC converter for wide output voltage range battery charging applications[J]. IEEE Transactions on Power Electronics, 2013, 28(12): 5437-5445. |
| [15] |
任小永, 阮新波. 适用于高压输入低压输出的两级式变换器[J]. 中国电机工程学报, 2005, 25(23): 153-157. REN Xiao-yong, RUAN Xin-bo. Two-stage converter for high voltage input and low voltage output[J]. Proceedings of the Chinese Society for Electrical Engineering, 2005, 25(23): 153-157. DOI:10.3321/j.issn:0258-8013.2005.23.028 |
| [16] |
KIM B C, PARK K B, KIM C E, et al. LLC resonant converter with adaptive link-voltage variation for a high-power-density adapter[J]. IEEE Transactions on Power Electronics, 2010, 25(9): 2248-2252. |
| [17] |
KIM J H, KIM M Y, YEON C O, et al. Analysis and design of Boost-LLC converter for high power density AC-DC adapter[C]//2013 IEEE ECCE Asia Downunder (ECCE Asia). Melbourne: IEEE, 2013: 6-11. http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=6579066
|
| [18] |
AGUILAR-NAJAR R, PEREZ-PINAL F, LARA-SALAZAR G, et al. Cascaded buck converter: a reexamination[C]//2016 IEEE Transportation Electrification Conference and Expo (ITEC). Busan: IEEE, 2016: 1-5. http://ieeexplore.ieee.org/document/7520211/
|
| [19] |
石健将, 章江铭, 龙江涛, 等. 高频变压器一次侧串联LLC+输出端并联Buck级联直流变换器[J]. 电工技术学报, 2015, 30(24): 93-102. SHI Jian-jiang, ZHANG Jiang-ming, LONG Jiang-tao, et al. A cascaded DC converter with primary series transformer LLC and output interleaved Buck[J]. Transactions of China Electrotechnical Society, 2015, 30(24): 93-102. DOI:10.3969/j.issn.1000-6753.2015.24.013 |