2. 上海市静安老年医院, 上海 200040
2. Shanghai Jing-an Geriatric Hospital, Shanghai 200040, China
脑卒中偏瘫患者表现为一侧的上肢或下肢活动受阻,患侧肌肉瘫痪或者呈现痉挛状态,另一侧肢体可正常活动和有功能[1].Brunnstrom的偏瘫恢复6阶段理论将患者划分为Ⅰ~Ⅵ级,分别从重度到协调运动大致正常.医学实验表明,双侧上肢肌群具有同时协调动作的能力,执行双侧对称性运动比非对称性运动的协调更稳定[2].相对于健侧作双侧共同运动,有助于大脑重组,进而促进患侧肢体恢复.
表面肌电(surface electromyography, sEMG)信号能够客观地反映神经肌肉活动水平和功能状态[3].该信号稳定性差,随机性强,受年龄、身体状况等因素的影响大[4].SEMG的运动检测旨在从连续采集的肌电信号数据流中判断出运动段,它是肌电信号应用于智能假肢控制、康复训练和评估以及人机交互等领域的重要参数和重要前提[5-8].当中重度偏瘫患者作双侧共同运动时,在患侧无明显运动的情况下,相较于健侧会存在明显杂乱的、幅值更大的肌电信号[9],在这类人群中,sEMG运动信号检测面临挑战.为此需要研究适合于偏瘫患者的运动检测算法,作为康复评估的一种定量指标,为后续的个体化肢体功能康复训练提供参考[10].
SEMG运动检测的算法主要有以下几种:幅值分析法,如绝对值均值(mean absolute value,MAV);各种统计模型法,如高斯分布模型[11-13]、能量模型[6]、广义似然比[14];描述肌电信号复杂度的熵法,如模糊熵[15](fuzzy entropy,FuzzyEn)、样本熵[5, 16](sample entropy,SampEn)或近似熵[17](approximate entropy,ApEn)等.这3种熵在sEMG的检测中都得到应用[18-20].幅值法与肌肉运动的幅度呈近似线性关系,因其简便快速,最早应用于sEMG运动检测.非线性的熵理论反映肌肉运动的不确定性和复杂性,是对给定信号序列的复杂程度的定量评估[21],在一定程度上解决了sEMG信号检测的不精确问题而逐渐成为热点[22].由于人体微弱的sEMG不可避免地带有噪声,上述算法大多采用固定信噪比(signal-to-noise ratio,SNR)模型的人工合成信号模拟肌电信号,如通过静息段和动作段不同比例合成[23],纯肌电信号添加随机噪声,肌电信号发生器添加高斯噪声[12]等.不同的模拟信号对实际的检测效果影响较大[24].由于噪声的不确定性,这些人工合成信号与实际的人体表面肌电信号有较大的差异[25].
Lee等[23]采用人体背部静息段的肌电信号,以不同比例添加到背部sEMG信号来进行算法鲁棒性的分析.本文采集不同等级偏瘫患者双侧腕伸动作时指伸肌(extensor digitorum,ED)和桡侧腕伸肌(extensor carpi radialis,ECR)的肌电信号.采用运动/静息比的方法,将静息段信号作为基准信号,计算不同等级患者sEMG信号的SNR[25-27].在滑动窗方法的基础上,分别计算MAV、FuzzyEn、SampEn、ApEn特征,评估适用于不同等级偏瘫患者sEMG信号的运动检测及潜在运动特征检测的算法.
1 方法简介 1.1 特征介绍绝对值均值(MAV)是信号幅值的最直接反映,也是最常见的时域特征, 表达式为
| $ {\rm{MAV = }}\sum\limits_{i = 1}^N {\left| {{u_i}} \right|/N.} $ | (1) |
式中:ui为信号当前值,其中i=1, 2, …, N,N为移动窗宽.
熵用于度量信号的复杂度,ApEn对于短时带噪的复杂生理信号均能够很好地处理.ApEn计算过程如下:设给定时间长度为N的1维时间序列{ui:1<i<N},重构m维向量Xi,i=1, 2, …, n, n=N-m+1,
| $ {X_i} = \left\{ {u\left( i \right), u\left( {i + 1} \right), \cdots, u\left( {i + m-1} \right)} \right\}. $ | (2) |
计算任意向量Xi与其余向量之间的距离:
| $ {d_{ij}} = \mathop {\max }\limits_{k \in \left( {0, m-1} \right)} \left| {u\left( {i + k} \right)-u\left( {j + k} \right)} \right|. $ | (3) |
给定阈值r,对每个向量Xi统计dij ≤r的数目并求出该数目与向量总数之比,记作Cim(r).将Cim(r)取对数,然后对所有的i对应的值求平均值,记作Φm(r).
| $ {\varphi ^m}\left( r \right) = \frac{1}{{N-m + 1}}\sum\limits_{i = 1}^{N-m + 1} {\ln C_i^m\left( r \right)} . $ | (4) |
定义Cim+1(r)表示在重构维数为m+1的情况下的Xi,重复式(1)~(3)的过程,
| $ {\rm{AEn}}\left( {m, r, N} \right) = {\varphi ^m}\left( r \right)-{\varphi ^{m + 1}}\left( r \right). $ | (5) |
ApEn包含自身匹配,结果是有偏估计量.为了克服这个统计缺点,Richman等[32]提出SampEn,解决了统计值有偏的问题,但连续性较差并且当参数较小时,会导致自身没有意义.Chen等[15]提出FuzzyEn.FuzzyEn引用模糊函数代替Heaviside函数,此处模糊函数使用指数函数exp[-(dijm/r)n],3种熵都包含r及m,FuzzyEn还有参数n,详细的定义见文献[28].
1.2 特征曲线的形成MAV、FuzzyEn、SampEn、ApEn 4种特征通过滑动窗运算进行sEMG运动检测.将滑动窗宽设为w=256,以固定步长s=64移动,对每个长度为w的窗内信号计算当前特征值,将计算好的数据归一化至[0, 1],便于后续不同特征的比较.针对每种特征,以时间为横坐标,特征值为纵坐标,如图 4、5所示,各形成一条表现sEMG运动检测的特征曲线.

|
图 4 Ⅴ级、Ⅳ级患者中4种特征算法信号检测效果对比 Fig. 4 Comparison of four algorithms in performance of signal detection with stage Ⅳ-Ⅴ patients |
|
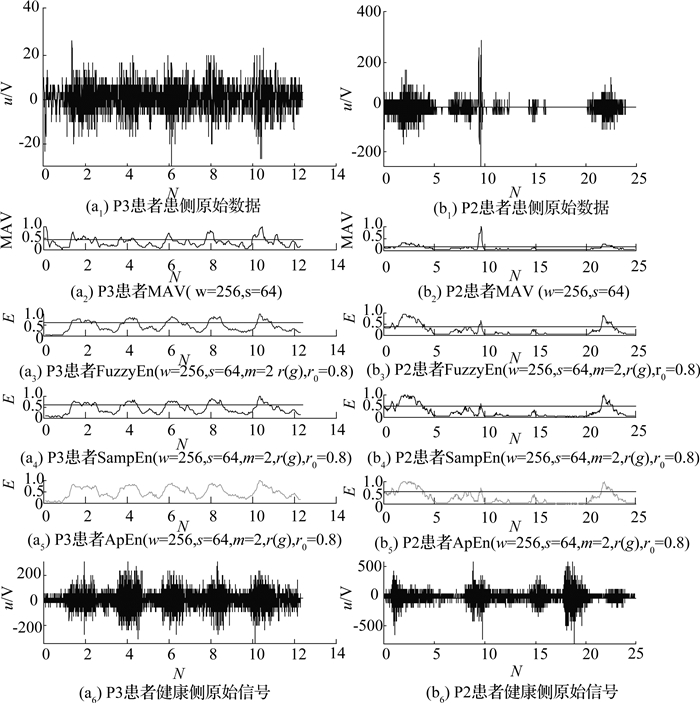
图 5 Ⅲ级、Ⅱ级患者4种特征算法信号检测效果对比 Fig. 5 Comparison of four algorithms in performance of signal detection with stage Ⅱ-Ⅲ patients |
熵值法的运算点数为窗内点数.3种熵均需设置匹配阈值r,匹配阈值为
| $ r\left( i \right) = {\rm{SD}}\left( i \right) \times {r_0};0 < {r_0} < 1, i = l、g. $ | (6) |
式中:r0为匹配阈值初始系数,i为局部或全局选项,r(l)为局部匹配阈值,r(g)为全局匹配阈值,SD(g)为整段数据的标准差.通过3.1节的比较,选用最佳的匹配阈值.所有的运算包括特征曲线的生成,均采用Matlab编程实现.
1.3 数据采集和处理流程肌电数据来自某康复医院的16名年龄56~85岁的偏瘫患者(12男4女)以及2名健康者,所有患者均已签署知情同意书,采集双侧ED和ECR的肌电信号[29].经医院Brunnstrom评测Ⅰ~Ⅴ级患者人数分别为3、4、4、3、2名,患病时间为1月至5年不等.肌电数据采集设备采用TeleMyo 2400T-G2型,采样频率为1 500 Hz,共16导双电极.实验中使用其中4个通道,每名被试者作5次前臂腕伸动作,对应20个sEMG运动信号,16名患者对应320个sEMG运动信号.对采集到的所有数据进行编组,依据患者等级将患侧信号编为5组,如Ⅴ级患者患侧信号编号为P5.将对应的健康侧信号作为对照组,健康被试者编号为N.
患者及健康者无外部肌肉损伤或疲劳,实验前已被告知整个测试流程,按图 1(a)所示的位置贴好电极.采集时,要求受试者手部及前臂置于支撑平面,掌心向下,前臂贴于支撑面,整体保持舒适姿态.按操作者指令重复5次前臂腕伸动作,动作要求5指合拢伸直.对于无运动能力的患侧肢体,提前告知患者意识上努力完成任务,采集潜在的肌电信号.

|
图 1 偏瘫患者数据采集与处理 Fig. 1 Data recording and processing from hemiplegic patients |
对采集到的肌电信号进行手动分割,计算SNR.使用健康者的肌电数据来比较和选择熵特征所需的参数,继而进行MAV、FuzzyEn、SampEn、ApEn的滑动窗运算,统计和比较在不同等级患者中各特征算法对尖峰及背景伪迹等噪声的敏感程度.提出适合于偏瘫患者sEMG运动检测的特征,数据采集和处理流程如图 1(b)所示.
2 不同Brunnstrom等级病人的信噪比计算针对各级偏瘫受试者,基于运动/静息比的方法,将静息段作为基准信号,计算腕伸动作的原动肌的SNR.参考对应对照组的数据,将每位受试者的腕伸数据分割成5段静息信号及5段动作信号.
设ui为信号幅值,N为信号段内的点数, u为均值,则
| $ {\sigma _{{\rm{state}}}}^2 = \frac{1}{{N-1}}\sum\limits_{i = 1}^N {{{\left( {{u_i}-\overline u } \right)}^2}} ;\left\{ {{\rm{state:}}\;{\rm{move, static}}} \right\}. $ | (7) |
肌电信号的信噪比为
| $ {\rm{SNR = 10lg}}\left( {\sigma _{{\rm{move}}}^2/\sigma _{{\rm{static}}}^2} \right). $ | (8) |
式中:σmove2为5次动作段信号的方差均值,σstatic2为5次静息段信号的方差均值.
根据式(7)、(8)计算各级患者双侧ED和ECR的信号SNR,如表 1所示.表中,ED(A)及ECR(A)对应患者的患侧.Ⅲ级以下患者的SNR接近于0甚至是负值,说明较低等级患者的患侧肌电信号混乱程度大.影响肌电信号幅值和频率的两个最重要因素是募集运动单元速度及运动单元放电速度[30].由图 4、5中第一行的患侧原始信号分析得出,Ⅲ级以下患者的每个动作占据较长的时间跨度,信号的稳定性明显不如健康者.
| 表 1 各等级受试者信号SNR Table 1 SNR of subjects with different stages |
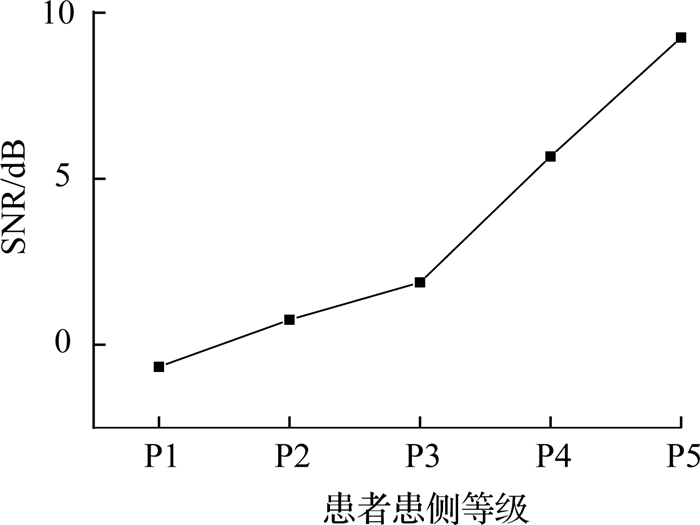
将同级患者患侧两个通道的SNR取均值发现,偏瘫患者的Brunnstorm等级与SNR呈线性正相关关系,如图 2所示.SNR越大,偏瘫患者等级越高,越接近于康复.随着偏瘫患者等级的降低,自身的肌肉组织相对更无序,导致患侧肌电信号的幅值逐渐减小,SNR呈逐渐降低的趋势.
|
图 2 各等级患者患侧信号SNR均值 Fig. 2 Average SNR of affected side signals under hemiplegic patients with different stages |
FuzzyEn、SampEn及ApEn的计算结果受参数取值的影响较大[15-31],因此使用这3种熵之前,有必要对涉及的参数进行选择.除了FuzzyEn的参数n以外,3种熵的特征计算主要与参数m、r的取值相关.根据所需的数据点数与采样时长确定,Wolf建议非线性动态分析中m维吸引子需数据点数为10m~30m,m初步取1、2、3.由式(6)可知,r的选择主要依赖于r0的初选,初步取r0为0.1、0.2、0.8.
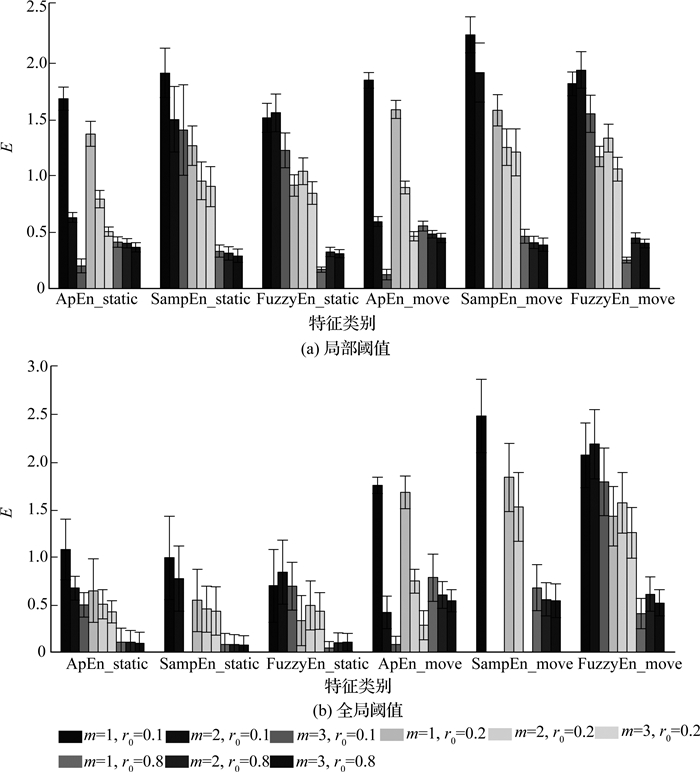
健康者肌电信号SNR高,无尖峰段,所以使用2名健康者原动肌的ED信号作为标准测试信号,选择熵的参数.取计算窗宽w=256,步长s=64,重叠度为75%,在m与r0各种取值组合下,计算局部阈值r(l)及全局阈值r(g)下的5个动作段及静息段信号的3种熵特征的均值与标准差,结果如图 3(a)、(b)所示.图中,E为熵.
|
图 3 不同参数下健康者的熵 Fig. 3 Entropy value of healthy subjectsunder different parameters |
静息段和动作段的均值差别越大,标准差越小,越有利于动态肌电检测.从图 3(a)可以看出,采用r(l)时3种熵在静息段和动作段的差别较小,不符合要求.从图 3(b)可以看出,采用r(g)时,静息段的熵明显低于动作段,满足这一要求,因此选择r(g).
从图 3(b)可以看出,采用r(g)时,当r0=0.1、0.2时,静息段和动作段的熵都较大,静息段的熵偏高并且标准差较大,不利于运动段sEMG信号的提取;当r0=0.8时,3种熵明显减小,对运动段的sEMG检测很有效,并且当r0=0.8时3种熵的变化相对稳定.选择r0=0.8.取r0=0.8,对比m=1、2、3时的熵与标准差.当m=1时,ApEn和SampEn的静息段和动作段的标准差最大;当m=3时,3种熵的动作段的幅值较小,不利于运动段sEMG的提取.m反映重构向量的长度,增大m会加大计算量和计算难度,但不提高性能[18];考虑计算量及有利于运动段sEMG提取,m取2.
sEMG运动检测所用熵的3种参数选择分为r(g)、r0=0.8和m=2.
3.2 各级患者sEMG运动检测利用上述不同等级偏瘫患者双侧腕伸动作时原动肌的肌电信号,分别计算MAV、FuzzyEn、SampEn、ApEn 4个特征,图像在Matlab中显示并作处理.如图 4、5所示分别为Ⅱ~Ⅴ级患者采集到的肌电信号和特征曲线图.图中,u为电压.根据对照组信号手动分割出5组静息段和5组运动段,在每幅图上添加一条平行于X轴的阈值线,将静息段熵的最大值作为阈值线高度,该值作为评判3种熵处理效果的一种依据.
如图 4(a)所示为某Ⅴ级偏瘫患者患侧ECR的肌电特征滑动窗图,SNR为12 dB.在第一个动作开始阶段及结束时有尖峰噪声,MAV法受尖峰噪声的影响较大,熵值法几乎不受影响.在后续动作的静息段中,噪声对MAV特征窗图的影响较明显,对熵值法影响几乎为0,其中FuzzyEn法的影响最小,SampEn和ApEn法受噪声的影响增大.MAV的整体效果明显不如3种熵的表现,静息段幅值在4种特征中最大.分析该患者的健侧原动肌滑动窗时,4种特征均表现良好.
如图 4(b)所示为某Ⅳ级患者患侧ED的肌电特征滑动窗图,信号SNR=9 dB,静息段中的平稳噪声对MAV的影响大.从熵值法尤其是FuzzyEn特征图中的静息段更接近0可得,FuzzyEn法受噪声的影响较小.
如图 5(a)所示为某Ⅲ级患者患侧ED的肌电信号,SNR=3 dB,SNR低且原始信号明显有毛刺状信号,可以用肉眼观察出静息段基准信号明显比高等级患者大.受其影响,3种熵值法滑动窗图中的静息段值均大于0,其中FuzzyEn静息段值最小,其次为SampEn、ApEn;可以看出,在SNR低且有毛刺信号的情况下,采用熵值法能够看出5个动作的波形.MAV幅值法受噪声影响没有规律,无法明显辨认出波形,对SNR低的sEMG运动信号失去检测能力.如图 5(b)所示为某Ⅱ级患者患侧ECR的信号(SNR为5 dB)检测结果.与高等级患者相比,熵值信号检测表现出对潜在运动的检测能力.对于Ⅰ级偏瘫患者,患侧均不能检测到sEMG运动特征.对于健康侧,只要SNR高,4种特征就都能检测到肌肉电活动;当SNR低时,熵的抗干扰能力显现出来.
4 结果与分析16名不同等级患者进行双侧共320个动作测试,对应320个运动段sEMG信号.运动sEMG信号经MAV、FuzzyEn、SampEn、ApEn 4种特征算法检测,统计所能适应的信号特点,如表 2所示,适应尖峰噪声、适应低信噪比、噪声敏感程度、潜在运动检测、偏瘫患侧等级、特征曲线连续性、可否在线使用等特性.从患者等级上统计,4名Ⅱ级患者中有2名患者的患侧及Ⅰ级所有患者患侧,4种特征均检测不到动作特征.原因是患者肌肉组织相对无序、肌力微弱、肌张力低,导致无法采集到自主意识上的收缩信号或者患者本身没有按要求靠意识完成收缩.对于Ⅲ级及以上的偏瘫患者患侧,熵值法比MAV占优势.对于Ⅳ、Ⅴ级患者患侧的信号,4种特征均有效.
| 表 2 4种特征算法统计差异 Table 2 Statistical differences of four algorithms |
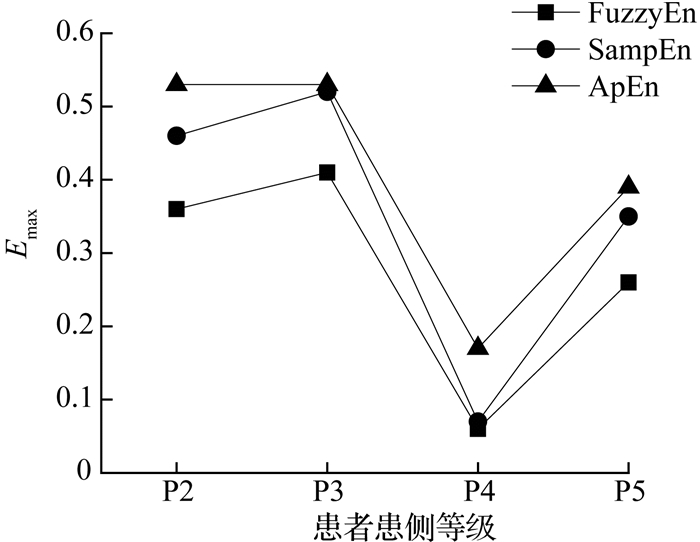
3种熵特征对SNR较低的肌电信号及其中的尖峰噪声的适应能力强,表现出了对潜在运动的检测能力,MAV不具备该优点.对于SNR高且无尖峰段的信号,熵值法与MAV均适用.在相同参数(r(g), m=2, r0=0.8)下,4种特征对噪声的敏感程度如下:FuzzyEn<SampEn<ApEn<MAV.如图 6所示,静息段3种熵特征中FuzzyEn更低,越接近于0,表明对背景毛刺噪声的敏感度低,有很强的抗干扰性.图中,Emax为静息段熵最大值.此外,从图 4、5的统计发现,SampEn的连续性较差,ApEn略受信号尖峰段的影响.
|
图 6 3种熵在不同等级患者情况下静息段熵最大值 Fig. 6 Maximum value of resting segment of three entropy algorithms in patients with different stages |
重度偏瘫患者患侧的肌电信号SNR低,属于弱肌电信号,其检测一直是备受关注的问题.在信号SNR高且无尖峰段时,熵特征的检测除耗时外均优于MAV,但MAV算法由于简单易行,运行时间短,可为首选算法;当分析SNR低的弱肌力信号时,熵值法的适应性明显强于MAV,对背景伪迹和尖峰噪声的敏感性较低,对运动状态误判的可能性较低,并且有检测潜在运动的潜力.FuzzyEn比SampEn和ApEn具有更好的表现,体现在静息段信号的FuzzyEn更接近0,对噪声的敏感程度更低,抗干扰性更强,这可能与FuzzyEn采用隶属度函数取代Heaviside函数有关.
5 结语本文针对不同等级偏瘫患者sEMG的运动检测问题,设计偏瘫患者的双侧腕伸共同运动实验.提取16名经过Brunnstrom分级患者,共320个运动sEMG信号的肌电数据,未加入任何人工合成成分.
以静息段信号为基准信号,作为信号SNR的计算依据,计算不同等级患者sEMG信号的SNR,得出肌电信号的SNR与偏瘫患者等级呈线性正相关性.
通过计算sEMG信号的MAV、FuzzyEn、SampEn、ApEn,得出在Ⅱ-Ⅲ级患者信号中,熵值法对噪声的敏感性较低,参数可调,具有对潜在肌肉电活动的识别能力,因此更适合于sEMG运动检测,其中FuzzyEn特征值的检测效果更好.在Ⅳ-Ⅴ级偏瘫患者中,MAV和熵值法均适用于sEMG运动检测,MAV法由于简单易行,算法的运算效率高,很适合在线检测,在无尖峰噪声时可以进行sEMG运动检测.
本文的研究为从Ⅱ-Ⅴ等级偏瘫患者中连续采集的肌电信号流中判断出运动段信号,为康复训练和评估及人机交互提供参考.今后的工作将扩大各等级偏瘫患者的实验样本,进一步验证该实验结论在低等级患者人群中的正确性.
| [1] |
FEIGIN V L. Stroke:practical management[J]. Journal of the American Medical Association, 2008, 300(19): 2311-2312. DOI:10.1001/jama.2008.633 |
| [2] |
杨钟亮, 唐智川, 陈育苗, 等. 面向双侧训练的前臂外骨骼肌肉力-电关系识别模型[J]. 浙江大学学报:工学版, 2014, 48(12): 2152-2161. YANG Zhong-liang, TANG Zhi-chuan, CHEN Yu-miao, et al. Force-sEMG relations recognition models of forearm exoskeleton for bilateral training[J]. Journal of Zhejiang University:Engineering Science, 2014, 48(12): 2152-2161. |
| [3] |
王健. sEMG信号分析及其应用研究进展[J]. 体育科学, 2000, 20(4): 56-60. WANG Jian. Some advance in the research of sEMG signal analysis and its application[J]. Sport Science, 2000, 20(4): 56-60. |
| [4] |
邱青菊. 表面肌电信号的特征提取与模式分类研究[D]. 上海: 上海交通大学, 2009. QIU Qing-ju. Feature extraction and pattern classification of electromyographic signals[D]. Shanghai: Shanghai Jiaotong University, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10248-2010033391.htm |
| [5] |
ZHOU P, ZHANG X. A novel technique for muscle onset detection using surface EMG signals without removal of ECG artifacts[J]. Physiological Measurement, 2014, 35(1): 45-54. |
| [6] |
LI X, ZHOU P, ARUIN A S. Teager-Kaiser energy operation of surface EMG improves muscle activity onset detection[J]. Annals of Biomedical Engineering, 2007, 35(9): 1532-1538. |
| [7] |
LI G, LI Y, YU L, et al. Conditioning and sampling issues of EMG signals in motion recognition of multifunctional myoelectric prostheses[J]. Annals of Biomedical Engineering, 2011, 39(6): 1779-1787. DOI:10.1007/s10439-011-0265-x |
| [8] |
ZHANG X, BARKHAUS P, RYMER W, et al. Machine learning for supporting diagnosis of amyotrophic lateral sclerosis using surface electromyogram[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering A Publication of the IEEE Engineering in Medicine and Biology Society, 2013, 22(1): 96-103. |
| [9] |
郭明远. 表面肌电对偏瘫患者肘关节痉挛评估的应用研究[D]. 广州: 南方医科大学, 2012. GUO Ming-yuan. Exploratory development of elbow spasticity assessment in Hemiplegic patients using sEMG[D]. Guangzhou: Southern Medical University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-90023-1013123862.htm |
| [10] |
付丽, 高晓平, 张旭, 等. 脑卒中后偏瘫上肢康复过程中表面肌电分析[J]. 中华物理医学与康复杂志, 2016, 38(5): 356-361. FU Li, GAO Xiao-ping, ZHANG Xu, et al. Surface-electromyographic analysis of the upper extremity muscles can aid in the rehabilitation of hemiparetic stroke survivors[J]. Chinese Journal of Physical Medicine and Rehabilitation, 2016, 38(5): 356-361. |
| [11] |
李瑞辉, 范志坚, 赵翠莲, 等. 利用sEMG能量高斯分布特性提取动作信号的方法[J]. 中国医疗器械杂志, 2014(3): 177-180. LI Rui-hui, FAN Zhi-jian, ZHAO Cui-lian, et al. Motion signal extraction method based on sEMG energy Gauss distribution characteristics[J]. Chinese Journal of Medical Instrumentation, 2014(3): 177-180. |
| [12] |
LINHARES N D, ANDRADE A O. Parametric sEMG muscle activity detection based on MAV and sample entropy[C]//Biosignals and Biorobotics Conference. [S. l. ]: IEEE, 2014: 1-6. http://www.researchgate.net/publication/268196018_parametric_semg_muscle_activity_detection_based_on_mav_and_sample_entropy
|
| [13] |
LIU J, YING D, RYMER W Z, et al. Robust muscle activity onset detection using an unsupervised electromyogram learning framework[J]. Plos One, 2015, 10(6): e0127990. DOI:10.1371/journal.pone.0127990 |
| [14] |
XU Q, QUAN Y, YANG L, et al. An adaptive algorithm for the determination of the onset and offset of muscle contraction by EMG signal processing[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering A Publication of the IEEE Engineering in Medicine and Biology Society, 2013, 21(1): 65-73. |
| [15] |
CHEN W, WANG Z, XIE H, et al. Characterization of surface EMG signal based on fuzzy entropy[J]. IEEE Transactions on Neural Systems and Rehabilitation Engineering A Publication of the IEEE Engineering in Medicine and Biology Society, 2007, 15(2): 266-272. DOI:10.1109/TNSRE.2007.897025 |
| [16] |
ZHANG X, ZHOU P. Sample entropy analysis of surface EMG for improved muscle activity onset detection against spurious background spikes[J]. Journal of Electromyography and Kinesiology Official Journal of the International Society of Electrophysiological Kinesiology, 2012, 22(6): 901-907. DOI:10.1016/j.jelekin.2012.06.005 |
| [17] |
AHMAD S A, CHAPPELL P H. Surface EMG classification using moving approximate entropy[C]//International Conference on Intelligent and Advanced Systems. [S. l. ]: IEEE, 2007: 1163-1167. http://www.researchgate.net/publication/224343570_Surface_EMG_classification_using_moving_approximate_entropy
|
| [18] |
MING L, XIONG C, ZHANG Q, et al. Fuzzy entropy-based muscle onset detection using electromyography (EMG)[J]. Lecture Notes in Computer Science, 2014, 8917: 89-98. |
| [19] |
XIE H B, GUO J Y, ZHENG Y P. Fuzzy approximate entropy analysis of chaotic and natural complex systems:detecting muscle fatigue using electromyography signals[J]. Annals of Biomedical Engineering, 2010, 38(4): 1483-1496. DOI:10.1007/s10439-010-9933-5 |
| [20] |
AO D, SUN R, SONG R. Comparison of complexity of EMG signals between a normal subject and a patient after stroke: a case study[C]//International Conference of IEEE Engineering in Medicine and Biology Society. Osaca: IEEE, 2013: 4965-4968. http://www.ncbi.nlm.nih.gov/pubmed/24110849
|
| [21] |
YU Z, ZHANG X, WANG D, et al. Study on relationship between surface EMG complexity and muscle strength[J]. Space Medicine and Medical Engineering, 2016, 29(2): 120-126. |
| [22] |
成娟, 陈勋, 彭虎. 基于样本熵的肌电信号起始点检测研究[J]. 电子学报, 2016, 44(2): 479-484. CHENG Juan, CHEN Xun, PENG Hu. An onset detection method for action surface electromyography based on sample entropy[J]. Chinese Journal of Electronics, 2016, 44(2): 479-484. |
| [23] |
LEE A S, CHOLEWICKI J, REEVES N P. The effect of background muscle activity on computerized detection of sEMG onset and offset[J]. Journal of Biomechanics, 2007, 40(15): 3521-3526. DOI:10.1016/j.jbiomech.2007.05.012 |
| [24] |
MERLO A, FARINA D, MERLETTI R. A fast and reliable technique for muscle activity detection from surface EMG signals[J]. IEEE Transactions on Biomedical Engineering, 2003, 50(3): 316-323. DOI:10.1109/TBME.2003.808829 |
| [25] |
KURODA Y, NISKY I, URANISHI Y, et al. Novel algorithm for real-time onset detection of surface electromyography in step-tracking wrist movements[C]//International Conference of the IEEE Engineering in Medicine and Biology Society. [S. l. ]: IEEE, 2013: 2056-2059. http://www.ncbi.nlm.nih.gov/pubmed/24110123
|
| [26] |
RASOO G, IQBAL K. Muscle activity onset detection using energy detectors[C]//International Conference of the IEEE Engineering in Medicine and Biology Society. [S. l. ]: IEEE, 2012: 3094-3097. http://www.ncbi.nlm.nih.gov/pubmed/23366579
|
| [27] |
SOLNIK S, RIDER P K, DEVITA P, et al. Teager-Kaiser energy operator signal conditioning improves EMG onset detection[J]. European Journal of Applied Physiology, 2010, 110(3): 489-498. DOI:10.1007/s00421-010-1521-8 |
| [28] |
PINCUS S. Approximate entropy (ApEn) as a complexity measure[J]. Chaos An Interdisciplinary Journal of Nonlinear Science, 1995, 5(1): 110. |
| [29] |
FAN Z, ZHAO C, LUO L, et al. Study on sEMG-based exercise therapy for upper limb of severe hemiplegic patients[C]//International Conference of the IEEE Engineering in Medicine and Biology Society. [S. l. ]: IEEE, 2013: 6643-6646. https://www.researchgate.net/publication/257602207_Study_on_sEMG-based_exercise_therapy_for_upper_limb_of_severe_hemiplegic_patients
|
| [30] |
KONRAD P. The ABC of EMG a practical introduction to kinesiological electromyography[EB/OL]. https: //doi. org/10. 1016/j. jacc. 2008. 05. 066. https://www.mendeley.com/research-papers/abc-emg-practical-introduction-kinesiological-electromyography/
|
| [31] |
CHEN W, ZHUANG J, YU W, et al. Measuring complexity using FuzzyEn, ApEn, and SampEn[J]. Medical Engineering and Physics, 2009, 31(1): 61-68. |


