光纤陀螺(fiber-optic gyroscope, FOG)是一种基于光学sagnac效应的角速度传感器,具有体积小、质量轻、精度范围广、无运动部件等优点[1-2],在航空、航天、航海及兵器等大型国防重点领域中发挥了重要的作用[3-4].
光纤陀螺的纯滞后指标是在高速惯导系统研发的背景下提出的一项新指标,在现有光纤陀螺频率特性测试条件难以满足极限带宽测试的情况[5]下,可以作为衡量光纤陀螺动态性能的重要标准.纯滞后时间定义为:从光纤陀螺接收到角速度冲击,到将该角速度冲击信号以陀螺数据的形式输出所需要的时间.
薛宁等[6]在专利《一种光纤陀螺输出延迟时间的测量装置及其方法》(申请号201110090599.9)中提出光纤陀螺纯滞后时间的测量系统.这种测试装置采用10 kHz的高采样速率查询光纤陀螺信号,正常工作的光纤陀螺数据帧频率一般在几kHz以内,因此该装置只能测试非正常工作状态下的查询式光纤陀螺,并且测试精度受采样速率的限制,测试精度较低.
本文在光纤陀螺数据测试系统的基础上,设计并实现了光纤陀螺纯滞后时间测试系统.该测试系统不改变陀螺正常的工作频率,能够同时适用于查询式和广播式陀螺,实现了较高的测试精度.利用该系统完成了光纤陀螺产品的纯滞后指标测试工作.光纤陀螺纯滞后时间测试系统的实现,对于高速武器系统应用中光纤陀螺产品的评价具有重要的意义.
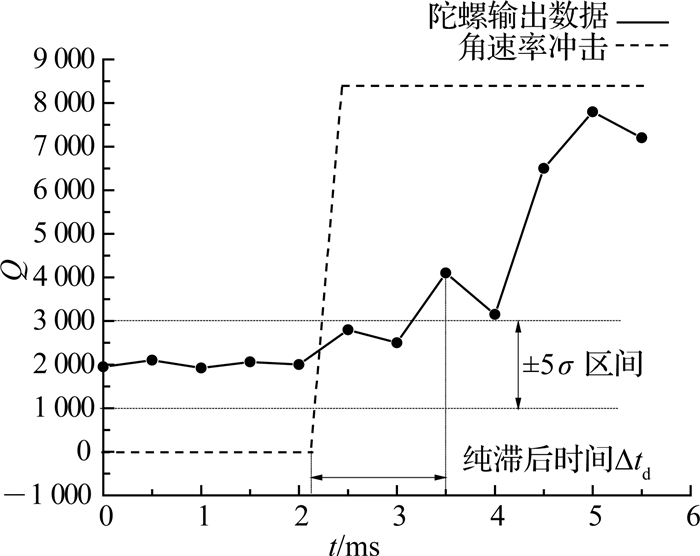
1 光纤陀螺纯滞后指标光纤陀螺纯滞后时间的定义如图 1所示.图中,Q为角速度所对应的陀螺数据量化值,该量化值与角速度成正比;t为时间.对于图 1所表述的光纤陀螺系统,数据输出周期是500 μs.当没有角速度冲击输入时,光纤陀螺输出数字量为2 000,光纤陀螺输出噪声为σ=200.在角速率冲击引入后,若光纤陀螺输出变化量达到了5σ以上(即1 000以上),则认为此时输出的光纤陀螺数据反映了角速率冲击,角速率冲击的开始时刻与陀螺输出有效数据的时刻之间的时间Δtd为光纤陀螺纯滞后时间.
|
图 1 光纤陀螺纯滞后时间的定义示意图 Fig. 1 Schematic diagram of definition of FOG pure lag time |
在实际的使用过程中,光纤陀螺的纯滞后特性与工作状态相关,如环境温度、数据帧频率、电磁环境等.需要在保持光纤陀螺正常工作状态的前提下,实现纯滞后时间的测量[7].对于一款光纤陀螺产品,能够实现的纯滞后时间的最小值称为光纤陀螺的极限纯滞后时间.
作为衡量光纤陀螺动态性能的重要参考标准,纯滞后指标直接反映了光纤陀螺输出的实时性以及对大动态角速度冲击信号的反馈能力,在大动态、高速兵器系统应用中是一项重要的考察指标.一般来说,工作频率达到1 kHz以上的光纤陀螺,即可认为其适用于高速系统应用.随着我国科研军工实力的不断增强,越来越多的快速反应武器的研发项目被提上了日程[8-9],其中不少项目都对光纤陀螺纯滞后指标提出了非常具体的要求,例如,对于以2 kHz频率输出陀螺数据的高速光纤陀螺,每帧陀螺数据的输出周期是500 μs;对于该款光纤陀螺的应用系统,要求该款光纤陀螺的极限纯滞后时间不得超过500 μs.
2 光纤陀螺纯滞后测试系统设计在介绍光纤陀螺纯滞后测试系统之前,有必要先对光纤陀螺数据测试系统进行说明.光纤陀螺数据测试系统是一个已经成熟并且广泛使用的测试系统.它能够接收正常工作状态的光纤陀螺数据,以此实现光纤陀螺的质量测试[10].光纤陀螺数据测试系统工作时,光纤陀螺原本的工作状态是得以保留的.
在不改变陀螺原有工作状态的前提下实现对纯滞后时间的测量,是设计该测试系统的关键.在光纤陀螺数据测试系统的基础上实现纯滞后测试系统,成为一种可行的技术方案.
按照该技术方案设计的纯滞后测试系统可以分为2部分:硬件触发模块和数据采集处理模块.
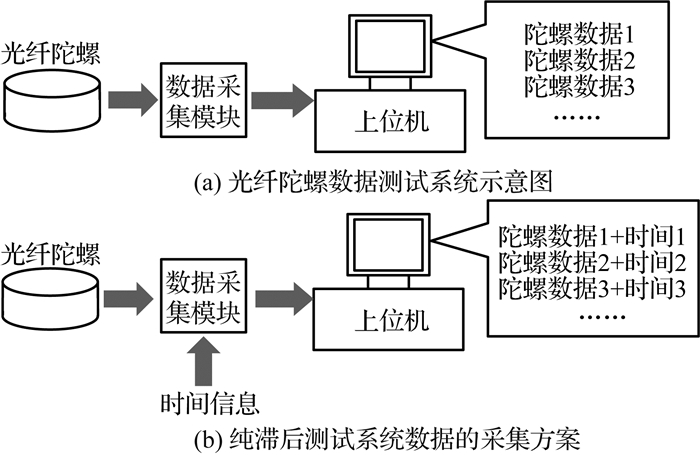
2.1 纯滞后测试系统测试方案在光纤数据测试系统中,光纤陀螺数据由光纤陀螺发出后,先由数据采集模块采集并进行预处理,再将预处理之后的数据交给上位机进行解算,如图 2(a)所示.
|
图 2 纯滞后测试系统与数据测试系统的对比 Fig. 2 Comparison of pure lag test system and data test system |
纯滞后测试系统的测试方案如下:光纤陀螺硬件和内部程序不作改动,在数据采集模块预处理陀螺数据的过程中,在接收到的每一帧原始陀螺数据中增加一个时间信息,该时间信息反映了外部角速度冲击发生到接收到此帧陀螺数据的时间.在上位机接收到的所有数据中,能够反映角速度冲击的第一帧陀螺数据所对应的时间,即为待测光纤陀螺的纯滞后时间.如图 2(b)所示,该方案可以在不修改光纤陀螺原本硬件、软件配置的前提下,实现纯滞后时间的测试.
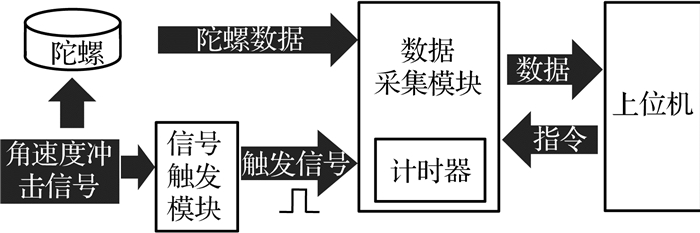
为了实现纯滞后测试系统,需要完成两个模块的设计,如图 3所示.首先是硬件触发模块,在角速度冲击施加给光纤陀螺的瞬间触发脉冲信号,作为计时器开始计时的信号;其次是数据采集模块的重新设计,需要在每一帧光纤陀螺数据中插入对应的时间信息.
|
图 3 光纤陀螺纯滞后测试系统设计方案 Fig. 3 Design scheme of FOG pure lag test system |
对于一个工作状态、数据传输帧率确定的光纤陀螺,存在极限纯滞后时间Δtdmin,它反映了光纤陀螺感受到角速率冲击到发出反应角速率冲击陀螺信号的极限时间.光纤陀螺按照数据的输出方式不同,可以分为2种:广播式光纤陀螺和查询式光纤陀螺.在光纤陀螺测试过程中,两种光纤陀螺均以固定的帧频率输出陀螺数据,每帧数据的间隔时间为Δtf.
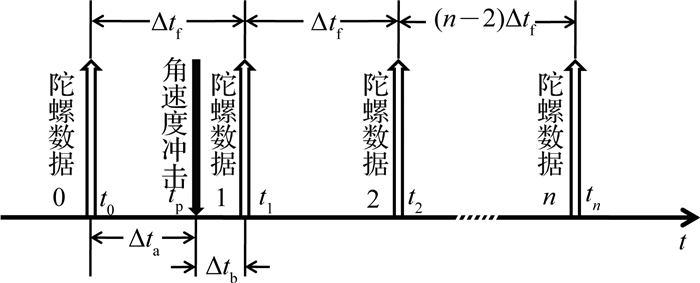
对于固定帧率输出的光纤陀螺,可以构建该陀螺在测试过程中的模型,如图 4所示.数据采集模块接收到陀螺数据0, 陀螺数据1, 陀螺数据2, …, 陀螺数据n的对应时刻分别为t0, t1, t2, …, tn,角速度冲击时刻tp发生在t0和t1之间,则有
| $ \Delta {t_{\rm{a}}} = {t_{\rm{p}}} - {t_{\rm{0}}}, $ | (1) |
| $ \Delta {t_{\rm{b}}} = {t_{\rm{1}}} - {t_{\rm{p}}}. $ | (2) |
|
图 4 光纤陀螺纯滞后时间测试原理模型 Fig. 4 Principle model of FOG pure lag time test |
式中:Δta为角速度冲击时刻tp距离前一帧陀螺数据时刻t0的时间间隔,Δtb为角速度冲击时刻tp距离后一帧陀螺数据t1时刻的时间间隔.
2.2.2 纯滞后时间测试原理对于该测试系统,在一次纯滞后测试中,角速率冲击时刻tp在t0和t1之间的位置是随机的,Δtb可能的取值范围为
| $ 0 < \Delta {t_{\rm{b}}} < \Delta {t_{\rm{f}}}. $ | (3) |
对于一个工作状态已经确定的光纤陀螺,极限纯滞后时间Δtdmin是一个固定的值.若对Δtdmin和Δtf的商作向下取整运算,则有
| $ \left\lfloor {\frac{{\Delta {t_{{\rm{dmin}}}}}}{{\Delta {t_{\rm{f}}}}}} \right\rfloor = m. $ | (4) |
式中:m为非负整数.随着角速率冲击时刻tp在t0和t1之间发生的位置不同,将会产生以下2种不同的情况.
1) 当Δtb满足关系:
| $ \Delta {t_{\rm{f}}} > \Delta {t_{\rm{b}}} > \Delta {t_{{\rm{dmin}}}} - m\Delta {t_{\rm{f}}} $ | (5) |
时,能够体现tp时刻的角速度冲击的陀螺数据编号为
| $ n = m + 1, $ | (6) |
测试结果Δtd为
| $ \Delta {t_{\rm{d}}} = \Delta {t_{\rm{b}}} + m\Delta {t_{\rm{f}}}. $ | (7) |
2) 当Δtb满足关系:
| $ \Delta {t_{{\rm{dmin}}}} - m\Delta {t_{\rm{f}}} > \Delta {t_{\rm{b}}} > 0 $ | (8) |
时,能够体现tp时刻的角速度冲击的陀螺数据编号n为
| $ n = m + 2, $ | (9) |
测试结果Δtd为
| $ \Delta {t_{\rm{d}}} = \Delta {t_{\rm{b}}} + \left( {m + 1} \right)\Delta {t_{\rm{f}}}. $ | (10) |
在一次纯滞后测试中,得到的测试结果为“纯滞后时间Δtd”和“反映角速度冲击的陀螺数据编号n”.多次测试之后,可以根据得到的多组测试结果分析,得到极限纯滞后时间Δtdmin的测试结果Δtdmin-result.
因为确定工作状态的光纤陀螺有固定的极限纯滞后时间Δtdmin,反映角速度冲击的陀螺数据编号n会确定得到两种测试结果n1和n2.n1、n2满足关系:
| $ {n_2} - {n_1} = 1. $ | (11) |
式中:n1和n2分别为在式(5)、(8)表述的情况下测得的n.根据式(6)、(9),可以确定式(4)的m:
| $ m = {n_1} - 1 $ | (12) |
或
| $ m = {n_2} - 2. $ | (13) |
对于测试结果n=n1的情况,结合式(5)、(7),根据测试结果Δtd,可得
| $ \Delta {t_{{\rm{dmin}}}} < \Delta {t_{\rm{d}}}. $ | (14) |
对于测试结果n=n2的情况,结合式(8)、(10),根据测试结果Δtd,可得
| $ \Delta {t_{{\rm{dmin}}}} > \Delta {t_{\rm{d}}} - \Delta {t_{\rm{f}}}. $ | (15) |
由上述2种情况可知,如果测试的样本数足够多,那么可以根据式(14)、(15)多次逼近确定Δtdmin.
如果在一次足够多样本数的测量中,n=n1所对应的所有测试结果Δtd的最小值为
| $ \Delta {t_{{\rm{dx}}}} = {\left[ {\left\{ {\Delta {t_{\rm{d}}}\left| {_{n = {n_1}}} \right.} \right\}} \right]_{\min }}. $ | (16) |
对于这类测试结果,定义Δtd为Δtdmin的上限元素,记为Δtdmin-H.
n=n2所对应的所有Δtd-Δtf的最大值为
| $ \Delta {t_{{\rm{dy}}}} = {\left[ {\left\{ {\left( {\Delta {t_{\rm{d}}} - \Delta {t_{\rm{f}}}} \right)\left| {_{{n_2}}} \right.} \right\}} \right]_{\max }}. $ | (17) |
对于这类测试结果,定义(Δtd-Δtf)为Δtdmin的下限元素,记为Δtdmin-L.
可以确定,最终采用这些测试样本能够逼近得到的Δtdmin极限取值范围为
| $ \Delta {t_{{\rm{dx}}}} > \Delta {t_{{\rm{dmin}}}} > \Delta {t_{{\rm{dy}}}}. $ | (18) |
Δtdmin的测试值为
| $ \Delta {t_{{\rm{dmin}} - {\rm{result}}}} = \frac{{\Delta {t_{{\rm{dx}}}} + \Delta {t_{{\rm{dy}}}}}}{2}. $ | (19) |
极限纯滞后时间Δtdmin测试的不确定度为
| $ {\delta _{{\rm{result}}}} = \frac{{\Delta {t_{{\rm{dx}}}} - \Delta {t_{{\rm{dy}}}}}}{2}. $ | (20) |
采用该测试系统得到的极限纯滞后时间Δtdmin的测试结果可以用Δtdmin-result±δresult的形式来表征,测试次数越多,得到的Δtd样本数越多,式(20)表征的不确定度越小,测试结果的精确度越高.
2.2.4 系统测试精度分析在每次测量过程中,角速率冲击时刻tp在t0和t1之间发生的位置是随机的,因此该系统的测试精度的实现是一个概率事件.
若采用该测试系统实施了2次测量,则达到±δresult的测试精度的概率为
| $ {P_2}\left| {_{{\delta _{{\rm{result}}}}}} \right. = 2\int_0^{{\delta _{{\rm{result}}}}} {\frac{{2{\delta _{{\rm{result}}}} - t}}{{{{\left( {\Delta {t_{\rm{f}}}} \right)}^2}}}{\rm{d}}t} = {\left( {\frac{{2{\delta _{{\rm{result}}}}}}{{\Delta {t_{\rm{f}}}}}} \right)^2}. $ | (21) |
若采用该系统进行了K次独立测试,则能够实现±δresult的测试精度的概率为
| $ {P_K}\left| {_{{\delta _{{\rm{result}}}}}} \right. = 1 - {\left( {1 - {P_2}} \right)^{C_K^2}} = 1 - {\left[ {1 - {{\left( {\frac{{2{\delta _{{\rm{result}}}}}}{{\Delta {t_{\rm{f}}}}}} \right)}^2}} \right]^{\frac{{K\left( {K - 1} \right)}}{2}}}. $ | (22) |
触发模块分为撞击结构和触发电路两部分,如图 5(a)所示.撞击结构由撞击滑块和被撞体构成,被撞体固定于转台,转台无机电结构且呈自由状态.自由状态的转台被撞击后,机械启动时间小于ns量级,可以忽略[11-12].释放撞击滑块后,滑块撞击被撞体会带动转台一起转动,从而传递角速度冲击给待测陀螺;撞击滑块与被撞体的接触部分有电极,撞击接触后会传递电信号给触发电路,从而使触发电路发出脉冲信号[13],如图 5(b)所示.触发模块可以保证在陀螺接收角速度冲击的同时,向计时器发送触发脉冲信号,实现撞击时刻的精准计时.
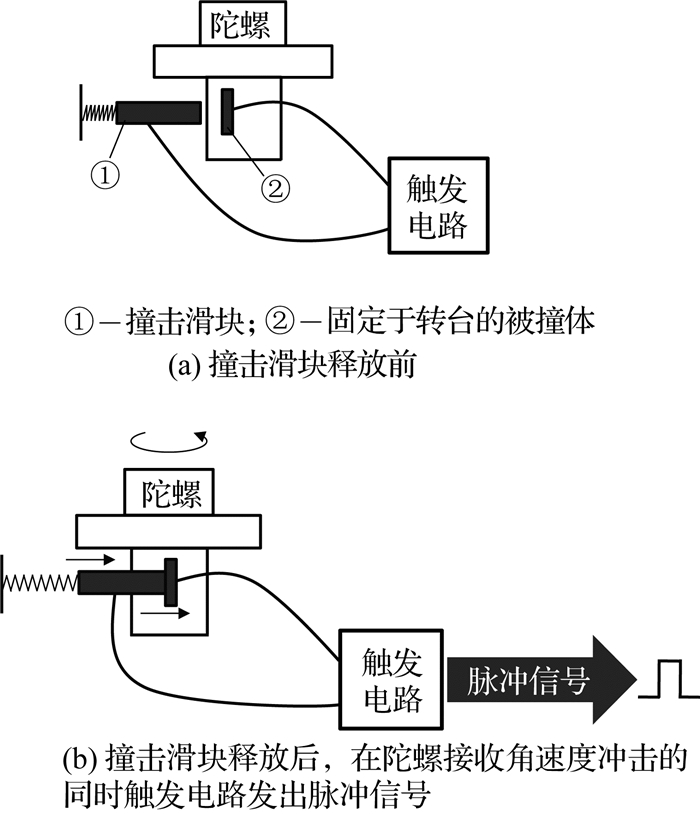
|
图 5 触发模块的功能设计示意图 Fig. 5 Schematic diagram of function design of trigger module |
数据采集处理模块采用F28M35双核DSP芯片作为处理核心,F28M35双核芯片由主核M3和副核C28组成[14],可以提供高达100 MHz的处理主频,实现陀螺数据的高速预处理;能够提供至少4个UART接口,可以同时实现四路陀螺的纯滞后时间测试,提高系统的测试效率[15-16].
数据处理模块的工作过程如图 6所示.UART串口实时接收陀螺数据,撞击发生后,触发模块发出的脉冲信号触发外部中断,M3核响应中断并开启计时器;随后UART每接收到一帧陀螺数据,M3核就将该帧数据和所对应的计时器时间打包在一起并放置于公共存储区;C28核负责抓取公共存储区的测试数据,控制USB模块,实现和上位机的实时通讯.USB数据的传输速率远高于串口波特率,避免了测试数据在数据处理模块内部的滞留问题.
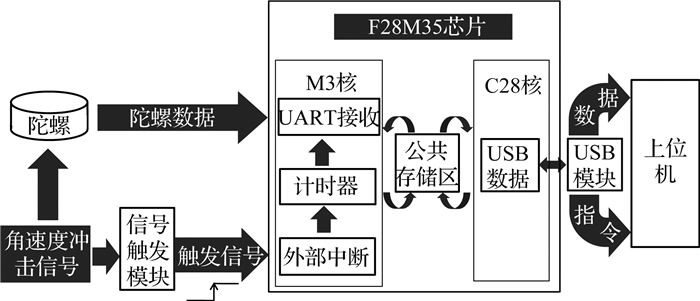
|
图 6 纯滞后测试系统数据采集处理模块的工作示意图 Fig. 6 Working schematic diagram of data acquisition and processing module of pure lag test system |
打包给上位机的测试数据由帧头、陀螺数据、时间信息3部分组成,由相邻帧之间陀螺数据的比较,可以判断陀螺数据是否反映角速度冲击信息,每一帧的时间信息反映了陀螺受到角速度冲击到数据处理模块接收到该帧陀螺数据的时间.第一帧反映角速度冲击信号的陀螺数据所对应的时间信息,即为被测光纤陀螺的纯滞后时间.
每一帧收到的时间信息数据格式由两个8位字节c1、c2共16位组成,其中最高位为flag标志位,flag置1代表发生了撞击;剩余15位为时间信息有效位,可以存储15位的时间信息.对于该测试系统,已知时间信息c1c2记满所有位数,即c2c1=0xffff时所对应的时间长度为ΔtFS,那么测试系统所对应的分辨率μ的计算公式为
| $ \mu = \frac{{\Delta {t_{{\rm{FS}}}}}}{{{2^{15}} - 1}}. $ | (23) |
完成后的纯滞后时间测试系统样机如图 7所示.使用该样机,对2支光纤陀螺产品(A和B)进行纯滞后时间测试,2支被测光纤陀螺均是广播式陀螺,通信帧率为2 kHz.结合1.2节的分析可知,对于这两款待测光纤陀螺产品,相邻陀螺数据之间的时间间隔Δtf=500 μs.一般认为测试精度为时间间隔的1/10,可以满足测试要求,即希望测试系统至少实现±25 μs的测量精度.

|
图 7 纯滞后时间测试系统样机 Fig. 7 Prototype of pure lag time test system |
结合式(22)可知,对于Δtf=500 μs的情况,如果有99%以上的概率实现±25 μs的测量精度,那么至少要进行Kx以上次数的测量,Kx满足如下关系:
| $ 99\% = 1 - {\left[ {1 - {{\left( {\frac{{50}}{{500}}} \right)}^2}} \right]^{\frac{{{K_{\rm{x}}}\left( {{K_{\rm{x}}} - 1} \right)}}{2}}}. $ | (24) |
由式(24)可得,Kx=31.
采用该系统进行31次测试,有99%以上的概率实现±25 μs的测量精度.
3.1 光纤陀螺A测试结果与测试精度±25 μs的测量精度对光纤陀螺A纯滞后性能的测试已经足够.为了实现更高的测量精度,对光纤陀螺A进行100次纯滞后时间测量(远高于31次).结合式(22)可知,该测试系统实现±5 μs以上测试精度的概率为
| $ {P_{100}}\left| {_{5\mu {\rm{s}}}} \right. = 1 - {\left[ {1 - {{\left( {\frac{{10}}{{500}}} \right)}^2}} \right]^{4950}} = 86.2\% . $ | (25) |
可以认为,100次测量的测试方案有很大概率实现±5 μs以上的测试精度.
为了方便分析,测试结果按照从小到大排序.因为篇幅限制,无法将所有100组测试数据全部列出,10组代表性测试数据如表 1所示.表中,序号1和序号10的数据分别是100组测试数据中的最大值和最小值,其余8组数据在100组测试数据中等间距采样并列出.
| 表 1 光纤陀螺A纯滞后时间测试结果 Table 1 Test results of pure lag time in FOG A |
表 1中,每次纯滞后时间的测试结果为Δtd,若测试结果小于Δtf(即500 μs),则认为此次测试符合式(5)、(6)所表征的情况.将测试时接收到的第一个能够反映角速度冲击的陀螺信号编号n记为n1,此时Δtd为Δtdmin的上限元素,记为Δtdmin-H.若测试结果大于Δtf,则认为此次测试符合式(8)、(9)所表征的情况,将测试时接收到的第一个能够反映角速度冲击的陀螺信号编号n记为n2,此时Δtd-Δtf为Δtdmin的下限元素,记为Δtdmin-L.
分析表 1数据可知,第1~5组的测试结果均小于Δtf(500 μs),符合式(5)、(6)所表征的情况,测试时接收到第一个能够反映角速度冲击的陀螺信号编号为n1,可以得到Δtdmin的上限元素Δtdmin-H;第6~10组的测试结果均大于Δtf,符合式(8)、(9)所表征的情况,测试时接收到第一个能够反映角速度冲击的陀螺信号编号为n2,可以得到Δtdmin的下限元素Δtdmin-L.
针对光纤陀螺A的测试结果,分析测试精度.由式(16)可知,Δtdmin的上限为
| $ \Delta {t_{{\rm{dx}}}} = {\left[ {\left\{ {\Delta {t_{\rm{d}}}\left| {_{n = {n_1}}} \right.} \right\}} \right]_{\min }} = 245.17\mu {\rm{s}}. $ | (26) |
由式(17)可知,Δtdmin的下限为
| $ \Delta {t_{{\rm{dy}}}} = {\left[ {\left\{ {\left( {\Delta {t_{\rm{d}}} - \Delta {t_{\rm{f}}}} \right)\left| {_{n = {n_2}}} \right.} \right\}} \right]_{\max }} = 239.30\mu {\rm{s}}. $ | (27) |
由式(19)、(26)、(27)可知,Δtdmin测量所得值为
| $ \Delta {t_{{\rm{dmin}} - {\rm{res}}}} = \frac{{\Delta {t_{{\rm{dx}}}} + \Delta {t_{{\rm{dy}}}}}}{2} = 242.23\mu {\rm{s}}. $ | (28) |
由式(20)、(26)、(27)可知,测量不确定度为
| $ {\delta _{{\rm{res}}}} = \frac{{\Delta {t_{{\rm{dx}}}} - \Delta {t_{{\rm{dy}}}}}}{2} = 2.96\mu {\rm{s}}. $ | (29) |
待测光纤陀螺的极限纯滞后时间测试结果为
| $ \Delta {t_{{\rm{dmin}} - {\rm{res}}}} \pm {\delta _{{\rm{res}}}} = \left( {242.23 \pm 2.96} \right)\mu {\rm{s}}. $ | (30) |
如果要测量Δtdmin更精确的值,需要对这支光纤陀螺进行更多次的重复测量,进而缩小式(29)所表征的不确定度,得到更高精度的测量结果.
3.2 光纤陀螺B测试结果与测试精度为了验证测试系统的兼容性,对光纤陀螺产品B进行20次纯滞后时间测量.结合1.2节的分析可知,实现±25 μs的测量精度的概率为
| $ {P_{20}}\left| {_{25\mu {\rm{s}}}} \right. = 1 - {\left[ {1 - {{\left( {\frac{{50}}{{500}}} \right)}^2}} \right]^{190}} = 85.2\% . $ | (31) |
可以认为,尽管没有达到31次的测量次数,但是20次测量仍有很大概率实现±25 μs测量精度的要求.10组代表性数据如表 2所示.
| 表 2 光纤陀螺B纯滞后时间测试结果 Table 2 Test results of pure lag time in FOG B |
下面针对光纤陀螺B的测试结果,分析测试精度.由式(16)可知,
| $ \Delta {t_{{\rm{dx}}}} = {\left[ {\left\{ {\Delta {t_{\rm{d}}}\left| {_{n = {n_1}}} \right.} \right\}} \right]_{\min }} = 358.26\mu {\rm{s}}. $ | (32) |
由式(17)可知,
| $ \Delta {t_{{\rm{dy}}}} = {\left[ {\left\{ {\left( {\Delta {t_{\rm{d}}} - \Delta {t_{\rm{f}}}} \right)\left| {_{n = {n_2}}} \right.} \right\}} \right]_{\max }} = 336.84\mu {\rm{s}}. $ | (33) |
由式(19)、(32)、(33)可知,Δtdmin测量所得值为
| $ \Delta {t_{{\rm{dmin}} - {\rm{res}}}} = \frac{{\Delta {t_{{\rm{dx}}}} + \Delta {t_{{\rm{dy}}}}}}{2} = 347.55\mu {\rm{s}}. $ | (34) |
由式(20)、(32)、(33)可知,测量不确定度为
| $ {\delta _{{\rm{res}}}} = \frac{{\Delta {t_{{\rm{dx}}}} - \Delta {t_{{\rm{dy}}}}}}{2} = 10.71\mu {\rm{s}}. $ | (35) |
待测光纤陀螺的极限纯滞后时间测试结果为
| $ \Delta {t_{{\rm{dmin}} - {\rm{res}}}} \pm {\delta _{{\rm{res}}}} = \left( {347.55 \pm 10.71} \right)\mu {\rm{s}}. $ | (36) |
该系统的测量精度和测试数据量相关,数据量越大,得到更高测量精度的概率越高;对于已经完成的测试系统,时间分辨率是确定的.结合1.3节的论述可知,在该样机系统中,经过测试可知时间信息c1c2记满所有15位信息,即c2c1=0xffff(最高位为撞击状态判断位)时所对应的时间长度ΔtFS=3 556.21 μs.由式(23)可得,系统分辨率为
| $ \mu = \frac{{\Delta {t_{{\rm{FS}}}}}}{{{2^{15}} - 1}} = \frac{{3556.21\mu {\rm{s}}}}{{{2^{15}} - 1}} = 108.5\;{\rm{ns}}{\rm{.}} $ | (37) |
理论上来说,如果测试的次数足够多,那么系统能够实现的极限精度等于系统分辨率.结合式(22)可知,如果要有99%以上的概率实现±108.5 ns的测量精度,那么至少要进行Kmax以上次数的测量.Kmax满足如下关系:
| $ 99\% = 1 - {\left[ {1 - {{\left( {\frac{{2 \times 0.1085}}{{500}}} \right)}^2}} \right]^{\frac{{{K_{{\rm{max}}}}\left( {{K_{{\rm{max}}}} - 1} \right)}}{2}}}. $ | (38) |
由式(38)可得,Kmax=6 993.
采用该系统进行6 993次测试,有99%以上的概率实现该系统的极限精度:±108.5 ns.
4 结语在大动态惯导系统的应用背景下,“纯滞后”作为光纤陀螺的一项新的测试指标被提出,本文设计并实现了光纤陀螺纯滞后时间的测试系统.该测试系统可以在保持陀螺原本工作状态的前提下,实现纯滞后时间的精确测试.
当用于测量极限纯滞后时间时,该系统的测量精度和测试数据量相关,数据量越大,得到更高测量精度的概率越高.对于2 kHz频率的光纤陀螺,若测试次数达到了31次,则有99%以上的概率实现±25 μs的测量精度.理论上来说,若测试次数足够多,则系统可以达到的极限精度等于系统的分辨率.
在后续研究中,可以考虑设计方案对角速度冲击时刻进行精确程序控制,以控制极限纯滞后时间的测量精度,提高测试效率.
| [1] |
张桂才. 光纤陀螺原理与技术[M]. 1版. 北京: 国防工业出版社, 2008, 2-3.
|
| [2] |
SANDERS G A, SANDERS S J, STRANDJORD L K. Fiber optic gyro development at Honeywell[C]//SPIE Commercial + Scientific Sensing and Imaging. Baltimore: SPIE, 2016: 985207. http://adsabs.harvard.edu/abs/2016SPIE.9852E..07S
|
| [3] |
MINAKUCHI S, SANADA T, TAKEDA N. Thermal strain in lightweight composite fiber-optic gyroscope for space application[J]. Lightwave Technology, 2015, 33(12): 2658-2662. |
| [4] |
WANG Y, MA L, YU H. Modeling and simulation on temperature performance in fiber optic gyroscope fiber coil of shipborne strapdown inertial navigation system[J]. Proceedings of the SPIE, 2016, 10158: 101580S. DOI:10.1117/12.2246797 |
| [5] |
赵政鑫, 于海成, 李超, 等. 基于等效角振动的光纤陀螺带宽测试方法[J]. 导航与控制, 2016, 15(1): 98-102. ZHAO Zheng-xin, YU Hai-cheng, LI Chao, et al. A bandwidth test method for fiber optic gyroscope based on equivalent angular vibration[J]. Navigation and Control, 2016, 15(1): 98-102. |
| [6] |
薛宁, 刘瑞, 张超, 等. 一种光纤陀螺输出延迟时间的测量装置及其方法: 201110090599. 9[P]. 2011-04-12.
|
| [7] |
陈贤, 周一览, 杨建华, 等. 一种准确评测光纤陀螺输出延迟时间的装置和方法: CN201510612439. 4[P]. 2014-05-11.
|
| [8] |
周一览. 过调制技术在光纤陀螺寻北中的应用[J]. 浙江大学学报:工学版, 2015, 49(8): 1817-1820. ZHOU Yi-lan. Application of over modulation technique in fiber optic gyroscope north-seeking[J]. Journal of Zhejiang University:Engineering Science, 2015, 49(8): 1817-1820. |
| [9] |
YOON Y G, LEE S M, KIM J H. Implementation of a low-cost fiber optic gyroscope for a line-of-sight stabilization system[J]. Journal of Institute of Control, 2015, 21(1): 168-172. |
| [10] |
刘思科, 陈明, 赵丽华. 一种光纤陀螺测试数据采集系统设计[J]. 计算机测量与控制, 2007, 15(6): 972-974. LIU Si-ke, CHEN Ming, ZHAO Li-hua. Design of fiber optical gyroscope test data collecting system[J]. Computer Measurement and Control, 2007, 15(6): 972-974. |
| [11] |
张林, 刘建斌, 郭竞尧, 等. 高速运动零件的碰撞特性实验研究[J]. 火炮发射与控制学报, 2017, 38(1): 79-83. ZHANG Lin, LIU Jian-bin, GUO Jing-yao, et al. Experimental study on the imepact property of high speed moving parts[J]. Journal of Gun Launch and Control, 2017, 38(1): 79-83. |
| [12] |
邹丽新, 孙海燕, 季晶晶, 等. 基于弹性体碰撞时间测定的杨氏模量测量[J]. 自动化仪表, 2009, 30(2): 50-53. ZOU Li-xin, SUN Hai-yan, JI Jing-jing, et al. Measuring young's modulus based on measurement of collision time ofelastomer[J]. Process Automation Instrumentation, 2009, 30(2): 50-53. |
| [13] |
王映宇, 周一览, 杨建华, 等. 一种用于光纤陀螺输出延迟时间自动测量的程控撞击装置: CN201320612757. 7[P]. 2013-09-29.
|
| [14] |
白亮, 严义, 周宏伟. 双核微处理器实时系统的软件架构方法[J]. 单片机与嵌入式系统应用, 2014, 14(8): 13-16. BAI Liang, YAN Yi, ZHOU Hong-wei. Software architecture method of real-time system with dual-core processor[J]. Microcontrollers and Embedded Systems, 2014, 14(8): 13-16. |
| [15] |
HOLZKE W, ADLER J, PAASCH W, et al. Operation and control of a three-level medium-voltage NPC inverter with TI F28M35 microcontroller[C]//PCIM Europe. Nuremberg: [s. n. ], 2015: 1-8. http://ieeexplore.ieee.org/document/7149180/
|
| [16] |
龚丹, 祝宇楠, 田正其, 等. 基于F28M35X的数字化电能表的设计[J]. 计算机测量与控制, 2017, 25(2): 228-230. GONG Dan, ZHU Yu-nan, TIAN Zheng-qi, et al. Design of digital input electricity meter based on F28M35X[J]. Computer Measurement and Control, 2017, 25(2): 228-230. |



