2. 西安电子科技大学 电子装备结构设计教育部重点实验室, 陕西 西安 710071
2. Key Laboratory of Electronic Equipment Structure Design, Ministry of Education, Xidian University, Xi'an 710071, China
构架式可展开索网反射面天线[1-2]的模块化设计理念使其既能满足大口径和高精度的要求,又具有形状构造灵活、设计过程较简捷、装配难度低、生产调试时间短和成本低等优点[3-6].目前,国内外对这种天线的研究处于理论完善阶段,NASA、JAXA、EADS(ESA)及俄罗斯等都先后研制了不同结构形式的构架式可展开天线[7-9].Meguro等[10]提出通过改变调整索的长度来提高天线反射面的精度,研究同步展开桁架结构作为天线支撑结构的特性;Ando等[11]在设计索网过程中考虑枕形误差及索网的重力,衡量桁架变形对索网精度的影响;Chu等[12]建立构架式天线几何模型并结合力密度方法对索网结构进行找形分析,利用单目标遗传优化算法对索网结构中的索单元进行拉力一致性优化,提高了索网结构在展开后的稳定性.
构架式可展开天线的索网反射面由各模块拼接组装而成,各模块的索网面上均铺有用于反射电磁波的、导电性能良好的金属丝网.在天线整体组装前,须分别对各模块进行设计和调试;为了实现单个模块索网张力的平衡,网格边界采用垂跨结构形式.垂跨结构能够改善索网中的张力分布均匀性,提高索网结构的力学性能,但使模块边界索网产生面积缺损,反射面上各模块之间出现缝隙,缝隙的存在会对天线电性能产生不良影响.
对于单个模块,若垂跨比减小,则该模块边界处索网单元的张力会显著增加,使得索网张力均匀性变差,索网结构的力学性能下降;反之,若垂跨比增大,则参与电波反射的反射面面积损失增大,天线的增益下降,副瓣电平、主瓣宽度和零深等其他电性能指标随之变化[13].对于位于确定位置上的某个缝隙,它对天线电性能的影响不仅与缝隙的面积有关,而且与该缝隙离反射面中心的距离有关.缝隙的面积越大、离反射面中心的距离越近,对天线电性能的影响越大.如何在保证索网结构力学性能的同时,削弱缝隙带来的电性能恶化问题,即同时考虑天线力学性能与电性能,合理设计各模块的索网垂跨比,成为构架式索网天线机电集成设计[14]的关键.因上述研究在构架式天线索网结构力学设计时,均未考虑缝隙带来的电性能问题,本文提出基于粒子群算法(PSO)的构架式索网天线机电集成设计方法.
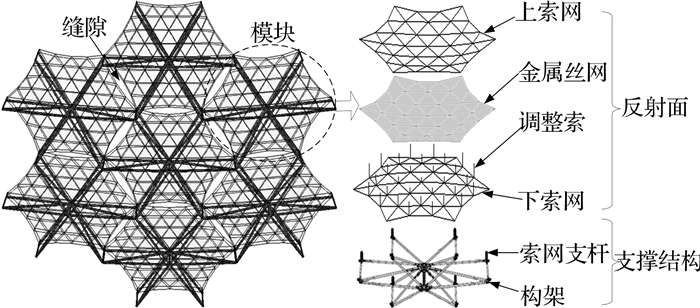
1 构架式天线的组成及网格设计构架式可展开索网反射面天线的结构组成如图 1所示.各模块单元均为六棱柱形式,由反射面和支撑结构两部分组成,且各模块的索网拓扑形式基本相同.天线各模块的上索网节点均位于抛物面上,下索网构成开口向下的抛物面形状.索网通过6个角点安装在索网支杆上,调整索与模块中心杆的方向平行,连接上、下索网.由于天线结构中各模块上的反射面在整个抛物面反射面中的位置各不相同,不同模块上的反射面的几何形状都不尽相同.
|
图 1 构架式可展开天线组成 Fig. 1 Composition of deployable truss antenna |
索网天线的网格结构形式众多,常用的索网结构形式有六边形网格、四边形网格、三角形网格及辐射状网格等[15].三向网格属于三角形网格的一种,这种索网的加工制作较复杂,但结构刚度较好;对于大型索网天线,采用正三角形面片拼合天线表面,可以在使用较少单元数的条件下达到所需的形面精度.本文以三向网格索网结构作为研究对象.
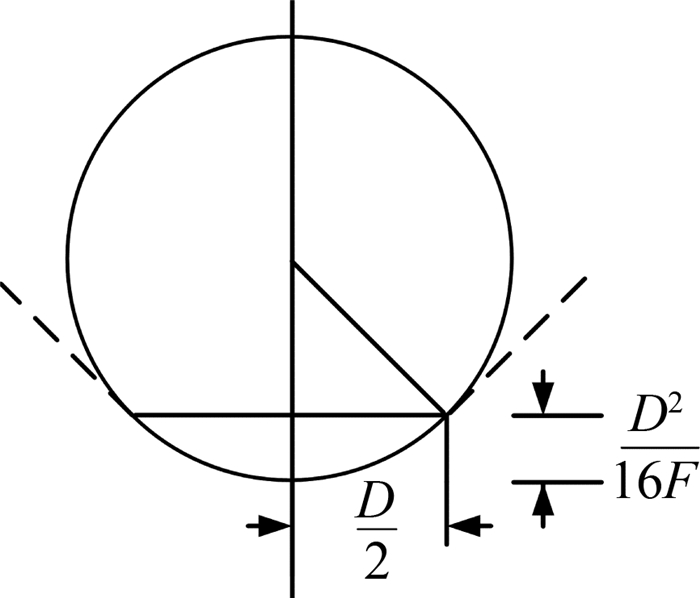
生成反射面网格的常用方法通常是在口径面内划分n环正三角形,然后将这些三角形的顶点投影到抛物面上形成空间三角形面片,从而构成天线的反射面.为了易于网格划分并确定网格三角形边长的上限lmax,特找出与抛物面最接近的半径为R的球面,如图 2所示,两者在抛物面顶点与开口的两点重合,于是有
| $ R = 2F + \frac{{D_{\rm{e}}^2}}{{32F}}. $ | (1) |
|
图 2 球面对抛物面的近似 Fig. 2 Approximation to parabploid of sphere |
反射面均方根误差εrms的容许值可以依据Ruze公式初步取为εrms=λ/ζ,其中λ为天线的工作波长,常数ζ通常取30~60.
三角形边长的最大值为
| $ {l_{\max }} = \sqrt {8\sqrt {15{{\bar \varepsilon }_{{\rm{rms}}}}R} } . $ | (2) |
若抛物线方程为4Fz=x2,则母抛物线的长度为
| $ \begin{array}{l} {S_1} = \int_0^{{D_{\rm{e}}}/2} {\sqrt {1 + {{\left( {\frac{{{\rm{d}}z}}{{{\rm{d}}x}}} \right)}^2}} {\rm{d}}x} = \\ \;\;\;\;\;\;\left[ {\frac{{{D_{\rm{e}}}}}{4}\sqrt {4{F^2} + \frac{{D_{\rm{e}}^2}}{4}} + 2{F^2}\ln \left( {\frac{{{D_{\rm{e}}}}}{2} + \sqrt {4{F^2} + \frac{{D_{\rm{e}}^2}}{4}} } \right)} \right] - \\ \;\;\;\;\;\;F\ln \left( {2F} \right). \end{array} $ | (3) |
三角形网格的分环数可以根据母抛物线长度和最大网格边长求得,即
| $ n = {\rm{CEIL}}\left( {{S_l}/{l_{\max }}} \right). $ | (4) |
式中:CEIL为对变量向正无穷方向取整的函数.
构架式天线的反射面由诸多模块组成,因此,需要根据整体反射面的网格分环数来确定各模块的分环数.设共有N层模块,各模块的索网分段数n′与天线整体索网分段数n之间满足几何关系:
| $ n' = n/\left( {2N - 1} \right). $ | (5) |
各模块边长即正六边形边长L与天线口径De之间满足几何关系:
| $ L = {D_{\rm{e}}}/\left[ {\sqrt 3 \left( {2N - 1} \right)} \right]. $ | (6) |
由此可得,口径面内各模块中三角形的边长为
| $ {l_\Delta } = \frac{L}{{n'}} = \frac{{{D_{\rm{e}}}}}{{\sqrt 3 n}}. $ | (7) |
根据lΔ在口径面内划分三角形网格,所得的索网可以满足设计精度.
2 天线电性能分析从面积损失的角度来考虑缝隙对天线增益的影响.由于离反射面中心距离不同的缝隙对天线电性能的影响不同,为反映这个差别,对反射面上的所有缝隙进行面积加权.设构架式天线中第i个缝隙在口径面上的投影面积为Si,S为整个天线反射面的有效面积;口径面上的照度因子为Q=0.7+0.3×(1-rj2/R02)[16],其中rj为反射面上某点j到天线反射面焦轴的距离,R0为口径面半径,则反射面上缝隙引入的天线效率损失比可以表示为
| $ {\eta _1} = \frac{{\sum\limits_{i = 1}^V {\int_{{S_i}} {Q{\rm{d}}{S_i}} } }}{{\int_S {Q{\rm{d}}S} }}. $ | (8) |
式中:∫SiQdSi与∫SQdS分别为照度因子在第i个缝隙的投影面积Si与整个反射面投影面积S上的积分,V为缝隙的总数.
将式(8)代入天线的增益公式:
| $ G = D\left( {1 - {\eta _1}} \right), $ | (9) |
可以分析缝隙对天线增益的影响.其中,D=(4πr2/(ηPrad))E*E为无缝隙反射面天线的方向系数;r为远场观察点到坐标中心的距离;η=120π为自由空间波阻抗;Prad为馈源的辐射功率;E为天线的远区辐射电场,可以利用物理光学法通过积分计算得到各个面片的远区辐射电场后,在远场对所有面片的辐射电场进行叠加得到.
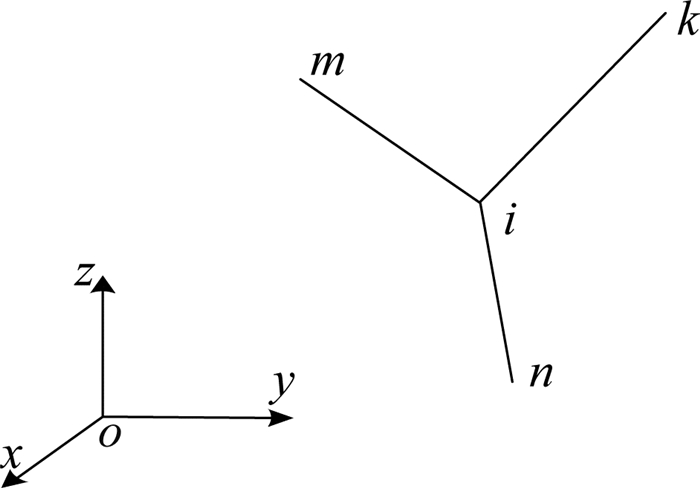
3 力学分析通过求解天线的静力平衡方程,来获得索段拉力分布,评估垂跨比对天线力学性能的影响.如图 3所示,空间索网结构平衡构型上的某个节点i在x、y、z方向上的力平衡方程为
| $ \sum {\frac{{{t_{ij}}}}{{{l_{ij}}}}\left( {{x_i} - {x_j}} \right)} = 0;j = m,n,k. $ | (10) |
| $ \sum {\frac{{{t_{ij}}}}{{{l_{ij}}}}\left( {{y_i} - {y_j}} \right)} = 0;j = m,n,k. $ | (11) |
| $ \sum {\frac{{{t_{ij}}}}{{{l_{ij}}}}\left( {{z_i} - {z_j}} \right)} = 0;j = m,n,k. $ | (12) |
|
图 3 索网结构中节点受力示意图 Fig. 3 Force of nodes on cable-net |
式中:tij为索力,lij为索段单元ij的长度,xi、yi、zi、xj、yj、zj为节点坐标值.
对索网中的每一个非约束节点列写式(10)~(12)的力平衡方程,并集成为矩阵形式,可得索网平衡方程:
| $ {\mathit{\boldsymbol{B}}_{3\left( {C - U} \right) \times E}}{\mathit{\boldsymbol{T}}_{E \times 1}} = {{\bf{0}}_{3\left( {C - U} \right) \times 1}}. $ | (13) |
式中:B3(C-U)×E为索网的平衡矩阵,索网第i个节点第j个单元在B中对应的子阵为Bi×j= [(xj1-xi)/lj, (yj1-yi)/lj, (zj1-zi)/lj]T,xi、yi、zi为节点i的坐标值,xj1、yj1、zj1为单元j上与节点i相连的节点1的坐标值,若无相连节点则记为0;TE×1为索段的预拉力列向量,C为索网节点总数,U为索网约束节点总数,E为索段总数.
通过求解方程(13)可得索网部分的张力,求解结果通过优化得到,将在后面介绍,这里不再赘述.
4 优化数学模型反射面上的缝隙大小主要由各模块索网的垂跨比决定.由于构架式天线各模块相对独立,各模块的垂跨比应当相互独立,将每个模块索网垂跨比作为设计变量,记为
| $ \mathit{\boldsymbol{\rho }} = {\left[ {{\rho _1},{\rho _2}, \cdots ,{\rho _{{N_{{\rm{sum}}}}}}} \right]^{\rm{T}}}. $ | (14) |
式中:ρi为第i个模块的垂跨比,Nsum为模块总数.
4.1 优化目标函数索网天线的设计须综合考虑电性能及力学性能的好坏,电性能的主要评价指标是天线增益,索网力学性能的好坏取决于索网最大最小张力比.由于星载可展开索网天线在太空中会受到复杂的太空环境影响,主要表现为空间不断变化的热载荷作用,索网的张力分布均匀情况将直接影响天线索网的稳定性.机电集成优化设计模型中的优化目标之一为增益最大化,可以等效为增益损失最小;另一优化目标是索网最大最小张力比最小.
| $ \left. \begin{array}{l} {f_1}\left( \mathit{\boldsymbol{\rho }} \right) = \Delta G = D\frac{{\sum\limits_{i = 1}^V {\int\limits_{{S_i}} {Q{\rm{d}}{S_i}} } }}{{\int\limits_S {Q{\rm{d}}S} }},\\ {f_2}\left( \mathit{\boldsymbol{\rho }} \right) = {\gamma _{\max }} = \sqrt {\sum\limits_{i = 1}^{{N_{{\rm{sum}}}}} {{{\left( {\frac{{{T_{i\max }}}}{{{T_{i\min }}}}} \right)}^2}/{N_{{\rm{sum}}}}} } . \end{array} \right\} $ | (15) |
式中:f1为实际反射面相对理想反射面的增益损失;f2为各模块索网的最大张力与最小张力比值的算术平均值.
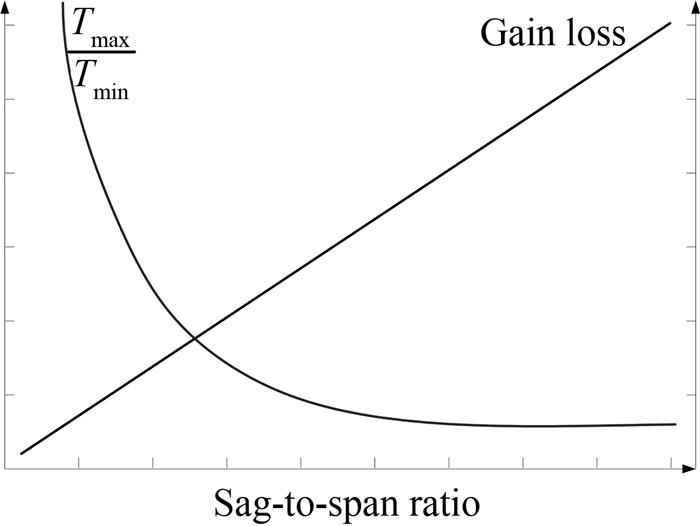
构架式索网天线机电集成设计问题为多目标优化问题,可以采用加权求和法可以进行简单、高效地求解,其中权系数的选取是求取有效解的关键.获得设计目标之间的支配关系,对多个目标的取舍与折中具有重要意义.如图 4所示为一个模块中各目标与设计变量的关系,可见当其中任何一个目标达到期望值时,另一个目标会被降低.对于多个模块来说,可以得到多组Pareto解.
|
图 4 各目标与自变量的关系[13] Fig. 4 Relationship between each objective and variables |
为了避免各子目标函数值存在数量级上的较大差别,导致权系数的作用失效,对目标函数分别进行归一化处理.设ΔG与γ为结构的特征量,引入
| $ {f_1}\left( \mathit{\boldsymbol{\rho }} \right) = \frac{{\Delta G}}{{\Delta \bar G}} = \frac{{\sum\limits_{i = 1}^V {\int\limits_{{S_i}} {Q{\rm{d}}{S_i}} } }}{{\sum\limits_{i = 1}^V {\int\limits_{{S_{i\max }}} {Q{\rm{d}}{S_{i\max }}} } }}, $ | (16) |
| $ {f_2}\left( \mathit{\boldsymbol{\rho }} \right) = \frac{{{\gamma _{\max }}}}{{2\bar \gamma }} = \frac{{\sqrt {\sum\limits_{i = 1}^{{N_{{\rm{sum}}}}} {{{\left( {\frac{{{T_{i\max }}}}{{{T_{i\min }}}}} \right)}^2}/{N_{{\rm{sum}}}}} } }}{{\sqrt {\sum\limits_{i = 1}^{{N_{{\rm{sum}}}}} {{{\left( {\frac{{{T_{i\max }}\left( {{\rho _{\min }}} \right)}}{{{T_{i\min }}\left( {{\rho _{\min }}} \right)}}} \right)}^2}/{N_{{\rm{sum}}}}} } }}. $ | (17) |
当构架式天线的模块间缝隙面积最大时,反射面相对理想反射面的面积损失最大,此时的天线增益可以作为ΔG;另外,可以取所有模块的垂跨比为优化范围下限值时计算得到的张力比为γ.
对每个目标函数乘以相应的权重,将多目标整合为单目标,因此优化的最终目标函数为
| $ \begin{array}{*{20}{c}} {f\left( \mathit{\boldsymbol{\rho }} \right) = \sum\limits_{j = 1}^2 {{\omega _j}{f_j}\left( \mathit{\boldsymbol{\rho }} \right)} = {\omega _1}\frac{{\sum\limits_{i = 1}^V {\int\limits_{{S_i}} {Q{\rm{d}}{S_i}} } }}{{\int\limits_S {Q{\rm{d}}S} }} + }\\ {{\omega _2}\frac{{\sqrt {\sum\limits_{i = 1}^{{N_{{\rm{sum}}}}} {{{\left( {\frac{{{T_{i\max }}}}{{{T_{i\min }}}}} \right)}^2}/{N_{{\rm{sum}}}}} } }}{{\sqrt {\sum\limits_{i = 1}^{{N_{{\rm{sum}}}}} {{{\left( {\frac{{{T_{i\max }}\left( {{\rho _{\min }}} \right)}}{{{T_{i\min }}\left( {{\rho _{\min }}} \right)}}} \right)}^2}/{N_{{\rm{sum}}}}} } }}.} \end{array} $ | (18) |
式中:ω1、ω2分别为f1与f2的权数(加权因子),且满足归一性条件与非负性条件,即∑j=12ωj=1,ωj≥0(j=1, 2).权数表示相应目标函数在优化模型中的重要程度,目标越重要,权数越大.
4.2 约束函数构架式索网天线机电集成设计问题中的约束条件如下. 1)索网中索段的张力平衡条件,为线性等式约束条件;2)索网中索段的预张力要在设计要求的范围内变化,为线性不等式约束;3)设计变量值的上、下限约束.约束条件的数学表述如下:
| $ {\rm{s}}.\;{\rm{t}}.\;\;\;\;g\left( \mathit{\boldsymbol{\rho }} \right) = {\mathit{\boldsymbol{B}}_{3\left( {C - U} \right) \times E}}{\mathit{\boldsymbol{T}}_{E \times 1}} = {{\bf{0}}_{3\left( {C - U} \right) \times 1}}. $ | (19) |
| $ {h_e}\left( \mathit{\boldsymbol{\rho }} \right) = \frac{{{T_e}\left( \mathit{\boldsymbol{\rho }} \right)}}{{{A_e}}} - {{\bar \sigma }_e} \le 0;e = 1,2, \cdots ,m. $ | (20) |
| $ {h_e}\left( \mathit{\boldsymbol{\rho }} \right) = - \frac{{{T_e}\left( \mathit{\boldsymbol{\rho }} \right)}}{{{A_e}}} + {{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\sigma } }_{m + e}} \leqslant 0;e = 1,2, \cdots ,m. $ | (21) |
| $ {q_i}\left( {{\rho _i},{\rho _{i\min }},{\rho _{i\max }}} \right) \le 0;i = 1,2, \cdots ,{N_{{\rm{sum}}}}. $ | (22) |
式中:Te(ρ)为第e个索单元的张力;Ae为第e个索单元的截面积;σe、σe为第e个索单元的应力上限值及下限值;qi(ρi, ρimin, ρimax)≤0为几何条件式,具体形式为ρimin≤ρi≤ρimax.
5 问题的求解对于4章给出的优化数学模型,采用粒子群算法[17](particle swarm optimization,PSO)进行求解.粒子群算法是一种新兴的智能优化技术,属于进化算法的一种,是群体智能中一个新的分支,它是对简单社会系统的模拟.该算法本质上是一种随机搜索算法,它从随机解出发,通过迭代寻找最优解,并通过适应度来评价解的品质.PSO比遗传算法规则更简单,它没有遗传算法的“交叉”和“变异”操作,通过追随当前搜索到的最优值来寻找全局最优,能够以较大的概率收敛于全局最优解.实践证明,它适合在动态、多目标优化环境中寻优,与传统的优化算法相比,具有更快的计算速度和更好的全局搜索能力.该算法以实现容易、精度高、收敛快等优点引起了学术界的重视,并且在解决实际问题时展示了优越性.
由于粒子群算法不能直接求解有约束的优化问题,在求解过程中需要将约束问题转化为无约束问题进行求解.
先将优化模型中的等式约束转化为不等式约束形式:
| $ {h_e}\left( \mathit{\boldsymbol{\rho }} \right) = \left| {g\left( \mathit{\boldsymbol{\rho }} \right)} \right| - \varepsilon \le 0;e = 2m + 1. $ | (23) |
式中:ε为允许公差(一个非常小的正值).当|g(ρ)|-ε≤0时,解ρ被认为是可行的.
构造适应度函数为
| $ F\left( \mathit{\boldsymbol{\rho }} \right) = \left\{ \begin{array}{l} f\left( \mathit{\boldsymbol{\rho }} \right),{h_e}\left( \mathit{\boldsymbol{\rho }} \right) \le 0;e = 1,2, \cdots ,2m + 1;\\ {f_{\max }}\left( \mathit{\boldsymbol{\rho }} \right) + \sum\limits_{i = 1}^{2m + 1} {\left( {h_e^f\left( \mathit{\boldsymbol{\rho }} \right)} \right)} ,其他. \end{array} \right. $ | (24) |
式中:fmax(ρ)为群体中最差可行个体的适应度;
| $ h_e^f\left( \mathit{\boldsymbol{\rho }} \right)\left\{ \begin{array}{l} {h_e}\left( \mathit{\boldsymbol{\rho }} \right),{h_e}\left( \mathit{\boldsymbol{\rho }} \right) > 0;\\ 0,\;\;\;\;{h_e}\left( \mathit{\boldsymbol{\rho }} \right) \le 0. \end{array} \right. $ |
于是,得到新的优化模型,记为
| $ \left. \begin{array}{l} {\rm{Find}}\;\;\;\mathit{\boldsymbol{\rho }} = {\left[ {{\rho _1},{\rho _2}, \cdots ,{\rho _{{{\rm{N}}_{{\rm{sum}}}}}}} \right]^{\rm{T}}}.\\ {\rm{Min}}\;\;\;\;F\left( \mathit{\boldsymbol{\rho }} \right) = \left\{ \begin{array}{l} f\left( \mathit{\boldsymbol{\rho }} \right),{h_e}\left( \mathit{\boldsymbol{\rho }} \right) \le 0;e = 1,2, \cdots ,2m + 1;\\ {f_{\max }}\left( \mathit{\boldsymbol{\rho }} \right) + \sum\limits_{i = 1}^{2m + 1} {\left( {h_e^f\left( \mathit{\boldsymbol{\rho }} \right)} \right)} ,其他. \end{array} \right.\\ {q_i}\left( {{\rho _i},{\rho _{i\min }},{\rho _{i\max }}} \right) \le 0,i = 1,2, \cdots ,{N_{{\rm{sum}}}}. \end{array} \right\} $ | (25) |
构架式索网天线的机电集成设计步骤可以表示如下.
1) 给出多目标权数ωi及设计变量的范围值ρimin、ρimax.
2) 设置PSO的控制参数.
3) 进行天线的电性能及力学性能分析.
4) 收敛判断.若连续5次迭代中种群最优值的相对误差小于设置值(本文中取为1%)且满足索网张力约束,或者达到最高迭代次数,则迭代停止;否则,转步骤5).
5) 更新结构模型,转步骤3).
6 算例分析某构架式索网天线的电口径De=108.3 λ,焦距F=86.4 λ,工作频率为f=2.5 GHz,下网面焦距为2F,模块层数为2层,模块索网分段数为3,天线上网面节点数为259,天线索段总数是1 477,其中调整索数为217.从中间模块逆时针往外的模块垂跨比依次为设计变量,由于电性能目标更重要,取权重因子ω1=0.6,ω2=0.4.PSO的一般控制参数分别如下:最大迭代次数为300;群体大小为24;算法的加速度参数c1、c2分别为2、2;随机因子r1、r2分别为0.9、0.4;参数的每步迭代最大允许值为MaxV,取变化范围的20%.
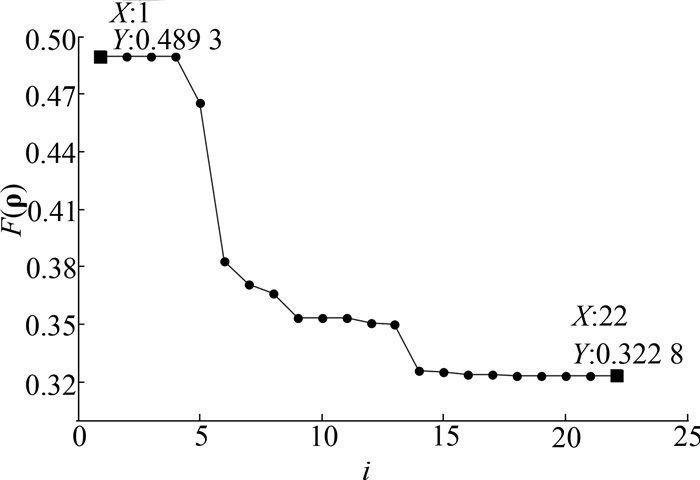
在优化过程中,目标函数的变化情况如图 5所示.图中,i为优化迭代次数.从图 5可以看出,随着优化迭代次数的增加,目标函数值不断减小.在22次迭代后,目标函数值的相对变化量较小,满足收敛条件.最终结果中的目标函数值为0.322 8,增益损失由1.405 8 dB下降至0.835 7 dB,张力比由5.688 4变为8.915 3.
|
图 5 目标函数迭代次数曲线 Fig. 5 Curve of target function and iteration number |
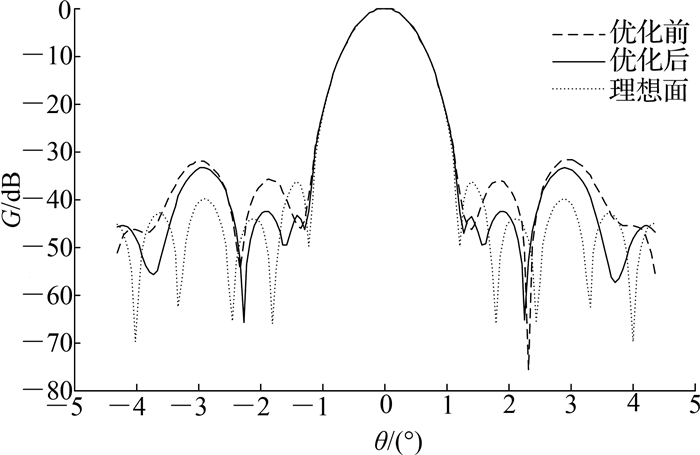
为了更直观地比较优化前、后天线远场方向图的零深及副瓣等电性能指标,将方向图进行归零处理后,如图 6所示.图中,G为天线增益.归零前的天线增益列于表 1.
|
图 6 天线远场方向图 Fig. 6 Far-field pattern of antenna |
| 表 1 优化前、后的天线电性能 Table 1 Electromagnetic performance before and after optimization |
由表 1可见,不同缝隙下远场方向图的半功率波瓣宽度2θ0.5相同;相比于优化前,优化后的方向图主瓣零深SLLmax下沉,增益增大约0.6 dB.结合图 6可知,优化后的方向图第一副瓣电平明显降低,天线电性能总体上优于优化前的结果.
优化前、后各参数值的对比如表 2所示.
| 表 2 优化前、后的天线参数 Table 2 Antenna parameters before and after optimization |
分析表 2中设计变量的优化值与初始值可以发现,优化后的天线结构中,反射面中心模块相较于其他模块其垂跨比明显下降,表明处于反射面中心部分的缝隙面积降至最低,这是因为中心区域的反射面对电性能的贡献较大,中心区域反射面面积的损失越小,电性能的损失越少;所有模块的垂跨比在保证天线整体索网力学性能的条件下,不同程度上都有下降,极大程度地降低了缝隙对天线电性能的影响.考虑到不同发射任务对天线增益、索网力学性能的要求不同,在天线的初始设计阶段,可以对两种性能进行平衡.决策者可以通过调整权重因子ω1及ω2来指导增益及张力比的重要程度,可以对PSO算法设置合适的参数,如种子数、c1、c2,或者增大终止次数来获取尽可能好的优化结果.
7 结论(1) 建立考虑缝隙影响的构架式天线索网机电集成设计优化模型.针对其中目标函数与设计变量的隐式函数关系,采用粒子群算法对以上机电集成设计优化模型进行求解.
(2) 算例的计算过程表明,粒子群算法适合于该机电集成设计优化模型的求解,具有要求简单、易实现的特点,收敛效果较好.
(3) 算例结果表明,所提的天线结构设计方法有效、可行,所设计的索网垂跨比不仅能够保证索网的力学性能在许可范围内,而且能够极大程度地降低反射面缝隙对天线电性能的影响.
| [1] |
EBISUI T, ISO A, ORIKASA T, et al. Characteristics of large deployable mesh reflector antennas for future mobile communications satellites[C]//14th International Communication Satellite Systems Conference and Exhibit. Washington: AIAA, 1992: 1586-1592. https://www.researchgate.net/publication/252329481_Characteristics_of_large_deployable_mesh_reflector_antennas_for_future_mobile_communications_satellites?ev=auth_pub
|
| [2] |
OZAWA S, TSUJIHATA A. Lightweight design of 30m class large deployable reflector for communication satellites[C]//52nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. Colorado: AIAA, 2011: 1829. 1-7. http://www.researchgate.net/publication/271375405_lightweight_design_of_30m_class_large_deployable_reflector_for_communication_satellites
|
| [3] |
OZAWA S, SHINTATE K, TSUJIHATA A. 30m class lightweight large deployable reflector[C]//Proceedings of the 5th European Conference on Antennas and Propagation (EUCAP). Rome: IEEE, 2011: 3354-3358. http://www.researchgate.net/publication/241183149_30m_class_lightweight_large_deployable_reflector
|
| [4] |
LI B, KONG W G, QI X Z. Modeling and design on modular deployable antenna[M]//DING X L, KONG X W, DAI J S. Advances in Reconfigurable Mechanisms and Robots Ⅱ. Switzerland: Springer, 2016: 1037-1048.
|
| [5] |
OZAWA S, SHINTATE K, TSUJIHATA A. Trifold deployable reflector for communication satellites[C]//29th AIAA International Communications Satellite Systems Conference. Nara: AIAA, 2011: 8022. 1-7. http://www.researchgate.net/publication/268579933_Tri-Fold_Deployable_Reflector_for_Communication_Satellites
|
| [6] |
MEGURO A, SHINTATE K, USUI M, et al. In-orbit deployment characteristics of large deployable antenna reflector onboard engineering test satellite Ⅷ[J]. Acta Astronautica, 2009, 65(9-10): 1306-1316. |
| [7] |
HENRIKSEN T K, MANGENOT C. Large deployable antennas[J]. CEAS Space Journal, 2013, 5(3-4): 87-88. DOI:10.1007/s12567-013-0055-4 |
| [8] |
SANTIAGO-PROWALD J, BAIER H. Advances in deployable structures and surfaces for large apertures in space[J]. CEAS Space Journal, 2013, 5(3-4): 89-115. |
| [9] |
PUIG L, BARTON A, RANDO N. A review on large deployable structures for astrophysics missions[J]. Acta Astronautica, 2010, 67(1-2): 12-26. DOI:10.1016/j.actaastro.2010.02.021 |
| [10] |
MEGURO A, MITSUGI J, ANDO K. A modular cable-mesh deployable structure for large-scale satellite communication antennas[J]. Electronics and Communications in Japan, 2010, 77(8): 90-100. |
| [11] |
ANDO K, MITSUGI J, SENBOKUYA Y. Analyses of cable-membrane structure combined with deployable truss[J]. Computers and Structures, 2000, 74(1): 21-39. |
| [12] |
CHU Z R, DEND Z Q, QI X Z, et al. Modeling and analysis of a large deployable antenna structure[J]. Acta Astronautica, 2014, 95: 51-60. |
| [13] |
马亚静, 张树新, 曹鸿钧, 等. 垂跨比对张拉天线力学、电磁特性影响[J]. 空间电子技术, 2014, 11(2): 36-41. MA Ya-jing, ZHANG Shu-xin, CAO Hong-jun, et al. Effects of sag-to-span ratio on mechanical and electromagnetic performance of tensegrity reflectors[J]. Space Electronic Technology, 2014, 11(2): 36-41. |
| [14] |
ZHANG S X, DU J L, DUAN B Y, et al. Integrated structural electromagnetic shape control of cable mesh reflector antennas[J]. AIAA Journal, 2015, 53(5): 1395-1399. DOI:10.2514/1.J053726 |
| [15] |
MORTEROLLE S, MAURIN B, QUIRANT J, et al. Numerical form-finding of geotensoid tension truss for mesh reflector[J]. Acta Astronautica, 2012, 76: 154-163. |
| [16] |
YANG D W, LIU J S, ZHANG Y Q, et al. Optimal surface profile design of deployable mesh reflectors via a force density strategy[J]. Acta Astronautica, 2017, 130: 137-146. DOI:10.1016/j.actaastro.2016.10.008 |
| [17] |
TIMAC G, BRAUT S, ZIGULI R. Comparative analysis of PSO algorithms for PID controller tuning[J]. Chinese Journal of Mechanical Engineering, 2014, 27(5): 928-936. DOI:10.3901/CJME.2014.0527.302 |



