2. 天津生态城能源投资建设有限公司, 天津 300480
2. Energy Investment and Construction Limited Company, Tianjin Eco-city, Tianjin 300480, China
太阳能由于具有分布广泛、清洁环保等优点,已经成为最重要的可再生能源之一.目前,有两种技术能够实现太阳能直接发电,分别为太阳能光伏发电及太阳能温差发电[1].作为一种成熟可靠的技术,太阳能光伏发电已经得到广泛应用.与光伏发电不同,太阳能温差发电首先将太阳能转化为热能,然后依靠温差发电器将热能转化为电能.温差发电器是利用热电效应将热能直接转化为电能的能量转化装置,无化学反应且无机械移动部件,因而具有无噪声、无污染、无磨损且小巧轻便、使用寿命长等优点,在余热回收中已得到广泛应用[2].
将温差发电技术应用到太阳能领域,最早可以追溯到1922年,Coblentz利用温差发电技术测量其他星球的红外辐射[3].此后,Telkes研制了太阳能温差发电机[4],发电效率达到3.35%,正式揭开了太阳能温差发电的序幕.温差发电的性能主要取决于冷热端温差及材料的性质,提高材料的优值系数以及增大冷热端温差均能够提高温差发电器的发电性能.对于太阳能温差发电装置来说,合理的聚焦倍率以及高效的冷却方式直接影响系统的发电性能[5-6].Chen[7]计算表明,使用Bi2Te3材料的太阳能温差发电器在小聚光比条件下可以达到约5%的发电效率.Amatya等[3]搭建了太阳能温差发电系统,在66倍聚光比条件下,发电效率达到3%.Li等[8]设计了一台聚光式太阳能热电发电器,采用数值模拟的方法对该发电器的性能进行研究;结果显示,当采用Bi2Te3、方钴矿和LAST合金作为热电材料时,热电发电器的效率分别为9.8%、13.5%和14.1%.Lauryn等[9]指出当入射热流为100 kW/m2,热端温度为1 000 ℃时,太阳能温差发电器可以实现15.9%的发电效率,使其可以与聚焦太阳能发电站相竞争.Li等[10]分析聚焦倍率、环境温度与风速对太阳能温差发电系统的影响.此外,针对冷却系统,Fernanda等[11]指出太阳能温差发电器的输出功率与冷端散热情况直接相关,输出功率在较低风速下急剧升高,在高风速下将收敛于一个稳定值.Chen等[12]分析热沉对太阳能温差发电系统的影响,指出采用水冷的方式可以获得更大的输出功率.
综上所述,目前关于太阳能温差发电系统的研究,更多地集中于温差发电器的发电性能,未考虑冷却系统自身消耗的功率,因此所得的结果不能反映太阳能温差发电系统的实际输出性能.本文在考虑冷却系统功耗的基础上,建立太阳能温差发电系统的数值模型.以净输出功率、净发电效率为指标,分析聚焦倍率及冷却水流量对太阳能温差发电系统的影响,获得了最优的运行参数,所得结果对于太阳能温差发电装置的优化设计具有一定的指导意义.
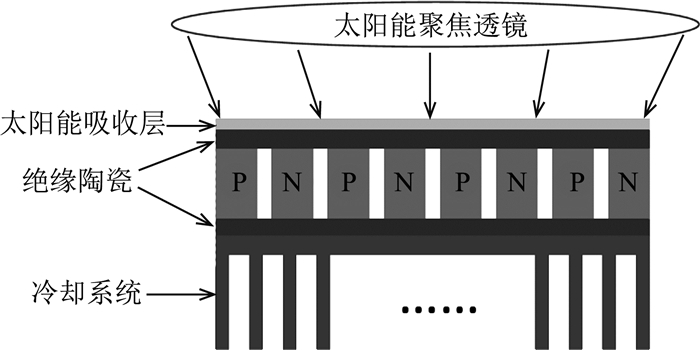
1 数值模型 1.1 太阳能温差发电系统数学模型太阳能温差发电系统如图 1所示,主要包括太阳能聚光系统、温差发电器及冷端散热系统.太阳能通过聚光系统后,被温差发电器表面的太阳能吸收层吸收转化为热能,从而形成温差发电器的热端;热能进入温差发电器,一部分转化为电能输出,剩余能量被冷端热沉吸收.为了简化模型,该模型作如下假设:
|
1)整个系统处于稳态;2)太阳能吸收层面积、陶瓷板横截面积及热沉底面积相同;3)热量传递仅在一维方向,忽略横向导热及温差发电器侧面的热损失;4)忽略接触热阻、接触电阻;5)忽略汤姆逊效应. 图 1 太阳能温差发电系统模型 Fig. 1 Solar thermoelectric generation system model |
在温差发电器热端,吸收来自太阳能聚光系统的太阳能Qin,由于吸热后表面温度升高,与外界环境存在对流换热Qc以及辐射换热Qr,剩余热量Qh将通过热端的陶瓷板到达PN节热端.太阳能温差发电器热端的能量方程可以表示为
| $ {Q_{{\rm{in}}}} = {Q_{\rm{c}}} + {Q_{\rm{r}}} + {Q_{\rm{h}}}. $ | (1) |
式(1)中的各部分能量可以根据下式计算:
| $ \begin{array}{l} GC\alpha S = {h_{\rm{a}}}S\left( {{T_{{\rm{si}},{\rm{h}}}} - {T_{\rm{a}}}} \right) + \varepsilon \sigma S\left( {T_{{\rm{si}},{\rm{h}}}^4 - T_{\rm{a}}^4} \right) + \\ \;\;\;\;\;\;\;\;\frac{{{\lambda _{{\rm{si}}}}\left( {{T_{{\rm{si}},{\rm{h}}}} - {T_{\rm{h}}}} \right)}}{{{\delta _{{\rm{si}}}}}}S. \end{array} $ | (2) |
式中:G为太阳能辐射强度,取1 000 W/m2;C为太阳能聚焦倍率;Tsi, h为温差发电器热端温度;Ta为环境温度,取293 K;S为模型的横截面积,取50 mm×50 mm;α为吸收层的吸收率,取0.9;ha为吸收层表面的换热系数;ε为吸收层的发射率,取0.08;σ为斯忒藩-玻耳兹曼常数;λsi为温差发电器陶瓷板的导热系数,取130 W/(m·K);δsi为陶瓷板的厚度,取0.25 mm.
温差发电器热端对流换热系数与环境的风速相关,可以由下式[13]求得:
| $ {h_{\rm{a}}} = 2.8 + 3{V_{\rm{a}}}. $ | (3) |
式中:Va为空气风速,取2 m/s.
在PN节的冷热端能量方程可以表示为
| $ {Q_{\rm{h}}} = {s_{{\rm{pn}}}}{T_{\rm{h}}}I + {K_{{\rm{pn}}}}\left( {{T_{\rm{h}}} - {T_{\rm{l}}}} \right) - 0.5{I^2}{R_{{\rm{pn}}}}, $ | (4) |
| $ {Q_{\rm{l}}} = {s_{{\rm{pn}}}}{T_{\rm{l}}}I + {K_{{\rm{pn}}}}\left( {{T_{\rm{h}}} - {T_{\rm{l}}}} \right) + 0.5{I^2}{R_{{\rm{pn}}}}. $ | (5) |
式中:spn为PN对的塞贝克系数;Th、T1分别为PN节热端与冷端温度;Kpn为导热参数;Rpn为PN节的电阻.根据文献[14]可知,所选的PN节参数如表 1所示.
| 表 1 PN节参数 Table 1 Parameters of PN junction |
电路中的电流I为
| $ I = \frac{{{s_{{\rm{pn}}}}\left( {{T_{\rm{h}}} - {T_{\rm{l}}}} \right)}}{{{R_{{\rm{pn}}}} + {R_{\rm{L}}}}}. $ | (6) |
式中:RL为外接电阻.
温差发电器的输出功率为
| $ P = {I^2}{R_{\rm{L}}}. $ | (7) |
PN节冷端的热量Q1最终进入冷却系统,可由下式计算:
| $ {Q_{\rm{l}}} = \frac{{{\lambda _{{\rm{si}}}}\left( {{T_{\rm{l}}} - {T_{{\rm{si,l}}}}} \right)}}{{{\delta _{{\rm{si}}}}}}S = {h_{\rm{c}}}\left( {{T_{{\rm{si,l}}}} - {T_{\rm{c}}}} \right)S. $ | (8) |
式中:Tsi, 1为温差发电器的冷端温度,Tc为冷却介质的温度,hc为冷却系统的换热系数.
对于翅片冷却系统,hc可由下式获得:
| $ {h_{\rm{c}}} = {h_{\rm{f}}}\frac{{2nH + W}}{W}. $ | (9) |
式中:n为翅片数量,取10;H为翅片高度,取50 mm;W为散热器的宽度,取50 mm;hf为翅片表面的换热系数,可以表示[15]为
| $ {h_{\rm{f}}} = \frac{{{\lambda _{\rm{c}}}Nu}}{L}. $ | (10) |
其中,λc为冷却介质的导热系数;L为散热器的长度,取50 mm;
| $ Nu = 0.664\mathit{R}{\mathit{e}^{0.5}}\mathit{P}{\mathit{r}^{1/3}}, $ | (11) |
Pr为冷却介质的普朗特数, Re为冷却介质的雷诺数,
| $ \mathit{Re} = \frac{{{V_{\rm{c}}}L}}{{{\mu _{\rm{c}}}}}, $ | (12) |
| $ {V_{\rm{c}}} = \frac{{{q_{{V_{\rm{c}}}}}}}{{nDH}}. $ | (13) |
D为翅片间距,取3 mm;Vc为冷却介质的流速;qVc为冷却介质的体积流量;μc为冷却介质的动力黏度.本文选取水作为冷却介质,冷却介质的温度取293 K.
沿肋片的压降为
| $ \Delta p = \frac{{12{\mu _{\rm{c}}}{V_{\rm{c}}}L}}{{{D^2}}}. $ | (14) |
冷却系统的功耗为
| $ {P_{\rm{c}}} = \frac{{{q_{{V_{\rm{c}}}}}\Delta p}}{{{\rho _{\rm{c}}}}}. $ | (15) |
对于整个系统来说,系统的净输出功率为
| $ {P_{{\rm{net}}}} = P - {P_{\rm{c}}}, $ | (16) |
则系统的净发电效率为
| $ {\eta _{{\rm{net}}}} = \frac{{{P_{{\rm{net}}}}}}{{GCS}}. $ | (17) |
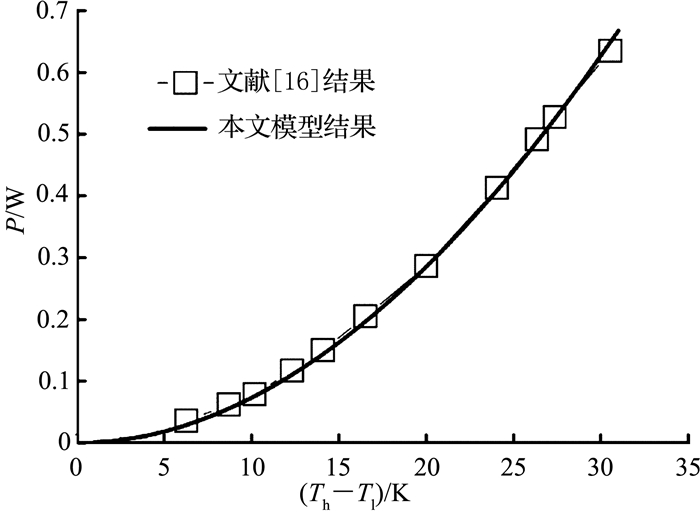
为了验证模型的正确性,参考文献[16]的实验条件,利用上述模型对温差发电器进行模拟计算.文献[16]所用的温差发电模块由199对PN节构成,每个PN节截面积为4×10-6 m2,高为6.4×10-4 m,P型材料与N型材料的塞贝克系数分别为2.15×10-4 V/K、-2.12×10-4 V/K,热导率分别为1.456、1.373 W/(m·K),电阻率均为1.04×10-5 Ω·m.温差发电片热端依靠加热器加热,冷端利用冷却水冷却,笔者通过实验获得不同温差条件下温差发电片的输出功率.本文模型的计算结果与文献[16]的实验结果对比如图 2所示.可以看出,利用该模型能够较好地预测实验结果,两者相差在±10%以内,说明该模型较可靠.
|
图 2 模型计算结果与实验结果对比图 Fig. 2 Comparison between calculated and experimental results |
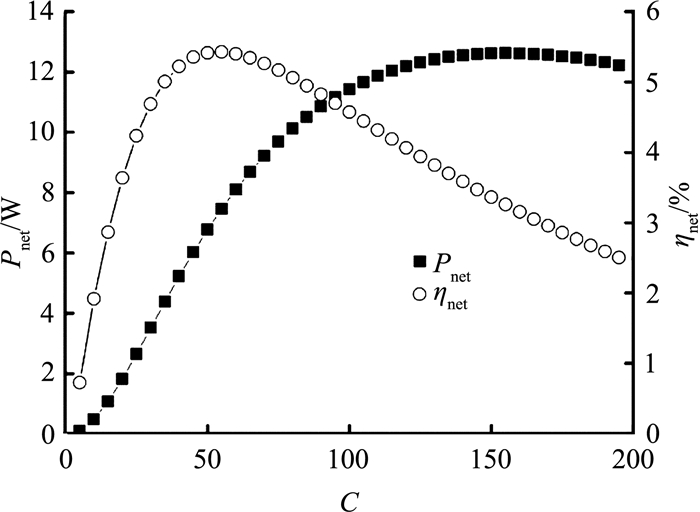
在太阳能温差发电系统中,聚焦倍率是一个关键性参数,直接影响系统的发电性能.本文首先计算了在qVc=1 L/s情况下,系统发电性能随聚焦倍率的变化规律,结果如图 3所示.随着聚焦倍率的增大,净发电效率逐渐增大;当聚焦倍率C=55时,净发电效率达到最大值5.43%;随后随着聚焦倍率的进一步增大,净发电效率逐渐减小.这是因为在冷却水流量固定的情况下,冷却系统冷却性能一定,随着聚焦倍率的增大,温差发电器热端温度升高,导致温差发电器冷、热端温差增大,系统净发电效率增大.随着聚焦倍率的进一步增大,由于冷端的散热能力有限,使得冷端的温度得不到足够的降低,因此使得冷、热端温差逐渐降低,系统净发电效率减小.此外,由于本文所选材料的ZT值不是很大,在400~500 K下,只有0.44~0.74,因此发电效率不是很大;若ZT值达到1(kpn=3.2),经计算可知,最大净发电效率能够达到13.53%.此外,从净输出功率来看,由于净发电效率在高聚焦倍率的情况下持续下降,净输出功率在C=155时达到最大值12.63 W.
|
图 3 系统发电性能随聚焦倍率的变化曲线 Fig. 3 Variation of power generation performance with concentration ratio |
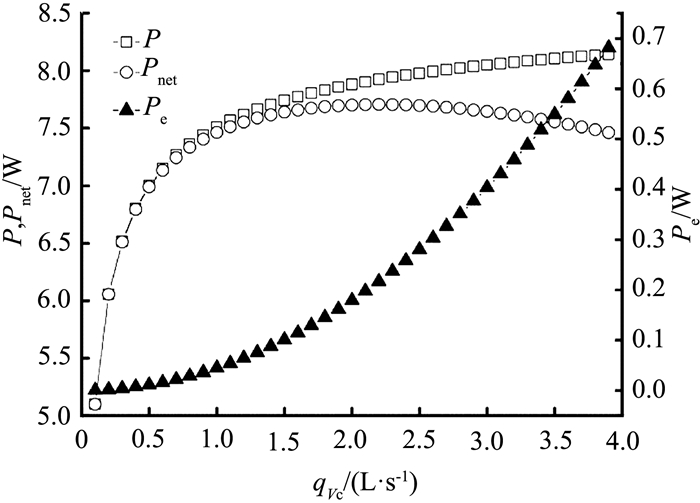
对于冷却系统而言,随着流速的增大,冷却换热系数增大,但同时消耗的功率增加,因此需要针对冷却水流量对系统发电性能的影响进行分析.图 4给出当C=55时,太阳能温差发电系统发电性能随冷却水流量变化的情况.可以看出,在冷却水流量较小的情况下,随着冷却水流量的增大,系统的输出功率急剧增大;随着冷却水流量的进一步增大,输出功率虽然增大,但增幅减小.对于冷却水功耗来说,随着流量的增大,功耗增幅逐渐增大.这些特点导致了当qVc=2.2 L/s时,净输出功率获得了最大值7.71 W.图 5给出当C=55时,太阳能温差发电器PN节冷热端温度随冷却水流量的变化.可以看出,随着冷却水流量的增大,冷、热端温度均会降低,但冷端温度获得更大幅度的降低,因此使得温差发电器冷、热端温差实际是增大的,这导致了输出功率随冷却水流量的增加能够逐渐增大的结果.
|
图 4 系统发电性能随冷却水流量的变化曲线 Fig. 4 Variation of power generation performance with cooling water flow rate |

|
图 5 PN节冷热端温度随冷却水流量的变化曲线 Fig. 5 Variation of hot-side and cold-side temperature of PN junction with cooling water flow rate |
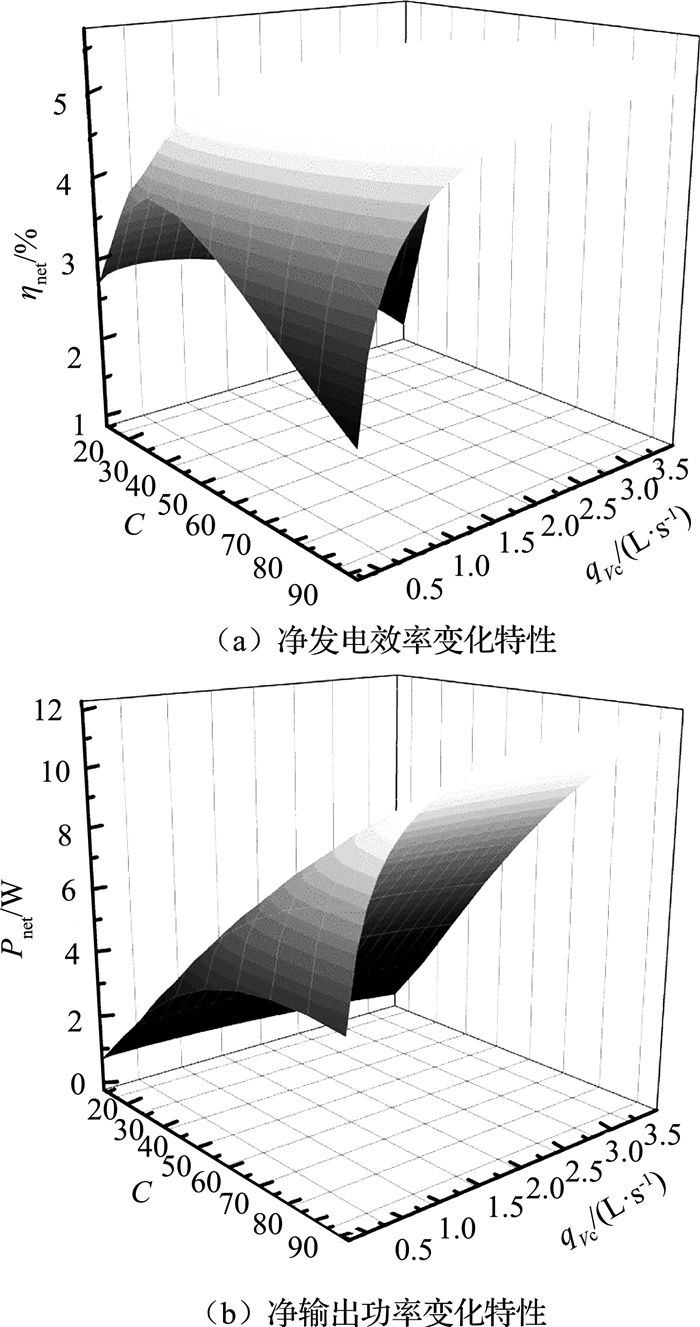
为了综合考虑聚焦倍率与冷却水流量对太阳能温差发电系统的影响,给出在不同聚焦倍率、不同冷却水流量下净输出功率与净发电效率的变化情况,如图 6所示.对于净发电效率来说,在不同的聚焦倍率下均存在最优的冷却水流量,使得净发电效率最大.随着聚焦倍率的增大,最优的冷却水流量增大.这是因为随着聚焦倍率的增大,温差发电器冷端温度升高明显,因此需要更高的冷却换热系数才能获得最大的净发电效率,最优的冷却水流量增大.此外,在冷却水流量固定的情况下存在最优的聚焦倍率,因此当C=65,qVc=2.5 L/s时,净发电效率取得最大值,为5.61%.从图 6(b)可以看出,当C<100,qVc=0~4 L/s时,净输出功率随着聚焦倍率及冷却水流量的增加而增大,系统在高聚焦倍率及高冷却水流量下,能够获得更高的净输出功率.在高聚焦倍率下,冷却水流量对净输出功率的影响更大,当C<100,qVc<4 L/s时,净输出功率未出现最大值.
|
图 6 低聚焦倍数情况下,系统发电性能变化曲线 Fig. 6 Variation of power generation performance in case of low concentration ratio |
图 7给出净发电效率与净输出功率在C>120下的变化情况,在高聚焦倍率情况下,净发电效率将会随着聚焦倍率的增大缓慢减小;对于净输出功率来说,当冷却水流量较小时,随着聚焦倍率的增大,净输出功率降低;当冷却水流量较大时,随着聚焦倍率的增大,净输出功率逐渐增大.总体而言,净输出功率存在最大值,当C=185,qVc=4.3 L/s时取得最大值15.86 W.此外,随着聚焦倍率的进一步增大,使得净输出功率最大时的最佳冷却水流量将会逐渐减小,这是由于在高聚焦倍率情况下,需要更高的冷却性能来提高发电性能.由于冷却水功耗随流量近乎指数增加,冷却换热系数增大引起的输出功率增加不足以抵消冷却系统的功耗,在高聚焦倍率情况下,需要寻求更加高效、低耗的冷却系统才能够使太阳能温差发电系统的发电性能得到进一步的提升.

|
图 7 高聚焦倍数情况下,系统发电性能的变化曲线 Fig. 7 Variation of power generation performance in case of high concentration ratio |
分析环境因素对太阳能温差发电系统的影响,结果如图 8所示.可以看出,与环境温度相比,风速对系统的发电性能响更大.随着环境温度的升高,系统的净输出功率增大,但变化幅度不是很明显.随着风速的增大,净输出功率的减小幅度更大,例如风速从2 m/s增大到8 m/s,净输出功率减少了近20%.这是因为当C=55时,温差发电器热端温度达到570 K左右,环境温度的降低与风速的增大均会导致向环境温度的散热量增大,但是风速引起表面换热系数的增大,使得散热量更大,因此风速对发电性能的影响更明显.此外,图 8给出将温差发电器热端进行真空隔热处理后,系统净输出功率随环境温度的变化曲线.在真空状态下,由于隔绝了温差发电器热端与环境之间的对流换热,减小了热端的热损失,从而提高了温差发电器热端的温度,增大了系统的净输出功率.在实际设计中,在不影响集光性能的情况下,应尽可能将温差发电器的热端进行必要的保温以减少散失热量,提高系统的发电性能.

|
图 8 系统输出功率随环境温度与风速的变化曲线(C=55, qVc=1 L/s) Fig. 8 ·Variation of output power with ambient temperature and wind velocity(C=55, qVc=1 L/s) |
(1) 随着聚焦倍率的增大,太阳能温差发电系统的净发电效率与净输出功率先增大后减小,且均存在最大值.随着冷却水流量的增大,系统输出功率和冷却系统功耗增大,因此存在最优的冷却水流量,使得系统净输出功率与净功率达到最大值.
(2) 当C=65,qVc=2.5 L/s时,净发电效率达到最大值5.61%;当C=185,qVc=4.3 L/s时,净输出功率取得最大值15.86 W.在高倍率聚光系统下,需要寻求更加高效、低耗的冷却方式来获得更高的发电性能.
(3) 环境温度的降低与风速的增大均会导致系统发电性能的降低,但是风速的影响更加明显.在实际设计中,应尽可能将发电器热端进行真空隔热,以减少系统的热损失,提高发电性能.
| [1] |
SUDHARSHAN K Y, PRAVEEN K V, HARISH C B. Performance evaluation of a thermally concentrated solar thermo-electric generator without optical concentration[J]. Solar Energy Materials and Solar Cells, 2016, 157: 93-100. |
| [2] |
陈伟, 梁燕, 胡长军, 等. 新型温差发电装置的结构设计[J]. 热能功力工程, 2016, 31(1): 125-128. CHEN Wei, LIANG Yan, HU Chang-jun, et al. Structure design of a new type thermoelectric generator[J]. Journal of Engineering for Thermal Energy and Power, 2016, 31(1): 125-128. |
| [3] |
AMATYA R, RAM R J. Solar thermoelectric generator for micro-power applications[J]. Journal of Electronic Materials, 2010, 39(9): 1735-1740. |
| [4] |
朱冬生, 吴红霞, 漆小玲, 等. 太阳能温差发电技术的研究进展[J]. 电源技术, 2012, 36(3): 431-434. ZHU Dong-sheng, WU Hong-xia, QI Xiao-ling, et al. Research of progress of solar thermoelectric generation[J]. Journal of Power Sources, 2012, 36(3): 431-434. |
| [5] |
毛佳妮, 江述帆, 方奇, 等. 新型太阳能温差发电集热体的传热特性[J]. 浙江大学学报:工学版, 2015, 49(11): 2205-2213. MAO Jia-ni, JIANG Shu-fan, FANG Qi, et al. Heat transfer characteristics of novel heat collector on solar thermoelectric power generation[J]. Journal of Zhejiang University:Engineering Science, 2015, 49(11): 2205-2213. |
| [6] |
林比宏, 陈晓航, 陈金灿. 太阳能驱动半导体温差发电器性能参数的优化设计[J]. 太阳能学报, 2006, 27(10): 1021-1026. LIN Bi-hong, CHEN Xiao-hang, CHEN Jin-can. Optimum design of the performance parameters of a solar-driven semiconductor thermoelectric generator[J]. Acta Energiae Solaris Sinica, 2006, 27(10): 1021-1026. DOI:10.3321/j.issn:0254-0096.2006.10.011 |
| [7] |
CHEN Gang. Theoretical efficiency of solar thermoelectric energy generators[J]. Journal of Applied Physics, 2011, 109: 104908-104908. DOI:10.1063/1.3583182 |
| [8] |
LI Peng, CAI Lan-lan, ZHAI Peng-cheng, et al. Design of a concentration solar thermoelectric generator[J]. Journal of Electronic Material, 2010, 39(9): 1522-1530. DOI:10.1007/s11664-010-1279-0 |
| [9] |
LAURYN L B, JEFFREY S G, ERIC S T. Concentrated solar thermoelectric generators[J]. Energy and Environmental Science, 2012, 5: 9055-9067. DOI:10.1039/c2ee22248e |
| [10] |
LI Chao, ZHANG Ming, MIAO Lei, et al. Effects of environmental factors on the conversion efficiency of solar thermoelectric co-generators comprising parabola trough collectors and thermoelectric modules without evacuated tubular collector[J]. Energy Conversion and Management, 2014, 86(10): 944-951. |
| [11] |
FERNANDA S M, LEANDRO C S, RAQUEL N A, et al. Solar thermoelectric generator performance relative to air speed[J]. Energy Conversion and Management, 2015, 99: 326-333. DOI:10.1016/j.enconman.2015.04.049 |
| [12] |
CHEN Wei-hsin, WANG Chien-chang, HUNG Chen-i, et al. Modeling and simulation for the design of thermal-concentrated solar thermoelectric generator[J]. Energy, 2014, 64: 287-297. DOI:10.1016/j.energy.2013.10.073 |
| [13] |
WU Ying-ying, WU Shuang-yin, XIAO Lan. Performance analysis of photovoltaicthermoelectric hybrid system with and without glass cover[J]. Energy Conversion and Management, 2015, 93: 151-159. |
| [14] |
JIAN Lin, LIAO Tian-jun, LIN Bi-hong. Performance analysis and load matching of a photovoltaic thermoelectric hybrid system[J]. Energy Conversion and Management, 2015, 105: 891-899. DOI:10.1016/j.enconman.2015.08.054 |
| [15] |
MEREU S, SCIUBBA E, BEJAN A. The optimal cooling of a stack of heat generating boards with fixed pressure drop, flowrate or pumping power[J]. International Journal of Heat Mass Transfer, 1993, 36(15): 3677-3686. DOI:10.1016/0017-9310(93)90047-A |
| [16] |
HSU Cheng-ting, HUANG Gia-yeh, CHU Hsu-shen, et al. Experiments and simulations on low-temperature waste heat harvesting system by thermoelectric power generators[J]. Applied Energy, 2011, 88(4): 1291-1297. |



