固定床鼓泡反应器是一种特殊的气液固三相反应器,具有催化剂与液相的接触效率高、液体分布均匀、催化剂床层较浅时转化率高等优点,适用于液相与少量气相的反应[1-2].然而,固定床鼓泡反应器存在返混程度较大的问题,这对反应器性能有着至关重要的影响[3-4].深入研究固定床鼓泡反应器内的返混特性,对反应器的设计、优化和放大具有重要意义.
目前,对于固定床鼓泡反应器返混特性的研究已有大量报道.Niranjan等[5-8]的研究发现,返混程度与气液表观速度以及填料直径有关,对于固定床鼓泡反应器,气泡尺寸和气泡运动行为是影响返混程度的重要因素.Cassanello等[9]将气泡直径与操作条件及物性参数相关联,得到返混程度和气泡直径的关联式,结果发现,返混程度随气泡直径的增大而增大.杨雨清[10]以空气-水-玻璃珠三相体系为研究对象,借助Bordas等[11]提出的气泡尺寸分布参数对反应器内的气泡尺寸分布进行预测,建立气相平均停留时间分布与气泡尺寸的经验关联式.以上研究主要针对气液比较大的情况,且反应器内产生的气泡尺寸较大;当固定床鼓泡反应器中气液比较低且产生的气泡直径较小(小于1 mm)时,液体的返混特性鲜有研究.
为了深入探讨在低气液比条件下μm级气泡对固定床鼓泡反应器内返混特性的影响规律,本文使用文丘里气泡发生器[12]产生大量μm级的小气泡,采用电解质示踪法测量固定床鼓泡反应器内液体的停留时间分布.分别考察表观气速、表观液速及填料直径对停留时间分布和返混特性的作用规律,以期为固定床鼓泡反应器的设计与应用提供理论指导.
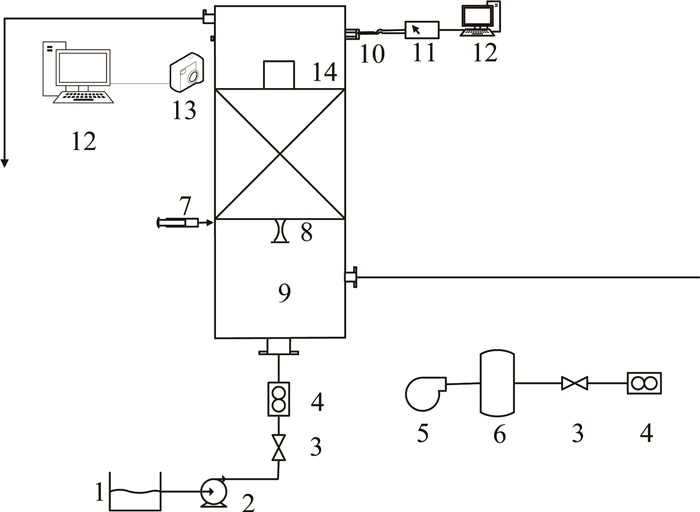
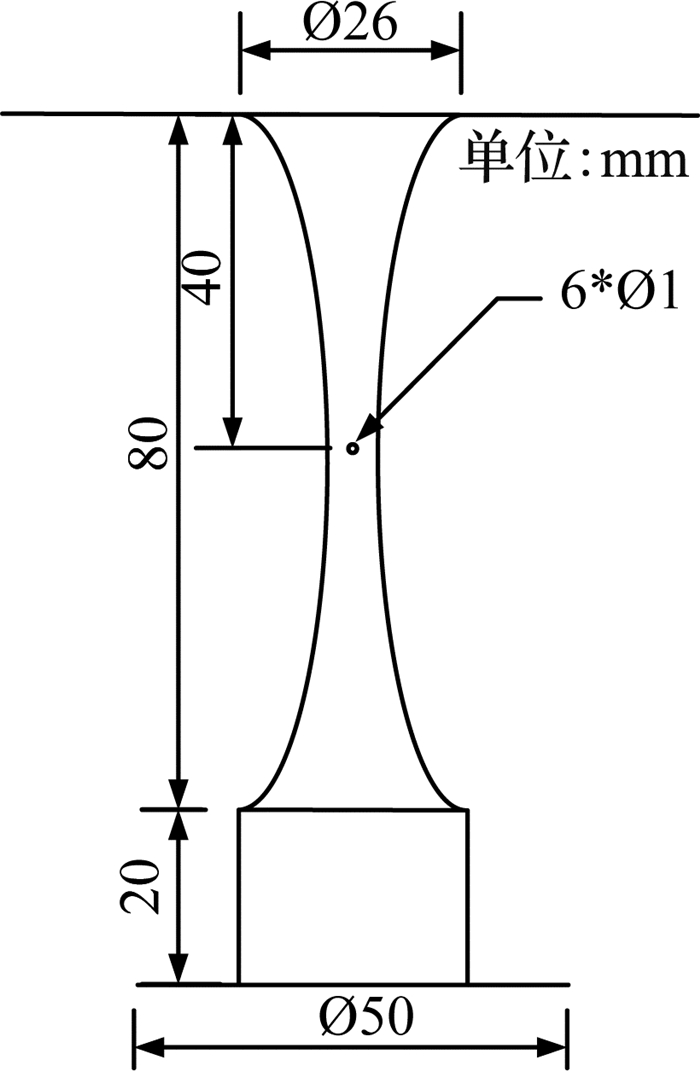
1 实验部分 1.1 实验装置与流程如图 1所示为固定床鼓泡反应器内返混程度测定的冷模实验流程图,包括固定床鼓泡反应器、气路系统、水路系统、检测仪器及计算机数据采集系统5个部分.反应器用有机玻璃制成,由上筒体、下筒体、液体注入管、气体注入管和文丘里气泡发生器等组成.反应器筒体的内径为140 mm,反应器上筒体的高度为500 mm,下筒体的高度为300 mm.其中,气泡拍摄区域14紧贴催化剂床层,大小为45 mm×45 mm.实验所用的文丘里气泡发生器结构如图 2所示.
|
1-水槽; 2-离心泵; 3-阀门; 4-流量计; 5-压缩机; 6-缓冲罐; 7-KCl注入装置; 8-文丘里气泡发生器; 9-反应器; 10-排水出口; 11-电导率仪; 12-计算机; 13-高速相机; 14-拍摄区域 图 1 固定床鼓泡反应器内返混程度测定实验流程图 Fig. 1 Schematic diagram of experimental setup for determination of backmixing degree in packed bubble column |
|
图 2 文丘里气泡发生器结构 Fig. 2 Structure of venturi bubble generator |
文丘里气泡发生器高度为80 mm,进出口处直径为26 mm,中部喉管直径为6 mm;喉管处小孔直径为1 mm,开孔数n=6,沿周向均匀分布;文丘里气泡发生器下方20 mm处安装直径为50 mm的圆形挡板.
实验在常温、常压下开展,将空气和水作为实验介质,空气由空气压缩机提供,经气体流量计后从反应器侧面的气体入口通入,控制气体体积流量为0.025~0.125 m3/h(表观气速UG为4.51×10-4~2.26×10-3 m/s);水由离心泵输送,经由液体流量计后从反应器底部通入,控制液体流量为0.1~0.4 m3/h(表观液速UL为1.81×10-3~7.22×10-3 m/s),对应的操作气液比为0.062 5~1.25.气体通过喉管处的小孔进入文丘里气泡发生器,并在高速流动液体的剪切作用下被破碎成微小的气泡,随液相一并向上流动进入催化剂床层.实验中采用的填料分别为直径为1、3、6、9和14 mm的氧化铝球形颗粒,密度为1 500 kg/m3,催化剂床层高度约为380 mm.
1.2 实验测试方法和数据处理将饱和KCl溶液作为示踪剂,采用脉冲法测量停留时间分布.实验开始前,向反应器内注入自来水至液面高度约为0.45 m,打开离心泵及空气压缩机,调整阀门开度,使得气液体积流量分别达到设定值;待流动稳定之后,将一定体积(20 mL)的饱和KCl溶液通过注入装置脉冲加入.为了消除气泡对检测结果的影响,在反应器上部检测点处安装带有除泡器的导管,将液体引出.采用电导率分析仪(上海雷磁公司,DDSJ-308A)测量液体电导率,将检测结果输入计算机内保存.每个数据点的实验次数不少于3次.实验所用自来水的电导率约为200 μS/cm,为了消除自来水电导率对实验结果的影响,对κ(t)进行归一化处理,得到无量纲的电导率:
| $ k\left( t \right) = \frac{{\kappa \left( t \right)-{\kappa _{\min }}}}{{{\kappa _{\max }}-{\kappa _{\min }}}}. $ | (1) |
式中:κmax为电导率最大值,κmin为实验开始时的初始电导率.当电导率达到初始电导率的99%~101%时,认为实验达到稳定.由k(t)可以计算得到相应的停留时间分布密度函数:
| $ E\left( t \right) = k\left( t \right)/\int_0^\infty {k\left( t \right){\rm{d}}t} . $ | (2) |
采取比较统计特征值的方法,对停留时间分布密度函数进行分析.根据E(t)的数学期望,可以求得平均停留时间:
| $ {t_{\rm{m}}} = \int_0^\infty {tE\left( t \right){\rm{d}}t} /\int_0^\infty {E\left( t \right){\rm{d}}t} = \int_0^\infty {tE\left( t \right){\rm{d}}t} . $ | (3) |
根据轴向扩散模型[13],利用停留时间分布密度函数E(t)的无量纲方差σθ2,可以求得模型参数Pe准数:
| $ \sigma _\theta ^2 = \frac{2}{{Pe}}-\frac{2}{{P{e^2}}}\left( {1-\exp \left( {Pe} \right)} \right). $ | (4) |
式中:
| $ \sigma _\theta ^2 = \sigma _t^2/t_{\rm{m}}^2, $ | (5) |
| $ \sigma _t^2 = \frac{{\int_0^\infty {{{\left( {t-{t_{\rm{m}}}} \right)}^2}E\left( t \right){\rm{d}}t} }}{{\int_0^\infty {E\left( t \right){\rm{d}}t} }} = \int_0^\infty {{{\left( {t-{t_{\rm{m}}}} \right)}^2}E\left( t \right){\rm{d}}t} . $ | (6) |
Pe可以由下式进行计算:
| $ Pe = \frac{{{U_{\rm{L}}}{d_{\rm{p}}}}}{{{\varepsilon _{\rm{L}}}{D_{{\rm{ax}}}}}}. $ | (7) |
式中:UL为液体有效流速,dp为填料直径,εL为持液率,Dax为有效轴向扩散系数.Pe准数与返混程度密切相关:Pe大,说明返混程度小;Pe小,说明返混程度大.
2 实验结果和讨论 2.1 填料直径对气泡直径的影响采用高速摄像法[14],采集文丘里气泡发生器产生的初始气泡分布图像.
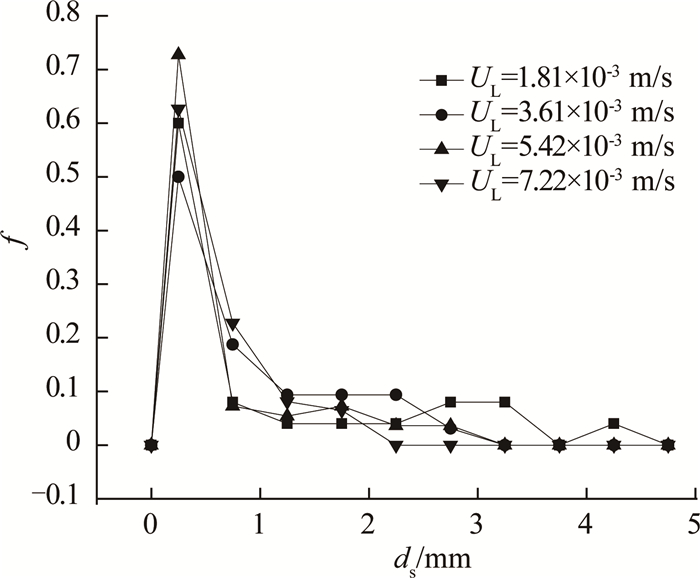
如图 3所示为气泡进入催化剂床层之前的分布图.可以看出,气泡在液相中的分散性较好,气泡总体直径较小.利用Matlab图像处理程序对气泡直径进行统计计算,得到进入催化剂床层之前的气泡直径分布比例f,如图 4所示.

|
图 3 进入催化剂床层之前的气泡分布图 Fig. 3 Bubble distribution before entering reactor (UG=4.51×10-4 m/s, UL=7.22×10-3 m/s) |
|
图 4 进入催化剂床层之前的气泡直径分布(UG=4.51×10-4 m/s) Fig. 4 Distribution of bubble diameters before entering reactor (UG=4.51×10-4 m/s) |
由图 4可以看出,在该实验条件下,文丘里气泡发生器所产生的气泡直径分布较宽.大多数气泡直径小于1 mm,为μm级气泡,也有少量直径为1~5 mm的大气泡.
与没有填料时相比,在固定床鼓泡反应器中,填料的存在会使得气泡的运动受到限制,导致气泡相互碰撞长大的概率增加,气泡直径增大.当加入不同直径的填料时,填料对气泡同时具有聚并和破碎作用[15],作用效果由初始气泡直径和填料间隙直径的相对大小决定[11].从催化剂床层出来的气泡在上升过程中,气泡内压力逐渐减小,气泡发生膨胀,气泡直径相应增大[16].
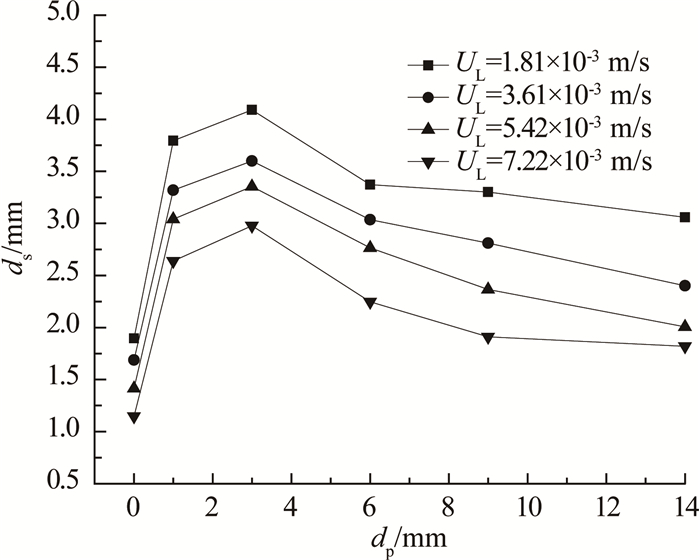
根据式(8),得到不同填料直径下图 1所示拍摄区域内气泡的Sauter平均直径ds,结果如图 5所示.
|
图 5 填料直径对平均气泡直径的影响(UG=4.51×10-4 m/s) Fig. 5 Effect of particle diameter on average bubble diameters (UG=4.51×10-4 m/s) |
| $ {d_{\rm{s}}} = \sum\limits_{i = 1}^n {d_{{\rm{b}}i}^3} /\sum\limits_{i = 1}^n {d_{{\rm{b}}i}^2} . $ | (8) |
式中:dbi为第i个气泡的等效圆直径,
| $ {d_{{\rm{b}}i}} = \sqrt {4{S_{{\rm{b}}i}}/{\rm{ \mathsf{ π} }}} . $ | (9) |
其中,
| $ {S_{{\rm{b}}i}} = 第i个气泡所占像素数 \times {\left( {\frac{l}{{l所占像素数}}} ~~~~~~\right)^2}, $ | (10) |
l为参考标尺的长度.
从图 5可以看出,在该实验条件下,与无填料时相比,填料的存在总会使得平均气泡直径增大;随着填料直径的增大,平均气泡直径先增大后减小,存在极大值.
填料间隙直径dv表示由填料堆积形成的空白区域大小的等效直径[17].不同直径填料形成的间隙直径根据下式计算:
| $ {d_{\rm{v}}} = {d_{\rm{p}}}\left( {\frac{2}{{\sqrt 3 }}-1} \right). $ | (11) |
结果如表 1所示.
| 表 1 不同填料的间隙直径 Table 1 Interval diameter of different packing particles |
比较气泡直径和填料间隙直径可以发现,当填料直径 < 3 mm时,气泡主体直径(约为0.5 mm)大于填料间隙直径,此时大气泡进入催化剂床层后受到明显的剪切作用,破碎效应较强;随着填料直径的增大,破碎效应逐渐减弱,平均气泡直径随之增大.当填料直径为3 mm时,气泡主体直径与填料间隙直径相当,此时气泡受到较强的毛细管力,气泡运动速度减小,在孔道内的停留时间变长,气泡之间的相互碰撞概率增加,聚并效应最强,平均气泡直径达到极大值.当填料直径>3 mm时,气泡主体直径小于填料间隙直径;随着填料直径的增大,气泡自由运动的空间增大,聚并效应逐渐减弱,平均气泡直径随之减小,与Collins等[18]的研究结果一致.
2.2 操作条件对停留时间分布和返混程度的影响反应器内物料的返混程度可以用停留时间分布函数来定量描述.分别对填料直径为1、3、6、9和14 mm时,不同表观气液速条件下液体的停留时间分布进行考察.结果发现,在不同填料直径的条件下,停留时间分布均表现出类似的变化规律.以直径为6 mm的氧化铝球形颗粒为例,不同表观气液速条件下液体的停留时间分布如图 6所示.
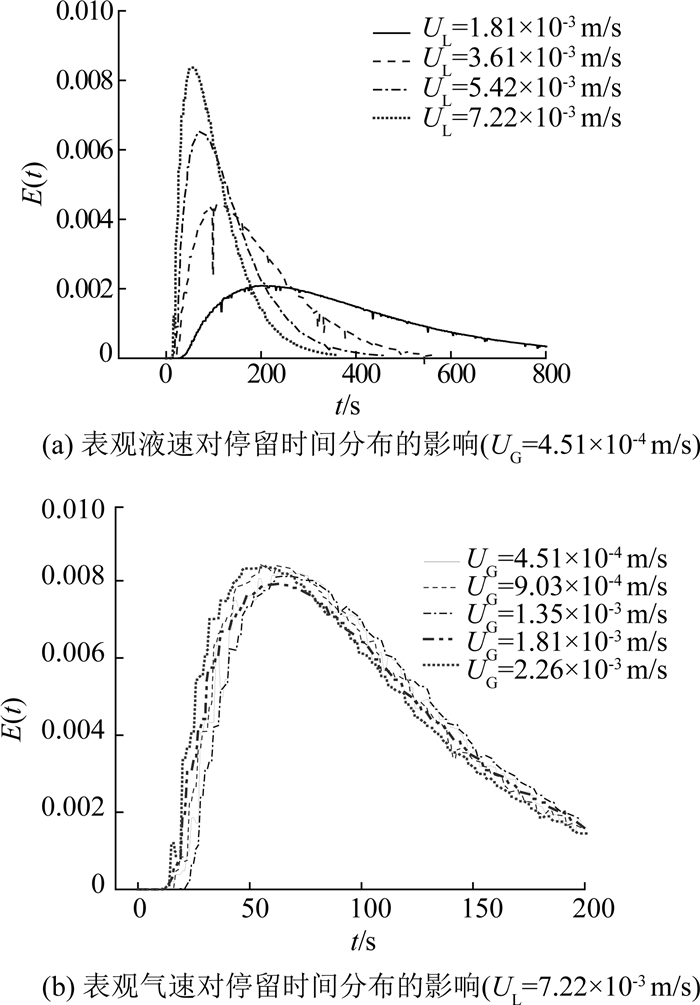
|
图 6 不同表观气液速条件下的停留时间分布密度函数 Fig. 6 Density function of RTD at different superficial gas and liquid velocities |
如图 6所示为不同表观气液速条件下的停留时间分布密度函数曲线.可以看出,不同操作条件下的停留时间分布密度函数曲线都存在拖尾现象,拖尾的程度与返混大小密切相关,返混越大时拖尾现象越明显.从图 6(a)可以看出,当表观气速一定时,随表观液速增大,停留时间分布密度函数曲线左移,同时曲线峰变高变窄,拖尾现象减弱;图 6(b)显示,当表观液速一定时,随着表观气速的增大,停留时间分布密度函数曲线的形状包括峰宽、峰高等没有明显变化.这说明在本文研究范围内返混程度受表观液速的影响较大,受表观气速的影响较小.对不同表观气液速条件下的Pe进行计算,结果如图 7所示.
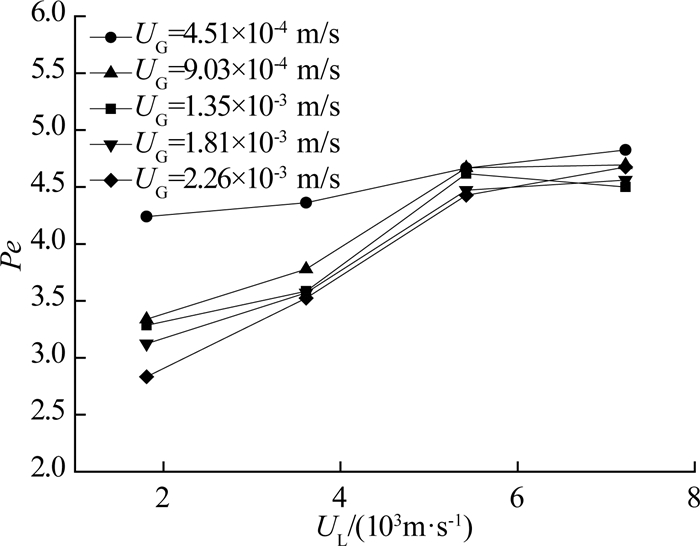
|
图 7 不同表观气、液速条件下的Pe准数 Fig. 7 Pe number at different superficial gas and liquid velocities |
从图 7可以看出,Pe随UL的增大而增大,说明提高表观液速有利于减小返混程度,使液相流动更接近平推流,这与文献[19, 20]的结果一致.当表观液速较低时,Pe随UG的增大而减小,且这种趋势随表观液速的增大而逐渐减弱;当表观液速增大到5.42×10-3 m/s时,表观气速的影响不再显著.这是因为当UL较小时,气液两相的流速差异较小,气体的引入对液体流动的扰动作用较强;在气流的推动作用下,可能产生涡流,加速液相的混合,使反应器内液体流动偏离理想流动状态,导致返混程度增大.随着UL的增大,这种扰动作用逐渐减弱,表观气速的影响变弱.
2.3 填料直径对停留时间分布和返混程度的影响分别使用直径为1、3、6、9、14 mm的氧化铝球形颗粒作为填料,通过实验测得不同填料直径下,固定床鼓泡反应器内的液相停留时间分布曲线以及无填料时反应器内的液相停留时间分布曲线,结果如图 8所示.
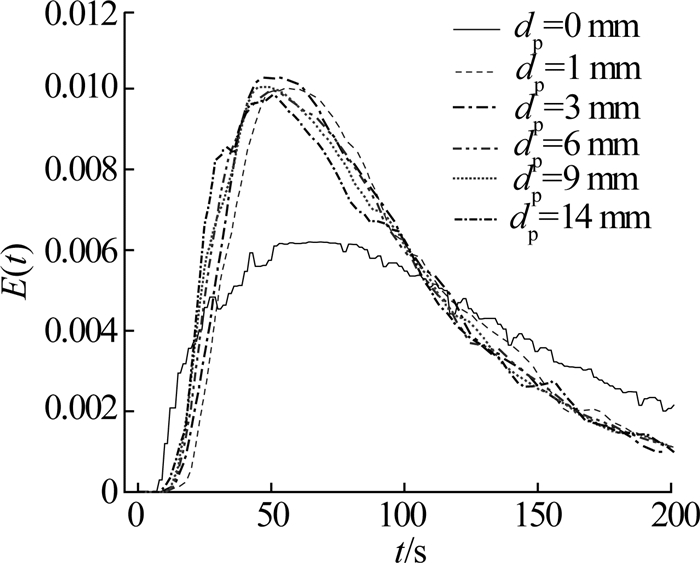
|
图 8 不同填料直径下的停留时间分布密度函数(UL=7.22×10-3 m/s,UG =4.51×10-4 m/s) Fig. 8 Density function of RTD with different particle diameters (UL=7.22×10-3 m/s, UG =4.51×10-4 m/s) |
从图 8可以看出,当反应器中没有填料(dp=0 mm)时,停留时间分布密度函数曲线的峰值较低且存在明显的拖尾现象,说明此时示踪剂进入反应器之后很快就被混合均匀,返混程度较大.在加入填料后,停留时间的分布密度函数曲线左移;曲线峰变高变窄,拖尾现象减弱,返混程度变小.对于不同直径的填料,停留时间分布密度函数的曲线形状变化不明显.
对不同条件下的Pe进行计算,得到Pe随填料直径的变化规律,如图 9所示.
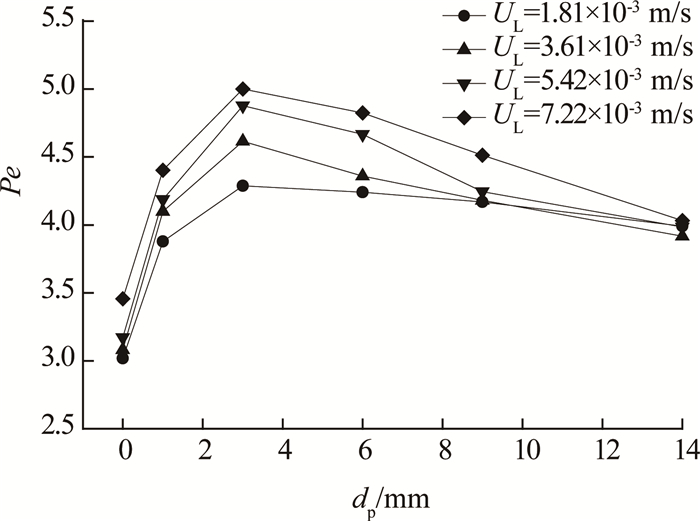
|
图 9 填料直径对Pe的影响(UG=4.51×10-4 m/s) Fig. 9 Effect of particle diameter on Pe number (UG=4.51×10-4 m/s) |
从图 9可以看出,与无填料(dp=0 mm)时相比,固定床鼓泡反应器内Pe有不同程度的增大.无填料时,由于文丘里管的射流作用,床层中心的液体速度远高于两侧,返混严重.在加入填料后,液体单元之间的相互质量交换受到阻碍,液体速度分布变得更加均匀,返混程度降低.从图 9可以看出,随着填料直径的增大,Pe先增大后减小,存在极大值点,即返混程度随填料直径的增大先减小后增大,存在极小值点.
填料直径对Pe的影响包含以下两方面的原因:1)使通过床层的有效液速[21]发生变化,进而改变返混程度;2)使气泡直径分布发生变化,从而改变气泡对液体的扰动程度,导致返混程度发生变化.Therning等[22]通过研究不同填料直径下固定床鼓泡反应器的流型及流动状况发现,当填料直径较小时,返混主要受微观扰动的影响;当填料直径较大时,返混主要受液体循环流动的影响.在该实验条件下,根据2.1节的实验结果可知,当填料直径 < 3 mm时,气泡主体直径大于填料间隙直径,此时催化剂床层对气泡的破碎作用占主导地位.随着填料直径的增大,催化剂床层对气泡的破碎作用逐渐减弱,气泡对液体的扰动作用随之变小,导致返混程度变小,Pe增大.当填料直径大于3 mm时,随着填料直径的增大,液体流通面积增大,有效流速减小,液体循环增强,导致返混程度增大,Pe减小.随着填料直径的增加,Pe呈现先增大后减小的变化趋势.
2.4 Pe准数经验关联式为了定量表征固定床鼓泡反应器内返混程度的变化规律,Bayraktar等[8]提出多种Pe计算的关联式,这些关联式大多将Pe和操作参数相关联,Niranjan等[5-6]将Pe和操作参数、填料直径相关联.本文根据不同操作条件和填料直径下的实验数据,提出固定床鼓泡反应器中Pe的经验关联式:
| $ Pe = R{e_{\rm{L}}}^xR{e_{\rm{G}}}^yf\left( {{d_{\rm{p}}}/{d_{\rm{c}}}} \right). $ | (12) |
式中:dc为反应器内径,液相雷诺数ReL=(dcULρL)/μL,气相雷诺数ReG=(dcUGρG)/μG,拟合得到x=0.16,y=-0.08,f(dp/dc)=-119.13(dp/dc)2+7.6(dp/dc)+1.78.从式(12)可以看出,ReL对返混程度的影响大于ReG对返混程度的影响,即返混程度对表观液速的变化更加敏感,与Bayraktar等[8]得到的Pe计算关联式Pe=0.166ReG-0.157(dp/dc)0.386差异较大.这是因为当表观气速和表观液速都发生改变时,Pe准数通常由流速较大的一方决定[23].在Bayraktar等[8]的实验中,操作气液比为16~300,表观气速较大,因而Pe准数主要受表观气速的影响.在该实验中,由于表观气速与表观液速接近(操作气液比为0.062 5~1.25),因此,Pe准数同时受表观气速和表观液速的影响,并且表观液速的影响更显著.同时,由于Bayraktar等[8]采用的是传统的孔板式分布器,而该实验采用文丘里气泡发生器,两者所产生的气泡直径不同,气泡直径与填料间隙直径之间的相对大小不同,最终导致Pe随着dp/dc的变化呈现出不一样的规律.
如图 10所示为Pe的实验值与计算值的比较.两者的相对偏差在±20%以内,模型的准确性较高.
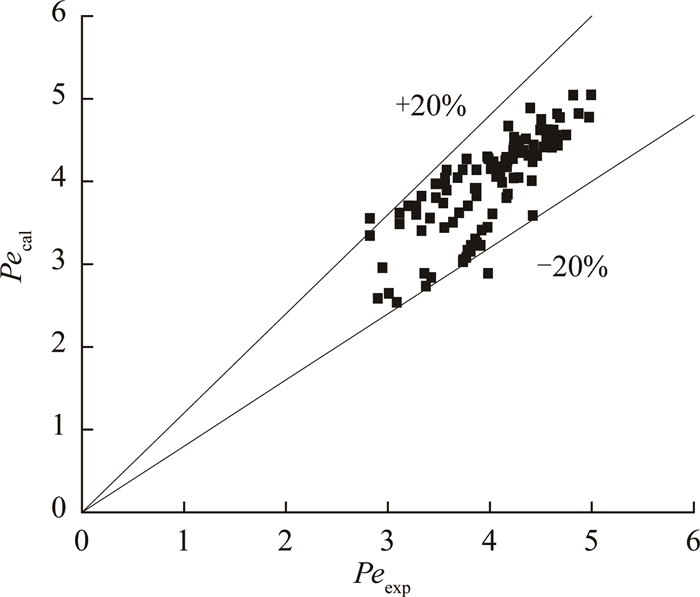
|
图 10 Pe实验值与计算值的对比 Fig. 10 Comparison between experimental and calculated results of Pe number |
(1) 与无填料时相比,填料的存在总会使得平均气泡直径增大,且随着填料直径的增大,平均气泡直径先增大后减小,存在极大值点.
(2) 在该操作气液比下,返混程度同时受表观气液速的影响,且表观液速的影响比表观气速的影响更显著.返混程度随着表观液速的增大而减小,随着表观气速的增大而增大;返混程度随着填料直径的增大,总体呈现先减小后增大的趋势,存在极小值点.
(3) 拟合得到Pe和液相雷诺数、气相雷诺数、填料直径的经验关联式,实验值与公式计算值的相对偏差在±20%以内.
| [1] |
MEDEROS F S, ELIZALDE I, ANCHEYTA J. Steady-state and dynamic reactor models for hydrotreatment of oil fractions:a review[J]. Catalysis Reviews, 2009, 51(4): 485-607. DOI:10.1080/01614940903048612 |
| [2] |
DUDUKOVIĆ M P, LARACHI F, MILLS P L. Multiphase catalytic reactors:a perspective on current knowledge and future trends[J]. Catalysis Reviews, 2002, 44(1): 123-246. DOI:10.1081/CR-120001460 |
| [3] |
VAN-GELDER K B, BORMAN P C, WEENINK R E, et al. Three-phase packed bed reactor with an evaporating solvent-Ⅱ. modelling of the reactor[J]. Chemical Engineering Science, 1990, 45(10): 3171-3192. DOI:10.1016/0009-2509(90)80062-J |
| [4] |
STVBER F, WILHELM A M, DELMAS H. Modelling of three phase catalytic upflow reactor:a significant chemical determination of liquid-solid and gas-liquid mass transfer coefficients[J]. Chemical Engineering Science, 1996, 51(10): 2161-2167. DOI:10.1016/0009-2509(96)00073-5 |
| [5] |
NIRANJAN K, PANGARKAR V G. Gas holdup and mixing characteristics of packed bubble columns[J]. Chemical Engineering Journal, 1984, 29(2): 101-111. DOI:10.1016/0300-9467(84)85031-5 |
| [6] |
CAMPOS J, CARVALHO J. A new experimental technique to study backmixing in packed bubble columns[J]. Chemical Engineering Science, 1992, 47(15): 4063-4067. |
| [7] |
THANOS A M, GALTIER P A, PAPAYANNAKOS N G. Liquid flow non-idealities and hold-up in a pilot scale packed bed reactor with cocurrent gas-liquid upflow[J]. Chemical Engineering Science, 1996, 51(11): 2709-2714. DOI:10.1016/0009-2509(96)00140-6 |
| [8] |
BAYRAKTAR E, MEHMETOGLU V. Back mixing and liquid hold-up in a cocurrent up-flow packed bed bioreactor[J]. Chemical Engineering Communications, 2001, 185(1): 125-140. DOI:10.1080/00986440108912859 |
| [9] |
CASSANELLO M, MARTÍNEZ O, CUKIERMAN A L. Liquid hold-up and backmixing in cocurrent upflow three-phase fixed-bed reactors[J]. Chemical Engineering Science, 1998, 53(5): 1015-1025. DOI:10.1016/S0009-2509(97)00196-6 |
| [10] |
杨雨清. 固定床鼓泡反应器的流体力学特性研究[D]. 上海: 华东理工大学, 2010: 41-44. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1650859
|
| [11] |
BORDAS M L, CARTELLIER A, SÉCHET P, et al. Bubbly flow through fixed beds:microscale experiments in the dilute regime and modeling[J]. AIChE Journal, 2006, 52(11): 3722-3743. DOI:10.1002/(ISSN)1547-5905 |
| [12] |
GORDIYCHUK A, SVANERA M, BENINI S, et al. Size distribution and sauter mean diameter of micro bubbles for a venturi type bubble generator[J]. Experimental Thermal and Fluid Science, 2016, 70: 51-60. DOI:10.1016/j.expthermflusci.2015.08.014 |
| [13] |
SABER M, HUU T T, PHAM-HUU C, et al. Residence time distribution, axial liquid dispersion and dynamic-static liquid mass transfer in trickle flow reactor containing β-SiC open-cell foams[J]. Chemical Engineering Journal, 2012, 185: 294-299. |
| [14] |
JO D, REVANKAR S T. Effect of coalescence and breakup on bubble size distributions in a two-dimensional packed bed[J]. Chemical Engineering Science, 2010, 65(14): 4231-4238. DOI:10.1016/j.ces.2010.04.019 |
| [15] |
JO D, REVANKAR S T. Investigation of bubble breakup and coalescence in a packed-bed reactor-Part 1:a comparative study of bubble breakup and coalescence models[J]. International Journal of Multiphase Flow, 2011, 37(9): 995-1002. DOI:10.1016/j.ijmultiphaseflow.2011.06.016 |
| [16] |
PELLICER J, GARCIA-MORALES V, HERNÁNDEZ M J. On the demonstration of the Young-Laplace equation in introductory physics courses[J]. Physics Education, 2000, 35(2): 144-168. DOI:10.1088/0031-9120/35/2/702 |
| [17] |
JO D, REVANKAR S T. Bubble mechanisms and characteristics at pore scale in a packed-bed reactor[J]. Chemical Engineering Science, 2009, 64(13): 3179-3187. DOI:10.1016/j.ces.2009.04.006 |
| [18] |
COLLINS J H P, SEDERMAN A J, GLADDEN L F, et al. Characterising gas behaviour during gas-liquid co-current up-flow in packed beds using magnetic resonance imaging[J]. Chemical Engineering Science, 2017, 157(10): 2-14. |
| [19] |
BELFARES L, CASSANELLO M, GRANDJEAN B P A, et al. Liquid back-mixing in packed-bubble column reactors:a state-of-the-art correlation[J]. Catalysis Today, 2001, 64(3): 321-332. |
| [20] |
SAROHA A K, KHERA R. Hydrodynamic study of fixed beds with cocurrent upflow and downflow[J]. Chemical Engineering and Processing:Process Intensification, 2006, 45(6): 455-460. DOI:10.1016/j.cep.2005.11.005 |
| [21] |
吉敏, 杨钊, 娄晓军, 等. 上流式反应器中流体流动及返混特性研究[J]. 化学工程, 2015, 43(11): 41-46. JI Min, YANG Zhao, LOU Xiao-jun, et al. Fluid flow and backmixing characteristics of up-flow reactor[J]. Chemical Eningeering, 2015, 43(11): 41-46. DOI:10.3969/j.issn.1005-9954.2015.11.009 |
| [22] |
THERNING P, RASMUSON A. Liquid dispersion and gas holdup in packed bubble columns at atmospheric pressure[J]. Chemical Engineering Journal, 2001, 81(1): 69-81. |
| [23] |
HAMAMCI H, RYU D D. Performance of tapered column packed-bed bioreactor for ethanol production[J]. Biotechnology and Bioengineering, 1987, 29(8): 994-1002. DOI:10.1002/(ISSN)1097-0290 |



