2013年,国务院部署开展地下综合管廊建设试点工作,2015年发布《关于推进城市地下综合管廊建设的指导意见》,鼓励由企业投资建设和运营管理地下综合管廊,推广运用公私合作(public-private partnerships,PPP)模式,至此,地下综合管廊PPP项目迎来发展热潮.设计出令项目利益相关者3满意的定价机制,是地下综合管廊PPP项目在特许经营期内稳定、健康运作的重要保证.
现阶段,国内专家学者对地下综合管廊及类似的PPP项目定价机制作了一定的研究.王曦等[1-2]建立基于管廊管理者与使用者间的博弈定价模型.刘妍等[3]建立社会资本的激励成本模型以及管线用户惩罚成本模型.崔启明等[4]提出管廊收费定价机制应考虑的5方面内容.杜娅妮[5]提出综合管廊收费方法可以分为管线年租费、运营维护费、一次性买断3种形式.王建[6]认为对综合管廊收费定价可以考虑空间比例分摊法和直埋成本法2种方式.丁晓敏等[7]分析广州大学城综合管廊费用定价,指出其费用构成包括入廊费和管理费.宋定[8]认为公共管廊的费用承担主体是政府部门和管线用户.李平[9]论述了综合管廊的定价原则及考虑因素.邱玉婷[10]指出在综合管廊费用分摊时,普遍采用成本配置法,包括比例法和增量法.王英[11]运用直埋成本法计算入廊费,根据管廊日常维护成本及合理利润确定日常维护费.杨卫华等[12-13]从风险角度,分别构建了收费公路PPP定价模型.杨俊萍[14]借助系统观思想,对PPP项目定价进行研究.王洪强[15]建立基于合同设计及风险收益对等的PPP项目定价模型.刘旭[16]以系统动力学为视角,分析高速公路PPP项目价格影响因素间的因果关系.综上所述,目前综合管廊或类似PPP项目定价采用的方法主要有直埋成本法、空间比例法、博弈定价及多目标规划定价.直埋成本法和空间比例法较传统普遍,但是模型中分摊因子确定的科学性存在诸多争议;博弈定价模型虽然能够较好地分析定价影响因素和各方定价决策机制,但模型设计建立在“完全信息博弈”的基础上,然而现实中管线用户和项目公司所掌握的信息通常很难全面;多目标规划模型将各方利益诉求作为约束条件,通过建立模型求得令多方满意的最优结果,方法合理且容易操作.本文选取多目标规划模型,对综合管廊价格制定进行探讨.
1 定价原则及影响因素地下综合管廊作为准经营性项目,应既具有生产服务的经营属性,又与其他公共产品一样具有公益属性[17].在制定项目价格时,既要使价格足以吸引到优质的社会资本来参与管廊项目的建设和运营,使收取的费用能够弥补建设投资和运营成本,并获得合理利润,又要考虑管线用户的承受能力,调动起管线用户的入廊积极性;同时,当收费不足时, 政府应给予自身能够承受且愿意承受的补贴额度[18].
地下综合管廊PPP项目的付费通常包括了可用性付费和日常维护付费,因此项目定价主要是进行入廊费和日常维护费的确定.入廊费是指管线用户为使用管廊而支付的费用,主要用于补偿社会资本建设管廊发生的成本;日常维护费主要用于弥补项目公司对管廊的日常维护和管理支出,由管线用户向项目公司逐期支付.由于地下综合管廊项目的建设投资巨大,仅靠管线用户支付入廊费来弥补是远远不够的,还需要政府提供必要的补贴;此外,假设入廊费和日常维护费都是在运营期内向项目公司逐期等额支付的.
在确定入廊费时应考虑的因素如下:1)地下综合管廊及附属设施的建设投资和合理回报;2)各入廊管线占所处管廊空间的比例;3)是否涉及需要单独建仓的特殊管线(如燃气管线);4)各管线按照以往方式单独敷设的成本;5)在管廊设计使用年限内,管线不入廊时所需的更新成本(不含管线自身费用);6)在管廊的设计使用年限内,因管线破损率以及水、热、气等漏损率降低而节省的管线维护费用和生产经营成本.在确定日常维护费时应考虑的因素如下:1)地下综合管廊及附属设施正常运营成本;2)项目公司的正常管理支出;3)社会资本方合理的经营利润;4)入廊管线占所处管廊空间的比例.
2 项目投资收益率确定项目投资收益率是社会资本方在进行项目投资时非常看重的一个因素,当面临多个投资方案时,社会资本方往往会优先选择投资收益率较大的投资项目[19].目前,项目投资收益率的确定方法有很多,资本资产定价模型(capital asset pricing model,CAPM)是一种考虑项目投资风险的定价模型,它将风险和收益紧密联系,即社会资本承担的风险越大,项目投资收益率越高[20].经典的Sharpe CAPM模型表示为
| $ R = {R_{\rm{f}}} + \beta \left( {{R_{\rm{m}}} - {R_{\rm{f}}}} \right). $ | (1) |
式中:R为项目投资收益率,Rf为无风险投资收益率,β为投资该项目的风险校正系数,Rm为市场平均投资收益率.
用国债收益率代替无风险投资收益率.通过中国人民银行官网统计了2016年6月1日至2017年5月31日共计251个工作日的中债国债收益率,如表 1所示.由于地下综合管廊PPP项目特许经营期大多为数十年,用10年期收益率平均值代表特许经营期在15年及以下项目的无风险投资收益率Rf1,用30年期收益率平均值代表特许经营期在15年以上项目的无风险投资收益率Rf2.求得:Rf1=3.065 9%,Rf2=3.547 9%.
| 表 1 中债国债收益率表 Table 1 Yields of government bonds |
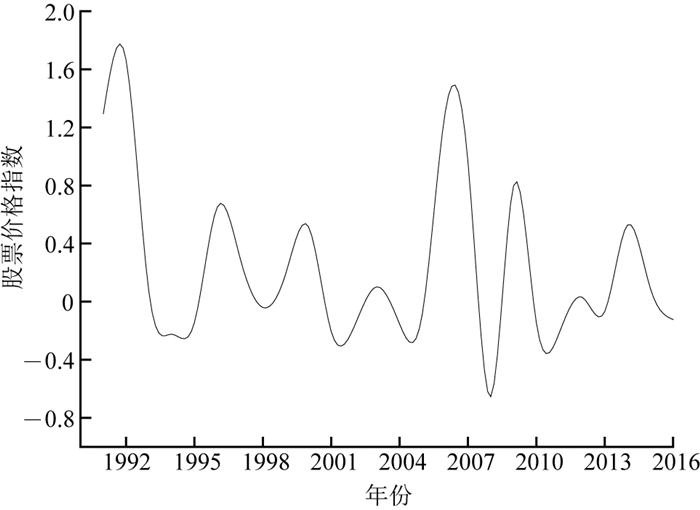
将通过上证综指求得的股票价格指数作为市场平均收益率的参考值,在东方财富网上统计了上证综合指数(000001)自1990年12月上市以来27年间年末最后一个交易日的收盘点(见表 2),以此计算得到1991~2016年的股票价格指数,画出如图 1所示的散点图.
| 表 2 上证综合指数数据统计 Table 2 SSE composite index data statistics |
|
图 1 股票价格指数散点图 Fig. 1 Stock price index scatter chart |
对数据异常值进行排查.根据概率统计中的3σ原则可知,若随机变量X服从正态分布,则有:P(μ-σ < X < μ+σ)=68.27%,即X偏离平均值超过1倍标准差的可能性为31.73%.为了提高数据准确度,可以设定该偏离平均值1倍标准差的区间为正常区间,若超出该区间,则视作异常数值.对本文的股票价格指数进行计算可知,μ=0.241 9,σ=0.566 3,由此得出股票价格指数的正常区间为(-0.324 4,0.808 2).分析数据可以发现,1991年、1992年、2006年、2007年及2008年的数据超出了正常区间,可以判定为异常数据.同时联系中国经济市场发展背景可以发现,在1991年与1992年,我国经济体制尚未完善,仅有少量股入市,供求关系极不平衡,出现了暴利的局面;2006年、2007年、2008年正值全球金融危机,中国股市受到了影响.本文认为在求股票的平均价格指数时,应该删除1991年、1992年、2006年、2007年以及2008年这5年的异常数据,通过对剩余21年的股票价格指数求平均值,得到市场平均收益率,Rm=8.16%.
对于地下综合管廊PPP项目,风险校正系数很难被直接估计,但它可以近似归属于证监会行业分类中的公共设施服务行业,因此可以用公共设施服务行业的风险校正系数来近似代替地下综合管廊PPP项目的风险校正系数.选取公共设施服务行业具有代表性的10家企业风险校正系数,求平均值作为该行业的风险校正系数.企业风险校正系数可以利用近5年企业股价数据,依据公式β=cov(R1, R2)/∂2(R2)来估计,其中R1为企业近5年来每月的股票价格指数,R2为上证综合指数近5年来每月的股票价格指数.
通过新浪财经网站,统计各公司从2012年6月至2017年5月共计60个月的股票数据,即每个月最后一个交易日的收盘价(不进行复权处理),计算出股票价格指数.利用同样的方式得到上证综指同时刻的价格指数,得到企业和上证综指价格指数的协方差和方差,如表 3所示.为了使统计的数据更加科学合理,将涉及停牌的企业从停牌当月至复牌前一个月的数据剔除.
| 表 3 公共设施服务板块上市公司风险校正系数 Table 3 Risk coefficient of listed companies for public service services |
通过以上计算可知,公共设施服务业的风险修正系数修正值为1.004,可以近似认为地下综合管廊PPP项目的风险修正系数为1.004.综上计算,能够得到特许经营期在15年及以下的地下综合管廊PPP项目投资收益率为R=3.065 9+1.004×(8.16-3.065 9)=8.18%;特许经营期在15年以上的地下综合管廊PPP项目投资收益率为R=3.547 9+1.004×(8.16-3.547 9)=8.178%.
在实际项目中,由于地下综合管廊项目投资巨大,社会资本方除使用自有资金外,必然会通过各种途径进行融资以满足项目投资需要.基于资本资产定价模型确定的项目投资收益率尚未考虑到项目因融资而产生的债务资金成本,加权平均资金成本法(weighted average cost of capital,WACC)综合考虑了项目股本资金成本和债务资金成本,将会使项目投资收益率测算更加合理,因此需要运用WACC对之前求得的项目投资收益率进行修正,计算公式为
| $ {\rm{WACC}} = {K_{\rm{e}}}\frac{E}{{E + D}} + {K_{\rm{d}}}\frac{D}{{E + D}}. $ | (2) |
式中:Ke为权益资金成本,可以用求得的项目投资收益率R替代;Kd为扣除所得税后的债务资金成本;E为项目股本资金;D为项目负债.
管廊项目的投资收益率包括了可用性资产回报率和日常维护利润率,本文假设两者均等于修正后的项目投资收益率.
3 基于多目标规划模型的入廊费和政府补贴确定地下综合管廊PPP项目的定价涉及政府、社会资本和管线用户3个利益主体,他们对于管廊项目价格的确定都有着自己的目标,因此在确定入廊费时要充分考虑三方的诉求.针对上述问题,可以借助多目标规划研究方法,综合考虑管线用户承受能力、政府财政能力和社会资本的合理预期收益,建立令三方满意的入廊费和政府补贴方案.
3.1 优先级的确定结合地下综合管廊PPP项目的实际情况,在模型构建时提出以下3个优化目标.1)管线用户的利益诉求;2)政府方的期望;3)社会资本方的利益诉求.
从项目属性及项目实施影响因素的角度,分别对这3个目标进行分析和优先级的确定.综合管廊的投资回报以及正常的运营管理维护需要有稳定的现金流作为支撑,综合管廊的主要收益来源是管线用户;因此,管线用户入廊与否是决定综合管廊项目能否成功的最关键因素,管线用户在利益诉求得到满足时才会积极入廊.可以将目标1确定为第1优先级.对于政府方而言,不仅希望综合管廊PPP项目的建设运营能够为社会公众提供优质的公共产品和服务,更希望能够通过该项目促进当地经济的发展,提升政府业绩.政府基于自身期望,对该项目制定的支持及补贴政策会对项目的进展产生较大的影响.可以将政府的期望作为第2优先级.此外,地下综合管廊PPP项目属于准公共产品,项目的实施目的是为了完善城市基础设施建设,不是鼓励社会资本一味地追求经济利益,应将社会资本的利益放在最后考虑,故社会资本的利益诉求处于第3优先级.
综合以上分析可以确定出:管线用户的优先级为P1,政府的优先级为P2,社会资本的优先级为P3.
3.2 目标函数和目标约束的搭建对于地下综合管廊项目使用者管线用户而言,入廊费越低越好,这样可以降低自身的使用成本;对于政府而言,期望是社会效益最大化,即一方面使社会资本获得适当的投资收益,另一方面是在管线用户承受能力许可的前提下,补贴越少越好,这样可以使财政资金有更多的发挥空间;对于社会资本而言,希望通过收取入廊费和政府补贴来弥补项目建设投资并获得预期的投资收益,出于商人逐利性的考虑,入廊费和政府补贴的总额越高越好.对于地下综合管廊项目的多目标规划,需要满足管线用户的承受能力、政府的财政支出能力和社会资本的投资收益3个目标.
对于管线用户来说,承受能力下的入廊费不应该超过期望目标值,因此管线用户的目标规划函数应该为min z=f(d+).
对于政府来说,补贴额度不应超过预期的补贴限额,政府的目标规划函数应为min z=f(d+).
对于社会资本来说,期望的入廊费收入和政府补贴额度之和不应低于根据合理收益率测算而来的总收费,因此社会资本方的目标规划函数应为min z=f(d-).
构建的目标函数为
| $ \min z = {P_1}d_1^ + + {P_2}d_2^ + + {P_3}d_3^ - . $ | (3) |
在构建目标函数后,需要确定目标函数的各个约束条件.从整体角度出发,首先应该满足社会资本获得的收入等于各管线用户缴纳的入廊费与政府补贴之和.假定管线用户从运营期第一年到最后一年以等额支付的方式向项目公司支付入廊费,政府每年提供的财政补贴额相等,故每年社会资本获得的收入Ws等于各管线用户每年缴纳的入廊费之和Wu与政府每年补贴R的总和,约束条件1为
| $ {W_{\rm{u}}} + R - {W_{\rm{s}}} = 0. $ | (4) |
最高优先级是管线用户.对于管线用户入廊费的计算方法主要有直埋成本法和多因素分析法.目前运用较广泛的是直埋成本法,它包括了以直埋方式敷设管线的直接成本和道路占用及挖掘修复等间接成本.优点是计算过程简单,管线用户可以清楚地比较入廊和不入廊产生的各自费用,得出的入廊费更容易被各管线用户接受;缺点是只考虑了管线用户因素,没有考虑到社会资本的项目建设投资对入廊费的影响,很难核算项目投资的回收期和收益.多因素分析法是综合考虑多方面因素后进行入廊费的计算,虽然计算过程相对复杂,且得出的入廊费结果相对偏高,但可以真实有效地反映管线用户真正应该承担多少入廊费,因此尝试采用多因素分析法求解入廊费.
首先,管线直埋成本是必须要考虑的因素.由于不同管线的直埋成本不同,假设一共有i种管线入廊,它们的直埋成本分别为ci.其次,要考虑直埋时管线更新带来的重新敷设成本因素.通常情况下,每种管线在使用了一定年限后都需要进行更新,故管线用户要为重新敷设支付成本(不包括管线费用).如果管线入廊,在更新管线时就不会产生这笔费用,假设每种管线在管廊设计使用年限内的更新次数为ki.此外要考虑到各管线置于综合管廊中,避免了管线破损及水热气泄漏等,从而节约成本,因此在入廊费的基础上设定系数α.为了简化计算,假设每家管线的入廊里程均和管廊所能提供的入廊里程相同.所有管线用户每年应缴纳的入廊费之和为
| $ {W_{{\rm{um}}}} = \alpha \sum {{c_i}{k_i}} \times \frac{{r{{\left( {1 + r} \right)}^{{t_2}}}}}{{{{\left( {1 + r} \right)}^{{t_2}}} - 1}}. $ | (5) |
式中:r为可用性资产回报率,t2为运营期.
通过多因素分析法计算得到的入廊费较高,管线用户的接受度较低,因此可以认为Wum是管线用户所能接受的最高价格,且管线用户更愿意支付比这个价格更低的费用,即Wu≤Wum,得到约束条件2:
| $ {W_{\rm{u}}} + d_1^ - - d_1^ + = {W_{{\rm{um}}}}. $ | (6) |
次优先级是政府.政府补贴主要包括了财政补贴和税收优惠两部分,其中财政补贴有中央专项补贴和地方补贴.《国务院办公厅关于推进城市地下综合管廊建设的指导意见》和财政部下发的《关于开展中央财政支持地下综合管廊试点工作的通知》中规定:中央财政对地下综合管廊试点城市提供专项资金补助,一共为期3年,直辖市、省会城市和其他城市每年分别补贴5亿、4亿和3亿.若该试点城市采用PPP模式运作综合管廊项目,则在上述补助的基础上增加补助10%.地方政府补贴是指为保证社会资本方获得合理收益,同时考虑使用者的承受能力,故由地方财政向项目公司提供财政补贴.上述文件提到,地方人民政府要在年度预算和建设计划中优先安排地下综合管廊项目,并纳入地方政府采购范围;但是地方政府的补贴是有一定限度的,即每年对当地所有PPP项目的财政补贴总额不能超过年度一般公共预算支出的10%,因此地方政府对地下综合管廊PPP项目每年的财政补贴额度需要综合考虑政府的补贴能力和补贴意愿.假设每年的财政补贴最高为Rf.
第二个是税收优惠方面.目前,我国关于PPP项目税收优惠政策的税种主要包括了企业所得税、增值税、耕地占用税、土地使用税、契税和印花税等.作为政府的另一种补贴方式,地下管廊项目根据地方政府关于PPP项目的优惠政策会获得相应的税收优惠,假设每年因税收优惠所获得的补贴最高为Rt.
通过上面的分析可知,政府每年的补贴限额为Rm=Rf+Rt,但是通常情况下政府有意愿将其中一部分补贴用于其他项目的扶持,所以每年的补贴额度应该小于或等于补贴限额,即R≤Rm,可得约束条件3:
| $ R + d_2^ - - d_2^ + = {R_{\rm{m}}}. $ | (7) |
最后一个优先级是社会资本.假设建设期为t1,运营期为t2,特许经营期为T(T=t1+t2).项目建设总投资额为S,建设总投资包括了工程费用、工程建设其他费用、预备费、专项费用和建设期利息,为了简化公式,假设建设投资均发生在建设期每年年初.由此测得的社会资本每年应收的可用性付费为
| $ {W_{{\rm{sr}}}} = \sum {{S_i}{{\left( {1 + r} \right)}^{{t_1} + 1 - i}}} \times \frac{{r{{\left( {1 + r} \right)}^{{t_2}}}}}{{{{\left( {1 + r} \right)}^{{t_2}}} - 1}}. $ | (8) |
式中:i表示建设期第i年,对应的Si表示该年建设投资,∑Si=S.
对于社会资本,期望的每年收入应该不低于Wsr,即Ws≥Wsr,可得约束条件4:
| $ {W_{\rm{s}}} + d_3^ - - d_3^ + = {W_{{\rm{sr}}}}. $ | (9) |
此外,在实际管廊的设计使用周期内,每种管线都会至少更新一次,没有一种管线可以在长达50~100年的时间内不进行更新.在考虑管线用户支付意愿的情况下,应对管线用户每年所缴纳的入廊费进行最小额度的限定,以区别于直埋成本法,即
| $ {W_{\rm{u}}} \ge {W_{{\rm{umin}}}} = 2\alpha \sum {{c_i}} \times \frac{{r{{\left( {1 + r} \right)}^{{t_2}}}}}{{{{\left( {1 + r} \right)}^{{t_2}}} - 1}}. $ | (10) |
通过以上分析研究,根据构建的目标函数和目标约束条件,得到如下的多目标规划模型:
| $ \left. \begin{array}{l} \min z = {P_1}d_1^ + + {P_2}d_2^ + + {P_3}d_3^ - ;\\ {W_{\rm{u}}} + R - {W_{\rm{s}}} = 0,\\ {W_{\rm{u}}} + d_1^ - - d_1^ + = {W_{{\rm{um}}}},\\ R + d_2^ - - d_2^ + = {R_{\rm{m}}},\\ {W_{\rm{s}}} + d_3^ - - d_3^ + = {W_{{\rm{sr}}}},\\ {W_{\rm{u}}} \ge {W_{{\rm{umin}}}},\\ {W_{\rm{u}}},R,{W_{\rm{s}}},{W_{{\rm{um}}}},{W_{{\rm{sr}}}},{R_{\rm{m}}},{W_{{\rm{umin}}}} \ge 0,\\ d_i^ + 、d_i^ - \ge 0;i = 1,2,3. \end{array} \right\} $ | (11) |
通过模型绘制函数图像求解,得到令三方满意的区域解;再根据优先级顺序,得到最终解.约定该最优点为A,所对应的每年政府补贴为RA,管线用户每年所缴纳的入廊费总额为WuA,通过反推求得各管线用户的入廊费.
4 日常维护费的确定日常维护费主要是用来补偿项目公司的日常维护和管理成本,由管线用户按年、季度或者月分期向项目公司支付.确定日常维护费主要考虑2个方面的问题:1)确定项目公司每年应该向各管线用户总共收取多少的日常维护费;2)确定各管线用户应该分别向项目公司缴纳多少的日常维护费.由于日常维护费远远小于入廊费的数额,各管线用户可以自行承担,假设日常维护费由各管线用户自己缴纳,政府不再对日常维护费进行补贴.
4.1 项目公司应收日常维护费的确定地下综合管廊项目的日常维护成本主要包括人工费、材料费、机械费、检测费、企业管理费、保险费、水电费、规费等几部分.根据管廊仓体类型的不同,各类型仓的日常维护成本不同.假定地下综合管廊有3种类型仓,它们每年的日常维护费分别为A1、A2和A3.通过以上研究可知,项目公司因提供管廊日常维护和管理服务,需要获得的日常维护利润率为r,因此项目公司每年应向各类型仓收取的日常维护费为Gi=Ai(1+r)(i=1, 2, 3).
4.2 各管线用户应缴日常维护费的确定在确定各管线用户应缴的日常维护费时,入廊管线占用管廊空间比例是一个必须要考虑的因素,因此将应缴的日常维护费拆分为各类型仓每个管线用户都必须缴纳的数额相等的基本维护费用B1和根据占用空间比例确定的空间占用费B2两部分.约定基本维护费用占应缴日常维护费的比例为λ1,空间占用费占应缴日常维护费的比例为λ2,其中λ1+λ2=1.
假设3种仓分别有管线ni种,每种管线的横截面积为Sij,每个仓所有管线的横截面积之和为Si,其中Si=∑Sij,i=1, 2, 3,j=1, 2, …, ni,故每个管线用户应缴纳的基本维护费用为
| $ {B_1} = \frac{{{\lambda _1}{G_i}}}{{{n_i}}}. $ | (12) |
每个管线用户应缴纳的空间占用费为
| $ {B_2} = \frac{{{S_{ij}}}}{{{S_i}}}{\lambda _2}{G_i}. $ | (13) |
综合式(12)、(13),可得每个管线用户每年应缴的日常维护费:
| $ B = {\lambda _1}\frac{{{G_i}}}{{{n_i}}} + {\lambda _2}\frac{{{S_{ij}}{G_i}}}{{{S_i}}}. $ | (14) |
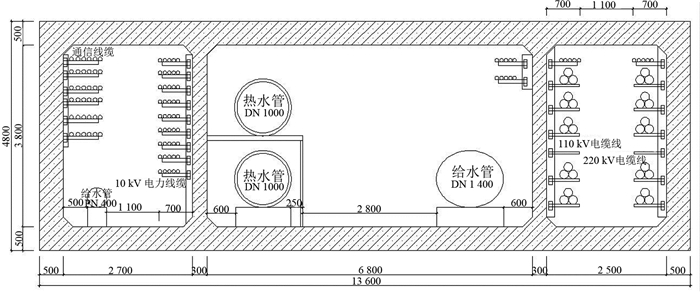
武汉沿江地下综合管廊PPP项目属于新建项目,管廊全长18.8 km,建设总投资549 364万元,合作期为30年,其中建设期为3年,运营期为27年,设计使用年限为100年.建设总投资在建设期内的各年投入比例分别为50%、30%、20%.项目股本资金占30%,融资成本为7%.综合管廊分3个舱室,分别是综合仓、管道仓和高压电力仓,共有4家单位管线入廊,分别是通信公司、电力公司、水务公司和供热公司,其中综合仓含通信、10 kV电力和给水3种管线,管道仓含给水和热水2种管线,高压电力仓含110 kV和220 kV 2种管线,综合管廊断面和各管线空间的占比情况分别如图 2和表 4所示.
|
图 2 武汉沿江地下综合管廊断面 Fig. 2 Wuhan Yanjiang utility tunnel section |
| 表 4 各入廊管线空间占比情况 Table 4 Proportion of each pipe line space |
首先,利用式(2)的WACC模型对项目投资收益率进行修正.结合案例所给的数据,可以得到可用性资产收益率和日常维护利润率为r=8.178%×30%+7%×70%×(1-25%)=6.13%.
经测算可知,通信管线一次性更新直埋成本约为4 366万元,电力管线一次性更新直埋成本约为13 077万元,给水管线一次性更新直埋成本约为7 659万元,热力管道一次性更新直埋成本约为11 574万元.通信管线的设计使用年限为15 a,电力管线的设计使用年限为20 a,给水管道的设计使用年限为50 a,热力管道的设计使用年限为50 a,因此它们在管廊设计使用年限内的更新次数分别为7次、5次、2次和2次.考虑现实情况,约定系数α=1.05.
根据式(5),可以得到所有管线用户每年应缴纳的入廊费之和最多为
| $ \begin{array}{l} {W_{{\rm{um}}}} = 1.05 \times \left( {4366 \times 7 + 13077 \times 5 + 7659 \times 2 + } \right.\\ \left. {11574 \times 2} \right) \times \frac{{6.13\% \times {{\left( {1 + 6.13\% } \right)}^{27}}}}{{{{\left( {1 + 6.13\% } \right)}^{27}} - 1}} = 10823\left( {万元} \right). \end{array} $ |
根据式(8),可以得到社会资本每年最少应收的可用性付费为
| $ \begin{array}{l} {W_{{\rm{sr}}}} = \left[ {549364 \times 50\% \times {{\left( {1 + 6.13\% } \right)}^3} + 549364 \times } \right.\\ \;\;\;\;\;\;30\% \times {\left( {1 + 6.13\% } \right)^2} + 549364 \times 20\% \times \\ \left. {\;\;\;\;\;\;{{\left( {1 + 6.13\% } \right)}^1}} \right] \times \frac{{6.13\% \times {{\left( {1 + 6.13\% } \right)}^{27}}}}{{{{\left( {1 + 6.13\% } \right)}^{27}} - 1}} = \\ \;\;\;\;\;\;48357\left( {万元} \right). \end{array} $ |
考虑武汉市政府的财政承受能力和支付意愿,参照当年的公共预算情况,得出政府每年能够对该项目提供的补贴限额为
| $ {R_{\rm{m}}} = 41000\left( {万元} \right). $ |
管线用户每年所缴纳的入廊费总和最小额度为
| $ \begin{array}{l} {W_{{\rm{umin}}}} = 2 \times 1.05 \times \left( {4366 + 13077 + 7659 + } \right.\\ \left. {11574} \right) \times \frac{{6.13\% \times {{\left( {1 + 6.13\% } \right)}^{27}}}}{{{{\left( {1 + 6.13\% } \right)}^{27}} - 1}} = 5906\left( {万元} \right). \end{array} $ |
通过以上数据,构建出多目标规划模型如下:
| $ \left. \begin{array}{l} \min z = {P_1}d_1^ + + {P_2}d_2^ + + {P_3}d_3^ - ;\\ {W_{\rm{u}}} + R - {W_{\rm{s}}} = 0,\\ {W_{\rm{u}}} + d_1^ - - d_1^ + = 10823,\\ R + d_2^ - - d_2^ + = 41000,\\ {W_{\rm{s}}} + d_3^ - - d_3^ + = 48357,\\ {W_{\rm{u}}} \ge 5906,\\ {W_{\rm{u}}}、R、{W_{\rm{s}}} \ge 0,\\ d_i^ + 、d_i^ - \ge 0;i = 1,2,3. \end{array} \right\} $ |
通过绘制函数图形求解,得到最优解A点,即每年政府补贴为41 000万元,管线用户每年所缴纳的入廊费总额为7 357万元.根据反推,可得各管线用户的入廊费.
通信公司每年应缴的入廊费为
| $ \begin{array}{l} \frac{{4366 \times 7}}{{4366 \times 7 + 13077 \times 5 + 7659 \times 2 + 11574 \times 2}} \times \\ \;\;\;\;\;\;7357 = 1673\left( {万元} \right) \end{array} $ |
电力公司每年应缴的入廊费为
| $ \begin{array}{l} \frac{{13077 \times 5}}{{4366 \times 7 + 13077 \times 5 + 7659 \times 2 + 11574 \times 2}} \times \\ \;\;\;\;\;\;7357 = 3579\left( {万元} \right) \end{array} $ |
水务公司每年应缴的入廊费为
| $ \begin{array}{l} \frac{{7659 \times 2}}{{4366 \times 7 + 13077 \times 5 + 7659 \times 2 + 11574 \times 2}} \times \\ \;\;\;\;\;\;7357 = 838\left( {万元} \right) \end{array} $ |
供热公司每年应缴的入廊费为
| $ \begin{array}{l} \frac{{11574 \times 2}}{{4366 \times 7 + 13077 \times 5 + 7659 \times 2 + 11574 \times 2}} \times \\ \;\;\;\;\;\;7357 = 1267\left( {万元} \right) \end{array} $ |
根据初步测算,了解到综合仓、管道仓和高压电力仓的运营及管理成本分别为25、35、20万元/(km·a).项目公司每年应向各类型仓收取的日常维护费分别为
| $ {G_1} = 25 \times 18.8 \times \left( {1 + 6.13\% } \right) = 498.8\left( {万元} \right), $ |
| $ {G_2} = 35 \times 18.8 \times \left( {1 + 6.13\% } \right) = 698.3\left( {万元} \right), $ |
| $ {G_3} = 20 \times 18.8 \times \left( {1 + 6.13\% } \right) = 399\left( {万元} \right). $ |
通过与政府、社会资本以及管线用户的访谈,约定基本维护费用占应缴日常维护费的比例为λ1=40%,空间占用费占应缴日常维护费的比例为λ2=60%.
在综合仓中,通信、10 kV电力、给水每年应缴的日常维护费分别为
| $ \begin{array}{l} {B_{11}} = 40\% \times \frac{{498.8}}{3} + 60\% \times 33.89\% \times \\ \;\;\;\;\;\;\;498.8 = 167.9\left( {万元} \right), \end{array} $ |
| $ \begin{array}{l} {B_{12}} = 40\% \times \frac{{498.8}}{3} + 60\% \times 45.48\% \times \\ \;\;\;\;\;\;\;498.8 = 202.6\left( {万元} \right), \end{array} $ |
| $ \begin{array}{l} {B_{13}} = 40\% \times \frac{{498.8}}{3} + 60\% \times 20.64\% \times \\ \;\;\;\;\;\;\;498.8 = 128.3\left( {万元} \right). \end{array} $ |
在管道仓中,给水和热力每年应缴的日常维护费分别为
| $ \begin{array}{l} {B_{21}} = 40\% \times \frac{{698.3}}{2} + 60\% \times 42.76\% \times 698.3 = \\ \;\;\;\;\;\;\;318.8\left( {万元} \right), \end{array} $ |
| $ \begin{array}{l} {B_{22}} = 40\% \times \frac{{698.3}}{2} + 60\% \times 57.24\% \times 698.3 = \\ \;\;\;\;\;\;\;379.5\left( {万元} \right). \end{array} $ |
在高压电力仓中,高压线每年应缴的日常维护费为B3=399(万元).
由此可知,通信公司、电力公司、水务公司和供热公司每年应缴的日常维护费分别为
| $ {C_1} = 167.9\left( {万元} \right), $ |
| $ {C_2} = 202.6 + 399 = 601.6\left( {万元} \right), $ |
| $ {C_3} = 128.3 + 318.8 = 447.1\left( {万元} \right), $ |
| $ {C_4} = 379.5\left( {万元} \right). $ |
分析计算结果可以发现,若按照该定价方式,可以在项目特许经营期的15年内回收全部建设投资,项目经济性良好.此外,每年应缴的日常维护费总和为1 596.1万元,高于每年的运营和管理成本1 504万元,即社会资本能够在该定价模式下获取一定利润.与该算例较类似的长沙高铁新城综合管廊项目作对比,两项目的建设年份、建设投资、特许经营期等基础数据较接近,长沙市综合管廊每年获得的入廊费和政府补贴约为3.5亿元,约占项目总投资的8.75%,每年向管线用户收取的日常维护费为80万元/km.在该案例中,每年入廊费和政府补贴之和约为4.8亿元,约占项目总投资的8.8%,日常维护费约为84.9万元/(km·a),可以认为计算结果与实际项目收费标准较接近,具有一定的参考价值.综上可以认为,研究的定价方法能够基本满足各方的利益诉求,结果有效可靠.
6 结语本文对地下综合管廊PPP项目的定价机制进行创新研究.与实际项目定价不同的是,本文采用资本资产定价模型和WACC模型确定项目可用性资产回报率和日常维护利润率.综合考虑管线用户承受能力、政府补贴能力以及社会资本合理收益等因素,构建令三方满意的多目标规划定价模型,从而得到各管线用户的入廊费和政府补贴方案.考虑入廊管线空间占比,求解各管线用户应缴的日常维护费,通过案例对研究内容进行验证分析.
本文在确定入廊费时,初次尝试使用多因素分析法.该方法综合考虑了影响综合管廊定价的多方面因素,能够切实反映出管线用户应缴纳的入廊费,弥补了使用直埋成本法时仅考虑管线用户因素而忽视社会资本投资因素对定价影响的不足;同时能够将PPP项目风险和收益紧密联系,这对综合管廊PPP项目的定价具有一定的参考价值.
| [1] |
王曦, 祝付玲. 基于博弈分析的城市综合管廊收费对策研究[J]. 地下空间与工程学报, 2013, 9(01): 197-203. WANG Xi, ZHU Fu-ling. Research of charge strategy for urban municipal utility tunnel based on game theory analysis[J]. Chinese Journal of Underground Space and Engineering, 2013, 9(01): 197-203. |
| [2] |
闫云辉. 梭鱼湾商务区综合管廊融资模式选择研究[D]. 大连: 大连理工大学, 2015. YAN Yun-hui. Reaearch of the financing mode selection about Suoyu bay business district municipal composite pipeline gallery[D]. Dalian: Dalian University of Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10141-1015355740.htm |
| [3] |
刘妍, 景凤梅, 姚丹阳, 等. 综合管廊PPP项目定价机制的设计研究[J]. 山西建筑, 2017, 43(16): 220-221. LIU Yan, JING Feng-mei, YAO Dan-yang, et al. On design for pricing mechanism of PPP program of comprehensive pipe gallery[J]. Shanxi Architecture, 2017, 43(16): 220-221. DOI:10.3969/j.issn.1009-6825.2017.16.120 |
| [4] |
崔启明, 张宏, 韦翔. 城市综合管廊收费定价模式探讨[J]. 建筑经济, 2016, 37(09): 11-15. CUI Qi-ming, ZHANG Hong, WEI Xiang. Research on the charge pricing model of urban utility tunnel[J]. Construction Economy, 2016, 37(09): 11-15. |
| [5] |
杜娅妮. 地下综合管廊项目PPP模式应用研究[J]. 建筑经济, 2016, 37(10): 58-61. DU Ya-ni. Application research on PPP model of underground pipe gallery project[J]. Construction Economy, 2016, 37(10): 58-61. |
| [6] |
王建. 城市地下市政综合管廊建设费分摊探讨[J]. 上海建设科技, 2008, 29(04): 66-67. WANG Jian. Discussion on construction fee allocation of urban underground pipe corridor[J]. Shanghai Construction Science and Technology, 2008, 29(04): 66-67. DOI:10.3969/j.issn.1005-6637.2008.04.024 |
| [7] |
丁晓敏, 张季超, 庞永师, 等. 广州大学城共同沟建设与管理探讨[J]. 地下空间与工程学报, 2010, 6(增1): 1385-1389. DING Xiao-min, ZHANG Ji-chao, PANG Yong-shi, et al. Discussion on construction and management of the common trench in Guangzhou university town[J]. Chinese Journal of Underground Space and Engineering, 2010, 6(supple.1): 1385-1389. |
| [8] |
宋定. PPP模式下公共管廊运营管理研究[D]. 北京: 北京建筑大学, 2014. SONG Ding. Research on the operations management of tube gallery based on PPP model[D]. Beijing: Beijing University of Civil Engineering and Architecture, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10016-1014332496.htm |
| [9] |
李平. 综合管廊定价标准研究[J]. 现代经济信息, 2016, 31(23): 338-340. LI Ping. Study on pricing standards of urban utility tunnel[J]. Modern Economic Information, 2016, 31(23): 338-340. |
| [10] |
邱玉婷. 我国城市共同沟项目的投融资分析[D]. 上海: 同济大学, 2008. QIU Yu-ting. Investment and financing model analysis for utility tunnel project in Chinese city[D]. Shanghai: Tongji University, 2008. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1245294 |
| [11] |
王英. 基于直埋成本法的地下综合管廊入廊费定价机制[J]. 建筑监督监测与造价, 2015, 8(6): 59-63. WANG Ying. The pricing mechanism for the urban utility tunnel's entrance fee based on the direct embedded cost method[J]. Supervision Test and Cost of Construction, 2015, 8(6): 59-63. |
| [12] |
杨卫华. 基于风险分担的高速公路BOT项目特许定价研究[D]. 大连: 大连理工大学, 2007. YANG Wei-hua. Concession pricing of BOT expressway projects based on risk allocation[D]. Dalian: Dalian University of Technology, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10141-2007211078.htm |
| [13] |
侯丽. 风险条件下收费公路PPP项目特许定价研究[D]. 昆明: 昆明理工大学, 2012. HOU Li. A study on the pricing of toll road PPP project under risk condition[D]. Kunming: Kunming University of Science and Technology, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10674-1012431392.htm |
| [14] |
杨俊萍. 基于系统观的PPP项目定价机制研究[D]. 重庆: 重庆大学, 2012. YANG Jun-ping. A study on the PPP project pricing mechanism based on the concept of system[D]. Chongqing: Chongqing University, 2012. http://d.wanfangdata.com.cn/Thesis/D305495 |
| [15] |
王洪强. 公共基础设施PPP项目定价研究[J]. 价格理论与实践, 2015(11): 141-143. WANG Hong-qiang. Research on PPP Pricing of Public Infrastructure[J]. Price Theory and Practice, 2015(11): 141-143. |
| [16] |
刘旭. 基于系统动力学的高速公路PPP项目定价研究[D]. 重庆: 重庆交通大学, 2016. LIU Xu. Research on the pricing of PPP expressway projects based on system dynamics[D]. Chongqing: Chongqing Jiaotong University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10618-1016165307.htm |
| [17] |
张宏, 崔启明, 韦翔. 城市综合管廊的PPP模式选择[J]. 价值工程, 2016, 35(33): 239-242. ZHANG Hong, CUI Qi-ming, WEI Xiang. The PPP Model Selection of Urban Utility Tunnel[J]. Value Engineering, 2016, 35(33): 239-242. |
| [18] |
刘光勇. PPP模式下地下综合管廊运营管理分析[J]. 城乡建设, 2016, 62(04): 31-33. LIU Guang-yong. Analysis of operation and management of urban utility tunnel using PPP mode[J]. Urban and Rural Development, 2016, 62(04): 31-33. DOI:10.3969/j.issn.1002-8455.2016.04.023 |
| [19] |
朱圆圆. 污水处理厂PPP项目的风险及投资决策的研究[D]. 杭州: 浙江大学, 2016. ZHU Yuan-yuan. PPP: the risk and investment decision in sewage treatment plant[D]. Hangzhou: Zhejiang University, 2016. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y3102755 |
| [20] |
屠新曙, 韦宏. 资本资产定价模型的适用条件分析[J]. 华南师范大学学报:自然科学版, 2013, 45(03): 36-39. TU Xin-shu, WEI Hong. The applicable condition analysis for capital asset pricing model[J]. Journal of South China Normal University:Natural Science Edition, 2013, 45(03): 36-39. |


