随着城市化进程的不断加快,“行车难、停车难”已成为我国新型城市化背景下的一大通病.国外一份报告里指出,城市交通中30%的交通拥堵是由于小汽车搜寻空余泊位导致的[1].
停车诱导信息系统(parking guidance and information system, PGIS)[2]和停车预约系统(parking reservation system, PRS)[3]作为两个停车智能化的应用,需要解决的一个共性问题是对停车场可用泊位的短时(单步)和长时(多步)预测.
对停车场泊位的预测方法主要分为两大类:统计分析方法[4-5]和机器学习方法[6-7].预测步长多为单步预测,少有对泊位的多步预测,Ji等[8]利用最大Lyapunov指数法进行多步预测,但由于计算复杂,无法满足实时性的要求.
目前很少有研究对停车场泊位占有率序列本身特性进行分析,未从数学角度对序列内部的动力学特性进行分析.Ji等[8-9]对停车场泊位占有率序列的短时预测研究的前提是占有率序列是混沌的,该结论暂无相关的理论依据,且应用混沌理论预测的精度无法满足停车预约系统的系统要求.
究其原因,停车场系统是一个典型的受人的行为影响的系统,如出行者的出行方式选择和到达目的地附近的停车行为选择都会对停车场的泊位变化产生影响.对于这种受人的行为影响的复杂系统,很难对该系统建立精确的数学模型并通过解析的方法研究该系统的原理.从系统的角度看,时间序列表征的是客观世界的某一动态过程,包括系统的行为特性和系统本身的固有特性等[10].传统的泊位预测仅将其作为一种一般的时间序列,从时域的角度统计的方法分析自相关系数、波动系数[6]等,未将其与停车场系统的本身特性联系起来,因此忽视了系统的本身的一些行为特性,这是将其简单地看作一组时间序列直接预测造成长时预测效果不佳的原因.
科学地对停车场泊位占有率序列的动力学特性进行研究,可以分析系统内部的非线性特性、序列的不规则程度等,对后续应用停车场的内部特性进行停车场运行效率分析、泊位预测、区域停车场诱导优化、缓解交通拥堵等具有重要意义.
本文分析泊位占有率序列的主分量谱判别序列的混沌特性,利用联合熵和改进的C0复杂度算法分别分析泊位占有率序列中的非线性动力学特性和不规则成分的含量.分析不同时段不同性质停车场的序列复杂性,基于复杂性测度分析提出在泊位长时预测时剔除不规则成分,对比分析该方法的预测效果.
1 时间序列动力学分析原理由于实际测量中,实测时间序列不可避免地带有噪声,这些噪声对时间序列分析带来一定困难.主分量分析法[11](principal components analysis, PCA)是一种有效区分噪声和混沌的方法,且对序列长度的要求较低,可以区分噪声和服从确定规律的信号(尤其是混沌序列).
在水文、控制、生物等领域,Lyapunov指数、分数维数和熵(如信息熵、Kolmogorov熵)等特征量[11]都被运用到序列非线性特性的研究中,但这些特征量的计算方法不成熟.比如,经典的Lyapunov指数计算方法很多种,如Wolf法、Jacobian法等,但由于受序列长度和噪声影响,只能在一定程度下可靠估计.由于频域分析在研究时间序列的周期波动等方面具有时域分析无法企及的优势,联合熵[12-14]可以表征两个信息之间的相关性,利用离散傅里叶变换对原始序列进行处理,分析原始序列中的非线性动力学特性;C0复杂度[15-16]可以度量序列中不规则成分的含量,分析序列的规则特性.本文从信号分析的角度出发,可以将一个时间序列看作各种周期扰动的叠加,应用离散傅里叶变换的思想对泊位占有率序列进行联合熵和C0复杂度的测度分析.
1.1 主分量分析(PCA)法主分量分析法是一种有效识别混沌和噪声的方法,具体的计算步骤如下.
1) 将原始时间序列X(n) (n=1, 2, …,N)以采样间隔τs进行相空间重构,嵌入维度为d(嵌入维度可以由混沌理论中的C-C方法[11]求解得到,本文对C-C法不作赘述,在实例分析中直接利用C-C法计算结果代入),计算该时间序列形成的轨线矩阵Xl×d(l=N-d+1):
| $ {\mathit{\boldsymbol{X}}_{l \times d}} = \frac{1}{{{l^{1/2}}}}\left[ {\begin{array}{*{20}{c}} {{x_1}}&{{x_2}}& \cdots &{{x_d}}\\ {{x_2}}&{{x_3}}& \cdots &{{x_{d + 1}}}\\ \vdots&\vdots &{}& \vdots \\ {{x_l}}&{{x_{l + 1}}}& \cdots &{{x_N}} \end{array}} \right] = \frac{1}{{{l^{1/2}}}}\left[ {\begin{array}{*{20}{c}} {{X_1}}\\ {{X_2}}\\ \vdots \\ {{X_l}} \end{array}} \right]. $ | (1) |
2) 计算协方差矩阵Ad×d:
| $ {\mathit{\boldsymbol{A}}_{d \times d}} = \frac{1}{l}\mathit{\boldsymbol{X}}_{l \times d}^{\rm{T}}{\mathit{\boldsymbol{X}}_{l \times d}}. $ | (2) |
3) 计算协方差矩阵Ad×d的特征值λi(i=1, 2, …, d)及各自对应的特征向量Ui(i=1, 2, …, d).将特征值按从大到小排序:λ1≥λ2≥…≥λd,则最大的特征值λ1对应的特征向量U1为主分量.
4) 计算所有特征值的总和γ:
| $ \gamma = \sum\limits_{i = 1}^d {{\lambda _i}} . $ | (3) |
5) 以i为x轴,ln (λi/γ)为y轴,作序列X(n)的主分量谱图.
由于混沌信号与噪声信号的主分量分布存在显著差异,噪声的主分量谱图是一条与x轴接近平行的直线,混沌信号的主分量谱图为过定点且斜率为负的直线.根据主分量谱图,可以有效地辨别序列是否为混沌信号.
1.2 联合熵计算方法在信息论[17]中,联合熵用来描述两个信息之间的相关性.从数学角度上讲,对于两个符号序列X、Y,状态数分别为m、n.联合熵是对符号集合XY上的每个元素对(xiyj)的联合自信息量的数学期望,数学表达式为
| $ H\left( {XY} \right) = - \sum\limits_{j = 1}^n {\sum\limits_{i = 1}^m {p\left( {{x_i}{y_j}} \right){{\log }_2}p\left( {{x_i}{y_j}} \right)} } . $ | (4) |
对时间序列信号X(n) (n=1, 2, …, N)进行符号化处理,对应的符号序列为S(n) (n=1, 2, …, N).定义序列划分状态数为M,研究中一般进行“四值符号化”[18]处理,即取M=4.按一定原则选取序列的M+1个分割点α(k),k=0, 1, …, M,以均值为界,将X(n)分为均值以下部分X1(n)和均值以上部分X2(n).选取α(0)=min(X(n)),α(1)=X1(n),α(2)=X(n),α(3)=X2(n),α(4)=max(X(n)).
按如下规则对序列符号化:
| $ \begin{array}{*{20}{c}} {{\rm{if}}\;\alpha \left( k \right) \le X\left( n \right) < \alpha \left( {k + 1} \right),{\rm{then}}\;\;\;S\left( n \right) = k.}\\ {n = 1,2, \cdots ,N,k = 0,1,2,3.} \end{array} $ | (5) |
特别地,若X(n)=max (X(n)),则S(n)=3,n=1, 2, …, N.
采用长度L=3的子序列分析几何分布率,共得到由M=4个符号组成的长度为3的子序列ML=43=64种状态.
利用联合熵对时间序列进行非线性动力学复杂性分析,需要对原始时间序列X进行离散傅里叶变换,对得到的功率谱各频率成分的相位作随机化变换,进行逆傅里叶变换,得到原始时间序列的替代序列Y.由于两序列的自相关函数不变,具有线性相关性.
具体的计算步骤如下.
1) 将原始时间序列X(n) (n=1, 2, …, N)进行离散FFT变换:
| $ \left. \begin{array}{l} x\left( k \right) = \sum\limits_{n = 1}^N {X\left( n \right)\exp \left[ { - \frac{{2{\rm{ \mathsf{ π} }}\left( {n - 1} \right)\left( {k - 1} \right)}}{N}i} \right];} \\ k = 1,2, \cdots ,N. \end{array} \right\} $ | (6) |
2) 将变换后的序列x(k) (k=1, 2, …, N)作相位随机化处理:
| $ \hat x\left( k \right) = x\left( k \right)\exp \left[ { - {\rm{i}}\varphi \left( k \right)} \right];k = 1,2, \cdots ,N. $ | (7) |
式中:φ(k)∈[-π, π],且满足斜对称条件[19],即当N为偶数时,
| $ \left. \begin{array}{l} \varphi \left( 1 \right) = \varphi \left( {N/2 + 1} \right) = 0,\\ \varphi \left( k \right) = \varphi \left( {N - k + 2} \right);k = 2,3, \cdots ,N/2 + 1. \end{array} \right\} $ | (8) |
当N为奇数时,
| $ \left. \begin{array}{l} \varphi \left( 1 \right) = 0,\\ \varphi \left( k \right) = - \varphi \left( {N - k + 2} \right);k = 2,3, \cdots ,\left( {N + 1} \right)/2. \end{array} \right\} $ | (9) |
3) 对
| $ \left. \begin{array}{l} Y\left( n \right) = \frac{1}{N}\sum\limits_{k = 1}^N {\hat x\left( k \right)\exp \left[ {\frac{{2{\rm{ \mathsf{ π} }}\left( {n - 1} \right)\left( {k - 1} \right)}}{N}i} \right];} \\ n = 1,2, \cdots ,N. \end{array} \right\} $ | (10) |
4) 对原始序列X(n)和替代序列Y(n)进行符号化处理,分别记作X0(n)和Y0(n),则联合熵为
| $ H\left( {{X_0},{Y_0}} \right) = - \sum\limits_{j = 1}^{{n_0}} {\sum\limits_{i = 1}^{{m_0}} {{p_{ij}}{{\log }_2}{p_{ij}}} } . $ | (11) |
式中:m0、n0分别为序列X0(n)和Y0(n)的状态数,pij为序列X0(n)的状态为i且序列Y0(n)的状态为j的概率.
根据信息论可知,联合熵越大,两者之间的相关性越弱.由于原始序列X(n)和替代序列Y(n)只有相同的线性特性,没有相同的非线性特性,两者的联合熵越大,说明序列的非线性动力学特性越明显,有更高的非线性动力学复杂性.
1.3 改进C0复杂度计算方法C0复杂度主要用来判别序列中非规则成分所占的比例,计算的主要思想是将序列分解成规则成分和不规则成分,具体的计算步骤如下.
1) 将原始时间序列X(n) (n=1, 2, …,N)进行离散FFT变换,得到序列x(k) (k=1, 2, …,N).
2) 计算功率谱x(k) (k=1, 2, …, N)的均方值为
| $ {G_N} = \frac{1}{N}\sum\limits_{k = 1}^N {{{\left| {x\left( k \right)} \right|}^2}} . $ | (12) |
按如下规则变换得到序列
| $ \hat x\left( k \right) = \left\{ \begin{array}{l} x\left( k \right),{\left| {x\left( k \right)} \right|^2} > r{G_N};\\ 0,其他. \end{array} \right. $ | (13) |
式中:r为参数,且r>1.
3) 对
| $ {\rm{C0}} = \frac{{\sum\limits_{n = 1}^N {{{\left| {X\left( n \right) - Y\left( n \right)} \right|}^2}} }}{{\sum\limits_{n = 1}^N {{{\left| {X\left( n \right)} \right|}^2}} }}. $ | (14) |
改进的C0复杂度算法通过引入参数r,随着r的增大,去掉的不规则部分越多,C0测度值将相应增加,推荐r的取值为5~10[16].
根据算法原理得出如下结论:对于周期序列或常数序列,当N→∞时,C0→0;对于均值为0的随机序列,当N→∞时,C0以概率1收敛于1.
2 停车场泊位占有率时间序列分析 2.1 停车场泊位序列预处理目前,停车场的管理模式逐步由人工管理向智能化管理改变,停车场进出口闸机的进出记录为有效分析停车场泊位占有率序列的动力学特性、预测停车场有效泊位等智能信息化应用提供了可能.本文采集的原始数据为杭州市某公共停车场进、出口闸机刷卡记录,停车场入口控制系统记录了停车场名称、出入口名称、车辆到达时间、车辆离开时间、车牌号、空余泊位数和停车数等15个字段(见表 1).
| 表 1 原始数据字段及含义说明 Table 1 Original data fields and meaning |
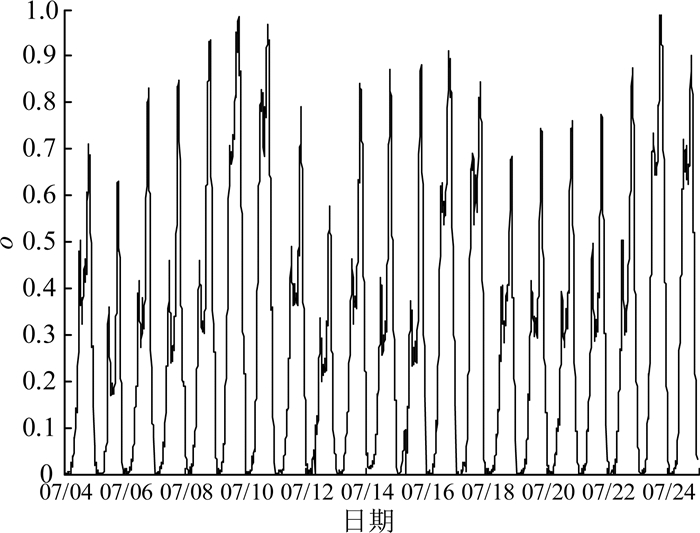
对原始数据进行校核,根据记录时间处理得到不同时间间隔的停车场实际泊位占有率序列.泊位占有率指当前时刻停车场中实际停放的车辆数占停车场容量的比例.如图 1所示为杭州市某停车场7月4日~7月24日共3周的泊位占有率变化图(采样时间间隔ts=5 min),其中o为泊位占有率,0 < ο < 1.
|
图 1 某公共停车场泊位占有率变化图 Fig. 1 Variation curve of public parking space occupancy |
选取线性序列、周期序列(正弦序列)、典型一维混沌序列(Logistic映射)、典型二维混沌序列(Henon映射)[11]和随机序列(高斯噪声),与实测泊位占有率序列对比.对比不同信号的主分量谱图,初步辨别泊位占有率信号的特性.所选取的对比序列如下.
1) 线性序列:x(t)=2t+3.
2) 周期序列:x(t)=sin (t/10).
3) 随机序列:产生均值为0、方差为1的高斯白噪声.
4) Logistic序列:x(t+1)=3.9x(t)(1-x(t))(舍弃前2 000点).
5) Henon序列:x(t+1)=1+y(t)-1.3x2(t), y(t+1)=0.3x(t)(舍弃前2 000点).
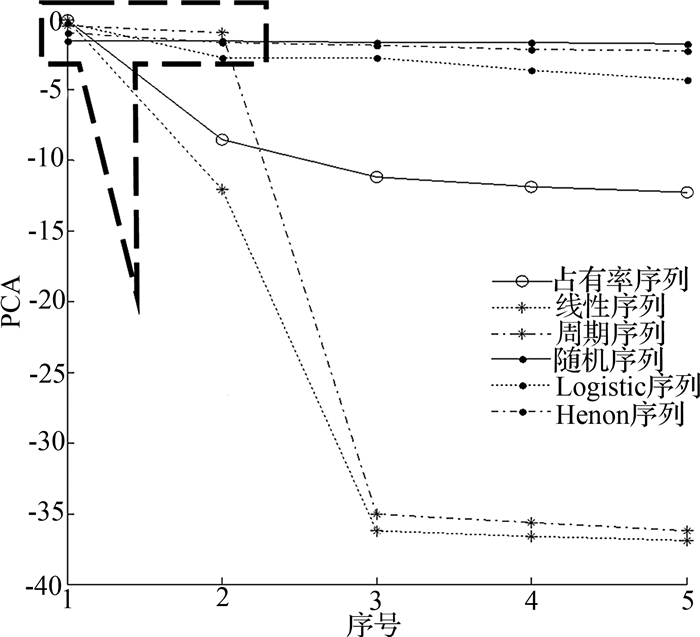
根据C-C法计算出泊位占有率序列的嵌入维度为5,计算并画出各序列的主分量谱,如图 2所示.图中,PCA为不同信号的分量值.
|
图 2 不同序列的主分量谱图 Fig. 2 Principal component spectra of different sequences |
由主分量谱图可以看出,噪声信号的主分量谱图近似为一条平行于x轴的直线,混沌序列的主分量谱近似一条斜率为负的直线,周期和线性序列的主分量谱集中在主分量和次主分量部分.由泊位占有率序列的主分量谱可以看出,泊位占有率序列的主分量过定点(1, 0),谱特征介于混沌序列和规则序列之间,偏向于混沌序列.可以初步判定,泊位占有率序列不是噪声信号,偏向于混沌信号.
2.3 停车场泊位占有率序列复杂性测度分析选取上述5种典型信号,分别计算不同序列长度下的联合熵和C0复杂度,验证提出的复杂性测度方法的有效性.如表 2、3所示分别为部分序列长度下的联合熵与C0复杂度测度结果.表中,H为联合熵的测度值,C为C0复杂度的测度值.
| 表 2 典型序列的联合熵 Table 2 Joint entropy of typical sequences |
| 表 3 典型序列的C0复杂度曲线 Table 3 C0 complexity of typical sequences |
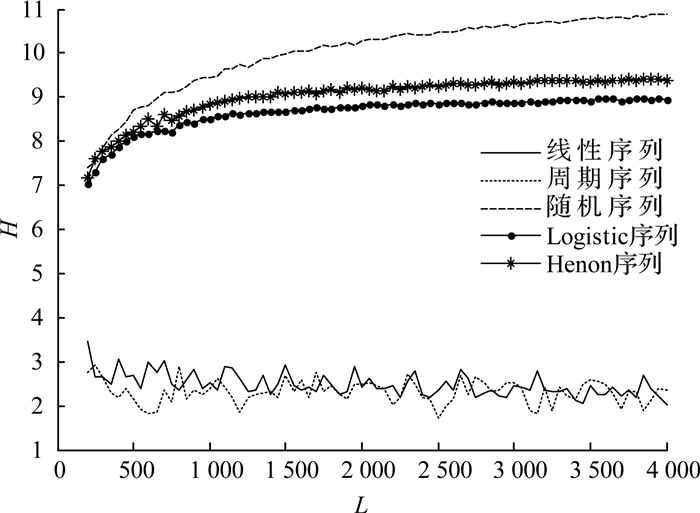
如图 3、4所示分别为不同序列长度下各种典型序列的联合熵与C0复杂度测度曲线.图中,L为序列长度.由图 3可以看出,线性序列和周期序列这两种有序序列的线性成分较大,因此联合熵较小,随机序列是无序序列,它的联合熵最大.两种混沌序列处于有序跟无序之间,当序列长度较短时,序列的随机性较大,因此联合熵与随机序列较接近,但随着序列长度的增加,混沌与随机序列的差别越来越明显.联合熵可以作为识别信号非线性特征的一个量度.
|
图 3 典型序列在不同序列长度下的联合熵曲线图 Fig. 3 Joint entropy of typical sequences at different sequence lengths |
|
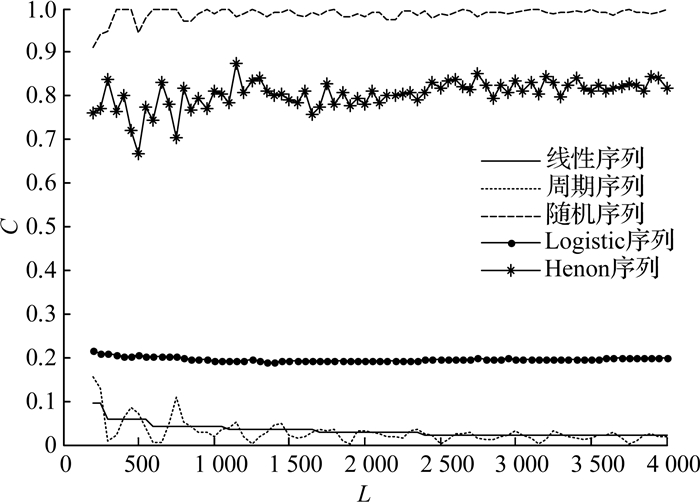
图 4 典型序列在不同序列长度下的C0复杂度曲线 Fig. 4 C0 complexity diagram of typical sequences at different sequence lengths |
由图 4可以看出,随着序列长度的增加,线性序列和周期序列两种有序序列的C0复杂度越来越小,逐渐趋近于0;随机序列的C0复杂度逐渐趋近于1.这与改进的C0复杂度性质吻合.混沌序列介于有序、无序之间,且一阶混沌序列(Logistic序列)的不规则成分明显比二阶混沌序列(Henon序列)小.C0复杂度可以作为识别信号不规则特征的一个量度.
对杭州市主城区5个典型公共停车场3周的泊位占有率序列进行分析,分别记作停车场A、B、C、D和E,停车场A、B、C主要服务附近商务办公,停车场D主要服务附近住宅小区,停车场E主要服务附近商业餐饮.
由于不同停车场的服务对象不同,工作日和周日的停车特征可能存在不同,对全周(7×3天)、工作日(5×3天)、周日(2×3天)3种不同时间的序列进行复杂性测度.由于停车场的泊位在夜间的变化较小,选取0:00—24:00和6:00—21:00两种不同时间段,对不同采样间隔下的泊位占有率序列进行复杂性测度分析.为了下文分析方便,对全周(7×3天)24 h分析记作情形1,对全周(7×3天)6:00—21:00分析记作情形2,对工作日(5×3天)24 h分析记作情形3,对工作日(5×3天)6:00—21:00分析记作情形4,对周日(2×3天)24 h分析记作情形5,对周日(2×3天)6:00—21:00分析记作情形6.由于停车场的泊位变化不像交通流变化快,过小的采样间隔会增加序列冗杂度,加重后续处理的速度且无实际意义;过长的采样间隔可能会遗失实际序列的某些特征,因此采用5、10、30 min 3种采样间隔.不同情形序列在不同采样间隔下的联合熵和C0复杂度测试结果分别如表 4、5所示.
| 表 4 实测泊位序列在不同采样间隔和情形下的联合熵 Table 4 Joint entropy of parking space occupancy series at different sampling intervals and different cases |
| 表 5 实测泊位序列在不同采样间隔和情形下的C0复杂度 Table 5 C0 complexity of parking space occupancy series at different sampling intervals and different cases |
对比几种典型序列的联合熵可知,泊位占有率序列的联合熵基本介于周期序列和混沌序列之间,且更接近于有序序列.说明泊位占有率序列有部分非线性动力学特性,但线性动力学特性更多,这是由停车场本身的属性决定的;停车场泊位的变化直接取决于车辆的到达率和停车率,间接与天气、停车行为选择等有关,车辆的到达率和停车率的特性决定了泊位占有率序列的动力学特性.分析C0复杂度测度值可知,泊位占有率序列的C0复杂度较小,更接近于线性序列或周期序列,这验证了联合熵的测度结果,说明泊位占有率序列的线性动力学特性更明显.
1) 随着采样时间间隔的增加,各情形下的联合熵和C0复杂度基本会略有上升,说明过大的采样间隔会增大序列的非线性和不规则性.特殊地,停车场E在情形6下C0复杂度随着采样间隔的增加略有下降,原因可能是停车场E主要服务周边商业,周末白天6:00—21:00的泊位变化较大,过大的采样间隔削去了序列中的不规则特征,造成部分原有信息的丢失.
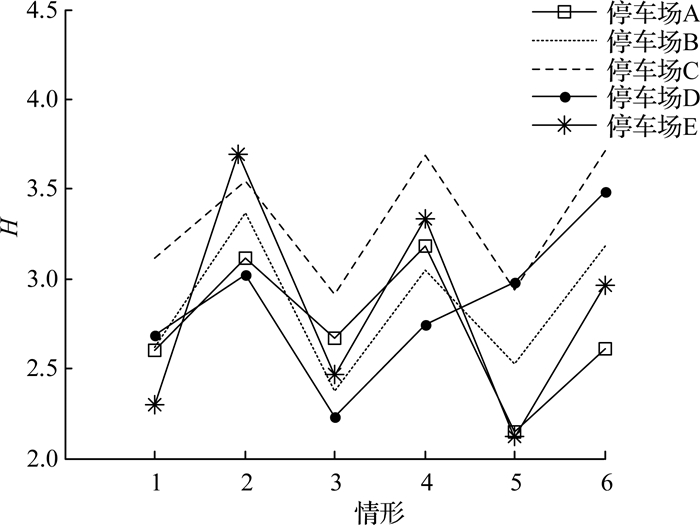
2) 在相同的采样间隔下,剔除21:00—第二天6:00期间的序列后,联合熵相较于全天24 h的联合熵明显大(见图 5),即夜间泊位变化的非线性特性较小.对比分析情形1、3、5(或者情形2、4、6)可知,同一停车场不管区不区分工作日与周末,联合熵基本相当,即泊位序列变化的线性特性受工作日或周末的影响较小.
|
图 5 不同情形下的联合熵变化曲线(ts=5 min) Fig. 5 Variation curve of joint entropy at different cases(sampling interval is 5 min) |
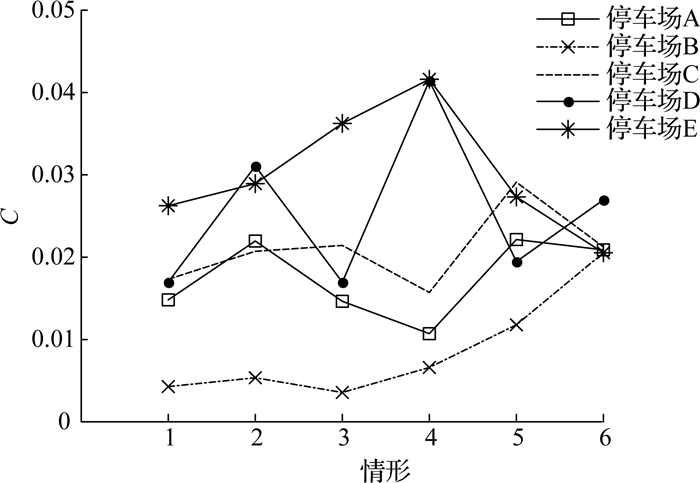
3) 在相同的采样间隔下,C0复杂度的变化特征比较复杂(见图 6),其C0复杂度值相差近一个数量级,这与停车场的服务性质相关.在不区分工作日和周日的情况下,剔除夜间的泊位序列后,C0复杂度均略有提高.在工作日情况下,剔除夜间的泊位序列后,停车场A、B和C的复杂度相当,因为这3个停车场主要服务周边商务办公,白天主要以通勤车辆为主,服务人群相对固定,C0复杂度较小;停车场D和E主要服务住宅小区和商业,白天停车行为的不规则性相较于全天会明显提高,因此C0复杂度较高.在周末情况下,除了停车场E完全服务于商业外,其余4个停车场周边也有一些商业,因此周末基于商业的出行行为基本相当,C0复杂度比较接近.
|
图 6 不同情形下的C0复杂度变化曲线(ts=5 min) Fig. 6 Variation curve of C0 complexity at different cases(sampling interval is 5 min) |
根据2种复杂性测度指标,可以得出如下结论:停车场泊位占有率序列有比较明显的规则特征,线性动力学特征较非线性特性明显,可以将其视作一种“拟周期”序列;泊位序列变化的线性特性受工作日或周末的影响较小;不同性质停车场根据服务性质区分C0复杂度有一定区别.
3 基于复杂度分析的泊位长时预测现有的泊位预测局限于单步预测(短时预测),对于长时预测的研究较少.根据停车场系统的“拟周期”特性,在长步预测时过滤非规则成分,提高预测精度.由于泊位序列中所包含的不规则成分很少,对极不规则部分序列的短时预测存在一定的可能,但在长步预测时很难预测,可能会增大预测偏差.
利用C0复杂度的计算思想,在多步预测时剔除极不规则的部分序列,直接对规则部分进行预测.为了验证该方法的有效性,采用遵循结构风险最小化(structural risk minimization, SRM)原则的核函数机器学习方法——最小二乘支持向量机[20](least squares support vector machine, LSSVM)进行验证.LSSVM与SVM的最大区别在于它将SVM中的不等式约束变成了等式约束,数学解析解相对固定,克服了NN方法训练结果不稳定的固有缺陷.
以停车场B和D的7月4日~7月7日的泊位序列为训练集,对7月8日的泊位进行长时预测(预测1~2 h后的泊位数量,步长为5 min).衡量指标取均方误差MSE:
| $ {\rm MSE }= \frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{{\hat y}_i} - {y_i}} \right)}^2}} . $ | (15) |
式中:yi为实际泊位数,
| 表 6 长时预测下的MSE结果 Table 6 Joint entropy of parking space occupancy series |
由表 6可以看出,在利用C0复杂度剔除掉极不规则成分之后,长时预测的精度大大提高,相比于直接利用LSSVM预测提高了26%~56%.另外可以看出,停车场B在剔除极不规则成分之后,预测MSE基本稳定,不像停车场D随着预测时长的增加而增加.分析两者工作日的C0复杂度可以看出,停车场B的C0复杂度较停车场D小得多,这是出现该现象的原因.
4 结语本文通过分析各种类型序列的主分量谱图,排除了停车场泊位占有率序列是噪声序列的可能性.通过分析序列的联合熵和C0复杂度两种复杂性测度指标,可以得出以下结论:1)停车场的泊位占有率序列有较明显的规则特征,线性动力学特征较非线性特性明显,可以看作是一种“拟周期”序列;2)泊位序列变化的线性特性受工作日或周末的影响较小;3)不同服务性质的停车场在工作日序列中的不规则成分含量有明显区别.应用C0复杂度的计算思想,在多步预测时剔除极不规则部分成分.结果表明,长时预测的精度大大提高.
本文方法的优势如下:1)将傅里叶变换的思想引入到停车场泊位占有率序列的分析中,从频域的角度分析停车场序列特性;2)利用C0复杂度算法思想剔除序列中不规则成分后进行长时预测,预测精度有较大提高.
在后续研究中,根据停车场系统的“拟周期”特性,从停车场系统的基本原理出发,分析引起停车场泊位占有率变化的外部输入变量特征.进一步挖掘系统中的规则特征,实现泊位占有率的实时多步的高精度预测.
| [1] |
SHOUP D. Cruising for parking[J]. Transport Policy, 2006, 13(6): 479-486. DOI:10.1016/j.tranpol.2006.05.005 |
| [2] |
THOMPSONR G, BONSALL P. Drivers' response to parking guidance and information systems[J]. Transport Reviews, 1997, 17(2): 89-104. |
| [3] |
LIU W, YANG H, YIN Y. Expirable parking reservations for managing morning commute with parking space constraints[J]. Transportation Research Part C Emerging Technologies, 2014, 44(4): 185-201. |
| [4] |
MAJIDI A, POLAT H, ÇETIN A. Finding a best parking place using exponential smoothing and cloud system in a metropolitan area[C]//International Istanbul Smart Grid Congress and Fair. Istanbul: [s. n. ], 2016. http://ieeexplore.ieee.org/document/7492439/
|
| [5] |
CALISKAN M, BARTHELS A, SCHEUERMANN B, et al. Predicting parking lot occupancy in vehicular Ad Hoc networks[C]//Vehicular Technology Conference. Dublin: [s. n. ], 2007: 277-281. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=4212497
|
| [6] |
JI Y, TANG D, BLYTHE P, et al. Short-term forecasting of available parking space using wavelet neural network model[J]. Journal of Southeast University, 2014, 9(2): 202-209. |
| [7] |
ZHENG Y, RAJASEGARAR S, LECKIE C. Parking availability prediction for sensor-enabled car parks in smart cities[C]//IEEE 10th International Conference on Intelligent Sensors, Sensor Networks and Information Processing. Singapore: IEEE, 2015. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=7106902
|
| [8] |
JI Y, TANG D, GUO W, et al. Forecasting available parking space with largest Lyapunov exponents method[J]. Journal of Central South University, 2014, 21(4): 1624-1632. DOI:10.1007/s11771-014-2104-3 |
| [9] |
陈群, 晏克非, 王仁涛, 等. 基于相空间重构及Elman网络的停车泊位数据预测[J]. 同济大学学报:自然科学版, 2007, 35(5): 607-611. CHEN Qun, YAN Ke-fei, WANG Ren-tao, et al. Parking space information prediction based on phrase construction and Elman neuraI network[J]. Journal of Tongji University:Natural Science, 2007, 35(5): 607-611. |
| [10] |
SHUMWAY R H, STOFFER D S. Time series analysis and its applications[M]. New York: Springer, 2009, 119-160.
|
| [11] |
吕金虎, 陆君安, 陈士华. 混沌时间序列分析及其应用[M]. 武汉: 武汉大学出版社, 2002, 49-92.
|
| [12] |
LI P, LI K, LIU C, et al. Detection of coupling in short physiological series by a joint distribution entropy method[J]. IEEE Transactions on Biomedical Engineering, 2016, 63(11): 2231-2242. DOI:10.1109/TBME.2016.2515543 |
| [13] |
李锦, 宁新宝, 马千里. 用联合熵分析短时心率变异信号的非线性动力学复杂性[J]. 生物医学工程学杂志, 2007, 24(2): 285-289. LI Jin, NING Xin-bao, MA Qian-li. Nonlinear dynamical complexity analysis of short-term heartbeat series using joint entropy[J]. Journal of Biomedical Engineering, 2007, 24(2): 285-289. |
| [14] |
张勇, 关伟. 基于联合熵和C0复杂度的交通流复杂性测度[J]. 计算机工程与应用, 2010, 46(15): 22-24. ZHANG Yong, GUAN Wei. Complexity measure of traffic flow based on union entropy and C0 complexity[J]. Computer Engineering and Applications, 2010, 46(15): 22-24. |
| [15] |
TONG C, HUANG Q, LIU H. Analysis on runoff time series dynamics character based on complexity theory[J]. Systems Engineering-theory and Practice, 2004, 9: 102-107. |
| [16] |
蔡志杰, 孙洁. 改进的C0复杂度及其应用[J]. 复旦学报:自然科学版, 2008, 47(6): 791-796. CAI Zhi-jie, SUN Jie. Modified C0 complexity and applications[J]. Journal of Fudan University:Natural Science, 2008, 47(6): 791-796. |
| [17] |
科费, 托马斯. 信息论基础[M]. 北京: 机械工业出版社, 2005, 7-13.
|
| [18] |
史永胜, 姜颖, 宋云雪. 基于符号序列联合熵的航空发动机健康监控方法[J]. 航空动力学报, 2011, 26(3): 670-674. SHI Yong-sheng, JIANG Ying, SONG Yun-xue. Aero-engine health monitoring method based on joint entropy of symbolic series[J]. Journal of Aerospace Power, 2011, 26(3): 670-674. |
| [19] |
雷敏, 王志中. 非线性时间序列的替代数据检验方法研究[J]. 电子与信息学报, 2001, 23(3): 248-254. LEI Min, WANG Zhi-zhong. Study of the surrogate data method for nonlinearity of time series[J]. Journal of Electronics and Information Technology, 2001, 23(3): 248-254. |
| [20] |
GESTEL T, SUYKENS J A K, BASTAENS D E, et al. Financial time series prediction using least squares support vector machines within the evidence framework[J]. IEEE Transactions on Neural Networks, 2001, 12(4): 809-821. DOI:10.1109/72.935093 |


