2. 上海交通大学 电力传输与功率变换控制教育部重点实验室, 上海 200240
2. Key Laboratory of Control of Power Transmission and Conversion, Ministry of Education, Shanghai Jiao Tong University, Shanghai 200240, China
预测控制在工业过程控制中得到了广泛应用, 已经发展成为一个具有丰富理论和实践内容的新的学科分支[1-2].从20世纪90年代以来, 不确定性系统的鲁棒预测控制迅速成为预测控制理论研究的热点[3-5].针对线性时变系统(linear parameter varying system, LPV system), 通过控制不变集和线性矩阵不等式方法(linear matrix inequality, LMI)设计鲁棒预测控制器, 取得了一系列的研究成果[6-16].
LPV系统中的时变参数, 一般可以分为当前可测和当前不可测两种情况.当LPV系统的时变参数不可测量时, Kothare等[6]引入椭圆不变集设计, 将鲁棒预测控制问题转化为半正定规划(SDP)问题.Ding等[17]通过在椭圆不变集外附加N个自由引导变量, 进一步扩大系统设计的自由度, 改善控制性能.Li等[18]提出多步控制集的概念, 在扩大初始可行域和提高控制性能方面可以取得很好的控制效果.Zheng等[19]提出设计基于单一控制律和参数增益调度控制律序列的多步混合反馈预测控制策略, 通过在首步椭圆集采用单一控制律, 在余下的椭圆集系列采用参数增益调度控制序列, 在计算量和控制性能之间实现了有效平衡; 当LPV系统的时变参数当前可测时, 利用时变参数的当前测量信息将有望进一步提高系统的控制性能.Park等[20-22]设计动态输出反馈鲁棒模型预测控制的综合方法.现有的状态反馈预测控制方法围绕参数变化速度有界的特殊情形, 开展控制器设计研究[23-26].Zheng等[23-25]首先预测系统未来模型, 不仅利用参数测量信息, 而且利用参数变化速度幅值受限信息, 改善对系统未来模型动态演化进行预测的精确度.随后, 通过设计优化算法以扩大鲁棒预测控制算法的自由度, 提高系统控制性能.Zheng等[26]在多步控制集的每一步椭圆集中均采用参数增益调度控制, 以增加在线计算量为代价, 有效地扩大了控制设计的自由度, 优点体现为改善控制性能, 缺点表现为在线计算量繁重.
本文考虑LPV系统参数可测但参数变化速度未知的一般化情形, 设计状态反馈预测控制器.鉴于Zheng等[26]采用参数增益调度控制可以扩大设计自由度和改善控制性能的优点, 本文尝试在控制算法设计过程中引入该设计思想, 以提高系统控制性能.直接引入文献[26]的控制设计思想, 虽然可以提高系统控制性能, 但会导致产生类似文献[26]具有的繁重在线计算负担.为了在系统控制性能和在线计算量之间进行有效的平衡, 本文设计基于参数增益调度反馈控制律和普通反馈控制律序列的混合反馈鲁棒预测控制策略, 即在多步控制集的首步椭圆集采用参数增益调度控制, 在余下的椭圆集序列采用普通反馈控制律序列.该设计方法弥补了文献[26]在多步控制集的每一步椭圆集中均采用参数增益调度反馈控制律所造成的繁重在线计算负担, 将以较低的优化计算量取得较优的控制性能, 在控制性能和在线计算量之间取得有效平衡.
1 问题描述考虑如下不确定系统:
| $ \mathit{\boldsymbol{x}}\left( {k + 1} \right) = \mathit{\boldsymbol{A}}\left( k \right)\mathit{\boldsymbol{x}}\left( k \right) + \mathit{\boldsymbol{B}}\left( k \right)\mathit{\boldsymbol{u}}\left( k \right). $ | (1) |
式中: x和u分别为可测的系统状态和控制输入, x ∈ Rn, u ∈ Rni.
系统模型的不确定性可以用多胞形式描述:
| $ \left. {\begin{array}{*{20}{c}} {\left[ {\mathit{\boldsymbol{A}}\left( k \right)\left| {\mathit{\boldsymbol{B}}\left( k \right)} \right.} \right] \in {\mathit{\boldsymbol{P}}_{{\rm{org}}}};}\\ {{\mathit{\boldsymbol{P}}_{{\rm{org}}}} = {\rm{Co}}\left\{ {\left( {{\mathit{\boldsymbol{A}}_1}\left| {{\mathit{\boldsymbol{B}}_1}} \right.} \right), \cdots ,\left( {{\mathit{\boldsymbol{A}}_{{n_{\rm{p}}}}}\left| {{\mathit{\boldsymbol{B}}_{{n_{\rm{p}}}}}} \right.} \right)} \right\}.} \end{array}} \right\} $ | (2) |
| $ \left[ {\mathit{\boldsymbol{A}}\left( k \right)\mathit{\boldsymbol{B}}\left( k \right)} \right] = \sum\limits_{l = 1}^{{n_{\rm{p}}}} {{\lambda _l}\left( k \right)\left[ {{\mathit{\boldsymbol{A}}_l}\left| {{\mathit{\boldsymbol{B}}_l}} \right.} \right]} . $ | (3) |
| $ \sum\limits_{l = 1}^{{n_{\rm{p}}}} {{\lambda _l}\left( k \right)} = 1;{\lambda _l}\left( k \right) \ge 0,l = 1,2, \cdots ,{n_{\rm{p}}}. $ | (4) |
式中:(Al|Bl)为多胞系统Porg的顶点; np为多胞系统的顶点数目; [A(k)B(k)]为多胞顶点的凸组合; λ(k)=[λ1(k), λ2(k), …, λnp(k)]T为当前k时刻的系统时变参数, 即凸组合系数, 并且假设该时变参数在当前时刻可测.可知, 在控制算法的设计过程中, 若能够有效地利用该参数可测信息, 则可以进一步提高系统的控制性能.
输入约束和状态约束为
| $ \left. \begin{array}{l} \left| {{u_i}\left( k \right)} \right| \le {{\bar u}_i}\left( {i = 1, \cdots ,{n_i}} \right),\left| {{\mathit{\boldsymbol{F}}_j}\mathit{\boldsymbol{x}}\left( k \right)} \right| \le {{\bar x}_j};\\ j = 1, \cdots ,{n_x}. \end{array} \right\} $ | (5) |
控制性能指标如下:
| $ J\left( k \right) = \sum\limits_{j = 0}^\infty {\left( {\left\| {\mathit{\boldsymbol{x}}\left( {k + j\left| k \right.} \right)} \right\|_\mathit{\boldsymbol{L}}^2 + \left\| {\mathit{\boldsymbol{u}}\left( {k + j\left| k \right.} \right)} \right\|_\mathit{\boldsymbol{R}}^2} \right)} . $ | (6) |
式中: L >0, R >0为对称加权矩阵.
通常, 无穷时域预测控制在线优化问题可以表示为
| $ \left. \begin{array}{l} \mathop {\min }\limits_{\mathit{\boldsymbol{u}}\left( {k + j\left| k \right.} \right),j \ge 0} \mathop {\max }\limits_{\left[ {\mathit{\boldsymbol{A}}\left( {k + j} \right)\left| {\mathit{\boldsymbol{B}}\left( {k + j} \right)} \right.} \right] \in {\mathit{\boldsymbol{P}}_{{\rm{org}}}},j \ge 0} J\left( k \right);\\ {\rm{s}}.\;{\rm{t}}.\;式\left( 1 \right) \sim \left( 6 \right). \end{array} \right\} $ | (7) |
针对描述的参数可测的LPV系统, 设计能够有效利用参数当前可测信息的鲁棒预测控制算法, 进而优化系统的控制性能.
考虑Zheng等[19]设计的多步混合反馈预测控制算法, 由于该算法在首步椭圆集内采用单一控制律, 该方法不能利用参数当前可测信息, 存在一定程度上的保守性.为了能够有效地利用参数当前可测信息, 在首步椭圆集采用参数增益调度控制律, 在余下的椭圆集系列采用多步控制律, 设计由参数增益调度控制律和普通反馈控制律序列组成的多步混合反馈鲁棒预测控制综合算法.该算法借助于在首步椭圆集采用参数增益调度控制律, 可以有效地利用可测的参数信息提高系统控制性能; 借助于在余下的椭圆集系列采用普通反馈控制律序列, 可以降低在线计算量, 从而有望在控制性能和计算负担间进行有效的平衡, 以较低的在线计算量取得较优的控制性能.
在控制策略设计中, 采用反馈控制序列π={ K(k), K(k+1), …, K(k+N)}.对当前时刻控制量u(k), 采用参数增益调度的反馈控制律:
| $ \mathit{\boldsymbol{u}}\left( k \right) = \mathit{\boldsymbol{K}}\left( k \right)\mathit{\boldsymbol{x}}\left( k \right). $ | (8) |
式中:
| $ \mathit{\boldsymbol{K}}\left( k \right) = \sum\limits_{l = 1}^{{n_{\rm{p}}}} {{\lambda _l}\left( k \right){\mathit{\boldsymbol{K}}_l}\left( k \right)} . $ | (9) |
式中:λl(k)为当前时刻可测的时变参数, Kl(k)分别为对应Porg各个顶点的状态反馈增益.显然, 式(8)表示参数依赖的状态反馈控制律.
对于j≥1等时刻的控制量u(k+j|k), 采用单一的反馈控制律:
| $ \mathit{\boldsymbol{u}}\left( {k + j\left| k \right.} \right) = \mathit{\boldsymbol{K}}\left( {k + j} \right)\mathit{\boldsymbol{x}}\left( {k + j\left| k \right.} \right);j = 1, \cdots ,\infty . $ | (10) |
反馈增益K(k+j)采用如下形式:
| $ \mathit{\boldsymbol{K}}\left( {k + j} \right) = \left\{ \begin{array}{l} {\mathit{\boldsymbol{K}}_j},\;\;\;\;N \ge j \ge 1;\\ {\mathit{\boldsymbol{K}}_N},j > N. \end{array} \right. $ | (11) |
将该min-max优化问题(7)转化为半正定规划(SDP)问题.首先定义二次函数:
| $ V\left( {k,j} \right) = \mathit{\boldsymbol{x}}\left( {k + j} \right)\mathit{\boldsymbol{P}}\left( {k,j} \right)\mathit{\boldsymbol{x}}\left( {k + j} \right). $ | (12) |
式中: P(k, j)= P(k, N), j>N.假设反馈控制序列π={ K(k), K(k+1), …, K(k+N)}满足如下鲁棒稳定性条件:
| $ \begin{array}{l} V\left( {k,j + 1} \right) - V\left( {k,j} \right) \le \\ - \left[ {\left\| {\mathit{\boldsymbol{x}}\left( {k + j\left| k \right.} \right)} \right\|_\mathit{\boldsymbol{L}}^2 + \left\| {\mathit{\boldsymbol{u}}\left( {k + j\left| k \right.} \right)} \right\|_\mathit{\boldsymbol{R}}^2} \right];j \ge 0. \end{array} $ | (13) |
在系统稳定的情况下, x(∞|k)= 0, V(∞|k)=0.将式(13)从j=0叠加到j=∞, 可得无穷时域性能指标上界:
| $ J\left( k \right) \le V\left( {k,0} \right). $ |
引入寻优变量γ, 假设满足:
| $ V\left( {k,0} \right) \le \gamma . $ | (14) |
可以将优化问题(7)转化为如下最小化问题:
| $ \mathop {\min }\limits_{\gamma ,{\mathit{\boldsymbol{K}}_l}\left( k \right),\mathit{\boldsymbol{K}}\left( {k + j} \right),\mathit{\boldsymbol{P}}\left( {k,j} \right)} \gamma . $ | (15) |
将约束条件转化为LMI, 进而将原优化问题转化为半正定规划问题.首先将式(13)改写为如下不等式:
| $ \begin{array}{l} \left\| {\mathit{\boldsymbol{A}}\left( {k + j} \right) + \mathit{\boldsymbol{B}}\left( {k + j} \right)\mathit{\boldsymbol{K}}\left( {k + j} \right)} \right\|_{\mathit{\boldsymbol{P}}\left( {k,j + 1} \right)}^2 - \\ \;\;\;\;\; \mathit{\boldsymbol{P}}\left( {k,j} \right) \le - \mathit{\boldsymbol{L}} - \left\| {\mathit{\boldsymbol{K}}\left( {k + j} \right)} \right\|_\mathit{\boldsymbol{R}}^2. \end{array} $ | (16) |
下面分j=0和j≥1两种情形进行处理.
当j=0时, 对于状态反馈律(8), 闭环系统的系统矩阵为
| $ \mathit{\boldsymbol{A}}\left( k \right) + \mathit{\boldsymbol{B}}\left( k \right)\mathit{\boldsymbol{K}}\left( k \right) = \sum\limits_{l = 1}^{{n_{\rm{p}}}} {{\lambda _l}\left( k \right)\left( {{\mathit{\boldsymbol{A}}_l} + {\mathit{\boldsymbol{B}}_l}\mathit{\boldsymbol{K}}\left( k \right)} \right)} . $ | (17) |
将状态反馈律(9)代入式(17), 引入文献[14]的半和策略, 可得
| $ \begin{array}{l} \mathit{\boldsymbol{A}}\left( k \right) + \mathit{\boldsymbol{B}}\left( k \right)\mathit{\boldsymbol{K}}\left( k \right) = \sum\limits_{l = 1}^{{n_{\rm{p}}}} {\lambda _l^2\left( k \right) \times \left( {{\mathit{\boldsymbol{A}}_l} + {\mathit{\boldsymbol{B}}_l}\mathit{\boldsymbol{K}}\left( k \right)} \right)} + \\ \;\;\;\;\;\;\;2\sum\limits_{l = 1}^{{n_{\rm{p}}} - 1} {\sum\limits_{i > l}^{{n_{\rm{p}}}} {{\lambda _l}\left( k \right){\lambda _i}\left( k \right) \times \frac{{{\mathit{\boldsymbol{A}}_l} + {\mathit{\boldsymbol{A}}_i} + {\mathit{\boldsymbol{B}}_l}{\mathit{\boldsymbol{K}}_i}\left( k \right) + {\mathit{\boldsymbol{B}}_i}{\mathit{\boldsymbol{K}}_l}\left( k \right)}}{2}} } , \end{array} $ | (18) |
| $ \begin{array}{l} \mathit{\boldsymbol{K}}\left( k \right) = \sum\limits_{l = 1}^{{n_{\rm{p}}}} {\lambda _l^2\left( k \right) \times {\mathit{\boldsymbol{K}}_l}\left( k \right)} + \\ \;\;\;\;\;\;\;2\sum\limits_{l = 1}^{{n_{\rm{p}}} - 1} {\sum\limits_{i > l}^{{n_{\rm{p}}}} {{\lambda _l}\left( k \right){\lambda _i}\left( k \right) \times \frac{{{\mathit{\boldsymbol{K}}_i}\left( k \right) + {\mathit{\boldsymbol{K}}_l}\left( k \right)}}{2}} } , \end{array} $ | (19) |
式中:
| $ \sum\limits_{l = 1}^{{n_{\rm{p}}}} {\lambda _l^2\left( k \right)} + 2\sum\limits_{l = 1}^{{n_{\rm{p}}} - 1} {\sum\limits_{i > l}^{{n_{\rm{p}}}} {{\lambda _l}\left( k \right){\lambda _i}\left( k \right)} } = 1. $ |
定义优化变量Yl(0)∈ Rni×n, Q0∈ Rn×n, Q0≥0.选取
| $ \left. \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Q}}_0}}& *&*&* \\ {{\mathit{\boldsymbol{A}}_l}{\mathit{\boldsymbol{Q}}_0} + {\mathit{\boldsymbol{B}}_l}{\mathit{\boldsymbol{Y}}_l}\left( 0 \right)}&{{\mathit{\boldsymbol{Q}}_l}}&{\bf{0}}&{\bf{0}}\\ {{\mathit{\boldsymbol{L}}^{\frac{1}{2}}}{\mathit{\boldsymbol{Q}}_0}}&{\bf{0}}&{\gamma \mathit{\boldsymbol{I}}}&{\bf{0}}\\ {{{\bf{R}}^{\frac{1}{2}}}{\mathit{\boldsymbol{Y}}_l}\left( 0 \right)}&{\bf{0}}&{\bf{0}}&{\gamma \mathit{\boldsymbol{I}}} \end{array}} \right] \ge 0;\\ l = 1, \cdots ,{n_{\rm{p}}}. \end{array} \right\} $ | (20) |
| $ \left. \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Q}}_0}}& *&*&* \\ {\frac{{\left( {{\mathit{\boldsymbol{A}}_l} + {\mathit{\boldsymbol{A}}_i}} \right){\mathit{\boldsymbol{Q}}_0} + {\mathit{\boldsymbol{B}}_l}{\mathit{\boldsymbol{Y}}_i}\left( 0 \right) + {\mathit{\boldsymbol{B}}_i}{\mathit{\boldsymbol{Y}}_l}\left( 0 \right)}}{2}}&{{\mathit{\boldsymbol{Q}}_1}}&{\bf{0}}&{\bf{0}}\\ {{\mathit{\boldsymbol{L}}^{\frac{1}{2}}}{\mathit{\boldsymbol{Q}}_0}}&{\bf{0}}&{\gamma \mathit{\boldsymbol{I}}}&{\bf{0}}\\ {{{\bf{R}}^{\frac{1}{2}}}\frac{{{\mathit{\boldsymbol{Y}}_l}\left( 0 \right) + {\mathit{\boldsymbol{Y}}_i}\left( 0 \right)}}{2}}&{\bf{0}}&{\bf{0}}&{\gamma \mathit{\boldsymbol{I}}} \end{array}} \right] \ge 0;\\ l = 1, \cdots ,{n_{\rm{p}}} - 1,i = l + 1, \cdots ,{n_{\rm{p}}}. \end{array} \right\} $ | (21) |
式中:(Al| Bl)分别为原多胞模型Porg的顶点, Q0、Q1为多步控制集.
输入约束和状态约束(5)可以转化如下.存在X0∈ Rni×ni和H0∈ Rnx×nx满足如下LMI:
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}_0}}& * \\ {{\mathit{\boldsymbol{Y}}_l}{{\left( 0 \right)}^{\rm{T}}}}&{{\mathit{\boldsymbol{Q}}_0}} \end{array}} \right] \ge 0;{X_{0,ii}} \le \bar u_i^2,i = 1, \cdots ,{n_i}. $ | (22) |
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{H}}_0}}& * \\ {{\mathit{\boldsymbol{Q}}_0}{\mathit{\boldsymbol{F}}^{\rm{T}}}}&{{\mathit{\boldsymbol{Q}}_0}} \end{array}} \right] \ge 0;{H_{0,ii}} \le \bar x_i^2,i = 1, \cdots ,{n_x}. $ | (23) |
当j≥1时, 对于状态反馈控制律(11), 综合文献[6]的控制不变集和文献[18]的多步控制集设计方法, 定义优化变量Y(j)∈ Rni×n, Qj∈ Rn×n, Qj≥0.选取K(k+j)= Y(j)Qj-1, P(k, j)=γQj-1, 可以将式(16)转化为如下LMI条件:
| $ \left. \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Q}}_j}}& *&*&* \\ {{\mathit{\boldsymbol{A}}_l}{\mathit{\boldsymbol{Q}}_j} + {\mathit{\boldsymbol{B}}_l}\mathit{\boldsymbol{Y}}\left( j \right)}&{{\mathit{\boldsymbol{Q}}_{j + 1}}}&{\bf{0}}&{\bf{0}}\\ {{\mathit{\boldsymbol{L}}^{\frac{1}{2}}}{\mathit{\boldsymbol{Q}}_j}}&{\bf{0}}&{\gamma \mathit{\boldsymbol{I}}}&{\bf{0}}\\ {{{\bf{R}}^{\frac{1}{2}}}\mathit{\boldsymbol{Y}}\left( j \right)}&{\bf{0}}&{\bf{0}}&{\gamma \mathit{\boldsymbol{I}}} \end{array}} \right] \ge 0;\\ l = 1, \cdots ,{n_{\rm{p}}},j = 1, \cdots ,N - 1. \end{array} \right\} $ | (24) |
| $ \left. \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Q}}_N}}& *&*&* \\ {{\mathit{\boldsymbol{A}}_l}{\mathit{\boldsymbol{Q}}_N} + {\mathit{\boldsymbol{B}}_l}\mathit{\boldsymbol{Y}}\left( N \right)}&{\mathit{\boldsymbol{Q}}_N}&{\bf{0}}&{\bf{0}}\\ {{\mathit{\boldsymbol{L}}^{\frac{1}{2}}}{\mathit{\boldsymbol{Q}}_N}}&{\bf{0}}&{\gamma \mathit{\boldsymbol{I}}}&{\bf{0}}\\ {{{\bf{R}}^{\frac{1}{2}}}\mathit{\boldsymbol{Y}}\left( N \right)}&{\bf{0}}&{\bf{0}}&{\gamma \mathit{\boldsymbol{I}}} \end{array}} \right] \ge 0;\\ l = 1, \cdots ,{n_{\rm{p}}}. \end{array} \right\} $ | (25) |
式中:(Al|Bl)分别为原多胞模型Porg的顶点, QN为控制不变集.
输入约束和状态约束(5)可以转化如下.存在Xj∈ Rni×ni和Hj∈ Rnx×nx满足如下LMI:
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}_j}}& * \\ {\mathit{\boldsymbol{Y}}{{\left( j \right)}^{\rm{T}}}}&{{\mathit{\boldsymbol{Q}}_j}} \end{array}} \right] \ge 0;{X_{j,ii}} \le \bar u_i^2,i = 1, \cdots ,{n_i},j = 1, \cdots ,N. $ | (26) |
| $ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{H}}_j}}& * \\ {{\mathit{\boldsymbol{Q}}_j}{\mathit{\boldsymbol{F}}^{\rm{T}}}}&{{\mathit{\boldsymbol{Q}}_j}} \end{array}} \right] \ge 0;{H_{j,ii}} \le \bar x_i^2,i = 1, \cdots ,{n_x},j = 1, \cdots ,N. $ | (27) |
基于式(20)、(21)、(24)和(25), 式(14)可以转化为如下LMI:
| $ \left[ {\begin{array}{*{20}{c}} 1& * \\ {\mathit{\boldsymbol{x}}\left( k \right)}&{{\mathit{\boldsymbol{Q}}_0}} \end{array}} \right] \ge 0. $ | (28) |
综上所述, 鲁棒预测控制问题已被转化为半正定规划问题, 可以设计如下多步混合反馈鲁棒预测控制算法.
算法1 对于不确定系统(1)~(5), 该系统在k时刻的初始状态为x(k)=x(k|k).若控制策略采用由式(9)、(11)组成的多步混合反馈控制序列π={ K(k), K(k+1), …, K(k+N)}, 则性能指标的优化问题可以转化为如下半正定规划问题:
| $ \left. \begin{array}{l} \mathop {\min }\limits_{\gamma ,{\mathit{\boldsymbol{Q}}_j},{\mathit{\boldsymbol{Y}}_l}\left( 0 \right),\mathit{\boldsymbol{Y}}\left( j \right),{\mathit{\boldsymbol{X}}_j},{\mathit{\boldsymbol{H}}_j}} \gamma ;\\ {\rm{s}}.\;{\rm{t}}.\;式\left( {20} \right) \sim \left( {28} \right). \end{array} \right\} $ | (29) |
式中:γ>0, Qj∈ Rn×n, Xj∈ Rni×ni, Y(j)∈ Rni×n, Yl(0)∈ Rni×n, Hj∈ Rnx×nx, l=1, …, np, j=0, 1, …, N.控制律
注1:由于Kothare等[6]的控制不变集方法和Li等[18]的多步控制集方法可以处理更一般化的参数不可测的LPV系统, 可以推知, 文献[6]和文献[18]的方法可以被应用来控制参数可测的LPV系统, 缺点在于无法有效利用当前可测的参数信息, 但可以在保证稳定性的基础上优化系统的控制性能, 且均以闭环反馈控制的形式实现了反馈预测控制.综上所述, 在随后对算法1的仿真验证环节中, 将和文献[6]、[18]和[26]的方法进行控制效果比较.
注2 :文献[6]要求当前时刻的系统状态位于控制不变集内, 严格意义上属于控制不变集设计, 存在保守性, 降低了系统控制性能.Li等[18]针对多胞模型的所有顶点, 采用多步控制集可以在一定程度上扩大自由度, 但由于对未来每一时刻均采用单一的反馈控制律, 控制性能有待提高.Zheng等[26]在多步控制集所对应的每一步椭圆集都采用参数增益调度控制, 可以有效地利用当前可测的参数信息, 有效地改善了控制性能.由于引入了较多的优化变量, 采用文献[26]的方法在线计算的负担繁重, 存在设计上的保守性, 难以在控制性能和在线计算量间进行有效平衡.算法1针对多胞模型的所有顶点, 对当前时刻采用参数增益调度控制, 对未来每一时刻采用单一反馈控制律, 设计了鲁棒预测控制综合算法.通过与文献[26]的方法比较可知, 算法1在降低优化变量数量的同时, 所设计的反馈控制序列可以有效地利用当前可测的参数信息, 将以较低的优化计算量取得较优的控制性能, 在控制性能和在线计算量之间实现有效的平衡.
上面通过半正定规划可以有效地优化系统控制性能, 下面给出可行性证明和稳定性证明.
定理1 对于系统(1)~(5), 如果在k时刻, 对于系统状态x(k|k), 算法1有可行解, 则算法1所设计的鲁棒预测控制器可以镇定该系统为渐近稳定.
证明: 设k时刻, 算法1是可行的, 优化问题的最优解是
| $ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^ * }\left( k \right) = \\ \;\;\;\;\;\;\left[ {{\gamma ^ * },Q_0^ * ,\mathit{\boldsymbol{X}}_0^ * ,{\mathit{\boldsymbol{Y}}_l}{{\left( 0 \right)}^ * },\mathit{\boldsymbol{H}}_0^ * ,\mathit{\boldsymbol{F}}_1^ * ,\mathit{\boldsymbol{F}}_2^ * , \cdots ,\mathit{\boldsymbol{F}}_N^ * } \right]. \end{array} $ |
式中:
| $ \mathit{\boldsymbol{F}}_j^ * = \mathit{\boldsymbol{Q}}_j^ * ,\mathit{\boldsymbol{X}}_j^ * ,\mathit{\boldsymbol{Y}}{\left( j \right)^ * },\mathit{\boldsymbol{H}}_j^ * . $ |
首先证明可行性.需要证明对于系统状态x(k+1)=x(k+1|k+1), LMI(20)~(28)可行, 即可证明可行性.为了证明可行性, 首先构造k+1时刻优化问题的可行解:
| $ \begin{array}{l} \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\left( {k + 1} \right) = \left[ {a{\gamma ^ * },a\mathit{\boldsymbol{Q}}_1^ * ,a\mathit{\boldsymbol{X}}_1^ * ,a\mathit{\boldsymbol{\vec Y}}{{\left( 1 \right)}^ * },a\mathit{\boldsymbol{H}}_1^ * ,} \right.\\ \left. {a\mathit{\boldsymbol{F}}_2^ * ,a\mathit{\boldsymbol{F}}_3^ * , \cdots ,a\mathit{\boldsymbol{F}}_N^ * ,a\mathit{\boldsymbol{F}}_N^ * } \right]. \end{array} $ |
式中:
| $ \left. \begin{array}{l} \mathit{\boldsymbol{\vec Y}}\left( 1 \right) = \underbrace {\left[ {\mathit{\boldsymbol{Y}}{{\left( 1 \right)}^ * }, \cdots ,\mathit{\boldsymbol{Y}}{{\left( 1 \right)}^ * }} \right]}_{{n_{\rm{p}}}},\\ a = V\left( {k,1} \right)/{\gamma ^ * }\left( k \right). \end{array} \right\} $ | (30) |
由式(20)、(21), 可以推得
| $ V\left( {k,1} \right) \le {\gamma ^ * }\left( k \right), $ |
进而可以推得0 < a≤1.由式(30), 可得
| $ \mathit{\boldsymbol{x}}\left( {k + 1} \right){\left( {a\mathit{\boldsymbol{Q}}_1^ * \left( k \right)} \right)^{ - 1}}\mathit{\boldsymbol{x}}\left( {k + 1} \right) = 1. $ |
综上所述, Γ(k+1)满足式(28).
注意到Qj*、Xj*、Y(j)*、Hj*在式(23)~(27)中呈仿射形式.因为Fj*满足式(23)~(27), 对式(23)~(27)分别乘以a>0, 可以推出Γ(k+1)满足式(23)~(27).
由于γ*、Q1*、X1*、Y(1)满足式(24)~(26), 可以推知aγ*、aQ1*、aX1*、
由于0 < a≤1, 可以推得
| $ \gamma \left( {k + 1} \right) = a{\gamma ^ * }\left( k \right) \le {\gamma ^ * }\left( k \right), $ |
闭环系统是渐近稳定的.
注3 :实现建立在稳定性基础上的预测控制性能优化, 涉及预测控制算法设计和理论分析两个方面, 除需要设计预测控制算法以优化系统控制性能外, 还需要证明在该算法控制下受控系统的稳定性.预测控制稳定性证明, 要求构造出未来时刻的可行解并且从数学上严格证明算法的递归可行性, 通常情况下这是预测控制算法理论分析和设计的瓶颈难点.由于算法1采用多步混合反馈鲁棒预测控制的特殊性, 使得稳定性分析过程中的递归可行性证明这一瓶颈难点, 进一步增加了证明难度.本文在定理1的证明过程中有效地构造了未来时刻的可行解, 并且从数学上严格证明了算法1的递归可行性, 解决了递归可行性分析这一瓶颈难点, 进而保证了受控系统的稳定性, 最终实现了建立在稳定性基础上的控制性能优化.
3 仿真验证通过仿真算例来验证所提出的鲁棒预测控制算法的有效性.鉴于注1所标注, 将算法1和文献[6]、[18]和[26]的方法进行控制性能比较, 验证控制算法1的控制效果.
考虑如下LPV系统:
| $ \left. \begin{array}{l} \mathit{\boldsymbol{x}}\left( {k + 1} \right) = \mathit{\boldsymbol{A}}\left( k \right)\mathit{\boldsymbol{x}}\left( k \right) + \mathit{\boldsymbol{B}}\left( k \right)\mathit{\boldsymbol{u}}\left( k \right);\\ \left[ {\mathit{\boldsymbol{A}}\left( k \right)\left| {\mathit{\boldsymbol{B}}\left( k \right)} \right.} \right] \in {\mathit{\boldsymbol{P}}_{{\rm{org}}}},\left[ {\mathit{\boldsymbol{A}}\left( k \right)\left| {\mathit{\boldsymbol{B}}\left( k \right)} \right.} \right] = \\ \sum\limits_{l = 1}^{{n_{\rm{p}}}} {{\lambda _l}\left( k \right)\left[ {{\mathit{\boldsymbol{A}}_l}\left| {{\mathit{\boldsymbol{B}}_l}} \right.} \right]} ,\sum\limits_{l = 1}^{{n_{\rm{p}}}} {{\lambda _l}\left( k \right) = 1} ,{\lambda _l}\left( k \right) \ge 0,\\ l = 1,2, \cdots ,{n_{\rm{p}}}. \end{array} \right\} $ |
多胞系统Porg的顶点如下:
| $ {\mathit{\boldsymbol{A}}_1} = \left[ {\begin{array}{*{20}{c}} 1&0\\ {0.05}&1 \end{array}} \right],{\mathit{\boldsymbol{B}}_1} = \left[ {\begin{array}{*{20}{c}} 1&{0.5}\\ {0.02}&{0.2} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{A}}_2} = \left[ {\begin{array}{*{20}{c}} 1&0\\ {3.5}&1 \end{array}} \right],{\mathit{\boldsymbol{B}}_2} = \left[ {\begin{array}{*{20}{c}} 1&{0.5}\\ {0.1}&{0.2} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{A}}_3} = \left[ {\begin{array}{*{20}{c}} 1&0\\ 3&{0.9} \end{array}} \right],{\mathit{\boldsymbol{B}}_3} = \left[ {\begin{array}{*{20}{c}} 1&{0.01}\\ {0.02}&{0.2} \end{array}} \right], $ |
| $ {\mathit{\boldsymbol{A}}_4} = \left[ {\begin{array}{*{20}{c}} 1&0\\ 1&{0.9} \end{array}} \right],{\mathit{\boldsymbol{B}}_4} = \left[ {\begin{array}{*{20}{c}} 1&{0.01}\\ {0.01}&{0.2} \end{array}} \right]. $ |
参数变化规律如下:
| $ {\lambda _1}\left( {k + 1} \right) = \left\{ {\begin{array}{*{20}{c}} {0,{\lambda _1}\left( {k + 1} \right) \le 0;}\\ {0.5,{\lambda _1}\left( {k + 1} \right) \ge 0.5;}\\ {{\lambda _1}\left( k \right) + {{\left( { - 1} \right)}^{\left\lfloor {k/6} \right\rfloor }}0.05,其他.} \end{array}} \right. $ |
| $ {\lambda _2}\left( {k + 1} \right) = \left\{ {\begin{array}{*{20}{c}} {0,{\lambda _1}\left( {k + 1} \right) \le 0;}\\ {0.5,{\lambda _2}\left( {k + 1} \right) \ge 0.5;}\\ {{\lambda _2}\left( k \right) + {{\left( { - 1} \right)}^{\left\lfloor {k/4} \right\rfloor }}0.03,其他.} \end{array}} \right. $ |
| $ {\lambda _3}\left( {k + 1} \right) = 0.3\left[ {1 - {\lambda _1}\left( {k + 1} \right) - {\lambda _2}\left( {k + 1} \right)} \right]. $ |
| $ {\lambda _4}\left( {k + 1} \right) = 1 - {\lambda _1}\left( {k + 1} \right) - {\lambda _2}\left( {k + 1} \right) - {\lambda _3}\left( {k + 1} \right). $ |
式中:
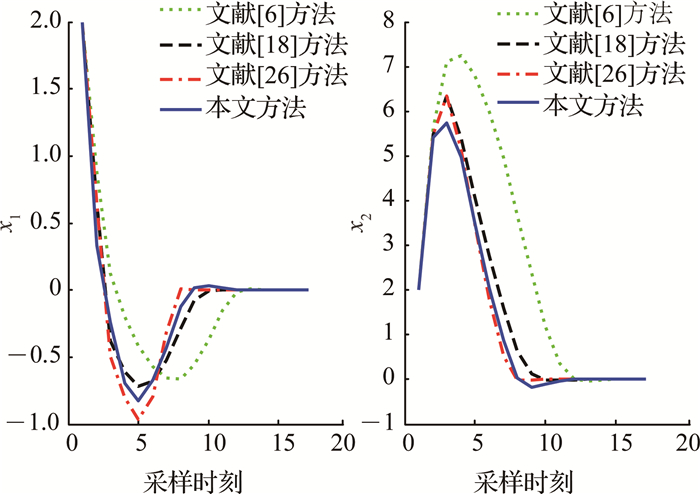
通过对算法1、文献[6]、[18]和[26]的方法进行仿真得到的系统闭环状态轨迹响应如图 1所示.图 1表明, 算法1对应的状态除收敛速度略慢于文献[18]外, 收敛速度比文献[6]、[18]的方法更快, 并且在算法1控制下, 受控系统闭环稳定.另外, 采用不同算法时的控制性能和平均优化时间如表 1所示.由表 1可知, 在列出的4种方法中, 利用文献[26]方法取得的控制性能最优, 算法1所对应的控制性能最接近于文献[26]方法的优异控制性能, 获得了比文献[6]、[18]方法更优的控制性能.采用不同算法时的平均优化时间t如表 1所示.另外, 算法1的平均优化时间为0.448 23 s, 文献[26]方法的平均优化时间为0.623 23 s, 算法1比文献[26]降低了大约30%的在线计算负担, 因此算法1具有比文献[26]更高的计算效率(接近于文献[6]、[18]方法的计算效率).综上所述, 利用算法1取得了比文献[6]、[18]方法更优的控制性能, 且以高效的计算效率(较低的在线计算量)取得了更接近于文献[26]方法的优异控制性能, 在控制性能与在线计算量之间取得了有效平衡.
|
图 1 系统闭环状态轨迹图 Fig. 1 Closed-loop system state responses |
| 表 1 采用不同算法时的控制性能和平均优化时间 Table 1 Comparison of control performance and average optimization time |
针对参数当前可测的LPV系统, 综合参数增益调度控制思想和多步控制集方法, 设计基于多步混合反馈控制律的鲁棒反馈预测控制算法, 降低了以往文献在多步控制集所对应的每一步椭圆集均采用参数增益调度控制律所导致的繁重在线计算负担, 以较低的优化计算量取得了较优的控制性能, 在控制性能和在线计算量之间实现了有效平衡.
| [1] |
席裕庚, 李德伟, 林姝. 模型预测控制:现状与挑战[J]. 自动化学报, 2013, 39(3): 222-236. XI Yu-geng, LI De-wei, LIN Shu. Model predictive control:status and challenges[J]. Acta Automatica Sinica, 2013, 39(3): 222-236. |
| [2] |
MAYNE D Q. Model predictive control:recent developments and future promise[J]. Automatica, 2014, 50(12): 2967-2986. DOI:10.1016/j.automatica.2014.10.128 |
| [3] |
GOODWIN G C, KONG H, MIRZAEVA G, et al. Robust model predictive control:reflections and opportunities[J]. Journal of Control and Decision, 2014, 1(2): 115-148. DOI:10.1080/23307706.2014.913837 |
| [4] |
MARTINS M A F, ODLOAK D. A robustly stabilizing model predictive control strategy of stable and unstable processes[J]. Automatica, 2016, 67(5): 132-143. |
| [5] |
何德峰, 丁宝苍, 于树友. 非线性系统模型预测控制若干基本特点与主题回顾[J]. 控制理论与应用, 2013, 30(3): 273-287. HE De-feng, DING Bao-cang, YU Shu-you. Review of fundamental properties and topics of model predictive control for nonlinear systems[J]. Control Theory and Applications, 2013, 30(3): 273-287. |
| [6] |
KOTHARE M V, BALAKRISHNAN V, MORARI M. Robust constrained model predictive control using linear matrix inequalities[J]. Automatica, 1996, 32(10): 1361-1379. DOI:10.1016/0005-1098(96)00063-5 |
| [7] |
CUZZOLA F A, GEROMEL J C, MORARI M. An improved approach for constrained robust model predictive control[J]. Automatica, 2002, 38(7): 1183-1189. DOI:10.1016/S0005-1098(02)00012-2 |
| [8] |
WAN Zhao-yang, KOTHARE M V. Efficient robust constrained model predictive control with a time varying terminal constraint set[J]. Systems and Control Letters, 2003, 48(5): 375-383. DOI:10.1016/S0167-6911(02)00291-8 |
| [9] |
LI De-wei, XI Yu-geng, GAO Fu-rong. Synthesis of dynamic output feedback RMPC with saturated inputs[J]. Automatica, 2013, 49(4): 949-954. DOI:10.1016/j.automatica.2013.01.010 |
| [10] |
LI De-wei, GAO Fu-rong, XI Yu-geng. Separated design of robust model predictive control for LPV systems with periodic disturbance[J]. Journal of Process Control, 2014, 24(1): 250-260. DOI:10.1016/j.jprocont.2013.10.010 |
| [11] |
HUANG He, LI De-wei, LIN Zong-li, et al. An improved robust model predictive control design in the presence of actuator saturation[J]. Automatica, 2011, 47(4): 861-864. DOI:10.1016/j.automatica.2011.01.045 |
| [12] |
DING Bao-cang, HUANG Biao, XU Fang-wei. Dynamic output feedback robust model predictive control[J]. International Journal of Systems Science, 2011, 42(10): 1669-1682. DOI:10.1080/00207721003624543 |
| [13] |
YU Shu-you, BOHM C, CHEN Hong, et al. Model predictive control of constrained LPV systems[J]. International Journal of Control, 2012, 85(6): 671-683. DOI:10.1080/00207179.2012.661878 |
| [14] |
WANG H O, TANAKA K, GRIFFIN M F. An approach to fuzzy control of nonlinear systems:stability and design issues[J]. IEEE Transactions on Fuzzy Systems, 1996, 4(1): 14-23. DOI:10.1109/91.481841 |
| [15] |
HE De-feng, HUANG Hua, CHEN Qiu-xia. Quasi-min-max MPC for constrained nonlinear systems with guaranteed input-to-state stability[J]. Journal of the Franklin Institute, 2014, 351(6): 3405-3423. DOI:10.1016/j.jfranklin.2014.03.006 |
| [16] |
黄骅, 何德峰, 俞立. 基于多面体描述系统的鲁棒非线性预测控制[J]. 自动化学报, 2012, 38(12): 1906-1912. HUANG Hua, HE De-feng, YU Li. Robust nonlinear predictive control based on polytopic description systems[J]. Acta Automatica Sinica, 2012, 38(12): 1906-1912. |
| [17] |
DING Bao-cang, XI Yu-geng, LI Shao-yuan. A synthesis approach of on-line constrained robust model predictive control[J]. Automatica, 2004, 40(1): 163-167. DOI:10.1016/j.automatica.2003.07.007 |
| [18] |
LI De-wei, XI Yu-geng. Design of robust model predictive control based on multi-step control set[J]. ACTA Automatica Sinica, 2009, 35(4): 433-437. DOI:10.1016/S1874-1029(08)60083-X |
| [19] |
ZHENG Peng-yuan, LI De-wei, XI Yu-geng, et al. A sophisticated RMPC design for LPV systems based on the mixed multi-step feedback control[C]//The 34th Chinese Control Conference. Hangzhou: IEEE, 2015: 4119-4123. http: //ieeexplore. ieee. org/document/7260274/
|
| [20] |
PARK J H, KIM T H, SUGIE T. Output feedback model predictive control for LPV systems based on quasi-min-max algorithm[J]. Automatica, 2011, 47(9): 2052-2058. DOI:10.1016/j.automatica.2011.06.015 |
| [21] |
SU Yang, TAN K K. Comments on "output feedback model predictive control for LPV systems based on quasi-min-max algorithm"[J]. Automatica, 2012, 48(9): 2385. DOI:10.1016/j.automatica.2012.06.100 |
| [22] |
平续斌, 丁宝苍, 韩崇昭. 动态输出反馈鲁棒模型预测控制[J]. 自动化学报, 2012, 38(1): 31-37. PING Xu-bin, DING Bao-cang, HAN Chong-zhao. Dynamic output feedback robust model predictive control[J]. Acta Automatica Sinica, 2012, 38(1): 31-37. |
| [23] |
ZHENG Peng-yuan, LI De-wei, XI Yu-geng. Constrained feedback RMPC for LPV systems with bounded rates of parameter variations and measurement errors[J]. International Journal of System Control and Information Processing, 2012, 1(2): 164-175. DOI:10.1504/IJSCIP.2012.052187 |
| [24] |
JUNGERS M, OLIVEIRA R, PERES P. MPC for LPV systems with bounded parameter variations[J]. International Journal of Control, 2011, 84(1): 24-36. DOI:10.1080/00207179.2010.536996 |
| [25] |
ZHENG Peng-yuan, LI De-wei, XI Yu-geng, et al. Improved future model prediction and robust MPC design for LPV systems with bounded rates of parameter variations[C]//The 9th Asian Control Conference. Istanbul: IEEE, 2013: 1-6. http: //ieeexplore. ieee. org/xpls/abs_all. jsp?arnumber=6606174
|
| [26] |
ZHENG Peng-yuan, LI De-wei, XI Yu-geng, et al. Improved model prediction and RMPC design for LPV systems with bounded parameter changes[J]. Automatica, 2013, 49(12): 3695-3699. DOI:10.1016/j.automatica.2013.09.024 |


