2. 武汉大学 测绘遥感信息工程国家重点实验室, 湖北 武汉 430079;
3. 上海师范大学 城市发展研究院, 上海 200234;
4. 中国科学院寒区旱区环境与工程研究所, 甘肃 兰州 730000
2. State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China;
3. Institute of Urban Studies, Shanghai Normal University, Shanghai 200234, China;
4. Cold and Arid Regions Environmental and Engineering Research Institute, Chinese Academy of Sciences, Lanzhou 730000, China
高光谱遥感技术能够获取地物从可见光至近红外的细微光谱响应信息, 更有利于识别地物的潜在差异[1]; 然而影像信息冗余且计算量大, 严重制约高光谱遥感技术的应用和推广[2].通常对高光谱进行波段选择的降维处理, 选取代表性波段来降低波段相关性和数据计算量, 更好地满足后续的生产应用[3-6].
近年来, 稀疏表达理论为高光谱影像的波段选择提供了新的研究思路和方法.该理论认为一个正常信号投影至低维特征空间能够得到信号的稀疏表达, 其中少数非零元素能够很好地继承原始信号的特性[7].稀疏表达目前已经应用于高光谱混合像元分解[8]、特征级融合[9]、特征提取[10]、异常探测[11]和分类[12-13]等众多领域.稀疏系数能够凸显高光谱影像的一些潜在结构信息, 可以用于波段选择[14].学者提出一些基于稀疏表达的高光谱波段选择方法, 如稀疏支持向量机方法[6]、稀疏自表达方法[4]、稀疏非负矩阵分解方法[5](sparse nonnegative matrix factorization, SNMF)和改进稀疏子空间聚类方法[15].然而以上方法得到的波段子集缺乏明确的物理或几何意义解释[3].
对称稀疏表达方法(symmetric sparse representation, SSR)假设波段子集和原始高光谱影像能够实现对称稀疏表达, 将波段选择问题转换为寻找高维光谱空间中波段对应的数据点构成的最小凸包的原型点问题, 通过求解非线性优化问题来估计适合的波段子集[3].然而, 波段的强相关性可能导致相邻波段对应的数据点差异较小而较难进行区分, 影响波段选择结果.另一方面, SSR方法的稀疏系数矩阵的限制条件导致稀疏重构得到的波段子集并非完全存在于原始的波段集合中.
本文基于常规SSR方法来提出改进核空间对称稀疏表达方法(improved kernel symmetric sparse representation, IKSSR), 更好地解决高光谱影像的波段选择问题.IKSSR采用以下两大策略来改进SSR以提升波段子集的分类效果.1)采用核函数映射高光谱波段向量到核参数特征空间, 扩大不同的波段对应的高维数据点间的差异, 解决SSR模型在光谱特征空间中容易选取较相近的原型点作为其代表性波段的问题.2)改变SSR中稀疏系数矩阵的限制条件来保证稀疏重构得到的波段子集完全存在于原始的波段集合中.类似于SSR方法, IKSSR将波段选择问题转换为寻找高维核空间中波段向量对应的数据集合的最小凸包的原型点来选取最佳波段子集, 所选的波段子集具有明确的物理意义.本文采用高光谱影像公开数据集, 包括Indian Pines和Pavia University(PaviaU), 开展实验分析, 验证提出IKSSR方法的有效性.
1 高光谱影像的对称稀疏表达模型[3]假设高光谱影像构成波段集合为Y={yi}i=1N∈RD×N, 其中D为像素个数, N为波段数量, yi∈RD×1为任一波段向量, Z={zl}l=1k∈RD×k为待求的波段子集, 其中k为波段子集的大小.高光谱影像的对称稀疏表达模型假设待选的波段子集和原始的波段集合能够实现彼此互相稀疏表达.一方面, 原始波段集合可以认为由波段子集进行稀疏表达和重构, 即
| $ \left. \begin{align} &\underset{D\times N}{\mathop{\mathit{\boldsymbol{Y}}}}\,=\underset{D\times k}{\mathop{\mathit{\boldsymbol{Z}}}}\,\cdot \underset{k\times N}{\mathop{\mathit{\boldsymbol{A}}}}\,+\underset{D\times N}{\mathop{\mathit{\boldsymbol{E}}}}\,; \\ &\text{s}\text{.t}\text{.}\ \ {{\mathit{\boldsymbol{a}}}_{i}}\ge 0,\left| {{\mathit{\boldsymbol{a}}}_{i}} \right|=1,i\in \left\{ 1,\ldots ,N \right\}. \\ \end{align} \right\} $ | (1) |
式中: A ={ai}i=1N为稀疏系数矩阵, E为由模型误差和随机噪声导致的误差项.约束条件ai≥0和|ai|=1是为了保证波段子集用以重构原始波段集合中任一波段的概率为1且任一波段的概率权重都大于0.另一方面, 对称稀疏表达模型认为波段子集能够被原始的波段集合进行稀疏表达和重构, 即
| $ \left. \begin{align} &\underset{D\times k}{\mathop{\mathit{\boldsymbol{Z}}}}\,=\underset{D\times N}{\mathop{\mathit{\boldsymbol{Y}}}}\,\cdot \underset{N\times k}{\mathop{\mathit{\boldsymbol{B}}}}\,,\text{diag}\left( \mathit{\boldsymbol{B}} \right)=0; \\ &{{\mathit{\boldsymbol{b}}}_{j}}\ge 0,\left| {{\mathit{\boldsymbol{b}}}_{j}} \right|=1,j\in \left\{ 1,\ldots ,k \right\}. \\ \end{align} \right\} $ | (2) |
式中: B={bj}j=1k为稀疏系数矩阵, diag(B)=0, bj≥0和|bj|=1保证任一原始波段用以重构波段子集的概率权重都大于0且重构概率为1.将式(1)、(2)进行整合, 得到对称稀疏表达模型如下:
| $ \left. \begin{align} &\underset{D\times N}{\mathop{\mathit{\boldsymbol{Y}}}}\,=\underset{D\times N}{\mathop{\mathit{\boldsymbol{Y}}}}\,\cdot \underset{N\times k}{\mathop{\mathit{\boldsymbol{B}}}}\,\cdot \underset{k\times N}{\mathop{\mathit{\boldsymbol{A}}}}\,+\underset{D\times N}{\mathop{\mathit{\boldsymbol{E}}}}\,; \\ &\text{s}\text{.t}\text{. }\!\!~\!\!\text{ }{{\mathit{\boldsymbol{b}}}_{j}}\ge 0,\text{ }{{\mathit{\boldsymbol{b}}}_{jj}}=0,\left| {{\mathit{\boldsymbol{b}}}_{j}} \right|=1,j\in \left\{ 1,\ldots ,k \right\}, \\ &\ \ \ \ \ \ \ \mathit{\boldsymbol{a}}{{~}_{i}}\ge 0,|{{\mathit{\boldsymbol{a}}}_{i}}|=1,i\in \left\{ 1,\ldots ,N \right\}. \\ \end{align} \right\} $ | (3) |
对称稀疏表达模型的求解可以转换为传统的原型分析的凸优化问题[3], 通过寻找高维光谱空间内包围原始波段向量对应的数据集合的最小凸包的原型点来得到波段子集.常用的非线性优化方法包括交替最小二乘法方法[16]、块坐标下降方法[17]和投影梯度方法[18]等.
2 改进核空间对称稀疏表达方法 2.1 改进核空间对称稀疏表达模型的构建对称稀疏表达模型认为波段选择为寻找高维波段空间下包围原始波段向量对应的数据集合的最小凸包的原型点[3].事实上, 高光谱波段的相关性较强导致相邻的光谱波段在高维光谱特征空间中对应的数据点差异较小而较难进行区分, 进而影响两者同时选为原型点时得到的波段子集结果.核函数通过映射原始高维数据至核特征空间, 被广泛应用于解决不同数据点的线性区分问题[19], 能够在核特征空间中来更好地区分相似波段向量.采用核函数来构建核特征空间, 实现原始波段向量向新的特征空间映射, 以扩大不同的波段对应的数据点的差异, 将波段选择问题转换为寻找高维核特征空间中波段向量对应的数据集合的最小凸包的原型点, 从而更好地选取波段子集.利用高维特征数据H∈RN×N替换原始的高光谱影像数据Y, 式(3)的对称稀疏表达模型转换为核空间下的表达形式:
| $ \left. \begin{align} &\underset{N\times N}{\mathop{\mathit{\boldsymbol{H}}}}\,=\underset{N\times N}{\mathop{\mathit{\boldsymbol{H}}}}\,\cdot \underset{N\times k}{\mathop{\mathit{\boldsymbol{B}}}}\,\cdot \underset{k\times N}{\mathop{\mathit{\boldsymbol{A}}}}\,+\underset{N\times N}{\mathop{{{\mathit{\boldsymbol{E}}}_{1}}}}\,; \\ &\text{s}\text{.t}\text{.}\ {{\mathit{\boldsymbol{b}}}_{j}}\ge 0,{{\mathit{\boldsymbol{b}}}_{jj}}=0,\left| {{\mathit{\boldsymbol{b}}}_{j}} \right|=1,j\in \left\{ 1,\ldots ,k \right\}, \\ &\ \ \ \ \ \ {{\mathit{\boldsymbol{a}}}_{i}}\ge 0,\left| {{\mathit{\boldsymbol{a}}}_{i}} \right|=1,i\in \left\{ 1,\ldots ,N \right\}. \\ \end{align} \right\} $ | (4) |
式中: B ={ bj}j=1k和A={ai}i=1N为稀疏系数矩阵, E1为由模型误差和随机噪声导致的误差项. H∈ RN×N为原始高光谱数据集合Y为映射至高维核空间下的特征数据, 通过核函数k(yi, yj)= < f(yi), f(yj)>计算得到, 其中高维空间的映射函数f(·)可以为线性函数、高斯函数、多项式函数和幂指数函数等.考虑到计算简单和方便性, 采用线性核函数k(yi, yj)=<yi, yj>, 转换原始波段向量至原始光谱空间下的超平面中, 得到核空间下的特征数据, 即H=YTY.
另一方面, 式(2)假设待求波段子集能够通过原始波段集合中所有波段向量的稀疏表达模型来进行重构, 采用迭代优化目标函数来随机产生满足最小重构误差约束条件的稀疏系数矩阵B和A.利用
| $ \left. \begin{align} &\underset{N\times N}{\mathop{\mathit{\boldsymbol{H}}}}\,=\underset{N\times N}{\mathop{\mathit{\boldsymbol{H}}}}\,\mathit{\boldsymbol{ }}\!\!\cdot\!\!\text{ }\underset{N\times k}{\mathop{\mathit{\boldsymbol{B}}}}\,\mathit{\boldsymbol{ }}\!\!\cdot\!\!\text{ }\underset{k\times N}{\mathop{\mathit{\boldsymbol{A}}}}\,+\underset{N\times N}{\mathop{{{\mathit{\boldsymbol{E}}}_{1}}}}\,; \\ &\text{s}\text{.t}\text{.}~\ {{\mathit{\boldsymbol{b}}}_{ij}}\in \left\{ 0,1 \right\},\left| {{\mathit{\boldsymbol{b}}}_{j}} \right|=1,j\in \left\{ 1,\ldots ,k \right\}, \\ &\ \ \ \ \ \ {{\mathit{\boldsymbol{a}}}_{i}}\ge 0,|{{\mathit{\boldsymbol{a}}}_{i}}|=1,i\in \left\{ 1,\ldots ,N \right\}. \\ \end{align} \right\} $ | (5) |
式中: bij∈{0, 1}和|bj|=1能够保证选取的Z为原始波段集合中的真正子集.
2.2 稀疏系数矩阵B和A的求解求解问题(5)可以转换为优化以下目标函数:
| $ \left. \begin{array}{l} \mathop {{\rm{argmin}}}\limits_{B, A} {\left\| {\mathit{\boldsymbol{H-HBA}}} \right\|_{\rm{F}}}^2, 1<k<N;\\ {\rm{s}}{\rm{.t}}\;{\mathit{\boldsymbol{b}}_{ij}} \in \left\{ {0, 1} \right\}, \left| {{\mathit{\boldsymbol{b}}_j}} \right| = 1, j \in \left\{ {1, \ldots, k} \right\}, \\ \;\;\;\;\;\;\;{\mathit{\boldsymbol{a}}_i} \ge 0, |{\mathit{\boldsymbol{a}}_i}| = 1, i \in \left\{ {1, \ldots, N} \right\}. \end{array} \right\} $ | (6) |
式中:‖·‖F为费罗宾尼斯范数.可以看出, 当稀疏系数矩阵B或A固定时, 非凸问题(6)转换为凸优化问题能够得以求解.
采用矢量量化编码方法[20]来初始化B和A, 运用块坐标下降策略来得到两者的最优解, 以得到待求的波段子集.矢量量化编码方法通过最小化量化编码误差来求解, 得到编码字典和与原始波段向量概率密度保持一致的高维波段数据点(称为质心).考虑到计算速度和有效性, 采用Linde-Buzo-Gray(LBG)算法来最小化编码误差并估计质心, 得到最初的波段子集[20], 具体过程如下:1)从原始波段集合中随机选取k个波段向量; 2)在每一次迭代中, 采用欧氏距离度量将每个波段向量对应的数据点编码至最近的离散泰森多边形, 通过移动至新的质心来更新编码向量; 3)当编码误差收敛至设定阈值时, 停止迭代并将对应的质心作为初始的波段子集Z(0).
块坐标下降方法通过依次迭代更新稀疏系数矩阵B和A, 求解得到局部最优解[18].在第t步迭代过程中, 目标函数(6)依次转换为求解以下两个子问题(7)和(8):
| $ \left. \begin{array}{l} \mathit{\boldsymbol{a}}_i^{(t + 1)} = {\rm{argmin}}\;\left\| {\mathit{\boldsymbol{h}}{_i}-\mathit{\boldsymbol{Za}}_i^{(t)}} \right\|_2^2;\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;{\mathit{\boldsymbol{a}}_i} \ge 0, \left| {{\mathit{\boldsymbol{a}}_i}} \right| = 1, i \in \left\{ {1, \ldots, N} \right\}. \end{array} \right\} $ | (7) |
| $ \left. \begin{array}{l} \mathit{\boldsymbol{b}}_j^{(t + 1)} = {\rm{argmin}}\;\left\| {\mathit{\boldsymbol{H}}-\mathit{\boldsymbol{H}}{\mathit{\boldsymbol{B}}^{(t)}}{\mathit{\boldsymbol{A}}^{(t + 1)}} + \mathit{\boldsymbol{H}}\left( {\mathit{\boldsymbol{b}}_j^{(t)}-\mathit{\boldsymbol{b}}_j^{(t + 1)}} \right){\mathit{\boldsymbol{a}}^j}} \right\|_2^2;\\ {\rm{s}}{\rm{.t}}{\rm{.}}\;{\mathit{\boldsymbol{b}}_{ij}} \in \left\{ {0, 1} \right\}, |{\mathit{\boldsymbol{b}}_j}| = 1, j \in \left\{ {1, \ldots, k} \right\}. \end{array} \right\} $ | (8) |
子问题(7)和(8)采用激活集方法[21]进行求解.当迭代次数达到设定最大值A(t+1)或B(t+1)满足‖H-HB(t+1)A(t+1)‖∞≤ε时停止迭代, 得到待求的波段子集为
改进核空间对称稀疏表达IKSSR的高光谱影像波段选择的流程如下.
1) 将三维的高光谱影像立方体转换为二维波段向量数据集Y, 以二维矩阵形式表示, 其中波段数为Y对应的矩阵的列数, 高光谱影像中的像素个数为Y的行数.
2) 利用式(5)构建高光谱影像波段数据集的改进核空间对称稀疏表达模型.
3) 将问题(5)的求解问题转换为式(6)的目标方程优化问题, 利用矢量量化编码方法和块坐标下降策略, 通过依次迭代求解目标问题(7)和(8)来得到稀疏系数矩阵
4) 利用稀疏重构表达式
Indian Pines数据来自美国普渡大学遥感应用实验室.数据由美国JPL成像光谱仪于1992年6月12日采集得到, 空间分辨率为20 m, 光谱分辨率为10 nm, 光谱区间为200~2 400 nm, 预处理后的波段数为200.如图 1所示为覆盖西拉法叶地区西部8 km的一小块区域, 包含145×145像素.图 1共包含16类主要地物, 地物分布的样本信息见表 1.表中, n为样本数.

|
图 1 Indian Pines数据 Fig. 1 Indian Pines data |
| 表 1 Indian Pines数据的地物真实样本信息 Table 1 Ground truth of all classes of ground objects on Indian Pines dataset |
PaviaU数据来自西班牙巴斯克大学计算智能课题组, 影像由ROSIS成像光谱仪采集得到, 共103波段, 空间分辨率为1.3 m, 光谱区间为430~860 nm.如图 2所示的影像为较大数据集中的一部分, 覆盖帕维亚大学区域, 包含350×340像素, 波段数为103, 包含9类地物(包括阴影).数据中各地物样本的真实空间分布信息如表 2所示.

|
图 2 PaviaU数据 Fig. 2 PaviaU data |
| 表 2 PaviaU数据的地物真实样本信息 Table 2 Ground truth of all classes of ground objects on PaviaU dataset |
利用提出的改进核空间对称稀疏表达方法IKSSR来分类Indian Pines和PaviaU数据集, 验证提出的波段选择方法的有效性.采用的波段选择对比方法包括最大方差主成分分析法(maximum-variance principal component analysis, MVPCA)[22]、基于稀疏的波段选择法(sparse based band selection, SpaBS)[23]、稀疏矩阵分解的波段选择法SNMF[5]和对称稀疏表达的波段选择方法SSR[3].实验采用支持向量机(support vector machine, SVM)和随机森林法(random forest, RF)来分类各对比方法的波段选择子集, 采用总体分类精度(overall classification accuracy, OCA)来定量评价分类结果.SVM分类器中采用径向基核函数, 方差和惩罚因子通过交叉验证获得.从每个数据集的训练和测试样本中随机抽取10次进行实验, 以下实验结果是10次独立实验的平均结果.
1) 不同波段数量下的分类结果对比.对比分析不同波段数下的IKSSR与MVPCA、SpaBS、SNMF和SSR方法的SVM与RF的分类结果.Indian Pines数据集中波段数的选择区间为2~44, PaviaU数据集中波段数的选择区间为2~50, 选定20%的地物真实样本作为训练样本进行实验, 其余的地物样本作为测试样本.在Indian Pines和PaviaU数据中, SpaBS方法的迭代次数设置为5次.利用交叉验证方法, Indian Pines数据集中, SNMF的正则化因子α和β分别设定为3.0和0.01;在PaviaU数据集中, SNMF方法的α和β分别设定为4.0和0.001.
如图 3所示为IKSSR和4种对比方法在Indian Pines和PaviaU数据集上得到的不同波段数目条件下的总体分类精度OCA的曲线图.可以看出, 随着波段数量的增加, 5种方法利用SVM和RF分类器得到的分类精度都逐渐上升后趋于较稳定的水平.在Indian Pines和PaviaU数据中, SpaBS的总体分类精度OCA整体最低; MVPCA曲线的OCA结果总体上高于SpaBS, 但明显低于SNMF、SSR和IKSSR方法.利用SSR方法得到的OCA结果优于SNMF, 但总体上低于IKSSR方法的结果, 这可以从SVM和RF分类器得到的曲线中看出; 因此, IKSSR在不同波段数量的条件下得到的OCA分类精度最高.
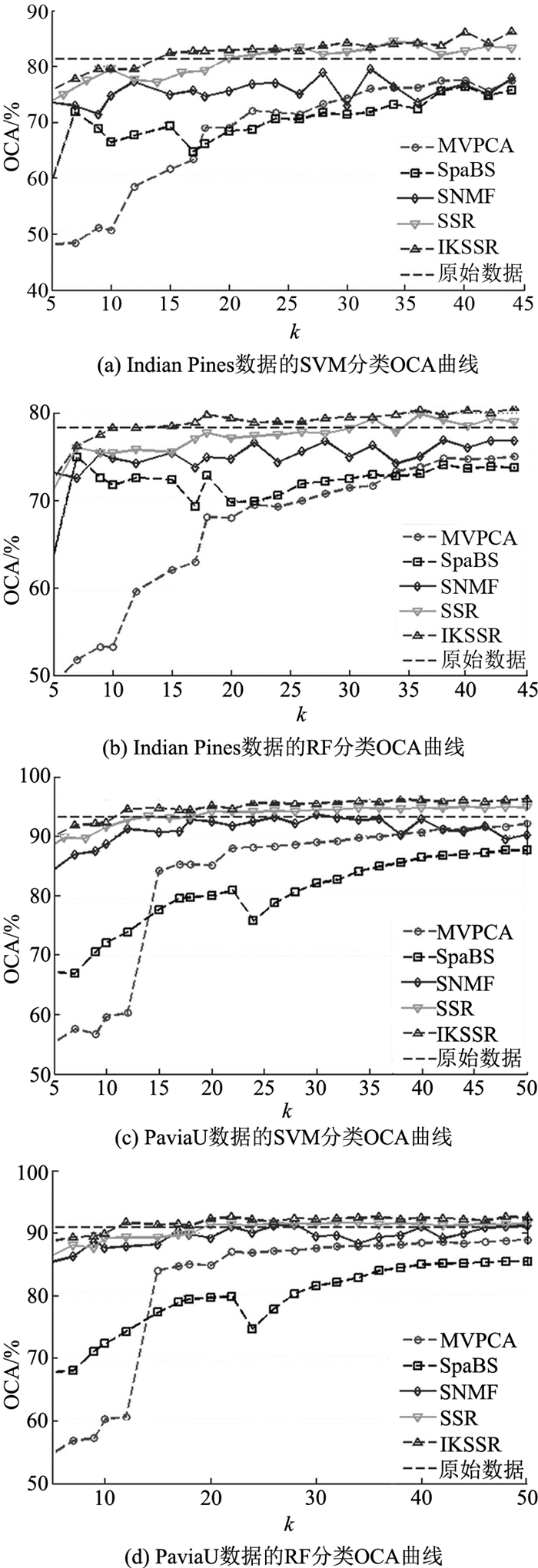
|
图 3 不同波段选择方法在Indian Pines和PaviaU数据中的总体分类精度曲线 Fig. 3 Overall classification accuracy curves of different band selection methods on Indian Pines and PaviaU datasets |
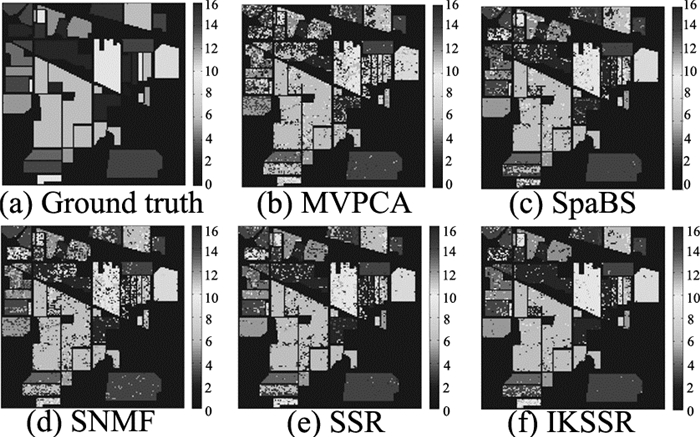
如图 4、5所示为5种波段选择方法在选定的波段数量条件下的SVM分类结果.其中, Indian Pines和PaviaU数据的波段数量k分别人为设定为12和20.可以看出, IKSSR的SVM分类图结果优于其他4种波段选择方法.

|
图 4 不同波段选择方法的Indian Pines数据的SVM分类结果 Fig. 4 SVM classification maps of different band selection methods on Indian Pines dataset |
|
图 5 不同波段选择方法的PaviaU数据的SVM分类结果 Fig. 5 SVM classification maps of different band selection methods on PaviaU dataset |
2) 不同波段数量下的计算时间对比.对比不同波段数量下各种波段选择方法的计算复杂度和计算效率.在Indian Pines和PaviaU数据集中, 波段数量k为[10, 20, 30, 40, 50].IKSSR和其他4种波段选择方法的参数设置与实验(1)保持一致.
IKSSR方法中, 高维核空间映射H=YTY的计算复杂度为O(N3); 矢量量化算法LBG的计算复杂度为O(3lkN), 其中l为LBG的迭代次数; 式(7)中更新稀疏矩阵A的计算复杂度为O(DNk+Nk2), 式(8)中更新稀疏矩阵B的计算复杂度为O(Dk2+kN2), 因此IKSSR的计算复杂度为O(3lkN+N3+kt(DN+Nk+N2+Dk)), 其中t为迭代的次数.考虑到k«N«D, IKSSR的计算复杂度可以近似表达为O(3lkN+N3+ktN(D+N)).如表 3所示为不同波段选择方法在Indian Pines和PaviaU数据中, 不同k下的计算时间tc.实验环境为WIN7台式计算机, 配置为Inter i5-4570四核CPU处理器和8 GB内存, 5种方法的代码执行环境为Matlab 2014a.可以看出, 5种波段选择方法的计算时间与k密切相关, 随着k的增加呈明显上升趋势.IKSSR方法的计算速度快于MVPCA、SpaBS和SNMF, 但略慢于SSR, 这是由于KSSR采用核函数和矢量量化编码来改进SSR, 导致计算复杂度上升.SpaBS方法的计算时间最长, 明显高于其他4种方法.5种波段选择方法的计算效率从高到低依次为:SSR、IKSSR、MVPCA、SNMF和SpaBS.
| 表 3 不同波段选择方法的计算时间对比 Table 3 Contrast in computation times of different band selection methods |
3) 不同训练样本大小下的分类结果对比.对比不同训练样本大小下, 利用IKSSR与MVPCA、SpaBS、SNMF和SSR方法得到的总体分类精度OCA结果.Indian Pines和PaviaU数据的训练样本随机采样于地物真实样本集, 采样比率为[0.03, 0.05, 0.08, 0.10, 0.13, 0.15, 0.18, 0.20, 0.25, 0.30, 0.40, 0.50].Indian Pines数据中, k设定为30;PaviaU数据中, k设定为20.IKSSR和其他4种波段选择方法的其他参数设置都与实验(1)保持一致.
如图 6所示为不同训练样本下5种波段选择对比方法在Indian Pines和PaviaU数据集中得到的总体分类精度曲线.图中, p为每一类地物训练样本的采样百分比.考虑到SVM和RF分类结果的相似性, 图 6列出SVM分类器得到的OCA曲线.可以看出, 随着训练样本子集大小的改变, IKSSR和其他4种波段选择方法的分类效果明显上升, 总体分类精度OCA提升较明显.2个高光谱数据集中, 在任何训练样本大小下, IKSSR的总体分类精度始终最高, 明显高于SSR、SNMF、SpaBS和MVPCA四种方法.SNMF得到的OCA曲线总体上低于SSR和IKSSR, 但明显优于MVPCA和SpaBS方法.5种方法中, SpaBS的总体分类精度最低; 因此, IKSSR在不同训练样本条件下得到的总体分类精度最高, 优于其他4种对比方法.
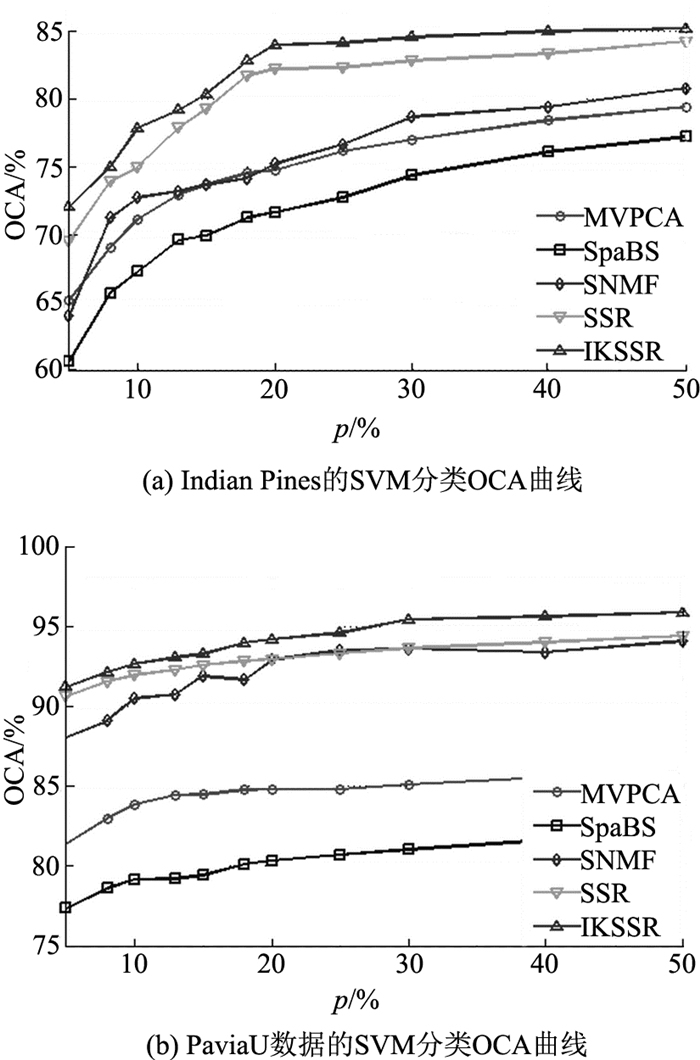
|
图 6 不同训练样本大小下各种波段选择方法的总体分类精度OCA曲线 Fig. 6 Overall classification accuracy curves of different band selection methods with different size of training samples per class |
本文提出改进核空间的对称稀疏表达方法IKSSR来解决高光谱影像的波段选择问题.IKSSR方法考虑高光谱影像的波段强相关问题, 采用核函数来改进对称稀疏表达模型SSR, 将波段选择问题转换为寻找高维核空间中波段向量对应的数据集合的最小凸包的原型点来进行求解.IKSSR采用块坐标下降策略, 将目标函数的非凸问题转换为凸优化问题进行求解; 采用矢量量化策略来选取初始波段子集, 加速收敛过程, 得到最优波段子集.利用Indian Pines和PaviaU两个高光谱数据集, 对比MVPCA、SpaBS、SNMF和SSR方法, 验证IKSSR进行波段选择的效果.实验结果表明, IKSSR在计算速度排名第二的情况下, 总体分类精度明显优于SSR和其他3种方法, 能够得到更好的分类结果.本文的研究结果需要下一步的研究工作来进一步完善.本文没有考虑自动选择最佳波段子集大小的问题, 只是对比不同方法在一定波段数量区间范围内的分类结果.在后续的研究中, 将细致研究自动选取波段子集大小来方便本文方法的实践应用; 考虑像元的空间邻域对IKSSR模型的影响, 提升波段选择效果来应用于高光谱影像数据处理.
| [1] |
TONG Q, XUE Y, ZHANG L. Progress in hyperspectral remote sensing science and technology in China over the past three decades[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(1): 70-91. DOI:10.1109/JSTARS.2013.2267204 |
| [2] |
BIOUCAS-DIAS J M, PLAZA A, CAMPS-VALLS G, et al. Hyperspectral remote sensing data analysis and future challenges[J]. IEEE Geoscience and remote sensing magazine, 2013, 1(2): 6-36. DOI:10.1109/MGRS.2013.2244672 |
| [3] |
SUN W, JIANG M, LI W, et al. A symmetric sparse representation based band selection method for hyperspectral imagery classification[J]. Remote Sensing, 2016, 8(3): 238. DOI:10.3390/rs8030238 |
| [4] |
孙伟伟, 蒋曼, 李巍岳. 利用稀疏自表达实现高光谱影像波段选择[J]. 武汉大学学报信息科学版, 2017, 42(4): 441-448. SUN Wei-wei, JIANG Man, LI Wei-yue. Band selection using sparse self-representation for hyperspectral imagery[J]. Geomatics and Information Science of Wuhan University, 2017, 42(4): 441-448. |
| [5] |
LI J M, QIAN Y T. Clustering-based hyperspectral band selection using sparse nonnegative matrix factorization[J]. Journal of Zhejiang University:Science C, 2011, 12(7): 542-549. DOI:10.1631/jzus.C1000304 |
| [6] |
CHEPUSHTANOVA S, GITTINS C, KIRBY M. Band selection in hyperspectral imagery using sparse support vector machines[C]//Proceedings of SPIE Defense+ Security. Baltimore: SPIE, 2014: 90881F-90881F-15. http://spie.org/x648.xml?product_id=2063812
|
| [7] |
DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [8] |
厉小润, 伍小明, 赵辽英. 非监督的高光谱混合像元非线性分解方法[J]. 浙江大学学报:工学版, 2011, 45(4): 607-613. LI Xiao-run, WU Xiao-ming, ZHAO Liao-ying. Unsupervised nonlinear decomposing method of hyperspectral imagery[J]. Journal of Zhejiang University:Engineering Science, 2011, 45(4): 607-613. |
| [9] |
WEI Q, BIOUCAS-DIAS J, DOBIGEON N, et al. Hyperspectral and multispectral image fusion based on a sparse representation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(7): 3658-3668. DOI:10.1109/TGRS.2014.2381272 |
| [10] |
LUO F, HUANG H, MA Z, et al. Semisupervised sparse manifold discriminative analysis for feature extraction of hyperspectral images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(10): 6197-6211. DOI:10.1109/TGRS.2016.2583219 |
| [11] |
XU Y, WU Z, LI J, et al. Anomaly detection in hyperspectral images based on low-rank and sparse representation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(4): 1990-2000. DOI:10.1109/TGRS.2015.2493201 |
| [12] |
ZHANG E, ZHANG X, JIAO L, et al. Spectral-spatial hyperspectral image ensemble classification via joint sparse representation[J]. Pattern Recognition, 2016, 59(1): 42-54. |
| [13] |
厉小润, 朱洁尔, 王晶, 等. 组合核支持向量机高光谱图像分类[J]. 浙江大学学报:工学版, 2013, 47(8): 1403-1410. LI Xiao-run, ZHU Jie-er, WANG Jing, et al. Hyperspectral image classification based on composite kernels support vector machine[J]. Journal of Zhejiang University:Engineering Science, 2013, 47(8): 1403-1410. |
| [14] |
DU Q, BIOUCAS-DIAS J M, PLAZA A. Hyperspectral band selection using a collaborative sparse model[C]//Proceedings of 2012 IEEE International Geoscience and Remote Sensing Symposium. Munich: IEEE, 2012: 3054-3057. http://ieeexplore.ieee.org/document/6350781/
|
| [15] |
SUN W, ZHANG L, DU B, et al. Band selection using improved sparse subspace clustering for hyperspectral imagery classification[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(6): 2784-2797. DOI:10.1109/JSTARS.2015.2417156 |
| [16] |
CUTLER A, BREIMAN L. Archetypal analysis[J]. Technometrics, 1994, 36(4): 338-347. DOI:10.1080/00401706.1994.10485840 |
| [17] |
CHEN Y, MAIRAL J, HARCHAOUI Z. Fast and robust archetypal analysis for representation learning[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Columbus: IEEE, 2014: 1478-1485. http://ieeexplore.ieee.org/document/6909588/
|
| [18] |
MORUP M, HANSEN L K. Archetypal analysis for machine learning and data mining[J]. Neurocomputing, 2012, 80(1): 54-63. |
| [19] |
KWAK N. Nonlinear projection trick in Kernel methods:an alternative to the Kernel trick[J]. IEEE Transactions on Neural Networks and Learning Systems, 2013, 24(12): 2113-2119. DOI:10.1109/TNNLS.2013.2272292 |
| [20] |
EQUITZ W H. A new vector quantization clustering algorithm[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(10): 1568-1575. DOI:10.1109/29.35395 |
| [21] |
NOCEDAL J, WRIGHT S. Numerical optimization[M]. 2nd ed. NewYork: Springer, 2006, 110.
|
| [22] |
CHANG C I, DU Q, SUN T L, et al. A joint band prioritization and band-decorrelation approach to band selection for hyperspectral image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 1999, 37(6): 2631-2641. DOI:10.1109/36.803411 |
| [23] |
LI S, QI H. Sparse representation based band selection for hyperspectral images[C]//Proceedings of 201118th IEEE International Conference on Image Processing. Brussels: IEEE, 2011: 2693-2696. https://dl.acm.org/citation.cfm?id=521706
|


