2. 中国船舶重工集团公司第七研究院 电子部, 北京 100192
2. Electronic Department, The Seventh Research Institute of China Shipbuilding Industry Corporation, Beijing 100192, China
严格来说, 目标威胁评估是一个NP困难问题[1].在进行威胁评估时, 难以给出一个各种因素与威胁程度的关系函数.王改革等[2]使用BP神经网络处理目标威胁评估问题, 获得了不错的效果, 但BP神经网络有着明显的缺点, 比如易陷入局部极值、学习率选择敏感等.笔者提出改进的灰狼算法(OGWO)优化小波神经网络的目标威胁评估模型.灰狼优化算法是由Mirjalili等[3]提出的模仿灰狼社会等级制度和捕食行为的新型仿生算法.该算法设置参数少、算法性能优越且模型简单, 因而得到广泛的应用.在处理复杂的优化问题时, GWO算法存在着求解精度不高、算法后期收敛速度变慢的问题[4].小波神经网络是以小波变换为基础发展而来的新型神经网络, 兼具小波变换良好的时频局部化特点与神经网络的自学习能力[5].传统WNN采用梯度修正法修正网络的权值和小波基函数参数, 存在易陷入局部最优和进化缓慢的缺点.为了解决以上缺点, 本文提出OGWO算法, 提高灰狼优化算法的求解精度和收敛速度.利用收集到的目标威胁度数据建立WNN空中目标威胁评估模型, 应用OGWO算法替代传统WNN中修正权值和参数使用的梯度下降法, 解决了WNN模型的参数优化问题.为了验证该模型的可靠性, 将该模型与其他几种神经网络模型进行对比研究.
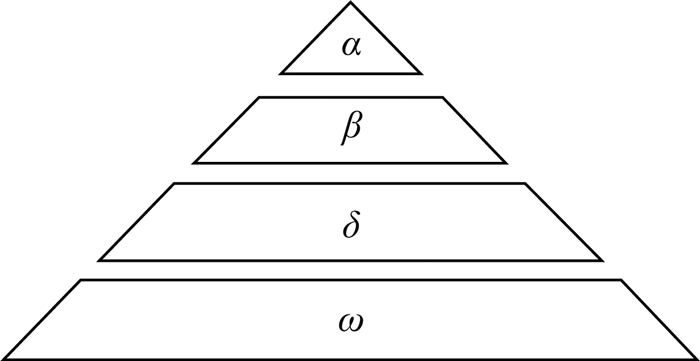
1 反向灰狼优化算法 1.1 基本灰狼优化算法灰狼是处于食物链顶端的群居食肉动物, 在狼群内有着严格的社会等级, 构成了灰狼种群等级金字塔[6].如图 1所示, 一个灰狼群的社会等级分为四层.金字塔第一层为灰狼群中的头狼, 称为α, 主要负责领导整个灰狼群体, 决策各项事务; 第二层称为β, 它协助头狼作出决策; 第三层称为δ, δ主要负责侦察、放哨、捕猎等任务; 最底层的称为ω, 跟随上三层并听从上层的指挥.
|
图 1 灰狼群等级金字塔 Fig. 1 Hierarchy of grey wolf |
灰狼群的种群等级制度在围猎中有着极其重要的作用, 围猎由头狼α带领实现.首先, 灰狼群以团队模式搜寻、追踪猎物, 并从各个方向逐渐包围猎物.当包围圈逐渐变小时, 狼群在头狼α的指挥下, 由最靠近猎物的β、δ率先发动攻击.当猎物逃跑时, 由其余个体ω补位防止猎物逃脱.最终, 在狼群不间断地多方位攻击下, 将猎物捕获.在GWO算法中, 由α、β、δ执行追捕行为, ω跟随前三者对猎物进行跟踪围捕.
GWO算法是基于对自然界灰狼群的社会等级制度和围猎行为的模拟[7].在D维搜索空间中, 定义种群X={X1, X2, …, Xn}, 其中n为种群中灰狼的个体数.定义Xi={Xi1, Xi2, …, XiD}为第i只灰狼的位置, 其中Xid为第i只灰狼个体在第d维上的位置.将在遍历中种群的当前最优解记为α, 将适应度当前排名次优的解记为β, 将适应度当前排名第三优的解记为δ, 种群中的其他个体记为ω, 猎物的位置即为优化问题的全局最优解.
在围猎过程中, 狼群根据下式对猎物进行包围:
| $ D = \left| {C{X_{\rm{p}}}\left( t \right)-X\left( t \right)} \right|. $ | (1) |
式中:Xp(t)为种群迭代至第t代时猎物的位置; X(t)为第t代灰狼个体的位置; 常数C为摆动因子,
| $ C = 2{r_1}, $ | (2) |
其中, r1=rand(0, 1).
根据下式更新灰狼个体的位置:
| $ X\left( {t + 1} \right) = {X_{\rm{p}}}\left( t \right)-AD. $ | (3) |
式中:A为收敛因子,
| $ A = a\left( {2{r_2}-1} \right) $ | (4) |
其中, a随着迭代次数的增加, 从2线性递减至0, r2=rand(0, 1).
在狼群中, α、β、δ最靠近猎物, 灰狼优化算法利用这3个个体来判断最优解.在灰狼群中, 个体围杀猎物行为的数学描述如下.
首先, 分别计算第t代时, α、β、δ对种群内灰狼个体位置的影响X1、X2、X3, 如下:
| $ {D_\alpha } = \left| {{C_1}{X_\alpha }\left( t \right)-X\left( t \right)} \right|, $ | (5) |
| $ {D_\beta } = \left| {{C_2}{X_\beta }\left( t \right)-X\left( t \right)} \right|, $ | (6) |
| $ {D_\delta } = \left| {{C_3}{X_\delta }\left( t \right)-X\left( t \right)} \right|, $ | (7) |
| $ {X_1} = {X_\alpha }\left( t \right)-{A_1}{D_\alpha }, $ | (8) |
| $ {X_2} = {X_\beta }\left( t \right)-{A_2}{D_\beta }, $ | (9) |
| $ {X_3} = {X_\delta }\left( t \right)-{A_3}{D_\delta }. $ | (10) |
式中:Xα(t)、Xβ(t)、Xδ(t)分别为种群迭代至第t代时α、β、δ的位置, X(t)为第t代灰狼个体的位置, C1、C2、C3和A1、A2、A3分别为不同的摆动因子与收敛因子.
根据下式计算第t轮迭代后种群内个体的新位置:
| $ X\left( {t + 1} \right) = \left( {{X_1} + {X_2} + {X_3}} \right)/3. $ | (11) |
通过研究可以发现, 对于标准灰狼优化算法, 随着迭代次数的增加, 所有灰狼个体都朝同方向运动, 使得灰狼群的趋同性变得严重[8].笔者采用反向学习策略[9-10]对标准灰狼优化算法的初始种群与迭代后的种群进行改进, 成功改善了算法的寻优范围和灰狼个体的分布特性, 提高了算法的收敛速度和精度.改进点如下.
1) 优化初始种群位置.
根据文献[11]可知, 一组优秀的初始种群能够较大地提高寻优的结果.在即使没有先验知识的情况下, 利用反向点, 能够获得一组较好的初始候选解.过程如下.
a) 随机初始化种群P.
b) 计算反向种群OP:
| $ {\rm{O}}{{\rm{P}}_{a, b}} = {\rm{mi}}{{\rm{n}}_a} + {\rm{ma}}{{\rm{x}}_a}-{P_{a, b}}. $ | (12) |
式中:a=1, 2, …, Np, b=1, 2, …, n, Pa, b和OPa, b分别为种群位置与反向种群位置中a维第b个变量的值, mina和maxa分别为第a维元素的最小、最大值, Np为数据维度.
c) 分别计算P与OP中个体的适应度, 选取其中适应度较好的n个体生成新的初始种群NP.
2) 优化迭代过程中的种群位置.
在迭代的过程中, 可以使用类似的反向学习方法, 提高算法的全局搜索能力, 避免算法出现早熟.设置反向学习优化选择率p, 每当完成一次迭代, 在计算出新的灰狼群位置后, 根据p来决定是否对种群进行反向学习优化.过程如下.
a) 生成一个随机数rand(0, 1).若rand(0, 1) < p, 则转入步骤b), 否则直接进入步骤d).
b) 计算动态反向种群OP:
| $ {\rm{O}}{{\rm{P}}_{a, b}} = {\rm{min}}_a^t + {\rm{max}}_a^t-{P_{a, b}}. $ | (13) |
式中:minat与maxat分别为第t次迭代后第a维元素的最小值与最大值.
c)利用适应度评价函数计算P和OP中个体的适应度.若f′i < fi, 则用OPi替代Pi, 全部比较、替换后的种群P即为新的种群.其中, fi、f′i分别为第i个个体和与对应的反向个体的适应度, OPi为第i个反向个体.
d) 进入下一轮OGWO迭代.
随着迭代次数的增加, 当前迭代的搜索区间远小于最初的搜索区间, 使得种群快速逼近最优解.
OGWO算法的具体流程如下.
a) 参数初始化, 即最大迭代次数I、种群规模N、p以及随机生成a、C和A.
b) 初始化种群位置, 根据式(12)计算初始反向种群并利用反向学习优化初始种群位置生成新的初始种群NP.
c) 利用适应度评价函数, 计算此时每个个体对应的适应度.根据适应度对灰狼个体进行排序, 将适应度前三的灰狼个体位置分别标记为α、β、δ, 作为灰狼群的决策层.
d) 根据式(5)~(7)分别计算种群中个体距α、β、δ的距离, 根据式(8)~(11)更新种群内每个灰狼个体的位置.
e) 生成rand (0, 1).若rand (0, 1) < p, 则根据式(13)计算动态反向种群, 并计算P与OP中个体的适应度.若f′i < fi, 则用OPi替代Pi, 生成新的种群, 否则直接进入步骤f).
f) 更新a、A、C等参数.
g) 判断是否达到最大迭代次数I.若是, 则输出种群最优适应度及对应的灰狼个体位置.否则, 重复步骤c)~步骤g), 直至达到最大迭代次数.
1.3 算法性能分析为了验证OGWO算法的寻优性能, 选择6个基准测试函数进行仿真分析, 并与标准GWO算法、PSO算法比较.测试函数如表 1所示.表中, f1、f2为单峰函数, f3~ f6为多峰函数.
| 表 1 基准测试函数 Table 1 Benchmark functions |
为了保证公平性, 3种算法的基本参数一致:初始种群规模为30, 最大迭代次数为200, 维度为10, 运行次数为10.特别地, OGWO中的反向学习优化选择概率p=0.5, PSO中的学习因子c1=c2=1.5, w=0.729 8.将10次寻优的最优值、最差值、平均值及标准差记录下来, 实验结果如表 2所示.
| 表 2 3种算法的性能比较 Table 2 Comparison of three algorithms |
根据表 2的实验结果可知, 除了在函数f4上GWO的最优值较优于OGWO(OGWO的均值最好), 在其余测试函数上, OGWO算法的性能均优于GWO算法、PSO算法, 能够取得更好的寻优效果.尤其在多峰函数上, OGWO算法表现得更优异, 拥有更强的鲁棒性.OGWO算法的良好表现, 为基于OGWO-WNN的目标威胁评估模型的建立奠定了基础.
2 基于OGWO-WNN的目标威胁评估 2.1 目标威胁评估因素在目标威胁评估问题中, 需要考虑很多因素, 例如天气情况、地貌、敌我兵力部署和指战员作战风格等[12-13].为了更方便地研究目标威胁评估问题, 在进行实验时, 通常需要考虑以下因素.
1) 目标类型:大型目标(如战略侦察机)、小型目标(如空空导弹)、武装直升机.
2) 目标距离:如10、20、30 km等.
3) 目标速度:如10、200、300 m/s等.
4) 目标方位角:如2°、4°、6°等.
5) 目标高度:低、中、高.
6) 目标抗干扰能力:无、弱、中、强.
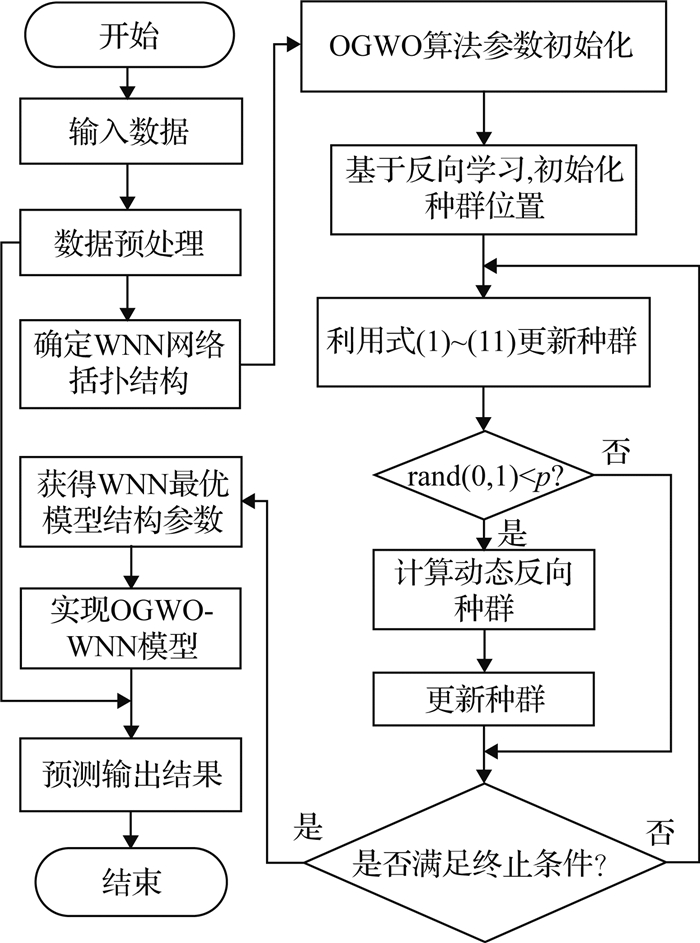
2.2 OGWO-WNN目标威胁评估模型小波神经网络是以BP神经网络拓扑结构为基础, 把小波基函数作为隐含层节点的传递函数, 在信号前向传播的同时误差反向传播的神经网络[14].Wang等[15]通过构造新的小波基函数来改进小波神经网络并应用于目标威胁评估, 取得了不错的效果.笔者从另一个角度改进小波神经网络, 传统的WNN权值参数修正算法采用梯度修正法, 修正网络的权值和小波基函数参数, 但梯度学习算法的进化缓慢并且容易陷入最小.为了解决上述问题, 笔者在采用WNN建立目标威胁评估模型的基础上, 利用OGWO算法替代梯度学习算法来优化小波神经网络的权值(ωij、ωjk)和小波基函数的平移因子bj与伸缩因子aj, 提出基于OGWO-WNN的目标威胁评估模型.模型的优化过程如图 2所示.具体步骤的详细解释如下.
|
图 2 基于OGWO-WNN的目标威胁评估模型 Fig. 2 Model of target threat assessment using OGWO-WNN |
1) 数据预处理.
采集若干组数据, 并分为两组分别作为训练集与测试集.部分原始数据如表 3所示.表中, v为速度, θ为方位角, h为高度, α为抗干扰能力, d为距离, T为威胁度.采用Miller的9级量化理论[16]对采集到的数据进行量化.对定性属性作如下量化处理.
| 表 3 部分威胁估计原始数据 Table 3 Part of original threat assessment data |
a) 目标类型:大型目标、小型目标、武装直升机依次量化为3、5、8.
b) 目标高度:超低、低、中、高, 依次量化为2、4、6、8.
c) 目标抗干扰能力:强、中、弱、无, 依次量化为2、4、6、8.
将量化后的目标类型、抗干扰能力、目标高度与目标距离、目标方向角和目标速度一起进行归一化操作, 使数据转化为OGWO-WNN模型能够识别的形式.
2) 确定WNN网络拓扑结构.
WNN隐含层节点数与输入层节点数和输出层节点数有关, 经过多次实验, 将隐含层节点数设置为11的效果较好, 所以WNN网络拓扑结构为6-11-1.采用国内外使用较多的Morlet母小波基函数作为OGWO-WNN模型的小波基函数.
3) OGWO参数初始化.
根据WNN网络中连接权值与小波基函数的参数个数决定灰狼个体的维度, 因为WNN网络的拓扑结构为6-11-1, 灰狼个体的编码长度为6×11+11+11+11=99.搜索空间为[-1, 1].确定种群规模、最大迭代次数和反向学习优化选择概率p.
4) 适应度评价函数为
| $ f = k\left( {\sum\limits_{i = 1}^n {\left| {{y_i}-{o_i}} \right|} } \right). $ | (14) |
式中:n为训练样本数, yi为模型的预测威胁度, oi为实际威胁度, k为不为0的常数.当利用OGWO算法优化WNN时, 使用的适应度评价函数为式(14).
5) 实现OGWO-WNN模型.
将通过OGWO算法优化得到的最优灰狼个体解码为WNN最优模型结构参数(即ωij、ωjk、bj、aj), 实现OGWO-WNN模型.
6) 预测输出结果.
将数据预处理后的测试集数据输入已经训练好的OGWO-WNN模型, 预测目标威胁度.将测试集实际威胁度与模型预测威胁度作比较, 检验模型的可靠性.
3 模型性能分析采集105组数据, 其中小型目标、大型目标和直升机各35组.随机选择3种类型、各30组数据作为训练集, 剩余15组作为测试集.为了验证OGWO-WNN目标威胁评估模型的有效性, 将测试数据分别输入训练好的OGWO-WNN、WNN、GWO-WNN、GWO-BP、PSO-WNN模型, 比较预测输出.
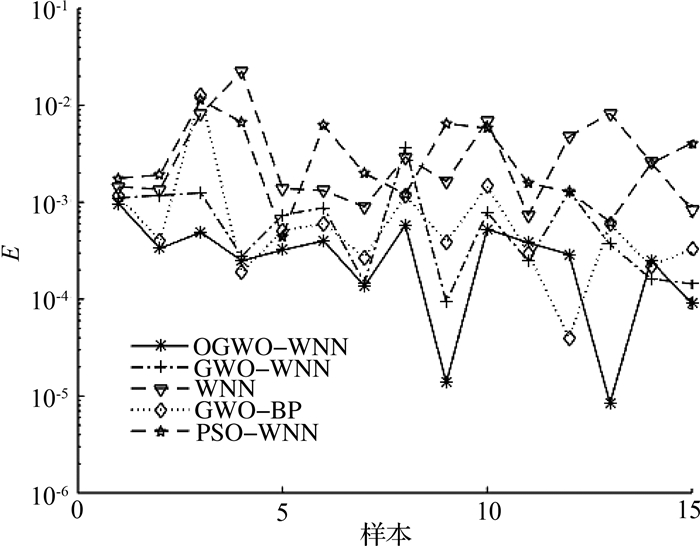
为了保证公平性, 5种模型的基本参数保持一致:种群规模为30、最大迭代次数为500.特别地, OGWO-WNN模型中的反向学习优化选择概率p=0.5.GWO-WNN模型、PSO-WNN模型的建立与OGWO-WNN相似, 仅将优化函数分别改成标准GWO算法和PSO算法.GWO-BP模型利用GWO算法优化BP神经网络的全部权值和阈值[17], 采用6-11-1的网络结构, 所以灰狼个体编码长度为6×11+11+11+1=89.将训练好的上述5种模型分别对相同的威胁度测试集进行预测, 实验结果如图 3、4和表 4所示.图中, T为目标威胁度, E为预测误差绝对值.

|
图 3 OGWO-WNN的预测威胁值与真实威胁值对比 Fig. 3 Comparison between forecasting values and real threat values based on OGWO-WNN |
|
图 4 5种模型的预测误差绝对值 Fig. 4 Absolute predictive error of five models |
| 表 4 5种优化方法的绝对预测误差平均值 Table 4 Mean absolute predictive error of five optimization methods |
由图 3可知, OGWO-WNN模型输出的预测威胁值与真实威胁值非常接近, 与真实威胁度的拟合度很高.由图 4、表 4可知, OGWO-WNN威胁评估模型的预测误差平均值小于其他4种威胁估计模型, 预测结果最接近真实值.除了在第4、11、12、14个样本处, OGWO-WNN模型预测误差不是最小(但十分接近最小误差), 其余样本点的预测误差均最小.5种模型的优异度排序为:OGWO-WNN>GWO-WNN>GWO-BP>PSO-WNN>WNN.实验结果显示, 构造的OGWO-WNN目标威胁评估模型能够较好地应对目标威胁评估问题, 模型性能优于另外4种模型.
4 结语本文针对多源信息融合中目标威胁评估的特点, 利用改进灰狼优化算法与小波神经网络, 建立基于改进灰狼优化算法优化小波神经网络的目标威胁评估模型, 提出该模型的算法.选取影响目标威胁评估的6个典型指标, 采集了105组数据用于仿真实验.实验结果表明, 相比于WNN、GWO-WNN、GWO-BP、PSO-WNN模型, OGWO-WNN模型能够更加准确、有效地预测目标威胁值, 为目标威胁评估提供了一种新的方法.
| [1] |
姚磊, 王红明, 郑锋, 等. 空中目标威胁估计的模糊聚类方法研究[J]. 武汉理工大学学报:交通科学与工程版, 2010, 34(6): 1159-1161. YAO Lei, WANG Hong-ming, ZHENG Feng, et al. Study fuzzy clustering method of air target threat assessment[J]. Journal of Wuhan University of Technology:Transportation Science and Engineering, 2010, 34(6): 1159-1161. |
| [2] |
王改革, 郭立红, 段红, 等. 基于萤火虫算法优化BP神经网络的目标威胁估计[J]. 吉林大学学报:工学版, 2013, 43(4): 1064-1069. WANG Gai-ge, GUO Li-hong, DUAN Hong, et al. Target threat assessment using glowworm swarm optimization and BP neural network[J]. Journal of Jilin University:Engineering and Technology Edition, 2013, 43(4): 1064-1069. |
| [3] |
MIRJALILI S, MIRJALILI S M, LEWIS A. Grey Wolf optimizer[J]. Advances in Engineering Software, 2014, 69(3): 46-61. |
| [4] |
MADADI A, MOTLAGH M M. Optimal control of DC motor using grey wolf optimizer algorithm[J]. Technical Journal of Engineering and Applied Science, 2014, 4(4): 373-379. |
| [5] |
DELYON B, JUDITSKY A, BENVENISTE A. Accuracy analysis for wavelet approximations[J]. IEEE Transactions on Neural Networks, 1995, 6(2): 332-348. DOI:10.1109/72.363469 |
| [6] |
SONG H, SULAIMAN M, MOHAMED M. An application of grey wolf optimizer for solving combined economic emission dispatch problems[J]. International Review on Modeling and Simulation, 2014, 7(5): 838-844. |
| [7] |
龙文, 赵东泉, 徐松金. 求解约束优化问题的改进灰狼优化算法[J]. 计算机应用, 2015, 35(9): 2590-2595. LONG Wen, ZHAO Dong-quan, XU Song-jin. Improved grey wolf optimization algorithm for constrained optimization problem[J]. Journal of Computer Applications, 2015, 35(9): 2590-2595. DOI:10.11772/j.issn.1001-9081.2015.09.2590 |
| [8] |
EI-GAAFARY A A M, MOHAMED Y S, HEMEIDA A M, et al. Grey wolf optimization for multi input multi output system[J]. Universal Journal of Communications and Networks, 2015, 3(1): 1-6. |
| [9] |
康岚兰, 董文永, 田降森. 一种自适应柯西变异的反向学习粒子群优化算法[J]. 计算机科学, 2015, 42(10): 226-231. KANG Lan-lan, DONG Wen-yong, TIAN Jiang-sen. Opposition-based particle swarm optimization with adaptive Cauchy mutation[J]. Computer Science, 2015, 42(10): 226-231. |
| [10] |
DEB S, DEB S, GANDOMI A H, et al. Opposition-based krill herd algorithm with Cauchy mutation and position clamping[J]. Neurocomputing, 2016, 177(C): 147-157. |
| [11] |
周新宇, 吴志健, 王晖, 等. 一种精英反向学习的粒子群优化算法[J]. 电子学报, 2013, 41(8): 1647-1652. ZHOU Xin-yu, WU Zhi-jian, WANG Hui, et al. Elite opposition-based particle swam optimization[J]. Acta E1ectronica Sinica, 2013, 41(8): 1647-1652. |
| [12] |
刘海波, 王和平, 沈立顶. 基于SAPSO优化灰色神经网络的空中目标威胁估计[J]. 西北工业大学学报, 2016, 34(1): 25-32. LIU Hai-bo, WANG He-ping, SHEN Li-ding. Target threat assessment using SAPSO and grey neural network[J]. Journal of Northwestern Polytechnical University, 2016, 34(1): 25-32. |
| [13] |
王改革, 郭立红, 段红, 等. 基于Elman_AdaBoost强预测器的目标威胁评估模型及算法[J]. 电子学报, 2012, 40(5): 901-906. WANG Gai-ge, GUO Li-hong, DUAN Hong, et al. The model and algorithm for the target threat assessment based on Elman_AdaBoost strong predictor[J]. Acta Electronica Sinica, 2012, 40(5): 901-906. |
| [14] |
KASIVISWANATHAN K S, HE J, SUDHEER K P, et al. Potential application of wavelet neural network ensemble to forecast stream flow for flood management[J]. Journal of Hydrology, 2016, 53(6): 161-173. |
| [15] |
WANG G, GUO L, DUAN H. Wavelet neural network using multiple wavelet functions in target threat assessment[J]. The Scientific World Journal, 2013, 13(1): 632437. |
| [16] |
YAO Y, ZHAO J, WANG Y, et al. MADM of threat assessment with attempt of target[J]. Advances in Technology and Management, 2012, 33(2): 171-179. |
| [17] |
HASSANIN M F, SHOEB A M, HASSANIEN A E. Grey wolf optimizer-based back-propagation neural network algorithm[C]//Computer Engineering Conference. Cairo: [s. n. ], 2017. http://ieeexplore.ieee.org/document/7856471/
|



