近年来, 遥感技术高速发展, 遥感图像地面分辨率大幅提高, 促进了高分辨率卫星在地理测绘、天气预报、军事侦察等民用和军用领域中的广泛应用.时间延迟积分电荷耦合元件(TDI-CCD)利用时间延迟积分推扫成像, 相比于普通面阵CCD具有更高的灵敏度和信噪比[1-2].TDI-CCD工作在N级积分级数下, N级电荷进行累加, 相当于延长积分时间, 为了获得清晰的图像, 像移速度和电荷转移速度需要持续保持匹配.卫星在轨摄像期间, 成像平台在姿态调整动量轮、调姿推力器以及外界扰动等因素下存在颤振, 导致地面目标在成像器件上发生像移, 形成像面模糊.
卫星上的颤振已经成为影响卫星光学成像质量的重要因素之一[3], 关于这方面的研究越来越多.在颤振检测和仿真模型方面, Timoner等[4]利用多维数字滤波器创建基于梯度的多幅图像配准算法, 实现了颤振运动的定量估测.Wu等[5]针对TDI退化图像PSF的空间变化性, 逐行根据颤振信息构建模糊核, 利用RL算法实现去模糊.冯华君等[6]通过构建模拟遥感成像的地面半物理仿真实验系统, 提出真正影响成像质量的颤振主要集中在大幅度的低频区和小幅度的高频区.孙韬等[7]采用稳定的相位幅角相关匹配算法进行波段间配准, 提出利用五谱段合一多光谱相机影像进行卫星颤振定量检测的方法.在退化图像的复原方面, 葛苹等[8]针对TDI-CCD的成像数据特点, 从遥感图像中获取刃边来计算成像系统MTF, 采用维纳滤波法及修正的逆滤波器法(MIF)对退化图像实现MTF补偿处理.Sun等[9]通过模拟实验分析不同颤振测量误差下, 维纳滤波、RL算法和全变分算法对退化图像的恢复情况, 测定不同算法对测量误差的最大容忍度.考虑到图像的复原效率, 目前针对TDI退化图像实现去模糊的算法多为传统的维纳滤波、RL滤波和全变分方法.3种方法中, 维纳滤波的效果最差; RL算法的去模糊效果良好, 会引入大量振铃; 全变分方法虽然能够有效地抑制振铃, 但会弱化图像边缘细节的复原效果.本文在全变分方法的基础上, 将数值保真项扩展至二阶, 结合文献[5]逐行根据颤振路径构建模糊核的方法, 对TDI退化图像进行复原.结果表明, 本文算法在抑制振铃的同时提升了图像的清晰度, 凸显边缘细节.
1 TDI遥感图像的去模糊 1.1 TDI遥感图像颤振过程图像的模糊过程可以等效于在考虑噪声因素的情况下, 原始清晰图像和颤振模糊核的卷积过程.该过程可以简单表示为
B =I*k+N.
式中:B、I、N分别为模糊图像、原始清晰图像和噪声, *为卷积运算.
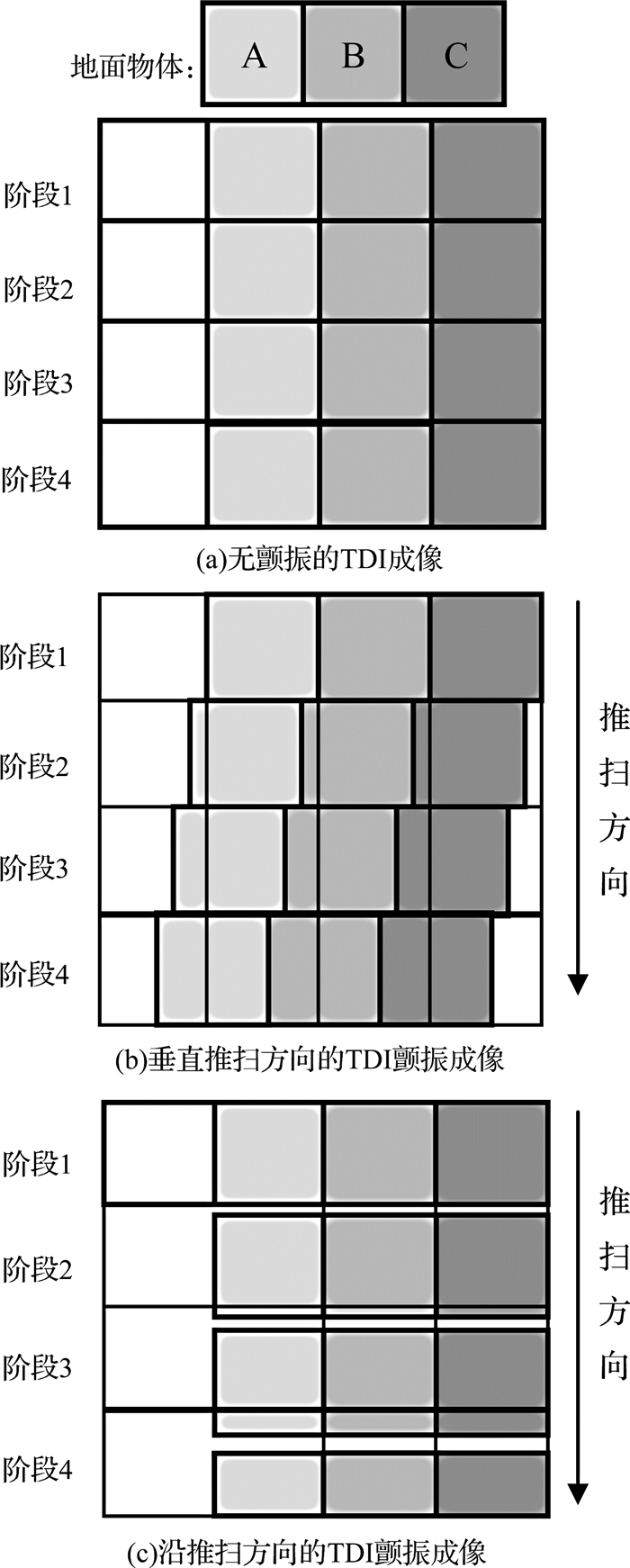
TDI-CCD颤振模糊成像和传统的图像模糊过程有区别, Yu等[10]在利用TDI-CMOS成像传感器实现遥感图像实时去模糊的阐述中有解释.图 1描述了不存在颤振和存在颤振时的TDI成像情况, A、B、C分别为3个地面物体, 设其在CCD上成像时所占像素面积都为1.如图 1(a)、(b)所示为CCD一行的不同成像阶段.使TDI推扫速度与CCD光生电荷包移动速度保持同步, 当不发生颤振时, 在每个阶段A、B、C都成像在CCD相同位置, 叠加不同阶段的成像数据, 可以获得清晰的遥感图像; 当发生颤振情况时, 每个阶段A、B、C在CCD的成像位置会发生偏移, 叠加不同阶段的成像数据后, 获得颤振模糊的遥感图.每个阶段的颤振路径可能不同, CCD每行根据颤振路径的模糊核不同, 因此TDI颤振图像的模糊核存在空间变化性.
|
图 1 TDI遥感成像 Fig. 1 TDI sensing imaging |
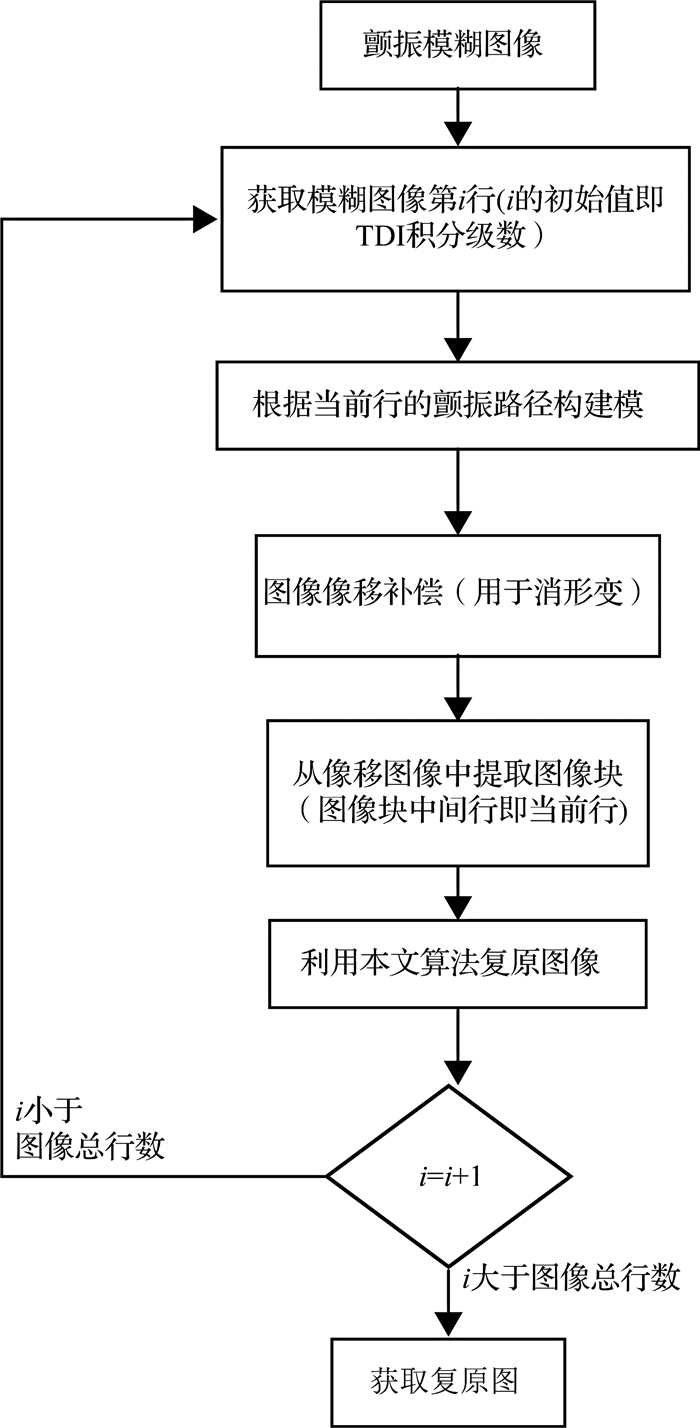
由于TDI颤振图像的模糊核存在空间变化性, 在文献[5]逐行估计模糊核的基础上, 采用将数值保真项扩展至二阶的方法对图像实现逐行去模糊, 再将复原的每一行拼接成复原图像.图像复原框架如图 2所示, 复原框架中, 关于逐行提取的图像块大小等细节问题, Wu等[5]进行了详细阐述.
|
图 2 颤振图像的复原框架 Fig. 2 Recovery framework of vibrated image |
Shan等[11]在盲去模糊过程中, 证实了将去模糊算法的数值保真项提升到二阶, 可以获得更精确的模糊核.Zoran等[12]以高斯混合模型为先验知识, 在图像块复原的基础上完成了图像的全局优化.Watanabe等[13]利用梯度域图像分解的凸优化方法, 实现模糊图像的复原.目前, 多数的图像复原方法主要针对自然图像的恢复, 算法的运行需要一定时间, 难以应用于模糊核空间变化的TDI颤振遥感图像中.本文在全变分方法的基础上, 将数值保真项增加至二阶.结果表明, 该方法在耗时相对较小的前提下, 可以恢复更多的高频信息, 提高图像的复原效果.
去模糊表述如下:
| $ {I_{{\rm{min}}}} = \left( {{\sum _{{\partial ^*} \in \vartheta }}{m_{k({\partial ^*})}}\left\| {{\partial ^*}I * k-{\partial ^*}B} \right\|_2^2} \right) + \mu {\left\| {\nabla I} \right\|_1}. $ | (1) |
式中:第一项为数值保真项, 第二项为正则化项; I表示原始清晰图像; B为模糊图像; k为卷积核; ϑ={∂0, ∂x, ∂y, ∂xx, ∂xy, ∂yy}, 包含了0阶到2阶的偏微分算子; μ为正则项权重因子; ∇为梯度算子.
对于式(1)的L1正则化项问题, 通过添加辅助变量∇w, 使用半二次分裂最小化方法[14]来求解:
| $ \begin{array}{l} {I_{{\rm{min}}}} = \left( {{\sum _{{\partial ^*} \in \vartheta }}{m_{k({\partial ^*})}}\left\| {{\partial ^*}I * k-{\partial ^*}B} \right\|_2^2} \right) + \\ \mu {\left\| {\nabla I} \right\|_1} + \lambda \left\| {\nabla I-\nabla w} \right\|_2^2. \end{array} $ | (2) |
之后, 对式(2), 通过固定其他变量交替最小化[15]I和∇w:
| $ \begin{array}{l} {I_{{\rm{min}}}} = \left( {{\sum _{{\partial ^*} \in \vartheta }}{m_{k({\partial ^*})}}\left\| {{\partial ^*}I * k-{\partial ^*}B} \right\|_2^2} \right) + \\ \lambda \left\| {\nabla I-\nabla w} \right\|_2^2, \end{array} $ | (3) |
| $ {\nabla _{{\rm{min}}}}w = \lambda \left\| {\nabla I-\nabla w} \right\|_2^2 + \mu {\left\| {\nabla w} \right\|_1}. $ | (4) |
通过傅里叶变换, 在频域中求解式(3), 可得
| $ {I_{{\rm{min}}}} = {F^{-1}}\left( {\frac{{\lambda F\prime \left( \nabla \right)F\left( {\nabla w} \right) + {\sum _{{\partial ^*} \in \vartheta }}{m_{k({\partial ^*})}}F\prime \left( {{\partial ^*}} \right)F\left( {{\partial ^*}} \right)F\prime \left( k \right)F\left( B \right)}}{{\lambda F\prime \left( \nabla \right)F\left( \nabla \right) + {\sum _{{\partial ^*} \in \vartheta }}{m_{k({\partial ^*})}}F\prime \left( {{\partial ^*}} \right)F\left( {{\partial ^*}} \right)F\prime \left( k \right)F\left( k \right)}}} \right). $ | (5) |
对于式(4), 可得
| $ w = \frac{{\nabla I}}{{\left| {\nabla I} \right|}}{\rm{max}}\left\{ {\left| {\nabla I} \right|-\frac{\mu }{\lambda }, 0} \right\}. $ | (6) |
由上述推导, 交替迭代式(4)、(5), 可以获得最终去模糊图像.其中mk(∂0)=mk(∂x)=mk(∂y)=1, mk(∂xx)=mk(∂xy)=mk(∂yy)=1, μ=0.002 5.关于λ的取值, 既需要保证优化的收敛速度, 又需要保证式(4)、(5)的迭代结果为式(1)的优化结果.取λ的初始值为0.002 5.每次迭代, λ翻倍, ∇w逐渐接近∇I.
2 仿真实验及分析为了验证该方法的有效性和普适性, 开展一系列仿真模拟实验.取TDI颤振积分级数为48, 颤振频率为100 Hz, 每行积分时间为3.71×10-4 s.由于颤振运动都可以利用不同类型的正弦运动组合而成[6], 垂直于推扫方向和沿推扫方向的TDI颤振展现了不同的模糊特性和复原情况, 分别从这两方向的正弦运动仿真TDI颤振模糊过程, 利用该算法实现退化图像的复原.关于颤振仿真模型的正确性和有效性, 冯华君等[6]通过构建模拟遥感成像的半物理实验系统得到验证.
如图 3所示为垂直于推扫方向的遥感图像清晰图、颤振模糊图及利用RL算法、全变分方法[16]和本文算法的复原图.如图 4所示为沿推扫方向的清晰图、颤振模糊图及3种复原图.由于卫星的遥感成像都显示在像面上, 为了研究方便, 颤振振幅单位取像素.设置颤振振幅都为6像素.根据图 3、4可知, RL算法的去模糊效果很好, 但振铃影响严重; 全变分算法虽然可以有效地抑制振铃, 但弱化了去模糊效果; 本文算法在抑制复原过程的振铃的同时, 保证图像有效去模糊, 边缘细节更清晰.如表 1所示为图 3、4中模糊图像和复原图像与原始图像的结构相似度ssim, 如表 2所示为对图像一行的复原时间t对比情况.由表 1、2可以看出, 该方法在耗时增加很少的情况下, 对图像的复原效果比RL算法和全变分方法高很多.

|
图 3 垂直于推扫方向的颤振图像复原效果对比图 Fig. 3 Comparision of recovery effect on vibrated image vertical to scanning direction |

|
图 4 沿推扫方向的颤振图像复原效果对比图 Fig. 4 Comparision of recovery effect on vibrated image horizontal to scanning direction |
| 表 1 3种算法复原颤振图像的ssim对比 Table 1 ssim value comparison of deblurred images by three algorithms |
| 表 2 3种算法对颤振图像一行的复原时间 Table 2 Recovery time of three algorithms |
比较在不同颤振条件下, 本文算法与RL算法、全变分方法对图像的复原情况.如表 3所示为当颤振幅度为6像素, 颤振频率为100 Hz, 积分级数分别为24、48、96时, 3种算法对颤振图像复原后的ssim比较.当积分级数较大时, 3种算法对颤振模糊图像的复原效果略好.在不同积分级数下, 该算法对颤振图像的复原效果都是最优.
| 表 3 不同积分级数下, 3种算法复原颤振图像的ssim对比 Table 3 ssim comparison of deblurred images by three algorithms in different integral series |
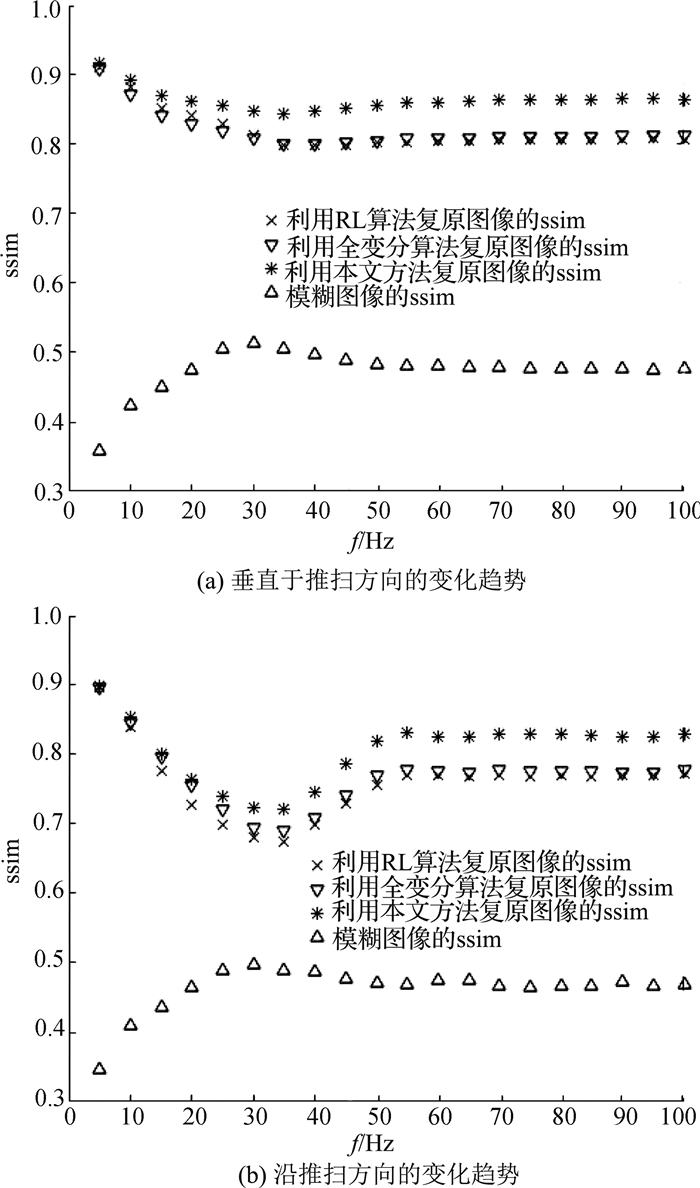
如图 5所示为当颤振幅度为6像素, 积分级数为48, 颤振频率f为0~100 Hz时, 3种算法对颤振图像的复原情况.可以发现, 虽然低频颤振对图像的降质影响较大, 但在低频处算法对图像的恢复效果很好.随着颤振频率的增加, 颤振对图像的降质影响和3种算法对图像的复原性能都趋于稳定.该算法在低频处对颤振模糊图像的复原和RL算法、全变分方法相差不多, 随着频率的增加, 该算法的优势逐渐明显.
|
图 5 3种复原算法下, ssim随频率的变化趋势 Fig. 5 Variation trend of ssim with frequency under three recovery algorithms |
根据图 3~5和表 3可以发现, 在不同积分级数、颤振频率下, 该算法对图像的恢复效果比RL算法和全变分方法好, 该算法对复原不同颤振条件的TDI模糊图像具有普适性.
3 结语本文在全变分去模糊的基础上, 提出将数值保真项扩展至二阶的方法, 不仅有效地抑制复原过程中产生的振铃, 而且保证图像的边缘纹理更清晰.将该算法应用到TDI遥感颤振的逐行去模糊中.实验表明, 无论是垂直于推扫方向还是沿推扫方向的颤振复原, 利用该算法复原后的图像ssim都高于传统RL算法、全变分方法, 证明了该算法能够有效地提升复原图像的清晰度, 凸显图像边缘细节.在不同的积分级数和颤振频率下, 利用图像复原后的ssim规律, 展示了该算法对复原不同颤振条件的TDI模糊图像都具有很好的普适性.
| [1] |
张媛. 星载TDICCD相机侧摆成像像移速度建模与分析[D]. 哈尔滨: 哈尔滨工业大学, 2013: 7. ZHANG Yuan. Modeling and analysis of image motion velocity for satellite borne TDICCD camera in roll attitude[D]. Harbin: Harbin Institute of Technology, 2013: 7. http://www.cnki.com.cn/Article/CJFDTOTAL-HFYG201306012.htm |
| [2] |
王凌, 徐之海, 冯华君, 等. 线阵推扫式CCD亚像元成像的列向动态调制传递函数[J]. 浙江大学学报:工学版, 2008, 42(2): 317-320. WANG Ling, XU Zhi-hai, FENG Hua-jun, et al. Transverse dynamic modulation transfer function of subpixel push-scanning imaging by linear CCD[J]. Journal of Zhejiang University:Engineering Science, 2008, 42(2): 317-320. |
| [3] |
WITTING M, HOLTS K, TUNBRIDGE D E L, et al. In-orbit measurements of microaccelerations of ESA's communication satellite OLYMPUS[C]//Free-Space Laser Communication Technologies Ⅱ. Los Angeles: SPIE, 1990, 1218: 205-215. http://spie.org/Publications/Proceedings/Paper/10.1117/12.18234
|
| [4] |
TIMONER S J, FREEMAN D M. Multi-image gradient based algorithms for motion estimation[J]. Optical Engineering, 2001, 40(9): 2003-2016. DOI:10.1117/1.1391495 |
| [5] |
WU Jia-gu, ZHENG Zhen-zhen, FENG Hua-jun, et al. Restoration of TDI camera images with motion distortion and blur[J]. Optics and Laser Technology, 2010, 42(8): 1198-1203. DOI:10.1016/j.optlastec.2010.03.010 |
| [6] |
冯华君, 邓勤, 郑珍珍, 等. 卫星颤振光学成像仿真模型分析[J]. 光电工程, 2013, 40(2): 1-7. FENG Hua-jun, DENG Qin, ZHENG Zhen-zhen, et al. Analysis of the simulation model based on remote sensing imaging under vibration[J]. Opto-Electronic Engineering, 2013, 40(2): 1-7. |
| [7] |
孙韬, 龙辉, 赵冬, 等. 基于五谱段合一多光谱相机影像的卫星颤振检测和补偿[J]. 光学学报, 2014, 34(7): 0728005. SUN Tao, LONG Hui, ZHAO Dong, et al. Detection and compensation of satellite flutter based on image from multispectral camera with five spectral combinations[J]. Acta Optica Sinica, 2014, 34(7): 0728005. |
| [8] |
葛苹, 王密, 潘俊, 等. 高分辨率TDI-CCD成像数据的自适应MTF图像复原处理研究[J]. 国土资源遥感, 2010, 22(4): 23-28. GE Ping, WANG Mi, PAN Jun, et al. A study of adaptive MTF image restoration of high resolution TDI-CCD image data[J]. Remote Sensing for Land and Resources, 2010, 22(4): 23-28. DOI:10.6046/gtzyyg.2010.04.06 |
| [9] |
SUN Xuan, ZHANG Wei, ZHI Xi-yang. Effects of vibration measurement error on remote sensing image restoration[C]//International Symposium on Optoelectronic Technology and Application. Beijing: SPIE, 2016: 10154. http://www.cs.bilkent.edu.tr/~gudukbay/citations/node3.html
|
| [10] |
YU Hang, QIAN Xin-yuan, GUO Meng-han, et al. A time delay integration CMOS image sensor with online deblurring algorithm[C]//International Symposium on VLSI Design, Automation and Test. [S. l. ]: IEEE, 2015: 1544-1554. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=6271566
|
| [11] |
SHAN Qi, JIA Jia-ya, AGARWALA A. High-quality motion deblurring from a single image[J]. ACM Transactions on Graphics, 2008, 27(3): 1-10. |
| [12] |
ZORAN D, WEISS Y. From learning models of natural image patches to whole image restoration[J]. International Comference on Computer Vision, 2011, 6126278: 479-486. |
| [13] |
WATANABE M, KYOCHI S, ONO S. Gradient-domain image decomposition for image recovery[C]//IEEE International Conference on Image Processing. [S. l. ]: IEEE, 2015: 4768-4772. http://ieeexplore.ieee.org/document/7351712/
|
| [14] |
XU Li, JIA Jia-ya. Two-phase Kernel estimation for robust motion deblurring[C]//European Conference on Computer Vision. Heraklion: [s. n. ], 2010: 157-170. http://dl.acm.org/citation.cfm?id=1886077
|
| [15] |
CHEN J, YUAN L, TANG C K, et al. Robust dual motion deblurring[C]//IEEE Conference on Computer Vision and Pattern Recognition. [S. l. ]: IEEE, 2008: 1-8. https://www.computer.org/csdl/proceedings/cvpr/2008/2242/00/04587830-abs.html
|
| [16] |
WANG Y, YANG J, YIN W, et al. A new alternating minimization algorithm for total variation image reconstruction[J]. SIAM Journal on Imaging Sciences 1, 2008, 1(3): 248-272. DOI:10.1137/080724265 |



