2. 华中科技大学 数字制造装备与技术国家重点实验室, 湖北 武汉 430074;
3. 浙江工商大学 工商管理学院, 浙江 杭州 310018
2. State Key Laboratory of Digital Manufacturing Equipment and Technology, Huazhong University of Science and Technology, Wuhan 430074, China;
3. School of Business Administraticn, Zhejiang Gongshang University, Hangzhou 310018, China
在现代社会中, 多目标决策问题十分常见, 决策的正误对决策者影响重大.在多数情况下, 被评价对象的很多表现难以准确度量;决策所用的指标很难不重复、也不遗漏地覆盖各个方面.不少多目标决策问题带有大量定性指标并且指标间存在交互作用[1-2].例如, 高中理科生的成绩可以用语文、数学、物理等指标评价, 这些指标不相互独立, 逻辑思维强的人往往数学和物理都好, 所以数学和物理有一定的抵消作用;语文需要表达能力, 兼有优秀的逻辑思维和表达能力是很难的, 所以语文和数学物理有互补作用.当评估供应商、生产线等系统时, 所涉及的定性指标数量更多, 指标间的交互作用更复杂.要做出合理的决策, 就要将交互作用合理地表达出来, 定性指标的评价值要用合理的方法表示.
传统的多目标决策方法包括多属性价值函数模型[3]、分层序列法[4]、目标规划法[5]、多属性效用法[6]、层次分析法[7]、理想解法[8]、数据包络法[9]、灰色综合评价法[10]等.这些方法虽然有的易于实现和操作, 有的对于某一类问题效果很好;但是他们大都假设指标之间是相互独立的, 使用线性方法集成评价值, 无法体现交互作用;评价值由专家以数值评分的形式给出, 专家水平对决策的影响极大, 对定性指标的评价不够准确.灰色综合评价法能够较好地处理带有灰色信息问题的决策, 广泛应用于因素分析[11]、多目标决策[12]等领域.现有的灰关联度模型如相似关联度[13]、周期关联度[14]、振幅关联度[15]及凸关联度[16]等都采用线性方法集成关联系数, 假设指标间独立, 不能表达交互作用.为了改进这一局限, 使用模糊测度表达交互作用是一种有效的手段, 相应地可以使用模糊积分进行评价数据的集成[17].
模糊积分理论由Sugeno[18]提出, 现已有多种模糊积分[19].其中, Choquet模糊积分最适于处理多目标决策中的非线性集成问题, 它可以完全表达指标间的交互作用[20].模糊测度有多种, 如K可加模糊测度、gλ模糊测度等[19].其中, gλ模糊测度易于计算, 能够完全表达一组指标的所有交互作用, 但每组指标只能表达1种交互作用.K可加模糊测度在K很小时易于计算, K很大时能够表达所有的交互作用, 两者不能兼得.常志朋等[21]提出基于2可加模糊测度的灰模糊积分关联度决策模型, 改进了灰色综合评价法的弊端, 但当指标个数较多时, 2可加模糊测度对交互作用的表达能力较弱[19].
针对带有大量定性指标并且指标间存在交互作用的多目标决策问题, 本文提出基于gλ模糊测度的灰模糊积分决策模型.1)使用模糊数表达专家对定性指标的评估值, 加强了评估的准确性.2)使用关联系数代替初始评估值, 减少了专家的主观性影响;使用Choquet模糊积分对关联系数进行集成, 使指标间的交互作用得到充分表达.3)使用gλ模糊测度表达交互作用, 设计了基于改进的教与学算法的gλ模糊测度辨识方法, 提高了指标权重的一致性.提出指标体系的构建原则, 弥补了gλ模糊测度的局限.4)通过实例证明了所提方法的可行性与合理性, 将该方法与灰色综合评价法进行比较.
1 相关理论简介下面对灰色综合评价法[22]、gλ模糊测度和Choquet模糊积分[23]及模糊数进行简要介绍.
1.1 灰色综合评价法众所周知, 现实世界中很多的系统是灰色的, 只能在一定程度上获取部分信息, 无法准确地获取全部信息;在对一个系统进行评价与决策时, 难免因为初始评价数据的不准确而有所偏颇.灰色综合评价法由我国著名学者邓聚龙教授提出, 它通过对部分已知信息的生成和开发, 实现对现实世界的准确认识, 即利用有限的已知信息来确定系统的未知信息.该方法对样本量和分布都没有要求, 适应面广, 能够很好地处理灰色系统, 下面将基本的方法简介如下.
1.1.1 获取原始评价数据和规范化处理设有n个指标, m个被评价对象.评价矩阵为
| $ \mathit{\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} {{j_1}\left( 1 \right)}&{{j_1}\left( 2 \right)}& \cdots &{{j_1}\left( n \right)}\\ {{j_2}\left( 1 \right)}&{{j_2}\left( 2 \right)}& \cdots &{{j_2}\left( n \right)}\\ \vdots&\vdots &{}& \vdots \\ {{j_m}\left( 1 \right)}&{{j_m}\left( 2 \right)}& \cdots &{{j_m}\left( n \right)} \end{array}} \right]. $ |
式中:ji(k)为第i个被评价对象在第k个指标上的评价值.
为了消除量纲与数量级的影响, 根据式(1)将原始评价值规范化为
| $ {C_i}\left( k \right) = \frac{{{j_i}\left( k \right) - \overline {{X_k}} }}{{{S_k}}}. $ | (1) |
式中:
由此可得规范化后的评价矩阵
| $ \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} {{C_1}\left( 1 \right)}&{{C_1}\left( 2 \right)}& \cdots &{{C_1}\left( n \right)}\\ {{C_2}\left( 1 \right)}&{{C_2}\left( 2 \right)}& \cdots &{{C_2}\left( n \right)}\\ \vdots&\vdots &{}& \vdots \\ {{C_m}\left( 1 \right)}&{{C_m}\left( 2 \right)}& \cdots &{{C_m}\left( n \right)} \end{array}} \right]. $ |
取C*=[C*(1), C*(2), …, C*(n)]为参考数列, 其中C*(i)为第i个指标所有评价值中的最优值.按式(2)计算第i个方案在第k个指标上的评价值相对于第k个指标的最优评价值的关联系数ξi(k), 即
| $ {\xi _i}\left( k \right) = \frac{{\mathop {\min }\limits_i \mathop {\min }\limits_k \left| {{C_ * }\left( k \right) - {C_i}\left( k \right)} \right| + \rho \mathop {\max }\limits_i \mathop {\max }\limits_k \left| {{C_ * }\left( k \right) - {C_i}\left( k \right)} \right|}}{{\left| {{C_ * }\left( k \right) - {C_i}\left( k \right)} \right| + \rho \mathop {\max }\limits_i \mathop {\max }\limits_k \left| {{C_ * }\left( k \right) - {C_i}\left( k \right)} \right|}}. $ | (2) |
式中:ρ∈[0, 1], 一般取0.5.由此可得关联系数矩阵为
| $ \mathit{\boldsymbol{ \boldsymbol{\varXi} }} = \left[ {\begin{array}{*{20}{c}} {{\xi _1}\left( 1 \right)}&{{\xi _1}\left( 2 \right)}& \cdots &{{\xi _1}\left( n \right)}\\ {{\xi _2}\left( 1 \right)}&{{\xi _2}\left( 2 \right)}& \cdots &{{\xi _2}\left( n \right)}\\ \vdots&\vdots &{}& \vdots \\ {{\xi _m}\left( 1 \right)}&{{\xi _m}\left( 2 \right)}& \cdots &{{\xi _m}\left( n \right)} \end{array}} \right]. $ |
若W=[w1, w2, …, wn]T为各评价指标的权重向量, 则第i个待评价方案的绝对关联度为
| $ {r_i} = \sum\limits_{j = 1}^n {\left[ {{w_j} \times {\xi _i}\left( j \right)} \right]} . $ | (3) |
ri越大, 表明Ci与最优指标C*越接近, 综合评价越好.
1.2 模糊测度与模糊积分模糊测度:设X为非空集合, P(X)是X的幂集, 若集函g:P(X)→[0, 1]满足以下3条性质, 则称g是P(X)的模糊测度.
1) g(Ø)=0, g(X)=1.
2) ∀A、B∈P(X), 若A⊆B, 则g(A)≤g(B).
3) 若{An}⊂P(X), A1⊆A2⊆…⊆An…, ∪n=1∞An∈P(X), 则limi=∞g(Ai)=g(limi=∞Ai).
若g满足附加性质:若A、B∈P(X)且A∩B=Ø, 则∃λ∈[-1, ∞), g(A∪B)=g(A)+g(B)+λg(A)g(B), 称为gλ模糊测度.当λ>0时, g(A∪B)≥g(A)+g(B), 即A与B组合的效果大于A与B各自效果之和, 两者为积极互补作用.类似地, 当λ < 0时, 两者为消极抵消作用.当λ=0时, 两者之间完全独立.若X={x1, x2, …, xn}为有限集, xi的模糊密度为gi, 则gλ可以根据下式计算得到:
| $ \begin{array}{l} {g_\lambda }\left( {\left\{ {{x_1},{x_2}, \cdots ,{x_n}} \right\}} \right) = \sum\limits_{i = 1}^n {{g_i}} + \\ \;\;\;\;\;\;\;\;\lambda \sum\limits_{{i_1} = 1}^{n - 1} {\sum\limits_{{i_2} = {i_1} + 1}^n {{g_{{i_1}}}{g_{{i_2}}} + \cdots + {\lambda ^{n - 1}}{g_1}{g_2} \cdots {g_n}} } = \\ \;\;\;\;\;\;\;\;\frac{1}{\lambda }\left| {\prod\limits_{i = 1}^n {\left( {1 + \lambda {g_i}} \right) - 1} } \right|. \end{array} $ | (4) |
当g(X)=1时, 可以由下式求出λ:
| $ \lambda + 1 = \prod\limits_{i = 1}^n {\left( {1 + \lambda {g_i}} \right)} . $ | (5) |
Sugeno教授在1974年提出模糊积分的概念, 它适用于处理指标间存在交互作用、主观性强的评价问题.后经多位学者发展, 提出多种不同的积分模型;其中, Choquet模糊积分考虑各种影响因素, 避免Sugeno模糊积分完全忽略次要因素影响的缺陷, 在综合评价中的应用较多[24].
Choquet模糊积分:不失一般性, 使第k个被评价方案在第i个指标上的评价值f(xik)按如下排列:f(x1k)≥…≥f(xik)≥…≥f(xnk), 则f(·)相对于g(·)在X上的Choquet积分为
| $ \begin{array}{l} \int {f{\rm{d}}g} = f\left( {x_n^k} \right){g_\lambda }\left( {{X_n}} \right) + \\ \;\;\;\;\;\;\;\left[ {f\left( {x_{n - 1}^k} \right) - f\left( {x_n^k} \right)} \right]{g_\lambda }\left( {{X_{n - 1}}} \right) + \cdots + \\ \;\;\;\;\;\;\;\left[ {f\left( {x_1^k} \right) - f\left( {x_2^k} \right)} \right]{g_\lambda }\left( {{X_1}} \right). \end{array} $ | (6) |
式中:gλ({Xn})=gλ({x1, x2, …, xn}), 表示相应指标集合的模糊测度.
1.3 模糊数在模糊数学中, 人们在对定性指标评价的过程中, 往往具有一定的模糊性, 因而用模糊数表示隶属程度.常用的有三角模糊和梯形模糊数.本文采用梯形模糊数.
梯形模糊数:模糊数
| $ f\left( x \right) = \left\{ \begin{array}{l} \frac{{x - {n_1}}}{{{n_2} - {n_1}}},{n_1} \le x < {n_2};\\ 1,{n_2} \le x < {n_3};\\ \frac{{x - {n_4}}}{{{n_3} - {n_4}}},{n_3} \le x < {n_4};\\ 0,\;\;\;\;\;\;\;其他. \end{array} \right. $ | (7) |
式中:0 < n1 < n2 < n3 < n4.
由梯形模糊数的性质和扩张原理, 可得数学运算如下.设模糊数
| $ \mathit{\boldsymbol{\tilde m}} \oplus \mathit{\boldsymbol{\tilde n}} \cong \left[ {{m_1} + {n_1},{m_2} + {n_2},{m_3} + {n_3},{m_4} + {n_4}} \right], $ | (8) |
| $ {\bf{\tilde m}} \otimes {\bf{\tilde n}} \cong \left[ {{m_1} \times {n_1},{m_2} \times {n_2},{m_3} \times {n_3},{m_4} \times {n_4}} \right]. $ | (9) |
设有m个被评价对象, K位专家参与评价.首先要根据决策者的目的和被评价对象的特点构建一套合理的指标体系, 分为P个层面, 各层面下有一些指标, 同一层面下的指标之间只有1种交互作用;当问题比较复杂时, 可以按树状结构继续划分层面, 直到满足同一层面的指标只有1种交互作用为止.基于gλ模糊测度的特点, 对这些层面逐个逐层处理.设某层面有n个评价指标, 其中有些指标是定性的, 评价值由K位专家以语意变量的形式给出;然后转换为对应的模糊数, 再经过整合与解模糊化可得明确值;有些指标是定量的, 评价值直接通过统计或测量的方法得到.部分重要的属性集的幂子集的权重数据由专家给出, 其余权重会在后续处理阶段通过计算获得.根据这些评价值和权重, 按照下面的方法进行处理, 最终得到每个对象在每个层面的综合得分及每个对象的整体综合得分.决策者可以根据分数的高低进行决策.
2.2 构建指标体系要做出科学的评价与决策, 首先要有科学的指标.评价指标的确定既要考虑实际问题的背景, 也要考虑所用方法的特点.本文总结了现有的原则, 结合灰模糊积分法的特点, 给出如下原则.
科学性原则:指标体系要能够准确而全面地反映被评价对象的所有方面, 定性与定量结合, 硬指标与软指标结合, 应避免某种指标数量过多而其他过少的情况, 形成层次清晰、权重合理的评价体系.
灵活性原则:指标体系要根据被评价对象的具体特点确定, 具体问题, 具体分析, 不能一概而论;要随着时代进步和技术革新的大环境不断调整, 与时俱进, 不能一成不变.
实用性原则:指标不宜过于繁杂, 避免只注重细节而不能反映整体性能.也不能过于粗略, 避免不能完整地反映被评价对象各方面的情况.指标不能涉及无法获取的被评价对象的机密.
分层与分组原则:采用gλ模糊测度, 局限是只能反映指标间的1种关系, 如互补、抵消或独立.现实中, 指标间往往各种关系都有, 评价误差较大.鉴于此, 宜采用分层分组的指标体系, 即先根据大方面分出几个层面, 这些层面之间几乎都是互补关系, 每个层面下再定具体指标, 这些指标间几乎都是抵消关系.若不满足, 可以继续分组直到1组内只有1种交互作用关系为止.然后对每个组分别应用1次基于gλ模糊测度的灰模糊积分模型, 逐层向上, 最终可以得出客观合理的评价.
2.3 初始数据的获取与处理 2.3.1 获取初始评估数据对于定量指标, 利用直接统计或测量的方法获取准确的评价数据.第i个对象在第k个指标上的评价值记为ji(k).对于定性指标, 请专家按语意评价集{极好, 很好, 好, 较好, 一般, 较差, 差, 很差, 极差}对各个被评价对象进行评价, 为方便计, 实际使用时, 用{z1, z2, z3, z4, z5, z6, z7, z8, z9}表示;根据表 1将专家给出的语意评价值转换为模糊数.第l位专家对i个被评价对象在k个指标上的模糊数记为
| 表 1 语意变量与模糊数对照表 Table 1 Corresponding table of linguistic values and fuzzy numbers |
在进行评价时, 模糊数不能参加运算, 因而要将模糊数解模糊化以转换为明确值.解模糊化的方法有很多, 各有优点和局限.如仅用单一公式转换, 计算太过简单, 无法验证其有效性.本文使用多种方法, 综合考虑之后再进行转换[25].
1) 距离测量法[26].根据相对距离公式, 模糊数
| $ {M_1}\left( {{{\mathit{\boldsymbol{\tilde x}}}_i}} \right) = \frac{{d_i^ - }}{{d_i^ - + d_i^ * }}. $ | (10) |
式中:0≤M1
| $ d_i^ - = \sqrt {\frac{1}{4}\left( {a_i^2 + b_i^2 + c_i^2 + d_i^2} \right)} , $ | (11) |
| $ \begin{array}{l} d_i^ * = \\ \sqrt {\frac{1}{4}\left[ {{{\left( {1 - {a_i}} \right)}^2} + {{\left( {1 - {b_i}} \right)}^2} + {{\left( {1 - {c_i}} \right)}^2} + {{\left( {1 - {d_i}} \right)}^2}} \right]} . \end{array} $ | (12) |
2) 中心值法[26].整体来看, 中心部分是最能够说明重要程度的区域.利用中心值法, 可以将模糊数
| $ \begin{array}{l} {M_2}\left( {{{\mathit{\boldsymbol{\tilde x}}}_i}} \right) = \frac{{{b_i} + {c_i}}}{2} + \frac{{\left[ {\left( {{d_i} - {c_i}} \right) - \left( {{b_i} - {a_i}} \right)} \right]}}{6} = \\ \;\;\;\;\;\;\;\;\frac{{2{b_i} + 2{c_i} + {d_i} + {a_i}}}{6}. \end{array} $ | (13) |
3) 重心法[27].利用重心法, 可以将模糊数
| $ \begin{array}{l} {M_3}\left( {{{\mathit{\boldsymbol{\tilde x}}}_i}} \right) = \\ \;\;\;\;\;\;\;\;\left\{ \begin{array}{l} {a_i},{a_i} = {b_i} = {c_i} = {d_i};\\ \frac{{d_i^2 + c_i^2 - b_i^2 - a_i^2 + {c_i}{d_i} - {a_i}{b_i}}}{{3\left( {{d_i} + {c_i} - {b_i} - {a_i}} \right)}},其他. \end{array} \right. \end{array} $ | (14) |
综合上面的3个结果取平均后, 得到综合解模糊值S(
| $ S\left( {{{\mathit{\boldsymbol{\tilde x}}}_i}} \right) = \frac{{{M_1}\left( {{{\mathit{\boldsymbol{\tilde x}}}_i}} \right) + {M_2}\left( {{{\mathit{\boldsymbol{\tilde x}}}_i}} \right) + {M_3}\left( {{{\mathit{\boldsymbol{\tilde x}}}_i}} \right)}}{3}. $ | (15) |
根据以上介绍的方法, 将
| $ \mathit{\boldsymbol{J}} = \left[ {\begin{array}{*{20}{c}} {{j_1}\left( 1 \right)}&{{j_1}\left( 2 \right)}& \cdots &{{j_1}\left( n \right)}\\ {{j_2}\left( 1 \right)}&{{j_2}\left( 2 \right)}& \cdots &{{j_2}\left( n \right)}\\ \vdots&\vdots &{}& \vdots \\ {{j_m}\left( 1 \right)}&{{j_m}\left( 2 \right)}& \cdots &{{j_m}\left( n \right)} \end{array}} \right]. $ |
根据下式对ji(k)进行规范化处理:
| $ {C_i}\left( k \right) = \frac{{{j_i}\left( k \right) - \overline {{X_k}} }}{{{S_k}}}. $ | (16) |
式中:
| $ \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} {{C_1}\left( 1 \right)}&{{C_1}\left( 2 \right)}& \cdots &{{C_1}\left( n \right)}\\ {{C_2}\left( 1 \right)}&{{C_2}\left( 2 \right)}& \cdots &{{C_2}\left( n \right)}\\ \vdots&\vdots &{}& \vdots \\ {{C_m}\left( 1 \right)}&{{C_m}\left( 2 \right)}& \cdots &{{C_m}\left( n \right)} \end{array}} \right]. $ |
取{C*(·)}={C*(1), C*(2)…, C*(n)}为参考数列;其中C*(i)为第i个指标所有评价值中的最优值, 对于高优指标, 取最大值;对于低优指标, 取最小值.按式(17)计算第i个方案在第k个指标上的评价值相对于第k个指标的最优评价值的关联系数ξi(k), 即
| $ \begin{array}{l} {\xi _i}\left( k \right) = \\ \frac{{\mathop {\min }\limits_i \mathop {\min }\limits_k \left| {{C_ * }\left( k \right) - {C_i}\left( k \right)} \right| + \rho \mathop {\max }\limits_i \mathop {\max }\limits_k \left| {{C_ * }\left( k \right) - {C_i}\left( k \right)} \right|}}{{\left| {{C_ * }\left( k \right) - {C_i}\left( k \right)} \right| + \rho \mathop {\max }\limits_i \mathop {\max }\limits_k \left| {{C_ * }\left( k \right) - {C_i}\left( k \right)} \right|}}. \end{array} $ | (17) |
式中:ρ∈[0, 1], 一般取0.5.可得关联系数矩阵:
| $ \mathit{\boldsymbol{ \boldsymbol{\varXi} }} = \left[ {\begin{array}{*{20}{c}} {{\xi _1}\left( 1 \right)}&{{\xi _1}\left( 2 \right)}& \cdots &{{\xi _1}\left( n \right)}\\ {{\xi _2}\left( 1 \right)}&{{\xi _2}\left( 2 \right)}& \cdots &{{\xi _2}\left( n \right)}\\ \vdots&\vdots &{}& \vdots \\ {{\xi _m}\left( 1 \right)}&{{\xi _m}\left( 2 \right)}& \cdots &{{\xi _m}\left( n \right)} \end{array}} \right]. $ |
根据公式λ+1=∏i=1n(1+λgi)求解λ, 但是当集合包含过多变量时, 该高阶多项式很难求解.
使用如下优化函数:
| $ \left. \begin{array}{l} f\left( {{C_j}} \right) = \min \left| {1 - \frac{1}{{{\lambda _j}}}\left[ {\prod {\left( {1 + {\lambda _j}{{\hat g}_i}} \right) - 1} } \right]} \right|;\\ {\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}\;\; - 1 < \lambda < \infty . \end{array} \right\} $ | (18) |
式中:
该方法可能陷入局部最优, 导致不满足模糊测度的数学特性.
以上两种方法均只考虑了模糊密度, 忽略了其他模糊测度, 即忽略了一部分指标间相互作用, 因而得出的解比较粗糙, 降低了模型对指标交互作用的表达能力.为了弥补这一局限, 提出基于TLBO算法的辨识方法, 考虑其他幂子集的权重.
2.5.2 基于TLBO算法的辨识Rao等[28]提出“教与学”优化算法.该算法是受教师教学及学生自学过程的启发, 通过老师教学、学生相互学习及学生自学等手段达到提高学习成绩的目的.与其他群智能优化算法比较, 教与学算法具有容易理解、参数较少、操作简便、收敛能力强、求解精度高并且运算速度快等优点, 因而被广泛采用.基于该思想, 设计出教与学算法来辨识gλ模糊测度, 算法的主要操作如下.
1) 编码与评价函数.输入值是专家给出部分重要子集权重
| $ f\left( {{X^j}} \right) = \sum\limits_{A \in \beta \left( x \right)} {\left| {{{\hat g}_\lambda }\left( A \right) - \frac{1}{{{\lambda ^j}}}\left[ {\prod {\left( {1 + {\lambda ^j}g_i^j} \right) - 1} } \right]} \right|} . $ | (19) |
由约束0≤gi≤1(i=1, 2, …, n), -1 < λ < ∞确定搜索边界.
2) 初始化.在搜索空间里随机地生成班级中的N个学生Xj=[g1j, g2j, …, gnj, λj](j=1, 2, …, N).
| $ \left. \begin{array}{l} X_i^j = X_i^{\rm{L}} + {\rm{rand}}\left( {0,1} \right) \times \left( {x_i^{\rm{U}} - x_i^{\rm{L}}} \right);\\ j = 1,2, \cdots ,N;i = 1,2, \cdots ,T. \end{array} \right\} $ | (20) |
式中:xiU为解变量第i个元素的上界, xiL为下界.
3) 教学阶段.在学生中, 按最小偏优策略选择1位老师Xteacher, 根据Xteacher和各科平均成绩mean之间的差异让每个学生学习.
| $ X_{{\rm{new}}}^i = X_{{\rm{old}}}^i + {\rm{difference}}, $ | (21) |
| $ {\rm{difference}} = {r_i} \times \left( {{X_{{\rm{teacher}}}} - {\rm{T}}{{\rm{F}}_i} \times {\rm{mean}}} \right). $ | (22) |
式中:ri为学习步长, 取(0, 1)之间的随机数.在实际学习中, 各个学生的接受能力不同, 因此学习的快慢有差异[29].教学因子为
| $ {\rm{T}}{{\rm{F}}_i} = \frac{{{X_i}}}{{{X_{{\rm{teacher}}\_i}}}}. $ | (23) |
4) 互学阶段.对每个学生, 随机选另1个学生, 通过分析他们的差异来相互学习.
| $ X_{{\rm{new}}}^i = \left\{ \begin{array}{l} X_{{\rm{old}}}^i + {r_i}\left( {{X^i} - {X^j}} \right),f\left( {{X^i}} \right) < f\left( {{X^j}} \right);\\ X_{{\rm{old}}}^i + {r_i}\left( {{X^j} - {X^i}} \right),f\left( {{X^j}} \right) < f\left( {{X^i}} \right). \end{array} \right. $ | (24) |
5) 自学阶段.自学是现实中最基础的学习方法, 自学可以使算法具有更强的局部搜索能力, 自学方法为
| $ \left. \begin{array}{l} X_{{\rm{newi}}}^j = X_{{\rm{oldi}}}^{\rm{L}} + {\rm{rand}}\left( {0,1} \right) \times \left( {x_i^{\rm{U}} - x_i^{\rm{L}}} \right);\\ j = 1,2, \cdots ,N;i = 1,2, \cdots ,T. \end{array} \right\} $ | (25) |
6) 解码.在算法的运行过程中, 每代都将成绩最好的学生进行更新, 确保历史上成绩最好的学生得以保存;当算法运行到给定代数后, 成绩最好的学生是该问题的解, 从中可以读出模糊密度和参数λ.
在辨识出参数λ和所有模糊密度后, 可以根据下式求出余下的所有幂子集的权重:
| $ \begin{array}{l} {g_\lambda }\left( {\left\{ {{x_1},{x_2}, \cdots ,{x_n}} \right\}} \right) = \\ \;\;\;\;\;\;\;\;\sum\limits_{i = 1}^n {{g_i}} + \lambda \sum\limits_{{i_1} = 1}^{n - 1} {\sum\limits_{{i_2} = {i_1} + 1}^n {{g_{{i_1}}}{g_{{i_2}}}} } + \cdots + {\lambda ^{n - 1}}{g_1}{g_2} \cdots {g_n} = \\ \;\;\;\;\;\;\;\;\frac{1}{\lambda }\left| {\prod\limits_{i = 1}^n {\left( {1 + \lambda {g_i}} \right) - 1} } \right|. \end{array} $ | (26) |
使用Choquet模糊积分, 将关联系数相对于各幂子集的模糊测度进行集成, 得到各被评价对象在该层面的综合得分.
定义:(灰模糊积分)设某被评价对象的评价值的关联度向量为ξ =[ξ(1), ξ(2), …, ξ(n)], 将它们按降序重新排列.为了表述方便, 记为ξ=[ξ(1), ξ(2), …ξ(n)](ξ(1)≥ξ(2)≥…≥ξ(n)).指标集X的所有幂子集的模糊测度已知, 则该被评价对象的灰模糊积分为
| $ \begin{array}{l} \int {\xi \left( \cdot \right){\rm{d}}g} = \xi \left( n \right){g_\lambda }\left( {{X_n}} \right) + \\ \;\;\;\;\;\;\;\left[ {\xi \left( {n - 1} \right) - {\xi _i}\left( n \right)} \right]{g_\lambda }\left( {{X_{n - 1}}} \right) + \cdots + \\ \;\;\;\;\;\;\;\left[ {\xi \left( 1 \right) - \xi \left( 2 \right)} \right]{g_\lambda }\left( {{X_1}} \right). \end{array} $ | (27) |
根据式(27), 可以依次计算每个被评价对象的综合积分.对于第i个被评价对象, 有
| $ \begin{array}{l} \int {{\xi _i}\left( \cdot \right){\rm{d}}g} = {\xi _i}\left( n \right){g_\lambda }\left( {{X_n}} \right) + \\ \;\;\;\;\;\;\;\left[ {{\xi _i}\left( {n - 1} \right) - {\xi _i}\left( n \right)} \right]{g_\lambda }\left( {{X_{n - 1}}} \right) + \cdots + \\ \;\;\;\;\;\;\;\left[ {{\xi _i}\left( 1 \right) - {\xi _i}\left( 2 \right)} \right]{g_\lambda }\left( {{X_1}} \right). \end{array} $ | (28) |
第i个对象在s层面的积分记为fis, 根据积分大小可以对各被评价对象在所分析的层面上进行优劣排序.
2.7 灰模糊积分决策模型流程1) 根据决策者的目的、偏好及被评价对象的特点, 设计出合理的指标体系.
2) 根据指标体系逐一获取评价数据, 定量指标通过统计测量方法获取初始评价值;定性指标评价值和各指标的权重由专家进行打分获得.
3) 将专家打出的模糊语意值转换为模糊数, 然后将模糊数进行整合并解模糊化, 获得各企业评价矩阵.
4) 对评价矩阵进行规范化处理, 计算各评价值相对于最优值的关联系数.
5) 根据各指标权重表运用基于教与学算法的辨识方法辨识出模糊密度和λ, 算出所有的模糊测度.
6) 对每个被评价对象, 计算关联系数对于模糊测度的Choquet积分, 即为综合评价值.
基于gλ模糊测度的灰模糊积分决策模型流程如图 1所示.
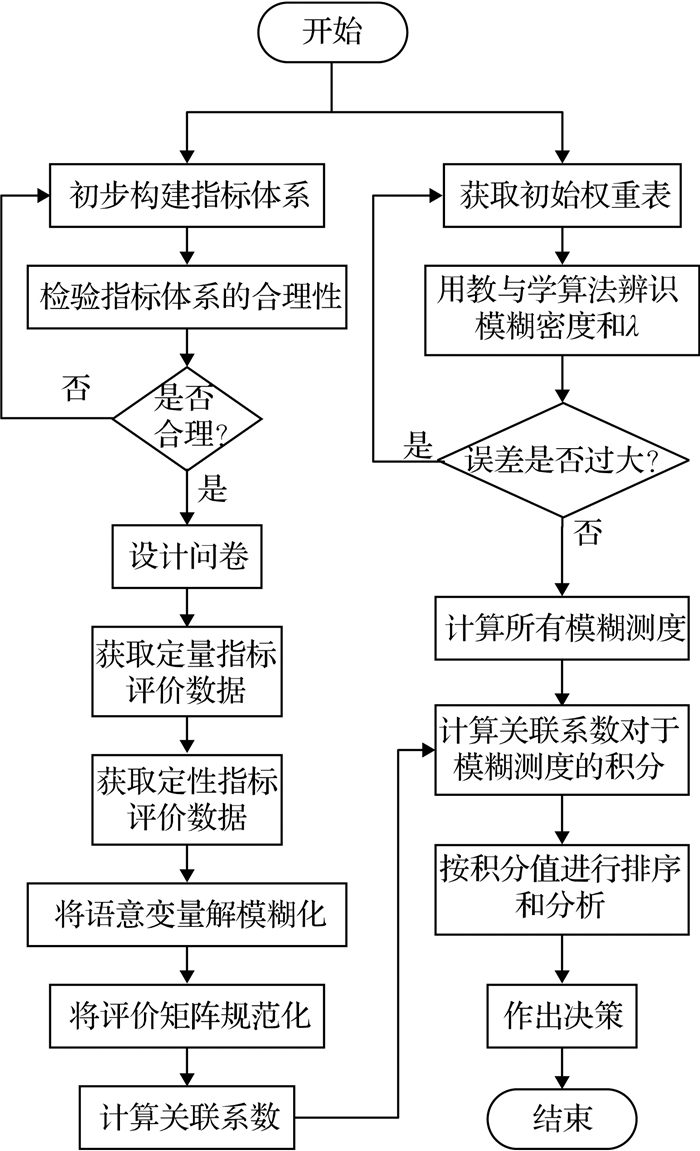
|
图 1 基于λ模糊测度的灰模糊积分评价方法流程图 Fig. 1 Flow chart of grey fuzzy integral evaluation method based on λ fuzzy measure |
下面以协作制造企业供应商评价与选择问题为例, 说明灰模糊积分评价模型的可行性与有效性.有5家备选供应商企业、12位评判专家.利用灰模糊积分评价模型, 对5家备选企业作出综合评估, 根据评估结果决定与哪家供应商合作.
3.1 构建指标体系和初始数据的获取根据协作制造企业的供应商选择问题的特点, 按照上述构建指标体系的原则, 结合前人研究[30], 设计出供参考的指标体系, 如图 2所示.

|
图 2 供应商评价指标体系 Fig. 2 Supplier evaluation index system |
限于篇幅, 仅给出质量水平层面的详细数据与详细计算过程、质量水平层面各企业评价值和各指标权重值, 如表 2、3所示.表 3中, 123表示指标a11、a12、a13合在一起的权重.
| 表 2 各企业评价表 Table 2 Evaluation table ofall enterprises |
| 表 3 各指标权重表 Table 3 Weights of each index |
根据式(8)~(17)将专家的语意变量整合, 解模糊化后得到各企业评价表, 如表 4所示.
| 表 4 各企业评价表 Table 4 Evaluation values of each enterprise |
根据式(16)将各企业评价表进行规范化处理, 得到规范化后的评价表, 如表 5所示.
| 表 5 规范化后的评价表 Table 5 Standard evaluation values |
取参考数列为C*=[1, 1.009 0, 1.120 0, 1.367 9, 0.979 3], 根据式(17)计算得到关联系数表, 如表 6所示.
| 表 6 关联系数表 Table 6 Correlation coefficients |
图 3中, 同一灰度表示同一企业.从图 3可以看出, 三者在趋势上是基本一致的, 但有细微的不同, 这说明标准化和计算关联系数的步骤是有效的;关联系数将原本的绝对评价值转换为相对评价值, 使得重要的差异被放大, 对于评价更具参考价值.
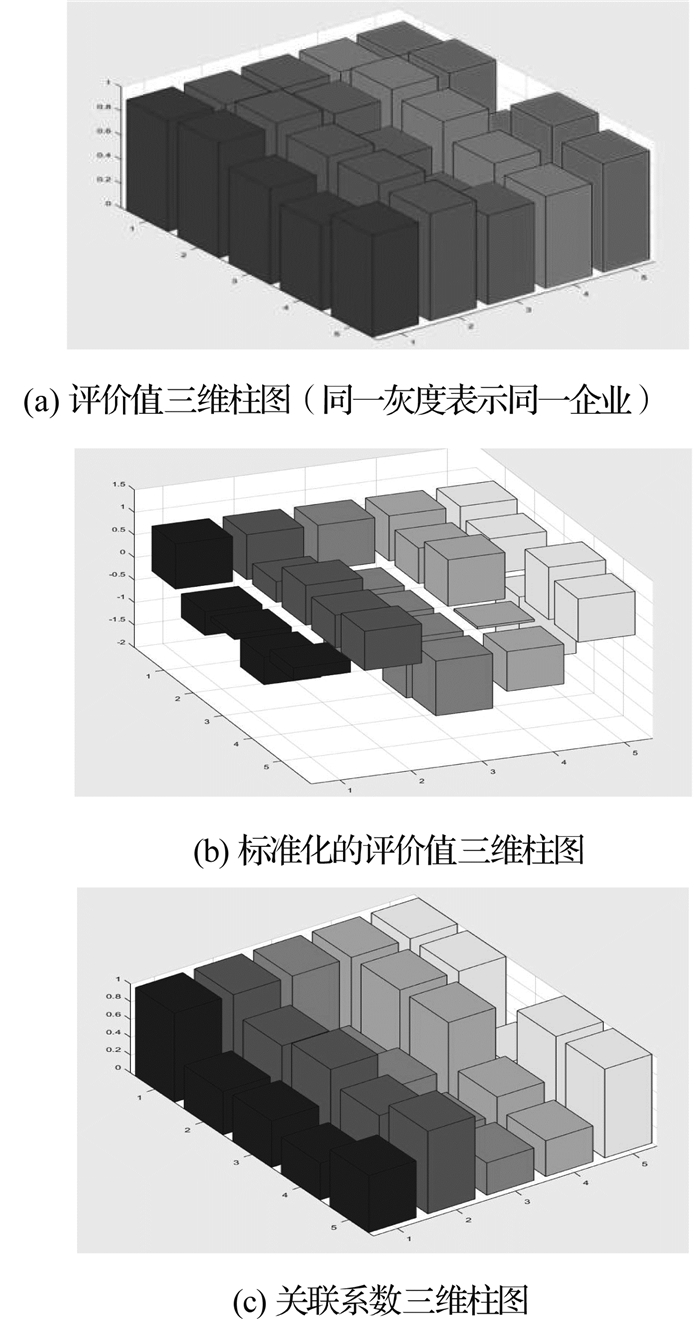
|
图 3 评价值、标准化的评价值、关联系数比较图 Fig. 3 Comparison of evaluation values, standardized evaluation values, correlation coefficients |
为了评估基于TLBO算法的gλ模糊测度辨识方法的有效性, 将该算法与朱娟[25]提出的基于遗传算法(GA)和Kiranyaz等[31]提出的基于粒子群算法(PSO)的辨识方法进行比较, 模糊测度辨识比较结果如表 7所示.可以看出, 基于TLBO算法的方法λ为-0.805 8, 误差为0.007 4;基于GA算法的方法λ为-0.699 7, 误差为0.096 6;基于PSO算法的方法λ为-0.804 2, 误差为0.010 9.测试结果显示, 提出的基于TLBO算法的方法能够获得更优的结果.根据表 7的数据, 根据式(4)计算出所有的模糊测度, 如表 8所示.
| 表 7 模糊测度辨识的比较 Table 7 Comparison of fuzzy densities identification |
| 表 8 所有模糊测度 Table 8 All fuzzy measures |
根据式(28), 计算各企业积分, 如表 9所示.
| 表 9 质量水平层面积分结果 Table 9 Integral result of quality level |
根据最终结果, 灰模糊积分法综合排序如下:企业5>企业4>企业2>企业1>企业3.灰色综合评价法综合排序如下:企业5>企业2>企业4>企业1>企业3.两种排序结果大致相同, 但是对于企业2和企业4的排序不同.企业5的各个方面都很优秀, 所有评价值都很高, 所以评价最好;企业3的各个方面都较差, 所有评价值都不太理想, 所以评价最差.利用这两种方法都可以识别出这样明显的优劣差异.企业2在各个方面都表现良好, 但是没有特别优秀的方面;企业4在质量认证情况、产品合格率、生产相关产品的经验这3个指标上都特别优秀, 是所有企业中最好的, 但是在质量控制能力和技术人员水平这两个指标上表现欠佳.从经验和感性角度来说, 企业在某几个方面做得特别优秀是很难的, 这比在大多数方面做到良好更难;在当今的供应链时代下, 关注点应放在企业最优秀的核心竞争力上, 不是所有的方面; 该组指标的参数λ达到-0.805 8, 这说明各指标间有强烈的消极抵消作用, 意味着这些指标之间存在冗余关系, 他们所反映的方面存在一定的共性, 所以各个指标都良好比某几个指标良好并不优秀多少;企业4比企业2更优秀, 这与灰模糊积分法的评价结果一致, 与灰色综合评价法的评价结果相反, 说明了灰模糊积分法在处理这一类问题时的可行性和有效性.
类似地, 重复以上过程, 计算出各层面的积分结果, 可以对各企业的各层面进行比较评价.将各层面的积分作为评价矩阵, 请专家给出各层面及重要组合的权重, 再次使用该模型可以求得综合评价值, 从而根据综合评价值进行决策.另外, 各个层面的积分结果可以帮助决策者了解各个企业在各个层面的具体表现和某个企业的优劣所在.
4 结语本文针对现有多目标决策方法要求指标之间相互独立, 应用于指标间存在交互作用且带有很多定性指标的多目标决策问题中效果不佳的弊端, 综合多学科知识, 提出基于gλ模糊测度的灰模糊积分决策模型用于多目标决策.利用关联度系数代替原始评价值, 在一定程度上修正了专家评价的主观倾向性影响;利用教与学算法辨识gλ模糊测度, 结合该模型的特点给出指标体系的构建原则和方法, 改善了专家打分的不一致性, 弥补了gλ模糊积分的局限;运用Choquet积分将关联系数对模糊测度进行集成, 不要求指标独立, 充分考虑到指标间的交互作用.将提出的灰模糊积分决策模型应用于某协作制造企业供应商评价与选择问题的实例, 证明了利用提出方法可以实现较准确、有效的评价与决策, 具有较广泛的推广性.
| [1] |
LIU H C, LIU L, LIN Q L. Fuzzy failure mode and effects analysis using fuzzy evidential reasoning and belief rule-based methodology[J]. IEEE Transactions on Reliability, 2013, 62(1): 23-36. DOI:10.1109/TR.2013.2241251 |
| [2] |
GRABISCH M, LABREUCHE C. A decade of application of the Choquet and Sugeno integrals in multi-criteria decision aid[J]. Annals of Operations Research, 2010, 175(1): 247-286. DOI:10.1007/s10479-009-0655-8 |
| [3] |
TSAI P F, LIN F M. An application of multi-attribute value theory to patient-bed assignment in hospital admission management:an empirical study[J]. Journal of Healthcare Engineering, 2014, 5(4): 439-456. DOI:10.1260/2040-2295.5.4.439 |
| [4] |
WANG X, CHEN X, HU H X, et al. Research on self-healing restoration strategy of urban power grid based on multi-agent technology[C]//International Conference on IEEE Advanced Power System Automation and Protection (APAP). [S. l. ]: IEEE, 2011: 1215-1218. http://ieeexplore.ieee.org/document/6180563/
|
| [5] |
WANG Y M, PARKAN C. A preemptive goal programming method for aggregating OWA operator weights in group decision making[J]. Information Sciences An International Journal, 2007, 177(8): 1867-1877. DOI:10.1016/j.ins.2006.07.023 |
| [6] |
TORRANCE G W, BOYLE M H, HORWOOD S P. Application of multi-attribute utility theory to measure social preference for health states[J]. Operations Research, 1982, 30(6): 1043-1069. DOI:10.1287/opre.30.6.1043 |
| [7] |
SAATY T L. Decision making with the analytic hierarchy process[J]. International Journal of Services Sciences, 2008, 1(1): 83-98. DOI:10.1504/IJSSCI.2008.017590 |
| [8] |
BORAN F E, GENC S, KURT M, et al. A multi-criteria intuitionistic fuzzy group decision making for supplier selection with TOPSIS method[J]. Expert Systems with Applications, 2009, 36(8): 11363-11368. DOI:10.1016/j.eswa.2009.03.039 |
| [9] |
SARRICO C S. Data envelopment analysis:a comprehensive text with models, applications, references and DEA-solver software[J]. Journal of the Operational Research Society, 2001, 52(12): 145-156. |
| [10] |
HUANG K. Study and implementation on the grey comprehensive evaluation support system of ecocity[J]. Journal of Southeast University:English Edition, 2002, 18(4): 356-360. |
| [11] |
卫海英, 张蕾, 梁彦明, 等. 多维互动对服务品牌资产的影响:基于灰关联分析的研究[J]. 管理科学学报, 2011, 14(10): 43-53. WEI Hai-ying, ZHANG Lei, LIANG Yan-ming, et al. The impact of multi-dimensional interaction on service brand equity-study based on grey relational analysis[J]. Journal of Management Sciences in China, 2011, 14(10): 43-53. |
| [12] |
金佳佳, 米传民, 徐伟宣, 等. 考虑专家判断信息的灰色关联极大熵权重模型[J]. 中国管理科学, 2012, 20(2): 135-143. JIN Jia-jia, MI Chuan-min, XU Wei-xuan, et al. Grey correlation entropy weight model considering the experts' judgment information[J]. Chinese Journal of Management Science, 2012, 20(2): 135-143. |
| [13] |
马保国, 成国庆. 一种相似性关联度公式[J]. 系统工程理论与实践, 2000, 20(7): 69-71. MA Bao-guo, CHEN Guo-qing. A formula of similarity correlation degree[J]. Systems Engineering and Theory Practice, 2000, 20(7): 69-71. |
| [14] |
施红星, 刘思峰, 方志耕, 等. 灰色周期关联度模型及其应用研究[J]. 中国管理科学, 2008, 16(3): 131-136. SHI Hong-xing, LIU Si-feng, FANG Zhi-geng, et al. Grey periodic correlation degree model and its application[J]. Chinese Journal of Management Science, 2008, 16(3): 131-136. |
| [15] |
施红星, 刘思峰, 方志耕, 等. 灰色振幅关联度模型[J]. 系统工程理论与实践, 2010, 30(10): 1828-2833. SHI Hong-xing, LIU Si-feng, FANG Zhi-geng, et al. Grey amplitude incidence model[J]. Systems Engineering:Theory and Practice, 2010, 30(10): 1828-2833. DOI:10.12011/1000-6788(2010)10-1828 |
| [16] |
吴利丰, 王义闹, 刘思峰. 灰色凸关联及其性质[J]. 系统工程理论与实践, 2012, 32(7): 1501-1505. WU Li-feng, WANG Yi-nao, LIU Si-feng. Grey convex relation and its properties[J]. Systems Engineering:Theory and Practice, 2012, 32(7): 1501-1505. DOI:10.12011/1000-6788(2012)7-1501 |
| [17] |
WU Y, GENG S, XU H, et al. Study of decision framework of wind farm project plan selection under intuitionistic fuzzy set and fuzzy measure environment[J]. Energy Conversion and Management, 2014, 87: 274-284. DOI:10.1016/j.enconman.2014.07.001 |
| [18] |
SUGENO M. Fuzzy measure and fuzzy integral[J]. Transactions of the Society of Instrument and Control Engineers, 1972, 8(2): 218-226. DOI:10.9746/sicetr1965.8.218 |
| [19] |
王熙照. 模糊测度和模糊积分及在分类器技术中的应用[M]. 北京: 科学出版社, 2008, 14-127.
|
| [20] |
HE Q, CHEN J F, YUAN X Q, et al. Choquet fuzzy integral aggregation based on g-lambda fuzzy measure[C]//International Conference on Wavelet Analysis and Pattern Recognition. Beijing: [s. n. ], 2007: 98-102. http://ieeexplore.ieee.org/document/4420644/
|
| [21] |
常志朋, 程龙生. 灰模糊积分关联度决策模型[J]. 中国管理科学, 2015, 23(13311): 105-111. CHANG Zhi-peng, CHENG Long-sheng. Grey fuzzy integral correlation degree decision model[J]. Chinese Journal of Management Science, 2015, 23(13311): 105-111. |
| [22] |
YAN T, FENG S, BI X L, et al. Grey correlation analysis and applications of drill stem failure in drilling engineering[C]//7th IEEE International Conference on Fuzzy Systems and Knowledge Discovery. [S. l. ]: IEEE, 2010: 1699-1702. http://ieeeexplore.com/xpl/articleDetails.jsp?tp=&arnumber=5569389&searchWithin%3Dp_Authors%3A.QT.Xue%2C+Liang.QT.
|
| [23] |
张国防, 何莉辉. 基于模糊积分的供应链网络优化方法[J]. 计算机工程与应用, 2014, 50(24): 231-235. ZHANG Guo-fang, HE Li-hui. Method based on fuzzy integral about construction and optimization of supply chain networks[J]. Computer Engineering and Applications, 2014, 50(24): 231-235. DOI:10.3778/j.issn.1002-8331.1305-0149 |
| [24] |
朱传军. 基于模糊测度与模糊积分的房地产评价方法与应用[M]. 北京: 科学出版社, 2011, 26-35.
|
| [25] |
朱娟. 中小企业产品创新测度与评价研究[D]. 哈尔滨: 哈尔滨理工大学, 2003. ZHU Juan. Study on measuring and evaluating product innovation of small and medium enterprises[D]. Harbin: Harbin University of Science and Technology, 2003. http://cdmd.cnki.com.cn/article/cdmd-11914-2003121454.htm |
| [26] |
DELGADO M, HERRERA F, HERRERA-VIEDMA E, et al. Combining numerical and linguistic information in group decision making[J]. Information Sciences, 1998, 107(1): 177-194. |
| [27] |
HERRERA F, MARTINEZ L. An approach for combining linguistic and numerical information based on the 2-tuple fuzzy linguistic representation model in decision-making[J]. International Journal of Uncertainty Fuzziness and Knowledge-Based Systems, 2011, 8(5): 539-562. |
| [28] |
RAO R V, SAVSANI V J, VAKHARIA D P. Teaching-learning-based optimization:a novel method for constrained mechanical design optimization problems[J]. Computer-Aided Design, 2011, 43(3): 303-315. DOI:10.1016/j.cad.2010.12.015 |
| [29] |
拓守恒, 雍龙泉, 邓方安. "教与学"优化算法研究综述[J]. 计算机应用研究, 2013, 30(7): 1933-1938. TUO Shou-heng, YONG Long-quan, DENG Fang-an. Survey of teaching-learning-based optimization algorithms[J]. Application Research of Computers, 2013, 30(7): 1933-1938. |
| [30] |
黄致远, 高勇. 浅谈制造企业供应商评价指标体系[J]. 物流科技, 2007, 30(09): 135-137. HUANG Zhi-yuan, GAO Yong. Primary study on manufacture enterprise supplier evaluation index system[J]. Logistics Sci-Tech, 2007, 30(09): 135-137. DOI:10.3969/j.issn.1002-3100.2007.09.043 |
| [31] |
KIRANYAZ S, INCE T, GABBOUJ M. Particle swarm optimization[M]. Berlin: Springer, 2014, 2212-2223.
|



