传感器输出的原始数据中往往包含高频噪声和低频漂移等干扰信息,消除和降低这些噪声,对于提高传感器分辨率、检出限和灵敏度等性能指标具有重要意义.表面等离子共振成像(surface plasmon resonance imaging, SPRi)传感器中存在两类噪声,分别是空间噪声和时间噪声.空间噪声是指由于光源分布不均造成的成像面上光强分布不均的情况,去噪方法通常为空间平均法、自参考法[1]或选取性能较好的区域作为有效区域[2].时间噪声包括高频随机噪声和长期基线漂移.随机噪声主要由光源波动、光电探测器热噪声等引起,基线漂移通常由环境温度变化产生的光学元件折射率变化、光源波动和探测器热噪声等引起.通用电气公司[3]发明了一种实时噪声降低的自适应线性滤波器,基于SPR传感图斜率和基于阀开闭、样品切换等事件发生的多个定时来确定滤波器的最佳长度,进行可变长度的滤波.该方法能够在有效降低噪声的同时,突显传感图中分析物与配体结合的关键生化过程.张玮等[4]针对自行研制的相位调制型SPR成像传感器,提出基于五步移相时域的变曝光时间图像采集法,通过增大信号幅值来提高光强测量信噪比,利用该方法可以将检测灵敏度提高35%.Chen等[5]采用希尔伯特-黄变换(Hilbert-Huang transform, HHT)方法处理SPR传感信号,有效地抑制了噪声,降低了检出限.
降低或消除噪声是传感技术研究的主要内容之一.本文以SPRi传感器的实验数据为例,介绍消除和降低时间噪声、从而提高传感器性能的数据处理方法和应用实例.利用课题组自行研制的偏振控制光强调制型SPRi传感器,开展NaCl折射率样品和BSA生物样品检测实验,得到两组原始数据,分析数据特征及噪声水平.研究分析零相移数字滤波、小波分析和HHT变换3种数据处理方法的相关理论及特点.运用这3种方法分别对上述两组实验数据进行滤波处理,并对处理结果进行分析比较.
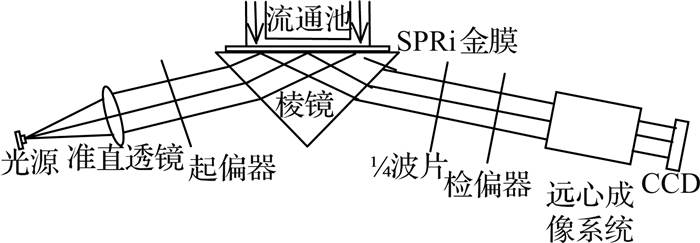
1 折射率样品与生物样品检测实验 1.1 实验装置偏振控制光强调制型SPRi传感器的原理如图 1所示.单色光源经准直起偏后,产生具有TE波和TM波的线偏振光,入射到棱镜-金膜界面后,TE波和TM波产生的相位变化不同,导致反射光为椭圆偏振光;再经过1/4波片和检偏器,将相位变化转换为光强信号;最后经过远心成像系统,在面阵CCD上成像.这种调制方式既具有相位检测的高灵敏性,又具有光强检测的简便性.
|
图 1 SPRi传感器的原理图 Fig. 1 Schematic of SPRi sensor |
课题组自行研制的传感器采用740 nm波长的LED和1 360×1 024像素的高分辨率CCD.CCD为12位,即具有4 096个灰度等级,以表征接收到的SPRi光强信号.在金膜上覆盖PDMS流通池,与注射泵相连,实现样品的注射.
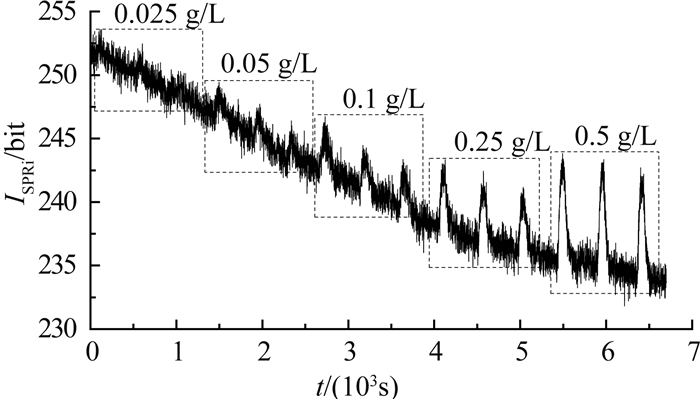
1.2 折射率样品检测实验与数据在室温条件下,SPRi传感器依次测量质量浓度为0.025、0.05、0.1、0.25、0.5 g/L的NaCl溶液,得到的实时监控曲线如图 2所示(每个质量浓度测量3次).图中,ISPRi为SPRi信号强度,t为时间. 1 s采集一个数据,基线为去离子水的SPRi信号,峰值为不同质量浓度NaCl溶液的SPRi信号.在动态范围内,SPRi信号随折射率的增大而增大,因此NaCl溶液浓度越高,SPRi信号越大.该实验属于折射率样品检测实验,结果可以用于传感器折射率分辨率、灵敏度和检出限等性能指标的分析.
|
图 2 不同质量浓度NaCl溶液的SPRi实时监控曲线 Fig. 2 SPRi real-time monitoring curve of NaCl solutions with different mass concentrations |
由图 2可知,传感器原始数据中存在高频噪声及持续下降的基线漂移.质量浓度为0.025和0.05 g/L的NaCl溶液的响应峰几乎被淹没在噪声中.需要研究合理可行的数据处理方法,消除或降低原始数据中的噪声,提高数据的信噪比和置信度,从而改善传感器的性能.
由于该实验的一次进样时间约为300 s,选取300 s的基线数据进行噪声计算(即标准偏差),结果为0.77.
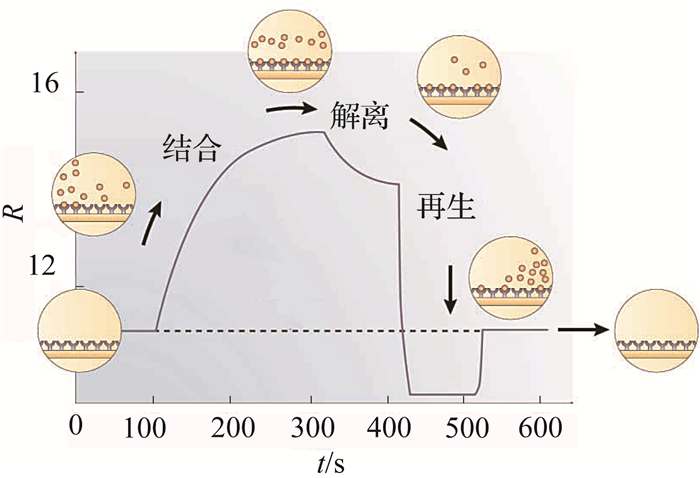
1.3 生物样品检测实验与数据在SPRi金膜上修饰可以与分析物特异性结合的配体,制备得到SPRi生物传感芯片,可以利用SPRi传感器开展生物分子相互作用实验,生物传感图如图 3所示[6].图中,R为折射率.首先在传感芯片表面流过缓冲液,得到基线;接着流过分析物,其与配体产生特异性结合,导致芯片的表面折射率增大,SPRi信号上升;然后通入缓冲液,带走游离在表面的分析物,SPRi信号稍有下降并趋于稳定;最后为了实现芯片的重复利用,通入再生液,将分析物从配体表面洗脱下来,完成芯片再生.
|
图 3 SPRi生物传感图 Fig. 3 Schematic of SPRi biosensing |
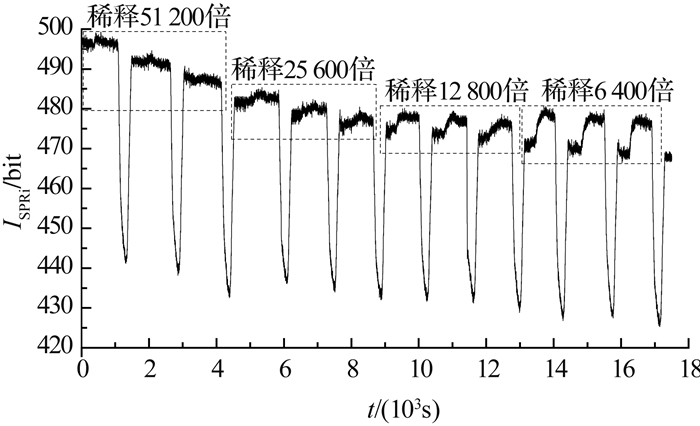
开展BSA抗原抗体相互作用的检测实验.首先需制备BSA传感芯片.由于BSA中含有大量巯基,流过金膜表面时,通过Au-S共价键与金膜结合,从而实现BSA的在线生长.具体制备过程如下:以“PBS缓冲液-2 mg/mL BSA溶液”的顺序进样数次,次数视SPRi信号而定.若某次进样后信号基本保持不变,则认为BSA在线生长完毕,即芯片表面生长的BSA已达到饱和状态.然后按标准的生物检测过程“缓冲液-BSA抗体-再生液(0.1 mol/L NaOH)”的顺序依次测量稀释51 200倍、25 600倍、12 800倍、6 400倍的BSA抗体溶液,每个浓度测量3次,得到的实时监控曲线如图 4所示.其中,BSA粉末(A0332)和BSA抗体原液(DAH1084)均购自生工生物工程公司.
|
图 4 BSA与不同质量浓度BSA抗体结合的SPRi实时监控曲线 Fig. 4 SPRi real-time monitoring curve of BSA binding to BSA antibody solutions with different mass concentrations |
与折射率样品检测实验的数据不同,图 4中每个浓度样品的实验数据均存在“基线—结合—解离—再生”的过程,但同样存在高频噪声和低频漂移,无法清晰地观测到较低浓度BSA抗体与BSA的结合响应,因此需要进行数据处理.
由于该实验的一次进样时间约为1 080 s,选取1 080 s的基线数据进行噪声计算,结果为1.36.
2 3种数据处理方法 2.1 零相移数字滤波巴特沃斯IIR数字滤波器的设计较简单,但相位变化非线性,滤波后易在信号端部出现失真[7-8].零相移数字滤波器可以有效地解决该问题,实现步骤如图 5所示.图中,X(z)为无限信号序列的双边Z变换,H(z)为普通滤波器的系统函数.图 5中的输出为

|
图 5 零相移数字滤波器实现步骤 Fig. 5 Implementation steps of zero-phase-shift digital filter |
| $ Y\left( z \right) = X\left( z \right)H\left( {1/z} \right)H\left( z \right). $ | (1) |
取z=ejw,则
| $ \begin{array}{l} Y({{\rm{e}}^{{\rm{i}}w}}) = {\rm{ }}X({{\rm{e}}^{{\rm{j}}w}})H({{\rm{e}}^{-{\rm{j}}w}})H({{\rm{e}}^{{\rm{j}}w}}) = \\ X({{\rm{e}}^{{\rm{j}}w}})|H({{\rm{e}}^{{\rm{j}}w}}){|^2}. \end{array} $ | (2) |
图 5的整个过程可以视为一个滤波器,则该滤波器的系统函数为H1(ejw)=|H(eiw)|2,相位偏移为0,即信号经过该滤波器后,相位不发生变化.
在实际生活中不存在无限信号序列,可以运用以下2个方法来解决这一问题:1)求解滤波器的初始状态,将其作为滤波时的初始态;2)拓展信号序列的开始和结尾两端,拓展的长度均为滤波器阶数的3倍.
2.2 小波分析小波分析是在傅里叶分析的基础上发展起来的一种时频分析方法.与傅里叶变换相比,小波变换是时域和频域的局部变换,因而能够有效地提取有效信息.在过去几十年中,小波分析已经成为信号处理领域的一个强有力的工具[9-12].
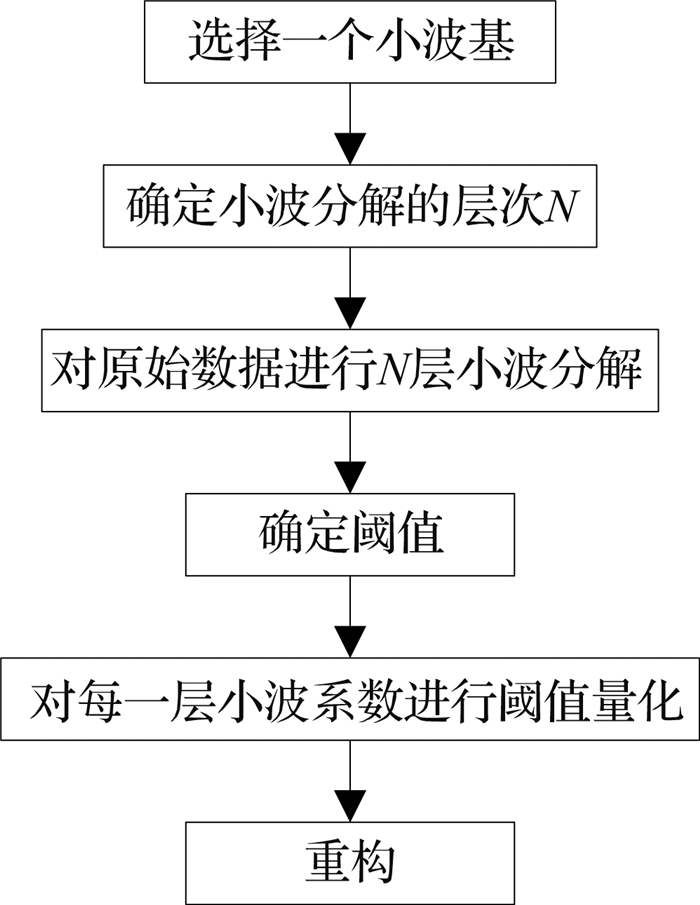
小波分析流程如图 6所示.其中,小波基的选择至关重要.根据不同小波基的特征[13-14],结合实际信号情况进行选择.为了更好地从原始数据中提取出样品信号特征,应选用具有紧支撑性的小波基,防止低频成分的影响和混入;短支撑长度的小波基具有良好的衰减特性;为了避免SPRi信号在多尺度分解与重构中过度失真,须采用具有对称性或近似对称性的双正交小波基;同时,应选择具有良好分频能力的高阶消失矩小波[15].其中,Db系列和Sym系列的小波基优于其他小波,它们拥有较短的支撑长度、相对适中的消失矩,是具有双正交性的紧支撑小波基.与Db系列小波基相比,Sym系列小波基具有更好的对称性,即能够更好地减少信号处理后的相位失真[16].选择Sym系列小波基.
|
图 6 小波分析流程图 Fig. 6 Flow chart of wavelet analysis |
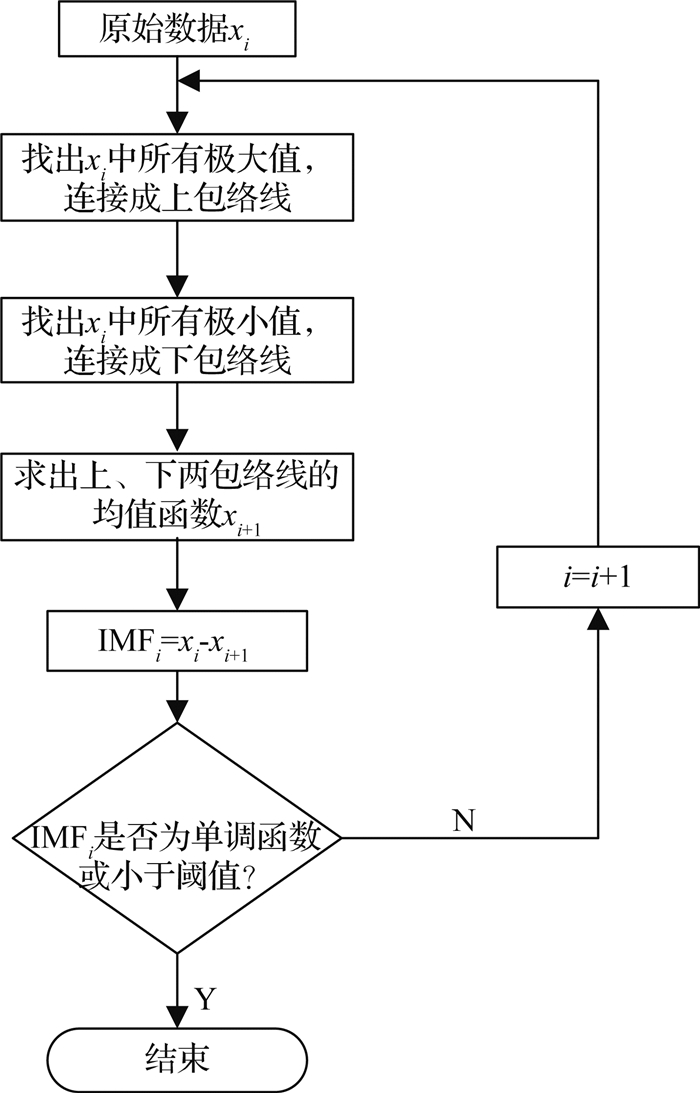
HHT是一种非平稳非线性信号处理方法,基本原理[17-19]是将信号进行经验模态分解(empirical mode decomposition, EMD),分解过程如图 7所示.获取有限数目的本征模态函数(intrinsic mode function, IMF),其中低阶次和高阶次的IMF分别为高频噪声和低频漂移;接着去除一定数量的高阶次和低阶次IMF,将其余IMF重构,可得抑制噪声后的传感器响应信号.
|
图 7 EMD分解流程图 Fig. 7 Flow chart of EMD decomposition |
对于不同的原始数据,通过HHT变换得到的IMF数量不等.这是因为HHT变换的基函数是根据实际数据自动确定,并不固定,这样保证了本征模态分解的自适应性.
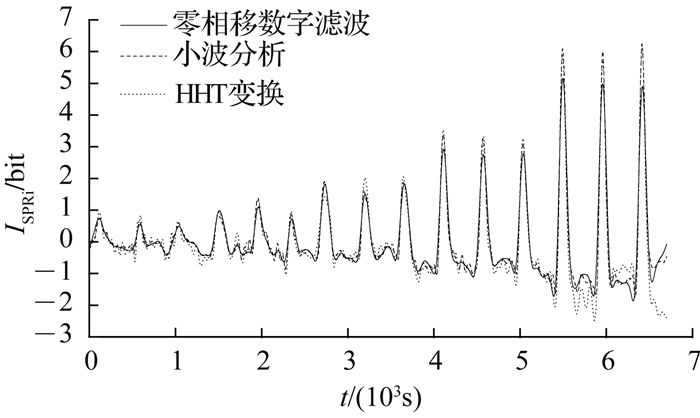
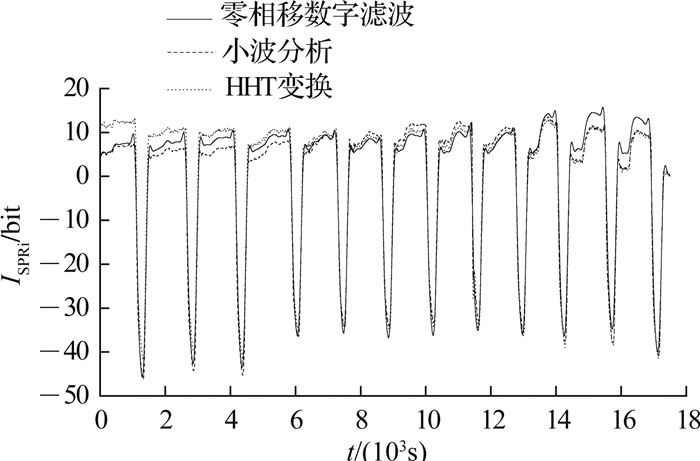
3 分析与讨论分别采用上述3种数据处理方法,对图 2的折射率样品实验数据和图 4的生物样品实验数据进行滤波处理,结果分别如图 8、9所示.对3种方法处理后的传感器性能参数进行计算比较,结果如表 1所示.表中,Ire为折射率样品实验噪声强度,S为灵敏度,ρc为Nacl溶液检出限,Ib为生物样品实验噪声强度,N为BSA抗体溶液检出限(稀释倍数).
|
图 8 3种方法处理后的折射率样品实验数据 Fig. 8 Data of refraction index sample experiment processed by three methods |
|
图 9 3种方法处理后的生物样品实验数据 Fig. 9 Data of biological sample experiment processed by three methods |
| 表 1 3种方法处理后的传感器性能参数 Table 1 Performance parameters of sensor processed by three methods |
对于零相移数字滤波方法,选取的滤波器阶数为3阶.由于图 2、4的数据差别较大,选取的通带范围不同,分别为0.001 ~0.01 Hz和0.000 1~0.01 Hz.
对于小波分析方法,采用sym8小波基.图 2、4中选取的分解层次分别为9和13,采用启发式软阈值去噪.
对于HHT变换方法,图 2分解得到11个IMF,去掉低阶次的高频噪声和高阶次的低频漂移,选取第6~9个IMF进行重构;图 4分解得到14个IMF,选取第6~13个IMF进行重构.
从图 8、9和表 1可见,3种方法在上述最佳设置下均取得了一定的滤波效果,有效降低了原始数据中的噪声,各浓度样品的信号均能清晰地观测出来,提高了信噪比.仔细分析对比后,可得如下结论.
1) 零相移数字滤波处理后,图 8中后两个浓度的信号明显被抑制;图 9中切换缓冲液和切换再生液时的突变噪声被放大.表 1表明,在折射率样品实验中,与小波分析和HHT变换相比,零相移数字滤波后,传感器的噪声较大,灵敏度较小,则导致信噪比低,折射率分辨率差.这是因为虽然数字滤波器可以实现各种选频功能,但实际上,所测得的有用信号与噪声往往会产生相互混叠.此时,数字滤波器无法通过简单的频域分析获得最优.小波和HHT都属于时频分析方法,在时、频两域都有表征信号局部特征的能力,能够有效地提取信息.
2) 小波分析和HHT变换处理后,折射率样品实验的基线噪声均降为约0.21 bit,灵敏度约为150 000 bit/RIU.由此得到传感器的折射率分辨率为1.4×10-6 RIU;生物样品实验的基线噪声均降为约0.47 bit.检出限定义为3倍噪声对应的样品响应浓度[5],则两组实验的检出限分别约为0.025 g/L NaCl溶液和稀释51 200倍的BSA抗体溶液.可见,滤波处理之后的噪声和检出限都大大降低,提高了传感器性能.
3) SPRi传感器的应用领域广泛,包括环境监测、食品安全、医学诊断和药物筛选等,不同实验的数据差别较大.结合以上2组实验数据的处理过程及结果,可以发现,对于不同的实验数据,零相移数字滤波器须调整滤波器阶数和截止频率;小波分析是非适应性的,须调整小波基及分解层次大小,对于非平稳非线性数据,不可能存在一个预定的基函数可以满足所有的物理性质;HHT变换能够通过原始数据本身自动产生自适应基函数,因此对不同的数据都具有较好的适应性,同时,分解出的一组IMF在时域上直观地体现出频域特征,可以根据数据特征选取其中几个IMF进行重构,能够取得较好的滤波效果,且操作简便.
4 结语本文研究分析零相移数字滤波、小波分析和HHT变换3种数据处理方法.SPRi传感器两组实验数据的处理结果表明,在最佳的参数设置下,采用这3种方法均能够在一定程度上有效地消除和抑制高频随机噪声和长期基线漂移.与零相移数字滤波器相比,利用小波分析和HHT变换这两种时频分析方法能够更好地提取有用细节信息,经这两种方法处理后,传感器的性能得到了明显提升,折射率分辨率改善为1.4×10-6 RIU,最小可检测0.025 g/L NaCl溶液和将原液稀释51 200倍的BSA抗体溶液.HHT变换具有自适应性,对于不同的实验数据,无需更改任何参数,即可完成滤波处理,因此应用范围最广,可以在传感器数据处理方面发挥较大的作用.
| [1] |
PILIARIK M, HOMOLA J. Self-referencing SPR imaging for most demanding high-throughput screening applications[J]. Sensors and Actuators B:Chemical, 2008, 134(2): 353-355. DOI:10.1016/j.snb.2008.06.011 |
| [2] |
SCARANO S, SCUFFI C, MASCINI M, et al. Surface plasmon resonance imaging (SPRi)-based sensing:a new approach in signal sampling and management[J]. Biosensors and Bioelectronics, 2010, 26(4): 1380-1385. DOI:10.1016/j.bios.2010.07.056 |
| [3] |
通用电气公司. 表面细胞质基因组共振系统中的实时噪声降低的自适应线性滤波器. 中国, 201080035292. 2[P]. 2010-07-15.
|
| [4] |
张玮, 邓焱, 王大千, 等. 基于变曝光时间图像采集法提高SPR相位成像检测灵敏度[J]. 清华大学学报:自然科学版, 2011, 51(4): 433-438. ZHANG Wei, DENG Yan, WANG Da-qian, et al. Improving SPR phase imaging system detection sensitivity by changing the exposure time periodically[J]. Journal of Tsinghua University:Science and Technology, 2011, 51(4): 433-438. |
| [5] |
CHEN H, WANG X. Study on the performance promotion of the surface plasmon resonance analytical system[J]. Instrumentation Science and Technology, 2012, 40(2/3): 226-237. |
| [6] |
COOPER M A. Optical biosensors in drug discovery[J]. Nature Reviews Drug Discovery, 2002, 1(7): 515-528. DOI:10.1038/nrd838 |
| [7] |
罗骋, 李宏生, 赵立业. 自适应Kalman和零相移滤波算法在重力信号处理中的对比[J]. 中国惯性技术学报, 2011, 19(3): 348-351. LUO Cheng, LI Hong-sheng, ZHAO Li-ye. Comparison of adaptive Kalman filter and zero-phase filter in processing gravity signal[J]. Journal of Chinese Inertial Technology, 2011, 19(3): 348-351. |
| [8] |
廖德春, 廖新浩. 几种常用滤波方法端部效应的比较[J]. 中国科学院上海天文台年刊, 2013(1): 50-56. LIAO De-chun, LIAO Xin-hao. Comparison of deformation at ends of the results obtained by some commonly used filters[J]. Annals of Shanghai Observatory Academia Sinica, 2013(1): 50-56. |
| [9] |
GALIANA-MERINO J J, PLA C, FERNANDEZ-CORTES A, et al. EnvironmentalWaveletTool:continuous and discrete wavelet analysis and filtering for environmental time series[J]. Computer Physics Communications, 2014, 185(10): 2758-2770. DOI:10.1016/j.cpc.2014.06.011 |
| [10] |
YAN R, GAO R X, CHEN X. Wavelets for fault diagnosis of rotary machines:a review with applications[J]. Signal Processing, 2014, 96: 1-15. DOI:10.1016/j.sigpro.2013.04.015 |
| [11] |
YAJNIK A. Novel technique of oversampling the broken images using wavelet transform[J]. Applied and Computational Harmonic Analysis, 2015, 39(2): 357-368. DOI:10.1016/j.acha.2015.01.002 |
| [12] |
KALE M C, ATAC G, GEREK Ö N. A biorthogonal wavelet design technique using Karhunen-Loéve transform approximation[J]. Digital Signal Processing, 2016, 51: 202-222. DOI:10.1016/j.dsp.2015.06.002 |
| [13] |
张斌, 王彤, 谷传纲, 等. 湍流信号分析中小波基的对比和选取[J]. 工程热物理学报, 2011, 32(4): 585-588. ZHANG Bin, WANG Tong, GU Chuan-gang, et al. Comparison and selection of wavelet functions in turbulent signal processing[J]. Journal of Engineering Thermophysics, 2011, 32(4): 585-588. |
| [14] |
张华, 陈小宏, 杨海燕. 地震信号去噪的最优小波基选取方法[J]. 石油地球物理勘探, 2011, 46(1): 70-75. ZHANG Hua, CHEN Xiao-hong, YANG Hai-yan. Optimistic wavelet basis selection in seismic signal noise elimination[J]. Oil Geophysical Prospecting, 2011, 46(1): 70-75. |
| [15] |
何正友, 钱清泉. 电力系统暂态信号分析中小波基的选择原则[J]. 电力系统自动化, 2003, 27(10): 45-48. HE Zheng-you, QIAN Qing-quan. Mother wavelet option method in the transient signal analysis of electric power systems[J]. Automation of Electric Power Systems, 2003, 27(10): 45-48. DOI:10.3321/j.issn:1000-1026.2003.10.010 |
| [16] |
焦飞, 陈璞, 朱少华. 小波消噪在光纤陀螺温度补偿中的应用[J]. 压电与声光, 2014, 36(5): 768-771. JIAO Fei, CHEN Pu, ZHU Shao-hua. The application of wavelet denoising to FOG temperature-induced drift compensation[J]. Piezoelectric and Acoustooptics, 2014, 36(5): 768-771. DOI:10.11977/j.issn.1004-2474.2014.05.023 |
| [17] |
HUANG N E. Hilbert-Huang transform and its applications[M]. Singapore: World Scientific Publishing, 2014, 27-125.
|
| [18] |
谭善文, 秦树人, 汤宝平. Hilbert-Huang变换的滤波特性及其应用[J]. 重庆大学学报, 2004, 27(2): 9-12. TAN Shan-wen, QIN Shu-ren, TANG Bao-ping. The filtering character of Hilbert-Huang Transform and its application[J]. Journal of Chongqing University, 2004, 27(2): 9-12. DOI:10.11835/j.issn.1674-4764.2004.02.004 |
| [19] |
LEI Y, LIN J, HE Z, et al. A review on empirical mode decomposition in fault diagnosis of rotating machinery[J]. Mechanical Systems and Signal Processing, 2013, 35(1): 108-126. |



