电动客车的续航能力与客车空调系统的性能息息相关，将电动客车冬季采暖主要由发动机余热与电加热组合方式改进为热泵系统供暖，有助于客车蓄电池的高效节能，因此开发高能效电动客车变频热泵空调系统有重要的意义.传统的空调设计方法需要制作大量的样机试验及调整系统结构参数，这不利于节能省材而且设计周期长.利用制冷系统仿真技术能够较准确地预测空调产品的性能，在一定误差范围内，能够模拟多种制冷及制热工况下空调的系统性能，代表空调系统设计的发展趋势.

国外对制冷系统计算机仿真的研究起步较早，制冷空调系统的仿真包含空气流场流动模拟、系统部件模拟、系统仿真3个部分.对于制冷系统空气局部流动模拟，多数采用Fluent计算流体动力学(CFD)软件进行仿真研究^[1].

电动客车空调系统的换热器均采用风冷管翅式换热器，管内制冷剂与管外空气进行耦合换热.广泛采用的换热器模型模拟算法选用多数研究者采用的效能-传热单元数(ε-NTU)算法.该算法的核心思路是将换热器中的换热管分成多个微元，根据各个微元段内制冷剂的状态，选用合适的换热和压降经验关联式来建立模型求解制冷剂和空气的出口状态.各个微元遵循相邻微元之间上一微元的出口状态作为下一微元的进口状态，直至最后一个微元的计算^[2].

由各个系统部件模型到整个系统模型的耦合，制冷空调系统的稳态仿真需要一定的仿真算法，系统耦合仿真算法主要有2大类：联立求解方程组方法和顺序模块方法.其中典型的联立方程组方法常用的有Euler法、Runge-Kutta法等^[3].发展至今最典型的系统仿真软件主要有美国橡树岭国家实验室开发的Mark软件和Purdue大学研发编写的系统仿真模型——ACMOEDEL.其中Mark模型可以模拟空调系统的多种工况，模拟结果与实验测试较吻合，但不足之处是换热器模型的管路连接方式不能自定义设计并且管路连接方式较简易.ACMODEL软件采用高级语言C++进行编写，换热器模拟采用ε-NTU算法，换热器模型计算的准确性较高.

本文围绕电动客车顶置式热泵空调系统，建立系统稳态仿真模型.结合实验数据，验证及修正仿真模型，建立精度较高的系统稳态仿真模型.基于优化设计目标，提出小管径换热器的优化设计方案.选用高效新型涡旋压缩机应用于客车热泵空调系统中，利用经过修正后的系统稳态仿真模型预测系统性能.

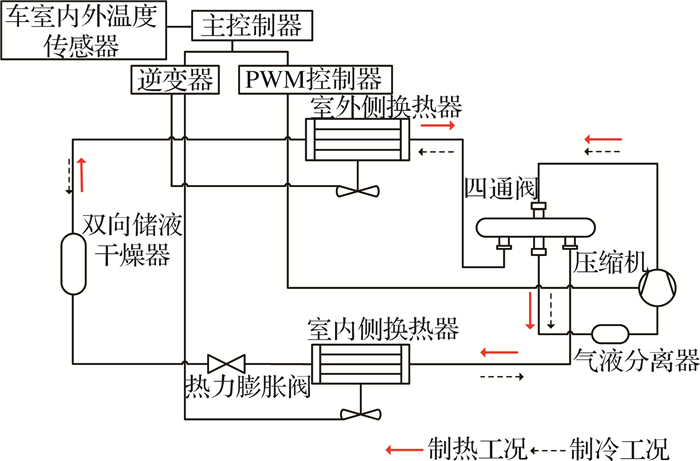
将电动客车变频热泵型空调系统安装于客车车顶，制冷剂为R410A，由变频器控制模块对空调系统进行调速控制，运行原理如图 1所示.系统的制冷循环过程如下：压缩机将低温低压的制冷剂蒸气压缩至高温高压蒸气状态，通过四通阀后进入室外侧换热器，与外界大气环境进行热交换后，制冷剂冷却至高温高压过冷状态；流经双向储液干燥器后，进入热力膨胀阀等焓节流至低温低压的气液两相混合状态；经分液头进入室内侧换热器蒸发吸热，将风道中的新风和回风进行冷却后吹入客车室内，对客车室内除湿降温，达到车室内热舒适性的要求.制冷剂在室内侧换热器中蒸发吸热后变成有一定过热度的过热蒸汽，再流经气液分离器后回到压缩机吸气口，至此完成一次制冷循环.在制热循环过程中，制冷剂的流向经四通阀变向，制冷剂在换热器中的流向与制冷循环时相反，如图 1所示为2种工况下的制冷剂流向.

图 1

图 1 电动客车热泵型空调系统原理图 Fig. 1 System schematic of HPAC in electric vehicle

热泵型空调系统的压缩机为HQB1D-80H510型直流变频卧式涡旋压缩机，本文采用工程上运用广泛的ARI compressor map方法来建立压缩机模型.该方法只需要已知压缩机吸气饱和温度(或吸气压力)和排气饱和温度(或排气压力)，就可以计算压缩机的功率、流量等参数.AHRI 10系数模型为

式中：Y可以表示压缩机耗功，也可以表示压缩机质量流量；t_e和t_c分别为蒸发温度和冷凝温度；C₁~C₁₀为压缩机性能方程的拟合系数.通过压缩机的全性能实验测试工况(环境温度为35 ℃，压缩机进口过热度为11.1 ℃，过冷度为8.3 ℃，简称为ARI标准工况)获取的实验数据拟合得到，由于原客车热泵空调系统的测试实验工况不能保证处在压缩机的全性能实验测试工况下，对实验测试压缩机的流量和耗功修正.修正公式^[4]为

式中：q_mAHRI和q_mact分别为ARI标准工况的系统质量流量和实际的质量流量；ρ_AHRI和ρ_act分别为ARI标准工况下压缩机进口吸气密度和实际的吸气密度；F₁为修正系数，对于封闭式压缩机，通常取0.75^[4]；W_AHRI和W_act分别为ARI标准工况和实际工况下压缩机的耗功；H_{in, AHRI}和H_{out, AHRI}分别为ARI标准工况下的压缩机进、出口焓，H_{in, act}和H_{out, act}分别为实际工况下的压缩机进、出口焓.热泵型空调系统的车内、外侧换热器均采用风冷翅片式管式换热器，换热模拟计算均采用效能-传热单元数(ε-NTU)算法，根据ε-NTU计算各小微元的换热量和总的换热量.系统运行制冷工况时，对于车外侧换热器而言，按制冷剂的状态和流动换热状况的不同，将车外侧换热器分为干壁面过热气体区、湿壁面过热气体区、两相冷凝区和过冷液体区来求解.对于车内侧换热器，按制冷剂的状态，一般将其分为液体区、两相沸腾区和过热气体区来求解.对各区域段模拟时，选用学术上用的较多的换热和压降计算关联式，如表 1所示.

表 1

表 1 各区域段换热和压降的计算关联式 Table 1 Calculation correlation of heat transfer and pressure drop in various district 求解区域 计算关联式 单相区换热 文献[5] 两相区换热 文献[6] 管内侧压降 文献[7] 风侧换热 文献[8] 风侧压降 文献[8]

表 1 各区域段换热和压降的计算关联式 Table 1 Calculation correlation of heat transfer and pressure drop in various district

车内、外侧换热器的结构参数如表 2所示.当进行系统稳态仿真时，实时调用换热器模型.系统运行制冷工况时，调用换热器模型须先判断换热器入口的制冷剂状态.若制冷剂处于过热蒸汽状态，则调用车外侧换热器模型；若制冷剂处于两相状态，则调用车内侧换热器模型.

表 2

表 2 管翅式换热器结构参数 Table 2 Structural parameters of TFHE 换热器 外形尺寸/m 管排数 每排 管数 排间距/ mm 管间距/ mm 排布方式 翅片厚度/ mm 翅片间距/ mm 车外侧换热器 1.68×0.64×0.14 8 30 12.7 21 24进12出 0.115 2.2 车内侧换热器 1.33×0.11×0.24 8 11 12.7 21 8进16出 0.115 2.2

表 2 管翅式换热器结构参数 Table 2 Structural parameters of TFHE

系统的四大部件由不同的管道连接，连接管道主要包括吸气管道、排气管道和输液管道等.对各管道模型搭建微元换热模型，换热方程为

式中：A_o为外表面换热面积；t_in、t_out分别为制冷剂在连接管道处的入口和出口温度；t_amb为连接管的环境温度；R_toatl为总的热阻，由外表面的对流热阻R₀、管壁的导热热阻R_m和内表面的对流热阻R_i组成.压降方程为

式中：f为管道沿程摩擦系数，L和D分别为等效管长、管径，G为单位面积的质量流量，ρ为制冷剂密度.

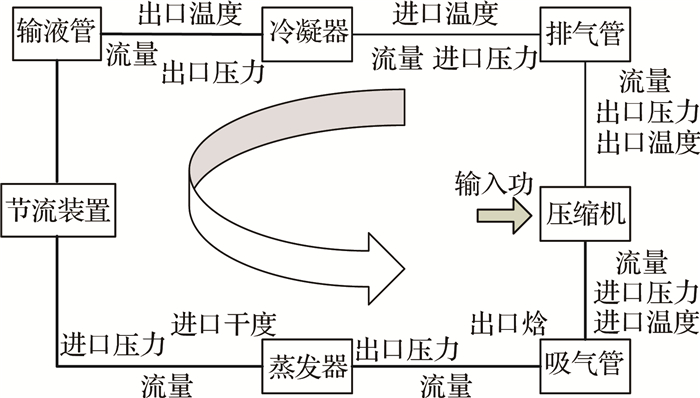
系统稳态仿真模型是在系统部件压缩机、换热器、连接管道等模型的基础上，将各部件耦合成完整的系统.系统各部件的耦合图^[9]如图 2所示.遵循上一部件的出口参数作为下一部件入口参数的原则，将各部件有机耦合成完整的空调系统.

图 2

图 2 空调系统的仿真部件耦合图 Fig. 2 Coupled map of HPAC's component

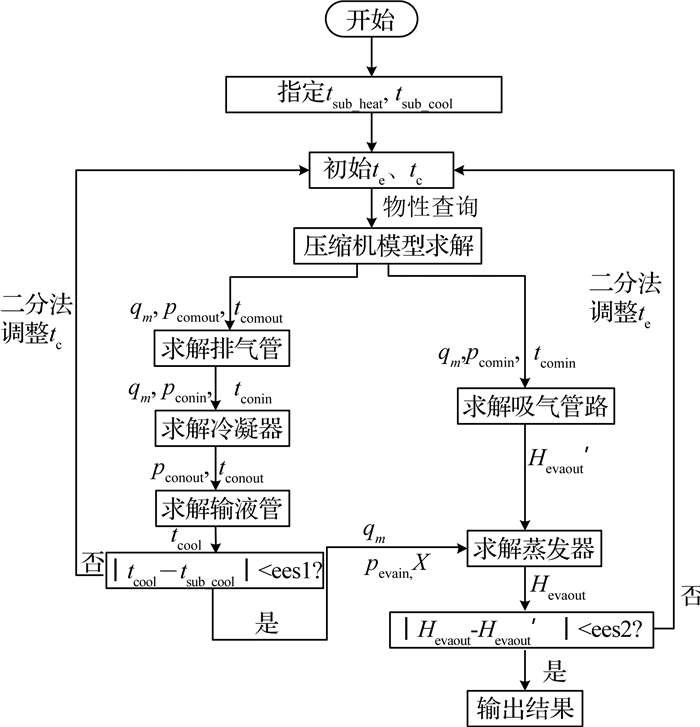
采用指定过热度和过冷度算法对制冷系统进行仿真迭代计算，流程图如图 3所示.图中，q_m为质量流量，p为压力，t为温度，H为焓，下标com表示压缩机，con表示冷凝器，eva表示蒸发器，in表示进口状态，out表示出口状态，X为干度.该算法的迭代循环主要通过获得冷凝器出口过冷度残差和蒸发器出口焓的残差，从而来判断调节冷凝温度和蒸发温度的方向，通过二分法来调节蒸发温度和冷凝温度，直至过冷度残差和蒸发器出口焓差满足允许的精度范围内完成迭代循环计算.

图 3

图 3 空调系统的稳态仿真迭代流程图 Fig. 3 Flow chart of steady state simulation of HPAC

空调系统的仿真模型与实际系统之间必然存在误差，需要用实际系统的实验数据来验证及修正系统仿真模型.对实际客车的空调系统实验测试了4组制冷工况(保持车内干球温度为27 ℃，变换车外侧干球温度为31、35、39、43 ℃)和2组制热工况(保持车内干球温度为20 ℃，变化车外侧干球温度为7、9 ℃)，所有的测试工况保持压缩机转速恒为3 300 r/min.基于实验数据，分别用1组制冷工况(车内侧温度为27 ℃，车外侧温度为31 ℃)和1组制热工况(车内侧温度为20 ℃，车外侧温度为7 ℃)实验数据来修正仿真结果，修正调整系数如表 3所示.表中，C_comm为压缩机流量调整系数，C_comw为压缩机功率调整系数，C_comoutt为压缩机排气温度调整系数，C_conQ为车外侧换热器换热量调整系数，C_conp为车外侧换热器压降调整系数，C_evaQ为车内侧换热器换热量调整系数，C_evap为车内侧换热器压降调整系数.基于修正后的系统仿真模型，对实验测试其余的制冷、制热工况进行仿真模拟，并与系统实测结果的对比如表 4、5所示.表 4中，t_out为车外侧干球温度，Q₀_act为制冷量实测结果，Q₀_sim为制冷量仿真结果，e__Q0为制冷量误差，EER_act为系统实际EER，EER_sim为系统仿真EER，e__EER为EER误差. 表 5中，Q_h_act为制热量实测结果，Q_h_sim为制热量仿真结果，e__Qh为制热量误差，COP_act为系统实际COP，COP_sim为系统仿真COP，e__COP为COP误差.从表 4可知，对比分析仿真模型对制冷工况的模拟和实际性能测试，仿真结果与实测结果的相对误差均不超过5%，在工程误差的允许范围内.从表 5可知，对比分析仿真模拟制热工况的仿真结果与实测数据可知，两者的相对误差不超过7%，因此该仿真模型可以用于实际空调系统性能预测和性能分析.

表 3

表 3 空调系统性能修正调整系数 Table 3 Adjustment coefficient of air-conditioning system performance 工况 Ccomm Ccomw Ccomoutt CconQ Cconp CevaQ Cevap 制热 1.024 1.003 0.988 1.003 1.730 0.981 1.358 制冷 1.007 1.003 0.984 0.977 1.134 0.918 2.390

表 3 空调系统性能修正调整系数 Table 3 Adjustment coefficient of air-conditioning system performance

表 4

表 4 空调系统仿真结果与实际结果对比(制冷工况) Table 4 Simulation result compared with test data (under cooling condition) tout/℃ Q0_act/kW Q0_sim/kW E_Q0/% EER_act EER_sim E_EER/% 35 22.1 22.32 0.91 3.37 3.42 1.48 39 20.3 20.94 2.95 2.83 2.92 3.18 43 18.4 18.72 1.63 2.33 2.37 1.72

表 4 空调系统仿真结果与实际结果对比(制冷工况) Table 4 Simulation result compared with test data (under cooling condition)

表 5

表 5 空调系统仿真结果与实际结果对比(制热工况) Table 5 Simulation result compared with test data (under heating condition) tout/℃ Qh_act/kW Qh_sim/kW E_Qh/% COP_act COP_sim E_COP/% 9 20.6 21.8 5.8 3.1 3.3 6.4

表 5 空调系统仿真结果与实际结果对比(制热工况) Table 5 Simulation result compared with test data (under heating condition)

蒸发器和冷凝器作为空调系统的2个重要组成部件，它的性能优劣直接影响到空调系统整体的性能.纯电动客车热泵空调对高度参数非常敏感，根据优化目标的要求，新设计的换热器安装高度由原来的260 mm降低至200 mm.若采用微通道换热器应用于热泵空调系统，会存在除霜、压降过大等问题.提出小管径换热器的优化设计方案，应用到客车热泵空调系统中.

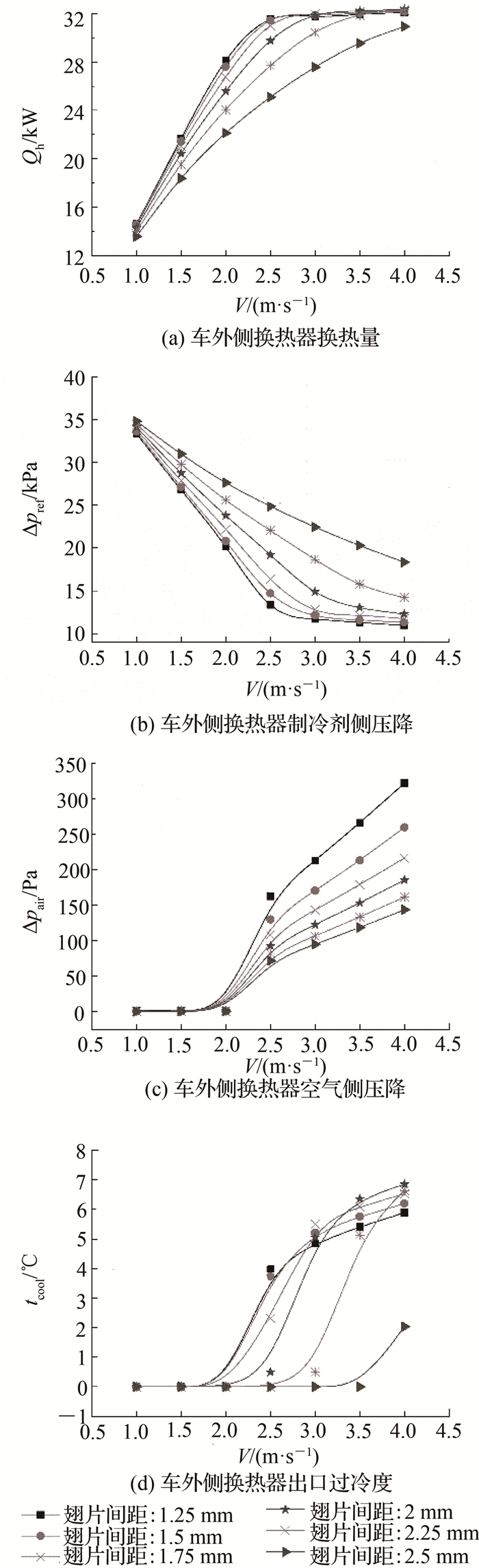
优化目标为额定制冷量(制热量)从22 kW(18 kW)提高到26 kW(22 kW)，制冷EER(制热COP)从2.8(2.5)提高到3.2(2.8)，将其作为小管径换热器优化设计的准则.根据车顶单元式空调安装几何尺寸的约束可知，换热器最大安装高度为200 mm，参考家用空调小管径换热器的铜管横向间距和纵向间距19 mm×12.7 mm，确定车外侧换热器为9排27列，车内侧换热器(单侧)为7排12列，管径为5 mm.采用管路枚举法，比较得出换热器较优的管路连接方式.客车空调系统额定制冷量的优化设计目标为26 kW，车内侧干球(湿球)温度为27 ℃(19 ℃)，车外侧干球(湿球)温度为35 ℃(27 ℃)，系统蒸发温度为7 ℃，冷凝温度为45 ℃，过热度为8 ℃，过冷度为6 ℃.经理论循环计算可知，车外侧换热器的换热量需达到31 kW，将31 kW作为车外侧换热器优化设计的一个目标值.在额定制冷工况下，不同翅片间距车外侧换热器的换热量、制冷剂侧压降、空气侧压降及出口过冷度随迎面风速的变化关系如图 4所示.图中，Q_h为换热量，V为迎面风速, Δp_ref为制冷剂侧压降，Δp_air为空气侧压降，t_cool为出口过冷度.

图 4

图 4 车外侧换热器不同翅片间距下性能随迎面风速的变化(额定制冷) Fig. 4 Performance of TFHE with different fin spacing along with wind speed (cooling condition)

从图 4可以看出，在同一风速下，翅片间距越小，换热器的换热量越大，较小的翅片间距减弱了换热器的排水除霜性能.在风速>3.0 m/s后，随着风速的增加，换热量的增长趋势缓慢.当风速为3.0 m/s时，换热器的换热量为31.84 kW，能够满足优化目标31 kW，并且换热器出口存在一定的过冷度.综合考虑换热量的优化目标值、排水除霜性能以及迎面风速，选定2 mm翅片间距为较优的翅片间距.当迎面风速为3.0 m/s，翅片间距为2 mm时，出口过冷度为1.95 ℃.

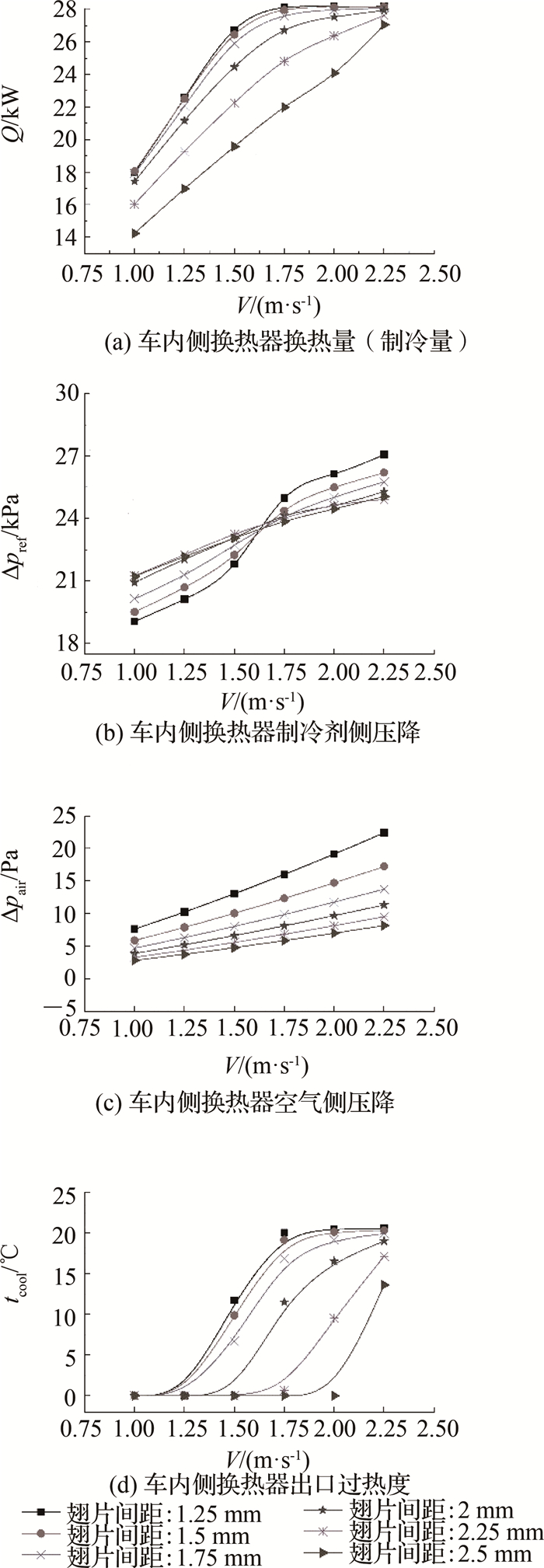
基于选定的迎面风速3 m/s，车外侧换热器翅片间距2 mm，在额定制冷工况下，不同翅片间距车内侧换热器的换热量、制冷剂侧压降、空气侧压降及出口过热度随迎面风速的变化关系如图 5所示.根据优化目标可知，额定制冷工况下车内侧换热器的制冷量(换热量)为26 kW.由图 5可以看出，当迎面风速超过2 m/s时，随着风速的增加，换热量基本保持不变.综合考虑换热量优化目标值、排水除霜性能及风机的耗功，选定2 mm翅片间距为较优的翅片间距.当迎面风速为2.0 m/s，翅片间距为2 mm时，车内侧换热器的换热量为27.64 kW，出口过热度为13.28 ℃.

图 5

图 5 车内侧换热器的性能下随迎面风速的变化(额定制冷) Fig. 5 Performance of TFHE with different fin spacing along with wind speed (heating condition)

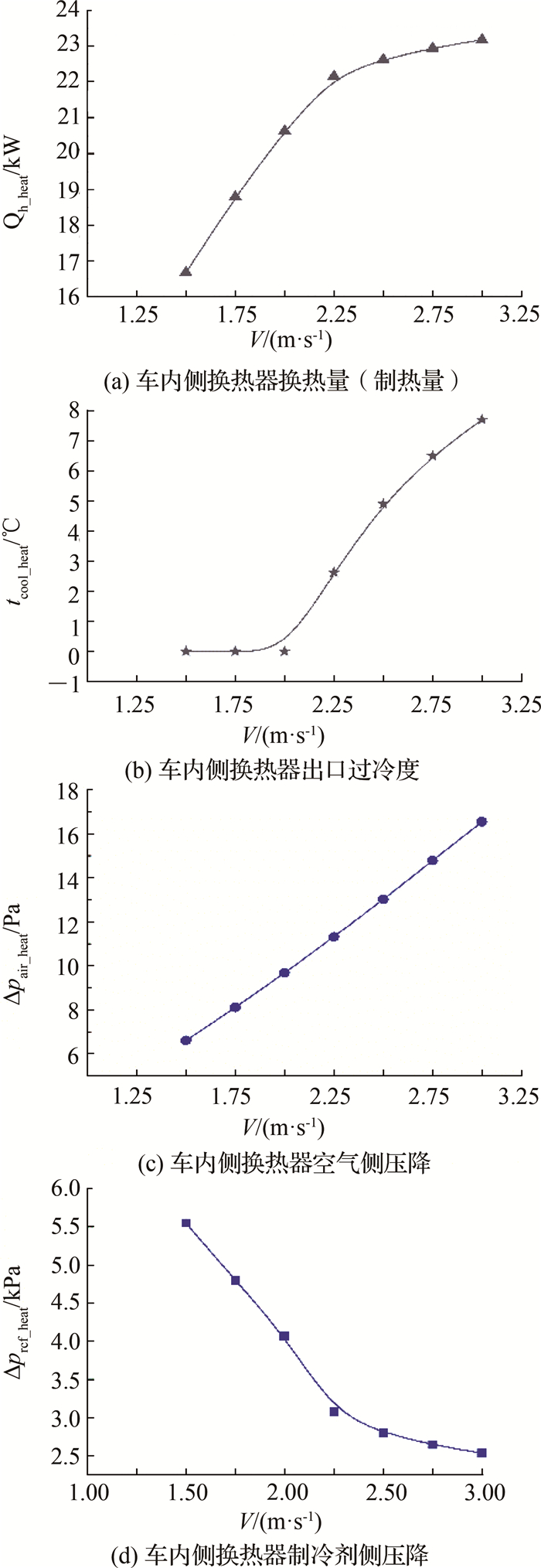
上述所设计的小管径换热器仅满足额定制冷目标，由于热泵空调系统在额定制热工况时，室内、外侧换热器置换了位置.为了满足额定制热量目标，需要对车内侧换热器(冷凝器)进行校核计算.额定制热工况的具体参数如下：蒸发温度为-2 ℃，冷凝温度为40 ℃，过热度为6 ℃，过冷度为6 ℃.基于选定冷凝器的翅片间距为2 mm，对其进行校核计算.在额定制热工况下，冷凝器的换热量、出口过冷度、制冷剂侧压降及风侧压降随迎面风速的变化如图 6所示.图 6中，Q_{h_heat}为换热量，V为迎面风速，Δp_{ref_heat}为制冷剂侧压降，Δp_{air_heat}为空气侧压降，t_{cool_heat}为出口过冷度.由图 6可知，当风速达到2.25 m/s以上时，冷凝器的换热量为22.3 kW，满足22 kW的额定制热量目标值，此时冷凝器的出口过冷度为3 ℃.

图 6

图 6 车内侧换热器(翅片间距为2 mm)的性能随迎面风速的变化(额定制热) Fig. 6 Performance of TFHE (fin spacing is 2 mm) along with wind speed (heating condition)

将小管径换热器应用于客车热泵空调系统，利用系统稳态仿真模型预测新热泵空调系统的性能.仿真结果如表 6所示.表中，t_e为蒸发温度，t_c为冷凝温度，W为压缩机功耗，Q₀(Q_h)为制冷(热)量，q_m为质量流量.由仿真结果可知，额定制冷量、COP、额定制热量与原客车空调系统相比，性能有所提升但离优化设计目标值有一段距离.根据额定制冷工况的理论计算结果可知，当达到额定制冷量26 kW时，系统循环质量流量为0.153 kg/s；在额定制热工况下，当满足优化目标制热量22 kW时，质量流量为0.11 kg/s.由此发现，原系统的HQB1D-80H510型号电动涡旋压缩机能力不足，须选用高效压缩机.

表 6

表 6 小管径换热器热泵空调系统性能仿真结果 Table 6 Simulation results of HPAC'S performance applied small diameter tube TFHE 工况 te/℃ tc/℃ W/kW Q0(Qh)/kW qm/(kg·s-1) EER(COP) 额定制冷工况 6.5 53.1 7.4 23.2 0.131 3.14 额定制热工况 -5.8 44.1 7.6 20.9 0.098 2.75

表 6 小管径换热器热泵空调系统性能仿真结果 Table 6 Simulation results of HPAC'S performance applied small diameter tube TFHE

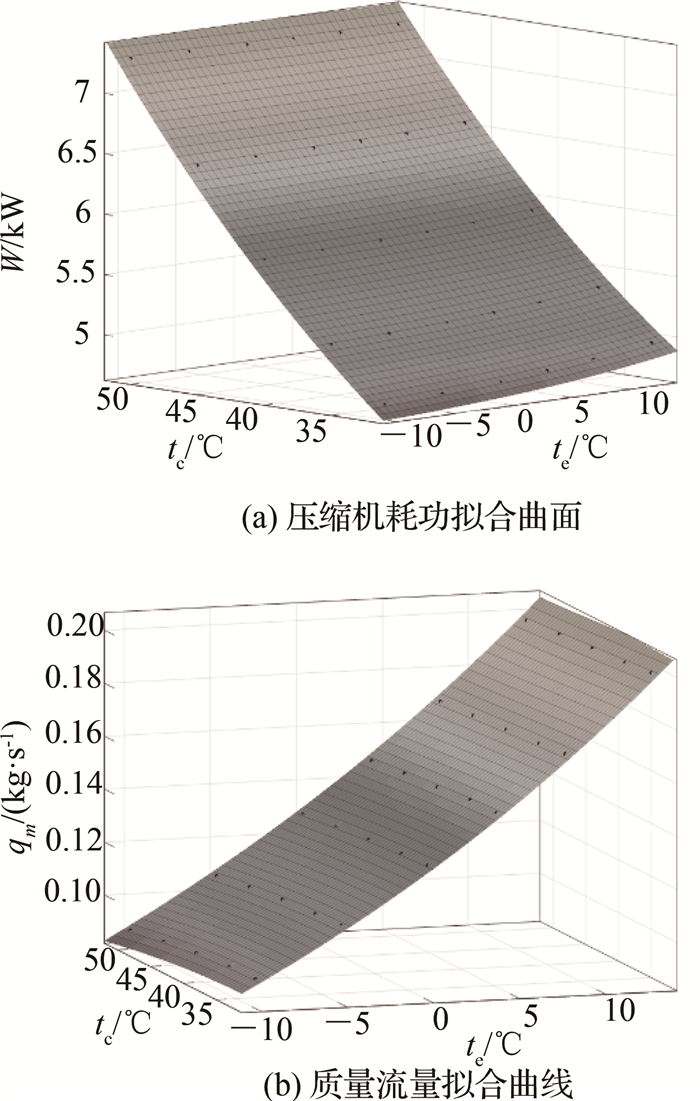
压缩机性能的提高，在相同运行工况下，能够降低压缩机功耗，提高系统COP.本文根据压缩机选型软件Product Selection Software，选用型号为ZP104KCE-TFD的电动涡旋压缩机，查询该型号压缩机在标准测试工况(压缩机吸气过热度为11.1 ℃，过冷度为8.3 ℃)下的性能参数，基于压缩机10系数模型进行拟合，如图 7所示.所选高效涡旋压缩机的10系数如表 7所示.

图 7

图 7 压缩机10系数模型拟合 Fig. 7 Fitting surface of 10 coefficient model for compress

表 7

表 7 ZP285KCE-TFD型压缩机模型系数 Table 7 ZP285KCE-TFD compress model coefficient Y C1 C2 C3 C4 C5 C6 C7 C8 C9 C10 qm 0.334 0.005 14 -2.74×10-7 7.38×10-5 -3.55×10-5 5.28×10-8 5.25×10-7 -4.44×10-7 4.63×10-7 -4.55×10-8 W 4.08 0.026 3 0.035 3 0.000 579 -0.000 586 0.000 31 0.000 006 33 -0.000 009 75 0.000 001 05 0.000 012 2

表 7 ZP285KCE-TFD型压缩机模型系数 Table 7 ZP285KCE-TFD compress model coefficient

在所设计的小管径换热器的基础上，选用ZP285KCE-TFD型高效新型压缩机应用在热泵空调系统中.基于系统稳态仿真模型，模拟新客车热泵系统在额定制冷、额定制热工况下的性能，并与原压缩机HQB1D-80H510结合小管径换热器的热泵空调系统性能仿真结果进行对比.额定制冷工况系统的仿真结果对比如表 8所示，额定制热工况系统的仿真结果对比如表 9所示.由表 8可知，采用新型高效压缩机结合小管径换热器后，系统制冷量由原来的23.2 kW增加至26.4 kW，提升了13.8%；系统制冷EER从3.14增加到3.62，提升了15.3%.由表 9可知，替换压缩机后，系统制热量由原来的20.9 kW增加至23.4 kW，提升了11.9%；系统COP从原来的2.75增加至3.16，提升了14.9%，基本达到优化目标.

表 8

表 8 替换压缩机前、后热泵空调系统性能的仿真结果(额定制冷) Table 8 Simulation results of HPAC'S performance compared with different compressor (under cooling conditioning) 系统 te/℃ tc/℃ W/kW Q0(Qh)/kW qm/(kg·s-1) EER 原压缩机系统 6.5 53.1 7.4 23.2 0.131 3.14 新压缩机系统 6.2 49.7 7.3 26.4 0.159 3.62

表 8 替换压缩机前、后热泵空调系统性能的仿真结果(额定制冷) Table 8 Simulation results of HPAC'S performance compared with different compressor (under cooling conditioning)

表 9

表 9 替换压缩机前、后热泵空调系统性能的仿真结果(额定制热) Table 9 Simulation results of HPAC'S performance compared with different compressor (under heating conditioning) 系统 te/℃ tc/℃ W/kW Q0(Qh)/kW qm/(kg·s-1) COP 原压缩机系统 -5.8 44.1 7.6 20.9 0.098 2.75 新压缩机系统 -1.5 48.8 7.4 23.4 0.122 3.16

表 9 替换压缩机前、后热泵空调系统性能的仿真结果(额定制热) Table 9 Simulation results of HPAC'S performance compared with different compressor (under heating conditioning)

(1) 利用计算机仿真手段，建立压缩机、车内外侧换热器、连接管路等部件模型，遵循上一部件的出口参数作为下一部件入口参数的原则，耦合各部件搭建出一套完整的热泵空调系统稳态仿真模型.依据原客车热泵空调系统的实验数据，验证并修正空调系统稳态仿真模型.运用修正后的热泵空调系统仿真模型，预测实验测试制冷工况下的系统性能.仿真结果表明，车内、外侧换热器换热量、压缩机耗功、制冷EER等仿真结果与实验数据的误差都小于5%；在实验测试制热工况下，热泵系统性能的仿真结果与实验数据的误差小于7%.所建立的客车热泵空调系统稳态仿真可以用于实际的工程应用，预测实际热泵空调系统的性能.

(2) 在换热器设计高度从260 mm降低到200 mm的前提下，为了满足客车热泵系统的优化设计目标，提出采用小管径换热器和高效涡旋压缩机的优化方案.利用系统稳态仿真模型预测新热泵空调系统的性能.仿真结果表明，在额定制冷(制热)工况下，系统制冷量(制热量)达到26.4 kW(23.4 kW)，整机制冷EER(制热COP)为3.62(3.18)，基本达到优化设计目标.