2. 南京磁谷科技有限公司, 江苏 南京 211102
2. Nanjing CIGU Limited Corporation, Nanjing 211102, China
磁悬浮轴承具有无机械接触、无摩擦、长寿命、免润滑、高效率、低噪声、可主动控制等优点.近年来,磁悬浮轴承在航空、化工、生产等领域的旋转机械得到了广泛应用[1],这使得磁悬浮旋转机械的振动稳定性问题评估尤为重要.如何准确地评价磁悬浮转子系统的稳定性,有效地控制转子振动、提高系统稳定性,成为目前急需解决的工业实际问题[2].
磁悬浮系统的振动稳定性研究有一定的工程实践意义,但现有的研究工作大多集中于实验室中,目前国内还没有一个行业普遍认同且行之有效的稳定性评估方法.ISO14839是对旋转机械ISO标准的补充与发展,由ISO/TC 108、机械振动与冲击的测量和评估等委员会提出.ISO14839规定了磁悬浮旋转机械振动方面的标准,包括术语定义、振动水平评估、稳定裕度评估和技术指南[3].其中,ISO14839-2于2004年初步修订,定义了磁悬浮轴承-转子系统的振动位移等级[4].ISO14839-3是磁悬浮轴承-转子系统的稳定裕度评估标准,于2006年初步修订,通过比较闭环系统灵敏度函数的幅频特性来衡量稳定裕度[5].
目前,国外引用ISO14839标准的振动稳定性研究已逐渐开展.Yoon[6]在磁悬浮压缩机喘振控制中,将ISO14839标准与传统的API标准对比,介绍了压缩机振动水平和稳定性评估方法;Li[7]利用ISO14839稳定裕度标准评估磁悬浮轴承转子系统潜在的局限性.国内利用ISO14839标准评估分析磁悬浮旋转机械振动稳定性的研究相对较少.
本文介绍ISO14839标准关于磁悬浮旋转机械系统的振动水平和稳定裕度两方面内容.以一磁悬浮轴承转子实验台为例,分析转子振动位移水平和系统稳定裕度.根据实验所得的磁悬浮转子系统振动水平和稳定裕度,分析系统的振动缺陷和不稳定因素,评价磁悬浮轴承转子系统的振动稳定性.
1 磁悬浮轴承ISO评估标准 1.1 振动位移评估ISO14839-2定义了磁悬浮轴承-转子系统在稳定工况下的振动位移等级.
磁悬浮轴承转子系统中影响转子振动水平的因素包括保护间隙Cmin[4].保护间隙是指保护轴承与转子之间的气隙.为了防止转子与电机定子及主动磁悬浮轴承定子相碰撞而损坏轴承系统,保护间隙应小于磁悬浮轴承与转子之间的气隙[8].
磁悬浮旋转机械可以通过位移传感器来采集转子动态位置信号,包括偏心距和振动轨迹.图 1中,xmax和ymax分别为传感器在径向方向上测得的最大振幅,Dmax为转子径向最大位移,可得
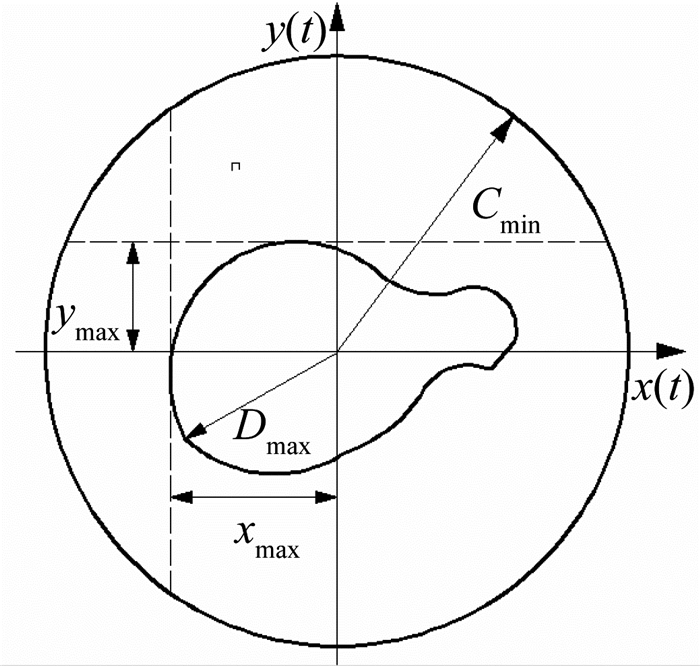
|
图 1 转子的振动位移轨迹 Fig. 1 Rotor orbit of vibration displacement |
| $ {D_{{\rm{max}}}} = {\rm{max}}[\sqrt {{x^2}\left( t \right) + {y^2}\left( t \right)}]. $ | (1) |
式中:x(t)、y(t)分别为转子位置坐标.
磁悬浮转子与保护轴承间应该保持足够间隙.径向保护轴承间隙为Cmin,应当满足
| $ {D_{{\rm{max}}}} < {C_{{\rm{min}}}}. $ | (2) |
同样地,转子轴向振动与保护轴承间隙应满足
| $ {D_{{\rm{max-axial}}}} < {C_{{\rm{min-axial}}}}. $ | (3) |
式中:Cmin-axial为转子轴向保护轴承单边间隙,Dmax-axial为转子轴向最大位移.
如表 1所示, ISO14839-2标准定义了对磁悬浮系统转子振动位移水平的等级.
| 表 1 推荐的振动等级限制标准 Table 1 Recommended criteria of zone limits |
等级A:一般为刚调试完成的新机器,性能良好.
等级B:在该水平下,设备能够长期稳定运行且不需要过多维护.
等级C:该水平下的设备需要定期维护才能保证稳定运行.
等级D:该水平下的设备在运行过程中出现失稳的可能性较大.
根据标准内容可知,在稳定工况下,若振动位移瞬间改变的幅值超过所划分等级B上限值0.4Cmin的25%,则需要分析振动位移变化的原因,避免潜在的问题.
1.2 稳定裕度评估ISO14839-3标准通过磁悬浮轴承转子系统稳定裕度评估振动稳定性.稳定裕度是用来衡量闭环系统相对稳定程度的指标,可以通过比较闭环系统灵敏度函数的幅值来评价[5].闭环系统灵敏度函数的幅值与系统稳定裕度成反比,因此,灵敏度函数幅值越小,对应的系统稳定裕度越大[7].
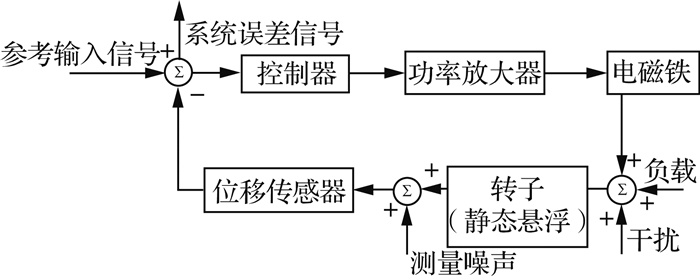
根据ISO14839-3可知,为了获得磁悬浮控制系统的灵敏度函数S(s),扰动和测量位置如图 2所示.
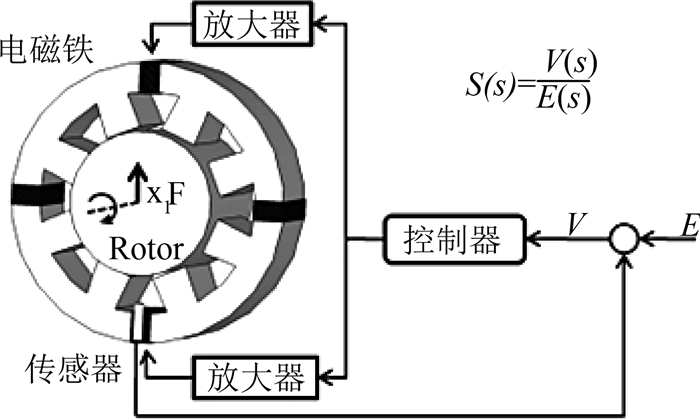
|
图 2 灵敏度函数测量位置 Fig. 2 Measurement points for sensitivity function |
系统的灵敏度函数为
| $ S\left( s \right) = \frac{{V\left( s \right)}}{{E\left( s \right)}}. $ | (4) |
式中:V(s)为闭环系统误差信号,E(s)为系统参考输入信号,S(s)为E(s)到V(s)的传递函数[9].
ISO14839-3将灵敏度函数峰值定义为4个等级,如表 2所示.表中,S为灵敏度函数峰值,等级限制值为3、4、5,对应灵敏度函数Bode图中的限制值分别为9.5、12和14 dB.
| 表 2 推荐的稳定裕度限制标准 Table 2 Peak sensitivity at zone limits |
稳定裕度等级A、B、C、D下对于机器性能的定义与振动位移等级下的定义类似,都是在系统稳定运行状况下划分的.
在测出不同磁悬浮作用力方向频域上的灵敏度函数后,可以得到整个磁悬浮轴承转子系统的灵敏度函数.各方向的灵敏度函数与整体灵敏度函数关系[5]如下:
| $ {S_{{\rm{max}}}} = \mathop {\max }\limits_i [{\rm{max}}|S({\rm{j}}w)|];w = 2{\rm{ \mathit{ π} }}f. $ | (5) |
式中:i为控制轴的数量,f为频率,w为相角.式(5)表示,系统整体评级取决于各个方向灵敏度函数的最差评级.
2 磁悬浮轴承-转子系统评估实验以实验室一磁悬浮轴承-转子实验台为例,对ISO14839标准进行研究.
磁悬浮轴承转子实验台的转子机械结构如图 3所示,xA、yA、xB、yB分别表示实验台A、B两端磁悬浮轴承径向控制力方向.径向位移传感器采用差动布置,分别固定在两端磁悬浮轴承外侧,轴向位移传感器固定在一侧端盖上.
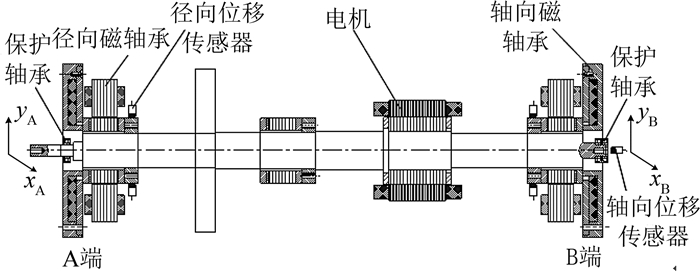
|
图 3 实验台转子的机械结构简图 Fig. 3 Mechanical structure diagram of test rig |
电涡流传感器检测转子的径向与轴向位移,将位移电压信号输入控制器.控制器计算出控制信号传递到功率放大器,功率放大器输出控制电流,经过转接开关到磁悬浮轴承线圈中,生成电磁力控制转子悬浮在所需要的位置[10].如图 4所示为实验现场图.

|
图 4 振动稳定性评估实验现场图 Fig. 4 Experimental site of vibration stability evaluation |
为了验证磁悬浮轴承-转子实验台径向悬浮的稳定性,开展旋转试验研究.
实验原理如图 5所示.采集转子转速频率为0~200 Hz下位移传感器检测到的振动位移信号,分析处理得到不同转速下转子的振动水平.本文中实验台保护轴承单边间隙Cmin为0.15 mm.
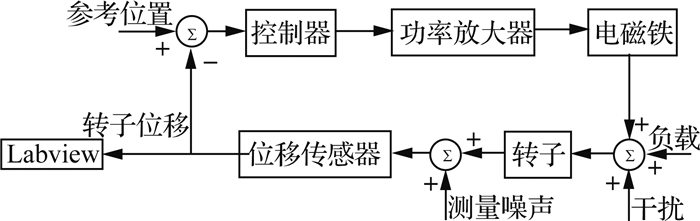
|
图 5 振动位移评估实验原理图 Fig. 5 Schematic diagram of vibration displacement evaluation |
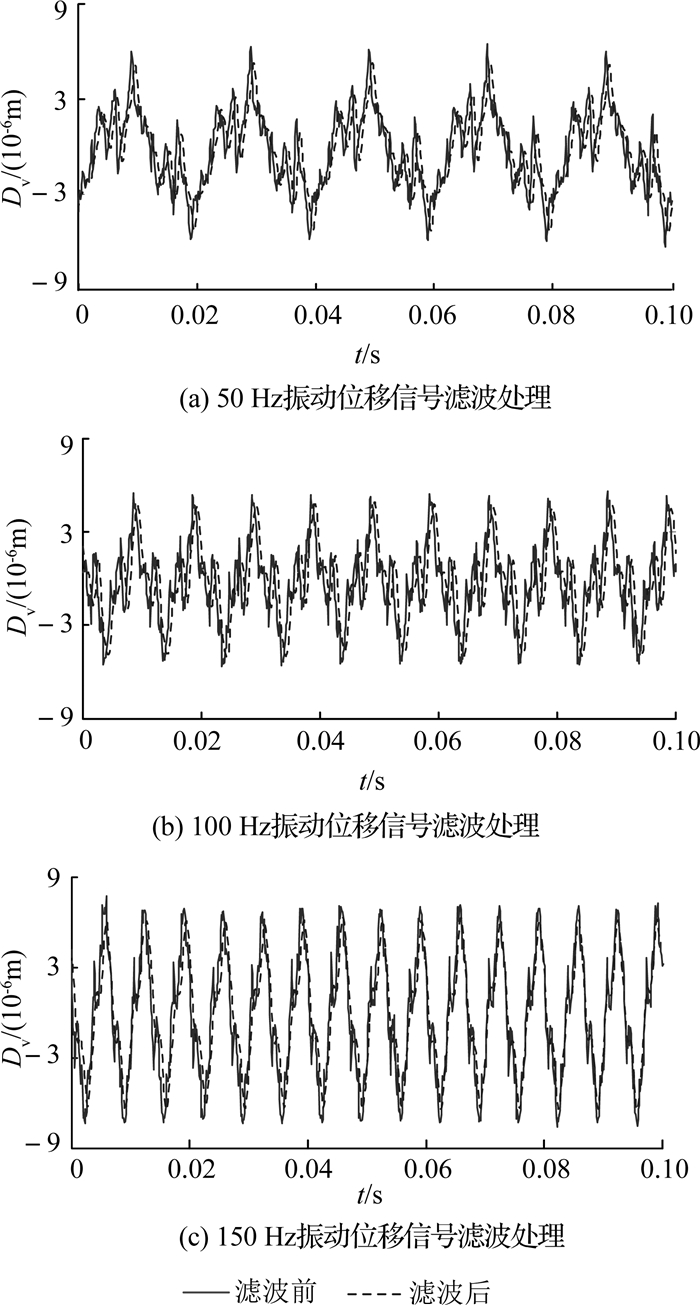
转子在旋转过程中偶尔伴随有尖锐的噪声,主要来源于电磁干扰、机械噪声以及空气动力噪声[11];因此可以通过增加低通滤波器来减少干扰信号的影响[12].如图 6所示分别为对50、100及150 Hz处的信号滤波处理结果.图中,t为时间,Dv为位移信号幅值.结果显示,滤波后,振动位移中的高频噪声和干扰等都有一定的衰减,能够得到所需的低频信号.
|
图 6 振动位移信号滤波处理 Fig. 6 Low pass-filter processing of vibration displacement signal |
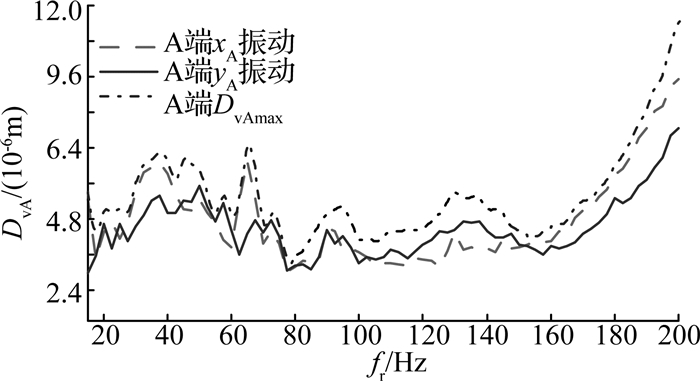
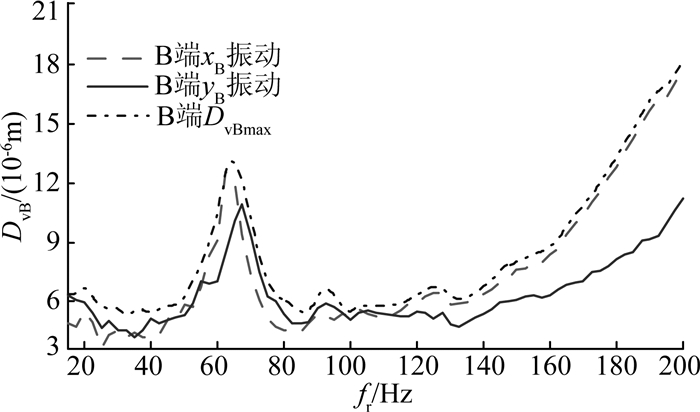
如图 7、8所示为径向磁悬浮力作用下转子的振动位移变化.图中,DvA和DvB分别为A、B端磁悬浮轴承的振动位移幅值,fr为转子转速频率.
|
图 7 A端磁悬浮轴承转子振动水平 Fig. 7 Vibration level of magnetic bearing A |
|
图 8 B端磁悬浮轴承转子振动水平 Fig. 8 Vibration level of magnetic bearing B |
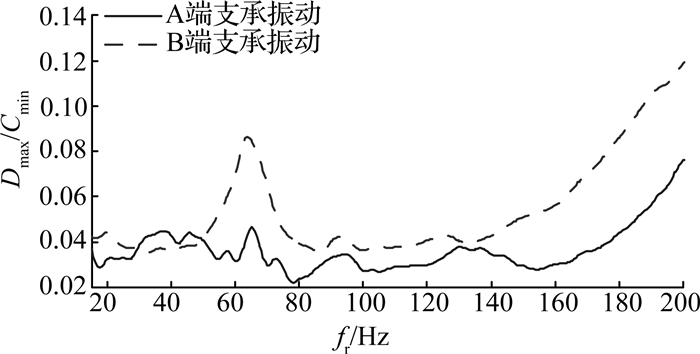
根据图 7、8,可得两端径向磁悬浮轴承的振动水平,即Dmax/Cmin,如图 9所示.可以看出,两端径向磁悬浮轴承的振动水平值均小于1/3,说明磁悬浮轴承转子实验台的振动位移水平在A等级内.
|
图 9 磁悬浮轴承转子振动水平 Fig. 9 Vibration level of magnetic bearings |
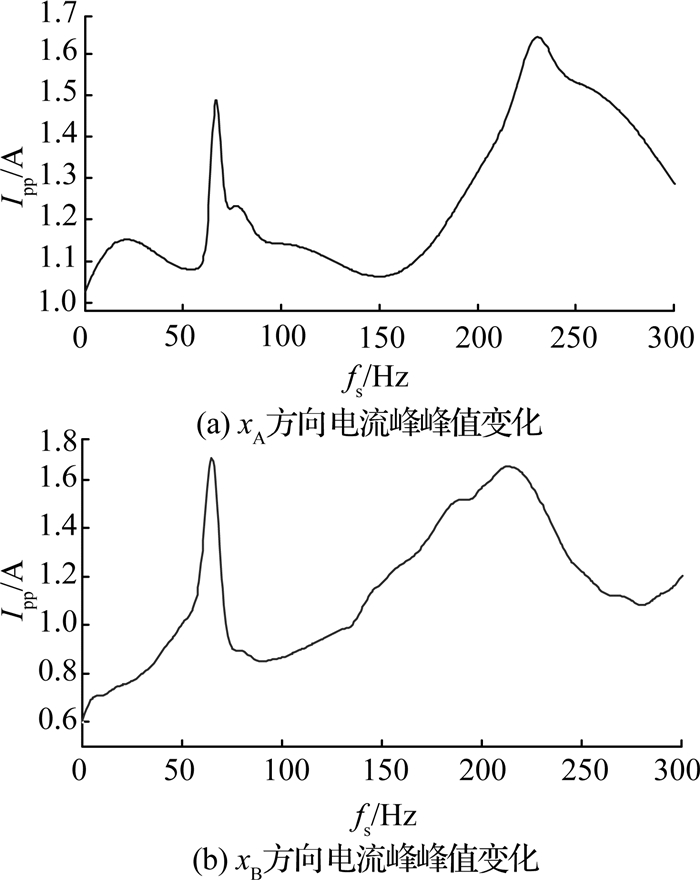
从图 9可以看出,转子在100 Hz后的振动位移呈明显的上升趋势,可以通过测量磁悬浮轴承在激振信号下的各方向电流变化[13],分析转子200 Hz后的振动水平趋势.如图 10所示为在0~300 Hz的激励信号下,xA和xB的电流峰峰值的变化.图中,Ipp为电流峰峰值,fs为激振信号频率.
|
图 10 xA和xB方向电流峰峰值变化 Fig. 10 Changes of peak-peak current of xA and xB |
从图 10可以看出,转子的一阶弯曲模态频率约为65 Hz,二阶弯曲模态频率约为225 Hz,这解释了图 7、8中在65 Hz处出现振动位移上升的情况.在225 Hz左右后振动位移再次减少.xA方向电流峰峰值在20 Hz处出现的峰值,经验证是由转子的一阶刚体模态频率产生.
从上述实验得到,实验台振动水平处于A等级,振动位移安全性能够得到保证.可以通过在线调试PID参数或动平衡实验[14],对磁悬浮轴承-转子实验台的振动水平进行进一步的优化.
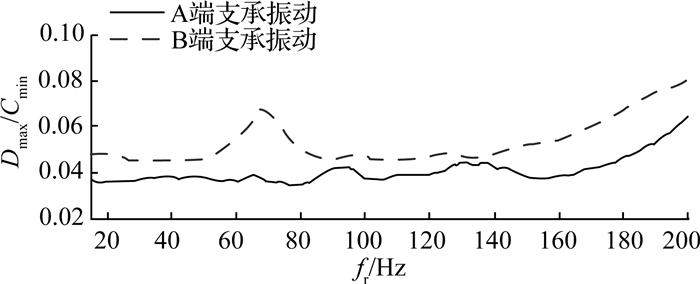
如图 11所示,对磁悬浮转子动平衡后,通过实验测量磁悬浮轴承端A、B的振动水平,振动水平得到优化.
|
图 11 动平衡后的磁悬浮轴承转子振动水平 Fig. 11 Vibration level of magnetic bearings after dynamic balancing |
进一步研究闭环系统的相对稳定性能,即系统的稳定裕度,评价系统的振动稳定性.
首先测量SISO系统的稳定裕度,再扩展到整体轴承转子系统中,综合评估整体的稳定裕度,具体的实验原理如图 12所示.
|
图 12 稳定裕度评估实验原理图 Fig. 12 Schematic diagram of stability margin assessment |
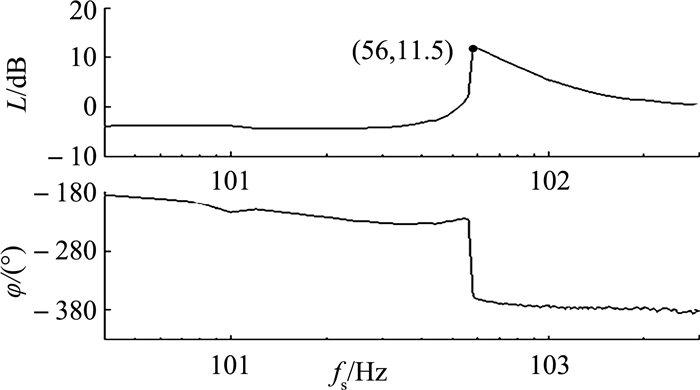
对实验台轴向系统进行扫频实验,采集闭环系统的误差信号,得到轴向系统参考信号到反馈信号的传递函数,即灵敏度函数Bode图,如图 13所示.图中,L为幅值,φ为相位差,fs为参考信号频率.
|
图 13 轴向系统灵敏度函数Bode图 Fig. 13 Bode diagram of transfer function of axial system |
从图 13可以看出,灵敏度函数Bode图的峰值为11.5 dB,对应灵敏度的峰值S为3.76,满足表 2中B区的幅值要求.
根据式(5)可知,整个轴承-转子系统的稳定裕度水平取决于各方向的综合评估.对其余方向分别进行闭环扫频后,得到径向A、B两端磁悬浮轴承x、y方向的灵敏度函数Bode图,如图 14所示.径向灵敏度函数Bode图峰值分别为10.82、10.75、11.6、11.39 dB,对应的灵敏度峰值S分别为3.48、3.45、3.81、3.71.各方向控制系统的稳定裕度都为等级B.
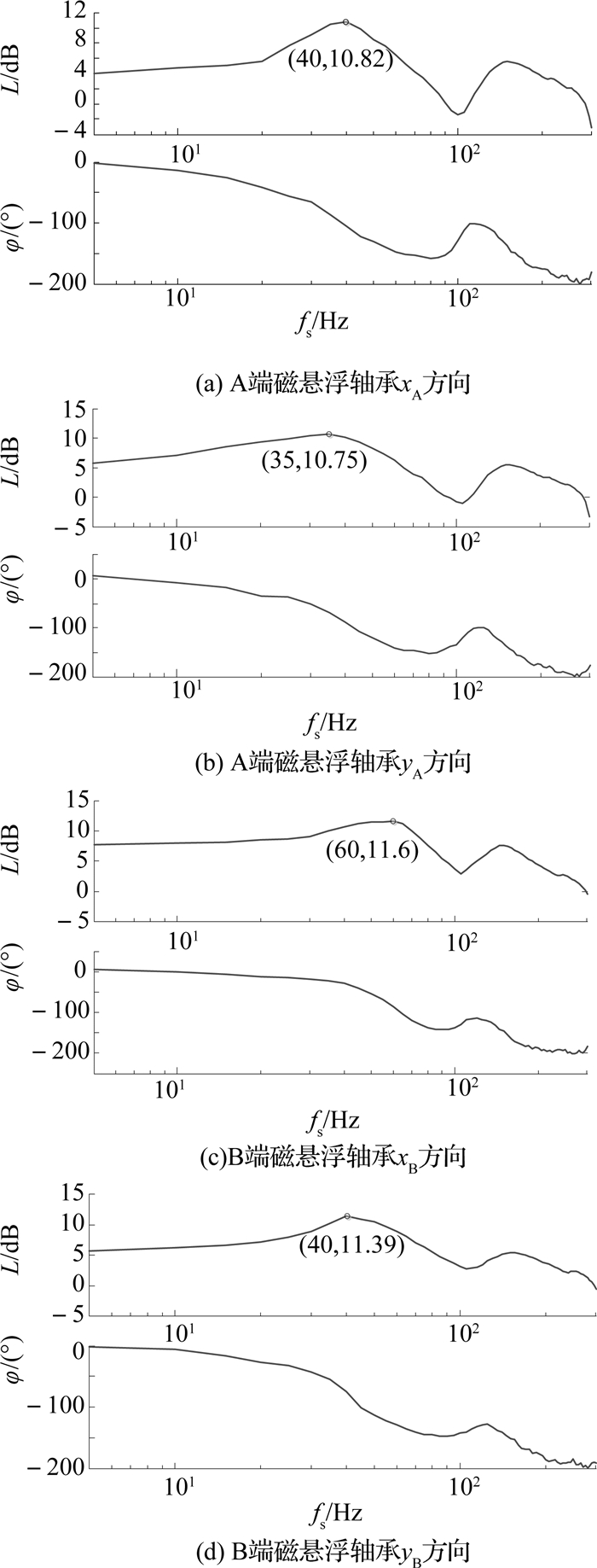
|
图 14 径向系统灵敏度函数Bode图 Fig. 14 Bode diagram of each radial axe's stability margin |
综合分析各方向系统的稳定裕度,得到整个磁悬浮轴承-转子系统的稳定裕度,如图 15所示.可以看出,在一阶弯曲模态频率附近60 Hz处达到峰值11.6 dB,对应的灵敏度峰值S为3.81,此时稳定裕度最小,在等级B范围内.
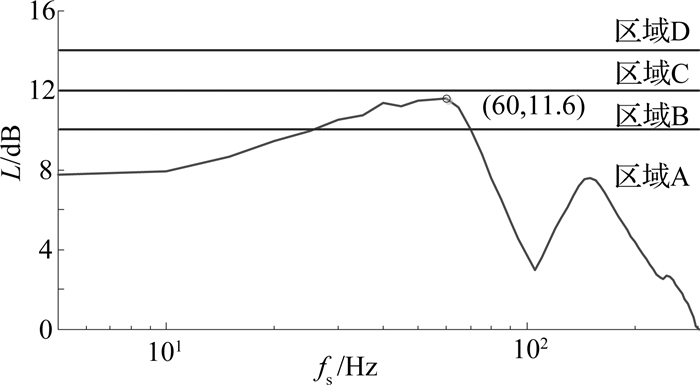
|
图 15 磁悬浮轴承系统整体稳定裕度 Fig. 15 Whole stability margin of magnetic bearing system |
整个磁悬浮轴承-转子系统的稳定裕度在B等级内,说明系统能够保证长期稳定运行,但是在一阶弯曲模态频率附近存在一定失稳的概率,可以通过设计固定中心频率的陷波器以稳定一阶弯曲模态[15-16],提高系统稳定性.
3 结语本文提出通过ISO14839标准分析磁悬浮旋转机械的振动稳定性,为系统的稳定控制和问题诊断提供指导.以一磁悬浮轴承转子实验台为例,实验评估分析磁悬浮转子振动位移水平和系统稳定裕度.分析结果表明,ISO14839标准能够为磁悬浮旋转机械的系统动力学设计、振动稳定性评估、系统状态监测等提供一种行之有效的方法,避免潜在的安全隐患,对提高磁悬浮旋转机械的工程应用可靠性具有一定的意义.
| [1] |
齐鹏逸. 基于电磁悬浮轴承的转子-轴承-密封系统的稳定性识别及振动控制[D]. 北京: 北京化工大学, 2011. QI Peng-yi.Rotor-bearing-seal system stability identification and Vibration control base on AMB[D].Beijing:Beijing University of Chemical Technology, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10010-1015562574.htm |
| [2] |
谢振宇, 徐龙祥, 李迎, 等. 磁悬浮轴承转子系统的稳定性及动态特性分析[J]. 机械科学与技术, 2004, 23(7): 765-767. XIE Zhen-yu, XU Long-xiang, LI Ying, et al. Analysis of the stability and dynamic characteristic of an active magnetic bearing system[J]. Mechanical Science and Technology for Aerospace Engineering, 2004, 23(7): 765-767. |
| [3] |
Active magnetic bearing-evaluation of stability margin:ISO TC108 SC2 WG7, N267[S]. London:Working Group Draft of International Standard, 2003.
|
| [4] |
Mechanical vibration-vibration of rotating machinery equipped with active magnetic bearings-Part 2:evaluation of vibration:ISO14839-2[S]. London:British Standard Institution, 2004. http://cds.cern.ch/record/1976519
|
| [5] |
Mechanical vibration-vibration of rotating machinery equipped with active magnetic bearings-Part 3:evaluation of stability margin:ISO14839-3[S]. London:British Standard Institution, 2006. http://cds.cern.ch/record/1976519
|
| [6] |
YOON S Y. Surge control of active magnetic bearing suspended centrifugal compressors[D]. Charlottesville:University of Virginia, 2011. https://search.proquest.com/docview/1018075088
|
| [7] |
LI G. Robust stabilization of rotor-active magnetic bearing systems[D]. Charlottesville:University of Virginia, 2007. http://adsabs.harvard.edu/abs/2007PhDT........36L
|
| [8] |
张钢, 殷庆振, 蒋德得, 等. 磁悬浮轴承-柔性转子系统的结构设计[J]. 轴承, 2010(6): 15-18. ZHANG Gang, YIN Qing-zhen, JIANG De-de, et al. Design of flexible rotor system supported by AMB[J]. Bearing, 2010(6): 15-18. |
| [9] |
SWANSON E, MASLEN E H, LI G, et al. Rotor dynamic design audit of amb supported machinery[C]//Proceedings of the 37th Turbo Machinery Symposium. Charlottesville:Texas A&M University, 2008:133-158. http://hdl.handle.net/1969.1/163121
|
| [10] |
吴桐. 主动磁悬浮轴承及其控制方法研究[D]. 沈阳: 沈阳工业大学, 2016. WU Tong. Research on active magnetic bearing and its control method[D]. Shenyang:Shenyang University of Technology, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10142-1016052519.htm |
| [11] |
XU X, CHEN S, ZHANG Y. Automatic balancing of AMB systems using plural notch filter and adaptive synchronous compensation[J]. Journal of Sound and Vibration, 2016, 374(4): 29-42. |
| [12] |
蒋森. 切比雪夫滤波器在磁悬浮控制系统中的应用[J]. 微电机, 2017, 50(3): 64-68. JIANG Sen. Application of Chebyshev filter for magnetic levitation control system[J]. Small and Special Electrical Machines, 2017, 50(3): 64-68. |
| [13] |
龙亚文, 谢振宇, 徐欣, 等. 基于变偏置电流控制方式的磁悬浮轴承系统控制策略[J]. 航空动力学报, 2014, 29(1): 118-124. LONG Ya-wen, XIE Zhen-yu, XU Xin, et al. Control strategy of active magnetic bearing system based on variable bias current control[J]. Journal of Aerospace Power, 2014, 29(1): 118-124. |
| [14] |
韩辅君, 房建成. 磁悬浮飞轮转子系统的现场动平衡方法[J]. 航空学报, 2010, 31(1): 184-190. HAN Fu-jun, FANG Jian-cheng. Field balancing method for rotor system of a magnetic suspending flywheel[J]. Acta Aeronautica Et Astronautica Sinica, 2010, 31(1): 184-190. |
| [15] |
汤恩琼, 房建成, 郑世强. 磁悬浮电动机柔性转子振动控制与试验研究[J]. 机械工程学报, 2015, 51(1): 106-116. TANG En-qiong, FANG Jian-cheng, ZHENG Shi-qiang. Vibration control and experimental study of flexible rotor in magnetically suspended motor[J]. Journal of Mechanical Engineering, 2015, 51(1): 106-116. |
| [16] |
SINA K İ. Robust control and unbalance compensation of rotor/active magnetic bearing systems[J]. Journal of Vibration and Control, 2012, 18(6): 817-832. DOI:10.1177/1077546310397560 |



