仿生柔性机械臂是从自然界软体动物的运动功能中获得灵感,基于功能仿生和结构仿生原理研制的新型机械臂,具有灵活性好、柔韧性高、运动范围广、能够在非结构化环境中工作等优点,在航天和深海探测领域有较好的应用前景.
近年来,国内外研究人员已经研制了多种驱动方式驱动的仿生柔性机械臂:气动驱动[1-3]、绳索驱动[4-6]、形状记忆合金(shape memory alloy,SMA)驱动[7-11]和电活性聚合物(electro active polymer,EAP)驱动[12].宾夕法尼亚大学与克莱姆森大学联合研制了柔性机械臂Oct-Arm [13-15].采用气动人工肌肉作为致动器,通过多段连续变形结构模拟章鱼腕与象鼻的柔性弯曲运动.气动柔性机械臂负载较大,但体积较大,且需要配备气源和相应的管路.欧盟“章鱼计划”项目资助了多家研究机构针对章鱼腕的组织结构和运动机理开展研究,研制仿章鱼柔性机械臂[16-20].该机械臂通过4组平行于中轴线的绳索模拟章鱼腕的纵肌,通过电机牵引绳索产生应力,从而使章鱼臂产生柔性弯曲、收缩和缠绕运动;采用SMA弹簧模拟章鱼腕的横肌,实现机械臂的伸长运动.该机械臂的运动柔性好,但结构复杂,需要电机驱动.浙江大学研制了仿生脊柱结构[21].该结构采用4组SMA丝平行于轴线分布并穿过若干间隔片,SMA加热收缩带动脊柱产生柔性弯曲运动,最大弯曲角度可以达到35°.该仿生结构驱动简单,实现了驱动与结构的一体化.美国斯坦福研究院研制了基于EAP驱动的圆柱形多功能驱动器[12].该驱动器总长度为65 mm,其中制动段长度为45 mm.该驱动器能够在强外电场(5.5 kV)下产生柔性弯曲,弯曲时驱动材料的应变最大可达26%.
本文针对水下非结构环境下操作对柔性机械臂柔性大变形的要求,基于章鱼腕肌肉结构的分析,提出SMA丝驱动仿生柔性机械臂结构.建立机械臂柔性变形的力学模型、SMA的本构模型和热力学模型,通过实验研究柔性机械臂的驱动性能,分析驱动参数对柔性弯曲运动的影响.
1 柔性机械臂结构设计与建模 1.1 SMA丝驱动柔性机械臂结构设计章鱼是一种常见的海洋软体动物,身体没有硬骨骼结构,由肌肉性静水骨骼来支撑[22],能够在肌肉组织的带动下实现大变形柔性动作并改变组织刚度.肌肉性静水骨骼的主要特征在于实现各种变形运动过程中的组织体积不变.
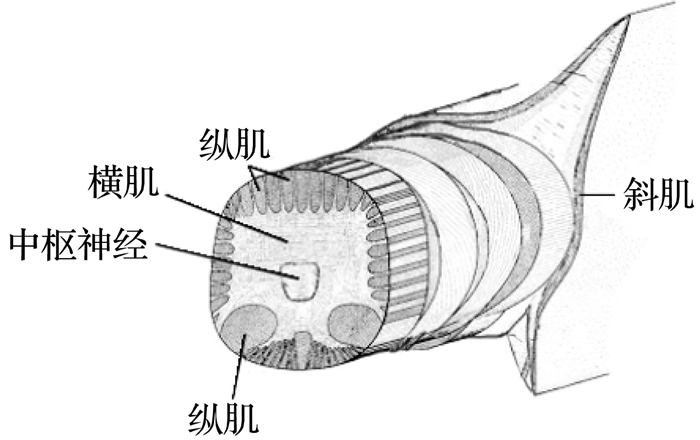
章鱼能够通过8条触腕来灵活地实现捕获和抓取动作,肌肉组织结构(见图 1)主要由横肌、纵肌、斜肌构成.横肌位于腕的中心位置,横肌收缩可以使腕自身的直径减小,由于静水肌肉组织的体积不变特性,而使得腕伸长;斜肌位于腕的外层,斜肌收缩可以拉动腕实现扭转;纵肌位于横肌的外侧,肌肉纤维方向为沿腕的长度方向,纵肌产生收缩时,能够拉动腕实现弯曲动作.
|
图 1 章鱼腕肌肉组织结构 Fig. 1 Muscle tissue structure of octopus's wrist |
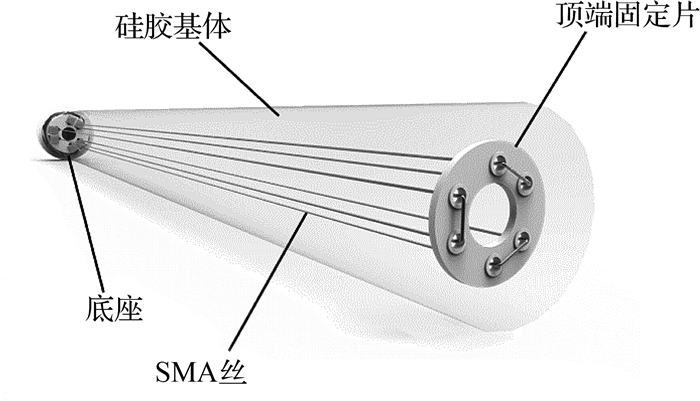
章鱼腕的大变形柔性弯曲运动是章鱼腕能够实现多自由度灵活运动的最主要动作.为了模仿章鱼腕肌肉性静水骨骼结构驱动的柔性大变形运动,设计了SMA丝驱动的仿章鱼腕柔性机械臂,结构如图 2所示.该柔性机械臂由底座、顶端固定片、SMA丝和硅胶基体组成,整体呈圆柱形.
|
图 2 柔性机械臂结构 Fig. 2 Structure of flexible manipulator |
底座是柔性机械臂的基座,3组SMA丝在柔性机械臂截面上沿圆周对称分布.每组SMA丝都是一根丝穿过顶端固定片后折返回来,丝的两端都固定在底座上,硅胶基体是柔性机械臂的本体结构,SMA丝嵌入在硅胶基体中.
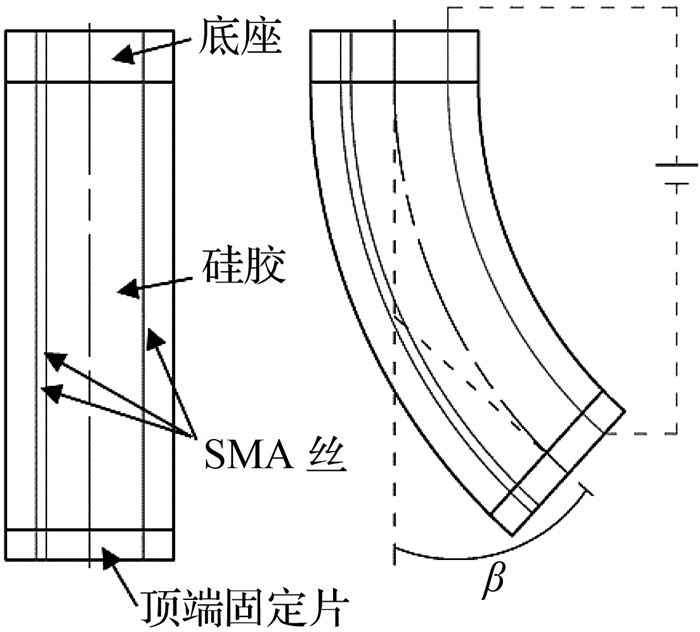
SMA丝为沿柔性机械臂长度方向布置,且与机械臂轴线平行,用以模仿章鱼腕的纵肌,SMA丝伸缩运动能够带动柔性机械臂向该侧柔性弯曲.机械臂主体由硅胶制成,硅胶具有不可压缩性,即具有近似的体积不变性,模拟章鱼腕的其他肌肉组织结构和结缔组织等肌肉性静水骨骼结构.任意一根SMA丝通电加热产生收缩应力时,机械臂可以发生柔性弯曲运动,动作如图 3所示.
|
图 3 柔性机械臂的弯曲动作原理 Fig. 3 Bending principle of flexible manipulator |
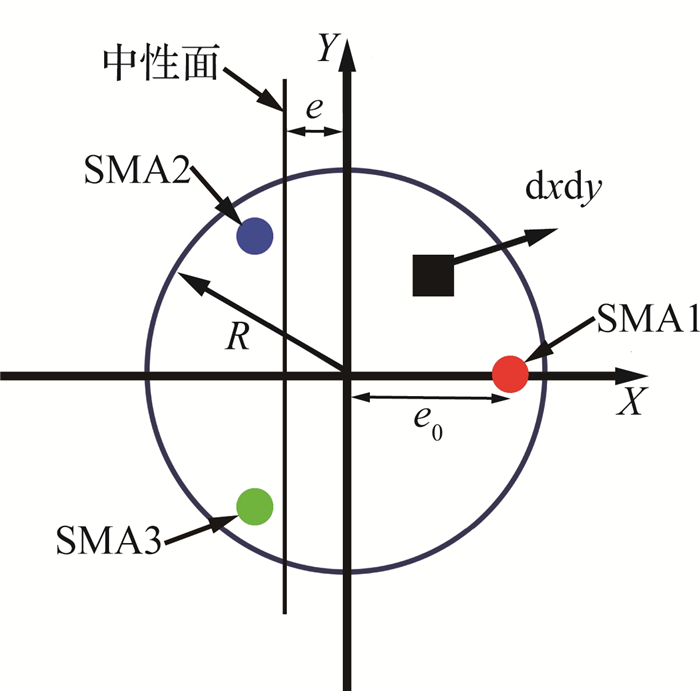
柔性机械臂在驱动SMA丝收缩力的作用下实现连续柔性弯曲运动,对应侧的冷态SMA丝被动拉伸.在达到最大弯曲角度时,柔性机械臂任意单元横截面内SMA丝和硅胶的作用力和作用力矩保持平衡.为了便于说明,取任意截面,以截面圆心为原点,建立相应的直角坐标系,X轴为沿原点指向SMA1圆心方向,Y轴过截面圆心与X轴垂直,如图 4所示.假设SMA1处于致动收缩状态,产生应力σSMA1;SMA2和SMA3处于被动拉伸状态,在机械臂弯曲变形过程中,中性面向反方向偏移,偏移距离为e,柔性机械臂弯曲角度可以表示为β=kls,其中k为机械臂轴线弯曲的曲率,ls为机械臂长度.SMA1产生的主动拉力为
|
图 4 柔性机械臂横截面示意图 Fig. 4 Cross section of flexible manipulator |
| $ {F_{{\rm{SMA1}}}} = {\sigma _{{\rm{SMA1}}}}{\rm{ \mathsf{ π} }}r_0^2. $ | (1) |
式中:r0为SMA丝半径.
SMA2和SMA3产生的被动拉力为
| $ {F_{{\rm{SMA2}}}} = {F_{{\rm{SMA3}}}} = {E_{\rm{M}}}{\varepsilon _{{\rm{SMA}}}}{\rm{ \mathsf{ π} }}r_0^2 = {E_{\rm{M}}}k\left( {\frac{1}{2}{e_0} - e} \right){\rm{ \mathsf{ π} }}r_0^2. $ | (2) |
式中:EM为SMA丝处于马氏体状态时的弹性模量,εSMA为SMA丝应变,e0为SMA丝距中轴线的距离.
将直角坐标系转化为极坐标系,计算硅胶的力和力矩.当机械臂产生弯曲运动时,硅胶由于发生弹性形变所产生的合力为
| $ {F_{\rm{S}}} = \int_0^{2{\rm{ \mathsf{ π} }}} {\int_0^R {E\varepsilon r{\rm{d}}r{\rm{d}}\theta } } . $ | (3) |
式中:E为硅胶弹性模量,ε为硅胶应变,R为柔性机械臂的半径.
硅胶由于发生弹性形变所产生的相对于中性面的合力矩为
| $ {M_{\rm{S}}} = \int_0^{2{\rm{ \mathsf{ π} }}} {\int_0^R {E\varepsilon \left( {r\cos \theta + e} \right)r{\rm{d}}r{\rm{d}}\theta } } . $ | (4) |
任意位置的硅胶应变及SMA丝应变计算公式均为
| $ \varepsilon = {\varepsilon _{{\rm{SMA}}}} = k\left( {r\cos \theta + e} \right). $ | (5) |
由式(1)~(5),可得截面上力平衡方程为
| $ \begin{array}{*{20}{c}} {{\sigma _{{\rm{SMA1}}}}{\rm{ \mathsf{ π} }}r_0^2 + 2{E_{\rm{M}}}k\left( {\frac{1}{2}{e_0} - e} \right){\rm{ \mathsf{ π} }}r_0^2 = }\\ {\int_0^{2{\rm{ \mathsf{ π} }}} {\int_0^R {Ek\left( {r\cos \theta + e} \right)r{\rm{d}}r{\rm{d}}\theta } } .} \end{array} $ | (6) |
截面上相对于中性面的力矩平衡公式为
| $ \begin{array}{*{20}{c}} {{\sigma _{{\rm{SMA1}}}}{\rm{ \mathsf{ π} }}r_0^2\left( {{e_0} + e} \right) - 2{E_{\rm{M}}}k\left( {\frac{1}{2}{e_0} - e} \right){\rm{ \mathsf{ π} }}r_0^2 = }\\ {\int_0^{2{\rm{ \mathsf{ π} }}} {\int_0^R {Ek{{\left( {r\cos \theta + e} \right)}^2}r{\rm{d}}r{\rm{d}}\theta } } .} \end{array} $ | (7) |
SMA在相变温度下产生相应的应力和应变变化,电加热方式是最方便的SMA致动方法,对SMA的加热采用PWM脉冲方式实现对SMA温度的控制,进而控制机械臂的弯曲运动.由欧姆定律及热力学基本公式可知,当SMA丝处于通电加热状态时,有
| $ mc\frac{{{\rm{d}}T}}{{{\rm{d}}t}} = \frac{{{U^2}}}{R}\tau - hA\left( {T - {T_0}} \right). $ | (8) |
式中:τ为占空比;m为SMA丝质量,m=ρSMAπr02l,其中ρSMA为SMA密度,l为SMA长度;T为SMA丝温度;R为SMA丝电阻,R=ρRl/(πr02),其中ρR为SMA电阻率;h为等效传热系数,基于温差修正方式,依据实验建立关系式h=h1+h2(T-T0);A为SMA丝传热面积,A=2πr0l;T0为环境温度;c为比热容;U为驱动电压.
当SMA丝处于断电散热状态时,即U=0,则有
| $ mc\frac{{{\rm{d}}T}}{{{\rm{d}}t}} = - hA\left( {T - {T_0}} \right). $ | (9) |
SMA丝相变过程中温度的变化,导致了SMA丝应力、应变和相变量等参数的关系.由于SMA自身的非线性及热迟滞等因素,使得SMA丝相变时的参数变化较复杂.Tanaka本构模型[23]描述了各参数的对应关系如下:
| $ \dot \sigma = E{{\dot \varepsilon }_{{\rm{SMA}}}} + \mathit{\Theta }\dot T + \mathit{\Omega }\dot \xi , $ | (10) |
| $ E = {E_A} + \xi \left( {{E_{\rm{M}}} - {E_{\rm{A}}}} \right). $ | (11) |
由马氏体向奥氏体相变时,马氏体所占的百分含量为
| $ \xi = \exp \left[ {a\left( {{A_{\rm{S}}} - T} \right) + b\sigma } \right]. $ | (12) |
由奥氏体向马氏体相变时,马氏体所占的百分含量为
| $ \xi = 1 - \exp \left[ {a\left( {{M_{\rm{S}}} - T} \right) + b\sigma } \right]. $ | (13) |
式中:AS为奥氏体相变开始温度,MS为马氏体相变开始温度,T为SMA丝的温度,ξ为马氏体百分含量,σ为SMA丝应力,E为SMA相变中的弹性模量,EA为SMA奥氏体的弹性模量,Ω为相变系数,Θ为热弹性系数,a、b为常量参数.
2 SMA驱动柔性机械臂性能实验研究 2.1 柔性机械臂样机选用TiNi基SMA丝作为柔性机械臂的制动器,直径为0.3 mm,电阻率为1.11×10-6Ω·m,密度为6.5×103 kg/m3,比热容为870 J/(kg·℃),As为66 ℃,Ms为78 ℃,EM为27 GPa,EA为65 GPa,Θ为0.55 MPa/℃.将3组SMA丝、顶端固定片和基底固定连接,连接后置入专用模具内(见图 5),灌注入A、B组份1:1配比的5度人体硅胶(弹性模量为2×104 MPa),完成柔性机械臂样机(见图 6)的制作.该样机长250 mm,直径为20 mm,e0为6 mm.

|
图 5 柔性机械臂样机的模具 Fig. 5 Mould for flexible manipulator prototype |

|
图 6 柔性机械臂样机实物图 Fig. 6 Flexible manipulator prototype |
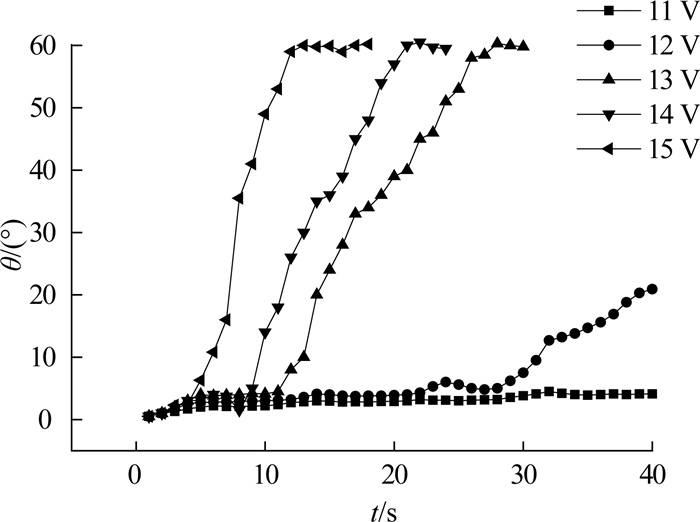
在机械臂的柔性弯曲控制中,需要选取合适的驱动电压,使得机械臂能够实现较大的柔性变形,同时能够保证使用寿命.过高的驱动电压能够提高SMA的响应速度,但会导致SMA丝的温度升高过快而过热;过低的驱动电压可能导致SMA丝应力无法带动机械臂弯曲或响应时间过长.为了研究不同驱动电压下机械臂弯曲角度随加热时间的变化情况,开展不同驱动电压下的加热实验.实验使用占空比为0.5的PWM直流电压脉冲驱动,单组SMA丝的驱动电压为11~15 V,实验水温为25 ℃.柔性机械臂单组SMA驱动时,弯曲角度θ随通电时间t的变化关系如图 7所示.
|
图 7 不同驱动电压下的弯曲角度与驱动时间关系 Fig. 7 Relationship between bending angle and driving time under different driving voltages |
由图 7可知,机械臂的最大弯曲角度约为60°(见图 8),机械臂的弯曲速度随电压的增大而提高.使用11 V驱动电压时,机械臂不能发生明显弯曲;使用12 V电压加热时,当加热至29 s时机械臂才发生较明显的弯曲,响应速度十分缓慢;使用13 V及以上电压加热时,随着电压的增大,机械臂的弯曲速度加快,且在全部柔性弯曲动作过程中,柔性机械臂能够保持沿长度方向的连续柔性变形,如图 9所示.

|
图 8 样机最大弯曲状态 Fig. 8 Maximum bending state of prototype |
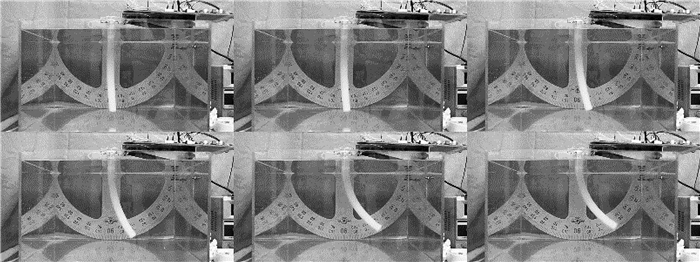
|
图 9 13 V电压下样机弯曲变形过程图像序列 Fig. 9 Bending deformation process image sequence of prototype under 13 V voltage |
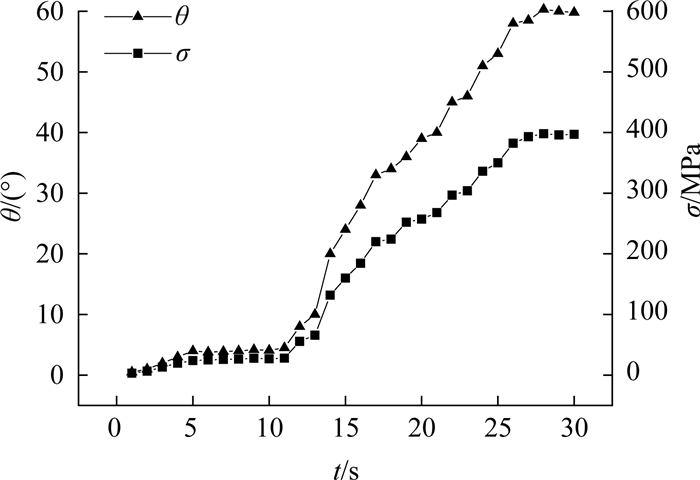
柔性机械臂的弯曲动作是在SMA丝通电加热收缩应力作用下实现的.为了研究SMA丝应力与柔性机械臂弯曲角度的对应关系,选用13 V驱动电压连续加热模式,对SMA丝的应力σ变化随时间t的变化关系和柔性机械臂的弯曲角度θ随时间t的变化关系进行实验研究,变化曲线如图 10所示.
|
图 10 SMA丝应力与弯曲角度的关系 Fig. 10 Relationship between stress and bending angle of SMA wire |
由图 10可见,在柔性机械臂的弯曲过程中,随着加热时间的增加,SMA丝的加热收缩应力逐渐增加,在应力作用下柔性机械臂的弯曲角度逐渐增加.机械臂弯曲角度和SMA丝收缩应力曲线的变化趋势相似,可知柔性机械臂弯曲角度和SMA丝应力呈近似线性关系.实验结果与基于力平衡方程建立的柔性机械臂弯曲模型基本吻合.
2.3 柔性机械臂驱动电压与动作时间关系柔性机械臂柔性弯曲和回复是周期性运动,虽然高电压能够提高动作响应,但SMA丝的冷却回复时间因为温度滞后而增加.为了获得最适合的驱动电压,开展不同驱动电压U下的响应与回复时间t实验.
在水温为25 ℃的实验水温条件下,控制加热PWM脉冲占空比为0.5,测量柔性机械臂达到最大弯曲角度的加热响应时间tres与冷却回复时间trec,如图 11所示.
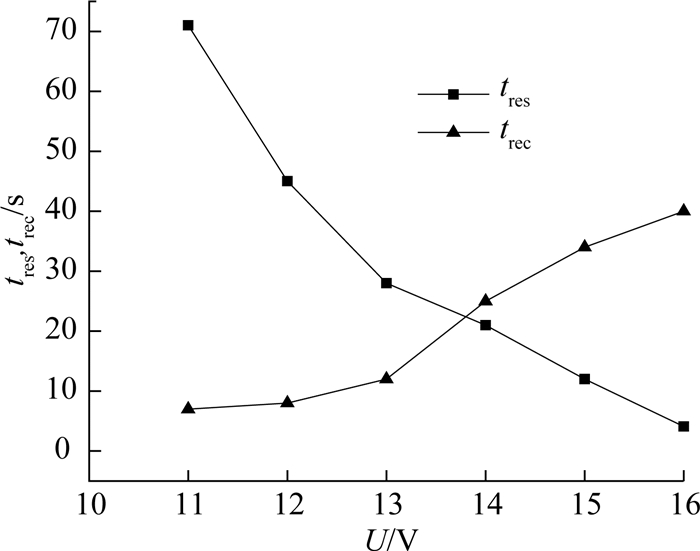
|
图 11 不同驱动电压下的响应时间与回复时间 Fig. 11 Response time and recovery time under different driving voltages |
由图 11可知,机械臂的响应时间随着驱动电压的增加而减小,回复时间随着驱动电压的增大而增大.在11 V和12 V电压驱动下,在稳定时未达到机械臂能够达到的最大弯曲角度,且响应时间很长;在15 V和16 V电压驱动下,回复时间较长,远大于达到最大弯曲角度的响应时间.在14 V电压驱动下,达到最大弯曲角度的响应时间和回复时间较接近,但回复时间明显大于13 V驱动电压状态.在13 V驱动电压下的响应时间略大于14 V电压时,但回复时间与11、12 V下的回复时间很接近.由于实验采用占空比为0.5的PWM脉冲加热,通过增加占空比的方式可以减小响应时间.由此可知,驱动电压选取13 V是较合适的,后续实验均采用13 V电压驱动.
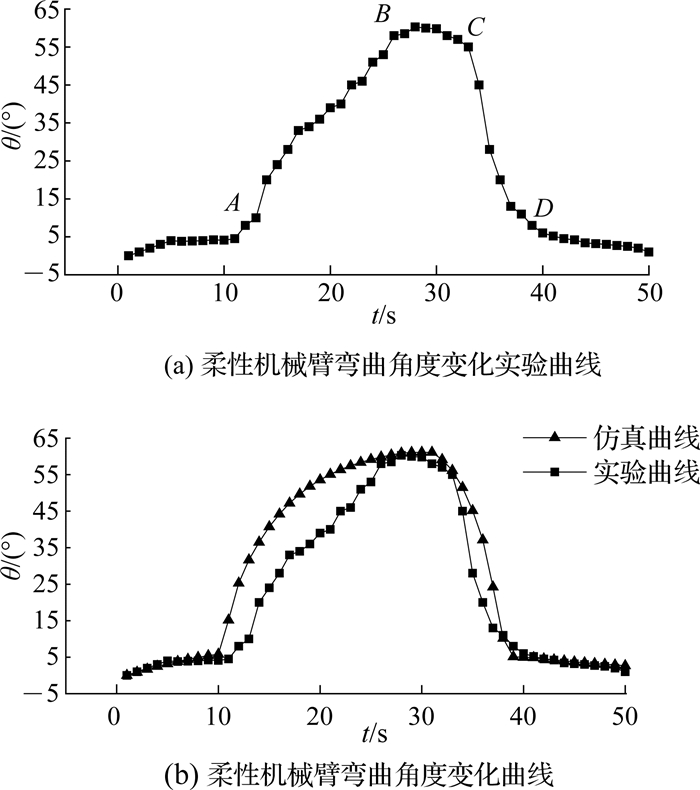
在13 V驱动电压下,PWM占空比为0.5,驱动时间为30 s,柔性机械臂柔性弯曲与回复角度θ随t变化的实验数据如图 12(a)所示.可见,柔性机械臂在A点开始弯曲角度迅速增大,即SMA丝的温度达到马氏体逆相变初始温度,开始发生马氏体逆相变,机械臂发生明显弯曲;在B点逆相变结束时,机械臂达到最大弯曲角度;在C点停止加热,SMA丝开始发生奥氏体相变,在D点相变结束时,机械臂基本恢复原长.
|
图 12 13 V电压下柔性机械臂弯曲角度的变化曲线 Fig. 12 Bending angle changing curve of flexible manipulator under 13 V voltage |
基于建立的柔性机械臂力学模型、SMA热力学模型和本构模型,选用表 1的相关参数,理论计算柔性机械臂的弯曲角度随时间变化的理论曲线和实验曲线之间的对比关系,如图 12(b)所示.可见,理论曲线和实验曲线较吻合,验证了理论模型的正确性.
| 表 1 SMA模型的理论计算参数 Table 1 Theoretical calculation parameters of SMA modeling |
采用固定占空比的PWM脉冲对机械臂的SMA丝进行加热,当加热时间足够大时,SMA最终会达到热平衡状态,SMA的温度会趋于一个定值.由于SMA的相变量与温度有关,在加热时间足够长的情况下,SMA丝的相变量与占空比有关.不同相变状态下的SMA丝表现出不同的电阻和应力,影响机械臂的弯曲角度.要实现柔性机械臂的准确控制,有必要对占空比、电阻与弯曲角的关系进行实验研究.
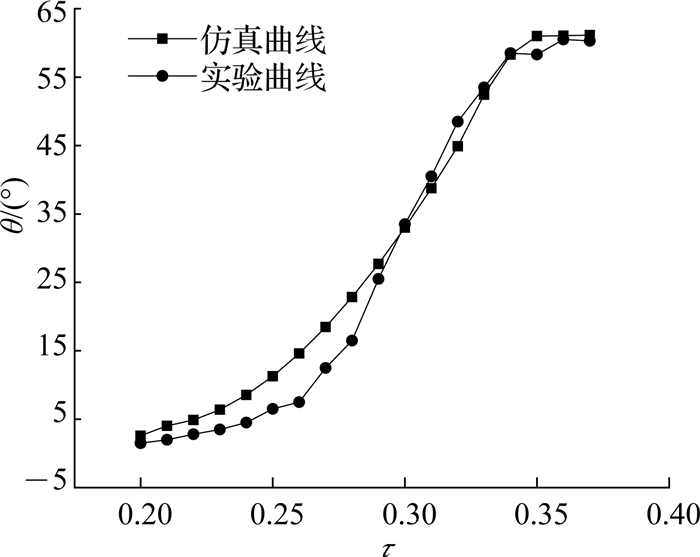
通过实验研究θ与τ的关系.实验采用的驱动电压为13 V,PWM驱动脉冲占空比从0.2开始每次增加0.01,每种占空比条件下,加热时间足够保证加热结束时SMA丝达到热平衡,温度保持恒定,机械臂角度保持稳定.不同占空比下的热平衡时的弯曲角度如图 13所示.当τ=0.20~0.25时,占空比较小,达到热平衡时的温度没有达到SMA丝逆相变开始温度,机械臂几乎不发生弯曲;当占空比为0.25~0.35时,SMA丝发生马氏体逆相变,热平衡时SMA丝相变量随占空比的增大而增大,机械臂弯曲角度随之增大;当τ>0.35时,SMA丝已经完全相变,机械臂达到最大弯曲角度.理论仿真数据和实验数据曲线基本吻合,表明对于柔性机械臂在任意角度下的精确控制,可以通过改变占空比实现柔性机械臂在任意弯曲角度的位置保持.
|
图 13 弯曲角度与占空比的关系 Fig. 13 Relationship between bending angle and duty cycle |
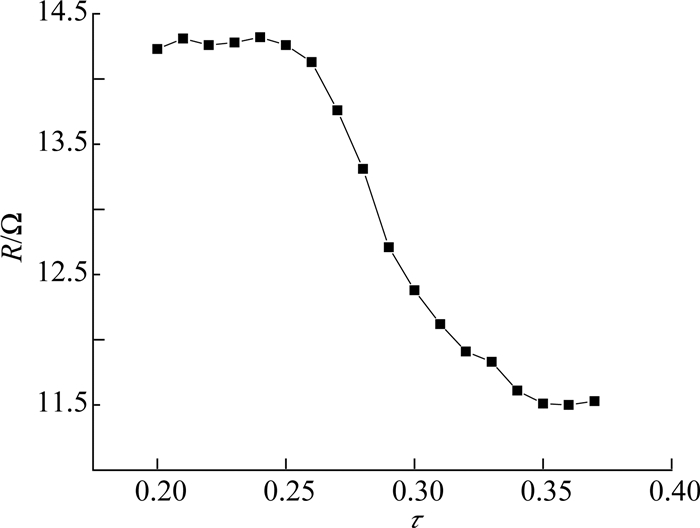
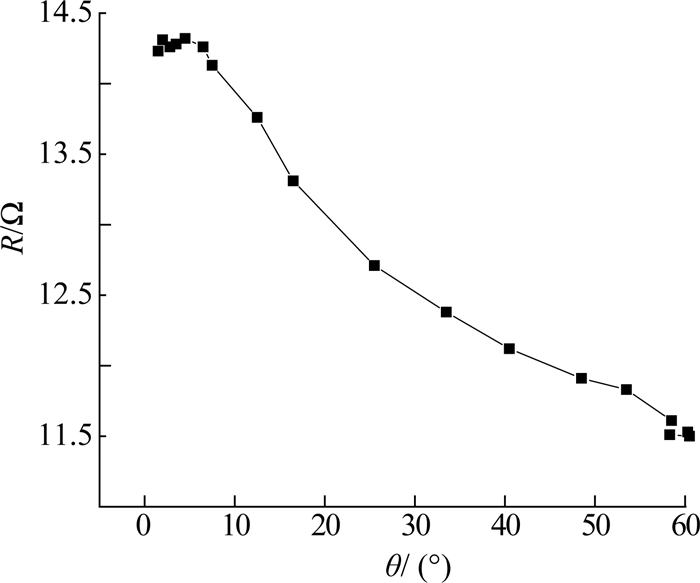
SMA具有自感知特性,电阻会随相变过程而变化.为了研究SMA电阻随相变过程的变化,开展SMA丝电阻与占空比的关系实验.在加热SMA丝达到热平衡状态时,测量不同占空比τ下SMA丝的电阻R,实验结果如图 14所示.可得θ与R的关系,如图 15所示.实验结果表明,占空比、电阻和柔性机械臂的弯曲角度有对应关系,在SMA相变阶段,弯曲角度与SMA电阻存在近似线性的关系.通过感知SMA的电阻状态,可以实现对柔性机械臂弯曲角度的精确控制.
|
图 14 SMA丝电阻与占空比的关系 Fig. 14 Relationship between SMA wire resistance and duty cycle |
|
图 15 SMA丝电阻与机械臂弯曲角度的关系 Fig. 15 Relationship between SMA wire resistance and bending angle of manipulator |
本文研制形状记忆合金丝驱动的柔性机械臂,针对该机械臂建立力学模型,基于形状记忆合金丝的热力学模型和本构模型,构建驱动电压和脉宽调制的占空比与柔性机械臂弯曲角度的理论关系.通过实验研究驱动电压、占空比对柔性机械臂弯曲角度、形状记忆合金丝电阻之间的变化规律.实验结果与理论分析结果较吻合,验证了理论模型的正确性,为未来仿生柔性机械臂的研制提供了一种可行的结构方案,并为下一步基于电阻反馈的柔性机械臂精确控制研究提供研究基础.
| [1] |
JONES B A, MCMAHAN W, WALKER I. Design and analysis of a novel pneumatic manipulator[C]//Proceedings of 3rd IFAC Symposium on Mechatronic Systems. Sydney:IEEE, 2004:745-750. http://www.academia.edu/15345301/An_octopus_anatomy-inspired_robotic_arm
|
| [2] |
WILLIAM M, JONES B A, WALKER I D.Design and implementation of a multi-section continuum robot:air-octor[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Edmonton:IEEE, 2005:2578-2585. http://ieeexplore.ieee.org/document/1545487/
|
| [3] |
EMANUELE G, NIKOS T, DARWIN G C, et al. An octopus anatomy-inspired robotic arm[J]. International Conference on Intelligent Robots and Systems, 2010, 6219(1): 3091-3096. |
| [4] |
SIMAAN N. Snake-like units using flexible backbones and actuation redundancy for enhanced miniaturization[C]//Proceedings of the 2005 IEEE International Conference on Robotics and Automation. Barcelona:IEEE, 2006:3012-3017. http://ieeexplore.ieee.org/document/1570572/
|
| [5] |
DEGANI A, CHOSET H, ZUBIATE B, et al. Highly articulated robotic probe for minimally invasive surgery[C]//International Conference of the IEEE Engineering in Medicine and Biology Society. Vancouver:IEEE, 2008:4167. http://europepmc.org/articles/PMC2923469
|
| [6] |
GIORELLI M, RENDA F, CALISTI M, et al. Learning the inverse kinetics of an octopus-like manipulator in three-dimensional space[J]. Bioinspiration and Biomimetics, 2015, 10(3): 035006. DOI:10.1088/1748-3190/10/3/035006 |
| [7] |
胡海燕, 王鹏飞, 孙立宁, 等. 线驱动连续型机器人的运动学分析与仿真[J]. 机械工程学报, 2010, 49(19): 1-8. HU Hai-yan, WANG Peng-fei, SUN Li-ning, et al. Kinematic analysis and simulation for cable-driven continuum robot[J]. Journal of Mechanical Engineering, 2010, 49(19): 1-8. |
| [8] |
VAVOURAKIS V, BAMPASAKIS D, KAZAKIDI A, et al. Generation of primitive behaviors for non-linear hyperelastic octopus-inspired robotic arm[C]//20124th IEEE RAS and EMBS International Conference on Biomedical Robotics and Biomechatronics. Rome:IEEE, 2012:725-730.
|
| [9] |
CIANCHETTI M, LICOFONTE A, FOLLADOR M, et al. Bioinspired soft actuation system using shape memory alloys[J]. Actuators, 2014, 3(3): 226-244. DOI:10.3390/act3030226 |
| [10] |
ZHENG T, YANG Y, DAVID T, et al. Controldesign of shape memory alloy based multi-arm continuum robot inspired by octopus[C]//2014 IEEE 9th Conference on Industrial Electronics and Applications. Hangzhou:IEEE, 2014:1108-1113. http://ieeexplore.ieee.org/document/6931331/
|
| [11] |
CIANCHETTI M, CALISTI M, MARGHERI L, et al. Bioinspired locomotion and grasping in water:the soft eight-arm OCTOPUS robot[J]. Bioinspiration and Biomimetics, 2015, 10(035003): 1-8. |
| [12] |
PEI Q, PELRINE R, STANFORD S, et al. Multifunctional electroelastomer rolls and their application for biomimetic walking robots[C]//International Society for Optics and Photonics, 2002, 4698(1):246-253. http://proceedings.spiedigitallibrary.org/proceeding.aspx?articleid=883269
|
| [13] |
MCMAHAN W, CHITRAKARAN V, CSENCSITS M, et al. Field trials and testing of the Oct Arm continuum manipulator[C]//Proceedings of 2006 IEEE International Conference on Robotics and Automation. Orlando:IEEE, 2006:23. http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1642051
|
| [14] |
RAHN C, WALKER I. Design and experimental testing of the OctArm soft robot manipulator[J]. Proceedings of SPIE, 2006, 6230(2). |
| [15] |
GODAGE I, MEDRANO G A, BRANSON D T, et al. Modal kinematics for multi-section continuum arms[J]. Bioinspiration and Biomimetics, 2015, 10(035002): 1-18. |
| [16] |
LASCHI C, MAZZOLAI B, MATTOLI V, et al. Design of a biomimetic robotic octopus arm[J]. Bioinspiration and Biomimetics, 2009, 4(015006): 1-10. |
| [17] |
CALISTI M, ARIENTI A, GIANNACCINI M E, et al. Study and fabrication of bioinspired octopus armmockups tested on a multipurpose platform[C]//20103rd IEEE RAS and EMBS International Conference on Biomedical Robotics and Biomechatronics. Tokyo:IEEE, 2010:461-466. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=5625959
|
| [18] |
CIANCHETTI M, ARIENTI A, FOLLADOR M, et al. Design concept and validation of a robotic arm inspired by the octopus[J]. Materials Science and Engineering, 2011, 31(6): 1230-1239. DOI:10.1016/j.msec.2010.12.004 |
| [19] |
MARGHERI L, MAZZOLAI B, PONTE G, et al. Methods and tools for the anatomical study and experimental in vivo measurement of the Octopus vulgaris arm for biomimetic design[J]. 20103rd IEEE RAS and EMBS International Conference on Biomedical Robotics and Biomechatronics (Bio Rob). Tokyo:IEEE, 2010, 467-472. |
| [20] |
EMANUELE G, NIKOS T, DARWIN G. An octopus anatomy-inspired robotic arm[C]//2010 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Taipei:IEEE, 2010:3091-3096.
|
| [21] |
WANG S, ZHU Q, XIONG R, et al. Flexible robotic spine actuated by shape memory alloy[J]. International Journal of Advanced Robotic Systems, 2014, 11(1): 56. |
| [22] |
KIER W, THOMPSON J. Muscle arrangement, function and specialization in recent coleoids[J]. Berliner Palobiol Abh, 2003(3): 141-162. |
| [23] |
TANAKA K. A thermomechanical sketch of shape memory effect:one-dimensional tensile behavior[J]. Res Mechanica, 1986, 18(3): 251-263. |


