自然界中绝大多数被认为无磁性的物质都具有抗磁性,如水、铜、硅、塑料等[1].抗磁性物质在磁场中可实现稳定悬浮.《Nature》杂志上报道了日本东京大学Ikezoe等在氧气介质中悬浮起水滴的研究工作[2],其所在实验室后续将磁悬浮技术应用于生物有机材料的分离研究[3-5].西北工业大学的商澎等利用稳态强磁场将磁悬浮应用于空间生物技术[6-7].Mirica等[8]提出一种新型磁悬浮装置用于检测抗磁性物质密度.利用两块同极相对且间距为45 mm的永磁铁使物质在顺磁介质中稳定悬浮,并且发现物质密度与悬浮高度之间呈线性关系,该测量方法随后被应用于物质分离[9]、食品药品检测[10-11]、法医鉴定[12]、自组装[13-14]、化学反应监测[15]、塑料制品检测[16]以及顺磁离子液体检测[17]等研究领域.作者所在课题组基于磁悬浮装置提出了塑料光学透镜的新型检测方法[18],并通过多项式拟合方法得到磁铁间距为60 mm时聚合物密度与悬浮高度之间的函数关系,其密度测量精度达到0.002 ~ 0.010 g/cm3[19].
目前,采用磁悬浮方法测量物质密度时,测量范围受到顺磁介质溶液密度的局限,很难超过2.3 g/cm3,Nemiroski等[20]提出利用倾斜装置来扩大密度测量范围的新方法.然而,该方法操作繁琐,且需要对溶液密度进行多次标定.本文提出全新的抗磁性高密度物质的磁悬浮测量方法,悬挂高密度样品,利用水平放置的磁悬浮装置来进行密度测量.通过对高密度样品在顺磁溶液中的受力分析,给出被测样品密度的计算公式,并结合样品横向悬浮位移,计算出抗磁性高密度样品的密度.该方法具有装置简单,操作简便,且适用于小尺寸样品等优势.
1 测量装置与理论 1.1 测量装置使用的抗磁性高密度物质密度测量装置包括磁悬浮装置和铝制三维运动平台,整体照片如图 1(a)所示.磁悬浮装置水平放置,由左、右两块相同的方形磁铁同极相对且间隔一段距离构成.该装置结构包括底座、磁铁座、磁铁和固定销四个部分,如图 1(b)所示,结构件采用3D打印成形.在实际测量时,高密度样品通过一定长度的细线悬挂于三维运动平台上的夹持装置,并通过运动平台调节夹持装置的位置,将样品置于磁悬浮装置中左侧磁铁表面的中心处.样品在磁悬浮装置中会受到重力、浮力、细线拉力和磁场力的综合作用,被推离左侧磁铁一定距离(横向悬浮位移),并保持稳定悬浮状态,如图 1(c)所示.为了保证照片效果,采用深灰色虚线标记图 1(c)的细线.

|
图 1 抗磁性高密度物质密度测量装置实物图 Fig. 1 Photograph of density measurement device for diamagnetic high-density materials |
磁铁选用北京久久高科磁性材料有限公司生产的N45牌号钕铁硼磁铁,尺寸均为50 mm×50 mm×25 mm,中心表面磁感应强度为(0.425±0.005) T.磁铁左、右各一块,两块磁铁以N极对N极的方式布置,磁铁间距为45 mm.细线长度为(200±0.5) mm.顺磁溶液为浓度为3.0 mol/L的MnCl2水溶液.
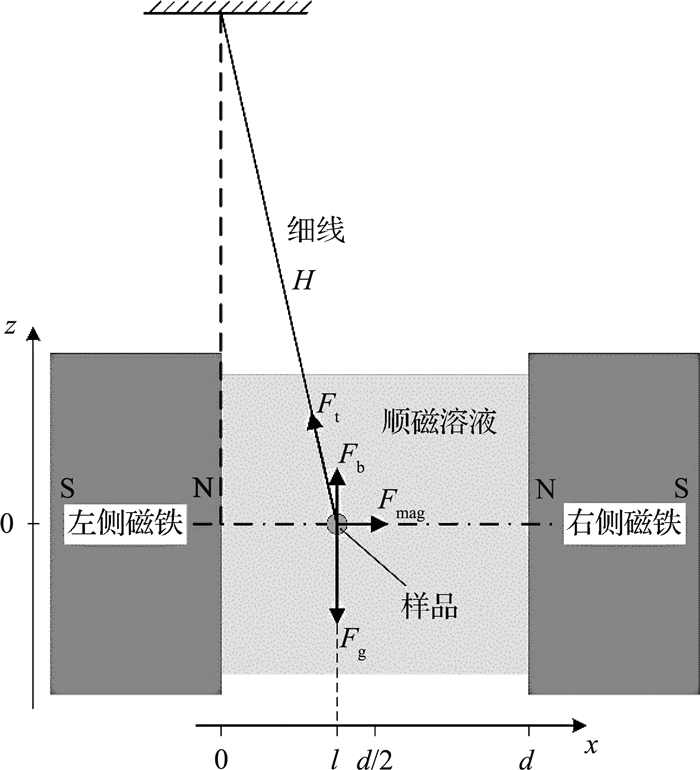
1.2 测量理论根据上述测量装置,高密度样品的磁悬浮密度测量示意图如图 2所示.左、右两块钕铁硼磁铁N极相对水平放置,间距为d,被细线悬挂的被测样品在顺磁溶液中稳定悬浮,细线长度为H,并产生横向悬浮位移l.根据样品的横向悬浮位移来计算被测样品的密度.本文中,d为45 mm,H为200 mm.
|
图 2 高密度样品的磁悬浮密度测量示意图 Fig. 2 Schematic diagram of density measurement by magnetic levitation for high-density materials |
高密度样品在顺磁性溶液中受到重力、浮力、细线拉力和磁场力的综合作用.当四力平衡时,样品达到稳定悬浮状态.平衡时的受力公式如下所示:
| $ {\mathit{\boldsymbol{F}}_{\rm{g}}} + {\mathit{\boldsymbol{F}}_{\rm{b}}} + {\mathit{\boldsymbol{F}}_{\rm{t}}} + {\mathit{\boldsymbol{F}}_{{\rm{mag}}}} = {\bf{0}}. $ | (1) |
式中:Fg为重力,Fb为浮力,Ft为细线拉力,Fmag为磁场对样品产生的作用力.式(2)、(3)分别描述了样品所受的重力与浮力.式(4)展示了在外加磁场B下,处于顺磁溶液内的抗磁样品所受的磁力Fmag.
| $ {\mathit{\boldsymbol{F}}_{\rm{g}}} = {\rho _{\rm{s}}}\mathit{\boldsymbol{g}}V, $ | (2) |
| $ {\mathit{\boldsymbol{F}}_{\rm{b}}} = - {\rho _{\rm{m}}}\mathit{\boldsymbol{g}}V, $ | (3) |
| $ \begin{array}{l} {\mathit{\boldsymbol{F}}_{{\rm{mag}}}} = \frac{{{\chi _{\rm{s}}} - {\chi _{\rm{m}}}}}{{{\mu _0}}}V\left( {\mathit{\boldsymbol{B}} \cdot \nabla } \right)\mathit{\boldsymbol{B}} = \\ \;\;\;\;\;\;\;\;\frac{{{\chi _{\rm{s}}} - {\chi _{\rm{m}}}}}{{{\mu _0}}}V \times \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {B_x}}}{{\partial x}}}&{\frac{{\partial {B_x}}}{{\partial y}}}&{\frac{{\partial {B_x}}}{{\partial z}}}\\ {\frac{{\partial {B_y}}}{{\partial x}}}&{\frac{{\partial {B_y}}}{{\partial y}}}&{\frac{{\partial {B_y}}}{{\partial z}}}\\ {\frac{{\partial {B_z}}}{{\partial x}}}&{\frac{{\partial {B_z}}}{{\partial y}}}&{\frac{{\partial {B_z}}}{{\partial z}}} \end{array}} \right] \times \left[ {\begin{array}{*{20}{c}} {{B_x}}\\ {{B_y}}\\ {{B_z}} \end{array}} \right]. \end{array} $ | (4) |
式中:χ为磁化率,ρ为密度,下标s与m分别表示样品与介质溶液;V为被测样品体积;B为磁感应强度;▽为向量梯度算子;g为重力加速度;μ0为真空磁导率,μ0= 4π×10-7N/A2.
重力与浮力在同一顺磁介质下保持不变.在三维直角坐标系下,z轴与重力方向平行,由于磁铁的对称性,系统中y和z轴是等价的,即xy平面与xz平面的磁场分布相同.本文使用的细线长度H=200 mm,使得样品在x轴方向推离时,在z轴方向的变化幅度小于±0.3 mm,不会影响到整体的受力分析结果.受力平衡发生在xz平面上,By必然为0,且(B ·▽) B在y轴方向上的分量为0;同时,(B ·▽) B在z轴方向上的分量(约10-5 T2/m)小于其在x轴上的分量(约10-3 T2/m);此外,在中心线周围Bz(约10-3 T)小于Bx(约10-1 T)两个数量级[8],因此,式(4)可以简化为
| $ {\mathit{\boldsymbol{F}}_{{\rm{mag}}}} = \frac{{{\chi _{\rm{s}}} - {\chi _{\rm{m}}}}}{{{\mu _0}}}V\left[ {\begin{array}{*{20}{c}} {{B_x}\frac{{\partial {B_x}}}{{\partial x}}}\\ 0\\ 0 \end{array}} \right]. $ | (5) |
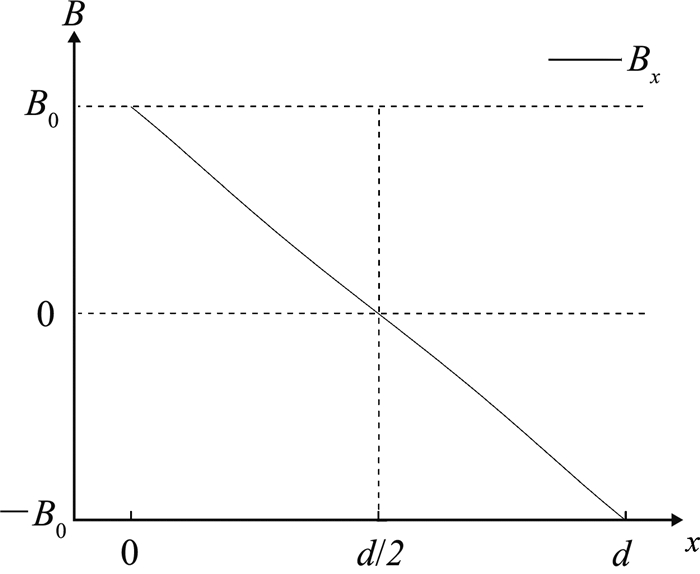
根据使用的磁铁(N45钕铁硼磁铁,尺寸为5 cm × 5 cm × 2.5 cm),Bx在x轴上(左侧磁铁到右侧磁贴表面)的变化几乎为线性的(R2=0.999).中心线上的Bx分布如图 3所示,从左侧磁铁表面(x=0)的最大值+B0变为右侧磁铁表面(x=d)的最小值-B0.磁悬浮装置中心线上的磁场强度B为
|
图 3 测量装置中心线上Bx分布情况 Fig. 3 Distribution of Bx at centerline of measurement device |
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} { - \frac{{2{B_0}}}{d}x + {B_0}}\\ 0\\ 0 \end{array}} \right]. $ | (6) |
利用力的平衡公式(1)及图 2,运用平行四边形法则,结合式(2)、(3)、(5)和(6),可得
| $ \frac{{\frac{{{\chi _{\rm{s}}} - {\chi _{\rm{m}}}}}{{{\mu _0}}}V\left( {\frac{{ - 2{B_0}}}{d}l + {B_0}} \right)\left( { - \frac{{2{B_0}}}{d}} \right)}}{{\left( {{\rho _{\rm{s}}} - {\rho _{\rm{m}}}} \right)gV}} = \frac{l}{H}. $ | (7) |
式中:ρs为物体密度,l为横向悬浮位移.求解式(7),可以得到
| $ {\rho _{\rm{s}}} = \frac{\alpha }{l} + \beta , $ | (8a) |
| $ \alpha = \frac{{ - 2B_0^2\left( {{\chi _{\rm{s}}} - {\chi _{\rm{m}}}} \right)H}}{{dg{\mu _0}}}, $ | (8b) |
| $ \beta = {\rho _{\rm{m}}} + \frac{{4B_0^2\left( {{\chi _{\rm{s}}} - {\chi _{\rm{m}}}} \right)H}}{{{d^2}g}}. $ | (8c) |
从式(8)可以看出,当给定顺磁溶液和磁铁以及细线长度时,ρs与l的倒数呈正比关系.
1.3 实验流程高密度样品的磁悬浮密度测量方法的实现流程主要包括以下5个步骤.
1) 配备顺磁溶液.溶质一般为高浓度盐,溶剂通常为水或醇溶液;本文使用的溶质为MnCl2,溶剂为水.
2) 将被测物体用一定长度的细线粘附,悬挂于三维运动平台的夹持装置上;通过运动平台调节夹持装置的位置,将样品置于磁悬浮装置中左侧磁铁表面的中心处,即样品自然下垂时,重心位于左侧磁铁表面的中心处.
3) 将盛有顺磁溶液的容器置于测量装置内,将悬挂的样品置于容器内并静置一段时间,使样品达到稳定悬浮状态.样品会在溶液中悬浮,并被推离左侧磁铁表面,产生横向悬浮位移.采用照相法[19],测量横向悬浮位移.每组实验保证相机在固定位置、高度以固定角度进行拍照,相机对焦到样品;在对焦面上放置已知长度的对比物体,待样品稳定悬浮后拍摄图像照片.
4) 所得照片采用图像处理软件,测量样品中心到左侧磁铁表面的像素点数目以及已知长度的对比物长度所对应的像素点数目.根据对比物的长度以及像素点数目之比,可以得到l.
5) 将l代入式(8),可以计算得到抗磁性高密度样品的密度.
2 实验结果与讨论 2.1 密度测量结果为了验证所提计算公式的正确性,选择铜球(H62黄铜)、铝球和玻璃球(直径≤5 mm)来进行磁悬浮密度测试实验.铜球、铝球和玻璃球的理论密度分别为8.500、2.710和2.500 g/cm3.铜球、铝球和玻璃球均为抗磁性物质,它们的磁化率均为10-6量级,大大小于顺磁溶液的磁化率.上述测试样品的磁化率均设置为χs=-5×10-6[8].顺磁溶液为浓度为3.0 mol/L的MnCl2水溶液,χm = 5.49×10-4,ρm = 1.292 g/cm3.
如图 4所示,铜球、铝球和玻璃球均不能在传统垂直放置的磁悬浮装置[8]中悬浮起来,因此,传统磁悬浮装置无法测量抗磁性高密度物质.

|
图 4 高密度样品在传统磁悬浮装置中无法悬浮 Fig. 4 High-density samples cannot be levitated in traditional magnetic levitation device |
在该实验装置中,两块磁铁间距为45 mm.通过COMSOL仿真,得到中心线上x方向磁感应强度呈线性分布(R2 = 0.999)且B0 = 0.375 T,将其代入式(6),可得
| $ {B_x} = 0.375 - 0.01667l. $ | (9) |
将式(9)代入式(8),可得ρs与l的函数关系:
| $ {\rho _{\rm{s}}} = - 1.20585 + \frac{{56.20159}}{l}. $ | (10) |
高密度样品在本文磁悬浮装置中的悬浮照片如图 5所示.为了保证照片效果,采用深灰色虚线标记图 5的细线.如图 5所示,铜球、铝球、玻璃球的横向悬浮位移分别为5.69、14.37和15.10 mm.根据式(10),计算得到它们的密度分别为8.667、2.705和2.517 g/cm3.测量结果与理论密度的误差分别为0.167、0.005和0.017 g/cm3,初步验证了所提方法的正确性.传统磁悬浮密度的测量范围为0.8 ~ 2.3 g/cm3,本文方法已准确测量出密度为2.5 ~ 8.5 g/cm3的高密度物质.理论上,本文方法的密度测量范围为1.1 ~ 22.0 g/cm3,测量下限由顺磁溶液密度决定,测量上限由被测样品的尺寸决定.

|
图 5 高密度样品在该磁悬浮装置中的悬浮照片 Fig. 5 Photograph of high-density samples are levitated in proposed magnetic levitation device |
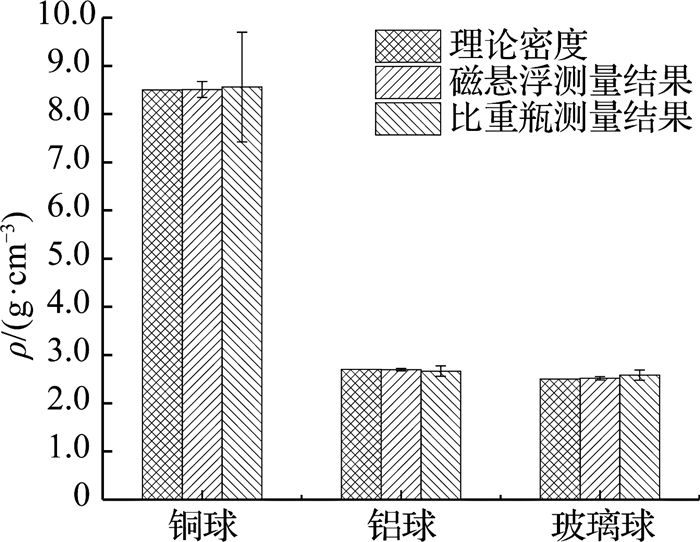
为了进一步验证所提计算公式的正确性与有效性,探讨分析磁悬浮密度测量方法的精度.采用该方法对铜球、铝球和玻璃球的密度进行10次重复测量;同时作为对比,利用比重瓶3次测量上述物质密度,理论密度、本文方法和比重瓶法的测量结果对比如图 6所示.本文方法的测量结果分别为8.509±0.165、2.696±0.034和(2.517±0.028) g/cm3,利用比重瓶的测量结果分别为8.562±1.138、2.665±0.109和(2.582±0.104) g/cm3.由图 6可知,与比重瓶法相比,本文方法具有非常好的重复测量精度.原因主要是本文样品都非常小(V约为6×10-8m3),比重瓶法需要精确测量样品的体积,提出的磁悬浮密度测量法不需要检测样品的体积.
|
图 6 磁悬浮测量结果与比重瓶测量结果对比 Fig. 6 Results comparison between magnetic levitation and pycnometer |
由图 6可知,本文方法随着样品密度的增加,偏差范围呈现增大趋势.对所提方法进行误差分析.
根据式(8)可知,对测量结果有影响的参数包括χm、ρm、χs、l、d、H和B0 7个参数.其中,χm、ρm不相互独立[8],这两个参数均与介质溶液浓度c和实验温度t相关.χm、ρm与浓度的关系分别如下:
| $ {{\rm{ \mathsf{ χ} }}_{\rm{m}}} = \frac{{{C_{{\rm{Cw}}}}}}{{t - \theta + 273.15}}c - 9 \times {10^{ - 6}}, $ | (11) |
| $ \begin{array}{l} {\rho _{\rm{m}}}\left( {t,c} \right) = {W_0} + {W_1}t + {W_2}{t^{3/2}} + Ac + \\ \;\;\;\;\;\;\;\;\;Bct + Cc{t^2} + D{c^{3/2}} + E{c^{3/2}}t + F{c^{3/2}}{t^2}. \end{array} $ | (12) |
式中:CCw为溶质的居里常数,θ为维斯常数;对于纯水,W0= 0.999 65,W1 = 2.043 8×10-4,W2 = -6.174 4×10-7;对于MnCl2,A = 0.102 2,B = 4.966×10-4,C= -1.307×10-5,D= -3.659×10-3,E= -1.631×10-4,F= 4.774×10-6.
式(8)中涉及的参数均转换为相互独立的参数,式(8)的综合误差为
| $ \begin{array}{l} {\rm{ \mathsf{ δ} }}{\rho _{\rm{s}}} = \left[ {{{\left( {\frac{{{\rm{ \mathsf{ δ} }}{\rho _{\rm{s}}}}}{{{\rm{ \mathsf{ δ} }}t}}{\rm{ \mathsf{ δ} }}t} \right)}^2} + {{\left( {\frac{{{\rm{ \mathsf{ δ} }}{\rho _{\rm{s}}}}}{{{\rm{ \mathsf{ δ} }}c}}{\rm{ \mathsf{ δ} }}c} \right)}^2} + {{\left( {\frac{{{\rm{ \mathsf{ δ} }}{\rho _{\rm{s}}}}}{{{\rm{ \mathsf{ δ} }}{{\rm{ \mathsf{ χ} }}_{\rm{s}}}}}{{\rm{ \mathsf{ χ} }}_{\rm{s}}}} \right)}^2} + {{\left( {\frac{{{\rm{ \mathsf{ δ} }}{\rho _{\rm{s}}}}}{{{\rm{ \mathsf{ δ} }}l}}{\rm{ \mathsf{ δ} }}l} \right)}^2} + } \right.\\ \;\;\;\;\;\;\;{\left. {{{\left( {\frac{{{\rm{ \mathsf{ δ} }}{\rho _{\rm{s}}}}}{{{\rm{ \mathsf{ δ} }}d}}{\rm{ \mathsf{ δ} }}d} \right)}^2} + {{\left( {\frac{{{\rm{ \mathsf{ δ} }}{\rho _{\rm{s}}}}}{{{\rm{ \mathsf{ δ} }}H}}{\rm{ \mathsf{ δ} }}H} \right)}^2} + {{\left( {\frac{{{\rm{ \mathsf{ δ} }}{\rho _{\rm{s}}}}}{{{\rm{ \mathsf{ δ} }}{B_0}}}{\rm{ \mathsf{ δ} }}{B_0}} \right)}^2}} \right]^{1/2}}. \end{array} $ | (13) |
在磁悬浮密度测量实验中,7个参数的测量误差分别为δt=±1 ℃, δc=±0.002 mol/L,δχs=±10×10-6, δl=±0.15 mm,δd=±0.5 mm,δH=±0.5 mm,δB0=±0.005 T.通过计算,这7个参数对铜球、铝球和玻璃球实验结果造成的总误差分别为:±0.54、±0.09、±0.08 g/cm3.如式(8a)所示,物体密度与横向悬浮位移的倒数呈正比关系;随着被测样品密度的增加,横向悬浮位移随之减小,横向悬浮位移的微小误差将被大幅放大.
3 结语针对现有磁悬浮方法密度测量范围很难超过2.3 g/cm3的瓶颈难题,提出新型抗磁性高密度物质的磁悬浮密度测量方法.该方法首先仿真出磁悬浮装置中心线上的磁感应强度分布,推导出样品横向悬浮位移与样品密度的关系函数,通过横向悬浮位移计算样品密度.实验结果表明:采用所提方法能够测量传统磁悬浮装置无法悬浮的高密度物质(如铜、铝和玻璃等)的密度.同时,本文方法无须检测样品的体积,与比重瓶法相比,具有更高的重复测量精度,特别是针对小尺寸样品.此外,由于物体密度与横向悬浮位移的倒数呈正比关系,随着样品密度的增加,本文方法的测量偏差范围呈现增大趋势.本文方法在扩大测量范围的同时,保证了操作流程简单、设备便宜,同时具有较高的精度,使得磁悬浮密度测量方法得到了极大的扩充,在密度检测方面具有广阔的应用前景.
| [1] |
DUNNE P A, HILTON J, COEY J M D. Levitation in paramagnetic liquids[J]. Journal of Magnetism and Magnetic Materials, 2007, 316(2): 273-276. DOI:10.1016/j.jmmm.2007.02.128 |
| [2] |
IKEZOE Y, HIROTA N, NAKAGAWA J, et al. Making water levitate[J]. Nature, 1998, 393(6687): 749-750. DOI:10.1038/31619 |
| [3] |
HIROTA N, KURASHIGE M, IWASAKA M, et al. Magneto-Archimedes separation and its application to the separation of biological materials[J]. Physica B-Condensed Matter, 2004, 346: 267-271. |
| [4] |
YOKOYAMA K, HIROTA N, IWASAKA M. Separation of collagen by magneto-Archimedes levitation[J]. IEEE Transactions on Applied Superconductivity, 2007, 17(2): 2181-2184. DOI:10.1109/TASC.2007.897197 |
| [5] |
HIROTA N, CHIBA H, OKADA H, et al. Separation of a mixture of particles into its individual components with the aid of the magneto-Archimedes separation[J]. Journal of Magnetism and Magnetic Materials, 2015, 380: 186-190. DOI:10.1016/j.jmmm.2014.11.007 |
| [6] |
曹建平, 尹大川, 骞爱荣, 等. 抗磁性物质磁悬浮方法在空间生物学与生物技术中的应用[J]. 空间科学学报, 2011, 31(01): 63-72. CAO Jian-ping, YIN Da-chuan, QIAN Ai-rong, et al. Application of magnetic levitation of diamagnetic materials for space biology and biotechnology[J]. Chinese Journal of Space Science, 2011, 31(01): 63-72. |
| [7] |
张大羽, 杨宪园, 商澎. 超导磁体大梯度强磁场中抗磁性物质表观重力分析[J]. 北京生物医学工程, 2013, 32(05): 441-448. ZHANG Da-yu, YANG Xian-yuan, SHANG Peng. Analysis on simulated gravity of diamagnetic substance in large gradient high magnetic field based on superconducting magnet[J]. Beijing Biomedical Engineering, 2013, 32(05): 441-448. DOI:10.3969/j.issn.1002-3208.2013.05.01 |
| [8] |
MIRICA K A, SHEVKOPLYAS S S, PHILLIPS S T, et al. Measuring densities of solids and liquids using magnetic levitation:fundamentals[J]. Journal of the American Chemical Society, 2009, 131(29): 10049-10058. DOI:10.1021/ja900920s |
| [9] |
ANDO T, HIROTA T, MAIE M. Development of recovery device for particulates in fluid by magneto-Archimedes separation[J]. Separation and Purification Technology, 2015, 149: 197-207. DOI:10.1016/j.seppur.2015.04.041 |
| [10] |
MIRICA K A, PHILLIPS S T, MACE C R, et al. Magnetic levitation in the analysis of foods and water[J]. Journal of Agricultural and Food Chemistry, 2010, 58(11): 6565-6569. DOI:10.1021/jf100377n |
| [11] |
NEMIROSKI A, KUMAR A A, SOH S, et al. High-sensitivity measurement of density by magnetic levitation[J]. Analytical Chemistry, 2016, 88(5): 2666-2674. DOI:10.1021/acs.analchem.5b03918 |
| [12] |
LOCKETT M R, MIRICA K A, MACE C R, et al. Analyzing forensic evidence based on density with magnetic levitation[J]. Journal of Forensic Sciences, 2013, 58(1): 40-45. DOI:10.1111/jfo.2013.58.issue-1 |
| [13] |
SUBRAMANIAM A B, YANG D, YU H D, et al. Noncontact orientation of objects in three-dimensional space using magnetic levitation[J]. Proceedings of the National Academy of Sciences of the United States of America, 2014, 111(36): 12980-12985. DOI:10.1073/pnas.1408705111 |
| [14] |
MIRICA K A, ILIEVSKI F, ELLERBEE A K, et al. Using magnetic levitation for three dimensional self-assembly[J]. Advanced Materials, 2011, 23(36): 4134-4140. DOI:10.1002/adma.201101917 |
| [15] |
MIRICA K A, PHILLIPS S T, SHEVKOPLYAS S S, et al. Using magnetic levitation to distinguish atomic-level differences in chemical composition of polymers, and to monitor chemical reactions on solid supports[J]. Journal of the American Chemical Society, 2008, 130(52): 17678-17680. DOI:10.1021/ja8074727 |
| [16] |
HENNEK J W, NEMIROSKI A, SUBRAMANIAM A B, et al. Using magnetic levitation for non-destructive quality control of plastic parts[J]. Advanced Materials, 2015, 27(9): 1587-1592. DOI:10.1002/adma.201405207 |
| [17] |
BWAMBOK D K, THUO M M, ATKINSON M B J, et al. Paramagnetic ionic liquids for measurements of density using magnetic levitation[J]. Analytical Chemistry, 2013, 85(17): 8442-8447. DOI:10.1021/ac401899u |
| [18] |
赵朋, 颉俊, 傅建中, 等. 塑料光学透镜的磁悬浮检测[J]. 光学精密工程, 2016, 24(4): 756-763. ZHAO Peng, XIE Jun, FU Jian-zhong, et al. Magnetic levitation detection for plastic optical lenses[J]. Optics and Precision Engineering, 2016, 24(4): 756-763. |
| [19] |
XIE Jun, ZHAO Peng, ZHANG Cheng-qian, et al. Measuring densities of polymers by magneto-Archimedes levitation[J]. Polymer Testing, 2016, 56: 308-313. DOI:10.1016/j.polymertesting.2016.10.032 |
| [20] |
NEMIROSKI A, SOH S, KWOK S W, et al. Tilted magnetic levitation enables measurement of the complete range of densities of materials with low magnetic permeability[J]. Journal of the American Chemical Society, 2016, 138(4): 1252-1257. DOI:10.1021/jacs.5b10936 |



