多裂纹脆性断裂问题一直是相关工程关注的重点,也是计算力学研究的难点.工程材料和结构内部往往包含如节理、断层等软弱结构面以及一系列微裂纹,在外载作用下产生宏观裂缝,进一步出现裂缝的扩展、交汇、贯通,最终导致结构破坏.为了探究脆性多裂纹扩展规律,国内外学者对典型多裂纹脆性板的破坏过程进行了大量的试验研究和数值模拟.Wong等[1]对含预置裂纹板受单轴压缩荷载作用下的破坏过程进行试验研究,分析了不同的预置裂纹布置方案对于裂纹扩展形式的影响.石路杨等[2]运用扩展有限元法分析裂纹间的相互作用,模拟了多条裂纹的扩展和交汇过程.刘丰等[3]采用基于移动最小二乘插值的数值流形法对多个经典的多裂纹扩展问题进行分析.Budyn等[4]运用扩展有限元法模拟了单轴拉伸荷载作用下多裂纹板的裂纹扩展过程.
近年来,基于非局部思想提出的近场动力学(peridynamics,PD)理论[5]以其在分析不连续力学问题方面的突出优势成为国际计算力学和相关工程领域的研究热点,在国内也受到越来越多的关注[6].刘肃肃等[7]基于态型PD理论对复合材料的材料非线性行为进行模拟分析.Zhou等[8-9]将PD方法引入到岩石材料的破坏分析中,模拟了含单裂纹、多裂纹板在单轴拉压作用下的裂纹扩展过程,与试验结果吻合较好.Gerstle等[10-13]运用PD方法对脆性材料混凝土构件的冲击破坏、失稳等问题进行分析.沈峰等[14-16]基于常规PD模型模拟了混凝土板的拉压和冲击破坏过程.然而,在已有的材料脆性断裂分析中,大部分依然采用常规的单参数微弹脆性(prototype microelastic brittle, PMB)PD本构模型[17],所能模拟的材料泊松比只能为固定值,且定量计算精度不高.为了解决这一问题,Gerstle等[11]尝试增加物质点对的转动自由度以突破常规模型的泊松比限制.Huang等[18-19]则引入能够反映物质点间非局部长程力尺寸效应的核函数修正项以提高PD方法的定量计算精度.
本文在现有研究基础上,提出能够同时考虑非局部长程力尺寸效应和物质点对转动自由度的PD模型,并构建相应的算法体系.通过方板变形定量分析确定最佳核函数修正项和近场尺寸.通过双裂纹巴西圆盘和多裂纹板的破坏过程模拟验证所提出的模型和算法.分组模拟单轴拉伸荷载作用下双裂纹板的破坏过程,并分析初始裂纹分布对结构破坏形式和承载能力的影响.
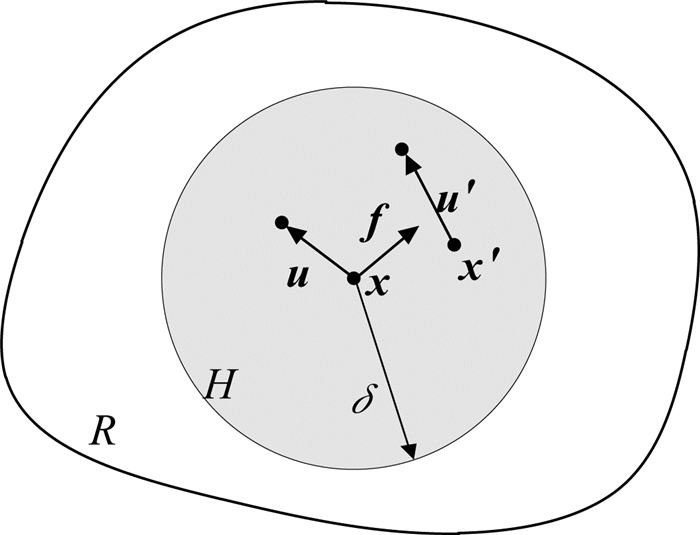
1 PD模型和算法 1.1 PD思想与模型如图 1所示,在任一时刻t,考虑某一空间域R内部任意物质点x与其一定范围H(近场范围,半径为δ的球域)内另一任意物质点x′存在单位体积相互作用力(点对力,本构力):
| $ \mathit{\boldsymbol{f}} = \mathit{\boldsymbol{f}}\left( {\mathit{\boldsymbol{u'}} - \mathit{\boldsymbol{u}}, \mathit{\boldsymbol{x'}} - \mathit{\boldsymbol{x}}, t} \right) = \mathit{\boldsymbol{f}}\left( {\mathit{\boldsymbol{\eta }}, \mathit{\boldsymbol{\xi }}, t} \right). $ |
|
图 1 物质点间的相互作用 Fig. 1 Interaction of material points |
式中:u、u′、x、x′分别表示两物质点的位移和位置,η、ξ表示两物质点的相对位移和相对位置.由此可以采用积分方程对物质点x处的内力密度进行描述,针对无记忆均质材料:
| $ \mathit{\boldsymbol{L}} = \int_H {\mathit{\boldsymbol{f}}\left( {\mathit{\boldsymbol{\eta }}, \mathit{\boldsymbol{\xi }}} \right)\;{\rm{d}}\mathit{V}'} . $ | (1) |
若将物质点对(键)看作中心弹簧的铰接杆单元,可得本构力表达形式为
| $ \mathit{\boldsymbol{f}}\left( {\mathit{\boldsymbol{\eta }}, \mathit{\boldsymbol{\xi }}} \right) = \frac{{\left( {\mathit{\boldsymbol{\xi }} + \mathit{\boldsymbol{\eta }}} \right)}}{{\left| {\mathit{\boldsymbol{\xi }} + \mathit{\boldsymbol{\eta }}} \right|}}\mathit{\boldsymbol{f}}\left( {\mathit{\boldsymbol{\eta }}, \mathit{\boldsymbol{\xi }}} \right) = \frac{{\left( {\mathit{\boldsymbol{\xi }} + \mathit{\boldsymbol{\eta }}} \right)}}{{\left| {\mathit{\boldsymbol{\xi }} + \mathit{\boldsymbol{\eta }}} \right|}}c\left( \xi \right)s. $ | (2) |
式中:c(ξ)称为物质点对(键)的拉伸微模量系数,表征物质点对的拉伸刚度,s=|ξ+η|/|ξ|-1,为物质点对(键)的伸长率.对于均匀各向同性材料且不考虑长程力尺寸效应时,物质点对的拉伸微模量系数c(ξ)=c,为常数.若令|ξ|=ξ,|η|=η,根据小变形假设可得η=sξ,类似于弹簧弹性变形能计算,则物质点对的弹性变形能(点对势能密度):
| $ \omega = f\eta /2 = c{s^2}\xi /2, $ |
由此任一物质点x的点对势能为
| $ \mathit{W} = \frac{1}{2}\int_H {\omega {\rm{d}}\mathit{V'}\mathit{.}} $ | (3) |
通过将物质点的点对势能与传统应变能进行等效,可以求得用传统力学参数描述的拉伸微模量系数c,针对本文所求解的平面应力问题可得
| $ c = \frac{{6E}}{{\pi {\delta ^3}\left( {1 - \nu } \right)}}, \;\;\nu = \frac{1}{3}. $ | (4) |
式中:E为材料宏观弹性模量,ν为泊松比.需要注意,此时泊松比被限制为1/3,对于各向同性的均匀材料,其平面和空间问题的力学属性描述往往需要使用E和ν两个维度,然而本模型仅考虑物质点对的法向作用,因此所得模型必然只有单一维度,表明泊松比限制存在的合理性,此模型即为经典的PMB[17]本构模型.
若考虑长程力的尺寸效应,引入Huang等[18-19]所提出的核函数修正项:
| $ \mathit{g}\left( \xi \right) = {\left( {1 - {\xi ^2}/{\delta ^2}} \right)^2}, $ |
此时拉伸微模量系数将被修正为c(ξ)=c(0, δ)g(ξ),当g(ξ)=1时,模型退化为PMB本构模型.针对平面应力问题,通过类似的能量等效可得
| $ c\left( {0, \delta } \right) = \frac{{105E}}{{4\pi {\delta ^3}\left( {1 - \nu } \right)}}, \;\nu = \frac{1}{3}. $ | (5) |
文献[18]曾定量验证引入核函数修正的PD本构模型具有更高的定量计算精度,但是该模型同样没有突破PMB本构模型中的泊松比限制.Gerstle等[10]将物质点对(键)的作用看作类似有限元中的欧拉梁单元,增加物质点对的弯曲约束,补充描述材料力学属性的另一个维度,得到双参数描述的PD微极模型.其本构力的修正表达形式为
| $ \mathit{\boldsymbol{f}}\left( {\mathit{\boldsymbol{\eta }}, \mathit{\boldsymbol{\xi }}} \right) = \mathit{\boldsymbol{D}}\left( \mathit{\boldsymbol{\xi }} \right) \cdot \mathit{\boldsymbol{\eta }}. $ | (6) |
式中:D(ξ)为PD微弹性矩阵,针对本文所求解的平面应力问题可得(详细推导见文献[10])
| $ \mathit{\boldsymbol{D}}\left( \mathit{\boldsymbol{\xi }} \right) = \left[{\begin{array}{*{20}{c}} {\frac{{c\left( \xi \right)}}{\xi }}&0\\ 0&{\frac{{12d\left( \xi \right)}}{{{\xi ^3}}}} \end{array}} \right]. $ | (7) |
其中d(ξ)=d(0, δ)g(ξ)为物质点对的弯曲微模量系数,对于均匀各向同性材料且不考虑长程力尺寸效应时,物质点对的拉伸、弯曲微模量系数均为常数,即c(ξ)=c、d(ξ)=d.此时点对势能密度
| $ \omega = \mathit{\boldsymbol{\eta }} \cdot \mathit{\boldsymbol{f}}/2 = \mathit{\boldsymbol{\eta }} \cdot \mathit{\boldsymbol{D}}\left( \mathit{\boldsymbol{\xi }} \right) \cdot \mathit{\boldsymbol{\eta }}/2. $ |
通过式(3)可得物质点的点对势能,进一步通过能量等效得到PD微极模型[10]中的2个微模量系数.若令ν=1/3,则d=0,模型退化为PMB本构模型[17]:
| $ \begin{array}{l} c = \frac{{6E}}{{\pi {\delta ^3}\left( {1 - \nu } \right)}}, \;\;d = \frac{{E\left( {1 - 3\nu } \right)}}{{6\pi \delta \left( {1 - {\nu ^2}} \right)}}, \;\;\\ \;\;\;\;\;\;\nu = \left( {\frac{1}{3} - \frac{{12d}}{{c{\delta ^2}}}} \right)/\left( {1 + \frac{{12d}}{{c{\delta ^2}}}} \right). \end{array} $ | (8) |
本文基于文献[10, 17-19]的研究,提出可以反映长程力尺寸效应的PD微极模型,引入满足式(9)的不同类型核函数修正项(式中Δ(ξ)为Dirac Delta函数),包括线形g1、多项式型g2和余弦型g3,推导相应的PD微模量表达式,如表 1所示.
| $ \left. \begin{array}{l} g\left( \xi \right) = g\left( { - \xi } \right), \\ \mathop {\lim }\limits_{\xi \to 0} g\left( \xi \right) = {\rm{max}}\ g\left( \xi \right), \;\;\mathop {\lim }\limits_{\xi \to 0} g\left( \xi \right) = 0, \\ \int_{ - \infty }^\infty {\mathop {\lim }\limits_{\xi \to 0} g\left( \xi \right)} = \int_{ - \infty }^\infty {\mathit{\Delta }\left( \xi \right){\rm{d}}\mathit{x} = 1} . \end{array} \right\} $ | (9) |
| 表 1 几类核函数及其PD微模量 Table 1 Various kernel functions and corresponding PD micromodulus |
本文采用与文献[19]相同的方式基于统计思想对损伤进行定义:
| $ \varphi \left( {x, t} \right) = 1 - \frac{{\int_H {\mu \left( {x, \xi, t} \right){\rm{d}}\mathit{V'}} }}{{\int_H {{\rm{d}}\mathit{V'}} }}. $ | (10) |
式中:μ为反映物质点对(键)断裂与否的间断函数,
| $ \mu = \left\{ \begin{array}{l} 1, \ 0 < s < {s_{{\rm{t0}}}}或0 > s > {s_{{\rm{c0}}}};\\ 0, \ 其他. \end{array} \right. $ | (11) |
其中,st0和sc0分别为物质点对的拉伸、压缩临界伸长率. Silling[17]、Gerstle[11]分别通过传统断裂参数以及材料宏观抗拉、压强度对此进行定义,本文采用后者进行计算:
| $ \left. \begin{array}{l} {s_{t0}} = \frac{{{f_{\rm{t}}}}}{E}, \;\;\;s > 0;\\ {s_{c0}} = - \frac{{{f_{\rm{c}}}}}{E}, \;\;\;s < 0. \end{array} \right\} $ | (12) |
其中,ft、fc分别为材料的宏观抗拉、压强度.
1.3 PD求解体系针对本文所研究的准静力问题,按文献[18]的求解思路,在物质点运动方程中引入人工阻尼加速收敛获得静力解:
| $ \rho \cdot {{\mathit{\boldsymbol{\ddot u}}}_\mathit{i}} + C \cdot {{\mathit{\boldsymbol{\dot u}}}_i} = {\mathit{\boldsymbol{L}}_i} + {\mathit{\boldsymbol{b}}_i}. $ | (13) |
式中:ρ为密度,C为人工阻尼,bi为外力密度.采用显式中心差分格式对时间序列进行均匀离散并带入式(13)可得迭代公式:
| $ \mathit{\boldsymbol{\dot u}}_i^{(t + \Delta t/2)} = \frac{{\left( {{\mathit{\boldsymbol{L}}_i} + {\mathit{\boldsymbol{b}}_i}} \right) + \left( {\frac{\rho }{{\Delta t}} - \frac{C}{2}} \right)\mathit{\boldsymbol{\dot u}}_i^{(t - \Delta t/2)}}}{{\frac{\rho }{{\Delta t}} + \frac{C}{2}}}. $ | (14) |
通过引用文献[18]中的时间迭代步长公式及收敛准则即可构建完备的PD求解体系,能够以统一的模型和算法模拟材料由弹性变形到脆性破坏的全过程,不需引入特殊的裂尖增强或奇异性处理技术,这是近场动力学方法处理破坏问题的独特优势.
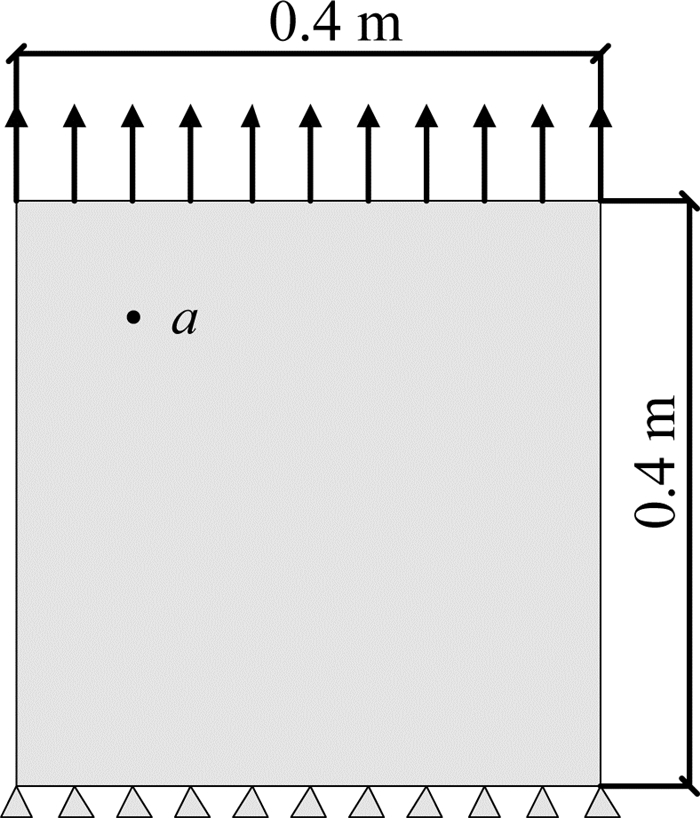
2 模型验证与分析 2.1 计算精度与求解稳定性验证在PD求解体系中,近场尺寸决定模型的计算精度和效率,本节通过对方板变形进行定量计算并与有限元结果比较,验证提出模型的定量计算精度和求解稳定性,进一步对近场尺寸的选取展开分析.取一边固定一边受均布拉伸荷载作用的方板进行分析,如图 2所示,方板边长为0.4 m,均匀离散间距Δx=0.002 m,均布荷载大小为0.25 MPa,按平面应力问题处理,材料参数如下:E=3×104 MPa,ν=0.2,ρ=2 400 kg/m3.为便于定量比较分析减小边界软化影响,记方板内部一点a(距左上角点竖直、水平0.08 m)为观测点,计算不同核函数和不同近场尺寸δ/Δx作用下方板的竖向位移.
|
图 2 方板受拉模型 Fig. 2 Square plate model under tension |
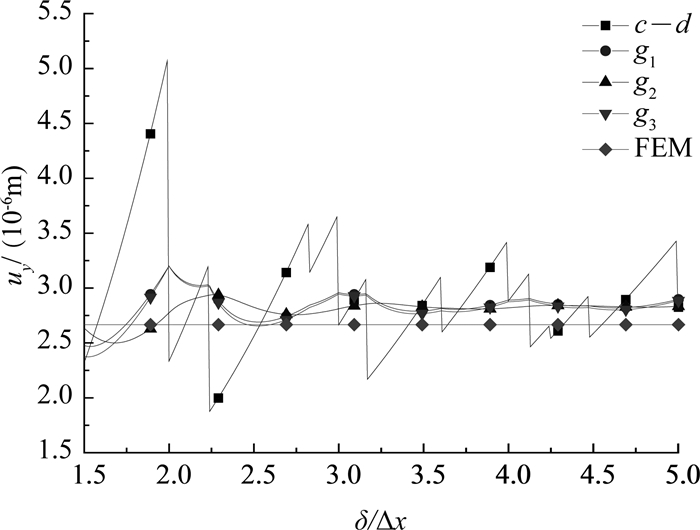
如图 3所示为不同核函数作用下观测点a的竖向位移uy随近场尺寸δ/Δx的变化曲线,无核函数作用时,计算结果会随着近场尺寸的变化而产生突变,当近场尺寸δ/Δx≈3时,PD方法的计算精度较高,证明文献[17]所选近场范围的准确性.当引入本文所提出的核函数修正项时,计算结果会随着近场尺寸增大而趋于稳定,且不产生突变,表明引入核函数可提高求解稳定性.由于本文引入动态松弛算法,收敛参数的选取会导致本文结果与较为精确的有限元解间存在稳定误差,随着近场尺寸δ/Δx的增大,误差保持不变.观察发现采用核函数g2修正的结果在δ/Δx>2.5时已趋于稳定,因此本文以下计算选择近场尺寸δ/Δx=2.5,核函数g2进行.对于本文所研究的平面应力问题,计算效率将提升25%,且不降低计算精度.
|
图 3 不同核函数作用下测量点的竖直位移 Fig. 3 Vertical displacement of measuring point with different kernel functions |
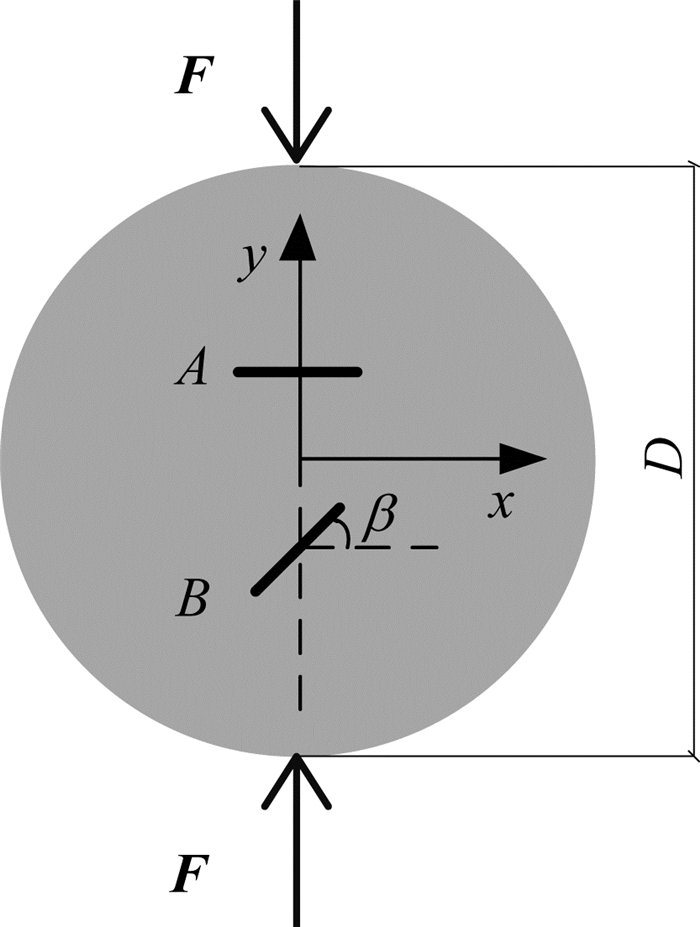
为了验证提出的模型和方法模拟脆性多裂纹扩展问题的可靠性,对文献[20]中进行的双裂纹巴西圆盘劈裂破坏试验进行数值模拟,如图 4所示,模型尺寸和材料参数与文献[20]一致.保持A裂纹不变,B裂纹倾角β (与水平方向夹角)分别取0°、30°、60°和90°进行数值模拟.
|
图 4 双裂纹巴西圆盘模型 Fig. 4 Brazilian disk model with double cracks |
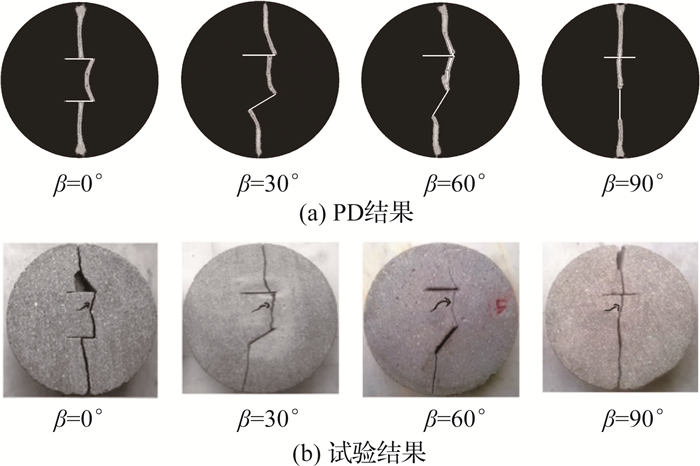
如图 5所示分别为PD模拟和试验所得圆盘最终破坏形式,4种初始裂纹布置下两者皆吻合较好,表明本文提出的PD模型和方法可以准确模拟脆性裂纹的扩展、交汇及贯通过程.
|
图 5 巴西圆盘的最终破坏形式 Fig. 5 Ultimate failure modes of Brazilian disk |
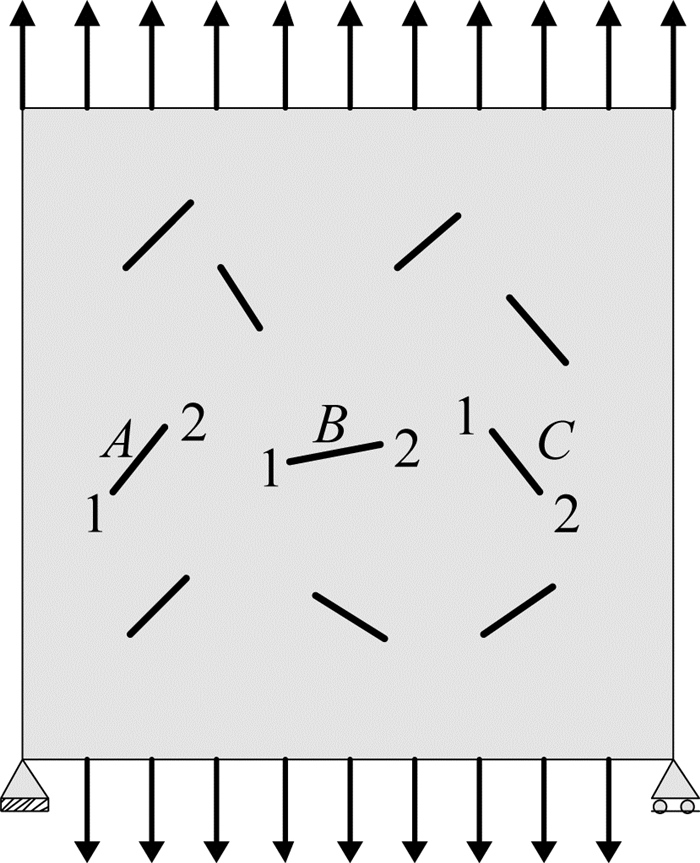
进一步采用本文方法对复杂多裂纹扩展问题进行建模分析.如图 6所示为含10条随机裂纹板受拉模型,该算例最早由Budyn等[4]采用扩展有限元法进行分析,徐栋栋等[21]采用数值流形法进行模拟.为便于比较分析,本文模型和材料参数与文献[21]一致.
|
图 6 含10条随机裂纹板模型 Fig. 6 Plate model with ten random cracks |
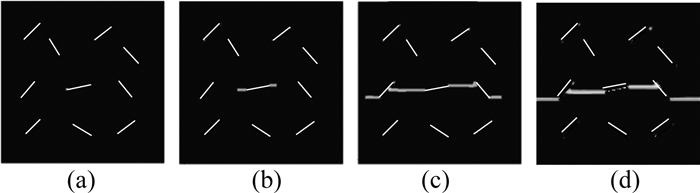
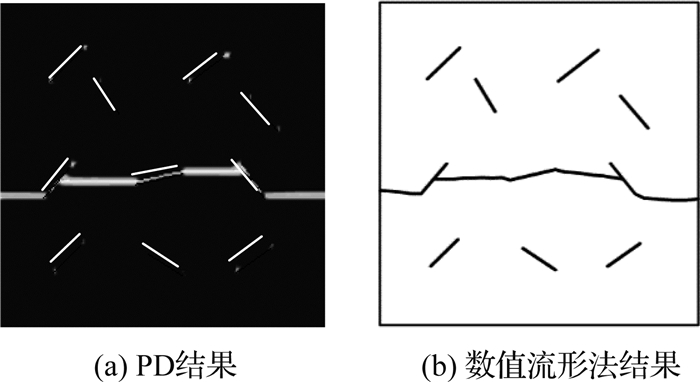
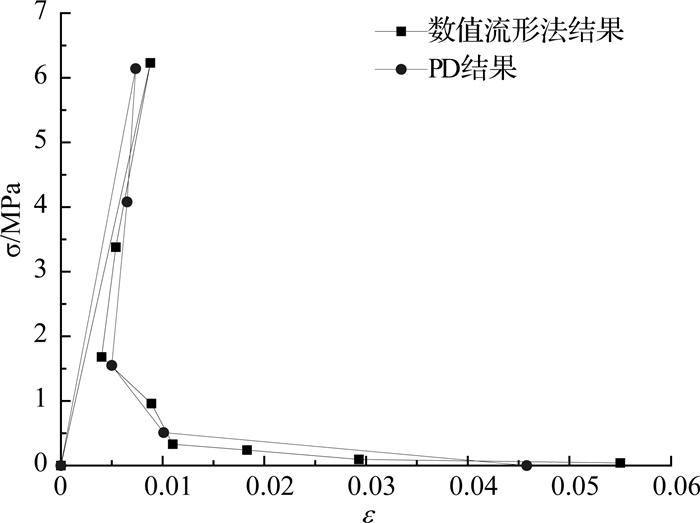
如图 7所示为本文PD方法模拟所得裂纹扩展过程,具体表现为,预置裂纹B率先发生扩展,进而与A、C两条预置裂纹发生交汇,最后形成贯通裂缝导致结构破坏.这一破坏过程与文献[21]中的描述一致.如图 8、9所示分别为本文模拟所得和文献[21]中的最终破坏形式与名义应力-名义应变(σ-ε)曲线,两者基本吻合.表明本文提出的PD模型和方法可以定性、定量模拟复杂多裂纹扩展全过程.
|
图 7 含10条随机裂纹板的裂纹扩展过程 Fig. 7 Crack propagation process of plate with ten random cracks |
|
图 8 含10条随机裂纹板的最终破坏形式 Fig. 8 Failure mode of plate with ten random cracks |
|
图 9 名义应力名义应变曲线 Fig. 9 Nominal stress-nominal strain curves |
如图 10所示为包含A、B两条裂纹的方板受拉模型,其模型尺寸和材料参数如下:方板边长d=0.05 m,E=690 MPa,ν=0.3,ρ=2 400 kg/m3,抗拉强度ft=20 MPa,抗压强度fc=150 MPa.保持A裂纹不变(A裂纹长度为0.01 m),改变B裂纹的长度l、位置h和初始倾角α进行模拟,探究不同初始裂纹布置对方板破坏形式和承载能力的影响.(分别取l/d=0.2、0.4,h/d=0、0.1、0.2,α=0°、45°、90°).

|
图 10 双裂纹方板受单轴拉伸作用 Fig. 10 Square plate with two cracks under uniaxial tension |
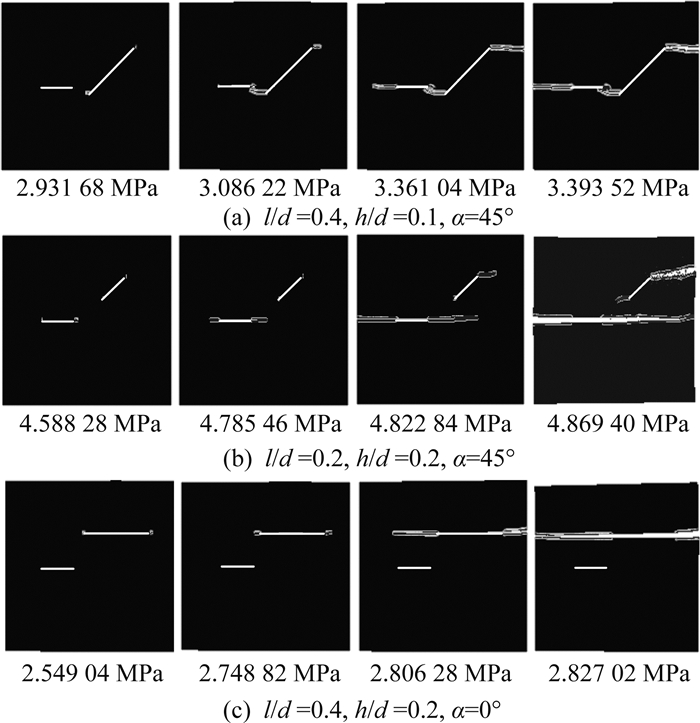
在不同的初始裂纹布置下主要存在3种破坏形式,分别如图 11所示:1) 2条裂纹先交汇形成长裂纹,进一步发生扩展形成贯通裂纹;2)单一裂纹扩展贯通,另一裂纹发生扩展,但未形成贯通裂纹;3)单一裂纹发生扩展贯通,另一裂纹未扩展.当h/d= 0、0.1时,结构破坏形式普遍为1)类,此时B裂纹位置为影响结构最终破坏形式的主要因素.当h/d=0.2时,结构破坏形式为第1)~3)类,B裂纹长度和角度均会影响结构的最终破坏形式.
|
图 11 不同初始裂纹方板破坏形式 Fig. 11 Failure mode of square plate with different initial cracks |
在不同h、l、α布置下,结构的起裂荷载σi和破坏荷载σu如表 2所示.相较于单A裂纹情况(l/d=0),B裂纹的存在会降低结构的承载能力,且不同B裂纹布置下结构的承载能力有明显差异.当h、l一定时,结构的承载能力随着α的增大而提升,当α=90°时,几种裂纹布置下结构的承载能力基本相同,仅略小于单裂纹情况,此时B裂纹的长度和位置几乎不会影响结构的承载能力;当α≠90°,结构的承载能力随着B裂纹长度的增加而明显减小,B裂纹长度为影响结构破坏荷载的主要因素.在本文研究中,α=0°时,结构的承载能力随着裂纹位置h的增大而提高,α=45°时,B裂纹位置对结构承载能力影响无明显规律.
| 表 2 方板的起裂荷载和破坏荷载 Table 2 Crack load and failure load of square plate |
(1) 本文在常规PMB近场动力学本构模型基础上构建的改进型PD模型可以消除原模型的泊松比限制,保证定量计算精度和求解稳定性,提高计算效率.同时通过方板变形定量计算,确定了最优核函数修正项和近场范围尺寸.
(2) 对含双裂纹巴西圆盘劈裂破坏过程和含10条随机裂纹板的受拉破坏过程进行数值模拟,所得裂纹扩展路径、最终破坏形式和名义应力-名义应变曲线等数值结果与已有结果吻合较好,表明本文的改进型PD模型和数值方法可以定性、定量分析脆性多裂纹扩展问题,为脆性多裂纹扩展问题的准确分析开辟了新的思路.
(3) 应用改进型PD方法分析了不同初始裂纹布置对双裂纹脆性方板受单轴拉伸荷载作用下破坏形式和承载能力的影响规律.结果表明:当h/d≤0.1时,B裂纹位置为影响结构破坏形式的主要因素;当h/d=0.2时,B裂纹的长度和角度均会影响结构的最终破坏形式.当h、l一定时,结构的承载能力随着α的增大而提升,当α=90°时,B裂纹的长度和位置几乎不会影响结构的承载能力;当α≠90°,B裂纹长度越大,结构的承载能力越低;当α=0°时,结构的承载能力随着裂纹位置h的增大而提升.
| [1] |
WONG R H C, CHAU K T, TANG C A, et al. Analysis of crack coalescence in rock-like materials containing three flaws, Part Ⅰ:experimental approach[J]. International Journal of Rock Mechanics & Mining Sciences, 2012, 38(7): 909-924. |
| [2] |
石路杨, 余天堂. 多裂纹扩展的扩展有限元法分析[J]. 岩土力学, 2014, 35(1): 263-272. SHI Lu-yang, YU Tian-tang. Analysis of multiple crack growth using extended finite element method[J]. Rock and Soil Mechanics, 2014, 35(1): 263-272. |
| [3] |
刘丰, 郑宏, 夏开文. 基于MLS的数值流形法模拟多裂纹扩展[J]. 岩石力学与工程学报, 2016, 35(1): 76-86. LIU Feng, ZHENG Hong, XIA Kai-wen. The MLS-based numerical manifold method and its applications to multiple crack propagation[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(1): 76-86. |
| [4] |
BUDYN É, ZI G, MOES N, et al. A method for multiple crack growth in brittle materials without remeshing[J]. International Journal for Numerical Methods in Engineering, 2004, 61(10): 1741-1770. DOI:10.1002/nme.v61:10 |
| [5] |
SILLING S A. Reformulation of elasticity theory for discontinuities and long-range forces[J]. Journal of the Mechanics and Physics of Solids, 2000, 48(1): 175-209. DOI:10.1016/S0022-5096(99)00029-0 |
| [6] |
黄丹, 章青, 乔丕忠, 等. 近场动力学方法及其应用[J]. 力学进展, 2010, 40(4): 448-459. HUANG Dan, ZHANG Qing, QIAO Pi-zhong, et al. A review on peridynamics method and its application[J]. Advance in Mechanics, 2010, 40(4): 448-459. DOI:10.6052/1000-0992-2010-4-J2010-002 |
| [7] |
刘肃肃, 余音. 复材非线性及渐进损伤的态型近场动力学模拟[J]. 浙江大学学报:工学版, 2016, 50(5): 993-1000. LIU Su-su, YU Yin. State-based peridynamic modeling of nonlinear behavior and progressive damage of composites[J]. Journal of Zhejiang University:Engineering Science, 2016, 50(5): 993-1000. |
| [8] |
ZHOU X P, GU X B, WANG Y T. Numerical simulations of propagation, bifurcation and coalescence of cracks in rocks[J]. International Journal of Rock Mechanics & Mining Sciences, 2015, 80: 241-254. |
| [9] |
WANG Y, ZHOU X, XU X. Numerical simulation of propagation and coalescence of flaws in rock materials under compressive loads using the extended non-ordinary state-based peridynamics[J]. Engineering Fracture Mechanics, 2016, 163: 248-273. DOI:10.1016/j.engfracmech.2016.06.013 |
| [10] |
GERSTLE W, SAU N, SILLING S A. Peridynamic modeling of concrete structures[J]. Applied Mechanics and Materials, 2007, 237: 1250-1258. |
| [11] |
GERSTLE W, SAU N, SAKHAVAND N. On peridynamic computational simulation of concrete structures[J]. Aci Special Publication, 2009, 265: 245-264. |
| [12] |
HA Y D, BOBARU F. Characteristics of dynamic brittle fracture captured with peridynamics[J]. Engineering Fracture Mechanics, 2011, 78(6): 1156-1168. DOI:10.1016/j.engfracmech.2010.11.020 |
| [13] |
KILIC B, MADENCI E. Structural stability and failure analysis using peridynamic theory[J]. International Journal of Non-linear Mechanics, 2009, 44: 845-854. DOI:10.1016/j.ijnonlinmec.2009.05.007 |
| [14] |
沈峰, 章青, 黄丹, 等. 基于近场动力学理论的混凝土轴拉破坏过程模拟[J]. 计算力学学报, 2013, 30(增1): 79-83. SHEN Feng, ZHANG Qing, HUANG Dan, et al. Damage and failure process of concrete structure under uni-axialtension based on peridynamics modeling[J]. Chinese Journal of Computational Mechanics, 2013, 30(Suppl. 1): 79-83. |
| [15] |
HUANG D, ZHANG Q, QIAO P Z. Damage and progressive failure of concrete structures using non-local peridynamic modeling[J]. Science China Technological Science, 2011, 54(3): 591-596. DOI:10.1007/s11431-011-4306-3 |
| [16] |
HUANG D, LU G, QIAO P. An improved peridynamic approach for quasistatic elastic deformation and brittle fracture analysis[J]. International Journal of Mechanical Sciences, 2015, 94/95: 111-122. DOI:10.1016/j.ijmecsci.2015.02.018 |
| [17] |
SILLING S A, ASKARI E. A meshfree method based on the peridynamic model of solid mechanics[J]. Computters & Structures, 2005, 83(17/18): 1526-1535. |
| [18] |
HUANG D, LU G, WANG C, et al. An extended peridynamic approach for deformation and fracture analysis[J]. Engineering Fracture Mechanics, 2015, 141: 196-211. DOI:10.1016/j.engfracmech.2015.04.036 |
| [19] |
顾鑫, 章青, 黄丹. 基于近场动力学方法的混凝土板侵彻问题研究[J]. 振动与冲击, 2016, 35(6): 52-58. GU Xin, ZHANG Qing, HUANG Dan. Peridynamics used in solving penetration problem of concrete slabs[J]. Journal of Vibration and Shock, 2016, 35(6): 52-58. |
| [20] |
HAERI H, SHAHRIAR K, MARJI M F, et al. Experimental and numerical study of crack propagation and coalescence in pre-cracked rock-like disks[J]. International Journal of Rock Mechanics & Mining Sciences, 2014, 67(4): 20-28. |
| [21] |
徐栋栋, 郑宏, 杨永涛, 等. 多裂纹扩展的数值流形法[J]. 力学学报, 2015, 47(3): 471-481. XU Dong-dong, ZHENG Hong, YANG Yong-tao, et al. Multiple crack propagation based on the numerical manifold method[J]. Chinese Journal of Theoretical and Applied Mechanics, 2015, 47(3): 471-481. DOI:10.6052/0459-1879-14-347 |



