硬岩隧道掘进机(tunnel boring machine, TBM)是典型的大型隧道掘进装备,适合于我国西部地区的硬岩隧道建设.由于TBM工作埋深大,掘进对象为岩石,需要提供的掘进载荷大,掘进载荷成为TBM设计制造的重要考虑因素.刀盘扭矩是TBM掘进载荷的重要组成部分,预测刀盘扭矩可以指导TBM掘进施工,避免TBM刀盘被卡受困,是掘进参数优化和保证TBM安全高效掘进的重要参考,是实现TBM智能控制和优化决策的前提.
针对TBM刀盘脱困的问题,刘统等[1]提出了基于液压变压器的二次调节系统协同变频电机的刀盘混合驱动方案,从驱动系统方面调节刀盘扭矩,解决脱困扭矩不足和欠负载工作效率低等问题.廖湘平等[2]设计了基于液黏离合器的刀盘驱动方案,提升脱困扭矩来使TBM脱困.以上研究均从TBM刀盘脱困出发,实际上,如果能够预测某一地质条件在设定掘进参数下需要的刀盘扭矩,就能够避免TBM刀盘被卡受困,因此需要进行刀盘载荷的建模和预测.
近年来,围绕刀盘载荷建模及预测的研究主要包括理论建模分析和工程数据分析.在理论建模分析方面,Roxborough等[3-7]应用接触力学和理论力学来分析盘形滚刀与岩石的载荷传递,获得了盘形滚刀载荷的理论公式;周思阳等[8]通过理论建模得到了TBM总推力的预测模型,结合工程实例验证了模型的合理性.在工程数据分析方面,宋克志等[9]对施工现场采集的数据进行多元回归分析,获得了盾构掘进速率与刀盘推力和扭矩的关系;施虎等[10]采用自适应神经模糊推理系统(adaptive network-based fuzzy inference system, ANFIS)分析盾构工程数据,讨论了推力等掘进数据与螺旋输送机转速的关系;Zhang等[11]利用工程数据反演识别载荷模型中的未知参数;Zhang等[12]采用机械解耦的分析方法得到了土压平衡盾构刀盘与掘进面的交互力表达式,并且据此提出了土压平衡盾构总推力的预测模型;Yang等[13]采用基于小波变换的灰色模型对盾构的刀盘载荷特征进行预测,基于此方法设计了刀盘模式控制策略,实现了刀盘驱动系统的能耗优化控制;Salimi等[14]利用人工智能算法预测FPI,对比了支持向量回归(support vector regression, SVR)算法与ANFIS算法,发现在TBM性能预测方面SVR模型优于ANFIS模型.
理论建模分析多为研究TBM单刀受力,由于TBM在掘进过程中刀盘载荷的影响因素的复杂性,理论模型不能完全符合实际掘进过程,预测结果往往具有较大的偏差.在工程数据的分析中,多数学者研究了盾构的刀盘载荷,而利用工程数据分析和预测TBM刀盘载荷的研究相对较少.
本研究结合吉林引松供水工程现场掘进的大量数据,分析TBM刀盘扭矩与掘进参数间的关系,将掘进参数作为输入变量,刀盘扭矩作为输出变量,运用机器学习方法中的非线性支持向量回归(nonlinear support vector regression, NSVR)学习方法建立TBM刀盘扭矩与掘进参数的NSVR预测模型,对预测模型进行评估并得出预测精度.
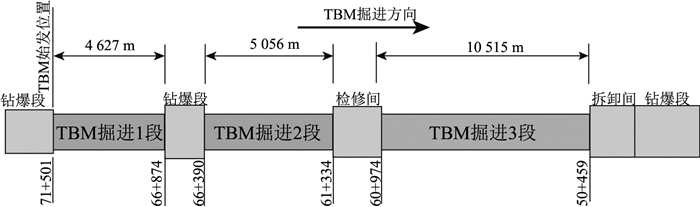
1 吉林引松供水工程 1.1 工程概况为了研究TBM刀盘扭矩与掘进参数和地质条件的关系,选取吉林引松供水工程现场掘进的大量典型数据进行分析.选取该工程的施工四标段(TBM3标),开挖断面为圆形,直径为7.93 m,开挖断面形状和开挖直径均为隧道工程中的常见选择.TBM3标中的TBM工区长度为20 198 m,分为3段:TBM掘进1段(71+501 m~66+874 m),TBM掘进2段(66+390 m~61+334 m),TBM掘进3段(60+974 m~50+459 m).TBM3的总体施工布置如图 1所示.
|
图 1 TBM3施工段总体布置 Fig. 1 Arrangement of TBM3 construction section |
TBM3施工段中采用水利水电HC法对围岩进行分类.本研究的工程数据取自TBM掘进1段和2段中约7.3 km的数据,统计7.3 km数据中各围岩类别里程长度的占比,得到Ⅱ类、Ⅲ类、Ⅳ类和Ⅴ类的占比分别为2.61%、64.94%、24.9%和7.54%.可见,本工程涉及4种围岩类别:Ⅲ类围岩为主要围岩,Ⅳ类围岩为常见围岩,Ⅱ类和Ⅴ类为少类围岩,相对较全面.
1.3 TBM主要技术参数TBM3施工段中采用国内常用的开敞式单对水平支撑TBM,刀盘驱动方式为变频电机驱动,主要技术参数如表 1所示.
| 表 1 TBM主要技术参数 Table 1 Main technical parameters of TBM |
在TBM掘进过程中,TBM操作者主要通过调节TBM刀盘转速和推进速度使得TBM输出不同的刀盘扭矩,从而适应不同的地质条件.在TBM结构参数给定的情况下,假设影响TBM刀盘扭矩的主要参数为表征TBM掘进状态的刀盘转速和推进速度,以及表征TBM所处地质条件的围岩类别.通过已有的7.3 km掘进数据,可以初步研究刀盘扭矩和推进速度、刀盘转速以及围岩类别之间的关系.
2.1 掘进数据预处理由于现场工程数据中存在非工作状态和异常的数据,需要对存储在数据库中的数据进行预处理.首先,从数据库中提取需要的数据,即刀盘扭矩、总推力、刀盘转速、推进速度和桩号.因为围岩类别是TBM掘进后判定,所以不存在于数据库中,需要根据桩号给每条数据记录标定围岩类别.为了去除非工作状态的数据,建立如下二值状态判别函数:
| $ D = \left\{ {\begin{array}{*{20}{c}} {1, }&{工作状态;}\\ {0, }&{停机状态.} \end{array}} \right. $ | (1) |
| $ D = f\left( F \right) \cdot f\left( v \right) \cdot f\left( T \right) \cdot f\left( n \right). $ | (2) |
| $ f\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {1, }&{x \ne 0;}\\ {0, }&{x = 0.} \end{array}} \right. $ | (3) |
式中:F为总推力,v为推进速度,T为刀盘扭矩,n为刀盘转速.
当二值状态判别函数D=0时,该数据记录为TBM非工作状态数据,应予以剔除.去除停机数据后,利用3倍标准差法剔除工作中产生的异常数据,进行刀盘扭矩与刀盘转速、推进速度和围岩类别的线性相关性分析,刀盘扭矩与刀盘转速、推进速度及围岩类别间的相关系数分别为0.61、0.41及-0.23.
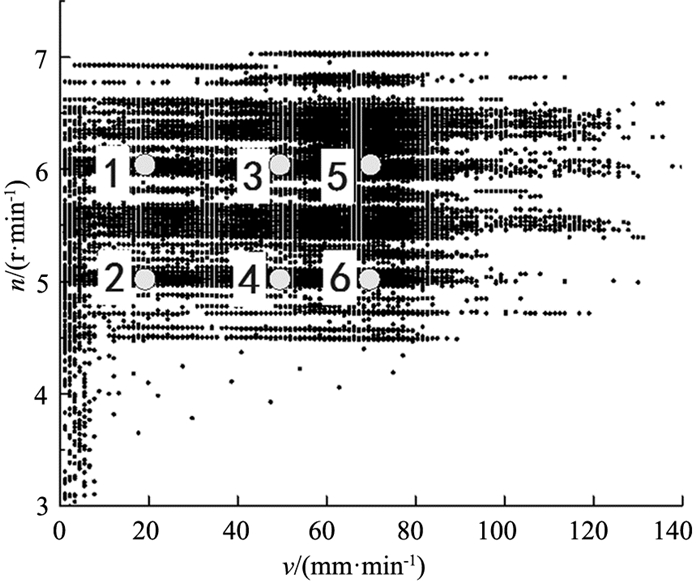
可以看出,刀盘扭矩与刀盘转速呈中度线性相关,与推进速度和围岩类别呈轻度线性相关,由此得出利用线性模型不能准确描述刀盘扭矩与刀盘转速、推进速度和围岩类别的关系.为了进一步确定刀盘扭矩与刀盘转速、推进速度和围岩类别的关系,从去除非工作状态和异常的数据中分别提取各类围岩下的数据,然后从各类围岩的数据中间隔提取不同刀盘转速对应不同推进速度下的特征点集,如图 2所示,1~6号样本点集即为选取的特征点集.
|
图 2 二类围岩的特征点集 Fig. 2 Feature point sets of rock type Ⅱ |
统计提取特征点集的信息如表 2所示,表中Pmin为各类围岩下提取的特征点集包含的样本点的最少数量,Pmax为各类围岩下提取的特征点集包含的样本点的最多数量.从表中可以看出,该工程中包含的刀盘转速范围和推进速度范围均涵盖了隧道掘进中的常见参数设置.特征点集中包含的样本点的数量最少为66个,对应的刀盘转速为6 mm/min,TBM每秒采集一个样本点,即提取的特征点集至少包含了TBM刀盘旋转6转的数据记录.将2.1节中提取的每个特征点集中的样本点的参数作均值化处理,得到在不同围岩下刀盘扭矩、刀盘转速和推进速度的均值点.
| 表 2 分析域的信息 Table 2 Information of analysis domain |
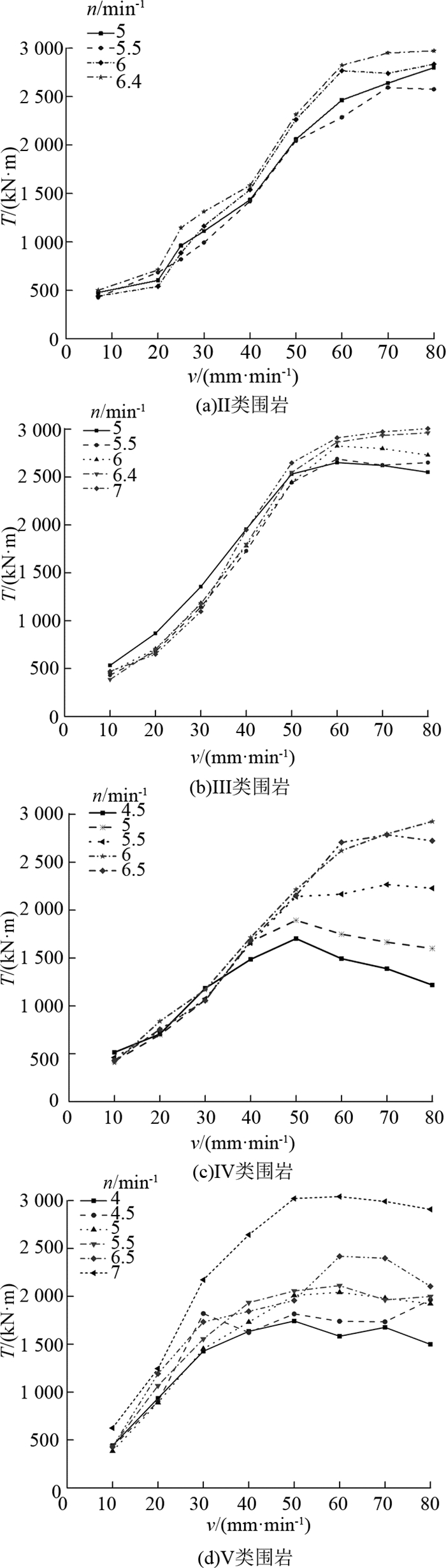
利用均值化后的点,研究刀盘扭矩随推进速度的变化关系,如图 3所示.从图中可知:1)在不同刀盘转速下,刀盘扭矩随着推进速度的增加而增加,当推进速度接近一定值后刀盘扭矩不再明显变化;2)当Ⅱ类、Ⅲ类、Ⅳ类和Ⅴ类围岩的推进速度分别超过约65、55、45和30 mm/min时,刀盘扭矩不再随推进速度明显变化,即随着围岩类别由Ⅱ类变到Ⅴ类,推进速度对刀盘扭矩的影响逐渐变弱;3)在不同的刀盘转速下,围岩类别由Ⅱ类变到Ⅴ类,刀盘扭矩与推进速度曲线间的差异性变大.
|
图 3 Ⅱ~Ⅴ类围岩刀盘扭矩与推进速度的关系 Fig. 3 Relationship between torque and advance speed of rock type Ⅱ to Ⅴ |
利用均值化后的点,研究刀盘扭矩随刀盘转速的变化关系,如图 4所示.从图中可以得出:1)在不同推进速度下,Ⅱ类和Ⅲ类围岩下刀盘扭矩随刀盘转速变化不明显,Ⅳ类和Ⅴ类围岩在推进速度较低时刀盘扭矩随着刀盘转速的变化不明显,但是当推进速度较高时刀盘扭矩随着刀盘转速的增加而增加,即随着围岩类别由Ⅱ类变到Ⅴ类,刀盘转速对刀盘扭矩的影响逐渐变强;2)由图 9和10可以看出,在高推进速度下,刀盘扭矩的值十分接近,即随着围岩类别由Ⅱ类变到Ⅴ类,不同的推进速度下,刀盘扭矩与刀盘转速曲线间的差异性变小,同样说明推进速度对刀盘扭矩的影响逐渐变弱.

|
图 4 Ⅱ~Ⅴ类围岩刀盘扭矩与刀盘转速的关系 Fig. 4 Relationship between torque and rotate speed of rock type Ⅱ to Ⅴ |
综上分析可以得出:刀盘扭矩受到围岩类别、刀盘转速和推进速度的影响.围岩类别由Ⅱ类变到Ⅴ类,推进速度对刀盘扭矩的影响逐渐变弱,刀盘转速对刀盘扭矩的影响逐渐变强.Ⅱ类围岩为硬岩,Ⅴ类围岩为软岩,即在硬岩条件下,TBM刀盘扭矩主要受推进速度影响,在软岩条件下,TBM刀盘扭矩主要受刀盘转速影响.
3 NSVR预测方法从第2章中的分析可知,刀盘扭矩受到推进速度、刀盘转速和围岩类别的影响,但是不能利用线性模型准确描述,尝试运用非线性模型来进行描述具有一定的可行性.因此本文利用NSVR对刀盘扭矩进行建模和预测.作为一种基于统计学理论的机器学习方法,NSVR能够有效地解决样本的非线性和高维度等实际问题.
3.1 NSVRNSVR是支持向量机(SVM)[15-17]在函数回归领域的应用,其解为全局最优解,称为支持向量(SV).利用SV构建的回归函数称为决策函数,可以输出特定实数.对于NSVR,给定训练样本集如下:
| $ S = \left\{ {\left( {{\mathit{\boldsymbol{x}}_1}, {\mathit{\boldsymbol{y}}_1}} \right), \left( {{\mathit{\boldsymbol{x}}_2}, {\mathit{\boldsymbol{y}}_2}} \right), \cdots, \left( {{\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{y}}_i}} \right), \cdots, \left( {{\mathit{\boldsymbol{x}}_n}, {\mathit{\boldsymbol{y}}_n}} \right)} \right\}. $ | (4) |
式中:xi∈Rm,为输入参数向量;yi∈Rd,为输出参数向量;i=1, 2, …, n. n为样本总数,m为输入向量的维度,d为输出向量的维度.
求解如下的最优化问题:
| $ \begin{array}{l} \mathop {\min }\limits_\alpha \frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\left( {{\alpha _i} - {{\alpha '}_i}} \right)\left( {{\alpha _j} - {{\alpha '}_j}} \right)} } k\left( {{\mathit{\boldsymbol{x}}_i}, {\mathit{\boldsymbol{x}}_j}} \right) + \\ \;\;\;\sum\limits_{i = 1}^n {{\alpha _i}\left( {\varepsilon - {\mathit{\boldsymbol{y}}_i}} \right)} + \sum\limits_{i = 1}^n {{{\alpha '}_i}\left( {\varepsilon + {\mathit{\boldsymbol{y}}_i}} \right)}, \\ \;\;\;{\rm{s}}{\rm{.t}}{\rm{.}}\sum\limits_{i = 1}^n {\left( {{\alpha _i} - {{\alpha '}_i}} \right)} = 0, \;\;0 \le {\alpha _i}, {{\alpha '}_i} \le C. \end{array} $ | (5) |
式中:ε为不敏感系数,C为惩罚系数,均为设定值,αi和α′i为引入的拉格朗日乘子,k(xi, xj)为将低维空间映射到高维空间的核函数,本文取高斯径向基核函数,即k(xi, xj)=exp (-γ·‖xi-xj‖),γ为高斯核函数中的系数,为设定值.
解式(5)得到最优解:α=(α1, α2, …, αn)T和α′=(α′1, α′2, …, α′n)T,从而得到用于预测的决策函数:
| $ {{\hat f}^{(\mathit{\boldsymbol{x}})}} = \sum\limits_{{x_i} = {\rm{SV}}} {\left( {{\alpha _i} - {{\alpha '}_i}} \right)k({\mathit{\boldsymbol{x}}_i}, \mathit{\boldsymbol{x}}) + b.} $ | (6) |
式中:b为函数中的偏置.
偏置b由位于不敏感区边界上的样本点确定,这些样本点称为标准支持向量(normal support vector, NSV),一般对所有NSV分别计算b对应的值,然后求其平均:
| $ \begin{array}{l} b = \frac{1}{{{N_{\rm{NSV}}}}}\left\{ {\sum\limits_{0 < {\alpha _i} < C} {\left[{{\mathit{\boldsymbol{y}}_i}-\sum\limits_{{x_j} = {\rm{SV}}} {\left( {{\alpha _j}-{{\alpha '}_j}} \right)k({\mathit{\boldsymbol{x}}_j}, {\mathit{\boldsymbol{x}}_i}) + \varepsilon } } \right]} } \right. + \\ \;\;\;\;\;\left. {\sum\limits_{0 < {{\alpha '}_i} < C} {\left[{{\mathit{y}_i}-\sum\limits_{{x_j} = {\rm{SV}}} {\left( {{\alpha _j}-{{\alpha '}_j}} \right)k({\mathit{\boldsymbol{x}}_j}, {\mathit{\boldsymbol{x}}_i})-\varepsilon } } \right]} } \right\}. \end{array} $ | (7) |
式中:NNSV为标准支持向量的数量.
3.2 序列最小最优化算法上述最优化问题在求解样本容量较大时比较低效,甚至不能使用.为了能够快速求解,引入序列最小最优化(sequential minimal optimization, SMO)算法.SMO算法由Scholkopf等[18-19]提出,该算法要求所有变量的解都满足该优化问题的KKT边界条件,如果违背了KKT条件,就选择其中2个变量并固定其他变量,再求解这2个变量的优化问题.SMO算法将原问题化为多个子问题来迭代求解,从而加快求解速度.
上述最优化问题可以变换为下式:
| $ \begin{array}{l} \mathop {\min }\limits_\beta f\left( \mathit{\boldsymbol{\beta }} \right) = \frac{1}{2}{\mathit{\boldsymbol{\beta }}^{\rm{T}}}K\mathit{\boldsymbol{\beta }} + \left[{\varepsilon {\mathit{\boldsymbol{e}}^{\rm{T}}}-y, \varepsilon {\mathit{\boldsymbol{e}}^{\rm{T}}} + y} \right]\mathit{\boldsymbol{\beta }}, \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;{\mathit{\boldsymbol{\chi }}^{\rm{T}}}\mathit{\boldsymbol{\beta }} = 0, \;{\rm{ }}0 \le {\beta _i} \le C, \;i = 1, \cdots, 2n. \end{array} $ | (8) |
式中:
通过变换,将求解α和α′的最优化问题转换为求解β的最优化问题,其中子问题为选取β的2个变量{βi, βj}的优化问题.
利用SMO算法求解式(8)描述的最优问题:
1) 初始化β1=0,∇f(β)=[εeT-y, εeT+y]T,∇f(β)为f(β)的梯度;
2) 如果βk是式(8)的驻点,即f(β)对βk的梯度∇f(βk)为0,而实际上迭代到0的代价巨大,因此选择最大梯度和最小梯度之差小于一个设定的数,称为停止准则,即如果最大梯度和最小梯度之差小于停止准则,则停止迭代.否则,需要选择2个变量的索引{i, j},来对这2个变量进行更新,使之满足KKT条件,选择依据如下式:
| $ \begin{array}{l} \;\;\;\;\;\;i = \mathop {\max }\limits_m {\rm{ }}\left\{ { - {\chi _m}\nabla f{{\left( {{\mathit{\boldsymbol{\beta }}^k}} \right)}_m}|m \in {S_1}} \right\}, \\ j = \mathop {\min }\limits_m \left\{ {\frac{{ - {\rm{ }}{{\left( { - {\chi _i}\nabla f{{\left( {{\mathit{\boldsymbol{\beta }}^k}} \right)}_i} + {\chi _m}\nabla f{{\left( {{\mathit{\boldsymbol{\beta }}^k}} \right)}_m}} \right)}^2}}}{{{K_{ii}} + {K_{mm}} - 2{K_{im}}}}} \right.|\\ \left. {\;\;\;m \in {S_2}, - {\chi _m}\nabla f{{\left( {\mathit{\boldsymbol{\beta }}{^k}} \right)}_m} < - {\chi _i}\nabla f{{\left( {{\mathit{\boldsymbol{\beta }}^k}} \right)}_m}.} \right\} \end{array} $ | (9) |
式中集合S1和S2表示如下:
| $ \begin{array}{l} {S_1} = \{ m|{\beta _m} < C, \;\;{\chi _m} = 1或{\beta _m} > 0{\rm{ }}, {\rm{ }}{\chi _m} = {\rm{ }} - 1\}, \\ {S_2} = \{ m|{\beta _m} < C, \;\;{\chi _m} = -1 或{\beta _m} > 0{\rm{ }}, {\rm{ }}{\chi _m} = {\rm{ }}1\} . \end{array} $ | (10) |
3) 将找出的索引{i, j}对应的2个变量记录为旧的βoldi, βoldj,然后更新βi, βj:
| $ \begin{array}{l} {\beta _i} = {\rm{ }}{\beta _{{\rm{old}}\mathit{i}}} + {\chi _i}\frac{{{{\left( { - {\chi _i}\nabla f{{\left( {\mathit{\boldsymbol{\beta }}{^k}} \right)}_i} + {\chi _j}\nabla f{{\left( {\mathit{\boldsymbol{\beta }}{^k}} \right)}_j}} \right)}^2}}}{{{K_{ii}} + {K_{jj}} - 2{K_{ij}}}}, \\ {\beta _j} = {\beta _{{\rm{old}}\mathit{j}}} - {\chi _j}\frac{{{{\left( { - {\chi _i}\nabla f{{\left( {\mathit{\boldsymbol{\beta }}{^k}} \right)}_i} + {\chi _j}\nabla f{{\left( {\mathit{\boldsymbol{\beta }}{^k}} \right)}_j}} \right)}^2}}}{{{K_{ii}} + {K_{jj}} - 2{K_{ij}}}}. \end{array} $ | (11) |
4) 在保证βi、βj和为定值的前提下再次更新βi、βj,若βi>C,令βi=C,若βi<0,令βi=0,根据和为定值修改βj值,再对βj判断,若βj>C,令βj=C,若βj<0,令βj=0,然后根据和为定值修改βi的值.
5) 按式(12)更新梯度,回到步骤2).
| $ \begin{array}{l} \nabla f{\left( {{\mathit{\boldsymbol{\beta }}^k}} \right)_m} = \nabla f{\left( {{\mathit{\boldsymbol{\beta }}^k}} \right)_m} + \left[{{K_{mi}}\left( {{\beta _i}-{\beta _{{\rm{old}}\mathit{i}}}} \right) + } \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {{K_{mj}}\left( {{\beta _j}-{\beta _{{\rm{old}}\mathit{j}}}} \right)} \right]. \end{array} $ | (12) |
求得最优化问题(8)的最优解β也就得到了α和α′,用于预测的决策函数同式(6).
4 TBM刀盘扭矩建模与预测 4.1 基于NSVR的TBM刀盘扭矩预测模型将去除非工作状态及异常的数据根据桩号以掘进里程10 cm为单位提取掘进段,并且剔除波动较大和每个推进行程启动段的数据,保留了约53%的数据,对掘进段的各参数作均值化处理,得到用于建模的样本集,部分数据如表 3所示.然后按照1:1划分训练样本集和测试样本集,样本总数为38 708,训练样本数和测试样本数均为19 854.
| 表 3 NSVR建模用的部分样本集 Table 3 Partial sample set for modeling |
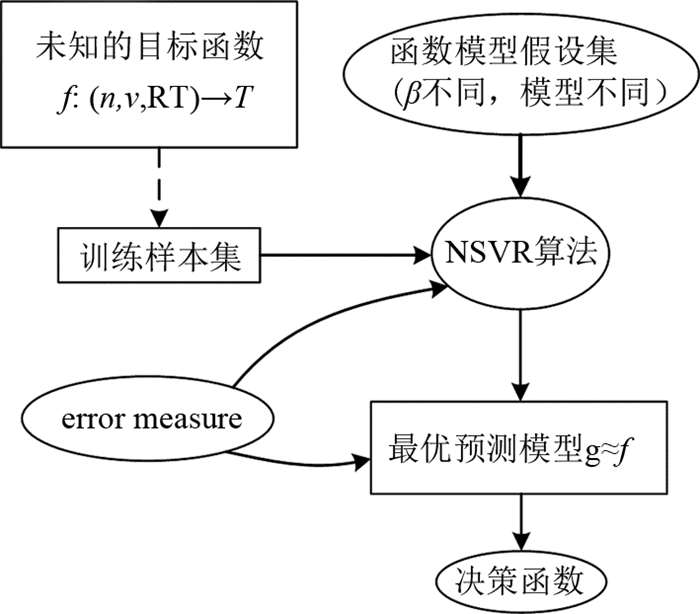
如图 5所示,为了得到刀盘扭矩的预测模型,将训练样本集的刀盘转速n、推进速度v和勘测的围岩类别作为输入,将其对应的实际产生的刀盘扭矩值T作为目标输出,设置停止准则为0.001,不敏感系数ε=0.001,惩罚系数C=6 000,高斯核函数中的系数γ=0.5,得到刀盘扭矩预测模型的决策函数.
|
图 5 创建决策函数 Fig. 5 Create decision function |
运用第4.1节中建立的决策函数,将刀盘转速n、推进速度v和勘测的围岩类别RT输入到决策函数中,分别对训练样本集和测试样本集的刀盘扭矩T进行预测,得到对应的刀盘扭矩预测值,应用式(13)计算单个样本相对预测误差,应用式(14)求取训练样本集和测试样本集的平均相对预测误差,最终求得的训练样本集的平均相对预测误差为11.3%,测试样本集的平均相对预测误差为12.9%.测试样本集中相对预测误差高于60%的有516个测试样本,占测试样本集的2.6%,其中最大相对预测误差为134.4%.
| $ {d_i} = \frac{{\left| {{T_{{\rm{r}}\mathit{i}}} - {T_{{\rm{p}}\mathit{i}}}} \right|}}{{{T_{ri}}}} \times 100\%, $ | (13) |
| $ \bar d = \frac{1}{n}\sum\limits_{i = 1}^n {{d_i}} =\frac{1}{n}\sum\limits_{i = 1}^n \frac{{\left| {{T_{{\rm{r}}\mathit{i}}} - {T_{{\rm{p}}\mathit{i}}}} \right|}}{{{T_{{\rm{r}}i}}}} \times 100\% . $ | (14) |
式中:di为第i个样本的相对预测误差,d为平均相对预测误差,Tri为第i个样本的刀盘扭矩实测值,Tpi为第i个样本的刀盘扭矩预测值.
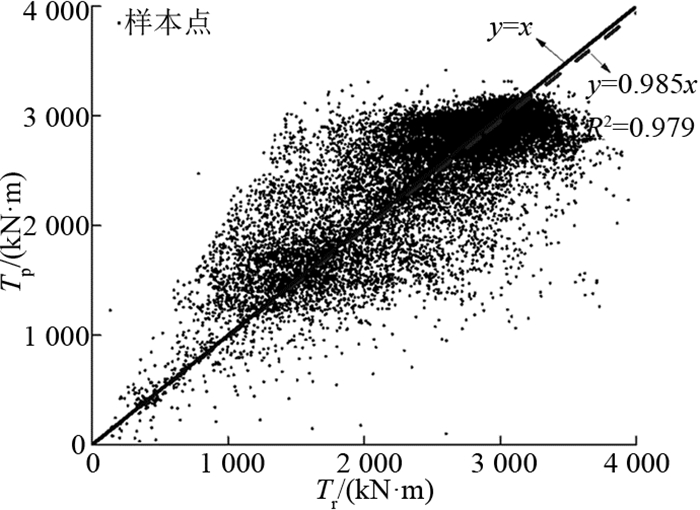
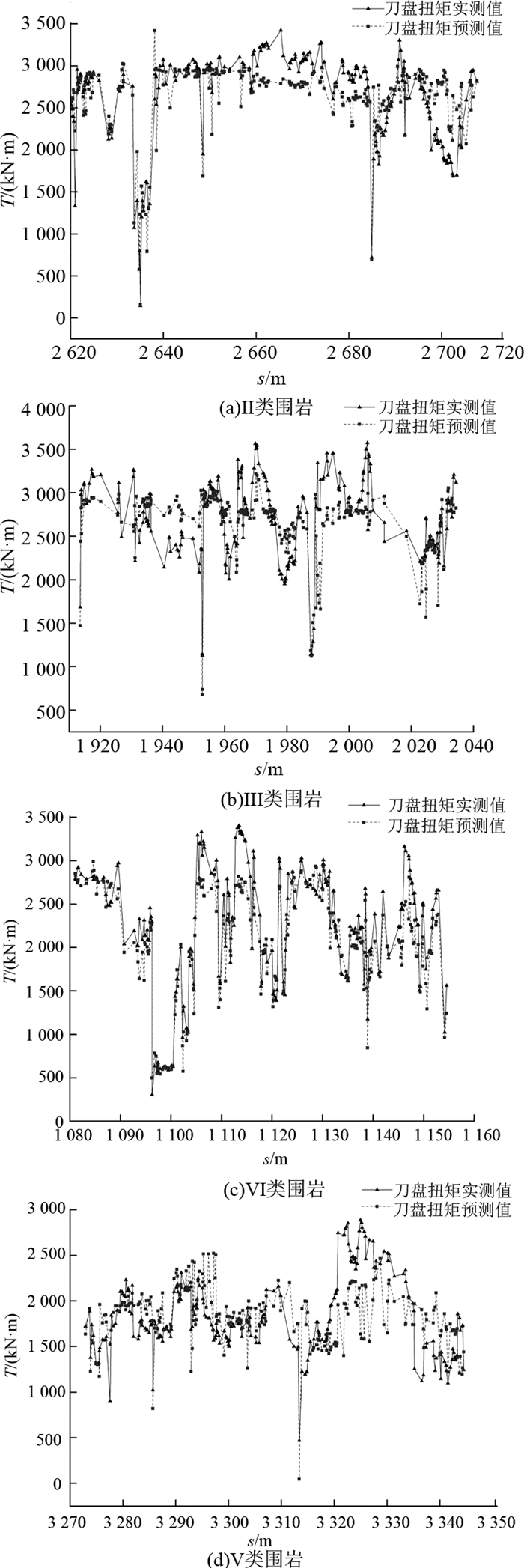
将测试集19 854个样本点的刀盘扭矩的实测值与预测值作对比,如图 6所示,预测值与实测值的相关系数平方为0.979,可见预测刀盘扭矩与实测刀盘扭矩吻合得很好.以掘进里程s为横坐标,分别查看在Ⅱ~Ⅴ类围岩条件下,测试集中刀盘扭矩预测值与实测值的吻合情况,如图 7所示.从图中可以看出,由NSVR模型给出的刀盘扭矩预测值与工程实测值吻合良好,并且预测值曲线变化较实测值曲线平稳.可见利用NSVR建立的模型在给定刀盘转速、推进速度和围岩类别的条件下能够较好地预测TBM刀盘扭矩.
|
图 6 刀盘扭矩实测值与预测值对比 Fig. 6 Cutterhead torque comparison between measured and predicted values |
|
图 7 Ⅱ~Ⅴ类围岩刀盘扭矩实测值与预测值 Fig. 7 Measured and predicted values of cutterhead torque in rock type Ⅱ to Ⅴ |
(1) 在各类围岩中,不同刀盘转速下,TBM刀盘扭矩随着推进速度的增加而增加,推进速度达到一定值后,刀盘扭矩不再随之明显变化.
(2) 在硬岩条件(Ⅱ类、Ⅲ类围岩)下TBM刀盘扭矩受刀盘转速影响较小,软岩条件(Ⅳ类、Ⅴ类围岩)下TBM刀盘扭矩在高推进速度下随着刀盘转速的增加而增加.
(3) 围岩类别由Ⅱ类到Ⅴ类,即围岩强度由强到弱,推进速度对刀盘扭矩的影响逐渐变弱,刀盘转速对刀盘扭矩的影响逐渐变强,即在硬岩条件下,刀盘扭矩主要受推进速度影响,在软岩条件下,刀盘扭矩主要受刀盘转速影响.
(4) 利用NSVR预测模型对按1:1划分的数据量均为19 854的训练样本集和测试样本集的刀盘扭矩进行预测,训练样本集的平均相对预测误差为11.3%,测试样本集的平均相对预测误差为12.9%,表明在给定刀盘转速、推进速度和围岩类别的条件下建立的NSVR预测模型能够很好的预测刀盘扭矩.
| [1] |
刘统, 龚国芳, 彭左, 等. 基于液压变压器的TBM刀盘混合驱动系统[J]. 浙江大学学报:工学版, 2016, 50(3): 419-427. LIU Tong, GONG Guo-fang, PENG Zuo, et al. Hybrid cutterhead driving system for TBM based on hydraulic transformer[J]. Journal of Zhejiang University:Engineering Science, 2016, 50(3): 419-427. |
| [2] |
廖湘平, 龚国芳, 彭雄斌, 等. 基于黏性耦合机理的TBM刀盘脱困特性[J]. 浙江大学学报:工学版, 2016, 50(5): 902-912. LIAO Xiang-ping, GONG Guo-fang, PENG Xiong-bin, et al. Jam breakout characteristic oftunnel boring machine based on hydro-viscous drive mechanism[J]. Journal of Zhejiang University:Engineering Science, 2016, 50(5): 902-912. |
| [3] |
ROXBOROUGH F F, PHILLIPS H R. Rock excavation by disc cutter[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1975, 12(12): 361-366. DOI:10.1016/0148-9062(75)90547-1 |
| [4] |
ROSTAMI J, OZDEMIR L. A new model for performance prediction of hard rock TBMs[C]//Proceedings of the Rapid Excavation and Tunneling Conference. Boston: RETC, 1993: 793-793. http://www.mendeley.com/research/new-model-performance-prediction-hard-rock-tbms/
|
| [5] |
张照煌, 叶定海. 盘形滚刀破岩模型及其侧向力的计算[J]. 应用基础与工程科学学报, 2004, 12(3): 294-299. ZHANG Zhao-huan, YE Ding-hai. The model of the disc cutter's broken-rock and the calculation of it's side-force[J]. Journal of Basic Science and Engineering, 2004, 12(3): 294-299. |
| [6] |
张照煌. 掘进机不同刀盘面上盘形滚刀工作时的侧滑分析[J]. 现代电力, 2003, 20(2): 16-18. ZHANG Zhao-huang. Side-slip analysis of disc cutter on all kinds of cutterheads of full face rock tunnel boring machine[J]. Modern Electric Power, 2003, 20(2): 16-18. |
| [7] |
顾健健. 地应力下TBM盘形滚刀载荷特性及破岩参数匹配研究[D]. 湖南: 中南大学, 2013. GU Jian-jian. Mechanical characteristics of TBM disc cutter under the crustal stress and the parameters matching researches of rock-breaking[D]. Hunan: Central South University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10533-1014145508.htm |
| [8] |
周思阳, 亢一澜, 苏翠侠, 等. 基于力学分析的TBM掘进总推力预测模型研究[J]. 机械工程学报, 2016, 52(20): 76-82. ZHOU Si-yang, KANG Yi-lan, SU Cui-xia, et al. Prediction of thrust force requirements for TBMs based on mechanical analysis[J]. Journal of Machanical Engineering, 2016, 52(20): 76-82. |
| [9] |
宋克志, 杨华勋, 安凯, 等. 复杂岩石地层盾构掘进速率预测模型研究[J]. 公路交通科技, 2008, 25(11): 105-108. SONG Ke-zhi, YANG Hua-xun, AN Kai, et al. Shield tunneling rate prediction model for complex rock stratum[J]. Journal of Highway and Transportation Research and Development, 2008, 25(11): 105-108. DOI:10.3969/j.issn.1002-0268.2008.11.022 |
| [10] |
施虎, 龚国芳, 杨华勇, 等. 盾构掘进土压平衡控制模型[J]. 煤炭学报, 2008, 33(3): 343-346. SHI Hu, GONG Guo-fang, YANG Hua-yong, et al. Control model of earth pressure balance for shield tunneling[J]. Journal of China Coal Society, 2008, 33(3): 343-346. |
| [11] |
ZHANG Q, QU C, KANG Y, et al. Identification and optimization of energy consumption by shield tunnel machines using a combined mechanical and regression analysis[J]. Tunnelling and Underground Space Technology, 2012, 28(1): 350-354. |
| [12] |
ZHANG Q, SU C, QIN Q, et al. Modeling and prediction for the thrust on EPB TBMs under different geological conditions by considering mechanical decoupling[J]. Science China Technological Sciences, 2016, 59(9): 1428. DOI:10.1007/s11431-016-6096-0 |
| [13] |
YANG X, GONG G, YANG H, et al. A cutterhead energy-saving technique for shield tunneling machines based on load characteristic prediction[J]. Journal of Zhejiang University-SCIENCE A, 2015, 16(5): 418-426. DOI:10.1631/jzus.A1400323 |
| [14] |
SALIMI A, ROSTAMI J, MOORMANN C, et al. Application of non-linear regression analysis and artificial intelligence algorithms for performance prediction of hard rock TBMs[J]. Tunnelling and Underground Space Technology, 2016, 58(2): 236-246. |
| [15] |
VAPNIK V, LERNER A. Pattern recognition using generalized portrait method[J]. Automation and Remote Control, 2008, 24(24): 774-780. |
| [16] |
BOSER B E, GUYON I M, VAPNIK V N. A training algorithm for optimal margin classifiers[C]//Proceedings of Annual ACM Workshop on Computational Learning Theory, Pittsburgh: ACM, 1996: 144-152. http://www.scienceopen.com/document?vid=21666ec6-8332-4fe0-ad28-53cfe5ec2810
|
| [17] |
VAPNIK V N. The Nature of Statistical Learning Theory[M]. Berliner: Springer, 2000, 988-999.
|
| [18] |
SCHOLKOPF B, BURGES J C, SMOLA A J. Advances in Kernel Methods:Support Vector Machine[M]. Cambridge: MIT Press, 1998, 1097-1105.
|
| [19] |
PLATT J C. Fast training of support vector machines using sequential minimal optimization[M]. Cambridge: MIT Press, 1999, 185-208.
|



