自然界中绝大多数物体都是抗磁性物质,抗磁性物质产生的附加磁场与外加激励磁场相反.密度是抗磁性物质的重要参数,现有的密度测量技术有:超声波法[1]、密度梯度柱法[2]、比重瓶法[3],这些方法不够方便,需要熟练的操作技巧或者昂贵的设备.2009年美国哈佛大学化学与生物化学实验室的Mirica等[4]首次提出采用磁悬浮装置检测样品密度,采用2块间距为45 mm的磁铁使得抗磁性样品稳定悬浮,实验发现样品密度与悬浮高度呈线性关系,据此可以检测样品密度,检测范围为0.8~2.3 g/cm3,检测精度达到0.000 2~0.020 0 g/cm3.目前磁悬浮装置的应用领域主要包括:聚合物的分离[5],食品检测分析[6],塑料制品质量检测[7],法医鉴定[8],蛋白质与配体结合、分离的实验分析[9],化学反应过程的监测[10],物体三维空间中取向的控制以及自组装[11],倾斜装置[12]等.笔者所在课题组基于磁悬浮装置提出了塑料光学透镜的新型检测方法[13],采用该装置测量聚合物密度[14],调整磁铁间距为60 mm,通过多项式拟合得到聚合物密度与悬浮高度之间的函数关系,密度测量精度达到0.002~0.010 g/cm3.
抗磁性物质的磁悬浮过程涉及磁学、流体力学、数学等多学科知识,属于流体-颗粒-磁场的多场耦合,目前尚未有学者研究磁悬浮过程的数值仿真,从而导致上述研究必须对磁悬浮装置进行特殊限定,如文献[4]限定磁铁间距为45 mm,存在较大的局限性.本研究开展多物理场耦合仿真研究,利用COMSOL软件模拟磁场分布,使用Fluent与EDEM软件进行流固耦合仿真,得到不同磁悬浮装置中样品密度与悬浮高度之间的定量函数关系.
1 磁悬浮检测装置及原理本研究中磁悬浮装置主要由2块相同的方形磁铁同极对置一定距离构成,装置支架采用3D打印聚乳酸(PLA)材料制成.选用合适的顺磁介质溶液,磁悬浮装置可使浸入介质溶液的抗磁性样品2块磁铁中心连线上达到稳定悬浮[4, 13-14],如图 1所示.

|
图 1 磁悬浮装置实物图 Fig. 1 Diagram of magnetic levitation device |
当样品处于装置中时,样品本身的势能由重力势能与磁势能2部分构成,磁势能是由磁悬浮装置中的样品受到磁场力作用引起的能量.以下方磁铁的上表面中心为原点,样品内部由磁场作用引起的势能密度[11]为
| $ {u_{{\rm{mag}}}} =- \frac{{{\mathit{\Delta}} \chi }}{{2{\mu _0}}}\mathit{\boldsymbol{B}} \cdot \mathit{\boldsymbol{B}}{\rm{.}} $ | (1) |
式中:Δχ=χs-χm,χs为样品的磁化率,χm为溶液的磁化率;μ0为真空磁导率;B =(Bx, By, Bz)为样品所在位置的磁感应强度向量.
样品内部由重力作用引起的势能密度为
| $ {u_{{\rm{grav}}}} ={\mathit{\Delta}}\rho \mathit{\boldsymbol{g}} \cdot \mathit{\boldsymbol{z}}. $ | (2) |
式中:Δρ=ρs-ρm,ρs为样品的密度,ρm为溶液的密度;g为重力加速度;z=(0, 0, z0),z0为样品的悬浮高度.
将势能密度对样品所在空间进行体积积分,得到系统总势能:
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;U = {U_{{\rm{mag}}}} + {U_{{\rm{grav}}}} = \\ \int_V { - \frac{{{\mathit{\Delta}} \chi }}{{2{\mu _0}}}\mathit{\boldsymbol{B}} \cdot \mathit{\boldsymbol{B}}{\rm{d}}\mathit{V}} + \int_V {{\mathit{\Delta}} \rho \mathit{\boldsymbol{gz}}{\rm{d}}\mathit{V}.} \end{array} $ | (3) |
式中:dV为样品内部的体积微元;V为样品所包含的空间.
由式(3)可知系统的总势能是样品悬浮高度的函数,当样品实现稳定悬浮时,系统的总势能达到最小值.因为样品在稳定悬浮时处于两磁铁中心连线上,所以仅对竖直方向进行分析即可得到样品密度与悬浮高度之间的关系.根据最小势能原理,样品的稳定悬浮高度z0应满足∂U/∂z=0,得到样品密度ρs与稳定悬浮高度z0之间的函数关系为
| $ \int_V { \left( {{\rho _{\rm{s}}} - {\rho _{\rm{m}}}} \right)\mathit{\boldsymbol{gk}}{\rm{d}}\mathit{V = }} \int_V {\frac{{{\mathit{\Delta}}\chi f\left( {{z_0}} \right)}}{{{\mu _0}}}{\rm{d}}\mathit{V}} . $ | (4) |
式中:k为竖直方向单位向量;样品与溶液的磁化率之差Δχ以及溶液密度ρm可以通过查表及实验手段测定得出;g、k、μ0均为已知常量.
2 密度-高度数值仿真由式(4)可知,要建立样品密度ρs与稳定悬浮高度z0之间的函数关系,需要得到磁感应强度B的表达式以及抗磁性样品的悬浮高度.通过COMSOL三维仿真,分析磁悬浮装置磁感应强度分布,建立磁感应强度数学模型,使用Fluent-EDEM耦合仿真模拟样品悬浮过程,得到样品的稳定悬浮高度.
2.1 磁场分布仿真COMSOLMultiphysics是基于有限单元法的数值仿真软件,以偏微分方程为基础,具有较强的计算功能,其中的交流/直流(alternating current/direct current,AC/DC)模块可模拟准静态电磁场[15].
在COMSOL Multiphysics 5.2中建立物理模型:创建2块对置的矩形磁铁模型,尺寸为50 mm×50 mm×25 mm,设置矩形磁铁的间距为45 mm.外部边界为边长为500 mm的正方体,设置磁铁以外、边界以内的材料为空气.文献[14]指出磁铁的表面磁感应强度大小并不影响空间磁感应强度的分布形式,因此参照现有材料,设置上方矩形磁铁的剩磁感应强度为1.32 T,方向沿z轴负方向,下方矩形磁铁剩磁感应强度与上方矩形磁铁大小相等,方向相反.整个模型内部磁通量守恒.通过COMSOL仿真得到该装置对称面上的磁感应强度的分布如图 2所示,图中Bx为x方向磁场强度.

|
图 2 磁悬浮装置x-z对称面上x方向磁感应强度云图 Fig. 2 Contour of x component of magnetic flux density on x-z symmetry plane for magnetic levitation device |
EDEM软件是利用现代化离散元模型来模拟和分析颗粒系统处理和生产操作的通用CAE软件,可以为固体颗粒系统建立参数化模型.通过添加力学性质和其他物理性质建立颗粒模型,同时结合其他CAE软件进行分析设计[16].Fluent软件是应用于流体动力学(CFD)领域最为全面的软件之一,具有广泛的物理模型,能够快速准确地得到CFD分析结果,具有强大的数值计算功能和前后处理功能[17].
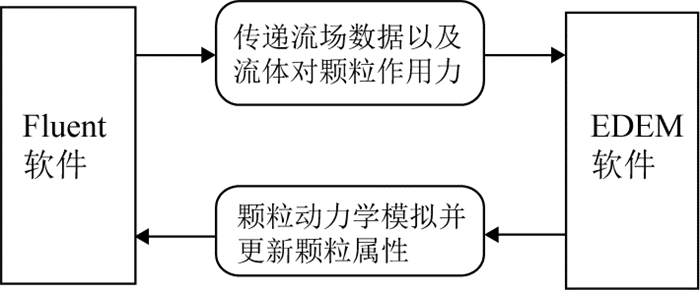
样品在磁悬浮装置中的运动属于流体-颗粒-磁场的多场耦合,采用Fluent-EDEM耦合可以进行多相流CFD仿真.颗粒相与流体相耦合的模型包括Eulerian-Eulerian法和Eulerian-Lagrangian法,由于本文仿真的固体颗粒占流体相的体积分数非常小,采用后者进行仿真.Fluent-EDEM耦合的流程图如图 3所示.
|
图 3 Fluent-EDEM耦合流程图 Fig. 3 Flow diagram of Fluent-EDEM coupling |
根据磁悬浮装置原理图,建立物理模型.首先创建尺寸为50 mm×50 mm×45 mm的长方体流体域,代表 2块磁铁中间的容器.长方体的顶部为入口,在Fluent 15.0中将边界条件定义为速度入口,由于模拟的是静水情况,将速度设为0,其他边界为壁面.在EDEM 2.7中建立一个半径为0.5 mm的球体,代表悬浮的样品.
根据磁感应强度表达式,编译磁场力数学模型,通过EDEM软件的API接口进行加载,设置样品在悬浮过程中受到磁场力的作用.设定样品释放的初始位置在距离容器底部竖直距离5 mm处,模拟样品的悬浮过程,并分析仿真结果.在EDEM软件的后处理模块中可以得到样品的稳定悬浮高度.
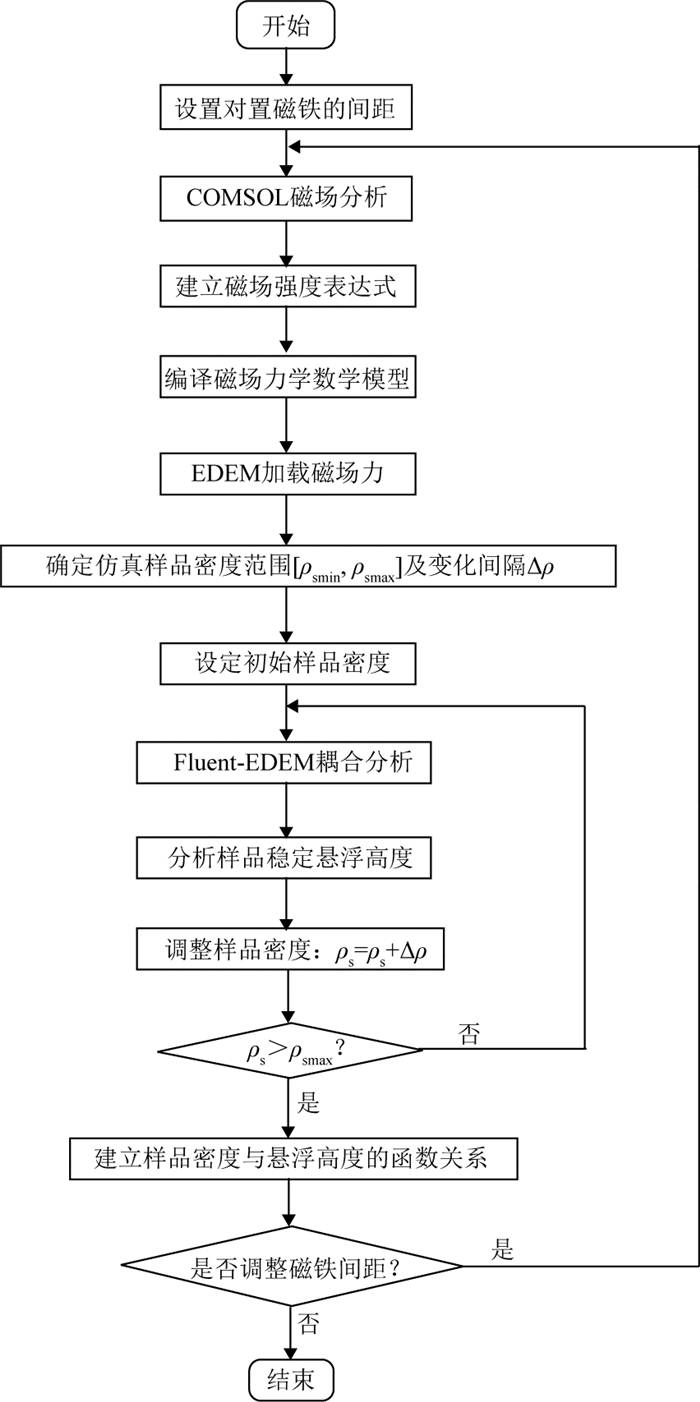
2.3 数值仿真步骤抗磁性物质的密度-高度检测方案实现流程图如图 4所示,由图可知,先设定上、下对置磁铁的间距,通过COMSOL分析该装置的磁感应强度分布,并建立中心线上磁感应强度表达式.编译磁场力数学模型,通过EDEM进行加载.通过Fluent-EDEM耦合仿真模拟样品悬浮过程,分析具有不同密度的样品其稳定悬浮高度的变化,并建立样品密度与悬浮高度的函数关系.
|
图 4 抗磁性物质的密度高度检测流程图 Fig. 4 Flow chart ofdiamagnetic materials' density-height detection |
在磁悬浮模型中调整2块磁铁的间距为45 mm,通过COMSOL仿真得到中心线上z方向磁感应强度分布.当磁铁间距为45 mm时,在中心线上的z方向磁感应强度分布呈线性关系.对z方向磁感应强度数据进行拟合,得到z方向磁感应强度的分布为
| $ {B_{z\_45}} = 0.377\;5 - 0.016\;7{z_0}, $ | (5) |
判定系数R2=0.999 1.
根据式(5)编译磁场力数学模型,通过EDEM软件进行加载.在EDEM软件中设置样品密度的取值范围为1.10 ~1.40 g/cm3,以0.05 g/cm3为间隔进行变化.通过Fluent-EDEM耦合仿真,分析不同样品密度下其稳定悬浮高度的变化.
对仿真数据拟合得到样品密度与悬浮高度的函数关系为
| $ {\rho _{\rm{s}}} = - 0.012 \ 5{z_0} + 1.574. $ | (6) |
判定系数R2=1.000 0.
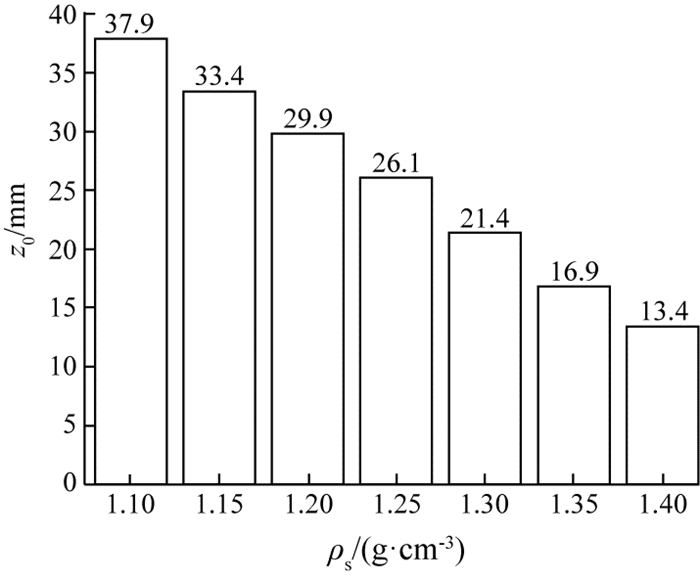
通过实验验证公式的正确性.实验磁铁选用北京久久高科磁性材料有限公司生产的牌号为N45的钕铁硼永磁体,中心表面的磁感应强度为0.425±0.005 T,2块磁铁以N极对N极的方式布置,磁铁间距为45 mm.顺磁介质溶液选用3.0 mol/L的氯化锰溶液,实验样品选用American Density Materials公司生产的标准密度球(密度标定精度为±0.000 2 g/cm3),密度间隔为0.05 g/cm3.将样品放入溶液中,当样品稳定悬浮时,记录样品的悬浮高度,实验结果如图 5所示.
|
图 5 当磁铁间距为45 mm时样品悬浮实验结果 Fig. 5 Experimental results for different samples with 45 mm separation distance |
实验中通过测量图像中像素点的方式来确定标准密度球的悬浮位置.每做1组实验保证相机在固定的位置与高度进行拍照.利用图像处理软件测量2块磁铁之间中心线的像素点数目,以及标准球中心到底部磁铁上表面的连线的像素点数目,根据2块磁铁的实际间距以及像素点数目的比例得到标准球的悬浮高度,具体参考文献[14].根据误差传递公式可以得到标准密度球的高度测量偏差小于0.4 mm.
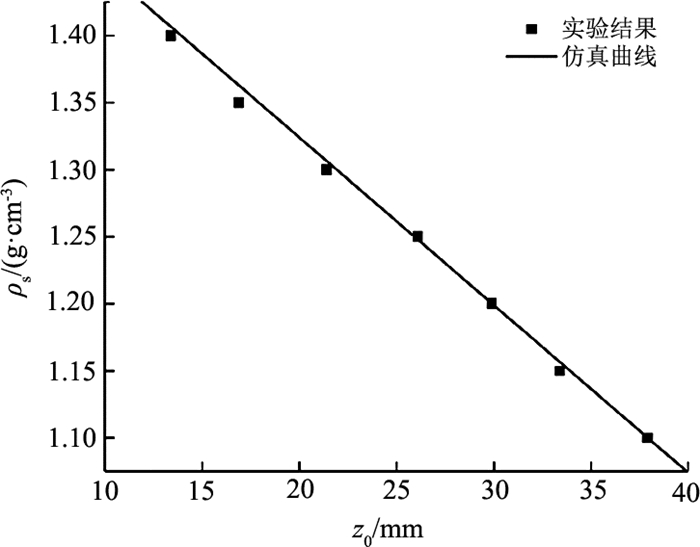
将实验得到的样品悬浮高度随样品密度的变化情况与仿真结果进行对比,如图 6所示.图 6中斜线为仿真结果,离散点为实验结果.由图可知,仿真曲线与实验结果吻合程度较高,仿真结果与实验结果相比,其偏差为-0.001 5~0.013 0 g/cm3.
|
图 6 当磁铁间距为45 mm时抗磁性物质密度与悬浮高度的仿真曲线和实验结果对比 Fig. 6 Comparison of simulation curves and experimental results for diamagnetic materials' density and levitation height with 45 mm separation distance |
将磁铁间距调整为60 mm,按照相同的方法分析中心线上的磁感应强度,通过拟合得到中心线上磁感应强度的分布,发现其中心线上z方向磁感应强度(Bz_60)不再符合线性分布.根据曲线趋势,选用3次多项式对曲线进行拟合:
| $ \begin{array}{l} {B_{z\_60}} = {\rm{ }} - 0.508\;3 \times 10 - 6z_0^3 + 4.616 \times 10 - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;4z_0^2 - 0.023\;29{z_0} + 0.421\;3, \end{array} $ | (7) |
判定系数R2=0.994 1.
根据式(7)编译磁场力数学模型,通过EDEM软件进行加载.在EDEM软件中设置样品密度的取值范围为1.08~1.30 g/cm3,以0.02 g/cm3为间隔进行变化.采用Fluent-EDEM耦合,模拟磁铁间距为60 mm情况下的样品悬浮高度.
对仿真结果拟合可以得到样品密度与稳定悬浮高度的函数关系:
| $ \begin{array}{l} {\rho _{\rm{s}}} = - 6.85 \times 10 - 6z_0^3 + 6.205 \times 10 - 4z_0^2\\ \;\;\;\;\;\;\;\;\;\;\;\; - 0.021\ 14{z_0} + 1.457, \end{array} $ | (8) |
判定系数R2=0.999 9.
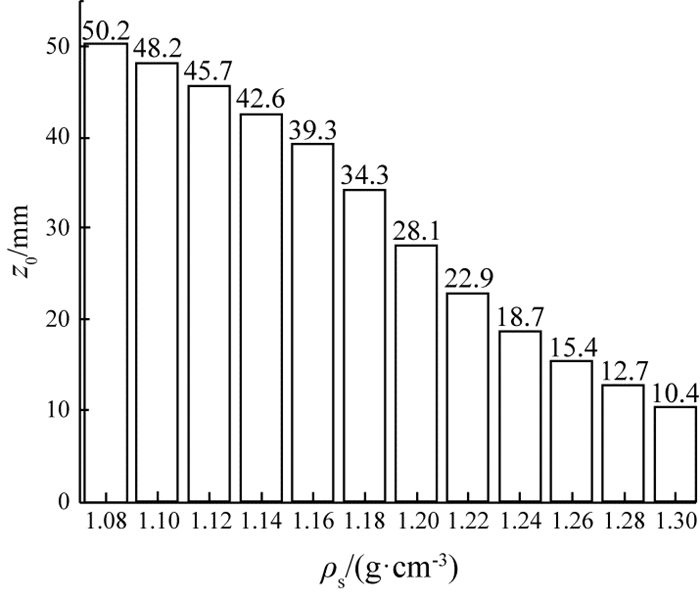
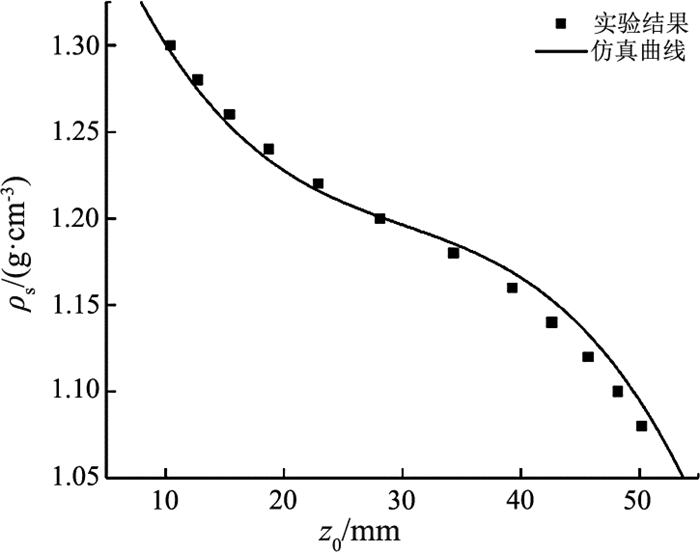
通过实验验证式(8)的正确性.采用与3.1节中相同的磁铁,控制磁铁间距为60 mm,标准密度球的密度间隔选为0.02 g/cm3.记录样品的悬浮高度,进行多组重复实验取平均值并与仿真结果进行比较.标准密度球的实验结果如图 7所示.将仿真结果与实验结果进行对比,得到图(8),其中散点为实验结果数据,曲线为拟合得到的密度-高度关系曲线.可以观察到仿真曲线与实验结果基本吻合,仿真结果与实验结果相比,其偏差为-0.006 4~0.013 0 g/cm3,仿真结果具有较高精度.
|
图 7 磁铁间距为60 mm时的样品悬浮实验结果 Fig. 7 Experimental results for different samples with 60 mm separation distance |
|
图 8 当磁铁间距为60 mm时抗磁性物质密度与悬浮高度的仿真曲线和实验结果对比 Fig. 8 Comparison of simulation curves and experimental results for diamagnetic materials' density and levitation height with 60 mm separation distance |
本文采用多物理场耦合,对磁悬浮密度检测技术进行仿真.通过COMSOL软件模拟磁场分布,得到磁感应强度的数学模型,并通过EDEM软件的API接口加载磁场力模型,使用Fluent-EDEM进行流固耦合仿真,得到磁铁间距分别为45、60 mm时样品密度与悬浮高度之间的关系曲线.由仿真结果可知,当磁铁间距为45 mm时,样品密度与悬浮高度呈线性关系,且其测量精度为-0.001 5~0.013 0 g/cm3;当磁铁间距为60 mm时,样品密度与悬浮高度服从多项式函数关系,其测量精度达到-0.006 4~0.013 0 g/cm3.所提的方法可实现抗磁性物质磁悬浮过程的数值仿真,大大增进对磁悬浮过程的理解与认识,可推进磁悬浮装置的应用与普及.
| [1] |
赵杨, 林莉, 李继承, 等. 基于超声波声压反射系数相位谱测定热障涂层密度的方法研究[J]. 稀有金属材料与工程, 2010, 39(增1): 255-258. ZHAO Yang, LIN Li, LI Ji-cheng, et al. Investigation on the principle for measuring inhomogeneous coating density by ultrasonic sound pressure reflection coefficient phase spectrum[J]. Rare Metal Materials And Engineering, 2010, 39(Suppl.1): 255-258. |
| [2] |
DAVIDSON S, PERKIN M. An investigation of density determination methods for porous materials, small samples and particulates[J]. Measurement, 2013, 46(5): 1766-1770. DOI:10.1016/j.measurement.2012.11.030 |
| [3] |
GHORBANI M, MOHAMMADI A H. Effects of temperature, pressure and fluid composition on hydrocarbon gas-oil interfacial tension (IFT):An experimental study using ADSA image analysis of pendant drop test method[J]. Journal of Molecular Liquids, 2017, 227: 318-323. DOI:10.1016/j.molliq.2016.11.110 |
| [4] |
MIRICA K A, SHEVKOPLYAS S S, PHILLIPS S T, et al. Measuring densities of solids and liquids using magnetic levitation:fundamentals[J]. Journal of the American Chemical Society, 2009, 131(29): 10049-10058. DOI:10.1021/ja900920s |
| [5] |
ATKINSON M B J, BWAMBOK D K, CHEN J, et al. Using magnetic levitation to separate mixtures of crystal polymorphs[J]. Angewandte Chemie, 2013, 52(39): 10208-10211. DOI:10.1002/anie.201305549 |
| [6] |
MIRICA K A, PHILLIPS S T, MACE C R, et al. Magnetic levitation in the analysis of foods and water[J]. Journal of Agricultural and Food Chemistry, 2010, 58(11): 6565-6569. DOI:10.1021/jf100377n |
| [7] |
HENNEK J W, NEMIROSKI A, SUBRAMANIAM A B, et al. Using magnetic levitation for non-destructive quality control of plastic parts[J]. Advanced Materials, 2015, 27(9): 1587-1592. DOI:10.1002/adma.201405207 |
| [8] |
LOCKETT M R, MIRICA K A, MACE C R, et al. Analyzing forensic evidence based on density with magnetic levitation[J]. Journal of Forensic Sciences, 2013, 58(1): 40-45. DOI:10.1111/jfo.2013.58.issue-1 |
| [9] |
SHAPIRO N D, SOH S, MIRICA K A, et al. Magnetic levitation as a platform for competitive protein-ligand binding assays[J]. Analytical Chemistry, 2012, 84(14): 6166-6172. DOI:10.1021/ac301121z |
| [10] |
MIRICA K A, PHILLIPS S T, SHEVKOPLYAS S S, et al. Using magnetic levitation to distinguish atomic-level differences in chemical composition of polymers, and to monitor chemical reactions on solid supports[J]. Journal of the American Chemical Society, 2008, 130(52): 17678-17680. DOI:10.1021/ja8074727 |
| [11] |
SUBRAMANIAM A B, YANG D, YU H D, et al. Noncontact orientation of objects in three-dimensional space using magnetic levitation[J]. Proceeding of the National Academy of Sciences of the United States of America, 2014, 111(36): 12980-12985. DOI:10.1073/pnas.1408705111 |
| [12] |
NEMIROSKI A, SOH S, KWOK S W, et al. Tilted magnetic levitation enables measurement of the complete range of densities of materials with low magnetic permeability[J]. Journal of the American Chemical Society, 2016, 138(4): 1252-1257. DOI:10.1021/jacs.5b10936 |
| [13] |
赵朋, 颉俊, 傅建中, 等. 塑料光学透镜的磁悬浮检测[J]. 光学精密工程, 2016, 24(4): 756-763. ZHAO Peng, XIE Jun, FU Jian-zhong, et al. Magnetic levitation detection for plastic optical lenses[J]. Optics and Precision Engineering, 2016, 24(4): 756-763. |
| [14] |
XIE J, ZHAO P, ZHANG C Q, et al. Measuring densities of polymers by magneto-archimedes levitation[J]. Polymer Testing, 2016, 56: 308-313. DOI:10.1016/j.polymertesting.2016.10.032 |
| [15] |
徐显金, 吴龙辉, 杨小俊, 等. 高压直流巡检机器人的磁力驱动方法[J]. 浙江大学学报:工学版, 2016, 50(10): 1937-1945. XU Xian-jin, WU Long-hui, YANG Xiao-jun, et al. Magnetic driving method of inspection robot for HVDC transmission lines[J]. Journal of Zhejiang University:Engineering Science, 2016, 50(10): 1937-1945. |
| [16] |
杨公波, 李郁, 陈定方. 基于EDEM仿真的斗轮堆取料机取料机理研究[J]. 武汉理工大学学报:交通科学与工程版, 2014, 38(3): 680-683. YANG Gong-bo, LI Yu, CHEN Ding-fang. Research of reclaiming mechanism of the bucket wheel stacker-reclaimer based on EDEM simulation[J]. Journal of Wuhan University of Technology:Transportation Science and Engineering, 2014, 38(3): 680-683. |
| [17] |
赵飞, 杨帅, 吴俊, 等. 基于Fluent的压力能交换器端面液膜支撑机理分析[J]. 浙江大学学报:工学版, 2014, 48(8): 1528-1533. ZHAO Fei, YANG Shuai, WU Jun, et al. Analysis on support mechanism of the axial film in Rotary Pressure Exchanger based on Fluent[J]. Journal of Zhejiang University:Engineering Science, 2014, 48(8): 1528-1533. |



