图像复原是图像处理中的一个重要问题,得到了研究人员的广泛关注.作为二维卷积运算的逆问题,它的病态性以及噪声等影响造成了求解上的困难.常用的解决方法是通过将模糊过程看作随机概率事件在贝叶斯框架下建立清晰图像的正则化约束得到复原结果.其中,盲复原问题由于模糊核知,求解更加困难.
近年来已经有学者提出了不少基于单幅图像的盲复原方法.Fergus等[1]采用2个混合高斯函数分别对图像梯度和模糊核(point spread function, PSF)的稀疏分布进行建模,通过变分法求解出PSF.Shan等[2]采用分段函数对自然图像梯度稀疏约束建模,简化了求解过程.Krishnan等[3]提出了一种归一化的稀疏分布模型作为复原的约束条件.Cho等[4]在模糊核估计时引入了滤波函数,并且该算法可以在频率域求解,显著提高了运算速度.Jia等[5-6]采用两步估计模糊核的方式较为稳定地估计出模糊核,同时提出了L0范数优化的图像复原方法.此外,围绕着建立更准确的图像先验概率分布[7-10]以及追求更准确稳定估计出模糊核[11-12]的盲复原算法也被不断提出.
在许多情况下,受限于存储空间或实时性等的要求,拍摄的图像在保存时会为了节省空间而采用有损压缩技术.特别在深空探测拍摄中,为了传输方便,会尽量压缩图像.其中,被最为广泛使用的是JPEG压缩格式,这种格式经过低比特率块编码压缩重构后的图像8×8小块边界往往会出现明显的块效应.这相当于在图像模糊的基础上又引入了进一步的退化.由于块效应破坏了图像的先验信息,常规的图像复原方法难以得到理想的复原结果.研究块效应明显的模糊图像复原方法具有重要意义.
本文提出了一种基于块效应抑制的压缩降质模糊图像盲复原算法.为了在有块效应的模糊图像下提高模糊核估计的稳定性,提出利用去块效应的模糊图像作为显著边缘估计的参考图像,并在正则化约束时加入模糊核的梯度约束保证模糊核的连续平滑性.在最终图像复原迭代阶段为了抑制块效应,在全变分(total variation, TV)正则化的基础上新增一项L2范数约束,逐步抑制块效应对复原带来的负面影响.
1 压缩降质模糊图像的模糊核估计压缩降质模糊图像的模糊核估计采用多尺度分解逐层进行.首先根据设定的金字塔层数降采样至金字塔顶层,在该层通过迭代算法估计出模糊图像的模糊核,以及该层的复原图像.之后,对该复原图像进行上采样,并估计出当前层的图像模糊核及复原图像,再上采样直至估计出原始图像大小的模糊核.得到块效应模糊图像的模糊核后,最后进行块效应抑制的图像复原,得到最终的复原图像.整体算法流程如图 1所示.
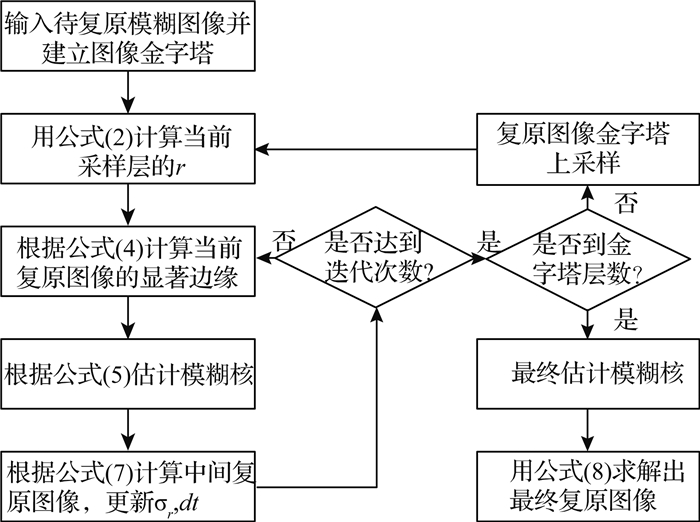
|
图 1 块效应模糊图像盲复原算法流程图 Fig. 1 Flow chart of compressed image restoration algorithm |
在显著边缘选择以及最终复原阶段,都需要对图像压缩块效应进行一定的抑制.常见的块效应处理方法主要包括基于离散余弦变换(DCT)域[13-14]以及基于空间域[15]的方法.本文采用逐点形状自适应DCT滤波器[13](SA-DCT)来抑制块效应的负面效应.该算法由Foi A在2007年提出,是比较成熟的兼顾去块效应效果与效率的滤波器.它的核心思想是:对图像中的像素点依据图像局部特征寻找其在不同方向的滤波长度,将不同方向的滤波端点连接构成一个形状自适应的待滤波区域.然后对该滤波区域水平和竖直方向分别做一维DCT变换并根据JPEG量化表与块效应严重程度对DCT系数进行相应的滤波处理.滤波过程用下式表示为
| $ t' = B\left( t \right). $ | (1) |
式中:t为待去块效应图像,t′为去块效应后图像,B为去块效应滤波器.
1.2 选择模糊核估计的显著边缘根据文献[16],图像中那些边缘宽度比模糊核尺寸还要小的边缘会对模糊核估计造成干扰,选择有效的显著边缘有助于排除干扰边缘从而估计出更准确的模糊核.被压缩后的模糊图像的模糊边缘会被块效应不同程度的破坏,直接从模糊图像选择的有效显著边缘虽然可以一定程度排除干扰边缘,但是也会由于块效应而影响最优有效显著边缘的选择.如果采用没有块效应存在的模糊图像的显著边缘区域进行模糊核估计,能够提高模糊核估计的精度.以某一层金字塔采样层为例,给出选择有效显著边缘的方法.
采用求边缘置信度[5]的基本思路,逐像素统计给定图像邻域范围内梯度和的绝对值与梯度绝对值之和的比值作为梯度边缘置信度.对模糊图像b用1.1节的去块效应滤波方法得到的图像作为计算时的参考图像,能够得到相对准确的边缘置信度r.定义其计算公式为
| $ r\left( i \right) = \frac{{\left| {\sum\nolimits_{j \in {N_u}\left( i \right)} {{D_x}{b_0}\left( j \right)} } \right| + \left| {\sum\nolimits_{j \in {N_u}\left( i \right)} {{D_y}{b_0}\left( j \right)} } \right|}}{{\sum\nolimits_{j \in {N_u}\left( i \right)} {\left( {\left| {{D_x}{b_0}\left( j \right)} \right| + \left| {{D_y}{b_0}\left( j \right)} \right|} \right) + 0.5} }}. $ | (2) |
式中:b0为对当前采样层的模糊图像去块效应后得到的图像.Nu(i)为以图像像素索引i为中心的u×u大小的邻域,j为邻域内的图像像素索引.Dx, Dy分别为图像水平与竖直方向的梯度算子.r(i)越大表示该像素越可能是有效显著边缘.选定一个阈值T1,记r>T1的像素集合为有效显著边缘区域M.
然后对迭代输入的当前图像进行双边滤波[17],空间域滤波参数σs设为2,初始值域滤波参数σr设定大小与模糊图像的块效应严重程度正相关.块效应不严重时一般取σr=0.5作为初始值.之后用shock滤波器[18]对双边滤波后的图像边缘进行强化,使得边缘变得更锐利,滤波公式为
| $ {{\tilde f}_{t + 1}} = {{\tilde f}_t} - {\rm{sign}}\left( {\Delta {{\tilde f}_t}} \right){\left\| {\nabla {{\tilde f}_t}} \right\|_2}{\rm{d}}t. $ | (3) |
式中:
在得到了经过强化的图像基础上,采用以下公式求解需要得到的有效显著边缘p的水平与竖直方向梯度Djp∈{Dxp, Dyp}.
| $ {D_j}p\left( i \right) = \left\{ \begin{array}{l} {D_j}{{\tilde f}_{t + 1}}\left( i \right),M\left( i \right)\sqrt {D_x^2{{\tilde f}_{t + 1}}\left( i \right) + D_y^2{{\tilde f}_{t + 1}}\left( i \right)} > {T_2};\\ 0,\;其他. \end{array} \right. $ | (4) |
式中:M(i)为有效显著边缘区域M中的第i个像素j∈{x, y},T2为梯度选择阈值,进一步滤除梯度过小的边缘,式(4)利用了有效显著区域并结合梯度大小筛选出有效的边缘,为后续模糊核求解奠定了重要基础.为了说明采用去块效应模糊图像求取有效显著边缘区域对复原的效果提升,对一张压缩模糊图像对比了在2种情况下的模糊核估计结果,分别如图 2(a)、(c)所示,对应的模糊核复原图像后的结构相似度(structural similarity index metric, SSIM) [19]分别为0.854 5和0.880 4.显见用去块效应图像估计显著边缘对模糊核估计精度有显著提高.

|
图 2 模糊核估计结果对比 Fig. 2 Comparison of kernel estimation results |
得到有效显著边缘梯度Dxp, Dyp后,就可以利用它们进行模糊核估计.提出的目标优化函数如下:
| $ \begin{array}{*{20}{c}} {h = \arg {{\min }_h}\sum\limits_{i \in \left\{ {x,y,xx,yy,xy} \right\}} {{\omega _i}\left\| {{D_i}p * h - {D_i}b} \right\|_2^2} + }\\ {{\gamma _1}\left\| h \right\|_2^2 + {\gamma _2}\sum\limits_{j \in \left( {x,y} \right)} {\left\| {{D_j}h} \right\|_2^2} .} \end{array} $ | (5) |
式中:b为当前采样层的模糊图像,h为待求解的模糊核,ωi为每一个代价项的权重系数,Di(·)表示对括号内的图像矩阵按照某一方向求梯度,比如Dxxb表示对模糊图像求二阶水平差分,Dxyp表示对Dxp求竖直方向梯度.γ1, γ2为对应正则化项的权重系数.由于该优化式中都是l2范数,可以在频率域进行求解,求解结果为
| $ \begin{array}{*{20}{c}} {F\left( h \right) = \frac{{\sum\limits_{i \in \left\{ {x,y,xx,yy,xy} \right\}} {{\omega _i}F{{\left( {{D_i}p} \right)}^ * } \circ F\left( {{D_i}b} \right)} }}{{\sum\limits_{i \in \left\{ {x,y,xx,yy,xy} \right\}} {{\omega _i}F{{\left( {{D_i}p} \right)}^ * } \circ F\left( {{D_i}p} \right) + {\gamma _1}} }} \cdot }\\ {\frac{1}{{{\gamma _2}\left( {F{{\left( {{D_x}} \right)}^ * } \circ F\left( {{D_x}} \right) + F{{\left( {{D_y}} \right)}^ * } \circ F\left( {{D_y}} \right)} \right)}}.} \end{array} $ | (6) |
式中:F为图像的傅里叶变换,因此式(6)的傅里叶逆变换即为h.“*”表示共轭运算,算符“°”表示2个图像矩阵的点乘积.由于式(5)的第3项梯度约束,使得从有块效应的模糊图像中估计出的模糊核形状连通性更高且准确性更优.对比了压缩模糊图像在有无梯度约束下的模糊核估计结果,如图 2(b)、(c)所示.没有增加模糊核梯度约束的复原图像SSIM为0.867,比增加此约束的复原指标低近0.02.而如果对无压缩情况下的模糊图像进行模糊核估计,是否增加这项约束的模糊核估计结果很相似,复原图像评价指标SSIM上相差小于0.005.这表明了模糊核梯度约束有助于提高有压缩块效应图像模糊核估计的精度.
估计出当前层的模糊核h后,即可求解当前层的图像复原中间结果.由于此时的复原图像仅仅是一个过渡的复原结果,目的是为了更好地估计模糊核,所以采用基于l2范数的图像正则化约束即可,优化公式如式(7)所示,
| $ \begin{array}{*{20}{c}} {f = \arg {{\min }_f}\sum\limits_{i \in \left\{ {x,y,xx,yy,xy} \right\}} {{\omega _i}\left\| {{D_i}f * h - {D_i}b} \right\|_2^2} + }\\ {\omega \left\| {f * h - b} \right\|_2^2 + \alpha \left\| f \right\|_2^2.} \end{array} $ | (7) |
式中:f为从当前估计的模糊核h中估计的清晰图像结果,α是图像约束正则化系数,ωi与Di意义同上.此问题也可以类似地在频率域进行求解.求解出中间层复原图像f后,再继续求解新的有效显著边缘以及估计模糊核,直至满足算法在该金字塔层的迭代次数.一般而言,对于每一个采样层需要的模糊核估计与图像解卷积轮转迭代次数为10次左右.
2 基于块效应抑制的图像复原估计出压缩降质模糊图像的模糊核h后,问题转化为图像非盲复原问题.如果采用常规的非盲复原方法,复原结果会使块效应更加明显.通过加大约束权重系数的方式能够一定程度抑制块效应负面效应,但得到的复原图像会过分平滑.针对这一问题,提出了基于块效应抑制的图像非盲复原方法,在TV正则化约束的图像复原方法基础上,将去块效应算法结合到复原迭代的过程中,使得在复原图像的过程中逐步抑制块效应带来的负面效应.提出的待优化代价函数为
| $ \begin{array}{*{20}{c}} {f = \arg {{\min }_f}\frac{\mu }{2}\left\| {h * f - b} \right\|_2^2 + {{\left\| {{D_x}f} \right\|}_1} + }\\ {{{\left\| {{D_y}f} \right\|}_1} + \frac{\xi }{2}\left\| {f - B\left( f \right)} \right\|_2^2.} \end{array} $ | (8) |
式中:μ, ξ为正则化系数,B(f)表示迭代过程中对上一次得到的复原图像f采用1.1节方法进行去块效应操作.‖·‖1, ‖·‖2分别表示l1与l2范数.公式(8)包含3项,第1项为损失项,第2项为清晰图像的先验约束项,这里采用TV-l1范数进行约束.第3项为块效应抑制项,由于该问题是通过迭代方式求解的,因此B(f)在每次迭代过程中都会发生变化,设计该项约束的目的就是使得求解的复原图像在满足清晰图像先验约束的前提下,也能逐步接近其去块效应图像.
为求解式(8),采用变量分离技术,将其引入2个辅助变量,转化为可方便求解的形式,
| $ \begin{array}{*{20}{c}} {\arg {{\min }_{{w_1},{w_2},f}}\frac{\mu }{2}\left\| {h * f - b} \right\|_2^2 + \frac{\xi }{2}\left\| {f - B\left( f \right)} \right\|_2^2 + }\\ {\sum\limits_{i = 1}^2 {{{\left\| {{w_i}} \right\|}_1}} + \frac{\beta }{2}\left\| {{w_1} - {D_x}f} \right\|_2^2 + \frac{\beta }{2}\left\| {{w_2} - {D_y}f} \right\|_2^2.} \end{array} $ | (9) |
式中:w1, w2为引入的辅助变量.β为迭代过程中的正则化系数,当β趋向于很大时,式(9)收敛于式(8).该问题可以转化为轮转迭代求解,在第t+1次迭代首先估计出辅助变量的解,采用阈值收缩公式可以得到辅助变量为
| $ \begin{array}{l} w_1^{t + 1} = \max \left( {\left\| {{D_x}{f^t}} \right\| - \frac{1}{\beta },0} \right)\frac{{{D_x}{f^t}}}{{\left\| {{D_x}{f^t}} \right\|}},\\ w_2^{t + 1} = \max \left( {\left\| {{D_y}{f^t}} \right\| - \frac{1}{\beta },0} \right)\frac{{{D_y}{f^t}}}{{\left\| {{D_y}{f^t}} \right\|}}. \end{array} $ | (10) |
之后在变换域求解出最终复原图像,求解公式如下:
| $ {f^{t + 1}} = {F^{ - 1}}\left( {\frac{{\mu F{{\left( h \right)}^ * } \circ F\left( b \right) + \beta \left( {F{{\left( {{D_x}} \right)}^ * } \circ F\left( {w_1^{t + 1}} \right) + F{{\left( {{D_y}} \right)}^ * } \circ F\left( {w_2^{t + 1}} \right)} \right) + \xi B\left( {{f^t}} \right)}}{{\mu F{{\left( h \right)}^ * } \circ F\left( h \right) + \beta \left( {F{{\left( {{D_x}} \right)}^ * } \circ F\left( {{D_x}} \right) + F{{\left( {{D_y}} \right)}^ * } \circ F\left( {{D_y}} \right)} \right) + \xi }}} \right). $ | (11) |
然后再对ft+1进行块效应滤波操作,作为下次迭代时块效应约束项的输入,并将β值更新为其原值的2倍,进行下一次迭代.在实际计算中,经过6~10次的轮转迭代后,得到最终的图像复原结果.复原算法因为可以在傅里叶变换域求解,算法的复杂度与TV正则化约束相当,需要多求一次矩阵傅里叶变换.算法计算时间增加主要由于迭代中需要调用去块效应方法.
3 实验与结果讨论本节采用Levin[16]的图像库进行图像盲复原与结果比较,库中包含8种已知参考模糊核的32幅实拍模糊图像,同时也包含清晰图像作为参考图,是较为广泛使用的图像复原效果比较库.选用图像库中4张255×255大小的清晰图像以及对应的模糊核与模糊图像,清晰图片与模糊核如图 3所示.实验所用的处理器为Intel Core i7,其主频3.6 GHz,内存8 GB.

|
图 3 实验选用的4张清晰图片与其对应的模糊核 Fig. 3 Four clear images and related PSFs used in experiment |
在图像库中选择图 3中模糊核所对应的4张模糊图像进行JPEG压缩.选用Matlab中保存成JPEG格式的压缩方法,该压缩方式可以设定压缩质量数值,范围是0~100,100表示无损压缩.在本节实验中,选择压缩质量40,此时保存的图像已经有较为明显的压缩块效应.分别对这4张压缩模糊图像进行图像盲复原求解,并与Cho等[4-5]提出的经典盲复原方法复原结果进行比较.限于篇幅,选取2组对比实验结果如图 4、5所示分别为场景人物图和卡通图,对应算法所估计的模糊核在复原图像右上角.

|
图 4 不同方法的场景人物图复原结果比较 Fig. 4 Comparison of restoration results of scene and character image using different methods |

|
图 5 不同方法的卡通图复原结果比较 Fig. 5 Comparison of restoration results of cartoon image using different methods |
从图 4中不同方法估计的模糊核结果可以看出,Cho等[4]方法估计的模糊核有断续感,而Jia等[5]方法的结果又太连续,本文方法估计相对准确.对比复原结果,由于原图像模糊程度比较剧烈,从常规方法的复原结果上看,块效应的负面效应被放大的较多,图像块的断续感很明显,特别是Jia等[5]的方法.本文方法的复原结果有效抑制了压缩块效应,目视效果最好.图 5是卡通图像的复原结果,卡通图像模糊相对较小,但模糊核形状比较复杂.从模糊核估计结果来看,Cho等[4]方法估计的模糊核依然有断续感,Jia等[5]方法的结果相对准确但模糊核形状中本应有的“孔”已经消失,本文方法估计的模糊核是最准确的.同时从复原结果上看,本文方法在图像细节丰富的区域取得了较好的块效应抑制复原效果,复原图明显最优.
为了对复原结果有客观的比较标准,选取了2种有代表性的评价指标峰值信噪比(PSNR)和结构相似度[19](SSIM)对在压缩质量40下的4张模糊图及不同方法复原图进行图像质量评价.2种评价参数均是数值越大表明复原效果越好.不同方法的质量评价参数如表 1所示.
| 表 1 3种方法的图像质量评价参数 Table 1 Quality assessment parameters of four algorithms |
从复原结果来看,几种盲复原方法的复原图像相比原压缩模糊图像均有一定程度的质量提高.本文方法的客观参数评价数值提高最多,从表中可知对于压缩降质模糊图像复原后的PSNR相对其他方法提高了2~3 dB,SSIM评价结果相对其他方法提高0.05~0.10.主观、客观评价均表明了提出方法对于改善模糊图像块效应负面效应的有效性.
3.2 块效应程度与复原效果关系为了研究块效应程度与复原图像质量的关系,选取Levin库中的人物特写图,对不同压缩质量下的模糊图像进行盲复原.如图 6所示为压缩质量选择20时的模糊图像,可以从图 6(b)的局部放大图中看到非常明显的8×8边界块效应.对此模糊图像用不同方法进行图像盲复原,得到的复原结果如图 7所示.从结果中可以看到,本文方法即使在压缩率较高的模糊图像复原上也能得到大幅改善的复原效果.

|
图 6 实验压缩模糊图像 Fig. 6 Compressed blur image in the experiment |
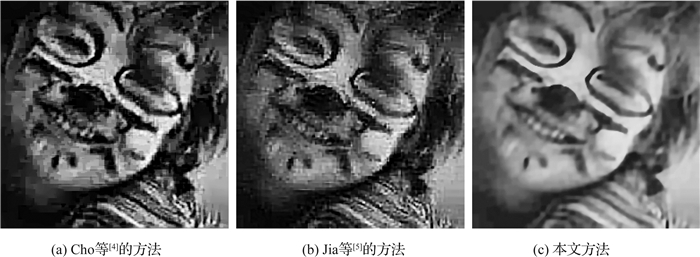
|
图 7 不同方法的人物特写图复原结果比较(压缩质量20) Fig. 7 Comparison of restoration results of character image using different methods (compress quality 20) |
同样地,在压缩质量分别设为40、60、80的时候,也采用相应的复原方法对其进行盲复原.为了客观比较复原质量,依然采用PSNR和SSIM对复原结果进行量化评价.如图 8和9所示分别直观地绘出了PSNR以及SSIM评价指标的柱状比较图.图中每一个压缩质量下的4根柱子分别为压缩降质模糊图像、Cho等[4]方法、Jia等[5]方法以及本文方法的复原图像评价指标.从图中可以看到,不同的压缩质量下的模糊图像的评价指标值相差较小,块效应影响的是局部观感,图像模糊仍然是导致像质退化的主要因素.但在压缩质量为20时,其他复原方法的复原质量甚至比原模糊图更为“糟糕”,说明由于模糊核估计不准以及复原时块效应引入的负面效应已经抵消了消除模糊对像质的指标提升.从整体趋势看,压缩质量越高也即压缩图像的块效应越不明显,模糊核估计准确性越好,复原图像的质量也越好.本文方法在各种压缩质量下的复原图像的评价指标都有显著提升,随着压缩质量的提高,是否在复原中考虑块效应对复原结果的影响逐渐变小.从图表中可以得出,在压缩块效应较为严重的图像中,也即压缩质量小于40的模糊图像,必须在盲复原算法中考虑块效应的影响;模糊图像块效应比较明显的图像,也即压缩质量在40至80之间,应用本文方法也会取得显著提升的复原结果;对于基本无压缩的模糊图像,也即压缩质量在80以上,复原结果相差已经较小,可以直接采用常规盲复原方法,无需对块效应进行特别处理.
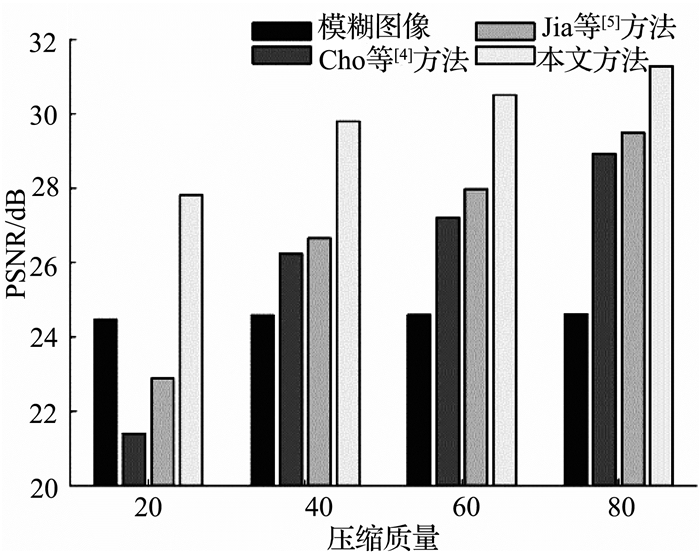
|
图 8 不同压缩质量下的图像复原结果PSNR对比 Fig. 8 Comparison of restoration result PSNR values under different compressed quality |
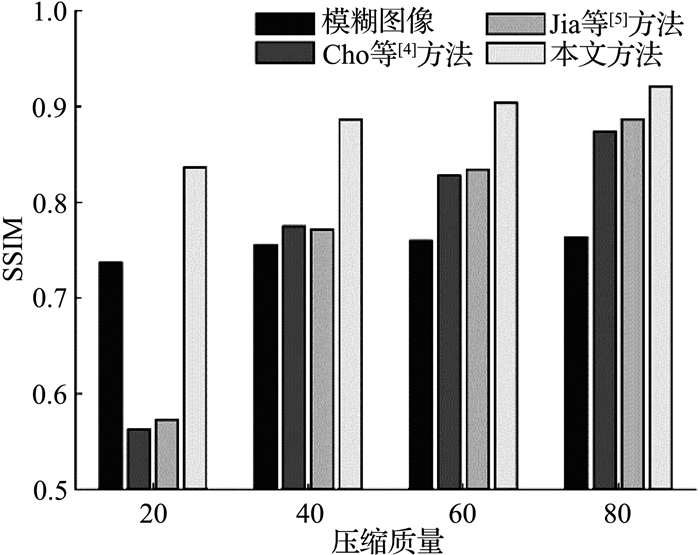
|
图 9 不同压缩质量下的图像复原结果SSIM对比 Fig. 9 Comparison of restoration result SSIM values under different compressed quality |
本文提出了一种基于块效应抑制的压缩降质图像盲复原方法,一定程度上解决了由于JPEG压缩而造成的复原图像质量变差的问题.在模糊核估计阶段,优化了有效显著边缘选择与模糊核约束方法.并在最终图像复原过程中,提出了在迭代过程中抑制块效应的正则化约束项.实验结果表明,采用本文方法有效提高了在盲复原过程中受块效应影响而进一步退化的模糊图像模糊核估计的准确性以及复原图像的质量.同时也指出了图像压缩质量与复原效果的关系,给出了块效应对复原不产生显著影响所对应的图像压缩质量值.
| [1] |
FERGUS R, SINGH B, HERTZMANN A, et al. Removing camera shake from a single photograph[J]. Acm Transactions on Graphics, 2006, 25(3): 787-794. DOI:10.1145/1141911 |
| [2] |
SHAN Q, JIA J, AGARWALA A. High-quality motion deblurring from a single image[J]. Acm Transactions on Graphics, 2008, 27(3): 15-19. |
| [3] |
KRISHNAN D, TAY T, FERGUS R. Blind deconvolution using a normalized sparsity measure[C]//IEEE Conference on Computer Vision and Pattern Recognition. Providence: IEEE, 2011: 233-240. http://ieeexplore.ieee.org/document/5995521/
|
| [4] |
CHO S, LEE S. Fast motion deblurring[J]. Acm Transactions on Graphics, 2009, 28(5): 89-97. |
| [5] |
JIA J, XU L. Two-phase kernel estimation for robust motion deblurring[C]//European Conference on Computer Vision. Greece: [s. n. ], 2010: 81-84. https://link.springer.com/chapter/10.1007/978-3-642-15549-9_12
|
| [6] |
XU L, ZHENG S, JIA J. Unnatural L0 sparse representation for natural image deblurring[C]//IEEE Conference on Computer Vision and Pattern Recognition. Washington: IEEE, 2013: 1107-1114. https://wenku.baidu.com/view/37775a4ef12d2af90242e6cf.html
|
| [7] |
DONG Wen-de, FENG Hua-jun, XU Zhi-hai, et al. Blind image deconvolution using the Fields of Experts prior[J]. Optics Communications, 2012, 285(24): 5051-5061. DOI:10.1016/j.optcom.2012.08.041 |
| [8] |
LAI Wei-sheng, DING Jian-jiun, LIN Yen-yu, et al. Blur kernel estimation using normalized color-line priors[C]//IEEE Conference on Computer Vision and Pattern Recognition. Boston: IEEE, 2015: 64-72. http://cmlab.csie.ntu.edu.tw/~jasonlai/colorline_deblur/
|
| [9] |
ZUO W, REN D, ZHANG D, et al. Learning iteration-wise generalized shrinkage-thresholding operators for blind deconvolution[J]. IEEE Transactions on Image Processing, 2016, 25(4): 1751-1764. |
| [10] |
王国栋, 徐洁, 潘振宽, 等. 基于归一化超拉普拉斯先验项的运动模糊图像盲复原[J]. 光学精密工程, 2013, 21(5): 1340-1348. WANG Guo-dong, XU Jie, PAN Zhen-kuan, et al. Blind image restoration based on normalized hyper laplacian prior term[J]. Optics and Precision Engineering, 2013, 21(5): 1340-1348. |
| [11] |
ZHANG X, WANG R, TIAN Y, et al. Image deblurring using robust sparsity priors[C]//IEEE Conference on Image Processing. Quebec: IEEE: 2015: 138-142. http://ieeexplore.ieee.org/document/7350775/
|
| [12] |
MICHAELI T, IRANI M. Blind deblurring using internal patch recurrence[J]. European Conference on Computer Vision. Zurich:[s.n.], 2014, 783-798. |
| [13] |
FOI A, KATKOVNIK V, EGIAZARIAN K. Pointwise shape-adaptive DCT for high-quality denoising and deblocking of grayscale and color Images[J]. IEEE Transactions on Image Processing, 2007, 16(5): 1395-1411. DOI:10.1109/TIP.2007.891788 |
| [14] |
LUO Y, WARD R K. Removing the blocking artifacts of block-based DCT compressed images[J]. IEEE Transactions on Image Processing, 2003, 12(7): 838-42. DOI:10.1109/TIP.2003.814252 |
| [15] |
WEERASINGHE C, LIEW W C, YAN H. Artifact reduction in compressed images based on region homogeneity constraints using the projection onto convex sets algorithm[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2002, 12(10): 891-897. DOI:10.1109/TCSVT.2002.804881 |
| [16] |
LEVIN A, WEISS Y, DURAND F, et al. Understanding and evaluating blind deconvolution algorithms[C]//IEEE Conference on Computer Vision and Pattern Recognition. Miami: IEEE, 2009: 1964-1971. http://ieeexplore.ieee.org/document/5206815/
|
| [17] |
TOMASI C, MANDUCHI R. Bilateral filtering for gray and color images[C]//IEEE International Conference on Computer Vision. Washington: IEEE, 1998: 839-846. http://homepages.inf.ed.ac.uk/rbf/CVonline/LOCAL_COPIES/MANDUCHI1/Bilateral_Filtering.html
|
| [18] |
OSHER S, RUDIN L I. Feature-oriented image enhancement using shock filters[J]. Siam Journal on Numerical Analysis, 1990, 27(4): 919-940. DOI:10.1137/0727053 |
| [19] |
WANG Z, BOVICK A C, SHEIKH H R, et al. Image quality assessment:from error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. DOI:10.1109/TIP.2003.819861 |



