2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
高精密装配作业是生产制造中一个重要的环节,耗费着大量的人力和物力.随着工业机器人技术的发展,制造业对机器人取代人工完成精密装配有着更加迫切的需求.
让机器人完成精密装配作业,是一件具有挑战的任务.以工业机器人大臂减速机的装配为例,工业机器人大臂装配孔的加工半径为67.50~67.52 mm,大臂减速机外围加工半径为67.48~67.50 mm,二者之间的配合公差小于40 μm.装配时,由于机器人在装配时,大臂和减速机都存在初始的位置偏差,不合适的调整,都很容易导致整个装配的失败,如减速机无法装入大臂,或装入后发生卡死的现象.高精密轴孔装配的难点在于采用常规的位置控制完全无法进行装配,工件的位置偏差无法通过示教和视觉定位的方式消除,装配件无法插入工件,为了解决该问题, 本文提出了工业机器人进行轴孔装配的装配流程和力/位混合控制策略,旨在让工业机器人能够顺利安全地完成装配作业.
目前让工业机器人进行精密装配主要采用两大类方法,一类是机械柔顺的方法,即利用一些能够吸收或储存能量的机械器件,如弹簧、阻尼等组成的机构,使机器人能够对外部作用力产生一定的自然顺从能力,如Lane等[1]设计遥轴顺应性装置(remote center compliance, RCC),但该方法主要缺陷为:需要为每个装配零件设计独自的柔顺部件专用性强,适应能力差,使用范围受到限制;另一类方法是柔顺控制的方法,指通过对伺服系统的主动控制,实现机器人的柔顺性.柔顺控制又包括无力/力矩传感器,和有力/力矩传感器.关于无力/力矩传感器的研究,Van等[2-4]通过基于电流的的方法估算机器人末端与环境的接触力,Stolt等[5-6]通过减小电机关节空间的PD系数,也称软伺服,是使机器人在有外界力影响的情况下,能够产生一定的位置偏差,具有一定的柔顺性.无力传感器的柔顺控制由于对外界力的估计存在局限,对于精度要求比较高的场合,无法很好地完成任务.有力传感器的柔顺控制,包括Hogan等[7-9]提出的阻抗控制和力/位混合控制,阻抗控制的柔顺性高,但不能很好地控制末端力,需要精确知道约束环境的刚度和位置.Mills等[10]提出力/位混合控制的方法可以较好地控制末端力,比较适用于具有高精度要求的装配作业的,也是当前商业机器人公司(如库卡、ABB等)普遍采用的方法.当前的力/位混合控制方法实现包括基于位置控制实现[11]和基于扭矩控制实现,基于位置控制实现的控制系统简单,适合于开放系统,如商业机器人公司库卡研发的力控制包,但基于位置控制的系统带宽小,响应速度慢,而基于扭矩实现的控制系统带宽大,但需要动力学补偿,系统复杂.还有一种是基于速度实现的方法,张庆伟等[12]进行相关的研究,但只进行仿真验证,本文在该方法基础上进行改进,提出了具有实际应用价值的基于速度控制的实现方法.
本文针对在高刚度环境下的高精度装配作业,以工业机器人装配大臂减速机的作业为例,提出了轴孔装配作业的装配流程和基于速度控制的力/位混合控制策略,旨在让工业机器人很好地完成轴孔装配类的作业任务,并进行实验的验证,该方法具有较大的工程应用价值.
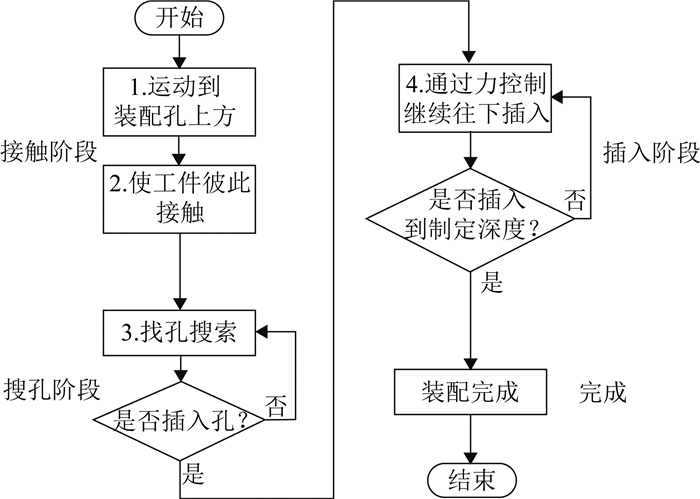
1 装配流程工业机器人大臂减速机的装配如图 1所示,装配流程如图 2所示,分为4个阶段,包括接近、搜孔、插入、完成.在每个阶段需要切换不同的控制模式,假设Z方向为孔的方向来描述每个阶段的模式切换.

|
图 1 工业机器人大臂及减速机装配 Fig. 1 Industrial robot big arm reducer assembly |
|
图 2 工业机器人精密装配流程 Fig. 2 Industrial robot high precision assembly process |
接触阶段:首先通过位置控制将装配轴运送到孔的上方,再通过速度控制使机器人彼此接触.
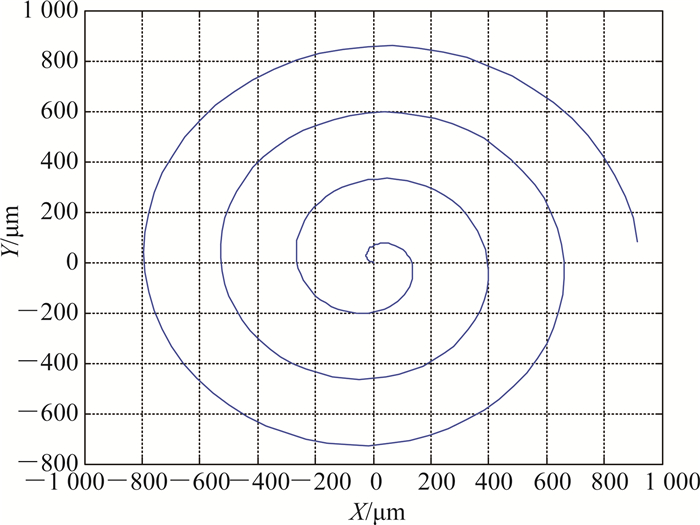
搜孔阶段:在搜孔阶段,采用力/位混合控制,例如在X、Y方向上进行位置控制,位置的轨迹为螺旋线的搜索方式,其搜索以接触点为起始点由内向外的轨迹进行,仿真结果如图 3所示.Z方向力控制,保持一个恒定的力值,使在找到孔的时候,能够进行插入.
|
图 3 螺旋线轨迹仿真 Fig. 3 Spiral trajectory simulation |
插入阶段:通过力控制把轴插入孔中,因为在此过程为了防止工件被卡住的现象,需要对工件进行姿态的调整,所以对X、Y方向不能进行位置控制,也需要进行力控制,即在此阶段,X、Y、Z这3个方向上包括3个姿态参数都采用力控制.
螺旋线方程是半径不断增大的圆方程,搜索的算法为
| $ \left. \begin{array}{l} X = r\left( t \right)\sin \left( {\omega t} \right) = vt\sin \left( {wt} \right),\\ Y = r\left( t \right)\cos \left( {\omega t} \right) = vt\cos \left( {wt} \right). \end{array} \right\} $ | (1) |
式中:t为搜索进行时间,ω为搜索角频率,体现为螺旋线的密度,r为搜索半径,v为搜索速度.
完成阶段:装配结束.
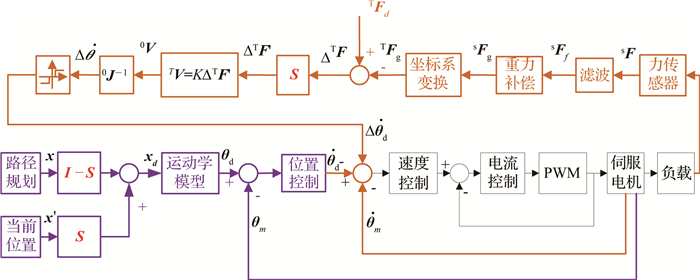
2 控制方案 2.1 基于速度环的力/位混合控制在力/位混合控制中,包含6个自由度空间,前3个自由度是进行力控制或位置控制,后3个自由度是进行力矩控制或姿态控制,每个自由度采用的控制方式由S选择矩阵(6×6对角型)决定,当S选择矩阵对应的自由度元素为1时,表示这个自由度采用力/力矩控制,当S选择矩阵对应的自由度元素为0时,表示这个自由度采用位置/姿态控制.基于速度环实现的力/位混合控制框图如图 4所示.整个机器人系统的控制结构分为上下2层,上层是机器人本体的控制,进行多轴机器人运动学和力控制的计算,下层是单轴电机的伺服控制,为商用伺服驱动器通用的三环控制结构.
|
图 4 基于速度环实现的力/位混合控制框图 Fig. 4 Hybrid force/position control system based on motor velocity control loop |
为了更清晰地描述力/位混合控制基于速度环的实现原理,以下分别描述位置控制的实现和力控制的实现,本节以机器人末端执行器在X轴、Y轴方向上进行位置控制,在Z轴方向上进行力控制为例,该方法的核心思想是:在X、Y方向上进行常规的位置控制,在Z方向上,机器人在保持当前位置的基础上,根据力的偏差进行速度信号的修正,从而达到力跟踪的目的.则此时的选择矩阵为
| $ \mathit{\boldsymbol{S}} = {\rm{diag}}\left( {0,0,1,0,0,0} \right). $ | (2) |
在进行位置控制时,包括2方面,一方面是X、Y方向上的位置控制,另一方面是Z方向上的位置控制.首先是X、Y方向上的位置控制,通过笛卡尔空间的路径规划,得到末端执行器期望位置和姿态的6维坐标矢量χ,通过选择矩阵I-S,则有(I-S)χ,表示在X、Y轴方向上进行位置控制,不进行力控制;其次是Z方向上的位置控制,Z轴方向不能位置给定值不能为零,而是需要保持上一次经过力控制之后的位置当前值,因此需要当前的末端执行器期望位姿χ′,通过选择矩阵S,则Sχ′,则最终在求解机器人运动学反解的位姿给定值χd,以此作为电机三环控制的位置给定值,从而实现了机器人在X轴、Y轴、Z轴方向上的所需要的位置给定.
| $ \mathit{\boldsymbol{\chi }} = {\left[ {{P_x},{P_y},{P_z},\alpha ,\beta ,\gamma } \right]^{\rm{T}}}. $ | (3) |
| $ \left[ {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{S}}} \right]\mathit{\boldsymbol{\chi }} = {\left[ {{P_x},{P_y},0,\alpha ,\beta ,\gamma } \right]^{\rm{T}}}. $ | (4) |
| $ \mathit{\boldsymbol{S\chi '}} = {\left[ {0,0,{{P'}_z},0,0,0} \right]^{\rm{T}}}. $ | (5) |
| $ \begin{array}{l} {\mathit{\boldsymbol{\chi }}_d} = \left[ {\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{S}}} \right]\mathit{\boldsymbol{\chi }} + \mathit{\boldsymbol{S\chi '}} = \\ {\left[ {{P_x},{P_y},{{P'}_z},\alpha ,\beta ,\gamma } \right]^{\rm{T}}}. \end{array} $ | (6) |
在进行力控制时,力传感器测得的数据SF,经过滤波、坐标系的变换等,得到TFg,T为工具坐标系.因为在Z轴方向上进行力控制,所以力的给定值为TFd,则力的偏差为ΔTF.经过选择矩阵S,则ΔTF′=ΔTF·S,通过阻尼矩阵K,将力的偏差转化为机器人笛卡尔空间的速度修正量ΔTV=KΔTF′,把速度修正量转化到基坐标系Δ0V,最后通过0J-1将笛卡尔空间速度的修正量Δ0V转化为关节空间的速度修正量
| $ {\Delta ^{\rm{T}}}\mathit{\boldsymbol{F'}} = {\Delta ^{\rm{T}}}\mathit{\boldsymbol{F}} \cdot \mathit{\boldsymbol{S}} = {\left[ {0,0,{\Delta ^{\rm{T}}}{f_z},0,0,0,} \right]^{\rm{T}}}. $ | (7) |
| $ {\Delta ^{\rm{T}}}\mathit{\boldsymbol{V}} = \mathit{\boldsymbol{K}}{\Delta ^{\rm{T}}}\mathit{\boldsymbol{F'}} = \left[ {\begin{array}{*{20}{c}} {{k_x}}&0&0&0&0&0\\ 0&{{k_y}}&0&0&0&0\\ 0&0&{{k_z}}&0&0&0\\ 0&0&0&{{k_\alpha }}&0&0\\ 0&0&0&0&{{k_\beta }}&0\\ 0&0&0&0&0&{{k_\gamma }} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 0\\ 0\\ {{\Delta ^{\rm{T}}}{F_z}}\\ 0\\ 0\\ 0 \end{array}} \right]. $ | (8) |
| $ \Delta \mathit{\boldsymbol{\dot \theta }} = {\left[ {\Delta {{\dot \theta }_1},\Delta {{\dot \theta }_2},\Delta {{\dot \theta }_3},\Delta {{\dot \theta }_4},\Delta {{\dot \theta }_5},\Delta {{\dot \theta }_6}} \right]^{\rm{T}}}. $ | (9) |
式中:ΔTFz为ΔTF′的元素,kx,ky, kz、kα、kβ、kγ为阻尼矩阵K的阻尼系数,
力/位混合控制的思想是,在需要位置/姿态控制的自由度I-S上,采用事先的笛卡尔空间的规划路径,通过运动学反解来取得电机的给定值;在需要力/力矩控制的自由度S上,在当前该自由度的位置基础上,通过对速度的修正,达到控制力的目的.
在本次装配任务中,接触和搜孔阶段只需要单自由度的力控制,S选择矩阵中Z方向对应的元素为1,其他元素为0.在插入阶段,为了防止装配件的卡住,在6个自由度上都进行力/力矩控制,S选择矩阵中对角线的6个元素都为1,其中只有Z方向设有不为零的期望力以进行插入,其他方向的期望力/力矩设为零,以进行位姿的调整,从而顺从插入时所受到的外力.
本次力控制策略通过阻尼关系矩阵,建立机器人末端的笛卡尔速度V和末端笛卡尔作用力F之间的关系,把笛卡尔力的误差信号转化为笛卡尔速度的修正量,再由雅可比逆矩阵把末端笛卡尔速度的修正量转化成关节角速度的修正量.
| $ {\Delta ^0}\mathit{\boldsymbol{V}} = \left[ \begin{array}{l} {\Delta ^0}\mathit{\boldsymbol{\upsilon }}\\ {\Delta ^0}\mathit{\boldsymbol{\omega }} \end{array} \right] = {}^0\mathit{\boldsymbol{J}}{\left( \mathit{\Theta } \right)_{6 \times 6}}\Delta \mathit{\boldsymbol{ \boldsymbol{\dot \varTheta} }}. $ | (10) |
式中:左上标表示笛卡尔速度所参考的坐标系,在本次机器人系统中表示为基坐标系.Δ0υ为基座标线速度,Δ0ω为基座标角速度,0J(Θ)6×6为基座标雅可比矩阵,ΔΘ为机器人关节的速度修正向量.
下面是雅可比矩阵的求解:因为操作臂末端的笛卡尔速度的产生是由6个关节轴的旋转产生的,所以操作臂末端的笛卡尔速度是有6个关节速度矢量叠加而成的,其中末端笛卡尔角速度ω等于6个关节的角速度矢量叠加,末端笛卡尔线速度υ等于6个关节的线速度矢量相加,又线速度等于角速度叉乘位置,则
| $ \mathit{\boldsymbol{\omega }} = {{\dot \theta }_1}{\mathit{\boldsymbol{e}}_1} + {{\dot \theta }_2}{\mathit{\boldsymbol{e}}_2} + \cdots {{\dot \theta }_6}{\mathit{\boldsymbol{e}}_6}. $ | (11) |
| $ \mathit{\boldsymbol{\upsilon }} = {{\dot \theta }_1}{\mathit{\boldsymbol{e}}_1} \times {\mathit{\boldsymbol{r}}_1} + {{\dot \theta }_2}{\mathit{\boldsymbol{e}}_2} \times {\mathit{\boldsymbol{r}}_2} + \cdots {{\dot \theta }_6}{\mathit{\boldsymbol{e}}_6} \times {\mathit{\boldsymbol{r}}_6}. $ | (12) |
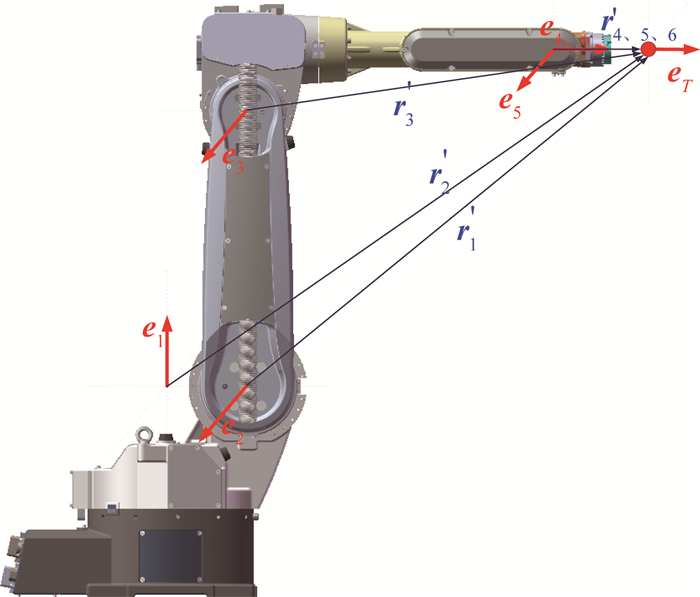
式中:e1、e2…e6表示为关节轴旋转方向的单位矢量;r1、r2…r6为以各个关节轴坐标系原点为起点,以末端为终点的位置矢量,表示每个关节旋转对末端运动的贡献.各个矢量如图 5所示,则得到雅可比矩阵为
|
图 5 工业机器人单位及位置矢量图 Fig. 5 Industrial robot unit and position vector |
| $ \mathit{\boldsymbol{J}}\left( \mathit{\Theta } \right) = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{e}}_1} \times {\mathit{\boldsymbol{r}}_1}}&{{\mathit{\boldsymbol{e}}_2} \times {\mathit{\boldsymbol{r}}_2}}& \cdots &{{\mathit{\boldsymbol{e}}_6} \times {\mathit{\boldsymbol{r}}_6}}\\ {{\mathit{\boldsymbol{e}}_1}}&{{\mathit{\boldsymbol{e}}_2}}& \cdots &{{\mathit{\boldsymbol{e}}_6}} \end{array}} \right]. $ | (13) |
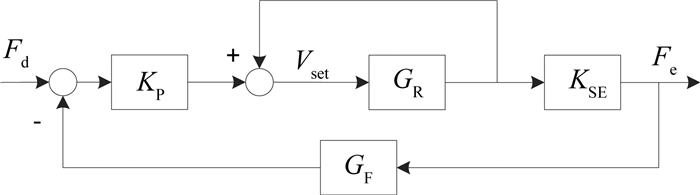
2.1节所提出的工业机器人力/位混合控制方法包括位置闭环和力闭环,本节只提炼分析其中力闭环(S选择矩阵中元素为1的回路),以分析该力闭环的稳定性及稳态误差.在力控制中,可以通过控制关节扭矩来达到控制末端力的作用,也可以通过控制末端位置来达到末端力的作用,本文力控制策略的核心思想是通过末端速度来达到控制末端力的目的,通过该方法也可以把速度进行积分可变为位置信号,加到位置环即可转换为位置的实现方式.本文所提出的工业机器人基于速度环的力控制系统模型框图如图 6所示.其中GR为机器人的速度控制系统特性,GF为力信号的滤波环节,KP为阻尼系数矩阵,KSE为接触环境的刚度,Fd、Fe为期望达力和环境的作用力.
|
图 6 基于速度环的力控制系统模型框图 Fig. 6 Force control block diagram based on velocity control |
机器人速度控制系统的传递函数为
| $ {G_{\rm{R}}} = \frac{1}{{{T_{\rm{R}}}s + 1}}\exp \left( { - s{T_{\rm{d}}}} \right). $ | (14) |
式中:Td为机器人系统的延迟时间(控制周期),TR为速度控制系统惯性环节的上升时间, s为拉普拉斯变换.图 6中速度控制环节GR的速度给定量Vset包括2部分,一个是机器人当前的速度,另一个是当前速度的修正量,通过力的偏差给出.比如当接触力偏小时Fe < Fd,则力的偏差ef=Fd-Fe>0,也就是速度的修正量为正,此时机器人往当前速度的正方向进行修正;当接触力偏大时Fe>Fd,则力的偏差ef=Fd-Fe < 0,也就是速度的修正量为负,此时机器人往当前速度的负方向进行修正.由于力负反馈外环存在,能够对当前的状态进行修正,保证了系统的稳定.该环节也可以用位置控制系统来替代,即转化为位置控制的实现方式,但是位置控制环节的上升时间Tr比速度控制系统的上升时间更长,力闭环的控制系统的带宽更小.
因为现在的工业机器人上层控制器的实时控制周期为Td=4 ms,很小,并且在每个控制周期内底层伺服驱动器能够进行线性插补,整个机器人系统可近视为连续系统,则
| $ \exp \left( { - s{T_{\rm{d}}}} \right) \approx \frac{1}{{{T_{\rm{d}}}s + 1}}. $ | (15) |
则有
| $ {G_{\rm{R}}} = \frac{1}{{{T_{\rm{R}}}s + 1}}\frac{1}{{{T_{\rm{d}}}s + 1}}. $ | (16) |
滤波环节传递函数为
| $ {G_{\rm{F}}} = \frac{1}{{{T_{\rm{F}}}s + 1}}. $ | (17) |
式中:TF为滤波时间常数.
由图 6控制系统框图和式(16)、(17),则可得整个力控制系统闭环传递函数为
| $ \begin{array}{*{20}{c}} {\mathit{\Phi }\left( s \right) = \frac{{{K_{\rm{P}}}{K_{{\rm{SE}}}}{G_{\rm{R}}}}}{{1 + {K_{\rm{P}}}{K_{{\rm{SE}}}}{G_{\rm{F}}}{G_{\rm{R}}} - {G_{\rm{R}}}}} = \frac{{{K_{\rm{P}}}{K_{{\rm{SE}}}}\frac{1}{{{T_{\rm{R}}}s + 1}}\frac{1}{{{T_{\rm{d}}}s + 1}}}}{{1 + \frac{1}{{{T_{\rm{R}}}s + 1}}\frac{1}{{{T_{\rm{d}}}s + 1}}\left( {{K_{\rm{P}}}{K_{{\rm{SE}}}}\frac{1}{{{T_{\rm{F}}}s + 1}} - 1} \right)}} = }\\ {\frac{{{K_{\rm{P}}}{K_{{\rm{SE}}}}\left( {{T_{\rm{F}}}s + 1} \right)}}{{{T_{\rm{R}}}{T_{\rm{d}}}{T_{\rm{F}}}{s^3} + \left( {{T_{\rm{R}}}{T_{\rm{d}}} + {T_{\rm{R}}}{T_{\rm{F}}} + {T_{\rm{d}}}{T_{\rm{F}}}} \right){s^2} + \left( {{T_{\rm{R}}} + {T_{\rm{d}}}} \right)s + {K_{\rm{P}}}{K_{{\rm{SE}}}}}}.} \end{array} $ | (18) |
由特征方程可求出稳定性条件为
| $ \begin{array}{l} \left( {{T_{\rm{R}}}{T_{\rm{d}}} + {T_{\rm{R}}}{T_{\rm{F}}} + {T_{\rm{d}}}{T_{\rm{F}}}} \right)\left( {{T_{\rm{R}}} + {T_{\rm{d}}}} \right) - \\ \;\;\;\;\;{T_{\rm{R}}}{T_{\rm{d}}}{T_{\rm{F}}}{K_{\rm{P}}}{K_{{\rm{SE}}}} > 0. \end{array} $ | (19) |
得
| $ \begin{array}{l} {K_{\rm{P}}} < \left( {T_{\rm{R}}^2{T_{\rm{d}}} + {T_{\rm{R}}}T_{\rm{d}}^2 + T_{\rm{R}}^2{T_{\rm{F}}} + T_{\rm{d}}^2{T_{\rm{F}}} + } \right.\\ \;\;\;\;\;\;\left. {2{T_{\rm{R}}}{T_{\rm{d}}}{T_{\rm{F}}}} \right)/\left( {{T_{\rm{R}}}{T_{\rm{d}}}{T_{\rm{F}}}{K_{{\rm{SE}}}}} \right). \end{array} $ | (20) |
近似为
| $ {K_{\rm{P}}} < 2/{K_{{\rm{SE}}}}. $ | (21) |
系统的误差
| $ \begin{array}{l} E\left( s \right) = {F_{\rm{d}}}\left( s \right) - {F_{\rm{e}}}\left( s \right){G_{\rm{F}}}\left( s \right) = \\ \;\;\;\;\;\;\;{F_{\rm{d}}}\left( s \right) - {F_{\rm{d}}}\left( s \right)\mathit{\Phi }\left( s \right){G_{\rm{F}}}\left( s \right) = \\ \;\;\;\;\;\;\;{F_{\rm{d}}}\left( s \right)\left[ {1 - \mathit{\Phi }\left( s \right){G_{\rm{F}}}\left( s \right)} \right]. \end{array} $ | (22) |
则系统的稳态误差为
| $ {e_{ss}} = \mathop {\lim }\limits_{s \to 0} sE\left( s \right) = \mathop {\lim }\limits_{s \to 0} s{F_{\rm{d}}}\left( s \right)\left[ {1 - \mathit{\Phi }\left( s \right){G_{\rm{F}}}\left( s \right)} \right]. $ | (23) |
由式(17)、(18)得
| $ \mathop {\lim }\limits_{s \to 0} \mathit{\Phi }\left( s \right) = \mathop {\lim }\limits_{s \to 0} {G_{\rm{F}}}\left( s \right) = 1 $ | (24) |
当输入信号为阶跃信号时Fd(s)=Fd/s,有
| $ \begin{array}{l} {e_{ss}} = \mathop {\lim }\limits_{s \to 0} sE\left( s \right) = \mathop {\lim }\limits_{s \to 0} s{F_{\rm{d}}}\left( s \right)\left[ {1 - \mathit{\Phi }\left( s \right){G_{\rm{F}}}\left( s \right)} \right] = \\ \;\;\;\;\;\;\mathop {\lim }\limits_{s \to 0} s\frac{{{F_{\rm{d}}}}}{s}\left[ {1 - \mathit{\Phi }\left( s \right){G_{\rm{F}}}\left( s \right)} \right] = {F_{\rm{d}}}\left( {1 - 1} \right) = 0. \end{array} $ | (25) |
为了验证本文所提出的基于速度控制方法,首先进行仿真,并以验证力控制系统的力跟踪性能为重点,包括了跃信号响应实验和正弦信号响应的实验.
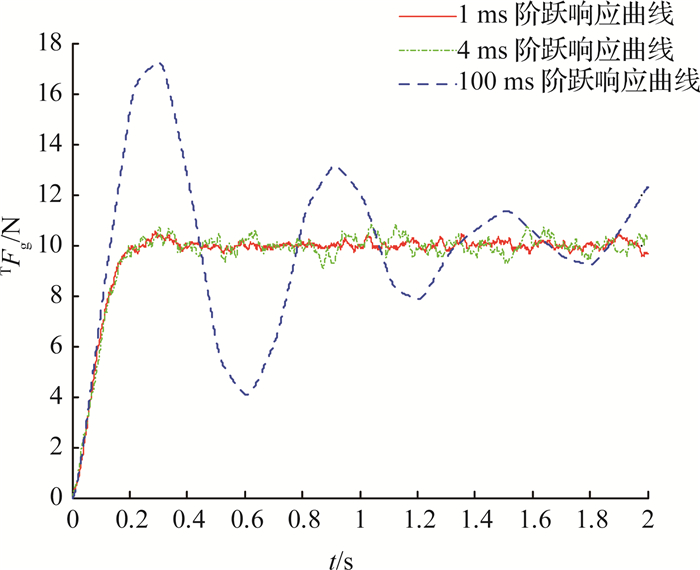
3.1 阶跃响应实验首先是力控制系统的阶跃响应,由于机器人和环境的高刚度,当二者接触时,短时间内会产生较大作用力,因此必须要考虑力控制周期对控制系统的影响,本次实验的采样周期分别为100、4、1 ms,控制系统的阶跃响应如图 7所示,图中t为时间,TFg为TFg的元素.该实验给定的期望力为10 N,从图中可以看出在100 ms采样周期时,系统也可以趋向稳定,但由于调节时间太长,会产生力的震荡的现象,导致系统不稳定,而4 ms采样周期和1 ms采样周期的阶跃响应具有快、准、稳的特点,能够很好地跟踪期望力,接近于连续系统的响应性能.并且在对阶跃信号的跟踪上,由于系统带宽主要受滤波器参数的影响,基于速度控制和基于位置控制的跟踪性能几乎一样,都能达到很好的跟踪效果.
|
图 7 力控制系统在不同采样周期下的阶跃响应 Fig. 7 Step response of force control under different sampling period |
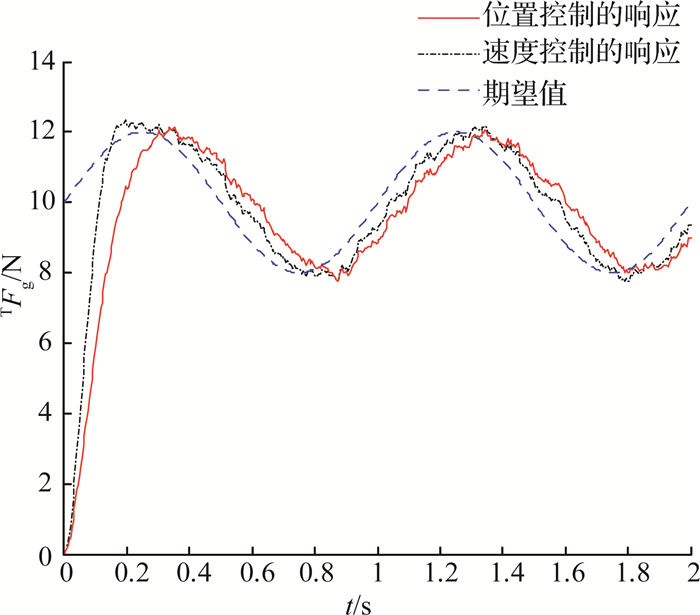
正弦响应实验分为力控制系统的正弦信号响应,分别给2个系统输入同样频率的正弦信号,看这2个系统的响应结果,以验证基于速度控制与基于位置控制[10]的系统带宽,以及系统在快速变化信号下的响应速度.当正弦输入信号的频率为1 Hz时,系统的响应如图 8所示.从图中可以看出2种控制方法都有一些滞后,基于位置控制的方法滞后稍多一点,但都能够较好跟踪到期望值.
|
图 8 力控制系统跟踪1 Hz正弦信号响应 Fig. 8 Sinusoidal response of force control to tracking 1 Hz signal |
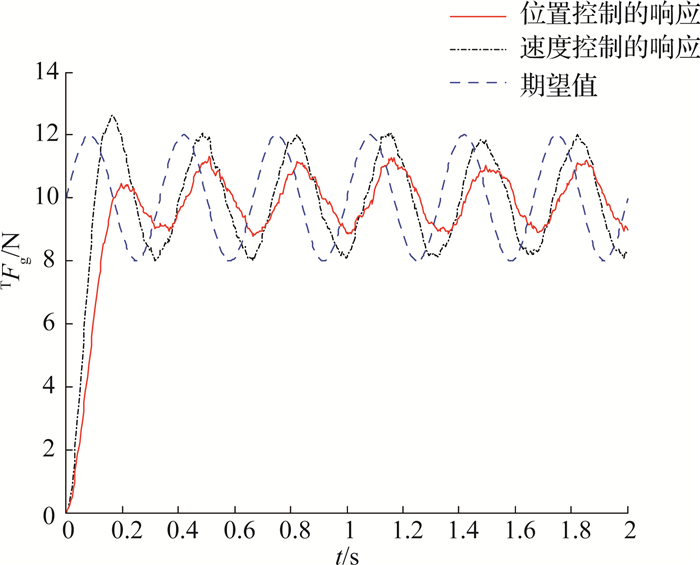
当正弦输入信号的频率为3 Hz,系统的响应如图 9所示.从图中可以看出在给定期望值的跟踪上,2种控制方法在时间上都有滞后,但基于速度控制方法的滞后更小,并且在幅值的跟踪上,基于速度的控制方法没有跟踪偏差,而基于位置控制有明显的衰减.
|
图 9 力控制系统跟踪3 Hz正弦信号响应 Fig. 9 Sinusoidal response of force control to tracking the 3 Hz signal |
从以上实验可以看出,基于速度控制的响应系统相对于基于位置控制的力控制系统具有更高的截止频率,更大的控制系统带宽,因此在跟踪变化较快的信号时,具有较快的响应速度和较好的跟踪性能.
4 实验为了验证本文提出的力控制精密装配方法,本次采用新松公司50 kg六轴工业机器人,进行工业机器人大臂减速机的装配实验,由于商用工业机器人一般都只开放位置环,因此本次实验是把速度信号积分转化为位置信号进行力闭环控制的.机器人末端装有ATI公司的六维力/力矩传感器,型号为FT17350,抓取的部件为负载6 kg的工业机器人大臂外壳,实验的目标是把大臂外壳装入减速机.整个机器人装配系统如图 10所示.

|
图 10 工业机器人大臂减速机装配系统 Fig. 10 Industrial robot big arm reducer assembly system |
实验分为2部分,一部分是阶跃响应实验,以验证力控制方法的力跟踪能力,另一部分是精密装配实验,以验证所提出装配方法可行性.在实验的过程中,把滤波截止频率设为5 Hz,这是因为力传感器含有噪声,包括来自机器人和工具的机械振动,来自电子部件的电磁干扰.
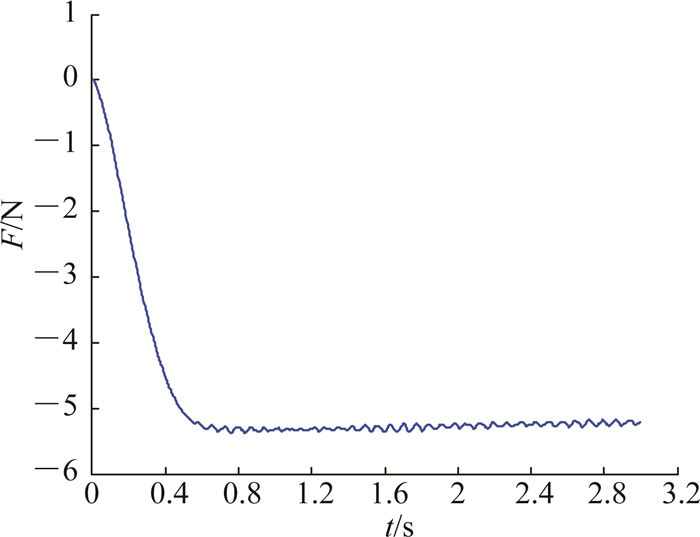
4.1 阶跃响应实验首先是阶跃响应实验,设定机器人在传感器坐标系下期望力为-5 N(期望力为负号是因为传感器坐标系和用户坐标系方向相反,即用户坐标系下期望力位+5 N),如图 11所示,机器人能够达到跟踪期望力的效果.
|
图 11 工业机器人的阶跃响应实验 Fig. 11 Step response of Industrial robot |
在实验过程中,如果末端执行器或环境刚度较小,具有线性的弹性形变时(如塑料、薄铝板等),该方法能够达到较好的力跟踪控制效果.但如果环境刚度过大,机器人在接触环境时微小的位移就会产生较大的力,因此在阶跃响应中为了达到期望力,机器人对末端位置/速度的修正量都是极其微小的,而一旦提高速度,即增加位置/速度的修正量,机器人和环境就会出现震荡的现象(机器人会脱离接触面),无法保持恒定的期望值.在实际生产过程中,由于设定修正速度一般都会超过理想力跟踪的修正速度,机器人此时只能达到在期望力附近波动的效果.
4.2 装配实验在实验时,让装配轴和装配孔有较大的位置偏差,以验证螺旋搜孔方式是否能够顺利找到装配孔.整个实验过程中力控制参数K设为1/300,机器人在接近过程中设定期望力为20 N,搜孔阶段设定期望力为3 N.如图 12所示是六维力Fx、Fy、Fz/力矩Tx、Ty、Tz传感器在6个方向上的力Fx、Fy、Fz和力矩Tx、Ty、Tz,其中, 0~38 s是螺旋搜孔的阶段,第0 s是接触的一瞬间,第38 s是搜索到装配孔,38~42 s是插入的阶段.

|
图 12 轴孔装配过程的力/力矩传感器数据 Fig. 12 Data of force/torque sensor in the peg-in-hole assembly process |
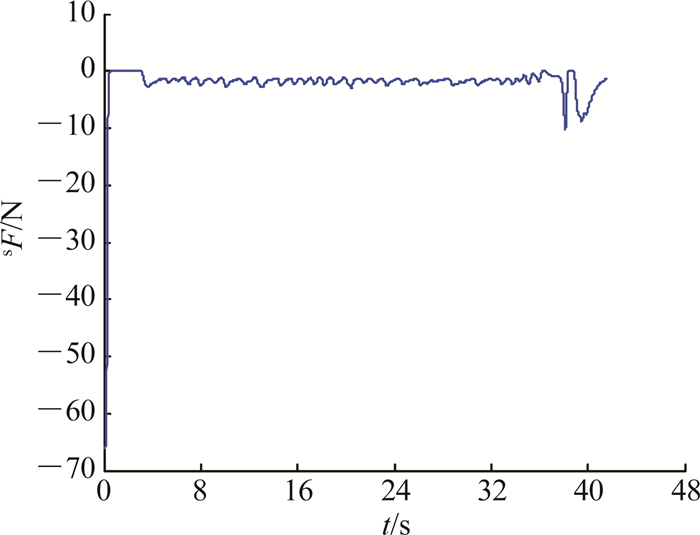
在整个装配过程中,只有Z方向是一直处于力控制的状态,并且除Z外其他方向上力/力矩变化不大,重点分析Z方向上的数据,如图 13所示,图中SF为SF的元素在接触的初期,力瞬间达到了66 N,并紧接归为0 N,这是因为在接近的过程中,期望力设为20 N,单位时间内位置修正量较大,可以缩小接近的时间,提高机器人的接近速度.在较快的接近速度下,初始接触力较大(力传感器安全的量程范围内),由于接触力过大,通过力控制的调节,产生了一次震荡,在再次进行接触时,开始了搜索阶段.搜索时,X、Y方向处于位置控制模式,机器人在X、Y的装配平面以初始接触点为起始点,随着时间的增加,以螺旋的形式从里往外搜索,公式(1)中的3个参数共同决定了搜索的效果,设定搜索速度v=0.1 rad/s,搜索时间t=50 s,即v和t共同决定了最大的搜索半径5 mm,搜索密度ω=0.5(决定搜索的半径内搜索的圈数的密度).Z方向处于力控制模式,设定的期望力为3 N,该设定对机器人末端在Z方向上位置/速度的修正量较小,使机器人以较小的接触力在装配表面进行搜孔;搜索到孔后,以设定的插入力进行插入,在插入的初始阶段由于轴和孔之间有微小的姿态偏差,在插入的过程中会产生额外的作用力,最终在力控制的调整下完成了整个轴孔装配过程.
|
图 13 轴孔装配Z方向上的力数据 Fig. 13 Force data of Z direction in peg-in-hole assembly process |
本文面向工业机器人高精密装配作业的背景,提出轴孔装配所需的装配流程,以及一种基于速度控制的力/位混合控制算法,该控制方案相对于基于位置控制的力控制系统,因为少了位置环,力闭环直接控制电机的速度值(相当于前馈),因此具有更大的控制系统带宽,在跟踪变化较快的信号时,具有较快的响应速度和较好的跟踪性能.而在跟踪阶跃信号时,慢速变化信号时,基于位置实现和基于速度实现差别不大.该控制方法系统最大的优点是原理清晰,结构简单,实现方便,它既适用于关节输入为速度信号的机器人系统,也可以适用于关节输入为位置信号(通过速度信号的积分)的机器人系统,为实现工业机器人力/位混合控制提供了一种新的实现方式,具有很大的工程应用价值.本文采用力/位混合控制和螺旋搜孔策略解决精密轴孔装配问题,并已应用于实际生产实践中,为了进一步提高工业机器人进行精密轴孔装配的装配效率,缩短装配时间,还有另外一个的研究重点是装配参数的优化工作,如优化搜索速度,搜索力,搜索半径,搜索圈数的密度等.
| [1] |
LANE J D. Evaluation of a remote center compliance device[J]. Assembly Automation, 1980, 1(1): 36-46. DOI:10.1108/eb004135 |
| [2] |
VAN DAMME M, BEYL P, VANDERBORGHT B, et al. Estimating robot end-effector force from noisy actuator torque measurements[C]//2011 IEEE International Conference on Robotics and Automation (ICRA). Shanghai, China: IEEE, 2011: 1108-1113. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?reload=true&arnumber=5980210
|
| [3] |
COLOMÉ A, PARDO D, ALENYA G, et al. External force estimation during compliant robot manipulation[C]//2013 IEEE International Conference on Robotics and Automation (ICRA). Karlsruhe, Germany: IEEE, 2013: 3535-3540. http://ieeexplore.ieee.org/document/6631072/
|
| [4] |
WAHRBURG A, ZEISS S, MATTHIAS B, et al. Contact force estimation for robotic assembly using motor torques[C]//2014 IEEE International Conference on Automation Science and Engineering (CASE). Taipei China: IEEE, 2014: 1252-1257. http://ieeexplore.ieee.org/document/6899487/
|
| [5] |
STOLT A, LINDEROTH M, ROBERTSSON A, et al. Force controlled robotic assembly without a force sensor[C]//2012 IEEE International Conference on Robotics and Automation (ICRA). Saint Paul. MN, USA: IEEE, 2012: 1538-1543. https://www.researchgate.net/publication/254041068_Force_controlled_robotic_assembly_without_a_force_sensor
|
| [6] |
CHEN H, WANG J, ZHANG G, et al. Robotic soft servo for industrial high precision assembly[C]//2008 IEEE Conference on Robotics, Automation and Mechatronics. Chengdu, China: IEEE, 2008: 24-29. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=4690877
|
| [7] |
HOGAN N. Impedance control:An approach to manipulation:Part Ⅱ-Implementation[J]. Journal of dynamic systems, measurement, and control, 1985, 107(1): 8-16. DOI:10.1115/1.3140713 |
| [8] |
ALBU-SCHÄFFER A, OTT C, HIRZINGER G. A unified passivity-based control framework for position, torque and impedance control of flexible joint robots[J]. The International Journal of Robotics Research, 2007, 26(1): 23-39. DOI:10.1177/0278364907073776 |
| [9] |
张庭, 姜力, 刘宏. 仿生假手抓握力控制策略[J]. 机器人, 2012, 34(2): 190-196. ZHANG Ting, JIANG Li, LIU Hong. A grasping force control strategy for anthropomorphic prosthetic hand[J]. Robot, 2012, 34(2): 190-196. |
| [10] |
MILLS J K, GOLDENBERG A A. Force and position control of manipulators during constrained motion tasks[J]. IEEE Transactions on Robotics and Automation, 1989, 5(1): 30-46. DOI:10.1109/70.88015 |
| [11] |
LI E, LI W. Hybrid force/position control for positional-controlled robotic manipulators in unknown environment[J]. Journal of China Coal Society, 2007, 6: 023. |
| [12] |
张庆伟, 韩利利, 徐方, 等. 基于打磨机器人的力/位混合控制策略研究[J]. 化工自动化及仪表, 2012, 39(7): 884-886. ZHANG Qing-wei, HAN Li-li, XU Fang, et al. Hybrid force/position control study based on grinding robot[J]. Control and Instruments in Chemical Industry, 2012, 39(7): 884-886. |



