2. 山东师范大学, 信息科学与工程学院, 山东 济南 250014;
3. 山东省网络环境智能计算技术重点实验室, 山东 济南 250012
2. School of Information Science and Engineering, Shandong Normal University, Jinan 250014, China;
3. Shandong Provincial Key Laboratory of Network based Intelligent Computing, University of Jinan, Jinan 250022, China
粒子群优化算法(PSO)是由Kennedy和Eberhart于1995年提出[1]{Kennedy, 1995 #1}, 该算法源于对鸟群觅食过程中的迁徙和群居行为的模拟, 是一种基于群体智能的随机搜索方法.群体中的每个粒子的位置代表搜索空间中的一个候选解.粒子个体之间通过位置信息的交流和学习来调整各自搜索方向.由于PSO算法概念简单, 收敛速度快, 参数调整方便, 容易实现等特点, 因此它在目标函数优化[2], 神经网络训练[3], 模糊控制系统[4], 模式识别[5], 信号处理[6], 图形图像处理[7], 统计学习模型参数优化[8], 机器学习模型参数优化[9]等诸多领域得到了广泛应用.
Vanden Bergh[10]证明了传统标准PSO算法高效, 但并不能保证一定收敛到全局最优点, 也不能保证搜索不到全局最优点, 而是以一定概率搜索到全局最优.针对PSO算法存在的问题国内外学者已提出了很多改进的方法, 这些方法大致可以归结为以下3种类型:参数调整的改进方法, 种群拓扑结构的改进方法和学习策略的改进方法.
基于参数调整的改进算法:标准PSO算法不能保证收敛到全局最优, 也不能保证搜索不到全局最优, 而是以一定的概率搜索到全局最优, 而选择最佳的参数会使最优解的坐标位置位于可行区域内的概率增大.Shi等[3]首次将惯性权重参数添加到标准PSO算法中, 提出全局PSO算法(Global version PSO, GPSO)[11], 分析参数选择对粒子群算法的影响.Clerc等[12]通过研究PSO算法的收敛性, 采用了压缩因子方法来控制粒子的搜索轨迹, 并提出局部版本的PSO算法(Local version PSO, LPSO)[13]. Nickabadi等[14]给出了权重调节的详细分析.Suganthan[15]提出了一种自适应加速因子的PSO算法, 这种算法比固定加速因子的算法实验效果相对较好.
基于种群拓扑结构改进的算法:该方法通过改变粒子之间相互学习的模式来提高种群的多样性.常见的粒子群拓扑结构包括:环形结构, 星形结构, 冯诺依曼结构.拓扑结构.不同拓扑结果对群体优势信息在种群内的传播有重要的影响. Mendes等[16]通过深入研究不同拓扑结构模型对算法性能的影响分析指出粒子群中粒子搜索过程中并非完全简单受到最优粒子的影响, 而是充分利用了所有粒子搜索的结果, 为此提出了一种基于全信息共享的PSO算法FIPS(Fully informed PSO, FIPS).Kennedy[11]指出粒子邻居数目较小的拓扑结构更有利于复杂问题的求解, 而粒子邻居数目较大的拓扑结构对于普通简单问题求解更好.Liang等[17]基于局部版本的PSO算法设计了一种动态非固定邻居模型的动态多种群PSO算法(dynamic multi-swarm PSO, DMSPSO).为避免粒子的所有维变量值向同一个目标粒子学习时产生的早熟现象, Liang等[18]提出了一种综合学习的算法(comprehensive learning PSO, CLPSO), 算法中对于每个粒子位置向量中的不同维度选择不同的粒子进行学习, 实验证明了该算法对多峰函数优化效果较好.基于拓扑结构的改进算法在不同程度上克服了标准PSO算法的早熟现象.
基于新的学习策略的改进算法:该类改进算法大多是通过设计新的学习策略使得算法更好的收敛.Peram等[19]提出一种基于适应度-距离比率的算法(Fitness-distance-ratio PSO, FDRPSO), 算法中粒子向着距离其较近且适应度较高的粒子飞行, 而不是飞向全局适应度最好的位置.Sun等[20]提出了一种基于量子行为的粒子群优化算法(Quantum behaved PSO, QPSO), 并从理论上证明了算法的全局收敛性.Kennedy等[21]提出一种基于高斯分布模型的粒子群优化算法(bar bone PSO, BBPSO).Zhan等[22]设计了一种基于正交学习策略的PSO算法.近年来,针对大规模全局优化中的问题解空间大,复杂度高的问题提出基于降维分解协同优化的解决方法[23],算法将高维空间分解为多个低维子空间, 然后算法轮流对这些子向量进行优化,最后合成一个完整的解向量,但是这类算法不适合求解变量间存在依赖性高的优化问题.
为解决PSO算法的过早收敛和种群多样性差问题,本文提出了一种基于随机维度划分的粒子群优化算法.随机维度划分和随机学习的双重动态随机机制, 使得算法在单峰多峰函数优化中具备较好的全局探测和局部挖掘能力.
1 PSO算法原理粒子群算法(PSO)与其他的进化算法(诸如遗传算法GA, 蚁群算法ACO, 人工蜂群算法ABC)类似, 都是通过群体中个体之间的信息共享和协作来指导种群的进化.PSO与其他进化算法的不同在于它将种群个体看成是在维搜索空间内没有质量和体积的粒子, 粒子的位置代表了搜索空间内的一个候选解, 粒子在搜索空间内以一定的速度运动, 粒子的飞行过程即解的搜索过程.粒子位置的优劣程度通常通过给定目标函数的适应度值来衡量.粒子的飞行速度可以根据粒子自身的飞行经验(即自身历史最优位置)和同伴的飞行经验(通常为种群中最佳粒子的位置)来进行动态调整.种群通过多次迭代来寻找搜索空间内的最佳粒子位置, 即待求解问题的最优解.
假设待优化问题的决策变量数目为D, 则问题的搜索空间为D维.在搜索空间内首先初始化M个粒子,其中每个粒子在空间中的位置采用一维向量x表示,粒子的空间移动速度用一维向量v表示.对于粒子i, 在第t次迭代时,粒子的位置向量可以表示为xi(t)=[xi, 1(t), xi, 2(t), …, xi, D(t)], 速度向量可表示为vi(t)=[vi,1(t), vi, 2(t), …, vi, D(t)].当算法搜索到第t代时, 粒子i的历史最好位置表示为pi(t)=[pi, 1(t), pi, 2(t), …, pi, D(t)], 整个种群在第t次迭代时搜索到的历史最好位置表示为pg(t)=[pg, 1(t), pg, 2(t), …, pg, D(t)].当粒子群算法迭代到下一代,即t+1代时, 第i个粒子的位置xi(t+1)和速度vi(t+1)可以通过式计算得到, 通过多次迭代,粒子可以在搜索空间中产生更多的可行解.
| $ \mathit{\boldsymbol{v}}_i^{\left( {t + 1} \right)} = \omega \mathit{\boldsymbol{v}}_i^{\left( t \right)} + {c_1}{r_1}\left( {\mathit{\boldsymbol{p}}_i^{\left( t \right)}-\mathit{\boldsymbol{x}}_i^{\left( t \right)}} \right) + {c_2}{r_2}\left( {\mathit{\boldsymbol{p}}_g^{\left( t \right)}-\mathit{\boldsymbol{x}}_i^{\left( t \right)}} \right), $ | (1) |
| $ \mathit{\boldsymbol{x}}_i^{\left( {t + 1} \right)} = \mathit{\boldsymbol{x}}_i^{\left( t \right)} + \mathit{\boldsymbol{v}}_i^{\left( {t + 1} \right)}. $ | (2) |
式中:ω为惯性权重, c1, c2为加速常数也称为学习因子, r1, r2为[0, 1]范围内服从均匀分布的随机数.粒子速度更新公式由3部分组成:第1部分是粒子飞行惯性部分, 说明了粒子目前的状态,起到平衡全局搜索和局部搜索的作用; 第2部分是认知学习部分(Cognition Modal), 表示粒子本身的思考,使粒子有了足够强的全局搜索能力,避免局部极小; 第3部分为社会部分(Social Modal), 体现粒子间的信息共享.这3个部分共同决定了粒子的空间搜索能力.式(1)中ω主要用来平衡粒子局部和全局的搜索能力.当惯性权重数值较大时, 算法偏向于全局搜索, 并提高群体的多样性, 相反ω设置较小时算法会倾向于局部搜索, 加快算法收敛的速度, 而随机惯性权重可以灵活地调节全局搜索和局部搜索能力, 且在求解动态非线性问题时具有一定优势.c1, c2主要作用是让粒子自我学习和向群体中其他优秀的粒子学习, 他们共同决定了粒子本身经验信息和其他粒子的经验信息对当前粒子的运动轨迹的影响.如果认知系数相对社会系数取值较大, 则将会导致个体在搜索空间内过度游离, 相反, 相对较大的社会认知系数将会使得个体快速进入局部最优区域, 致使算法过早收敛.因此, 为了平衡粒子随机因素的作用, 一般将认知系数和社会系数都同时设置为2, 即c1=c2=2.0.
2 基于随机维度划分与学习的算法基于随机维度划分与学习的群优化算法同其他改进的PSO算法目的是提高全局和局部搜索性能, 同时保持群体的多样性, 防止算法在进化的过程中出现过早收敛.在标准PSO算法中, 每个粒子采用完整的向量来表示问题的一个可行解, 该算法通过迭代来不断更新粒子的空间位置.这种更新策略可以让粒子在某些维度上更接近最优解, 但同时也可能让某些原来已经接近最优解的某些维度偏离最优解.为此, 提出了基于维度划分与学习的粒子群优化算法.该算法首先通过随机维度划分方法将粒子的位置向量随机划分为多个不同长度大小的子向量段.然后算法为每个子向量段随机分配一种学习算子来对粒子维度数值进行更新.
2.1 随机维度划分假设给定问题的搜索空间为D维, 则群体中的每一个粒子可被表示为一个D维的向量.随机维度划分就是将粒子的D维向量随机划分成多个子段, 每个子段内包含的元素个数至少为m(m≥2).通常算法将m设置为2.在进行粒子维度划分时, 为保证维度划分的有效性和准确性, 划分过程将根据公式产生多个划分节点, 进而实现粒子全维度划分:
| $ \begin{array}{l} {S_i} = {\rm{rand}}\left( {{S_{i- 1}} + m, D- 1- m} \right), \\ \;\;\;\;\;\;{S_i} \in \left[{0, D-1-m} \right]. \end{array} $ | (3) |
式中:rand(a, b)为随机划分函数, 函数的2个参数分别表示划分的起点位置和终点位置.rand函数的数值在整数区间[a, b]中产生.Si表示当前分割点位置; Si-1表示上一个分割点的位置, 该位置决定了下一个分割点取值的范围.
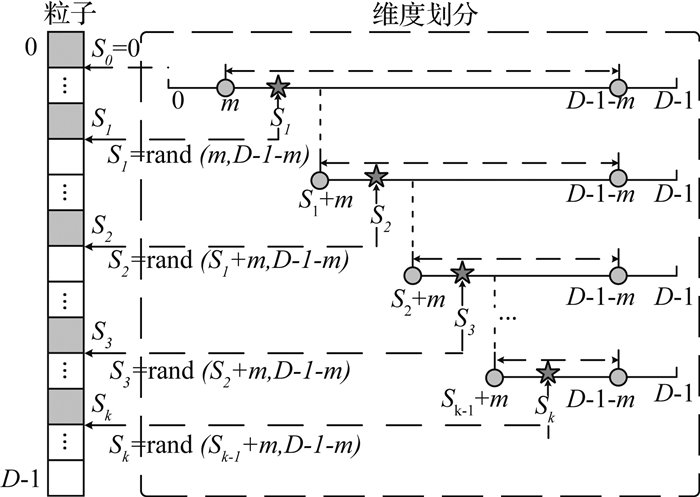
假设粒子的搜索空间为D维, 进行维度划分时算法首先通过公式(3)随机生成k个分割点, 这k个分割点可将粒子划分为k+1段.分割点的位置和分割点的数目均由算法自动生成, 无需手工干预.由于划分后的每个子段内至少包含m个元素, 所以分割点的个数k取值范围满足k∈[0, D/m].粒子随机划分的过程如图 1所示.该图描述了从起始维度位置处逐渐生成每个分割点(星形标注)的过程.基于分割点的随机维度划分方法, 可以将粒子全维度随机划分为多个不同子段, 通过不同对子段之间的协作优化来实现目标问题最优解的计算.
|
图 1 随机维度划分过程示意图 Fig. 1 Process of random dimensional partition |
当粒子完成维度随机划分后,该算法就开始就对粒子i的每个子维度段随机分配一种学习算子(中心学习算子或离散学习算子).假设算子用符号OP标记.算子分配按照随机公式OP=rand()%2+1进行.如果OP=1, 则为该维度段分配中心学习算子; 如果OP, 则分配离散学习算子.
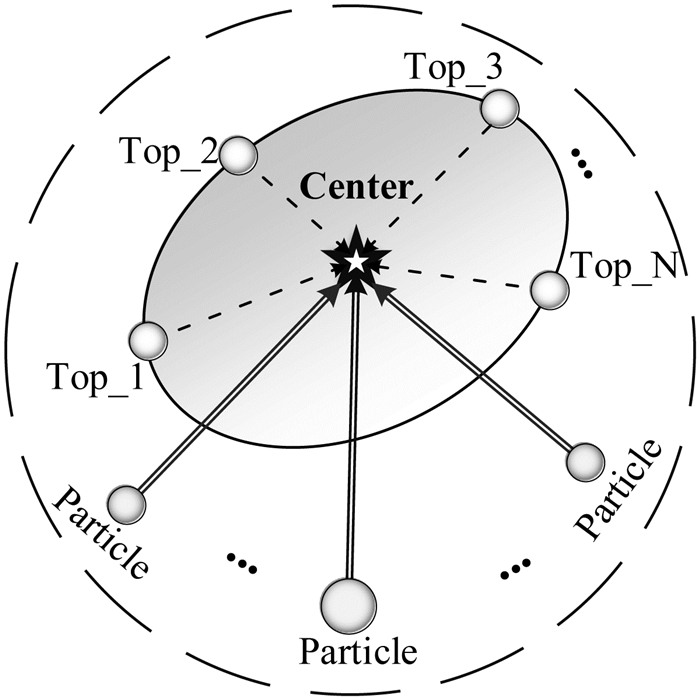
2.2 中心学习算子通过标准PSO算法的速度更新公式可以看出标准PSO算法中种群的信息共享机制并不是建立在全体粒子的层面.粒子除了自身的历史记忆之外, 只有全局最优粒子可以与其他粒子共享信息.标准PSO信息的共享是单向的, 即只有全局最优粒子的认知才有可能向整个群体传播.为此, 算法中设计了一种基于粒子排名的机制的中心学习算子, 将适应度排名靠前的N个粒子的平均中心位置Center(t)作为认知源引导种群进化, 避免单一粒子信息的传播机制.在中心算子学习策略中, 该算法进化到第t+1代时, 粒子i的速度和位置根据下面的式(4)到(6)进行更新.图 2给出了中心学习算子示意图, 星形标记为多个精英粒子的平均中心位置, 算法在进化过程中, 中心认知信息将在种群内传播.
|
图 2 中心学习算子示意图 Fig. 2 Center learning operator |
| $ \mathit{\boldsymbol{v}}_{\rm{i}}^{\left( {{\rm{t}} + 1} \right)} = \omega \mathit{\boldsymbol{v}}_i^{\left( t \right)} + {c^*}{r^*}\left( {{\rm{Cente}}{{\rm{r}}^{\left( t \right)}}-\mathit{\boldsymbol{x}}_i^{\left( t \right)}} \right), $ | (4) |
| $ \mathit{\boldsymbol{x}}_i^{\left( {t + 1} \right)} = \mathit{\boldsymbol{x}}_i^{\left( t \right)} + \mathit{\boldsymbol{v}}_i^{\left( {t + 1} \right)}, $ | (5) |
| $ {\rm{Cente}}{{\rm{r}}^{\left( t \right)}} = \frac{1}{N} \cdot \sum\limits_{l = 1}^N {{\rm{pbest}}_l^{\left( t \right)}} . $ | (6) |
式中:惯性权重ω在迭代过程中变化范围可由0.9线性递减到0.5.N为精英粒子的个数(N=4~6), c=2.0, 是加速因子, r是[0, 1]之间符合均匀分布的随机小数, 它主要用来控制搜索的方向.Center位置向量为精英粒子的平均中心位置.在中心算子迭代公式中,将惯性权重设定为0.721,加速系数设定为2.0时算子搜索性能最佳.
算法中根据种群中各粒子历史最优位置的适应度值排序来确定精英个体, 适应度排名在前N位的粒子个体将被选择参与中心信息源的计算.式(4)共包含2部分内容, 第1部分是粒子的惯性项, 模拟了生物习惯性作用, 第2部分是粒子个体的社会认知项, 它蕴含了精英团队的智慧认知, 扩展了标准PSO算法中基于单一个体的认知.此外, 在种群进化的过程中每个粒子都有机会进入到精英团队, 并将其信息传播到种群, 进而帮助种群实现快速进化.
2.3 离散学习算子在标准PSO算法中, 每个粒子采用全维度向量来表示搜索问题的可行解, 粒子每次通过全维度数值的更新来实现位置的更改, 即解的搜索.对于简单搜索问题, 比如单峰优化问题, 这种更新策略可以让粒子在整体维度上逐渐靠近全局最优解, 但对于某些复杂问题, 比如复杂多峰优化问题, 搜索过程中粒子的某些维度值更接近最优解, 但同时也可能让某些维度值偏离最优解.因此, 在算法中设计了一种去中心化离散学习算子.每个粒子个体的某个维度信息都有机会被其他粒子效仿学习.种群间的信息互动也更频繁, 这种群体间基于维度交流学习的方式更有利于复杂问题的搜索.算法进化到第t+1代时, 粒子i的速度和位置可根据式(7)和(8)进行更新.
| $ \mathit{\boldsymbol{v}}_{^i}^{\left( {t + 1} \right)} = \omega \mathit{\boldsymbol{v}}_i^{\left( t \right)} + {c^*}{r^*}\left( {{\rm{pbest}}_{{r_i}\left( j \right)}^{\left( t \right)}-\mathit{\boldsymbol{x}}_i^{\left( t \right)}} \right), $ | (7) |
| $ \mathit{\boldsymbol{x}}_i^{\left( {t + 1} \right)} = \mathit{\boldsymbol{x}}_i^{\left( t \right)} + \mathit{\boldsymbol{v}}_i^{\left( {t + 1} \right)}, {\gamma _i}\left( j \right) \in \left[{0, M-1} \right]. $ | (8) |
式中:惯性权重设置为0.6,加速系数设定为1.0时算子搜索性能较佳, γi(j)表示当前粒子i在第j维度上要学习的其他某个粒子的编号, 该编号可以通过2轮制锦标赛选择方法随机获取.
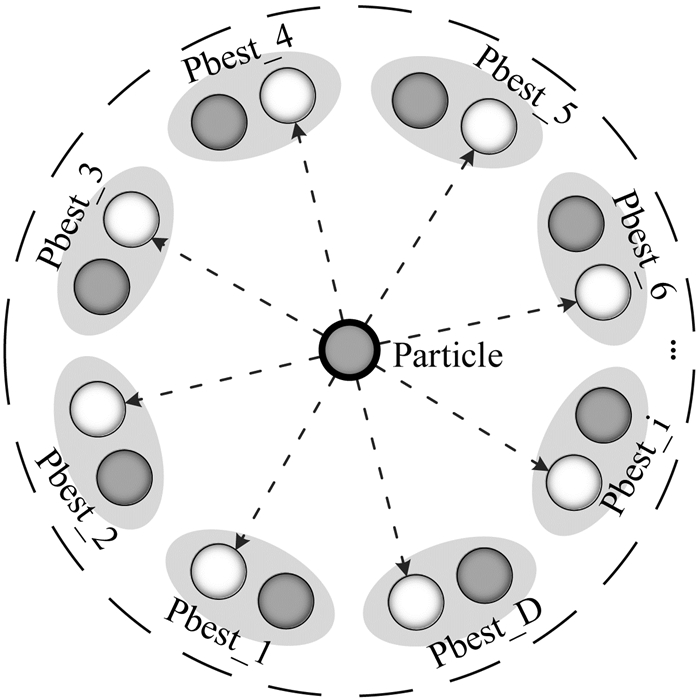
离散学习算子的速度更新形式和中心学习算子的速度更新公式区别在于粒子的认知目标不再依赖于群体中的精英个体, 而是在不同子维度上选择不同的学习目标.图 3给出了粒子i的离散学习示意图, 图中椭圆形内的2个粒子为算法在某个维度上进行随机选择学习的候选目标.假设问题解的搜索空间为D维, 则粒子i对应有D个随机学习目标.这种离散学习的方式可以丰富种群的多样性, 同时也可以避免粒子在搜索过程中过早聚拢到局部极值点的情况.
|
图 3 离散学习算子示意图 Fig. 3 Decenter learning operator |
离散化学习策略提高了粒子空间搜索的均匀性与自由性.算法在进化过程中对每个粒子历史最优位置更新次数进行统计, 当监测到某个粒子的历史最优位置未更新的次数超过2次时, 算法将对该粒子重新进行随机维度划分, 并重新分配学习算子.反之粒子将按照自己原来的划分和学习继续进化.算法的过程分为3个阶段:初始化, 各粒子维度划分, 算子分配.算法的具体执行过程可参见算法1.
算法1.基于随机维度划分与学习的粒子群优化算法
输入:最大迭代次数T, 种群大小M, 问题解的维度D.
输出:全局最优解x′(t);
1. t←1
2.初始化种群:
3. FOR i=1 TO M
4.初始化粒子i的位置向量xi(t)和速度向量vi(t);
5.根据公式(3)对粒子i进行维度随机划分;
6.对粒子i的每个子维度随机分配一种学习算子
7. WHILE f(xi(t))≥ε ORt≤T
8. FOR i=1 TO M
9.计算粒子i的适应度值f(xi(t));
10.更新粒子i的局部位置xi(t), 统计未升级次数Δi;
11.更新粒子种群的全局最优位置x′(t),如下:
12. IF f(xi(t))≤f(x′(t))
13. x′(t)=xi(t);
14. FOR i=1 TO M
15. IF Δi> 2
16.根据公式(3)对粒子i全部维度随机划分;
17.对粒子i的各子维度随机分配一种学习算子;
18. Δi←0;
19.更新粒子i的位置向量xi(t)和速度向量vi(t);
20. t←t+1;
21.返回全局最佳位置向量x′(t);
3 实验与分析 3.1 算法及参数设置本文选取8个经典改进的PSO算法与提出的算法进行比较.这些算法涵盖了文中介绍的多种改进策略.基于参数改进的算法, 如FDRPSO; 基于学习策略改进的算法, 如GPSO算法, LPSO算法, QPSO算法, BBPSO算法; 基于邻域拓扑结构改进的算法, FIPS算法, DMSPSO算法, CLPSO算法.这些算法都是经典高效的改进算法.实验过程中算法的参数均设置为各自对应文献中的默认参数, 具体的参数设置如表 1所示.
| 表 1 各对比算法实验参数设置 Table 1 Parameter settings ofcompared algorithms |
实验中为保证各算法测试的公正性, 各算法的适应度数值评估的最大次数设定为D×104, 种群的大小M设置为40.为减少实验测试的误差, 所有算法重复测试30次, 每次测试记录各算法的最佳适应度数值,并将各算法多次独立重复测试结果的平均值(Mean)和适应度值的标准方差(Std.)作为算法评估的标准.
3.2 基准测试函数为了评估算法的收敛精度,收敛速度和全局搜索能力,本文中选用了文献[24]中采用的10个基准测试函数来评估各算法的性能, 这些测试函数大部分取自国际进化计算会议中设定的测试函数.基准测试函数中包含单峰函数优化问题以及多峰函数优化问题, 其中函数F1~F4为单峰函数, 该类函数中只有一个峰值点, 且为全局最优点; 函数F5~F10为多峰函数, 此类函数中存在多个局部极值点或局部最优点, 多峰函数通常可以用来检验算法的全局搜索能力和局部搜索能力.相对单峰函数, 多峰函数的全局最优解搜索相对较难, 如果算法的全局搜索能力不足, 就很容易陷入到搜索空间内的某个局部极值点中.表 2列出了这些基准测试函数的详细信息, 具体包括函数名称, 函数表达式, 各维度数值搜索空间, 各函数的全局最优解位置x*, 以及全局最优位置对应的函数全局最佳适应度值f(x*).
| 表 2 基准测试函数 Table 2 Test Benchmark functions |
本节将测试算法中的最小划分间隔m对实验性能的影响.算法在进化过程中粒子维度划分的分割点根据公式(3)自动产生.各粒子的维度划分方式为随机非完全均匀划分, 分割后的每个维度段内包含至少m个元素(即最小分割距离为m).整数m的大小对划分段数k有着直接地决定性作用.当最小划分间隔确定后,粒子维度分割点的个数k的数值范围则确定,且满足k∈[1, D/m].由于k的数值是随机的,因此粒子总体划分的段数也相应具有随机性.假如某个粒子共随机产生了2个分割点, 那么划分的段数就是3段, 而另外一个粒子随机生成了3个分割点, 那么划分的段数就是4段.通常如果某粒子的分割间隔越大, 则划分段数越少, 粒子搜索优化趋向于传统的全维度优化; 如果某粒子的分割点越多, 则划分段数越多,粒子的搜索趋向于多元协同优化.
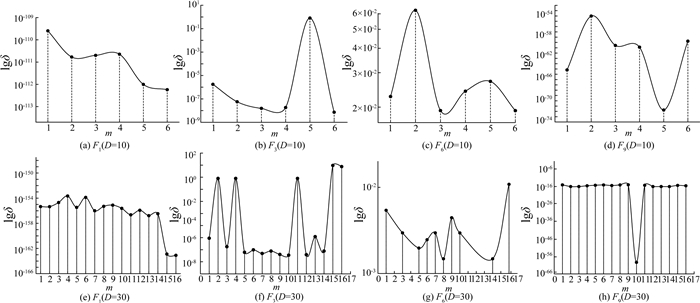
为测试最小分割距离对实验性能的影响,实验中选择了4个具有代表性的基准函数,其中包括2个单峰函数(F1,F3)和2个多峰函数(F6,F9).各函数适应度评估的最大次数设定为D×104, 种群规模设定为40.实验测试维度为10维度和30维度.函数的最佳适应度数值均值作为实验比较标准.图 4给出了测试函数在不同分割距离上的实验测试结果(10维:a~d,30维:e~h),其中,lgδ为不同分割距离对应的平均最佳精度的对数值.纵坐标的数值越小表示算法的适应度数值越好.从图 4中可以看出不同的测试函数对应的最佳分割距离彼此互有不同,但同一函数在不同维度的测试中最佳分割距离具有一定相似性,此外,对于单峰函数,极值点即全局最优点,算法中的中心学习算子或离散学习算子均可进行独立优化,图 4中对于单峰函F1,F3,分割距离设定的数值越大,算法的求解精度越高.对于多峰函数,基于单一算子的全维度优化实验效果相对混合算子优化效果相对较差.为了提高划分的多元性和问题求解的普适性,在基本RVPLO算法中,算法统一将维度划分间隔设定为最小分割距离m=2.
|
图 4 维度划分距离对实验精度的影响 Fig. 4 Effect of dimensional partition interval on experimental accuracy |
本文在基准测试函数F1~F10上测试了各算法在30维和100维上的全局优化性能.各算法平均最佳适应度值和标准方差作为评估的标准.如表 3、4所示列出各对比算法在30维和100维的实验测试结果(采用科学计数法表示).表中加粗的数值表示各个比较算法在相应测试函数上取得的最好结果.表中h为显著性统计标记.当h=‘+’时, 表示RVPLO算法显著优于当前被比较的算法, 当h=‘=’时, 表示当前算法和比较算法的实验结果无显著统计性, 当h=‘-’时表示当前算法实验结果显著差于当前被比较算法.从实验结果统计上可以看出RVPLO算法在大部分测试函数上都取得了较好的效果.在这些测试函数中, F1~F4为单峰函数, 他们的极值点的数目只有一个且是全局最优点.各对比测试算法在该类函数上都能搜索到全局最优点, 但是算法在收敛速度和精度上较大差异.RVPLO算法在所有的单峰函数上收敛精度较高, 搜索性能优势明显.在单峰函数中, F3是较为特殊的单峰函数,特点为非凸, 病态函数, 且在一些变量之间有明显的相互作用, 普通算法很难搜索到全局极小点.相对其他算法, RVPLO在F3上依然取得了较好的搜索结果.在多峰函数搜索上, 除了函数F8外, RVPLO算法性能整体表现优异, 并在多峰函数F6和F7上具有更好的搜索效果.通常多峰函数中存在多个局部极值点, 当种群多样性差, 搜索性能低时算法很容易陷入到局部极值而产生过早收敛现象, 因此, RVPLO在多峰函数上较好的搜索结果进一步验证了算法内种群的多元性及较好的全局搜索和局部搜索能力.为了验证算法测试结果的置信度, 文中进一步对表 3和4的测试结果进行双侧t检验,置信水平设置为α=0.05.表 3和4中的h值表示t-test的显著性统计结果.
| 表 3 对比算法在标准测试函数上的优化结果(D=30) Table 3 Comparison results of RVPLO and other algorithms on 30-dimensional problems |
| 表 4 各对比算法在标准测试函数上的优化结果(D=100) Table 4 Comparison results of RVPLO and other algorithms on 100-dimensional problems |
通过表 3, 4中的结果可以看出, 在30维优化问题的搜索中, RVPLO算法在所有测试函数上(除了函数F8外), 收敛精度平均优于其他各对比算法.此外, 在高维即100维函数优化过程中, 单峰搜索性能最佳, 其多峰搜索性能与经典的针对多峰函数优化的算法CLPSO相当.对比算法CLPSO在多峰优化中表现相对较好.BBPSO算法则在单峰优化中表现较好, 性能仅次于RVPLO算法.表 3和4给出了各算法收敛精度的均值Mean,方差Std.以及所有测试过程中平均最佳适应度值对应的显著性统计结果h.表 3和4的最后一行统计了RVPLO算法在进行函数优化时相对其他比算法在搜索性能上表现为显著更优, 相同和显著更劣的函数的个数.通过统计结果可以进一步看出, RVPLO算法在整体测试中相比其他算法显著更优的函数个数更多, 整体表现出显著更好的综合搜索性能.RVPLO的维度随机划分机制和算子动态分配机制强化了算法的全局搜索能力和局部挖掘能力.
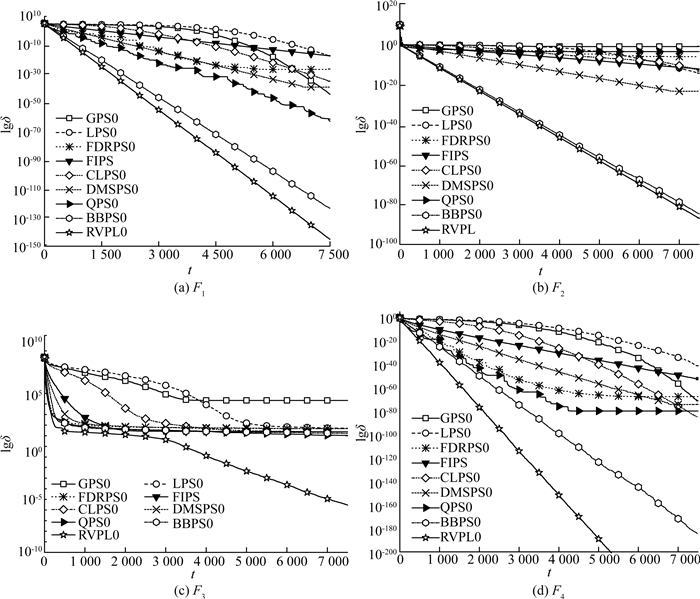
3.5 收敛速度算法的收敛速度反映了算法寻找最优解搜索速度, 这个指标对于解决实际应用问题具有重要的意义.为比较各测试算法的收敛速度,文中测试了RVPLO算法和其他8个算法在10个基准测试函数基于30维优化问题上的函数优化收敛曲线,实验测试结果如图 5和6所示.
|
图 5 测试算法在单峰测试函数上的收敛性能曲线图 Fig. 5 Convergence curves of compared algorithms on unimodal functions |

|
图 6 测试算法在多峰测试函数上的收敛曲线图 Fig. 6 The convergence curves of the compared algorithms on multimodal functions |
本文各算法在函数优化实验测试过程中均采用相同的迭代次数, 且每次迭代的次数设定为评估次数的最大值.算法每次运行中的最佳平均适应度数值和标准方差作为实验比较的依据. 图 5和6给出了各算法在基准测试函数上的测试结果.图中t表示为算法迭代的次数, 函数F1~F4为单峰函数, 函数最大值即极值点的数值各个算法在这类函数上收敛精度较高且收敛速度较快, 其中RVPLO和BBPSO算法的收敛速度和收敛精度优于其他各对比算法.多峰函数能够考察算法的综合搜索性能, 即全部搜索能力和局部搜索能力.从各函数的平均进化收敛曲线可以看到RVPLO算法在大部分函数上收敛速度较快.除了函数F8外, RVPLO算法在其他函数上均取得了最佳或近似最佳的收敛速度.
RVPLO算法通过随机维度划分机制在种群内产生更多的可行解,当种群陷入局部极优时,通过该策略可以进一步丰富种群的多样性, 使得算法能够在复杂环境中能够产生更多高质量的候选解. RVPLO的双重动态随机调整机制强化了算法自适应全局寻优能力.
3.6 算法复杂度在本节中对比分析了RVPLO算法和标准PSO算法的复杂度.标准PSO算法在进化过程中主要包含3个阶段:初始化阶段, 评估阶段, 位置和速度更新阶段.各阶段的复杂度均为O(MD), 不同的算法在不同阶段的时间复杂度不同, RVPLO算法采用随机维度划分和随机学习策略的方式进行种群的迭代和更新.相对于PSO算法, RVPLO算法初始阶段时间复杂度为O(MD), 迭代过程分为2个阶段:随机维度划分及算子分配阶段,以及粒子的位置和速度向量更新阶段.
在随机维度划分阶段, 算法复杂度为O(D);在粒子位置速度更新阶段, 算法复杂度为O(MD), 总的时间复杂度为O(MD), 因此总的时间复杂度上限为O(MD), 算法并没有增加额外的时间复杂度开销. RVPLO算子在时间上与标准PSO算法的空间复杂度相同.空间上, RVPLO相对标准PSO算法, 额外增加的内存空间用于记录各粒子的维度划分位置和对应的学习算子.由于进化过程RVPLO的粒子的数目小于50, 因此总体上RVPLO算法的时间复杂度与空间复杂度相当.
4 结语本文提出一种基于维度随机划分与策略的群优化算法RVPLO, 该算法采用维度划分策略对各个粒子维度进行随机分割, 分割后算法为每个子向量随机分配一种学习算子用以对粒子维度进行更新操作.中心学习算子将种群中顶层精英簇的平均位置信息共享给其他粒子,使得群体具备快速迁移和局部感知的能力.离散学习算子通过不同粒子间各个维度之间的相互学习和借鉴来增强各自的全局搜索能力以及群体协同搜索的能力.传统粒子群算法中的粒子个体的学习目标仅限于粒子自身和当前全局最优个体, 缺乏多元学习的能力.RVPLO算法拓展了传统粒子学习的方式,并通过随机维度划分和随机算子分配的双重动态机制提高了PSO算法在函数优化问题上的求解能力.
为了评估算法的综合优化性能,文中将RVPLO算法与其他8个改进算法在多种不同类型函数上的全局优化性能进行了对比测试,实验测试结果及统计结果表明RVPLO算法在单峰, 多峰函数上具备较高的收敛精度和较快的收敛速度.
下一步将在该算法基础上研究基于局部搜索策略和差分操作等方法来提高算法在复杂环境下的全局寻优能力,此外,也将研究基于随机维度划分策略在大规模复杂工程优化领域中的搜索性能,设计出面向大规模优化领的更加高效的全局优化算法.
| [1] |
KENNEDY J, EBERHART R. Particle swarm optimization[C]//Proceedings of the IEEE International Conference on Neural Networks. 1995 Proceedings, Perth, WA, Australia: [s. n. ], 1995, 4: 1942-1948. https://en.wikipedia.org/wiki/Particle_swarm_optimization
|
| [2] |
迟玉红, 孙富春, 王维军, 等. 基于空间缩放和吸引子的粒子群优化算法[J]. 计算机学报, 2011, 34(1): 11-130. CHI Yu-hong, SUN Fu-chun, WANG Wei-Jun, et al. An improved particle swarm optimization algorithm with search space zoomed factor and attractor[J]. Chinese Journal of Computers, 2011, 34(1): 115-130. |
| [3] |
TAORMINA R, CHAU K W. Neural network river forecasting with multi-objective fully informed particle swarm optimization[J]. Journal of Hydroinformatics, 2014, 17(1): 99-113. |
| [4] |
SAFARI S, ARDEHALI M M, SIRIZI M J. Particle swarm optimization based fuzzy logic controller for autonomous green power energy system with hydrogen storage[J]. Energy Conversion & Management, 2013, 65(1): 41-49. |
| [5] |
AGHDAM M H, HEIDARI S. Feature selection using particle swarm optimization in text categorization[J]. Journal of Artificial Intelligence & Soft Computing Research, 2015, 5(4): 38-43. |
| [6] |
DE B P, KAR R, MANDAL D, et al. Optimal selection of components value for analog active filter design using simplex particle swarm optimization[J]. International Journal of Machine Learning & Cybernetics, 2014, 6: 1-16. |
| [7] |
LIU Y, MU C, KOU W, et al. Modified particle swarm optimization-based multilevel thresholding for image segmentation[J]. Soft Computing, 2015, 19(5): 1311-1327. DOI:10.1007/s00500-014-1345-2 |
| [8] |
RASMUSSEN T K, KRINK T. Improved Hidden Markov Model training for multiple sequence alignment by a particle swarm optimization evolutionary algorithm hybrid[J]. Biosystems, 2003, 72(1): 5-17. |
| [9] |
SHRIVASTAVA N A, KHOSRAVI A, PANIGRAHI B K. Prediction interval estimation of electricity prices using pso-tuned support vector machines[J]. IEEE Transactions on Industrial Informatics, 2015, 11(2): 322-331. DOI:10.1109/TII.2015.2389625 |
| [10] |
FRANS V D B. An analysis of particle swarm optimizers[D]. University of Pretoria, 2007. https://www.researchgate.net/publication/33786643_An_Analysis_of_Particle_Swarm_Optimizers
|
| [11] |
KENNEDY J. Small worlds and mega-minds: effects of neighborhood topology on particle swarm performance[C]//Proceedings of the Evolutionary Computation, Washington, DC, USA: IEEE, 1999. https://www.researchgate.net/publication/3810337_Small_worlds_and_mega-minds_Effects_of_neighborhood_topology_on_particle_swarm_performance
|
| [12] |
CLERC M. The swarm and the queen: towards a deterministic and adaptive particle swarm optimization[C]//Proceedings of the Evolutionary Computation. Washington, DC: IEEE, 1999. http://ieeexplore.ieee.org/document/785513/
|
| [13] |
KENNEDY J, MENDES R. Population structure and particle swarm performance[C]//Proceedings of the Evolutionary Computation on 2002 Congress. Honolulu, HI, USA: IEEE, 2002, 1671-1676. http://ieeexplore.ieee.org/document/1004493/
|
| [14] |
NICKABADI A, EBADZADEH M M, SAFABAKHSH R. A novel particle swarm optimization algorithm with adaptive inertia weight[J]. Applied Soft Computing, 2011, 11(4): 3658-3670. DOI:10.1016/j.asoc.2011.01.037 |
| [15] |
SUGANTHAN P N. Particle swarm optimiser with neighbourhood operator[C]//Proceedings of the Evolutionary Computation. Washington, DC, USA: IEEE, 1999. http://ieeexplore.ieee.org/document/785514/
|
| [16] |
MENDES R, KENNEDY J, NEVES J. The fully informed particle swarm:simpler, maybe better[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3): 204-210. DOI:10.1109/TEVC.2004.826074 |
| [17] |
LIANG J J, SUGANTHAN P N. . Dynamic multi-swarm particle swarm optimizer with local search[C]//Evolutionary Computation, The 2005 IEEE Congress on. Edinburgh, Scotland, UK, IEEE, 2010: 522-528. https://wenku.baidu.com/view/fbca74097cd184254b3535e1.html
|
| [18] |
LIANG J J, QIN A K, SUGANTHAN P N, et al. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J]. IEEE Transactions on Evolutionary Computation, 2006, 10(3): 281-295. DOI:10.1109/TEVC.2005.857610 |
| [19] |
PERAM T, VEERAMACHANENI K, MOHAN C K. Fitness-distance-ratio based particle swarm optimization[C]//Proceedings of the Swarm Intelligence Symposium. Indianapolis, IN, USA: IEEE, 2003: 174-181. http://ieeexplore.ieee.org/document/1202264/
|
| [20] |
SUN J, FENG B, XU W. Particle swarm optimization with particles having quantum behavior[C]//Proceedings of the Evolutionary Computation. Portland, OR, USA: IEEE: 2004, 1571-1580. http://ieeexplore.ieee.org/document/1330875/
|
| [21] |
KROHLING R A, MENDEL E. Bare bones particle swarm optimization with Gaussian or cauchy jumps[C]//Evolutionary Computation. Trondheim, Norway: IEEE, 2009: 3285-3291. http://ieeexplore.ieee.org/lpdocs/epic03/wrapper.htm?arnumber=4983361
|
| [22] |
ZHAN Z H, ZHANG J, LI Y, et al. Orthogonal Learning Particle Swarm Optimization[J]. IEEE Transactions on Evolutionary Computation, 2009, 15(6): 1763-1764. |
| [23] |
FRANS V D B, ENGELBRECHT A P. A cooperative approach to particle swarm optimization[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3): 225-239. DOI:10.1109/TEVC.2004.826069 |
| [24] |
夏学文, 刘经南, 高柯夫, 李元香, 曾辉.具备反向学习和局部学习能力的粒子群算法[J].计算机学报, 2015, 38(7):1397-1407. XIA Xu-Wen, LIU Jing-Nan, GAO Ke-fu et al. Particle Swarm optimization algorithm with reverse-learning and local-learning behavior[J]. Chinese Journal of Computers, 2015, 38(7):1397-1407. https://www.researchgate.net/publication/283110535_Particle_swarm_optimization_algorithm_with_reverse-learning_and_local-learning_behavior |



