薄壁钢构件弹塑性屈曲稳定的理论和试验研究受到许多研究者^[1-4]青睐，关于I型^[5]、箱形截面^[6-7]的理论研究成果很丰富.除此之外，冷弯薄壁槽钢截面短柱^[8]、矩形切角截面钢桥塔节段^[9]、钢箱梁梯形肋加劲板^[10]也是稳定理论问题的主要研究对象，屈曲形态、考虑初始缺陷的极限承载力是这些稳定问题的关注热点.此类钢材的屈曲特性试验研究也主要集中于工字形和箱形截面^[11]，但对Q500qE高性能钢箱形压弯构件的稳定性能的研究仍较少，尤其是设置外伸翼缘的构件.

结构或构件屈曲形态主要关注整体屈曲和局部屈曲、平面内和平面外屈曲等^[1-3].整体失稳模态在日本JSCE^[12]规范中划分为分歧点失稳、极值点失稳、跳跃失稳和缺陷敏感型失稳模态.对于轴向圆柱壳发生的不稳定分歧点失稳，也属于缺陷敏感型失稳^[1].与分歧点失稳相比，偏心压弯构件的极值点失稳的平衡状态不发生变化^[12].屈曲半波数描述了加劲薄壁板局部屈曲形态，有R-模态和F-模态^[12].

影响屈曲特性的因素主要包括结构材料特性、截面对称性、加劲肋和翼缘板刚度匹配、板件长细比的影响等^[3]，还包括宽厚比、屈曲系数及模态、长细比、有效屈曲长度限值等因素^[12-15].

对压弯构件强度和稳定的验算，现有公路设计规范^{[12-13, 15]}和铁路TB10091规范^[14]分别采用极限状态法和容许应力法.外伸翼缘加劲钢箱形压弯构件稳定问题在国内外规范^{[13, 15]}中暂未列出，为此，现行规范强度和稳定验算对此类截面的适用性需要进行验证.

本文主要采用模型试验的方法，从荷载-位移曲线、屈曲形态等角度，研究外伸翼缘薄壁箱形压弯构件的整体和局部屈曲特性，并通过有限元计算验证试验结果，验证现有规范中的强度和稳定相关公式对Q500qE高性能钢外伸翼缘箱形压弯构件强度和稳定相关公式的适用性.

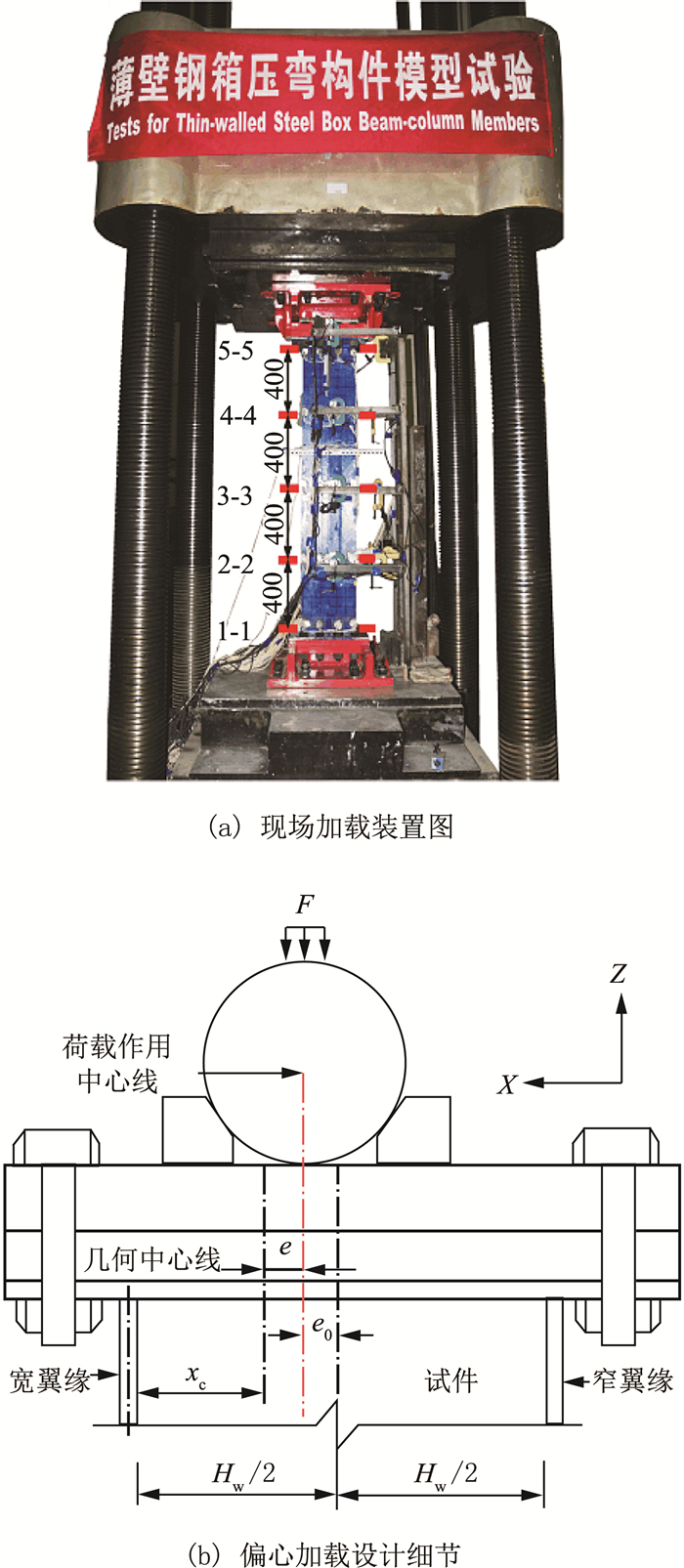
如图 1所示为本试验加载系统的设计及现场布置情况.图 1(a)中构件底部通过高强螺栓与基座固定，而上端沿弯矩作用方向单向转动.4个试件分别命名为SA、SB、SC和SD.沿试件螺栓连接面至连接板加载顶面的高度均为1.68 m.加载顶连板上方预先设置荷载偏心距，其中偏心距e和e₀见图 1(b).

图 1

图 1 加载设计简图及现场布置情况 Fig. 1 Diagram of test design and in-site arrangement

静力加载前，每个试件沿图 1(a)中长度方向的1-1 ~ 5-5截面作为焊接缺陷测试截面.当静力加载过程中，同时测定整体屈曲变位和翼缘板面局部变位，其中整体屈曲变位通过电测位移计测试；翼缘板板面局部屈曲变形通过微型位移计测试.数据采集系统采用35951B IMP板收集.

静力加载试验过程按3个阶段进行.预压阶段预压荷载值为100 kN.正式加载阶段在材料弹性范围内按照荷载控制加载，加载速率为20~30 kN/min，一旦达到材料非线性阶段改为位移控制加载，其加载速率为0.01~0.02 mm/min.卸载阶段采用位移控制，其卸载速率为0.1~0.2 mm/min.

试验构件分别由Q500qE和Q345B这2种材料组成.8 mm厚的Q500qE钢板与沪通长江大桥钢梁中的板件为同一批生产制造，其钢板材料特性由河北和辽宁某钢厂各取2件试验得到，而2件8 mm厚的Q345B试验钢材的材料特性由内蒙古某钢厂试验得到.这6组材性试验实测值、平均值及变异系数分别见表 1.表中，σ_y为名义屈服程度，σ_cr为名义极限强度，δ_s为伸长率，σ_y/σ_cr为比值.从表中可知，Q500qE板的σ_y和σ_cr平均值分别为545和657 MPa，与中国铁道科学院的潘永杰^[5]和鞠晓臣^[11]的试验结果相比，误差不超过0.6%.Q345B板的σ_y和σ_cr平均值分别为434和555 MPa，与王萌等^[16]的试验结果相比，误差不超过5.77%.故2种材料试验的名义屈服强度和抗拉强度取值可靠.

表 1

表 1 Q500qE和Q345B材料特性实测值 Table 1 Tested material properties of Q500qE and Q345B 材料 σy/MPa σy变异系数 σcr/MPa σcr变异系数 δs/MPa δs变异系数 σy/σcr/MPa σy/σcr变异系数 测试值 平均值 测试值 平均值 测试值 平均值 测试值 平均值 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4 Q500qE 546 570 546 518 545 0.79 665 667 655 640 657 0.50 20 21 19.5 27.5 22 8.14 0.82 0.85 0.83 0.81 0.83 14.46 Q345B 435 432 — — 434 0.28 566 543 — — 555 0.61 30 24 — — 27 6.41 0.77 0.8 — — 0.79 15.19

表 1 Q500qE和Q345B材料特性实测值 Table 1 Tested material properties of Q500qE and Q345B

试验基座、顶压座、中间连接板均采用Q345B钢材，图 1中SA、SB和SD试件的1.68 m区段采用Q500qE钢材，SC试件全截面段采用Q345B钢材.2种材料的弹性模量E均取为2.1×10⁵ MPa, δ_s平均值分别为22 %和27 %.

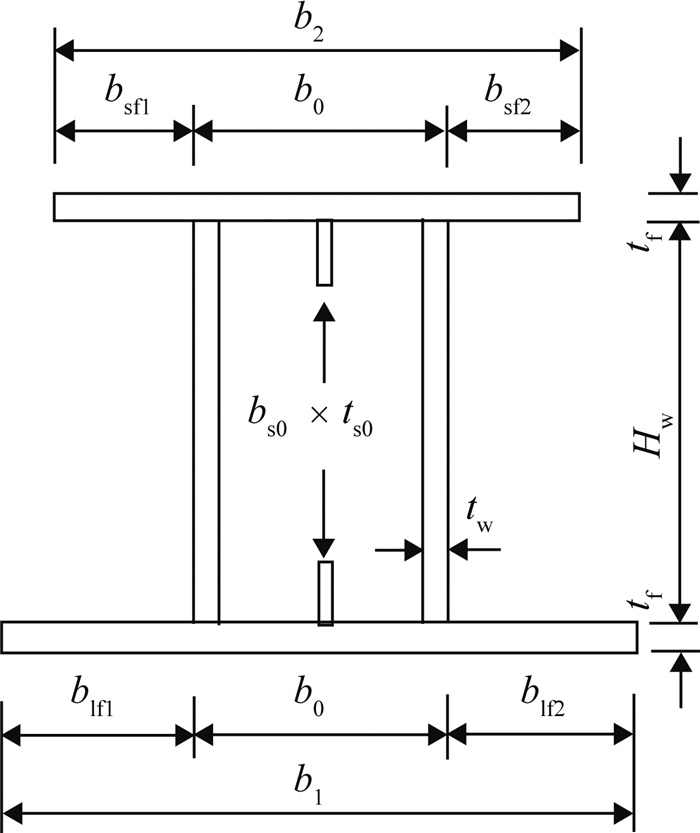
试件SA, SB, SC和SD的截面形式如图 2所示，其截面相应的几何参数如表 2所示，x_c为宽翼缘外侧边线至惯性矩中心线的距离，截面中心关于y轴对称，且在x轴方向上设置偏心距来设置弯矩.

图 2

图 2 试件截面设计示意图 Fig. 2 Design schemes of cross section

表 2

表 2 试件设计几何参数 Table 2 Geometry parameters of specimens 试件 Hw/mm b1/mm b0/mm blf1/mm blf2/mm b2/mm bsf1/mm bsf2/mm tf/mm tw/mm bs0/mm ts0/mm xc/mm EIy/EIx λcx λcy SA 160 420 112 154 154 340 114 114 8 8 22 6 78 1.60 0.267 0.206 SB 160 340 112 114 114 240 64 64 8 8 22 6 75 1.04 0.267 0.267 SC 160 322 112 105 105 224 64 64 8 8 22 6 75 1.16 0.270 0.270 SD 160 128 112 8 8 128 8 8 8 8 22 6 84 0.44 0.298 0.453

表 2 试件设计几何参数 Table 2 Geometry parameters of specimens

相对长细比λ_c^[17]是反映结构杆件的整体失稳的特征值.λ_c与材料弹性模量E、材料屈服强度σ_y、沿杆件平面外的回转半径r_sy和r_sz、有效长度系数μ以及杆件长度L有关.考虑圆柱体支座作用中心至连接板荷载作用面之间的距离为60 mm, 则L应取杆件的有效计算长度L_eff，即1 740 mm.对于一端简支、一端固支杆件，μ取为0.7.σ_y按表 1中相应的名义屈服强度确定.4个试件的相对长细比λ_cx和λ_cy见表 2.从表中可知，随着外伸翼缘板宽度增大，y向截面刚度EI_y、x向截面刚度EI_x均增大，EI_y/EI_x也增大，λ_cx和λ_cy均减小.

公路规范^[13]规定了箱形截面梁截面尺寸的限值要求.表 2中4个试件的腹板高与中间翼缘板宽度的比值为1.43(小于6)；翼缘板横向约束点之间的距离与中间翼缘板宽度的比值均为14.29 (小于＜65·(345/σ_y))，均能满足公路规范^[13]的要求.

中间翼缘、腹板和加劲肋的宽厚比分别为14、20和3.67，4个试件外伸翼缘的宽厚比共有19.25、14.25、13.125、8和1等5种.规范^{[12, 15]}规定了板的宽厚比限值公式为$ b/t \le k\;\sqrt {E/{\sigma _y}} $，该限值与弹性屈曲系数k、弹性模量E及材料屈服强度σ_y相关.对于单边支撑板，k=0.56，对于两端支撑板k=1.4，两者限值与TB10091^[14]中宽厚比限值基本相同.4个试件中四边支撑板，如中间翼缘板和腹板，均能满足铁路规范限值^[14]的要求.

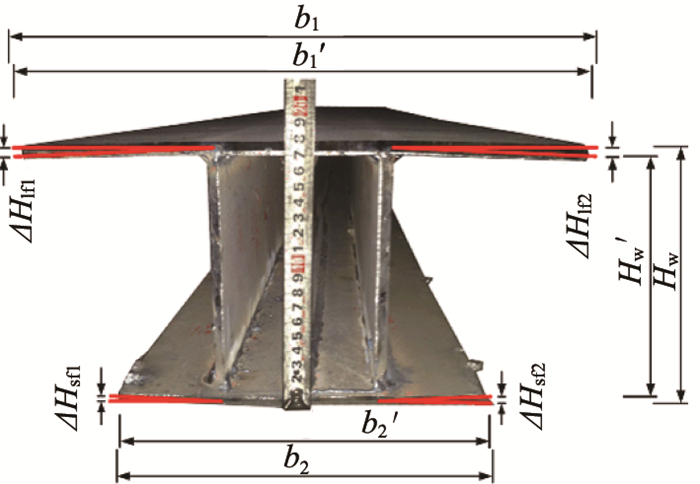
初始缺陷包括焊接变形造成的缺陷和荷载作用偏心初始缺陷2部分.缺陷幅值的增大会导致截面延性下降段出现越早^[18], 故在数值计算^{[5, 11]}中均需考虑初始缺陷的影响.对于焊接初始缺陷，受压柱、自由外伸翼缘板、中间翼缘板、腹板初始弯曲分别按照JSCE^[12]中推荐的L/1 000、b_f1/100、b₀/150和H_w/250公式计算，可知，试件纵向初始缺陷的最大值不超过2 mm，小于板件局部初始缺陷(如图 3所示).4个试件长细比位于13 ~ 28之间，小于30，属于短柱，按照文献[11]公式，可不计焊接引起的杆件纵向弯曲，故这里将外伸翼缘板自由边在平面外的变位作为构件的初始缺陷.

图 3

图 3 焊接后的试件截面变形示意图 Fig. 3 Section deflection diagram of welded members

图 1中试件1-1 ~ 5-5截面的初始缺陷最大实测值如表 3所示.表中翼缘板焊接后与设计值差Δb₁=b₁-b₁', Δb₂=b₂-b₂'；ΔH_lf1, ΔH_lf2分别表示宽翼缘左、右外伸翼缘板在平面外相对于中间翼缘的变位；ΔH_sf1, ΔH_sf2表示窄翼缘中左、右外伸翼缘板在平面外相对于中间翼缘的变位.最大翼缘边变位ΔH_fmax取ΔH_lf1, ΔH_lf2, ΔH_sf1和ΔH_sf2中的最大值；最大翼缘边的初始缺陷ΔD_max取ΔH_fmax、翼缘板之间截面实际高度与设计高度之差ΔH_w和腹板之间实际间距与设计间距之差Δb₀中的最大值，试件SA、SB、SC外伸翼缘板的最大转角分别为2.23°、2.01°和1.01°.4个试件的ΔD_max值分别为6、4、3、3 mm，这些初始缺陷将用于有限元数值计算中.

表 3

表 3 试件焊接初始缺陷/mm Table 3 Initial welding imperfection of specimens /mm 试件 Δb1/mm Δb2/mm ΔHlf1/mm ΔHlf2/mm ΔHsf1/mm ΔHsf2/mm ΔHfmax/mm ΔHw/mm Δb0/mm ΔDmax/mm ΔDmax·L-1/‰ SA -1 1 6 6 1 1 6 2 2 6 3.57 SB 1 0 4 4 3 1.5 4 2 3 4 2.38 SC -1 -1 2 2 0 0 2 3 -1 3 1.19 SD 1 1 0 0 0 0 1 -1 3 3 0.60

表 3 试件焊接初始缺陷/mm Table 3 Initial welding imperfection of specimens /mm

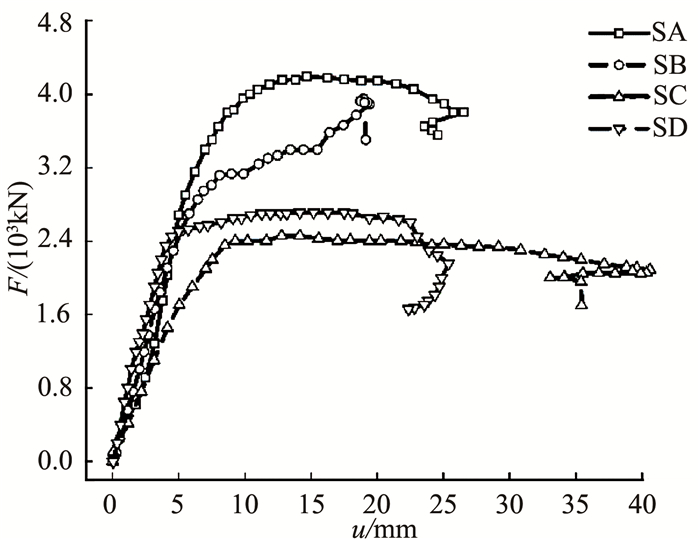
如图 4所示为4个试件试验过程中的荷载F与杆顶端竖向位移u的关系曲线.SA、SB、SC和SD试件的极限加载值分别为4 199、3 943、2 501、2 747 kN.较Q345B制成的SC试件，Q500qE制成的SA、SB和SD试件的极限荷载明显增大.对于不同外伸翼缘宽度的SA、SB和SD试件，由表 1知三者的EI_y/EI_x值分别为1.60、1.04和0.44，相对于试件SD的三者极限荷载比值分别为1.53、1.44和1.00，故采用Q500qE高性能钢和设置外伸翼缘可有效提高薄壁箱形压弯构件极限承载力.

图 4

图 4 试件荷载位移曲线 Fig. 4 Load-deflection curve of specimens

为考察外伸翼缘薄壁钢箱压弯构件屈曲特性，分析如图 5所示中4个试件在试验过程中的压弯屈曲特性.

图 5

图 5 屈曲模态及其特征 Fig. 5 Buckling modes and characteristics

由图 5可知，在试验过程中，压弯构件失稳形式为整体-局部耦合屈曲模态.对于整体屈曲，4个构件均在0.7倍构件长度的位置区域发生一阶受弯屈曲，与一端固定、一端简支的经典屈曲验算公式中的有效屈曲长度系数吻合.

对于整体失稳，由图 4的荷载-位移曲线可知，试验中带外伸翼缘的薄壁钢箱压弯构件整体失稳模态不止一种.按照JSCE^[12]失稳分类，试件SA、SB、SC和SD在加载过程中均表现为极值点失稳特性(EPI).

另外，从构件整体变形位置处的表面凹凸变形区可知，SA、SB、SC和SD试件截面虽关于中间加劲肋对称，但在对称翼缘板两侧的局部屈曲并非对称.试件SA、SB和SC，特别是SD，在发生受弯屈曲(FB)同时发生了局部扭转屈曲(TB)，即发生了弯扭耦合屈曲(FTB)，发生弯扭耦合屈曲变形幅度从大到小分别为SD、SC、SB和SA.其原因主要是，当作用荷载较小时，构件仅发生平面内受弯屈曲(FB)；当作用荷载增大时，在构件翼缘板因初始缺陷造成局部区域应力提前进入塑性状态，随着塑性区域的增大荷载偏心距也随之增大；当荷载偏心距继续增大且当板件平面外刚度不足以抵抗荷载时，局部变形区段发生不均匀内凹或鼓曲，使得整体屈曲模态由平面内受弯屈曲(FB)模态向平面内和平面外弯扭耦合屈曲(FTB)模态转化.而SA、SB和SC试件外伸翼缘增大了构件的横向刚度，大大限制了中间翼缘的扭转变形，进而改善了平面外弯扭耦合屈曲特性.

从局部屈曲角度，通过对图 5(b)中4个试件试验加载过程观测，试件SC和SD在距杆底向上的0.7倍杆长位置处受压翼缘侧中部区域出现较大的内凹塑性区，而试件SA和SB截面中间翼缘上内凹塑性区较小.此外，随着简支端的偏心荷载增大，外伸翼缘上出现局部屈曲(EFLB)或中间翼缘上出现局部屈曲(MFLB)，整体受弯屈曲(FB)明显增大；翼缘板发生局部屈曲后，构件截面发生应力重分布，翼缘板传递给腹板内的剪应力明显增大.因腹板宽厚比达到20，腹板自身的平面外刚度小于其平面内刚度，即在腹板发生平面外局部屈曲(WLB).由此可见，外伸翼缘可改善薄壁钢箱压弯构件屈曲特性.

从局部屈曲半波数角度描述外伸翼缘板局部屈曲特征.如表 4所示统计了图 5中在宽、窄翼缘板上发生的局部屈曲半波数试验实测情况.表 4中LF, SF分别表示试件的宽翼缘和窄翼缘；-L和-R分别表示每个翼缘板的左、右边缘.从翼缘板局部屈曲模态来看，SA和SB主要发生R-模态，SC兼有R-模态和F-模态，SD主要发生F-模态.SC试件在整体屈曲最大位置处发生2个局部屈曲半波数，在宽翼缘底部因受压也出现2个局部半波数；SD试件仅在距底部以上0.7倍距离处的中间翼缘和腹板处出现1个屈曲半波数；而试件SA和SB宽厚比为154/8和114/8的宽翼缘上出现的屈曲半波数明显多于宽厚比为114/8和64/8的窄翼缘，即宽厚比越大，屈曲半波数越多.当板宽厚比b/t小于规范限值$ 0.56\ \sqrt{E/{{\sigma }_{y}}} $时屈曲半波数相对较少.

表 4

表 4 翼缘板局部屈曲试验实测半波数和屈曲形态 Table 4 Half wave numbers and buckling modes of FLB by tests 翼缘边 SA SB SC SD LF-L 3 2 2 1 LF-R 3 3 2 1 SF-L 1 2 2 1 SF-R 1 1 2 1 FLB屈曲模态[11] R R R+F F

表 4 翼缘板局部屈曲试验实测半波数和屈曲形态 Table 4 Half wave numbers and buckling modes of FLB by tests

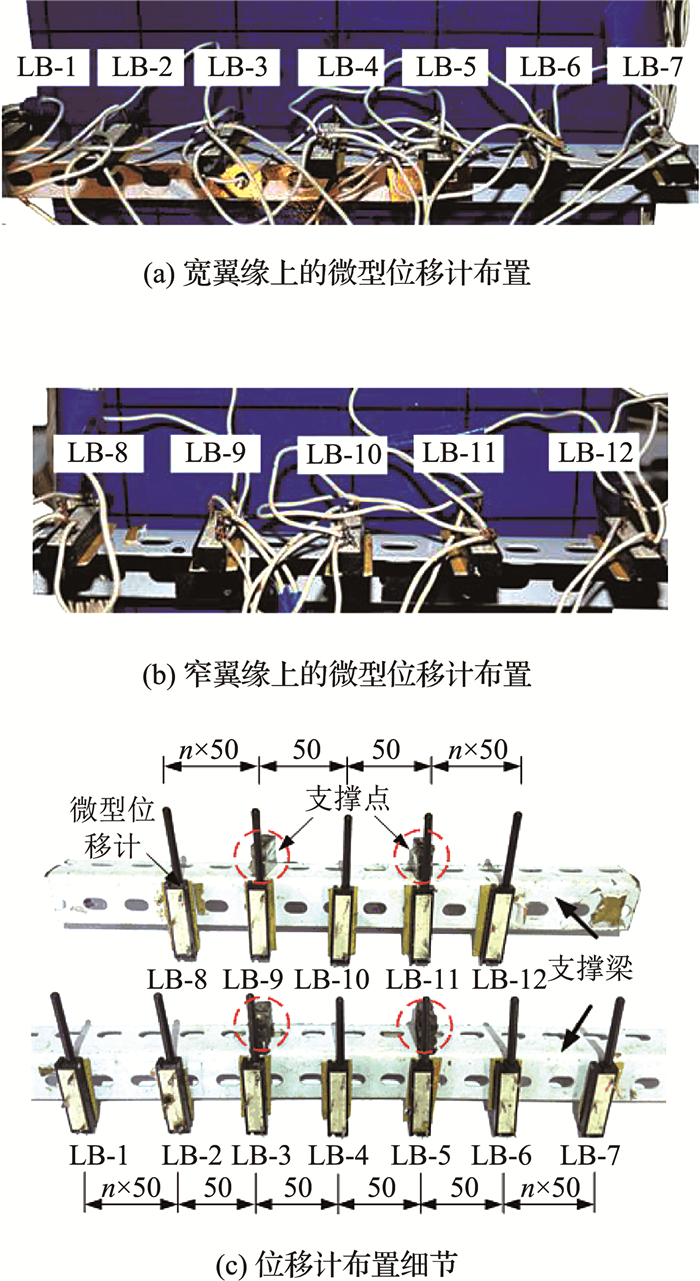
影栅云纹法^[8]用于反映板件表面局部变形的波形特征.本试验设计了一种通过微型位移计DUNCAN测得翼缘板局部屈曲位移的方法.在宽、窄翼缘上分别布置了LB-1 ~ LB-7等7个和LB-8 ~ LB-12等5个微型位移计，其中位移计LB-3 ~ LB-5和LB-9 ~ LB-11分别为观测宽、窄翼缘上的中间翼缘的观测点，其他测点为外伸翼缘测点，如图 6所示.

图 6

图 6 局部屈曲位移计及其布置 Fig. 6 Displacement gauges and its arrangement for local buckling tests

这些位移计按照图 6(c)的间距布置分别安装在两角钢支撑横梁上(见图 6(a)~6(c))，并设置间距100 mm的两支撑点将支撑横梁固定于试件表面，图 6中两支撑点正好位于两腹板与翼缘板相交位置处.图 6(c)中n为最外侧位移计距相邻位移计50 mm的倍数.对于试件SA，n=2；试件SB和SC，n=1，试件SD，n=0.

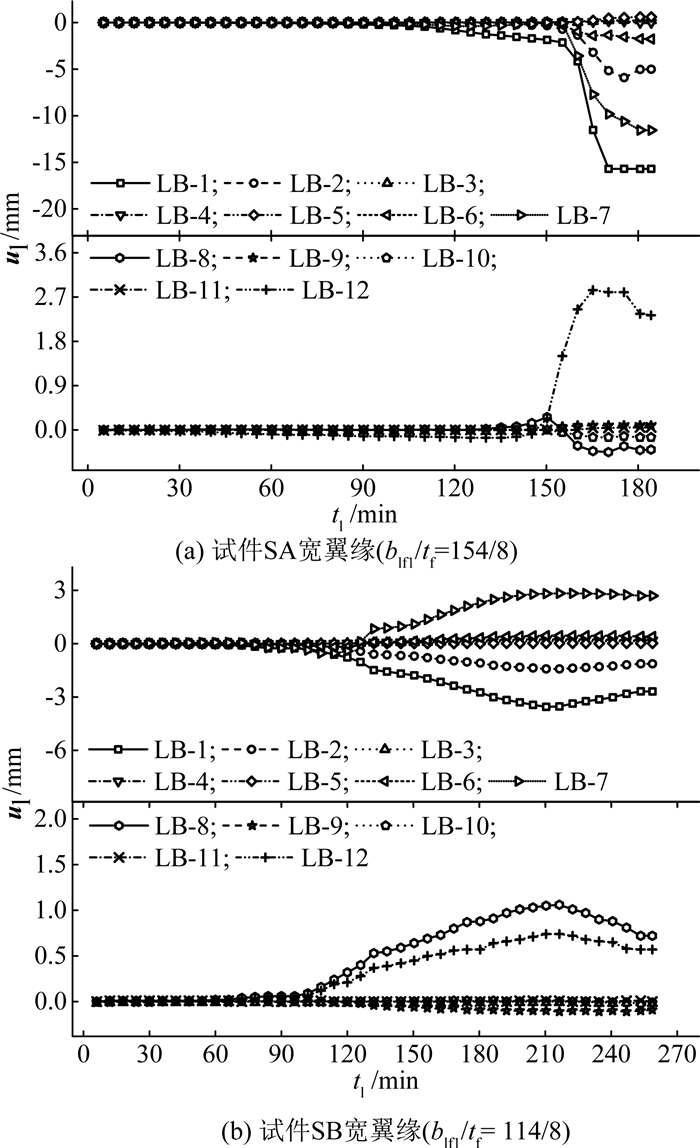
如图 7所示为距试件底部1.0 m处在试验过程中随加载时间t_l变化的局部屈曲相对于腹板与翼缘板相交点的位移u_l变化情况，其中位移以朝向腹板内侧的屈曲变形为负，以远离腹板内侧屈曲变形为正.由图 7-(a)和(b)，在相同时间条件下，测点LB-1, LB-2和LB-7远大于测点LB-3 ~ LB-6位移, 测点LB-8和LB-12位移大于测点LB-9 ~ LB-11上位移.即外伸翼缘局部屈曲变位(EFLB)大于中间翼缘局部屈曲变位(MFLB).对比SA和SB局部位移值，试件SA的宽翼缘最外侧测点LB-1和LB-7的最大位移超过15 mm，远大于试件SB宽翼缘相应的最外侧测点最大位移；试件SA的窄翼缘最外侧测点LB-8和LB-12的最大位移接近3 mm，大于试件SB窄翼缘相应的最外侧测点1.0 mm.由此可见外伸翼缘宽厚比越大，其自身的局部屈曲变位影响越大.

图 7

图 7 翼缘板实测局部位移 Fig. 7 Local displacements of tested flanges

外伸翼缘宽厚比154/8、114/8、64/8对应的局部屈曲位移分别为15、3、1 mm，位移与宽度比分别为0.78、0.21和0.125.前两者宽厚比均已超过规范^{[12, 15]}宽厚比限值$ 0.56\ \sqrt{E/{{F}_{\rm{y}}}} $或TB10091^[14]规范条文第5.3节中对应限值要求.故这种带外伸翼缘薄壁钢箱压弯构件的外伸翼缘宽厚比限值采用现有规范中限值是合理的.

采用ANSYS有限元软件中SOLID95实体单元, 计算分析4个模型试件的弹塑性屈曲特性.其数值分析试件边界条件为一端简支、一端固支.假定圆柱体支座在顶压座槽内滑动很小，故简支端承受竖向荷载，模拟加载系统中的圆柱体支座作用.

弹塑性屈曲求解的基本步骤为先进行静力线性计算，再通过Block Lanczos法求解弹性屈曲特征值及相应的屈曲模态.利用弹性屈曲特征值，计算构件的极限承载力.根据牛顿拉普森法并考虑几何非线性和材料非线性.对于材料非线性，考虑采用多线性随动硬化法则(KINH)法.数值计算中考虑了表 3中的焊接初始缺陷.计算结果见图 8和表 5.

图 8

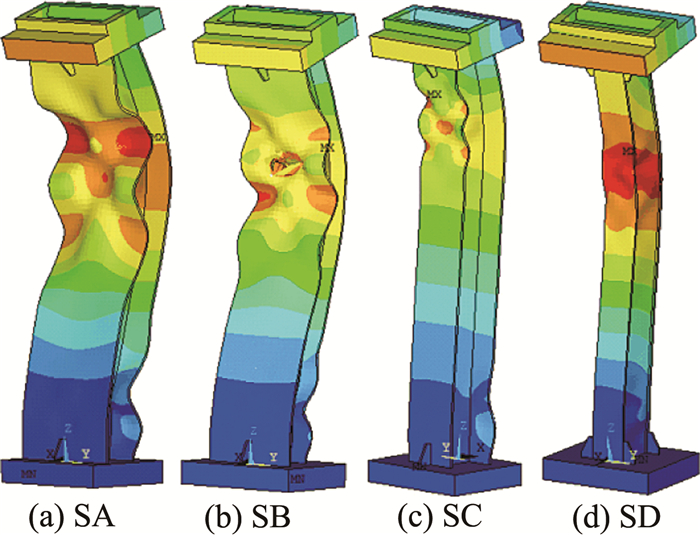
图 8 数值计算极限状态 Fig. 8 Ultimate states by numerical analysis

表 5

表 5 屈曲荷载实测值与数值计算值比较 Table 5 Comparison of buckling loads between test results and numerical analysis 试件 Leff/mm y/mm e0/mm e/mm e·Leff-1/‰ FPT/kN MT/kN·m FCA/kN FEA/kN FPT/FCA FPT/FEA SA 1 740 82 13 7 4.02 4 199 29.39 4 078 4 660 1.03 0.90 SB 1 741 79 13 4 2.30 3 943 15.77 3 768 6 787 1.046 0.58 SC 1 741 80 -13 -21 -12.1 2 501 -52.52 2 443 7 477 1.023 0.33 SD 1 742 88 13 13 7.47 2 747 35.71 2 621 11 779 1.048 0.23

表 5 屈曲荷载实测值与数值计算值比较 Table 5 Comparison of buckling loads between test results and numerical analysis

由图 8中有限元计算结果与图 5中试验实测值对比，发现4组试件的数值计算结果试件屈曲形态与试验结果基本吻合，大致均在靠近试件总长的0.7倍区域范围内弯曲变形，局部屈曲发生的位置也基本一致.如SD试件中翼缘板处发生内凹变形，同时在腹板面外产生凸起变形.

表 5中列出了4组试件屈曲荷载试验实测值与数值计算值的情况，其中F_PT、F_CA、F_EA、M_T分别表示试验极限荷载、数值计算极限荷载、弹性屈曲荷载、试验等价弯矩.极限荷载的实测值与计算值误差在2.3% ~ 4.8%之间，吻合度较好.考虑非线性的极限荷载与弹性屈曲荷载之间的比值F_PT/F_EA位于0.23~ 0.90之间.

本节讨论Q500qE高性能外伸翼缘箱形压弯构件试验值采用现有规范稳定验算公式的适用情况.选取基于容许应力法的铁路TB10091^[14]规范强度验算公式与基于极限状态法的美国AASHTO LRFD^[14]中压弯构件稳定验算公式.

AASHTO LRFD^[15]规范稳定验算式详见式(1).其中F_u、M_ux、M_ax分别为极限轴力、极限弯矩和等效弯矩.抗力分项系数φ_c=0.9, φ_b=0.9；对于一端简支、一端固定压弯构件，弯矩等效系数β_mx=0.6.

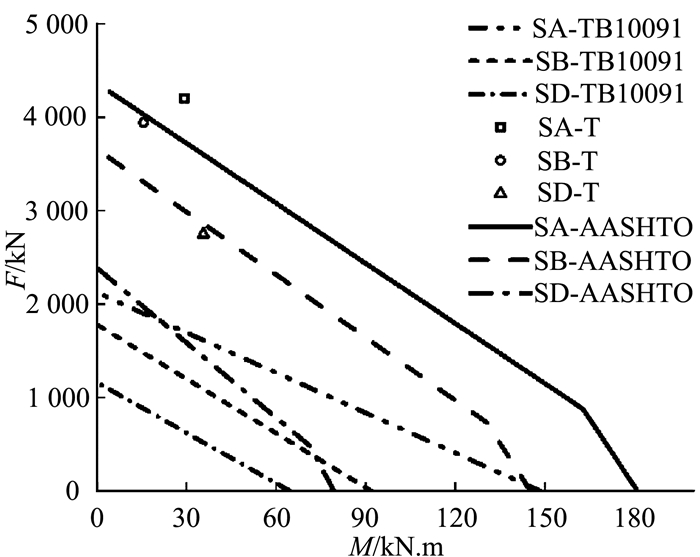
铁路TB10091规范^[14]稳定验算公式按照规范条文中4.2.2公式进行验算.对于Q500qE，其容许应力值为285 MPa，再由长细比小于30，查得规范中试件平面内整体稳定系数φ₁，对于翼缘板，φ₁=0.837；对于腹板及焊接箱形，φ₁=0.867.构件只在一个主平面内受弯的容许应力折减系数φ₂和考虑弯矩因构件受压而增大所引用的值μ₁分别由规范条文中表3.2.6和表4.2.2查得.通过以上两规范^[14-15]稳定验算公式，建立Q500qE高性能钢SA、SB和SD试件稳定验算F-M关系曲线，与表 5中试验值的比较见图 9.

图 9

图 9 试验构件稳定验算F-M关系曲线 Fig. 9 Stability correlation curve between axial force and bending Moment for beam-columns

由TB10091^[14]容许应力法计算得到的弹性稳定F-M关系曲线，明显低于AASHTO LRFD中极限状态法计算得到的相应弹塑性稳定N-M关系曲线.3个试件极限荷载和弯矩，均处于2种规范稳定范围外.故采用容许应力法和极限状态法验算外伸翼缘箱形压弯构件弹塑性稳定，均能满足规范要求.

为研究Q500qE高性能钢外伸翼缘薄壁箱形压弯构件屈曲特性，通过模型试验研究4个构件的荷载-位移曲线、屈曲模态及外伸翼缘宽厚比对局部屈曲变形的影响等3个方面的屈曲特性，并将试验值与现有规范稳定验算公式计算结果进行比较，得出如下结论：

(1) 材料强度和外伸翼缘宽厚比明显影响极限承载力、屈曲模态和局部屈曲变位.

(2) 与Q345B比较，Q500qE钢材料强度能够明显提升极限承载力.较无外伸翼缘钢箱压弯构件，设置外伸翼缘能增大构件平面外横向刚度、提高极限承载力和改善构件的整体屈曲特性.

(3) 带外伸翼缘的薄壁钢箱形压弯构件在加载过程中的失稳模态不止一种.其中整体屈曲由极值点受弯屈曲转向弯扭耦合屈曲，局部屈曲可能由外伸翼缘局部屈曲或中间翼缘局部屈曲转向兼有腹板局部屈曲的局部耦合屈曲模态.

(4) 4个试件均在0.7倍构件长度的位置区域发生整体屈曲，与一端固定、一端简支的有效屈曲长度系数吻合.

(5) 局部屈曲试验表明，外伸翼缘宽厚比越大，屈曲半波数越多，且局部屈曲影响幅度越大；外伸翼缘薄壁钢箱压弯构件的外伸翼缘宽厚比采用现有规范中对应限值限制是合理的.

(6) 考虑焊接初始变形的有限元计算结果与试验结果误差不超过4.8%，符合较好.

(7) 采用容许应力法和极限状态法验算Q500qE高性能钢外伸翼缘箱形压弯构件能够满足现有规范弹塑性稳定要求.