2. 同济大学 岩土及地下工程教育部重点实验室, 上海 200092;
3. 上海隧道工程有限公司, 上海 200232
2. Key Laboratory of Geotechnical and Underground Engineering of Ministry of Education, Tongji University, Shanghai 200092, China;
3. Shanghai Tunnel Engineering Limited Company, Shanghai 200232, China
盾构法经过一百多年的发展,已经逐渐成为软土地层隧道施工的主导工法.圆形隧道受力合理、适合机械化施工,但从空间利用率来看,圆形断面明显低于矩形或马蹄形断面,大直径圆形断面的问题更为突出,不利于地下空间资源的高效利用.上世纪七十年代以来,日本相继开发了矩形盾构、双圆盾构等异形盾构技术[1-2].双圆盾构是城市地铁双线双洞隧道的一种替代方案,但上海地铁的施工实践表明,双圆盾构对地层扰动较大,尤其是两圆交接处凹槽部位的"海鸥型"板构造,在盾构推进时产生背土效应[3-4].类矩形盾构在吸收双圆盾构优点的基础上改进产生,特点是取消了双圆盾构的"海鸥形"板构造,并优化注浆孔位,以降低施工扰动.类矩形盾构作为全新的断面形式,推广价值较高,但是盾构推进的地层扰动等问题还有待研究.
部分研究者针对圆形盾构、双圆盾构、顶管等引起的地层变形做了相应研究.张冬梅等[5]推导了单圆盾构正面附加推力引起土中附加应力的分布;孙统立等[6]分析了双圆盾构正面附加推力、盾构与土体摩阻力引起的土体附加应力;魏刚等[7]推导了单圆盾构正面附加推力、盾壳摩阻力以及土体损失引起的地表沉降;林存刚等[8]研究了单圆盾构掘进中隧道坡度对地面隆陷的影响;在异形断面隧道方面,部分研究者[9-10]总结了矩形盾构和顶管在中国的工程案例和技术特点;也有研究者[11-12]对小断面矩形顶管施工中的地表沉降进行理论分析和现场实测.已有的研究大都针对单圆、双圆盾构,且未考虑盾尾注浆压力对地层变形的影响;而针对小断面矩形顶管施工的分析结果,由于工艺差异也不能直接运用于类矩形盾构中.宁波轨道交通3号线的类矩形盾构属于国内首次设计、首次制造、首次应用的案例工程,掘进引起的地表变形问题值得关注.
本文以国内第1条类矩形盾构隧道——宁波轨道交通3号线区间隧道为例,采用弹性力学Mindlin解和数值积分方法,考虑刀盘正面附加推力、壳体与土体之间非均匀摩阻力以及盾尾同步注浆压力3大因素,计算分析类矩形土压平衡盾构施工引起的地表变形,并和现场实测数据对比,为后续类矩形盾构施工的地层扰动控制提供理论依据.
1 类矩形盾构概况2015年,宁波轨道交通3号线在国内率先设置类矩形隧道区间,采用国产11.83 m×7.267 m类矩形土压平衡盾构进行施工,如图 1所示.

|
图 1 类矩形盾构机 Fig. 1 Quas-rectangle shield |
如图 2所示,类矩形盾构的断面边界由两对不同半径的圆弧构成,分为两腰
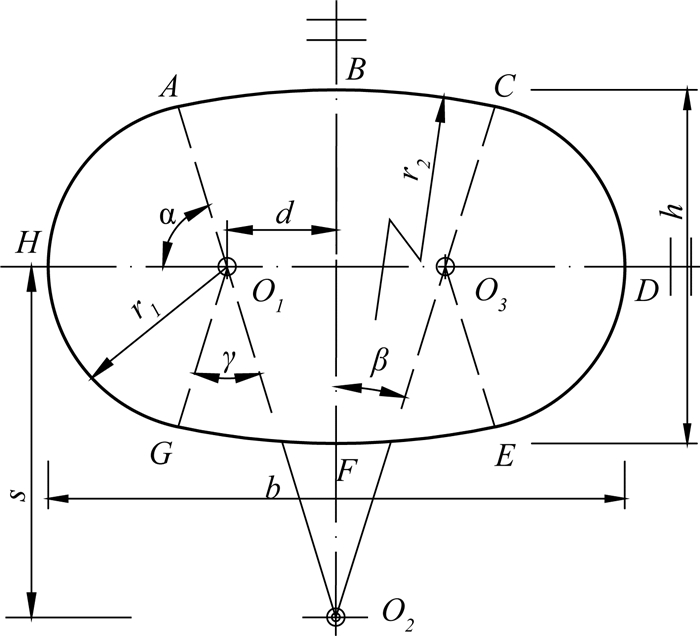
|
图 2 类矩形盾构断面 Fig. 2 Cross section of quasi-rectangle shield |
| 表 1 盾构机主要尺寸 Table 1 Geometry of the quasi-rectangle shield machine |
建立如图 3所示力学模型,分析类矩形盾构掘进中,刀盘正面附加推力p1、壳体与土体之间非均匀摩阻力p2,同步注浆压力p3以及土体损失这4类因素共同作用产生的地表变形.为简化分析,模型作如下假定:1)不考虑盾构掘进时土体的排水固结;2)盾构沿水平方向正常掘进,不考虑盾构纵向坡度以及偏转的影响;3)正面附加推力p1沿开挖面均匀分布;4)土层为均质、线弹性的半无限体;5)类矩形盾构采用2对大开口的双辐条式刀盘,其对开挖面土体的扭矩效应相比面板式刀盘的圆形盾构小,分析中暂不考虑刀盘扭矩的影响.
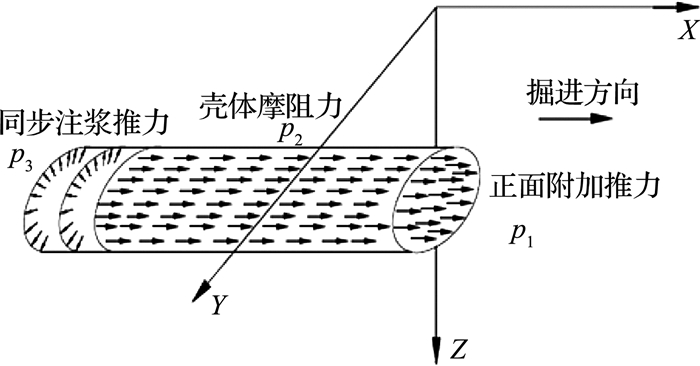
|
图 3 类矩形盾构掘进力学模型 Fig. 3 Analysis model of ground deformation induced by tunneling |
关于盾构正面附加推力p1,现有文献中多简化设定为20 kPa左右[7-8].但上海某直径6.34 m单圆面板式土压平衡盾构现场实测数据表明,刀盘到达时产生的附加推力可达170~190 kPa,辐条式双圆盾构为27~50 kPa[13].实测说明,现有研究中p1的取值低估了刀盘正面附加推力值.王洪新认为,盾构正面附加推力p1由刀盘转动产生的挤压力和切口切入土体产生的挤压力2部分组成,并提出了相应的定量计算公式[13].本文正面附加推力p1的取值,即采用该计算公式:
| $ {p_1} = \frac{{10.13\left( {1 - \mu } \right){E_{\rm{u}}}{\rm{ \mathsf{ π} }}v{{\left( {1 - \xi } \right)}^2}}}{{\left( {1 + \mu } \right)\left( {3 - 4\mu } \right)Dk{n_1}}} + \Delta p'. $ | (1) |
式中:μ为土体泊松比;Eu为土体不排水弹性模量(MPa),按照文献[14]的研究结论进行取值为(2.5~3.5)Es0.1~0.2,其中Es0.1~0.2为土体压缩模量(MPa);v为盾构机掘进速度(cm/min);ξ为刀盘开口率;D为刀盘直径(m);k为刀盘闭口部分幅数;n1为盾构机刀盘转速(r/min);Δp'为切口切入土体产生的挤压力,范围为10~25 kPa.
1.2 非均匀摩阻力p2现有研究中,多假定盾构壳体与土体之间的摩阻力沿盾构全长、全周均匀分布[7-8],而不考虑侧向压力沿盾壳竖向的变化.盾壳与土体的摩擦特性,应考虑盾壳推进产生的壳-土接触面摩阻力的软化效应,参考桩土界面摩阻力的研究结果[15-16], 盾壳-土体界面摩阻力的表达式为
| $ {p_2} = \eta {\sigma _\theta }\tan \varphi . $ | (2) |
式中:η为摩阻力软化系数,参考文献[15],范围为0.83~0.97;σθ为壳体θ角处的正应力,可根据一点的应力状态进行换算;φ为盾构壳体与土体的摩擦角,Potyondy[17]根据黏土-光滑钢材界面剪切试验,给出了6.5°~9°的建议值.
1.3 同步注浆压力p3盾尾注浆能够及时填补管片与地层的间隙,减小地面沉降.注浆压力会对管片外地层产生挤推效应,使土体产生背离盾构的位移.类矩形盾构共设置8处同步注浆管路,以确保浆液能够迅速均匀地填充管片外地层间隙.本文假定同步注浆压力p3沿管片外侧均匀分布于盾尾后两环管片范围(2.4 m),不考虑其沿纵向及径方向的衰减变化.由于注浆压力的水平分量对地层竖向位移的影响很小,本文仅考虑注浆压力的竖向分量对地层竖向位移的影响.根据宁波轨交3号线的现场施工实践,注浆压力p3取为250 kPa.
1.4 土体损失软土地层中隧道掘进将不可避免地产生土体损失.目前针对圆形盾构施工引起的土体损失展开的研究较多,而对于双圆、矩形等异形盾构的土体损失,大都根据面积相等原则将其等效为圆形断面,并在此基础上进行一些参数修正.已有的现场实测数据[18]表明,这种等效可以满足工程精度的要求.由于类矩形盾构属于首次设计和应用,本文在计算其土体损失引起的地面变形时,采取断面面积相等的原则,将类矩形截面等效为圆形截面,进而计算土体损失引起的变形.
3 类矩形盾构施工引起的地表变形 3.1 Mindlin应力解如图 4所示,Mindlin推导了各向同性弹性半无限体内部,分别作用一水平集中力ph和竖向集中力pv时,弹性体内任意一点的位移值[18].
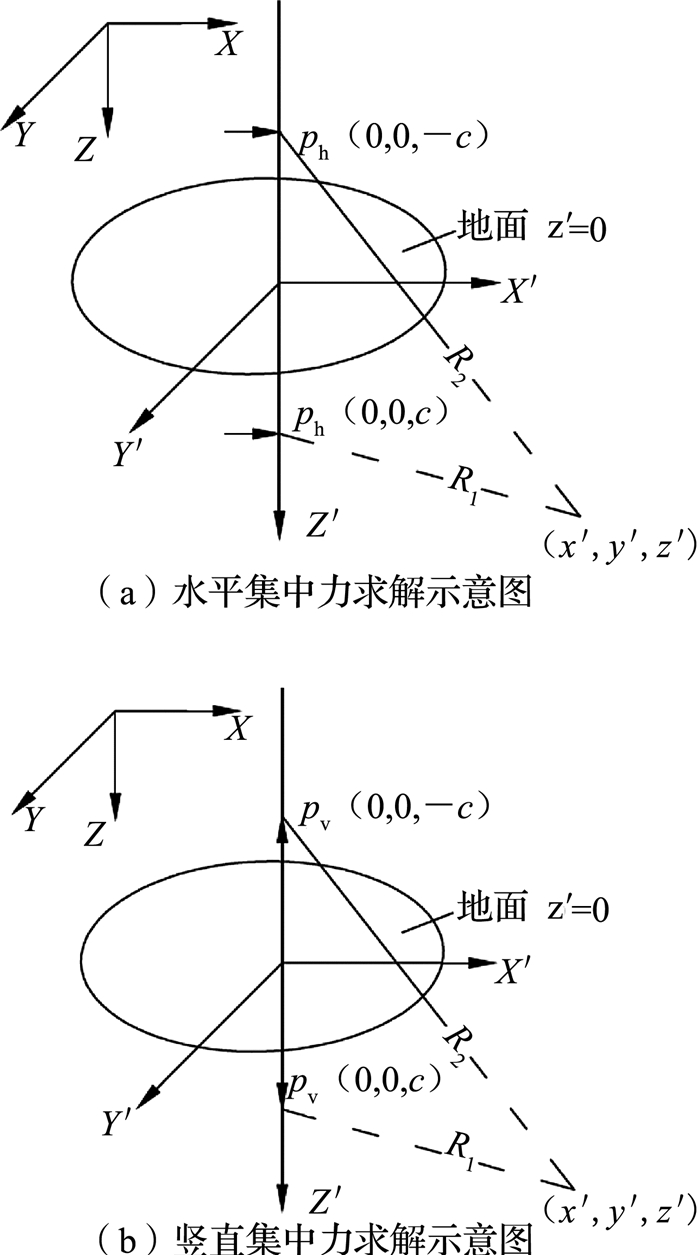
|
图 4 Mindlin解示意 Fig. 4 Map of Mindlin solution |
由于Mindlin解中,集中力位于Z轴(0, 0, c)处,后续积分不便进行.梁荣柱等[15],采用坐标变换的方式,推导任一点集中力作用下Mindlin解的一般式.
如图 5所示,设整体坐标系XYZ,局部坐标系X'Y'Z'.两坐标系对应坐标轴互相平行,局部坐标系原点在整体坐标系下的坐标为(l, m, n).根据坐标变换公式,有以下关系:
| $ \left. \begin{array}{l} x' = x - l\\ y' = y - m\\ z' = z - n \end{array} \right\}. $ | (3) |
|
图 5 正面附加推力引起地表变形分析模型 Fig. 5 Analysis model of ground surface deformation induced by excess pressure |
得到任意一点分别作用水平集中力ph和竖向集中力pv所引起的竖向位移解答,如式(4)和(5)所示.弹性力学以拉应变为正,而土力学以压应变为正,所以对Mindlin解需做符号修正,文中以地层隆起变形为正,沉降变形为负.
| $ \begin{array}{*{20}{l}} {{\omega _{\rm{h}}} = \frac{{{p_{\rm{h}}}\left( {x - l} \right)}}{{16{\rm{\pi }}G\left( {1 - \mu } \right)}}\left( {\frac{{z - n - c}}{{R_1^3}} + \frac{{\left( {3 - 4\mu } \right)\left[ {z - n - c} \right]}}{{R_2^3}} - } \right.}\\ {\left. {\frac{{6c\left( {z - n} \right)\left[ {z - n{\rm{ + }}c} \right]}}{{R_2^5}} + \frac{{4\left( {1 - \mu } \right)\left( {1 - 2\mu } \right)}}{{{R_2}\left( {{R_2} + z - n + c} \right)}}} \right) = }\\ {H\left( {x,y,z} \right).} \end{array} $ | (4) |
| $ \begin{array}{l} {\omega _{\rm{v}}} = \frac{{{p_{\rm{v}}}}}{{16{\rm{ \mathsf{ π} }}G\left( {1 - \mu } \right)}}\left( {\frac{{\left( {3 - 4\mu } \right)}}{{{R_1}}} + \frac{{8{{\left( {1 - \mu } \right)}^2} - \left( {3 - 4\mu } \right)}}{{{R_2}}} + } \right.\\ \frac{{{{\left( {z - n - c} \right)}^2}}}{{R_1^3}} + \frac{{\left( {3 - 4\mu } \right){{\left( {z - n + c} \right)}^2} - 2c\left( {z - n} \right)}}{{R_2^3}} + \\ \left. {\frac{{6c\left( {z - n} \right){{\left( {z - n + c} \right)}^2}}}{{R_2^5}}} \right) = V\left( {x,y,z} \right). \end{array} $ | (5) |
式中:G为土体剪切模量,H(x, y, z)和V(x, y, z)分别为单位集中力ph和pv作用下点(x, y, z)处产生的竖向位移,c为水平集中力作用点到地面的距离,R1、R2分别为Mindlin解中集中力作用点及其对称点到待求应力点间的距离,可表示为
| $ \left. \begin{array}{l} {R_1} = \sqrt {{{\left( {x - l} \right)}^2} + {{\left( {y - m} \right)}^2} + {{\left( {z - n - c} \right)}^2}} ,\\ {R_2} = \sqrt {{{\left( {x - l} \right)}^2} + {{\left( {y - m} \right)}^2} + {{\left( {z - n + c} \right)}^2}} . \end{array} \right\} $ | (6) |
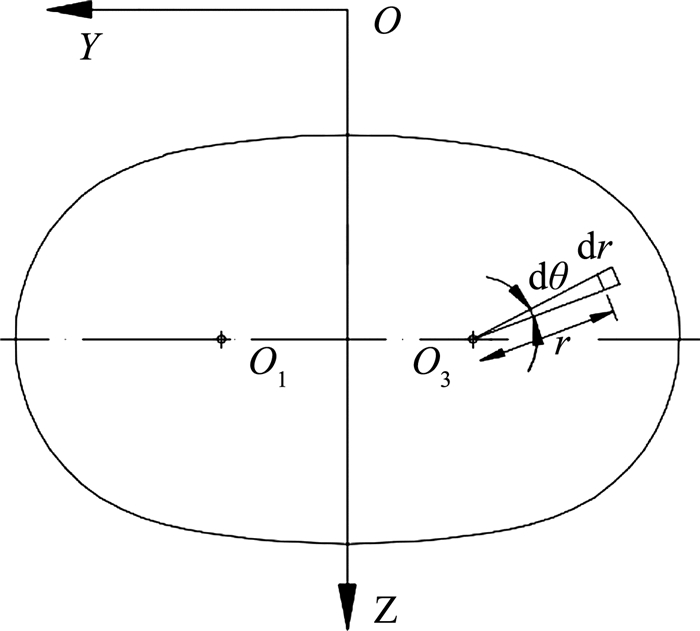
如图 5,取开挖面正面面积微元rdrdθ,其上作用的荷载为p1rdrdθ,在整个开挖面上积分,即可求得正面附加推力p1引起的附加应力.
| $ {\omega _1} = \iint {H\left( {r,\theta } \right){\rm{d}}r{\rm{d}}\theta }. $ | (7) |
式中:ω1为p1作用下引起的地表变形表达式(z=0)
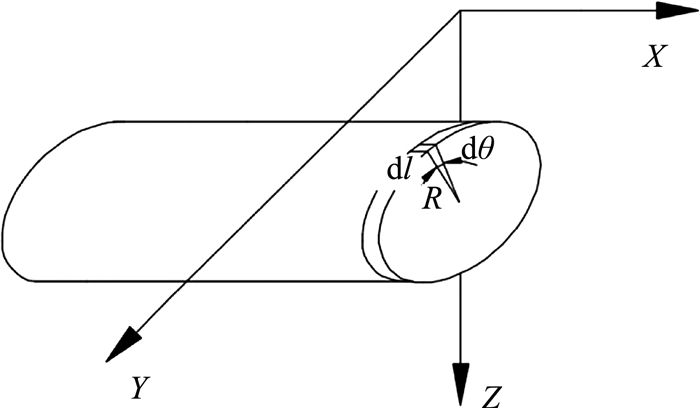
3.3 壳体非均匀摩阻力p2引起的地表变形如图 6所示,取壳体表面面积微元Rdθdl,则微元上的荷载为p2Rdldθ.沿壳体边界和盾构全长进行积分.
| $ {\omega _2} = \iint {H\left( {l,\theta } \right){\rm{d}}l{\rm{d}}\theta }. $ | (8) |
|
图 6 壳体摩阻力引起地表变形分析模型 Fig. 6 Analysis model of ground surface deformation induced by friction force around skin |
式中:ω2为p2作用下引起的地表变形表达式(z=0)
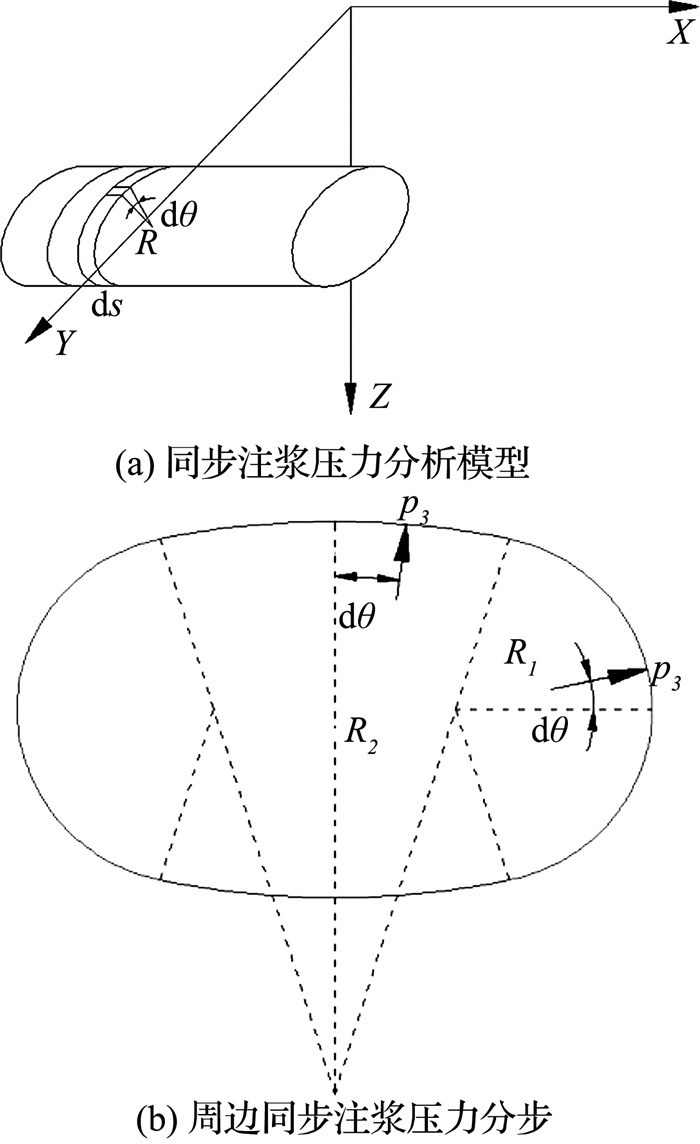
3.4 同步注浆压力p3引起的地表变形如图 7所示,取管片表面面积微元Rdθds,则微元上的荷载为p3Rdsdθ.取同步注浆压力的竖向分量,沿管片边界和两环管片长度进行积分.
| $ {\omega _3} = \iint {V\left( {s,\theta } \right){\rm{d}}s{\rm{d}}\theta }. $ | (9) |
|
图 7 同步注浆压力引起地表变形分析模型 Fig. 7 Analysis model of ground surface deformation induced by tailskin grouting |
式中:ω3为p3作用下引起的地表变形表达式(z=0)
3.5 土体损失引起的地表变形Loganathan等[20]在假定土体不排水的前提下,推导了圆形盾构在椭圆非等向土体位移情况下土体损失引起的地层变形公式,本文在其研究结果基础上,将类矩形截面按面积相等的原则等效为圆形截面,进而考虑土体损失对地表变形的影响,得到土体损失引起的地表沉降表达式如下:
| $ \begin{array}{l} {\omega _4} = 2\left( {1 - \mu } \right)\frac{{{V_{{\rm{loss}}}}{h_0}}}{{{\rm{ \mathsf{ π} }}\left( {{y^2} + h_0^2} \right)}}\left( {1 - \frac{x}{{\sqrt {{x^2} + {y^2} + h_0^2} }}} \right) \times \\ \;\;\;\;\;\;{\;^ * }\exp \left( { - \frac{{1.38{y^2}}}{{{{\left( {{h_0} + {R_{\rm{e}}}} \right)}^2}}}} \right). \end{array} $ | (10) |
| $ A = {\rm{ \mathsf{ π} }}R_{\rm{e}}^2. $ | (11) |
| $ {V_{{\rm{loss}}}} = \varepsilon {\rm{ \mathsf{ π} }}R_{\rm{e}}^2. $ | (12) |
式中:ω4为土体损失引起的地表变形,h0为隧道的中心埋深;Re为类矩形盾构的等效半径;A为类矩形盾构截面面积,取为73.14 m2;Vloss为地层损失;ε为地层损失率,魏纲[21]统计了全国各地盾构施工的土体损失率,在饱和软黏土地层土体损失介于0.35%~2.02%之间,本文取0.8%.
3.6 类矩形盾构施工引起的地表变形综合以上4类因素,得到类矩形盾构施工引起的地表变形为
| $ \omega = {\omega _1} + {\omega _2} + {\omega _3} + {\omega _4}. $ | (13) |
宁波轨道交通3号线类矩形盾构试验段以始发井加固区为起点,隧道轴线平均埋深H=13.1 m,主要穿越淤泥质黏土层,土层力学参数见表 2.
| 表 2 积分计算参数 Table 2 Integration parameters |
类矩形盾构刀盘开口率ξ=80%,刀盘直径D=6.72 m,闭口部分幅数k=4,推进速度v=1.9 cm/min,刀盘转速n1=0.9 r/min.数值积分计算参数见表 3,表中γ0为上覆土层的加权重度, k0为静止侧压力系数.
| 表 3 土层力学参数 Table 3 Mechanical parameters of soil |
采用MATLAB软件编制程序进行积分计算,以下针对积分结果进行分析.
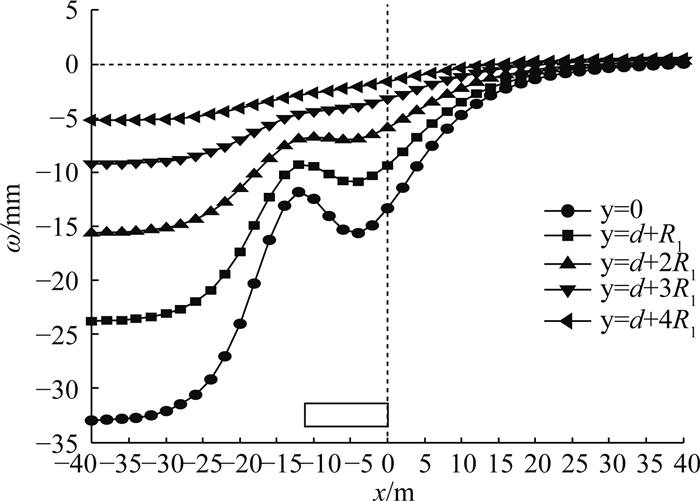
4.2 地表变形ω沿x方向的分布情况如图 8所示为地表变形ω沿x方向(盾构掘进方向)的分布情况.计算结果表明:沿盾构掘进方向地面均表现沉降,在盾构中轴线位置(y=0)的变形最大.以中轴线位置为例,在盾构开挖面前方,沉降值随着距开挖面的距离的增加而快速减小,在x>10 m范围内沉降已小于5 mm,表明类矩形盾构施工的地层扰动主要集中在开挖面前方10 m范围内;在盾构开挖面后方,地表变形在x=-14 m附近(同步注浆边界)达到最小,经分析这是由于同步注浆压力p3引起的地表隆起抵消了部分沉降,在x<-14 m范围内地表沉降迅速增大,最终在盾构开挖面后方约35 m处趋于稳定,沉降量约为33 mm.
|
图 8 地表变形沿x方向的分布情况 Fig. 8 Ground surface deformation along x direction |
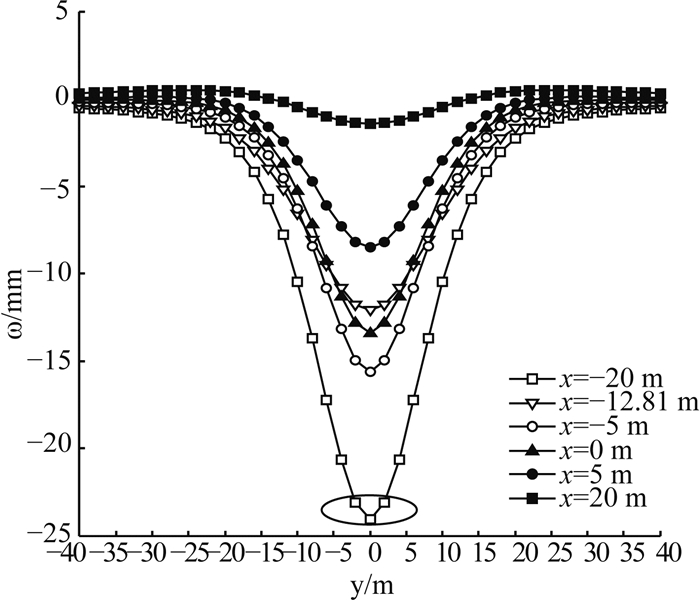
考虑地表变形ω沿y方向(垂直于盾构掘进方向)的分布情况,如图 9所示为不同断面位置地表变形的计算结果(即横向沉降槽).从图 9中分析可知,地表变形沿盾构中轴线左右对称,在盾构开挖面前方,地表变形值随着距开挖面的距离的增加而逐渐减小(图中x=0、5、20 m).横向地表变形分布表明,地表变形主要集中于盾构中轴线两侧约13 m范围内(地表沉降>5 mm);在盾构开挖面后方地表变形均表现为沉降;在盾构开挖面前方一定范围之外(如x=20 m, |y|>16 m),地表变形表现为轻微的隆起,这是由于土体损失的影响迅速减弱造成的.随着距中轴线距离的增加,地表变形值逐渐降低,盾构掘进的扰动影响减小.
|
图 9 地表变形沿y方向分布情况 Fig. 9 Ground surface deformation along y direction |
为了进一步分析4种因素单独作用下地表变形的特点,作盾构沿中轴线方向(y=0)的地表变形图如图 10所示,在正面附加推力p1作用下,开挖面前方表现为隆起,最大隆起位于盾构前方约10 m处;开挖面后方表现为沉降,最大沉降发生在后方约10 m处.积分计算结果表明,在p1作用下地表变形在-0.5~0.5 mm之间,说明p1对地表变形影响很小.非均匀摩阻力p2产生的地表变形,以盾构开挖面后方约6 m位置为界(x=-6 m),沿掘进方向依次表现为沉降和隆起,最大隆起约为1.34 mm,发生在开挖面前方约8 m处,最大沉降为1.33 mm,发生在开挖面后方约18 m处.比较p1和p2这2种因素作用的结果,非均匀摩阻力产生的地表变形远大于正面附加推力作用结果.以开挖面前方10 m位置为例,由p1和p2产生的地表变形分别为0.45和1.32 mm.且p1和p2作用下的地表变形分别关于对称截面呈S形反对称,前者对称位置在开挖面处,后者对称位置在开挖面后方约-4 m处.
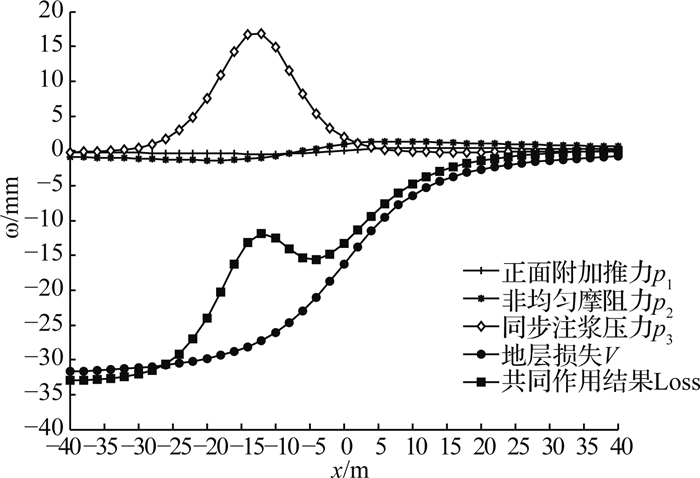
|
图 10 4种因素对地表变形的贡献比较 Fig. 10 Comparison of effects of three factors on ground surface deformation |
分析图 10结果,同步注浆压力p3引起的地表隆起十分明显.p3的主要影响范围为-20 m<x<2 m,在该范围内地表表现为隆起;最大隆起为16.87 mm,位于开挖面后方约14 m处(x=-14 m).土体损失则在纵向引发地表沉降,沉降值的变化主要集中在-32 m<x<10 m内,并随着x的增大沉降迅速增大,最终在开挖面后方约32 m处趋于收敛,此时沉降值约为32 mm.
从图 10中可以看出,同步注浆压力p3产生的隆起(最大约16.8 mm)可以抵消相当部分土体损失引发的沉降变形,在4种因素的共同作用下,沉降值在开挖面后方约14 m位置处出现局部极小值,此即为盾尾同步注浆的影响.因此,施工中合理设置同步注浆压力p3以及在盾尾后方补充二次注浆,可以抵消部分土体损失引发的地表沉降,尤其有利于控制盾构开挖面后方的地表变形.
4.5 实测数据对比分析结合宁波地铁3号线类矩形盾构区间工程的现场实测数据,将理论计算结果与实测结果进行对比分析.
如图 11所示为横向沉降槽的对比情况,图中实测的沉降槽数据来源于盾构区间第181环管片位置处的监测结果.由图 11可知,基于本文公式计算得到的该断面位置处最大沉降量为33 mm,且沉降槽影响范围为盾构中轴线两端各15 m范围;现场实测的最大沉降量为38 mm,沉降槽影响范围为中轴线两端各12 m范围,呈深"Ⅴ"型.
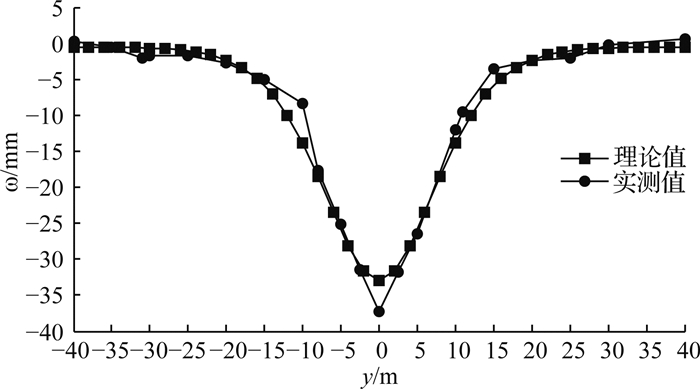
|
图 11 横向沉降槽实测对比 Fig. 11 Comparison of settlement values from theoretic calculation and on-site monitoring |
如图 12所示为纵向地表变形的对比情况,其中盾构开挖面前方的实测值波动较大,且与理论分析值相差较大,分析可能是由于实际施工过程中刀盘的推力较大且不稳定造成;在盾构开挖面后方,理论计算的稳定沉降值约为34 mm,实测值约为38 mm,2条曲线虽有一定差异,但误差值满足工程实际精度要求.值得注意的是,理论和实测值均反映了同步注浆压力对地表具有一定的抬升作用.
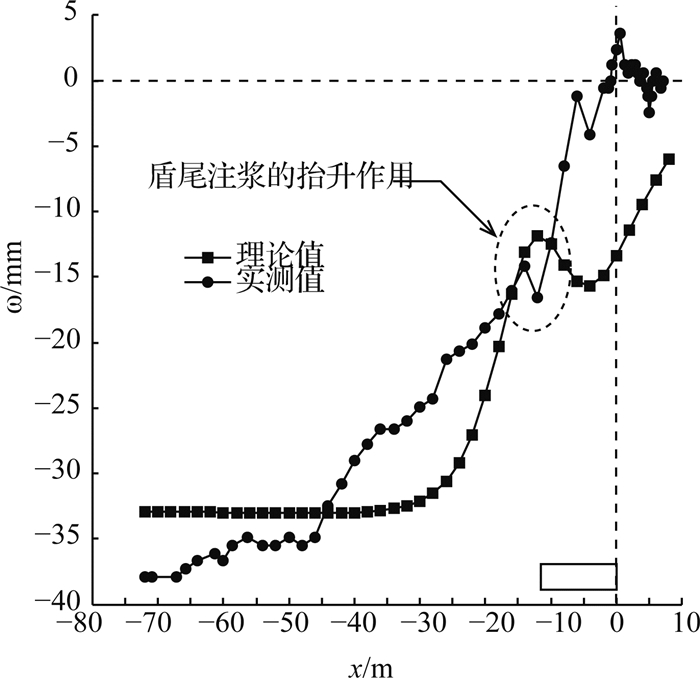
|
图 12 纵向地表变形对比 Fig. 12 Comparison of longitudinal settlement values from theoretic calculation and on-site monitoring |
本文以宁波轨道交通3号线类矩形盾构隧道工程为背景,基于弹性力学Mindlin解分析了刀盘正面附加推力、壳体与土体间摩阻力、同步注浆压力以及土体损失4类因素共同作用引起的地表变形.理论分析结果表明:
(1) 类矩形盾构掘进施工引起地表变形,其在盾构机前后一定范围内表现为沉降,最大的稳定沉降值约33 mm.施工期间横向沉降影响区主要集中于轴线两侧各约15 m范围内.
(2) 同步注浆压力在其作用范围内产生隆起(最大隆起值约16.8 mm),其对土体损失引起的地表沉降具有较大抵消作用,并使得整体沉降变形曲线在盾尾注浆边界处出现局部极小值(约12 mm),因而合理设置同步注浆以及二次注浆有利于控制施工期的地表沉降.
(3) 在4类因素中,正面附加推力以及盾壳与土体的摩阻力两者引起的地表变形极其微小(约1.6 mm),根据本文分析结果,在注浆压力作用范围内,两者引起的地表沉降值约为注浆压力作用下隆起量值的1/10,尚不及土体损失作用下沉降值的1/10,因而类矩形盾构施工中注浆压力和土体损失对地表沉降起决定性作用.
(4) 结合现场监测数据,基于本文计算的沉降槽比实际监测结果稍宽,纵向沉降结果也有一定差异,但已满足实际工程的精度要求.
本文在地表变形分析过程中将类矩形盾构等效为圆形截面可能会有一定误差,同时注浆压力均匀分布的假定也不尽合理,后期研究中针对异形盾构的地层损失分布以及非均匀注浆压力下的地表变形,尚需要进一步探究.
| [1] |
KASHIMA Y, KONDO N, INOUE M. Development and application of the DPLEX shield method:results of experiments using shield and segment models and application of the method in tunnel construction[J]. Tunnelling and Underground Space Technology, 1996, 11(1): 45-50. DOI:10.1016/0886-7798(96)00053-3 |
| [2] |
KONDA T. Shield tunneling method[J]. Civil Engineering, Japan Society of Civil Engineers, 2001, 39: 23-27. |
| [3] |
盛佳韧, 叶冠林, 桥本正, 等. 双圆盾构盾尾注浆对地层沉降的影响分析[J]. 地下空间与工程学报, 2014, 10: 201-205. SHENG Jia-ren, YE Guan-lin, Tadashi H, et al. Influence of backfill grouting on ground settlement in DOT shield[J]. Chinese Journal of Underground Space & Engineering, 2014, 10(1): 201-205. |
| [4] |
周文波, 顾春华. 双圆盾构施工技术[J]. 现代隧道技术, 2004, 04: 22-32. ZHOU Wen-bo, GU Chun-hua. Construction technique of DOT shield[J]. Modern Tunnelling Technology, 2004, 04: 22-32. |
| [5] |
张冬梅, 黄宏伟, 林平, 等. 地铁盾构推进引起周围土体附加应力分析[J]. 地下空间, 1999, 19(5): 379-382. ZHANG DONG-mei, HUANG Hong-wei, LIN Ping, et al. Additional stress analysis of subway shieldtunneling[J]. Underground Space, 1999, 19(5): 379-382. |
| [6] |
孙统立, 张庆贺, 韦良文, 等. 双圆盾构掘进施工扰动土体附加应力分析[J]. 岩土力学, 2008, 29(8): 2246-2251. SUN Tong-li, ZHANG Qing-he, WEI Liang-wen, et al. Analysis of additional stresses of soil disturbance induced by propulsion of double-O-tube shield[J]. Rock & Soil Mechanics, 2008, 29(8): 2246-2251. |
| [7] |
魏纲, 张世民, 齐静静, 等. 盾构隧道施工引起的地面变形计算方法研究[J]. 岩石力学与工程学报, 2006, 25(增1): 3317-3323. WEI G, ZHANG S, QI J, et al. Study on calculation method of ground deformation induced by shield tunnel construction[J]. Yanshilixue Yu Gongcheng Xuebao/Chinese Journal of Rock Mechanics and Engineering, 2006, 25(supp.1): 3317-3323. |
| [8] |
林存刚, 刘干斌, 梁荣柱, 等. 隧道坡度对盾构掘进引起地面隆陷的影响[J]. 岩土工程学报, 2014, 36(7): 1203-1212. LIN Cun-gang, LIU Gan-bing, LIANG Rong-zhu, et al. Influences of tunnel slope on shield tunnelling-induced heave and subsidence of ground surface[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(7): 1203-1212. DOI:10.11779/CJGE201407003 |
| [9] |
傅德明, 张冠军. 我国矩形掘进机隧道施工技术发展与应用[J]. 上海建设科技, 2008, 02: 4-5. FU De-ming, ZHANG Guan-jun. Technical development and application of rectangular shieldtunnelling in china[J]. Shanghai Construction Science & Technology, 2008, 02: 4-5. |
| [10] |
郭昊. 矩形顶管机下穿郑州市中州大道工程简介[J]. 中国市政工程, 2013, 05: 53-55. GUO Hao. Brief Introduction of Zhengzhou Zhongzhon Ave.underpass project using rectangular pipe jacking machine[J]. China Municipal Engineering, 2013, 05: 53-55. |
| [11] |
周顺华, 廖全燕, 刘建国, 等. 矩形顶管隧道顶进过程的地层损失[J]. 岩石力学与工程学报, 2001, 20(3): 342-345. ZHOU Shun-hua, LIAO Quan-yan, LIU Jian-guo, et al. Stratum loss during pipe jacking of rectangle tunnel[J]. Chinese Journal of Rock Mechanics & Engineering, 2001, 20(3): 342-345. |
| [12] |
邓长茂, 彭基敏, 沈国红. 软土地区矩形顶管施工地表变形控制措施探讨[J]. 地下空间与工程学报, 2016, 12(4): 1002-1007. DENG Chang-mao, PENG Jim-in, SHEN Guo-hong. Discussion on control methods of ground surface settlement caused by rectangular pipe jacking construction in soft soils[J]. Chinese Journal of Underground Space & Engineering, 2016, 12(4): 1002-1007. |
| [13] |
王洪新. 土压平衡盾构刀盘挤土效应及刀盘开口率对盾构正面接触压力影响[J]. 土木工程学报, 2009, 42(07): 113-118. WANG Hong-xin. Effect of cutterhead compressing the front soil and influence of head aperture ratio on contact pressure of EPB shield to the front soil[J]. Tumu Gongcheng Xuebao/China Civil Engineering Journal, 2009, 42(7): 113-118. |
| [14] |
杨敏, 赵锡宏. 分层土中的单桩分析法[J]. 同济大学学报:自然科学版, 1992, 04: 421-428. YANG Min, ZHAO Xi-hong. An approach for a single pile in layered soil[J]. Journal of Tongji University:Natural Science, 1992, 04: 421-428. |
| [15] |
梁荣柱, 夏唐代, 林存刚, 等. 盾构推进引起地表变形及深层土体水平位移分析[J]. 岩石力学与工程学报, 2015, 34(3): 583-593. LIANG Rong-zhu, XIA Tan-dai, LIN Cun-gang, et al. Analysis of ground surface displacement and horizontal movement of deep soils induced by shield advancing[J]. Yanshilixue Yu Gongcheng Xuebao/chinese Journal of Rock Mechanics & Engineering, 2015, 34(3): 583-593. |
| [16] |
张乾青, 李连祥, 李术才, 等. 成层土中单桩受力性状简化算法[J]. 岩石力学与工程学报, 2012, 31(z1): 3390-3394. ZHANG Qian-qing, LI Lian-xiang, LI Shu-cai, et al. Simplified analytical method for response prediction of single pile embeded into layered soils[J]. Yanshilixue Yu Gongcheng Xuebao/chinese Journal of Rock Mechanics & Engineering, 2012, 31: 3390-3394. DOI:10.3969/j.issn.1000-6915.2012.z1.106 |
| [17] |
POTYONDY J G. Skin friction between various soils and construction materials[J]. Geotechnique, 1961, 11(4): 339-353. DOI:10.1680/geot.1961.11.4.339 |
| [18] |
吕虎, 张庆贺. 地铁双圆盾构施工引起的地面沉降模型[J]. 建井技术, 2006, 27(1): 32-34. LV Hu, ZHANG Qing-he. Analysis model of surface settlement induced by subway double-O-tube shield[J]. Mine Construction Technology, 2006, 27(1): 32-34. |
| [19] |
MINDLIN R D. Force at a point in the interior of a semi-infinite solid[J]. Physics, 1936, 7(5): 195-201. DOI:10.1063/1.1745385 |
| [20] |
LOGANATHAN N, POULOS H G. Analytical prediction for tunneling-induced ground movement in clays[J]. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(9): 846-856. DOI:10.1061/(ASCE)1090-0241(1998)124:9(846) |
| [21] |
魏纲. 盾构隧道施工引起的土体损失率取值及分布研究[J]. 岩土工程学报, 2010, 32(9): 0-0. GANGW E I. Selection and distribution of ground loss ratio induced by shield tunnel construction[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(9): 1354-1361. |



