坡面流是指在降雨量超过土壤入渗及地面洼蓄能力后产生的、在重力作用下沿坡面运动的浅层水流,有时也称为片流或漫流[1].它是形成河道水流的主要组成部分,也是土壤侵蚀及泥沙输移的重要动力.因此,研究坡面流,无论是对丰富和完善水力学理论,还是解决水土侵蚀等工程问题,都具有重要意义.
坡面流阻力系数是反映坡面流特性的一个关键参数,然而,由于坡面流水深极浅(毫米级),极易受坡面地形地貌特征、土壤类型、植被覆盖以及降雨等条件影响,导致阻力特性规律比河道水流复杂的多.
目前,国内外学者主要通过室内外人工降雨试验放水冲刷试验,对坡面流阻力特性规律进行研究,并得到了很多有益的研究成果.然而,由于试验条件、测量手段和工况设计的不同,许多结论不尽相同,甚至有的截然相反.例如,Emmett[2]在0.17°~ 4.47°的坡面上研究发现坡面流阻力系数与坡度呈负相关关系;Savat[3]通过对2.8° ~ 30°坡面的研究认为,在层流状态下,坡面流阻力系数与坡度呈正相关关系;翟艳宾[4]在坡度为0°~ 15°范围内,采用变坡水槽试验研究表明,阻力系数随着坡度的增大而增大.刘元臣等[5](2016)通过变坡水槽试验研究了坡度为0 ~ 1.7°范围内坡面流的阻力特性,结果表明,坡度是影响阻力系数的重要因素之一,随着坡度增大阻力系数先逐渐变大后变小.王俊杰等[6]在坡度为5°~ 25°范围内,采用人工降雨和径流冲刷相结合的方法,试验得出,阻力系数随着坡度的增加呈现先增加后减小的趋势.陈国祥等[7]研究了降雨对浅层水流阻力特性的影响,研究表明降雨可使浅层水流的阻力系数增大.梅欣佩[8]研究了雨滴打击强度对坡面薄层水流阻力特性的影响,水槽试验结果表明阻力系数与雨滴打击强度正相关,土槽试验结果表明阻力系数与雨滴打击强度负相关.潘成忠等[9]通过放水冲刷和模拟降雨试验,研究表明降雨对阻力系数无显著影响.张小娜等[10]通过模拟降雨试验得出了阻力系数随雨强的增大呈现先增加后减小的趋势.迄今为止,阻力系数与坡度、降雨的关系,尚无定论.
在自然界,尤其是山区,四五十度的陡坡十分常见.然而,由于物理模型试验条件的限制,大多数试验是在15°以内的缓坡下进行[2, 4, 5],部分试验坡度达到了25°[3, 6, 11],但均未超过30°.另外,目前针对坡面流阻力特性的研究,大多是研究坡面平均阻力系数[12-13],不能反映阻力系数在不同时刻、不同断面的分布情况.
本文采用18场人工降雨物理模型试验数据对基于物理概念的水文响应数值模型进行了率定验证,然后使用数值模型虚拟150种工况,定量研究了坡度5° ~ 55°,雨强30 ~ 240 mm/h范围内,坡面流阻力系数的时空分布规律,以及雨强和坡度对坡面流阻力系数的影响.
1 材料与方法 1.1 人工降雨物理模型试验 1.1.1 试验装置人工降雨土槽模型试验装置由针管式模拟降雨系统、固定式液压升降试验土槽、径流收集装置3部分组成(如图 1所示).其中,针管式模拟降雨系统可以实现不同的降雨强度以及可以控制降雨发生器的运动路径,针管式雨滴发生器的降雨面积为1 m × 1 m,距离土槽垂直高度12 m;固定式液压升降试验土槽可调节坡度,尺寸为长5 m,宽1 m,深0.5 m;为减少边界条件的影响,土槽土壤铺设的净尺寸为长4 m,宽1 m,厚0.3 m;底部为不透水层;在坡面下游出口处,放置一个金属容器,用于收集和测量径流.
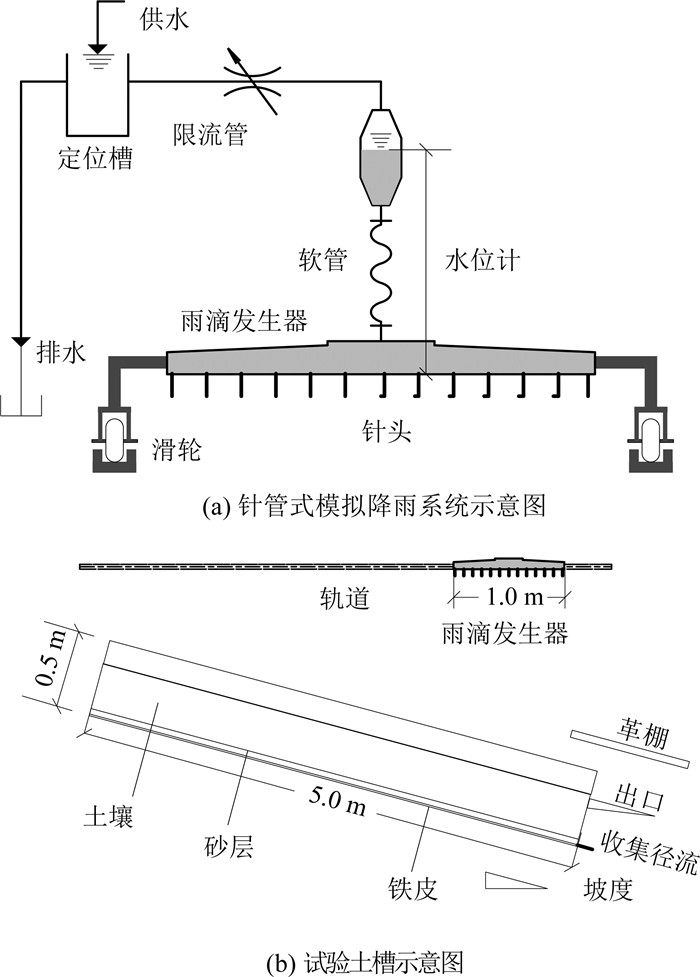
|
图 1 人工降雨物理模型试验装置示意图 Fig. 1 Experimental setup of artificial rainfall physical model |
本次物理模型试验共计18场次,试验坡度S为15°和20°;降雨形式包括固定降雨和向上、向下的移动降雨;降雨强度(I)为60 ~ 210 mm/h不等;降雨历时(t)为15 ~ 120 min不等.具体工况如表 1所示.
| 表 1 室内人工降雨试验工况设置 Table 1 Experimental setting of indoor artificial rainfall |
自产流起,径流收集装置每1 min收集一次径流量,直至降雨结束.将4 m长的坡面均分为4个坡段,则使用秒表和染色剂(KMnO4)示踪法测量各个坡段的表面流速.通过流速修正系数计算平均流速:
| $ V = \alpha {V_{{\rm{sur}}}}. $ | (1) |
式中:V为平均流速(m/s);α为流速修正系数;Vsur为实测表面流速(m/s).
目前坡面薄层水流的阻力特性规律和内在机理尚未明晰,因此,长期以来一直借用明渠流的概念和表达式.由于Darcy-Weisbach阻力系数表达式具有良好的物理意义且量纲和谐,因此,在坡面流阻力特性研究中被广泛应用[5-15].本研究亦采用Darcy-Weisbach公式计算阻力系数:
| $ f = \frac{{8gRJ}}{{{V^2}}}. $ | (2) |
式中:f为Darcy-Weisbach阻力系数;g为重力加速度(m/s2);R为水力半径,近似于水深(m);J为水力坡度,近似于sin θ,θ为土槽坡度.
1.1.2 土壤参数试验所用土壤为西安附近的黄土,分层填土(每层5 cm)并压实,因此认为土壤密实度均一,饱和导水率各向同性.土壤样品用烘干法实测土壤干质量浓度为1.296 g/cm3,经查阅资料[16],取土壤的颗粒密度为2.60 g/cm3,经计算,土壤孔隙度约为0.50.烘干法实测土壤体积含水量为25.0 %.采用BT-9300H激光粒度分析仪对土壤颗粒进行级配分析,如表 2所示,其中d为土壤粒径(mm), wB为各粒径土壤所占百分比(%).根据土壤粒径级配,推算出土壤水分特征曲线Van-Genuchten模型参数为,α=1.04,n=1.64,sr=0.1.为保证每次试验土壤初始条件一致,避免土壤初始含水量的变化及降雨结皮对土壤特性的影响,每次试验均重新换土,分层填土并整平.
| 表 2 试验土壤粒径级配 Table 2 Particle size gradation of soil |
基于物理概念的分布式水文/侵蚀数值模型(intergrated hydrology model, InHM)是由VanderKwaak[17]在Waterloo大学开发的,后经Stanford大学地质水文研究组的Loague等[18-20]不断改进和完善,其模拟范围包括:地下水的三维运动、地表水的二维坡面流动、二维河道流动及地表泥沙搬运.现已被成功应用于流域尺度下的地貌演变[20]、泥沙侵蚀模拟[21]等领域,尤其适用于小尺度下的水文响应模拟[22-24].相比于应用经验半经验公式来描述自然过程的传统水文数值模拟模型,InHM模型最大的优势在于用基本物理定律来描述自然过程.
1.2.1 边界条件与初始条件如图 2所示为InHM模拟土槽的三维网格示意图.三维网格的边界包括不透水边界(A-D-E-F, B-C-H-G, E-F-G-H, C-D-E-H)、流量过程边界(A-B-G-F)和径流出口边界(A-B-C-D).数值模拟中,降雨荷载以降雨强度的形式施加在降雨区域的每一个网格节点上.

|
图 2 InHM模型三维网格 Fig. 2 3D mesh used inInHM simulations |
初始条件的设置主要是针对初始含水量,根据1.1.2,设置初始含水量为25%.
1.2.2 率定验证主要是针对InHM数值模型参数饱和导水率ks的率定和验证.将上述18场物理模型试验均分为2组,取其中一组的9场试验数据用于率定,另外9场的试验数据用于验证.首先,比较实测洪峰流量(qVo)与模拟洪峰流量(qVs),以相关系数r和纳什效率系数E为数值模拟效果优劣的衡量标准,率定阶段r=0.98,E=0.82,验证阶段,r=0.92,E=0.74,如图 3(a)所示,说明参数率定可靠,模型模拟效果良好.另外,由于本次阻力特性规律研究需要用到分布式精细化的数据,如坡面沿程的流速、水深等,因此,为了保证数值模拟的结果的可靠度,用所有坡面各断面实测流速(V)与模拟流速(Vs)对率定结果做进一步验证.流速验证显示r=0.80,E=0.57,如图 3(b)所示.由以上的出口处洪峰流量的率定验证以及坡面分布式流速信息的验证,避免了“异参同效”现象,可以认为此次数值模拟对水文响应的把握比较准确.
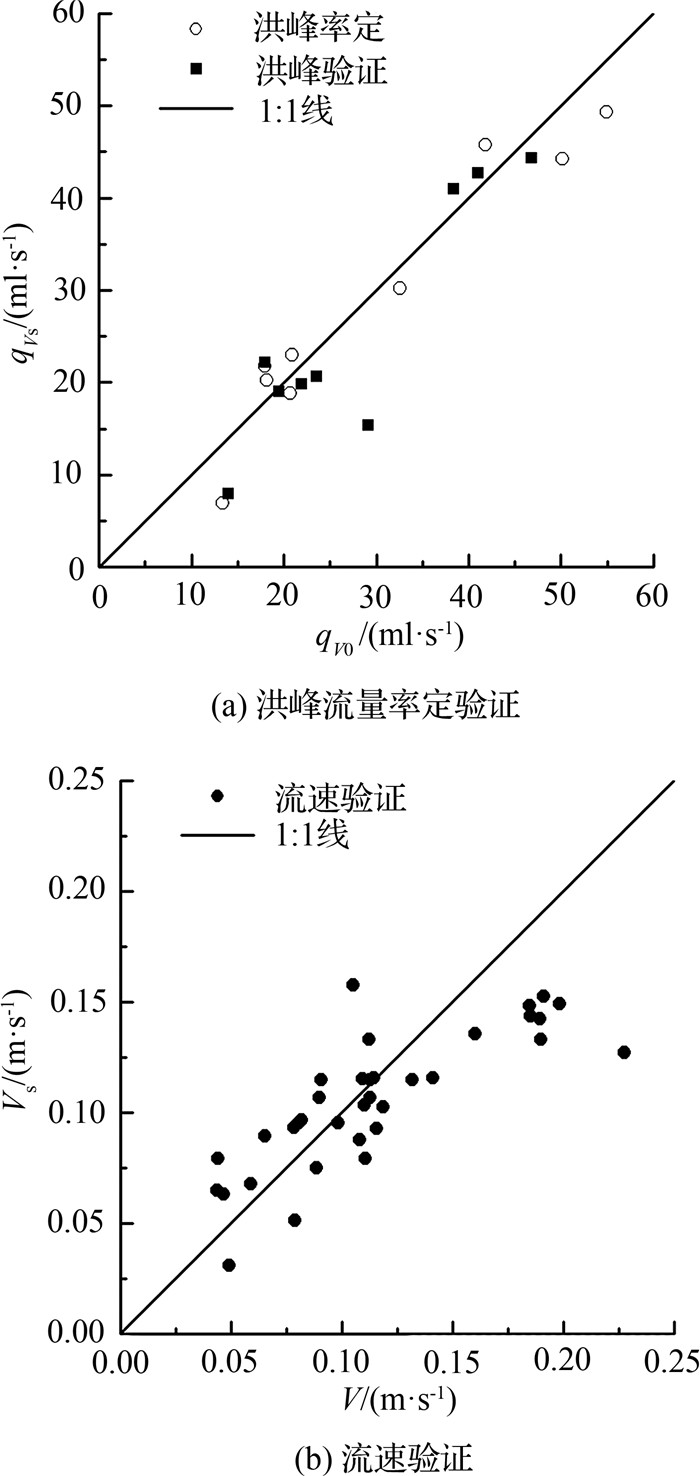
|
图 3 洪峰流量及流速对InHM模型参数(饱和导水率ks)的率定验证 Fig. 3 Calibration and verification of saturated hydraulic conductivity ks using peak flow and velocity |
经过率定验证,得到了土壤饱和导水率ks=2×10-7m/s.地表糙度在查阅资料[25]的基础上,经过微调率定,取值为0.015.1.1.2的实测土壤参数和1.2.2率定得到土壤参数整理如表 3所示, 表中w为初始含水量.
| 表 3 试验土壤关键特征参数 Table 3 Key parameters of experimental soil |
经初步计算,雨强为60 mm/h,坡度为20 °工况的坡面平均雷诺数为Re=724>500,流态为紊流,故,可将工况拓展到更大坡度,更大雨强.
虚拟工况坡度为:5° ~ 55°范围内的15种坡度(每间隔5°设置一个坡度,以及由于进一步研究需要,新增坡度8°,12°,13°,14°);
虚拟工况雨强为:30、60、120、180、240 mm/h等5种雨强;降雨历时:1 h.
另外,考虑到在定坡长条件下,坡度变化会影响受雨面积,而定受雨面积的条件下,坡度变化会影响坡长.因此,对于坡面尺寸,设计了定坡长(4 m)和定受雨面积(4 m2)2个系列,均为全坡面固定降雨,共计150种虚拟工况.
2 结果与讨论InHM模型输出的信息非常丰富,包括任何时刻任何位置的水深、流速、流量、土壤含水量等信息.因此,可以通过提取坡面上的水深和流速信息,用Darcy-Weisbach公式计算得到任意时刻任意位置的阻力系数.
2.1 阻力系数的时空分布规律由于150种工况的坡面流阻力系数的时空分布具有相似的定性规律,故随机选取了降雨强度为60 mm/h,坡度为30°的工况做展示.由于固定受雨面积的情况下,不同坡度对应的坡长不一致,为了便于分析比较,将其坡面点距坡顶的距离做归一化处理,l=l0/L,其中,l为归一化的坡面点距离坡顶的距离,无量纲,l0为实际距离,L为全坡长.
如图 4所示为S=30°、I=60 mm/h的工况,在t=600、900、1 500、3 300 s时刻的阻力系数分布图,由图 4可以看出,在时间上,随着降雨历时的增加,坡面各个位置的阻力系数均呈减小趋势,且产流初期阻力系数变化相对明显,随后,坡面阻力系数逐渐趋于稳定.
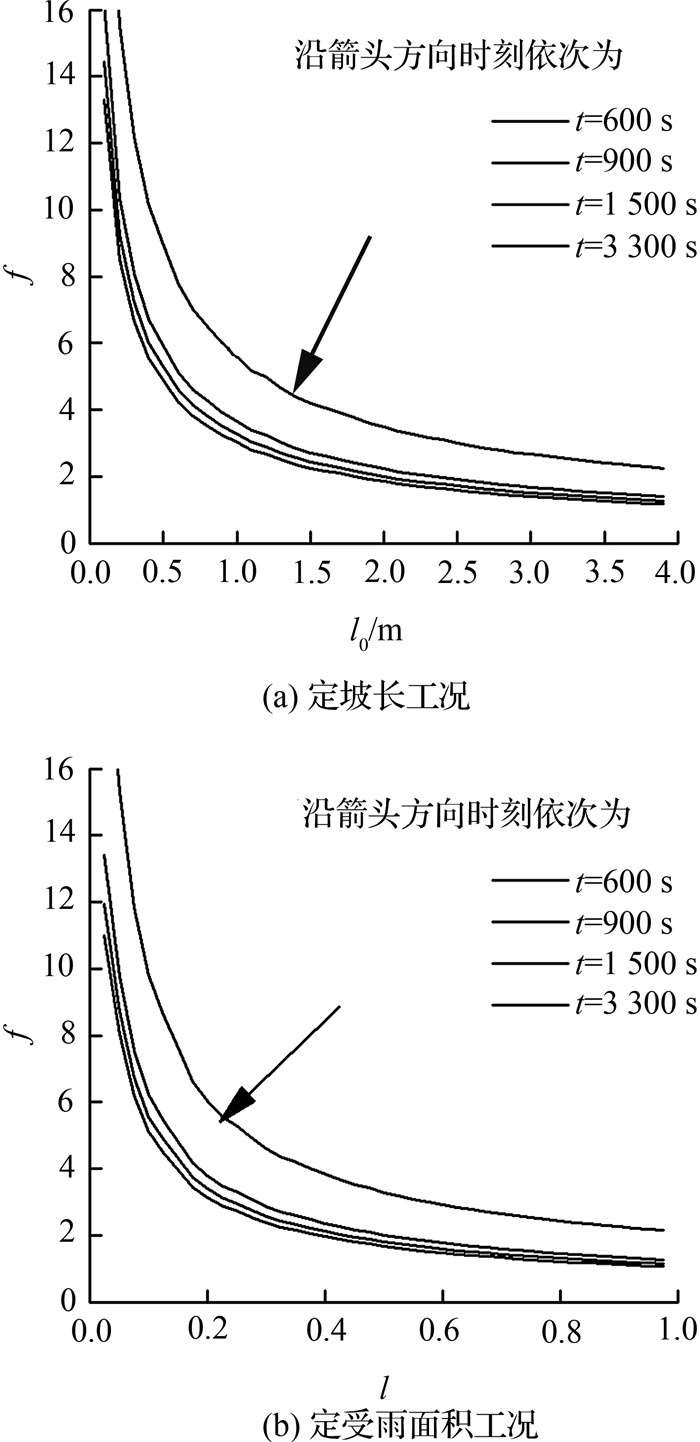
|
图 4 阻力系数时间分布 Fig. 4 Temporal distribution of resistance coefficient |
如图 5所示为坡度为30°,雨强为60 mm/h、t=3 300 s产流稳定时刻,流速(V)、水深(D)和阻力系数的空间布图,由图 5可以看出,在空间上,坡面流阻力系数从上游到下游呈现递减趋势,且递减趋势逐渐减小,当距离坡顶超过1 m之后,阻力系数逐渐趋于平稳.分析原因为,水深沿程变化不大,维持在1.0 ~1.3 mm之间,而流速沿程变化显著,靠近坡顶的位置,流速较低,由于重力加速作用,越向坡脚处,流速越大,导致阻力系数沿程递减.
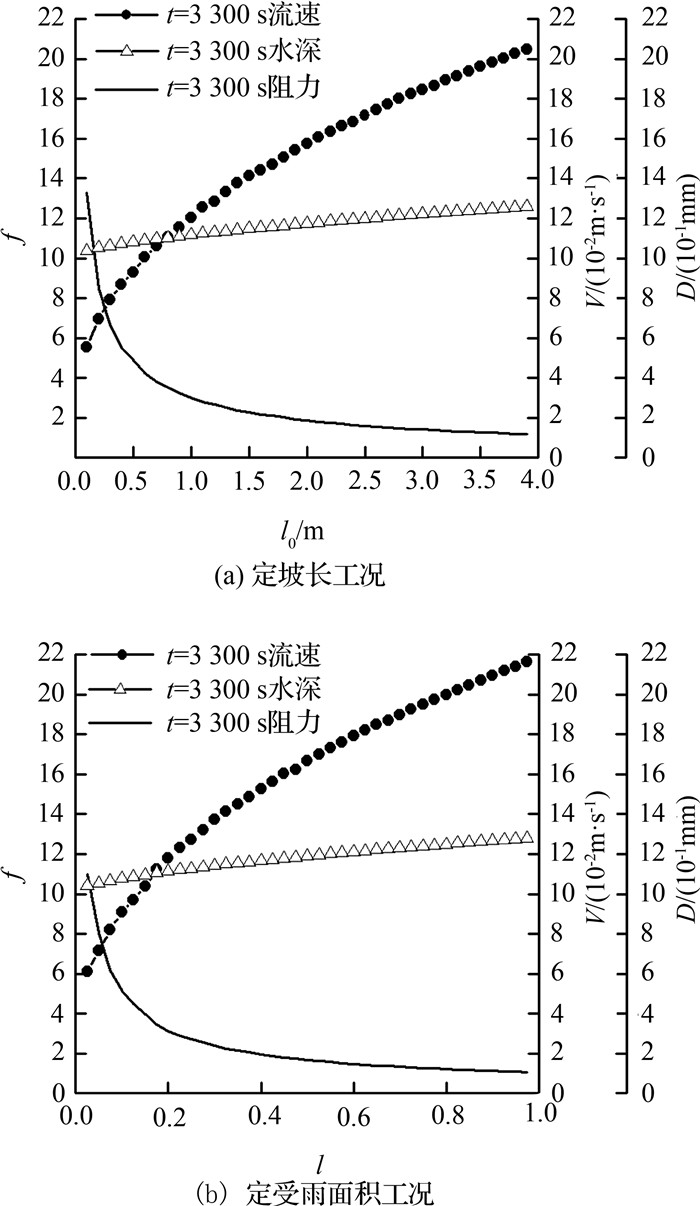
|
图 5 流速、水深、阻力系数空间分布图 Fig. 5 Spatial distribution of velocity, water depth and resistance coefficient |
由2.1节可知,时间上,随着降雨历时的增长,阻力系数递减并趋于稳定;空间上,在距坡顶距离大于1 m之后,坡面流阻力系数趋于平稳.为研究坡度和雨强对阻力系数的影响,便于对比分析,取每种工况的第3 300 s时刻(产流稳定),距离坡顶1 m开外(阻力系数平稳)的坡面的沿程平均阻力系数进行分析研究.
如图 6所示为坡度和雨强对150种工况的坡面平均阻力系数的影响.由图 6可以看出,对于I=30~240 mm/h的任意雨强,在坡度5° ~ 55°范围内,对于定坡长坡面,坡面流阻力系数随着坡度的增加而增加;对于定受雨面积坡面,坡面流阻力系数与坡度的关系跟雨强有一定关系,在I=30 mm/h时,阻力系数随坡度的增加而增加,当I>60 mm/h时,阻力系数随坡度的增加先增加,当坡度到达30°~ 35°左右时,阻力系数随坡度的增加有轻微回落趋势.分析原因为,在缓坡下,坡度对阻力系数起主要影响作用,当坡度超过30°之后,由于在同等雨量的情况下,坡长过大,导致入渗增加,水深减小,且坡度越大,对流速有促进作用,因此,深流比减小,此时,深流比占主导作用,因此在大陡坡下,阻力系数f随坡度略有回落.
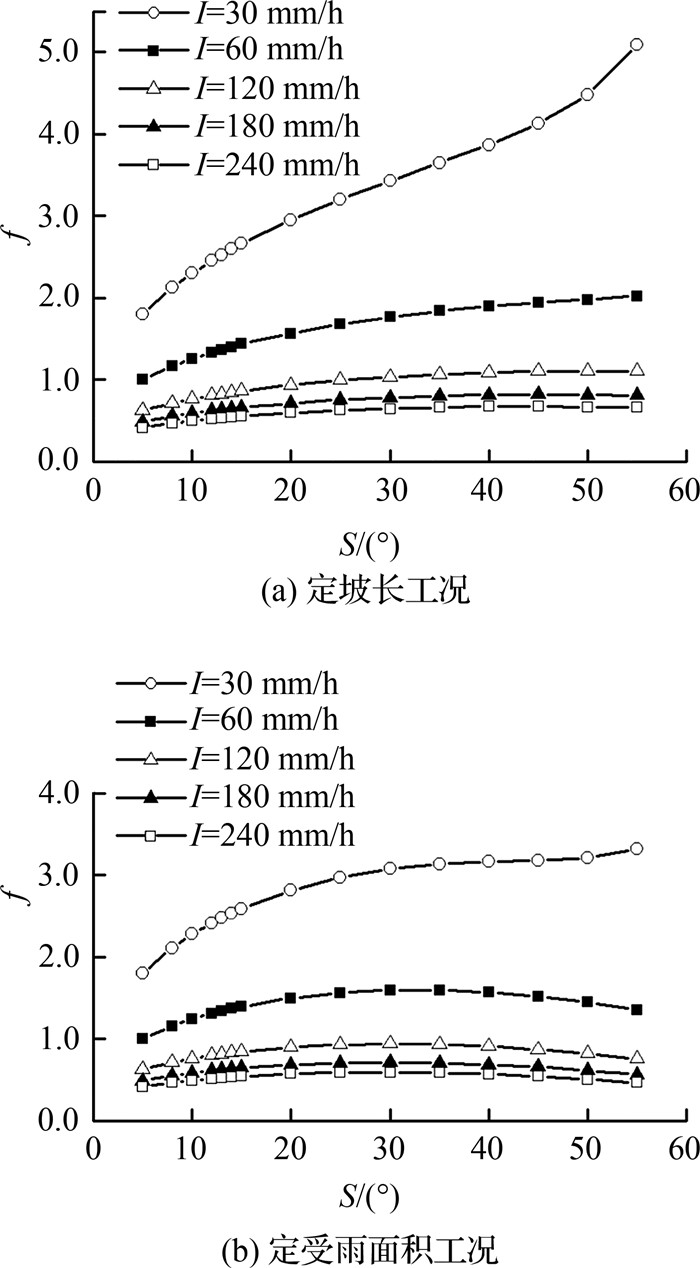
|
图 6 坡度和雨强对坡面平均阻力系数的影响 Fig. 6 Influence of slope and rainfall intensity on resistance coefficient |
如图 6所示,无论对于定坡长(图 6(a))还是定受雨面积(图 6(b))工况,雨强越大,坡面流阻力系数越小,且雨强越大,雨强增量对于阻力系数的影响效果越微弱.这与王瑄[27]通过天然降雨径流小区试验得到的阻力系数则随降雨强度的增大而减小的结论一致.而且,相比于坡度对坡面流阻力系数的影响,从图 6中可以看出雨强(流量)对坡面流阻力系数起主导作用.
图 6中,在中低雨强(30、60 mm/h)下,坡度对阻力系数的影响较为为显著;当雨强较大时(120、180、240 mm/h),坡度对阻力系数的影响较小,说明雨强较大时,雨强为主要影响因子.这与张光辉[12]变坡试验水槽研究的Darcy-Weisbach阻力系数主要受流量控制的结论一致.
如图 7所示为坡度和雨强对黏性底层厚度η的影响.在物理层面分析阻力系数随坡度的增大而增大的原因,由图 7中可以看出,在同一雨强下,随着坡度的增加,坡面黏性底层的平均厚度逐渐减小,变化范围是0.11 ~ 0.37 mm.本试验所采用的黄土,经整平,表面绝对粗糙度大概1 mm左右.因此,本试验坡面流处于紊流粗糙区,且随着坡度增大,粘性底层越薄,产生的附加切应力越大,所以阻力系数越大.
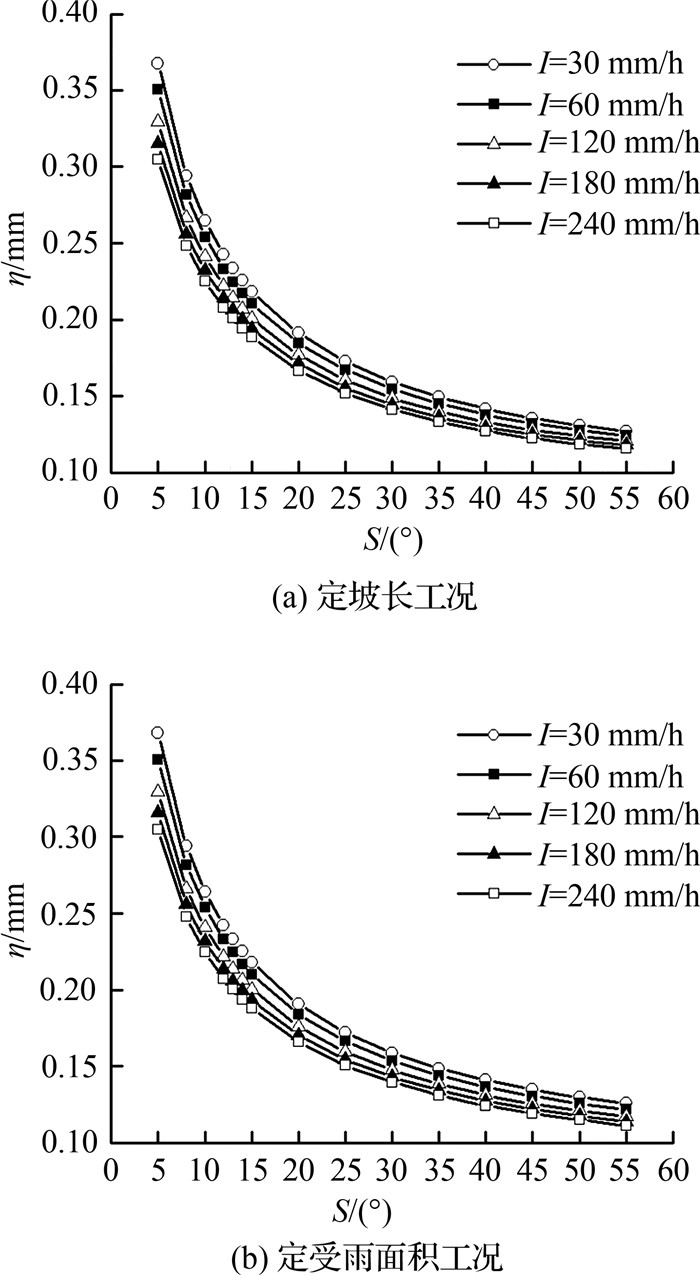
|
图 7 坡度和雨强对黏性底层厚度的影响 Fig. 7 Influence of slope and rainfall intensity on viscous bottom thickness |
对于雨强影响阻力系数的原因,可以从总能量和黏性底层2方面可分析.如图 7所示,在同一坡度下,随着雨强的增大,黏性底层的厚度变小,附加切应力增大,然而,图 6的结果显示,阻力系数却减小了.从能量的角度分析,虽然随着雨强的增加,阻力的绝对数值增大,沿程能量损耗增大,然而,雨强增大意味着坡面流总能量的大幅增加,程能量损耗/总能量反而减小了.而且,也正因为大雨强下,总能量较大,所以坡度对阻力系数的影响不显著.
另外,经统计分析,在同一雨强下,定坡长平均阻力系数比定受雨面积的高30.6% ~ 37.2%,且雨强越大,差距越小.分析其原因,定坡长系列的受雨量小,一定程度上有增大阻力系数的作用;定受雨面积系列的坡长较大,有减小阻力系数的作用.随着雨强的增大,2个系列的阻力系数的差距减小,说明坡长的影响作用减弱.这与赵小娥[28]通过人工降雨试验得到的,随雨强的增大,坡长对流速的影响逐渐减小的结论,有相似之处.
另外,张科利[26]在研究黄土细沟水流阻力特性规律时,发现阻力系数与水流雷诺数(Re),在缓坡条件下表现为负相关,在陡坡条件下则表现为正相关,临界坡度大约在10° ~ 12°之间.为进一步研究临界坡度问题,本试验在10°附近增加了8°、12°、13°、14°这4种工况(如图 6、7加密部分),然而研究并未发现存在临界坡度的现象.本试验中阻力系数与雷诺数的关系,在任何坡度下,均为负相关(如图 8所示,篇幅所限,仅列出一种情况).分析原因,可能为,张科利使用的是黄土的径流冲刷试验,在缓坡下,床面未发生明显侵蚀,地表糙度无显著变化,与本试验的结论相同,阻力系数随着雷诺数的增大而减小;然而,在流量较大坡度较大的情况下,张科利试验床面发生了明显的侵蚀现象,下垫面糙度的变化和切沟形态增大了对水流的阻碍作用,因此在陡坡下,产生了阻力系数随着雷诺数的增加而增大的现象.
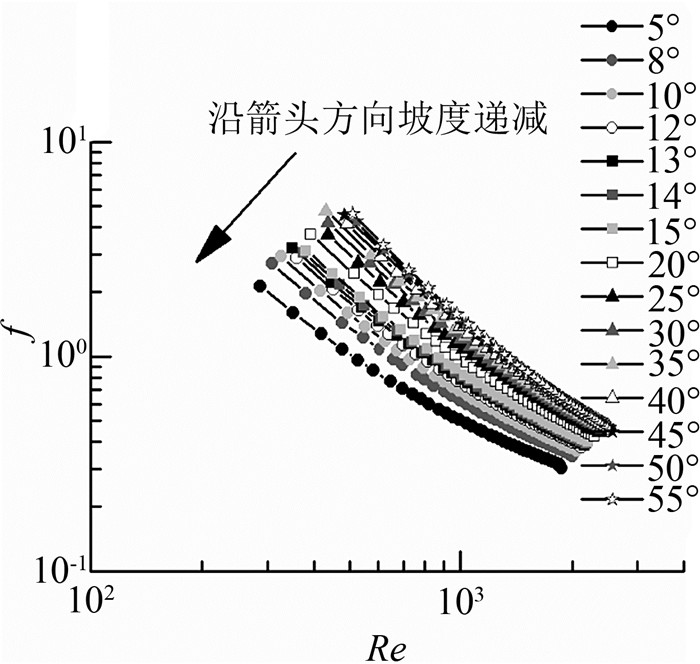
|
图 8 阻力系数与雷诺数的关系(定坡长系列,雨强为60 mm/h) Fig. 8 Relationship between the resistance coefficient and Reynolds number(Constant slope length, i=60mm/h) |
研究重点为产流稳定时刻的坡面流阻力系数,产流开始后,坡面流很快达到产流平稳状态.可以得出,时间对于坡面阻力系数的影响可以忽略.雨强(流量),底坡坡度和坡面质点的空间位置,对于阻力系数均有显著影响.经分析发现,阻力系数与底坡坡度正相关,与雨强和坡面点距离坡顶的距离均存在负相关关系.使用origin多元参数拟合,对5 850组数据进行回归分析得:
| $ f = 39.274{\rm{ }}{S^{0.409I-0.955l-0.651}}. $ | (3) |
相比于前人建立的阻力系数与流量、雷诺数、弗劳德数、坡度等参数的阻力系数公式[12, 15, 29-30],公式(3)中的底坡坡度、雨强、空间距离这3个自变量,更加直观,也更易测量.而且,将坡面点距坡顶的距离这一要素引入阻力系数公式,实现了对坡面流阻力系数的的空间分布式研究.
2.4 讨论本试验的设计初衷在于研究坡面流阻力系数分布规律,重点探讨雨强、坡度等因素对于坡面流阻力系数的影响.设计了定坡长和定受雨面积2套方案.这对雨强和坡度对阻力系数影响的定性分析略有干扰,然而对于阻力系数公式拟合的定量分析并无影响.
关于物理模型试验中的实测流速,由于染色剂示踪法测量的是表面流速,需要乘以流速系数α,得到测深平均流速.多数研究经常根据流态选取流速系数[11],例如层流α=0.67[31],过渡流α=0.7[32],紊流α=0.8[2],或者直接指定流速系数0.75[30].目前,也有更多针对坡面流的流速系数的研究问世[33-34],然而考虑到坡面薄层水流的复杂性及试验条件的显著差异,本试验并未直接采用上述流速系数.由于在本试验的人工降雨物理模型试验过程中,观察到雨滴的溅击有减缓染色剂流动速度的效果,张宽地[13]、田凯[35]等也指出雨滴溅击有减缓流速的作用,因此,本试验流速系数取值为α=1.
本研究的不足之处为:
1) 由于土槽中布设的是4 m×1 m×0.3 m的黄土,在人工模拟降雨土槽试验过程中,会产生泥沙,床面有轻微侵蚀,但未产生明显细沟,因此床面的微小变形可以忽略.但含沙量会对水流阻力系数有一定的影响[36, 37],未考虑含沙量的影响是本研的不足之处.含沙量对阻力系数的影响有待继续深入研究.
2) 仅研究了单一土壤类型、单一糙度的裸坡.研究结果也只适用于以颗粒阻力为主的裸坡.对于复杂下垫面条件及有植被覆盖的坡面有待深入研究.
3) 本文研究的是小尺度理想平整坡面,且在人工降雨物理模型试验中未产生冲沟.然而,在自然界中的大尺度坡面上,容易产生冲沟,且冲沟对于坡面流特性具有重要影响.关于冲沟对坡面流阻力特性的影响有待进一步研究.
最后,本试验中使用的流速测量技术仍然是传统的染色剂(KMnO4)示踪法.然而,此种测量方法测得的是表面流速,需要进行二次修正.而且在降雨条件下,又会受到雨滴打击的影响,流速修正系数的取值难以确保妥当.由于坡面流水深极浅,其水深和流速的测量是一大难题.不能精确的测量流速、水深等数据,是制约坡面流水力学特性研究的重要因素.因此,针对这方面的不足,今后的研究中,应加强对试验设备和测量技术方面的研发投入.另外,不同学者采用的试验设备、试验条件、测量方法的不同,所得到的结果也不尽相同.针对这个问题,应逐渐规范试验设备和测量技术的使用标准,以便提高不同研究者的工作成果的可比性,有利于试验数据的积累和坡面流理论研究的进展.
3 结论本文采用18场人工降雨物理模型试验数据对基于物理概念的水文响应数值模型进行了率定验证,然后使用数值模型虚拟150种工况,在坡度5° ~ 55°,雨强30 ~ 240 mm/h范围内,研究了坡面流阻力系数的时空分布规律,定量分析了坡度、雨强对于坡面流阻力系数的影响,最后通过对数值模型试验数据的回归分析得出了反映雨强、坡度和坡面点距坡顶距离的坡面流阻力系数公式.主要结论如下:
(1) 在时间上,坡面阻力系数随着时间的增加呈减小趋势,自产流开始后,很快趋于平稳;在空间上,向下游出口处,阻力系数沿程递减.
(2) 在雨强一定的前提下,对于定坡长系列工况,阻力系数随坡度的增加而平缓增长,其本质原因为粘性底层厚度越薄,附加切应力越大;对于定受雨面积系列工况,阻力系数随坡度的增加现增加后减小,临界坡度在30°~ 35°左右.
(3) 在坡度一定的前提下,雨强越大,阻力系数越小,且雨强越大,雨强增量对阻力系数的影响程度越小.
(4) 经多元参数回归分析得出了考虑空间位置的分布式坡面流阻力系数公式.
| [1] |
陈国祥, 姚文艺. 坡面流水力学[J]. 河海科技进展, 1992, 12(2): 7-13. CHEN Guo-xiang, YAO Wen-yi. Slope flow hydraulics[J]. Advances in Science and Technology of Hohai University, 1992, 12(2): 7-13. |
| [2] |
EMMETT W W. The hydraulics of overland flow on hillslopes[M]. [S. l]: US Government Printing Office, 1970.
|
| [3] |
SAVAT J. The hydraulics of sheet flow on a smooth surface and the effect of simulated rainfall[J]. Earth surface processes, 1977, 2(2/3): 125-140. |
| [4] |
翟艳宾. 缓坡面薄层水流水动力学特性的试验研究[D]. 杨凌: 西北农林科技大学, 2013. ZHAI Yan-bin. Study on hydrodynamic characteristics of sheet flow on lower slope surface[Master's degree thesis] [D]. Yangling: Northwest A & F University, 2013. http://cdmd.cnki.com.cn/article/cdmd-10712-1013347734.htm |
| [5] |
刘元臣, 张升堂, 张景洲, 等. 坡变化对坡面流水动力学特性影响研究[J]. 人民长江, 2016, 47(16): 99. LIU Yuan-hen, ZHANG Sheng-ang, ZHANG Jing-zhou, et al. Study on slope influence on overland flow dynamic characteristics[J]. Yangtze River, 2016, 47(16): 99. |
| [6] |
王俊杰, 张宽地, 龚家国, 等. 降雨和坡度对坡面水流阻力规律影响研究[J]. 灌溉排水学报, 2016, 35(5): 43-49. WANG Jun-jie, ZHANG Kuan-di, GONG Jia-guo, et al. Influence of rainfall and slope on the overlan flow resistance[J]. Journal of Irrigation and Drainage, 2016, 35(5): 43-49. |
| [7] |
陈国祥, 姚文艺. 降雨对浅层水流阻力的影响[J]. 水科学进展, 1996, 7(1): 42-46. CHEN Guo-xiang, YAO Wen-yi. The influence of rainfall on the resistance of shallow water flow[J]. Advances in Water Science, 1996, 7(1): 42-46. |
| [8] |
梅欣佩. 降雨条件下坡面薄层水流水动力学特性试验研究[D]. 西安: 西安理工大学, 2004. MEI Xin-pei. Experimental study on hydrodynamic characteristics of sheet flow on slop under rain[D]. Xian: Xi'an University of Technology, 2004 http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D012795 |
| [9] |
潘成忠, 上官周平. 降雨和坡度对坡面流水动力学参数的影响[J]. 应用基础与工程科学学报, 2009, 17(6): 843-851. PAN Cheng-zhong, SHANGGUAN Zhouping. The influence of rainfall and slope on overland flow hydrodynamic parameters[J]. Journal of Basic Science and Engineering, 2009, 17(6): 843-851. |
| [10] |
张小娜, 冯杰, 张超, 等. 不同雨强下土壤大孔隙对坡面流水动力学参数的影响[J]. 河海大学学报:自然科学版, 2012, 40(3): 264-269. ZHANG Xiaona, FENG Jie, ZHANG Chao, et al. Influence of soil macropore on hydrodynamic parameters of overland flow with different rainfall intensities[J]. Journal of Hohai University:Natural Sciences, 2012, 40(3): 264-269. |
| [11] |
PAN C, MA L, WAINWRIGHT J, et al. Overland flow resistances on varying slope gradients and partitioning on grassed slopes under simulated rainfall l[J]. Water Resources Research, 2016, 52(4): 2490-2512. DOI:10.1002/2015WR018035 |
| [12] |
张光辉. 坡面薄层流水动力学特性的试验研究[J]. 水科学进展, 2002, 13(2): 159-165. ZHANG Guang-hui. Experimental study on sheet flow hydrodynamic properties[J]. Advances In Water Science, 2002, 13(2): 159-165. |
| [13] |
张宽地, 王光谦, 吕宏兴, 等. 模拟降雨条件下坡面流水动力学特性研究[J]. 水科学进展, 2012, 23(2): 229-235. ZHANG Kuan-di, WANG Guang-qian, LV Hong-xing, et al. Overland flow hydrodynamic characteristics study under simulated rainfall[J]. Advances in Water Science, 2012, 23(2): 229-235. |
| [14] |
敬向锋, 吕宏兴, 张宽地, 等. 不同糙率坡面水力学特征的试验研究[J]. 水土保持通報, 2007, 27(2): 33-38. JING Xiang-feng, LV Hong-xing, ZHANG Kuan-di, et al. Experimental study of overland flow hydromechanics under different degrees of roughness[J]. Bulletin of Soil and Water Conservation, 2007, 27(2): 33-38. |
| [15] |
施明新, 李陶陶, 吴秉, 等. 地表粗糙度对坡面流水动力学参数的影响[J]. 泥沙研究, 2015(4): 59-65. SHI Xin-ming, LI Tao-tao, WU Bing, et al. , Influence of surface roughness on over land flow hydrodynamic parameters[J]. Journal of Sediment Research, 2015(4): 59-65. |
| [16] |
马玉莹, 雷廷武, 庄晓晖. 测量土壤颗粒密度的体积置换法[J]. 农业工程学报, 2014, 30(15): 130-139. MA Yu-ying, LEI Ting-wu, ZHUANG Xiao-hui. Volume replacement methods for measuring soil particle density[J]. Transactions of the Chinese Society of Agricultural Engineering:Transactions of the CSAE, 2014, 30(15): 130-139. DOI:10.3969/j.issn.1002-6819.2014.15.018 |
| [17] |
VANDERKWAAK J E. Numerical simulation of flow and chemical transport in integrated surface-subsurface hydrologic systems[J]. National Library of Canada Bibliothèque nationale du Canada, 1999. |
| [18] |
LOAGUE K, HEPPNER C S, ABRAMS R H, et al. Further testing of the Integrated Hydrology Model (InHM):Event-based simulations for a small rangeland catchment located near Chickasha, Oklahoma[J]. Hydrological Processes, 2005, 19(7): 1373-1398. DOI:10.1002/(ISSN)1099-1085 |
| [19] |
HEPPNER C S, RAN Q, VANDERKWAAK J E, et al. Adding sediment transport to the integrated hydrology model (InHM):Development and testing[J]. Advances in Water Resources, 2006, 29(6): 930-943. DOI:10.1016/j.advwatres.2005.08.003 |
| [20] |
RAN Q. Regional scale landscape evolution: Physics-based simulation of hydrologically-driven surface erosion[D]. Palo Alto: Stanford University, 2006.
|
| [21] |
冉启华, 史致男, 许月萍. 降雨移动方向对坡面侵蚀泥沙浓度的影响[J]. 浙江大学学报:工学版, 2013, 5: 011. RAN Qi-hua, SHI Zhi-nan, XU Yue-ping. Impacts of moving rainfall on sediment concentration of soil erosion[J]. Journal of Zhejiang University:Engineering Science, 2013, 5: 011. |
| [22] |
冉启华, 富强, 苏丹阳, 等. 降雨移动方向对坡面径流的影响机理[J]. 浙江大学学报:工学版, 2009, 43(10): 1915-1922. RAN Qi-hua, FU Qiang, SU Dan-yang, et al. Impact of rainfall-movement direction on hillslope runoff generation[J]. Journal of Zhejiang University:Engineering Science, 2009, 43(10): 1915-1922. |
| [23] |
冉启华, 钱群, 许月萍. 降雨因素对土壤表面结皮发育的影响[J]. 清华大学学报:自然科学版, 2011, 51(6): 770-776. RAN Qi-hua, QIAN Qun, XU Yue-ping. Impact of rainfll factors on soil-surface seal formation[J]. Journal of Tsinghua University:Science and Technology, 2011, 51(6): 770-776. |
| [24] |
冉启华, 梁宁, 钱群, 等. 移动降雨时空分布对坡面产流的影响[J]. 清华大学学报:自然科学版, 2013(5): 636-641. RAN Qi-hua, LIANG Ning, QIAN Qun, et al. investigation of hillslope runoff due to moving storms in flume-scale experiments[J]. Journal of Tsinghua UniversityScience and Technology), 2013(5): 636-641. |
| [25] |
ENGMAN E T. Roughtness coefficience for routing surface runoff[J]. Journal of Irrigation and Drainage Engineering, 1986, 112(1): 39-53. DOI:10.1061/(ASCE)0733-9437(1986)112:1(39) |
| [26] |
张科利. 黄土坡面细沟侵蚀中的水流阻力规律研究[J]. 人民黄河, 1998, 20(8): 13-15. ZHANG Ke-li. Study on water flow resistance law of rill erosion on loess slope[J]. Yellow River, 1998, 20(8): 13-15. |
| [27] |
王瑄, 雷洋. 天然降雨条件下坡面侵蚀动力学特性研究[J]. 沈阳农业大学学报, 2010, 41(5): 598-601. WANG Xuan, LEI Yang. Study ondynamic characteristics of slope erosion under natural rainfall conditions[J]. Journal of Shenyang Agricultural University, 2010, 41(5): 598-601. |
| [28] |
赵小娥, 魏琳, 曹叔尤, 等. 强降雨条件下坡面流的水动力学特性研究[J]. 水土保持学报, 2009(6): 45-47. ZHAO Xiao-e, WEI Lin, CAO Shu-you, et al. Study oncharacteristics of overland flow with higher rain intensity[J]. Journal of Soil and Water Conservation, 2009(6): 45-47. |
| [29] |
曹颖, 张光辉, 唐科明, 等. 地表模拟覆盖率对坡面流阻力的影响[J]. 水土保持学报, 2010(4): 86-89. CAO Ying, ZHANG Guang-hui, TANG Ke-ming, et al. Impact of simulated surface cover on resistance coefficient of overland flow[J]. Journal of Soil and Water Conservation, 2010(4): 86-89. |
| [30] |
王龙生, 蔡强国, 蔡崇法, 等. 黄土坡面细沟与细沟间水流水动力学特性研究[J]. 泥沙研究, 2013(6): 45-52. WANG Long-sheng, CAI Qiang-guo, CAI Chong-fa, et al. Hydrodynamic characteristics of rill and between-rill on loess slope[J]. Journal of Sediment Research, 2013(6): 45-52. |
| [31] |
HORTON R E, LEACH H R, VAN VLIET R. Laminar sheet-flow[J]. Eos, Transactions American Geophysical Union, 1934, 15(2): 393-404. DOI:10.1029/TR015i002p00393 |
| [32] |
LUK S H, MERZ W. Use of the salt tracing technique to determine the velocity of overland flow[J]. Soil technology, 1992, 5(4): 289-301. |
| [33] |
LI G, ABRAHAMS A D, ATKINSON J F. Correction factors in the determination of mean velocity of overland flow[J]. Earth surface Processes and landforms, 1996, 21(6): 509-515. DOI:10.1002/(ISSN)1096-9837 |
| [34] |
ZHANG G, LUO R, CAO Y, Et al. Correction factor to dye-measured flow velocity under varying water and sediment discharges[J]. Journal of Hydrology, 2010, 389(1): 205-213. |
| [35] |
田凯, 李小青, 鲁帆, 等. 坡面流侵蚀水动力学特性研究综述[J]. 中国水土保持, 2010, 2010(4): 4. TIAN Kai, LI Xiao-qing, LU Fan, et al. Review of hydrodynamic characteristics of erosion on slope[J]. Soil and Water Conservation in China, 2010, 2010(4): 44-47. |
| [36] |
赵春红, 高建恩, 王飞, 等. 含沙量对坡面流水动力学特性的影响研究[J]. 农业机械学报, 2013(09): 79-85. ZHAO Chun-hong, GAO Jian-en, WANG Fei, et al. Effects of sediment load on hydrodynamic characteristics of overland flow[J]. Transactions of the Chinese Society for Agricultural Machinery, 2013(9): 79-85. DOI:10.6041/j.issn.1000-1298.2013.09.015 |
| [37] |
ABRAHAMS A D, LI G. Effect ofsaltating sediment on flow resistance and bed roughness in overland flow[J]. Earth Surface Processes and Landforms, 1998, 23(10): 953-960. DOI:10.1002/(ISSN)1096-9837 |



