索穹顶是美国工程师Geiger^[1]提出的一种高效的大跨度空间结构形式，已应用于众多的大型体育场馆等标志性建筑中^[2-4].索穹顶的结构构成机理与常规结构存在较大区别，需要依靠初始预张力来维持形态的稳定性并提供结构刚度^[5]，因此索穹顶的结构分析设计理论在近些年来成为研究热点.应该注意到，服役时间最长的索穹顶结构已经超过30年，但有关如何进行此类既有结构性能监测和评价的研究报道还非常少.作为结构检测的一种重要方法，动力测试^[6]在结构健康监测中非常受欢迎.但索穹顶的模态频率非常密集，使得常规方法的模态识别误差较大，从而不能有效地完成刚度重构、模型修正等后续工作.

传统的模态识别方法一般分为频域法和时域法^[7].当利用环境激励时，由于通常引入近似白噪声的假定，这2类方法都只需要利用响应信号便可进行模态识别.环境激励只能被动接受，不能通过对激励的主动优化来控制参振模态，因此模态识别的精度不能保证.当采用人工激励时，频域法需要同时测量激励信号和响应信号，而时域法一般只需要测量后者.通过优化人工激励来激发结构的待识别模态，可以改善密集模态的识别精度^[8-9].当前研究一般针对激振器和冲击锤等激励装置对人工激励进行优化，而对阶跃激励优化研究较少.应该看到，阶跃激励可通过在结构上吊挂荷载，然后同时瞬间卸载使结构产生自由振动，并可对结构输入较大的能量，工程上非常适用于大跨度结构的模态测试^[7]，但需要配合时域法进行模态识别.

本文针对索穹顶密集模态识别问题，提出一种基于优化阶跃激励与模态识别时域法相配合的模态测试方法.首先介绍了稀疏时域法(sparse time domain method, STD)^[10]的基本原理，分析了密集模态识别精度低的原因.其次，推导了自由振动响应的模态贡献指标，给出了激发待识别模态的目标模式向量，并采用遗传算法来实现阶跃激励的优化.最后，对所提方法进行算例分析.

1 STD法及误差灵敏度分析 1.1 STD法基本原理

采用时域法中经典的STD法配合阶跃激励优化进行索穹顶的模态识别.1987年，在Ibrahim时域法(ibrahim time domain, ITD)^[11]的基础上提出了STD法.它是一种利用结构自由振动响应的位移、速度或加速度时域信号进行模态识别的方法.基于黏性阻尼线性多自由度系统的自由振动响应在理论上可以表示为各阶模态组合，STD法根据同时测得的自由衰减响应信号(位移、速度或加速度)，构造不同延时的采样数据矩阵和Hessenberg矩阵，建立特征方程，求解特征对后再估算各阶模态参数.相比ITD法，STD法具有更高的计算效率和识别精度.

基于复模态理论的结构自由振动位移响应为

$ \mathit{\boldsymbol{u}} = \sum\limits_{j = 1}^{2n} {\left( {{\mathit{\boldsymbol{\psi }}_j}\exp \left( {{\lambda _j}t} \right)} \right)} . $

(1)

式中：ψ_j为第j阶复振型，ψ_n+j= ψ_j^*, (j=1, 2, …, n)；λ_j为复特征值，λ_n+j=λ_j^*, (j=1, 2, …, n)；上标*表示复共轭；n为识别模态数；t为时间.

假设采样间隔为Δt，取采样点数、测点数(含虚拟测点)均为m，且令m=2n，将m个测点数据代入式(1)，得到

$ \mathit{\boldsymbol{U}} = \mathit{\boldsymbol{\psi }} \times \mathit{\boldsymbol{E}}. $

(2)

其中

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{U}} = \left[ {\begin{array}{*{20}{c}} {{u_{11}}}&{{u_{12}}}& \cdots &{{u_{1m}}}\\ {{u_{21}}}&{{u_{22}}}& \cdots &{{u_{2m}}}\\ \vdots&\vdots &{}& \vdots \\ {{u_{m1}}}&{{u_{m2}}}& \cdots &{{u_{mm}}} \end{array}} \right],}\\ {\mathit{\boldsymbol{\psi }} = \left[ {\begin{array}{*{20}{c}} {{\psi _{11}}}&{{\psi _{12}}}& \cdots &{{\psi _{1m}}}\\ {{\psi _{21}}}&{{\psi _{22}}}& \cdots &{{\psi _{2m}}}\\ \vdots&\vdots &{}& \vdots \\ {{\psi _{m1}}}&{{\psi _{m2}}}& \cdots &{{\psi _{mm}}} \end{array}} \right],}\\ {\mathit{\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}} {\exp \left( {{\lambda _1}{t_1}} \right)}&{\exp \left( {{\lambda _1}{t_2}} \right)}& \cdots &{\exp \left( {{\lambda _1}{t_m}} \right)}\\ {\exp \left( {{\lambda _2}{t_1}} \right)}&{\exp \left( {{\lambda _2}{t_2}} \right)}& \cdots &{\exp \left( {{\lambda _2}{t_m}} \right)}\\ \vdots&\vdots &{}& \vdots \\ {\exp \left( {{\lambda _m}{t_1}} \right)}&{\exp \left( {{\lambda _m}{t_2}} \right)}& \cdots &{\exp \left( {{\lambda _m}{t_m}} \right)} \end{array}} \right].} \end{array} $

(3)

式中：u_ij为第i个测点在采样点时间t_j上的位移；ψ_ij为第j个复振型在第i个测点的分量；t_j=(j-1)Δt.将U中的采样点数据均延时Δt，得到新的方程为

$ \mathit{\boldsymbol{\tilde U}} = \mathit{\boldsymbol{\tilde \psi }} \times \mathit{\boldsymbol{E}} = \mathit{\boldsymbol{\psi }} \times \mathit{\boldsymbol{\chi }} \times \mathit{\boldsymbol{E}}. $

(4)

式中：$ \mathit{\boldsymbol{\chi }} = {\rm{diag}}(\exp ({\lambda _1}\Delta t), \exp ({\lambda _2}\Delta t), \exp ({\lambda _3}\Delta t), \cdots, \exp ({\lambda _m}\Delta t)) $.在式(2)、(4)左右两侧分别右乘E^-1，整理后得到

$ \mathit{\boldsymbol{\tilde U}}{\mathit{\boldsymbol{E}}^{ - 1}} = \mathit{\boldsymbol{\tilde U}} \times {\mathit{\boldsymbol{E}}^{ - 1}} \times \mathit{\boldsymbol{\chi }}. $

(5)

采样数据矩阵U和延时采样数据矩阵$ \mathit{\boldsymbol{\tilde U}} $之间存在线性关系.

$ \mathit{\boldsymbol{\tilde U}} = \mathit{\boldsymbol{UB}}. $

(6)

式中：B是仅含有1列未知元素的Hessenberg矩阵，如下式所示：

$ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} 0&0&0& \cdots &0&{{b_1}}\\ 1&0&0& \cdots &0&{{b_2}}\\ 0&1&0& \cdots &0&{{b_3}}\\ \vdots&\vdots&\vdots &{}& \vdots&\vdots \\ 0&0&0& \cdots &1&{{b_m}} \end{array}} \right]. $

(7)

式中：b_i为B中最后一列第i个元素.结合式(6)和(7)，可知

$ {{\mathit{\boldsymbol{\tilde U}}}_m} = \mathit{\boldsymbol{Ub}}. $

(8)

式中：$ {\mathit{\boldsymbol{\tilde U}}_m}$和b分别为$ \mathit{\boldsymbol{\tilde U}} $和B的第m列.根据实测的$ {\mathit{\boldsymbol{\tilde U}}_m} $和$\mathit{\boldsymbol{\tilde U}} $, 由式(8)可按下式求解b的最小二乘解：

$ \mathit{\boldsymbol{b}} = {\left( {{\mathit{\boldsymbol{U}}^{\rm{T}}}\mathit{\boldsymbol{U}}} \right)^{ - 1}}{\mathit{\boldsymbol{U}}^{\rm{T}}}{{\mathit{\boldsymbol{\tilde U}}}_m}. $

(9)

于是将式(6)代入式(5)中，经整理得到

$ \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{E}}^{ - 1}} = {\mathit{\boldsymbol{E}}^{ - 1}} \times \mathit{\boldsymbol{\chi }}. $

(10)

上式是一个标准的特征方程.由矩阵B的特征值χ_j=exp (λ_jΔt)可以求得复特征值的实部和虚部分别为

$ {\sigma _j} = - \frac{1}{{2\Delta t}}\ln {\left( {{\mathop{\rm Re}\nolimits} \left( {{\chi _j}} \right)} \right)^2} + {\left( {{\mathop{\rm Im}\nolimits} \left( {{\chi _j}} \right)} \right)^2}, $

(11)

$ \begin{array}{*{20}{c}} {{\omega _{{\rm{d}}j}} = \frac{1}{{\Delta t}}\left( {\arctan \frac{{{\mathop{\rm Im}\nolimits} \left( {{\chi _j}} \right)}}{{{\mathop{\rm Re}\nolimits} \left( {{\chi _j}} \right)}} + b{\rm{ \mathsf{ π} }}} \right),}\\ {b = 0,1,2, \cdots .} \end{array} $

(12)

进而得到复模态j的无阻尼圆频率和阻尼比分别为

$ {\omega _j} = \sqrt {\omega _{dj}^2 + \sigma _j^2} ,{\zeta _j} = \frac{{{\sigma _j}}}{{{\omega _j}}}. $

(13)

将式(10)求得的特征向量(E^-1)_j左乘式(2)两边，得到ψ_j.假设实际测点数为q，则取ψ_j中前q个实际测点对应的元素即组成模态j的识别振型.当采用速度或加速度响应信号时，式(2)~(13)给出的模态识别过程同样适用.研究表明，当所识别的结构具有比例阻尼时，所识别出的复振型虚部即为结构的实振型^[12].此外，需要引入模态置信准则来剔除虚假模态^[7].

1.2 噪声灵敏度分析

假设由于响应时程的噪声引起特征矩阵误差为ΔB.根据文献[13]给出的特征值与特征向量同刚度变化与质量变化之间的一阶灵敏度关系，将特征矩阵B代替文献[13]中的刚度矩阵，得到仅由ΔB引起的特征值χ_j和特征向量(E^-1)_j的误差分别为

$ {{\rm{ \mathsf{ χ} }}_j} = \left( {\mathit{\boldsymbol{E}} - 1} \right)_j^{\rm{T}}\Delta \mathit{\boldsymbol{B}}{\left( {{\mathit{\boldsymbol{E}}^{ - 1}}} \right)_j}, $

(14)

$ \Delta {\left( {{\mathit{\boldsymbol{E}}^{ - 1}}} \right)_j} = \sum\limits_{s = 1}^m {{C_{js}}{{\left( {{\mathit{\boldsymbol{E}}^{ - 1}}} \right)}_j}} . $

(15)

式中：

$ {C_{js}} = \left\{ \begin{array}{l} 0,\;\;\;\;\;j = s;\\ \frac{{\left( {{\mathit{\boldsymbol{E}}^{ - 1}}} \right)_s^{\rm{T}}\Delta \mathit{\boldsymbol{B}}{{\left( {{\mathit{\boldsymbol{E}}^{ - 1}}} \right)}_j}}}{{{{\rm{ { χ} }}_j} - {{\rm{ { χ} }}_s}}},\;\;\;j \ne s. \end{array} \right. $

(16)

由式(14)、(15)可知，当χ_j与χ_s很接近时(即模态j和s的频率很接近)，组合系数C_js的分母非常小，因此特征向量(E^-1)_j对误差ΔB非常敏感.相对而言，特征值χ_j对ΔB的敏感性较低.反映到所识别的模态参数上，模态频率对噪声相对不敏感，而密集模态振型对噪声非常敏感.这是采用STD法进行模态识别时密集模态振型识别精度低的根本原因.其他时域方法用于密集模态识别时对噪声的敏感性与此类似.

2 自由振动响应的模态贡献

索穹顶的动力模态方程为

$ \left( {{\mathit{\boldsymbol{K}}_{\rm{T}}} - {\eta _j}\mathit{\boldsymbol{\bar M}}} \right){\mathit{\boldsymbol{\theta }}_j} = {\bf{0}}. $

(17)

式中：K_T为索穹顶的切线刚度矩阵^[5]；M为一致质量矩阵；η_j、θ_j分别为模态j的特征值和对质量矩阵归一化的振型向量.

在荷载p作用下，索穹顶结构的静力平衡方程为

$ {\mathit{\boldsymbol{K}}_{\rm{T}}}{\mathit{\boldsymbol{u}}_0} = \mathit{\boldsymbol{p}}. $

(18)

式中：u₀为静力位移.由于振型θ_r (r=1, …, n)构成自由度空间的基，总是存在$ {\mathit{\boldsymbol{u}}_0} = \sum\limits_{r = 1}^n {{\alpha _r}{\mathit{\boldsymbol{\theta }}_r}} $，其中α_r表示振型θ_r的组合系数，或称广义静力位移.将其代入式(18)，并在方程左右两边左乘θ_j^T，有

$ \mathit{\boldsymbol{\theta }}_j^{\rm{T}}{\mathit{\boldsymbol{K}}_{\rm{T}}}\left( {\sum\limits_{r = 1}^n {{\alpha _r}{\mathit{\boldsymbol{\theta }}_r}} } \right) = \mathit{\boldsymbol{\theta }}_j^{\rm{T}}\mathit{\boldsymbol{p}}. $

(19)

考虑式(17)，并利用θ_j (j=1, …, n)的正交性及其对质量矩阵的归一化，可知广义静力位移为

$ {\alpha _j} = \frac{{\mathit{\boldsymbol{\theta }}_j^{\rm{T}}\mathit{\boldsymbol{p}}}}{{{\eta _j}}}. $

(20)

假设荷载p作用在结构上，待静力位移u₀稳定后突然卸载，则结构发生在u₀扰动后的自由振动，其位移响应为^[7]

$ \mathit{\boldsymbol{u}} = \sum\limits_{j = 1}^n {{\mathit{\boldsymbol{\theta }}_j}{\alpha _j}\exp \left( { - {\zeta _j}{\omega _j}t} \right)\cos \left( {{\omega _{{\rm{d}}j}}t + {\varphi _j}} \right)} . $

(21)

式中：$ {\omega _{{\rm{d}}j}} = {\omega _j}\sqrt {1-\zeta _j^2} $为模态j的阻尼固有圆频率；φ_j为模态j的相位.

将式(21)对时间t求导可以求出速度与加速度自由振动响应的表达式.不难发现，无论是位移、速度还是加速度自由振动响应，模态j对自由振动的贡献都可以用| α_j |的大小来衡量.| α_j |大的模态能量特征明显，容易识别；反之，| α_j|小的模态容易被噪声湮没.前面已说明，密集模态的频率识别较准确，但振型识别效果较差.为了能更好地识别密集模态振型，应当增强待识别模态对结构振动的贡献(即激发待识别模态)，并抑制其邻近模态参与振动.这样密集模态识别问题就转化成为孤立模态识别问题，从而提高模态识别精度.可以通过激励优化来调节各参振模态对结构振动的贡献.

3 阶跃激励优化

本文采用突然卸载的方式对结构施加阶跃激励.考虑在索穹顶的若干节点施加荷载，使结构产生静力位移并稳定后，再突然卸载，结构将发生具有初始位移扰动的自由振动.不同的荷载分布(作用点数量、位置和大小)会使结构产生不同的初始位移，造成各阶模态对结构振动的贡献也不同.

参照式(21)，仅考虑前后各两阶相邻模态对模态j的影响，可定义相对广义静力位移向量(或称模式向量)为

$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\varphi }}_j} = \left\{ {\left| {{\alpha _{j - 2}}/{\alpha _j}} \right|,\left| {{\alpha _{j - 1}}/{\alpha _j}} \right|,1,} \right.}\\ {{{\left. {\left| {{\alpha _{j + 1}}/{\alpha _j}} \right|,\left| {{\alpha _{j + 2}}/{\alpha _j}} \right|} \right\}}^{\rm{T}}}.} \end{array} $

(22)

记$ {\mathit{\boldsymbol{\tilde \varphi }}_j} = {\left\{ {0, 0, 1, 0, 0} \right\}^{\rm{T}}} $，称为模态j的目标模式向量.显然，当$ {\mathit{\boldsymbol{\varphi }}_j} = {\mathit{\boldsymbol{\tilde \varphi }}_j} $时，模态j被完全激发而邻近模态则被完全抑制.可以采用遗传算法^[14]来优化荷载分布(包括位置和大小)，使实际模式向量φ_j尽量接近$ {\mathit{\boldsymbol{\tilde \varphi }}_j} $，从而达到激发出模态j的目标.遗传算法模仿自然界生物进化机制，是一种具有较高搜索效率和鲁棒性的随机全局搜索和优化方法.在指定荷载作用点数量时，可以基于遗传算法给出荷载分布优化策略.对于模态j，设荷载作用点向量为X_j，这些作用点上对应的荷载向量为F_j，候选作用点集合为E_X.以实际模式向量与目标模式向量之间的欧式距离作为优选指标，取其倒数作为遗传算法的适应度函数f(X_j, F_j)，则阶跃激励优化问题的数学描述为

$ \begin{array}{*{20}{c}} {{\rm{find}}\;{\mathit{\boldsymbol{X}}_j} = {{\left[ {\begin{array}{*{20}{c}} {{X_{j1}}}& \cdots &{{X_{ji}}}& \cdots &{{X_{jh}}} \end{array}} \right]}^{\rm{T}}},}\\ {{\mathit{\boldsymbol{F}}_j} = {{\left[ {\begin{array}{*{20}{c}} {{F_{j1}}}& \cdots &{{F_{ji}}}& \cdots &{{F_{jh}}} \end{array}} \right]}^{\rm{T}}},}\\ {\max f\left( {{\mathit{\boldsymbol{X}}_j},{\mathit{\boldsymbol{F}}_j}} \right) = \frac{1}{{{{\left\| {{\mathit{\boldsymbol{\varphi }}_j} - {{\mathit{\boldsymbol{\tilde \varphi }}}_j}} \right\|}_2}}};}\\ {{\rm{s}}.\;{\rm{t}}.\;\;\;\;{\mathit{X}_{ji}} \in {\mathit{\boldsymbol{E}}_X},{F_{\min }} \le {F_{ji}} \le {F_{\max }}.} \end{array} $

(23)

式中：h为荷载作用点数量；‖‖₂表示欧氏距离；X_ji为激发模态j时第i个荷载作用点的节点号；F_ji为对应X_ji的荷载大小；F_min和F_max为荷载限值.

应用遗传算法进行阶跃激励优化的步骤如下：

1) 给出初始条件并编码.确定荷载作用点数量h、待识别模态j和候选作用点集合E_X.采用浮点数编码方案.将节点号与浮点数建立映射关系，从而使节点号为整数.

2) 生成初始种群.每个个体包含的基因由荷载作用点向量X_j和相应的荷载向量F_j组成.随机生成若干个个体，生成的个体应各不相同以保证初始种群的多样性.

3) 计算适应度值f(X_j, F_j).将种群中每个个体对应的荷载代入式(20)计算各阶模态的广义静力位移，并分别根据式(22)和(23)计算模式向量和适应度函数.

4) 选择.以个体的适应度值占种群总适应度值的比例作为其被选择的概率，依据“赌轮盘”(即比例越高的个体被选择的概率越大)和保存最优个体(即最优的个体直接保存)的策略，选择适应度值高的个体.

5) 交叉.对种群中的个体随机两两配对，依据交叉概率对每组配对个体进行判断，决定是否需要交换随机生成的基因点处的基因(即交换部分作用点位置和荷载大小).

6) 变异.依据变异概率对种群中的每个个体进行判断，决定是否需要改变其某个基因点处的基因(即改变部分作用点位置和荷载大小)，需要变异个体的基因变异位置随机生成.完成步骤(4)~(6)后，种群进化为新一代.

7) 重复步骤(3)~(6)，直到获得最优解.

本文种群数取40，交叉概率和变异概率分别取为0.90和0.015.荷载作用点数量h从1开始逐步增加，由上述策略获得对应的最优模式向量.当荷载作用点数量增加后得到的最优模式向量改善有限时，此时的荷载分布将产生最优阶跃激励.将最优荷载施加到结构，突卸荷载后测量自由振动响应时程，再采用基于自由振动响应的时域法进行模态识别(本文采用STD法).

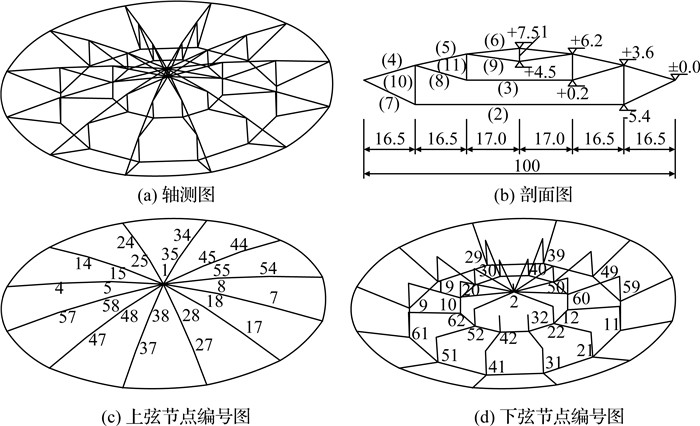
4 数值算例 4.1 模型参数

如图 1所示为某100 m跨度轴对称Geiger索穹顶，索穹顶周边节点均三向固定支承于刚性环梁上.构件分组和施工成型后(考虑预应力和自重)的节点位置如图 1(b)所示.上、下弦节点编号如图 1(c)、1(d)所示.索和杆的材料密度均为7 850 kg/m³，弹性模量分别为1.70×10¹¹和2.06×10¹¹ N/m².构件截面面积A、构件内力F如表 1所示.

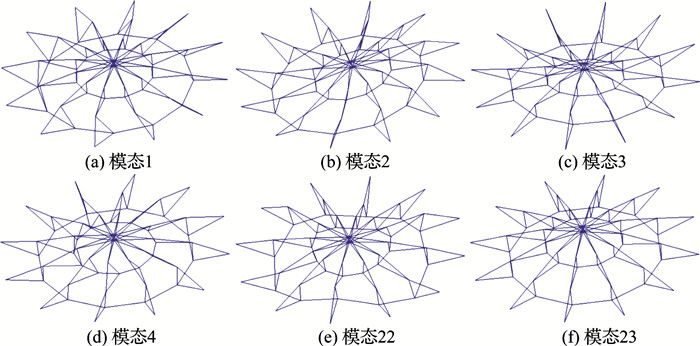
对其进行模态分析(未考虑节点质量的影响)，只考察前30阶模态.表 2给出了这些模态的固有频率.模态j的固有频率f_j=ω_j/(2π)，由表 2可知，索穹顶结构的模态频率非常密集.如图 2所示为6个典型模态的振型图.除模态2、23可以较为直观地判断是竖向振动为主之外，其余模态的主要振动方向较难直观判断.经分析，调整预应力水平或考虑节点质量的影响，均不会改变索穹顶模态密集的特点.

4.2 可激发的模态

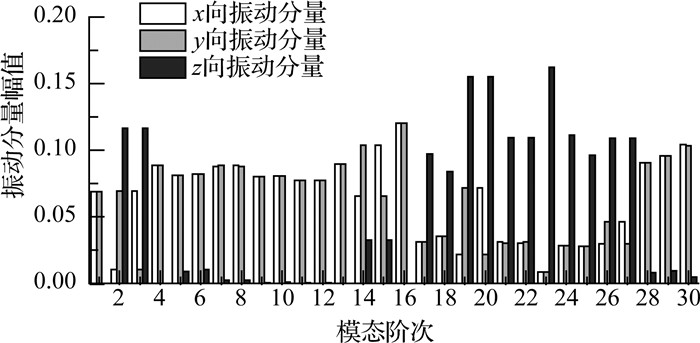
考虑到现场测试的易操作性，本算例只考虑竖向荷载悬挂在下弦节点的情况.考虑到广义荷载θ_j^Tp实际上是振型与荷载向量的点积，因此当施加竖向悬挂荷载时，以竖向振动为主的模态容易获得较大的广义静力位移.如图 3所示给出了前30阶模态在x、y、z这3个方向的振动分量幅值(将各个方向的振型幅值绝对值相加).可见，第2、3、17~27阶模态都是以竖向振动为主，这些模态容易被竖向悬挂荷载激发.

4.3 阶跃激励优化

分别取第2、3、17~23共9阶模态作为待识别模态.由于本算例只考虑竖向悬挂荷载，故取荷载限值为F_min=0，F_max=1.对每一阶待识别模态，将激励点数量(即荷载作用点数量)从1开始逐渐增加，按照3.3节遗传算法策略求解得到给定激励点数量下的最优解.当激励点数量增加后得到的模式向量与当前模式向量之间的欧氏距离小于0.05时，当前解即认为是阶跃激励优化的最优解.表 3给出了这些模态在阶跃激励优化后得到的荷载作用点数量h、荷载分布(包括荷载作用点对应的节点号向量X_j与荷载向量F_j)、以及最优模式向量φ_j.可见只需少数挂点就能得到最优模式向量.对于第2、3、23阶模态，只需要1个挂点，就可以得到非常接近目标模式向量的优化结果.对于第19~23阶模态，需要6个挂点才能得到最优模式向量.观察第21、22阶模态的最优模式向量φ_j，可以发现第23阶模态相对这两阶模态的参振贡献比依然高达0.47和0.46.即使进一步增加激励点数量，该参振贡献比也不能进一步被降低.表明在分别激发这两阶模态时，第23阶模态也总是被激发出来，这是由此类结构的动力特性决定的.

4.4 模态识别

假设结构为瑞利阻尼，取阻尼矩阵为C=0.08M + 0.0008 K_T.根据经典的有效独立法(effectiveness independence method, EI)^[15]进行测点布置优化，取9个测点.每阶待识别模态都需要进行单独的模态测试(即阶跃激励优化与模态识别).每次模态测试，均需要调整挂点位置，将优化荷载(表 3中的荷载大小须乘以50 000)施加于结构，待位移稳定后同时释放使结构产生自由振动.设定传感器采样频率50 Hz，采样时长20 s.为模拟实测噪声影响，给所测加速度时程添加上限为采样点幅值30%的白噪声.采用STD法进行模态识别以后，各阶模态频率、阻尼比与归一化振型的识别值同理论值的比较分别如表 4~5所示.表 4中，e_fj、e_ζj分别为模态频率和阻尼比识别值与理论值之间的相对误差；表 5中，θ_j与$ {\mathit{\boldsymbol{\tilde \theta }}_j} $分别为测点位置归一化后的理论振型和识别振型.采用模态置信准则(modal assurance criteria, MAC)^[16]来衡量理论振型θ_j与识别振型$ {\mathit{\boldsymbol{\tilde \theta }}_j} $之间的相关性，定义MAC系数为

$ {\rm{MAC}}\left( {{{\mathit{\boldsymbol{\bar \theta }}}_j},{{\mathit{\boldsymbol{\tilde \theta }}}_j}} \right) = \frac{{\left| {\mathit{\boldsymbol{\bar \theta }}_j^{\rm{T}}{{\mathit{\boldsymbol{\tilde \theta }}}_j}} \right|}}{{\left| {\mathit{\boldsymbol{\bar \theta }}_j^{\rm{T}}{{\mathit{\boldsymbol{\bar \theta }}}_j}} \right|\left| {\mathit{\boldsymbol{\bar \theta }}_j^{\rm{T}}{{\mathit{\boldsymbol{\tilde \theta }}}_j}} \right|}}. $

(24)

MAC系数介于0~1之间.MAC系数越接近1，则2个振型之间相似程度越高.各阶振型识别值与理论值的MAC系数如表 5所示.

由表 4可知，模态频率、模态阻尼比识别精度较高.虽然第22阶模态的频率识别误差最大，但相对误差仅为-1.55%，绝对误差为0.05 Hz；第2阶模态的阻尼比识别误差最大，相对误差为8.6%.

由表 5可知，即使噪声水平高达30%，第2、3、17~20、23阶模态的振型识别值与理论值也吻合较好，MAC系数大于0.99.可见，进行阶跃激励优化后这些密集模态的识别问题都有效地转化为孤立模态识别问题，识别精度得到提高.相比之下，第21、22阶模态的振型识别效果相对较差，这主要是受到了同时被激发的23阶模态的干扰.

常规模态测试流程一般并不进行激励优化，而且是一次性识别所有模态.不失一般性，针对该索穹顶随机生成一组节点荷载作为阶跃激励，并获得该激励引起的自由振动加速度响应时程，也同样引入30%的白噪声.采用STD法进行模态识别，结果如表 6所示.从表中可以看出，在不进行激励优化的情况下，该方法进行模态频率识别的精度还较高，但模态阻尼比识别结果与表 4相比误差大大增加.与表 5相比，其振型识别结果则是完全失败，所有模态的MAC系数均小于0.1.以上对比也印证了1.2节理论分析的正确性.

5 结论

(1) 以STD法为例进行的噪音灵敏度分析表明，在噪音干扰下，密集模态的特征值识别精度较高，但振型的识别精度却往往较低.

(2) 对初始位移扰动下自由振动响应的模态贡献分析表明，广义静力位移是衡量各阶模态参与结构自由振动的贡献指标.

(3) 以增强待识别模态并同时抑制邻近模态参与结构振动的贡献为目标，采用遗传算法可以获得最优荷载分布.将最优荷载施加于结构，突然卸载后使结构产生自由振动，再利用STD法进行模态识别，即完成待识别模态的测试流程.

(4) 当限定下弦节点和竖向荷载条件时，算例表明：大部分模态(第2、3、17~19、23阶)经阶跃激励优化后能够抑制邻近模态的参振贡献，模态识别精度较高；而由于结构动力特性的原因，少部分模态(第21、22阶)即使经过阶跃激励优化，也难以排除邻近模态(第23阶)的干扰，振型识别误差相对较大，但结果要远远好于不考虑激励优化的常规识别方法的结果.

对于以水平振动为主的密集模态，采用滑轮导向也能够实现阶跃激励，其模态测试流程与竖向模态的流程(见算例)相同.总的来说，提出的模态测试方法对于筛选可激发模态，提高索穹顶密集模态的识别精度效果较好.方法也同样适用于其他具有密集模态的大跨度结构，如网架、网壳、索桁架等.值得指出的是，实际结构与有限元模型的模态信息会有所不同，如何提高阶跃激励优化在既有结构模态测试中的鲁棒性是下一步需要重点解决的问题.