常力机构是一种末端输出在一定尺寸范围或者变形范围内时,输出力近似常力的机构.常力机构在输出端与外部环境接触,变形不可预知,而接触力需要保持常力的场合特别有用.在某些任务场合,工业机器人或者机床在对部件,抓取、加工或者打磨抛光时,往往需要末端执行器与外部环境接触时接触力保持常值.例如研磨抛光精密零部件的表面,希望接触抛光力是常值,这样可以提高零部件表面的质量[1-3],再或者在切割玻璃时,若接触力保持常力,切割的玻璃不容易出现裂纹[4].但通常的基于力传感器的力的控制,在实际工业应用中难以精确的实现,这是由于设备振动、外部环境的恶劣以及传感器技术的限制,力传感器采集到的信号比较杂乱,很难准确地将期望的力信号分离出来.柔顺常力机构不需要增加额外的传感器能够保持末端输出的常力,易于工程的实现.
1997年,Midha等[5]提出了柔顺常力机构,并申请了专利.采用型综合的方法总结出了28种平面柔顺常力机构的基本构型.随后Pedersen等[6]提出了拓扑优化方法用来设计柔顺常力机构.Meaders等[7]对匹配未知情况下的近常力弹簧做了优化研究工作,这有助于近常力弹簧在常力机构中的应用.2014年,Rahman等[8]提出了一种插值法用来设计柔顺常力机构.Chao等[9-10]利用正负刚度结合的原理提出了一种自适应机器人末端执行器的柔顺常力机构.Prakashah等[11]利用变宽度样条曲线综合出常力矩机构.Volkan Parlaktas等[12-15]研究了初始位形在同一个平面的空间单自由度空间曲柄滑块机构(spatial crank slider mechanism, RSSP)型柔顺常力机构.由于机构初始位形各杆件位于同一平面,机构的空间设计就会受到限制.初始位形对于RSSP空间柔顺常力机构的影响很大,不同的初始位形,所得到优化结构参数是完全不同的.因而,初始位形位于同一平面下的优化结构参数,不能够用于指导一般初始位形的空间柔顺常力机构的设计.本文研究的是一般初始位形下的RSSP空间柔顺常力机构,通过理论建模,优化结构参数并开展相应的实验,为RSSP空间柔顺常力机构的实际设计做理论指导.
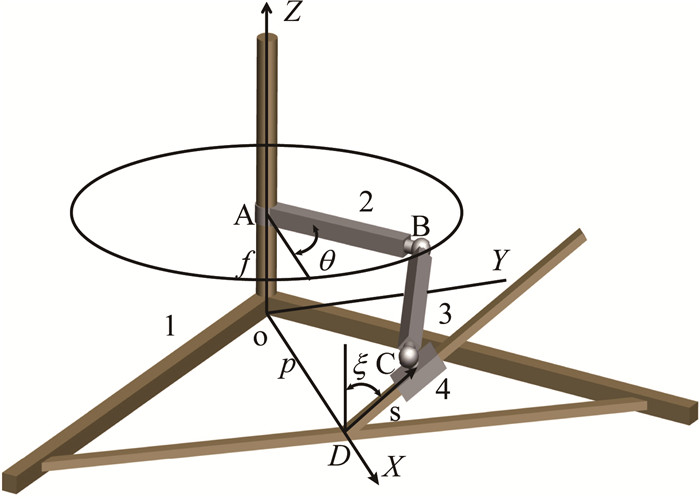
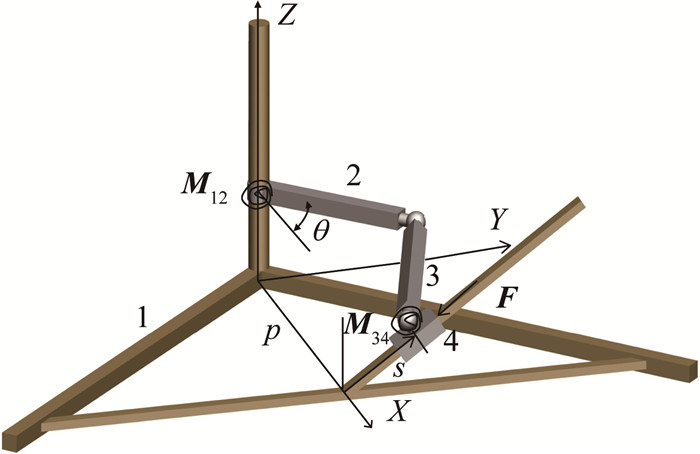
1 空间RSSP机构运动学建模与分析空间RSSP机构如图 1所示,杆1为机架,杆2为曲柄,其长度为a2,杆3为连杆,其长度为a3,4为滑块.参考坐标系O-XYZ建立过程如下:z轴为曲柄转动轴线方向,X轴为Z轴与滑块导轨矢量线的公垂线方向,与Z轴的交点为原点O.图中,p为曲柄转动轴到滑块导轨矢量线的垂直距离,s为滑块的导程,即滑块中心位置到X轴的距离.f为OA的长度,即曲柄所在平面与OXY平面间的距离.θ为曲柄输入角,即曲柄与XOZ所构成平面在X轴正方向的半平面之间的夹角.ξ为滑块所在轨道与XOZ所构成平面在Z轴正方向的半平面之间的导路方向角.为了使得本文的分析方法更加具有一般性,将机构的参数进行无量纲化处理.选择连杆3为基本杆,曲柄长度a2,f和p相比于a3,得到的无量纲参数r1、r2和r3分别为
|
图 1 空间RSSP机构构型 Fig. 1 RSSP mechanism |
| $ {r_1} = {a_2}/{a_3},{r_2} = f/{a_3},{r_3} = p/{a_3}. $ | (1) |
采用闭合矢量法,RSSP机构的位置方程可以得到
| $ \begin{array}{*{20}{c}} {{s^2} - 2s\left( {f\cos \xi + {a_2}\sin \xi \sin\theta } \right) + }\\ {{p^2} + a_2^2 + {f^2} - a_3^2 - 2p{a_2}\cos \theta = 0.} \end{array} $ | (2) |
式(2)两边同时除以a32,则可以写成如下形式:
| $ \begin{array}{*{20}{c}} {{{\left( {\frac{s}{{{a_3}}}} \right)}^2} - 2\frac{s}{{{a_3}}}\left( {{r_1}\sin \xi \sin \theta + {r_2}\cos \xi } \right) - }\\ {2{r_1}{r_3}\cos \theta + r_1^2 + r_2^2 + r_3^2 - 1 = 0.} \end{array} $ | (3) |
如果以杆2作为输入,那么对于任一给定的θ值,相对位移s/a3可以表示为以下形式:
| $ \frac{s}{{{a_3}}} = v \pm {\sqrt {\mathit{\Lambda }}} . $ | (4) |
式中:v=r1 sin ξ sin θ+r2 cos ξ,Λ=(r1 sin ξ×sin θ)2+(r2 cos ξ)2+2r1r2 sin ξ cos ξ sin θ-r12-r22+1+2r1r3 cos θ-r32.
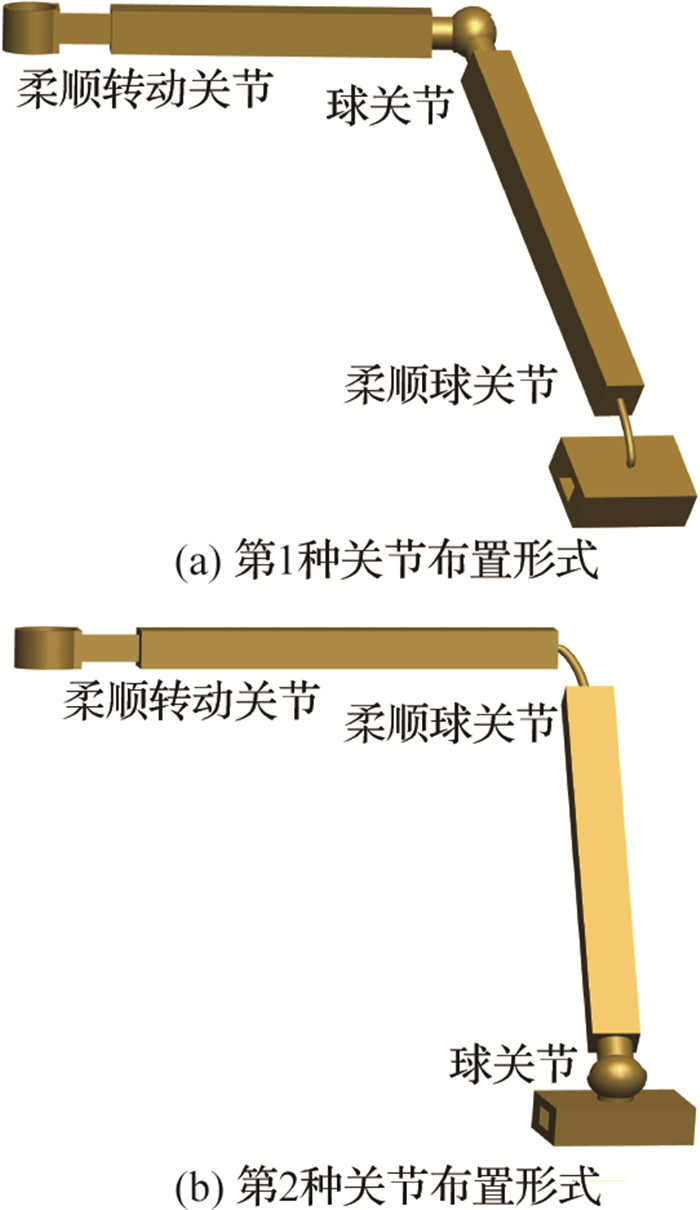
根据文献[14],当将RSSP的2个球关节全部替换成柔顺关节时,连杆在机构运动中会产生扭矩.因此,只将其中一个球关节替换成三自由度柔顺球关节,另外一个球关节的存在可以消除额外的扭矩,降低分析的复杂度.根据柔顺关节替换球关节的位置,可以得到2种基本的柔顺RSSP构型,如图 2所示.根据文献[13],图 2(b)中的第2种构型的机构在运动中,三自由度柔顺球关节的初始位置向量,会随着曲柄输入角度的变化而变化,这使变形量的分析变得复杂,而第1种构型的三自由度柔顺球关节的初始位置向量在机构运动过程中不会随着曲柄输入角变化,其变形量的分析比较简单.本文选择图 2(a)中的第1种构型进行分析.
|
图 2 柔顺关节的布置图 Fig. 2 Layout of compliant joint |
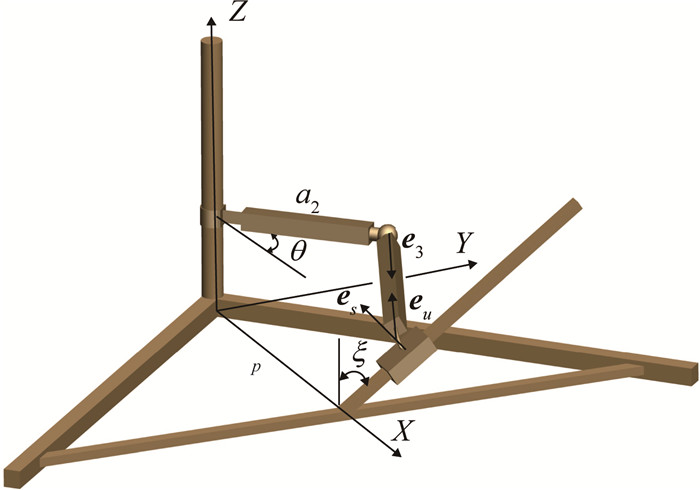
如图 3所示,RSSP柔顺机构初始位形时,曲柄杆和滑块导轨不在同一个平面内,即r3≠0. e3是沿着杆3的单位向量,杆3的向量可以表示为
|
图 3 初始位形下位置参数表示 Fig. 3 Parameters of the initial configuration |
| $ {\mathit{\boldsymbol{e}}_3} = {\left[ {l,m,n} \right]^{\rm{T}}}. $ | (5) |
式中:l、m、n为e3在参考坐标系各坐标轴上的分量,可以计算得到
| $ l = {r_3} - {r_1}\cos \theta , $ |
| $ m = \frac{s}{{{a_3}}}\sin \xi - {r_1}\sin \theta , $ |
| $ n = \frac{s}{{{a_3}}}\cos \xi - {r_2}. $ |
在初始位形下,eu为三自由度柔顺关节的初始位置向量,初始定义为eu=-e3.假设曲柄初始输入位置在θ=θc,此时eu为
| $ {\mathit{\boldsymbol{e}}_{\rm{u}}} = \left( \begin{array}{l} {r_1}\cos {\theta _{\rm{c}}} - {r_3},\\ {r_1}\sin {\theta _{\rm{c}}} - {s_{\rm{c}}}\sin \xi ,\\ {r_2} - {s_{\rm{c}}}\cos \xi . \end{array} \right) $ | (6) |
式中:θc为柔性关节的初始未偏转角,sc=sθc/a3,sθc为初始输出位置. eu只在滑块导轨上的平移运动,因而eu方向不变.
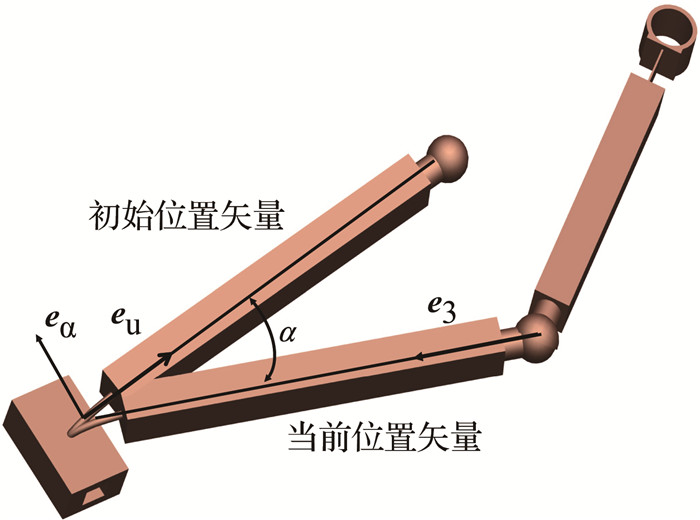
如图 4所示,eα为垂直于三自由度柔顺关节初始位置矢量eu与连杆当前位置矢量e3的单位向量,其方向定义为柔顺球关节的瞬时轴,α为连杆初始位置和当前位置的夹角.α表征三自由度柔顺关节变形量的大小.其大小可以表示为
|
图 4 瞬时柔顺关节的位置 Fig. 4 Instantaneous position of the compliant joint |
| $ \alpha = {\cos ^{ - 1}}\left[ {{\mathit{\boldsymbol{e}}_{\rm{u}}} \cdot \left( { - {\mathit{\boldsymbol{e}}_3}} \right)} \right]. $ | (7) |
eα为
| $ {\mathit{\boldsymbol{e}}_\alpha } = \frac{{{\mathit{\boldsymbol{e}}_{\rm{u}}} \times \left( { - {\mathit{\boldsymbol{e}}_3}} \right)}}{{\left| {{\mathit{\boldsymbol{e}}_{\rm{u}}} \times \left( { - {\mathit{\boldsymbol{e}}_3}} \right)} \right|}}. $ | (8) |
eα对于运动后杆件的每一个位置都是确定的,在没有扭矩存在的情况下,柔顺球关节的分析能够简单地当作单自由度柔顺关节进行处理.由于柔顺球关节上的瞬时轴是由其初始位置和当前位置决定的,因而其当前位置可以看做是初始位置围绕着瞬时轴偏转了一个角度.对于横截面是圆形的弯曲关节,三自由度柔顺关节就可以当作单自由度柔顺关节处理.
如图 3所示,es是垂直于滑块表面的方向轴,基本参数u是es与eu之间的夹角,
| $ {\mathit{\boldsymbol{e}}_{\rm{s}}} = {\left[ {0, - \cos \xi ,\sin \xi } \right]^{\rm{T}}},u = {\cos ^{ - 1}}\left[ {{\mathit{\boldsymbol{e}}_{\rm{u}}} \cdot {\mathit{\boldsymbol{e}}_{\rm{s}}}} \right]. $ | (9) |
伪刚体模型的概念是用具有等效力-变形关系的刚体构件模拟柔性部件的变形,刚体机构的理论可以用来分析柔顺机构.一般初始位置的RSSP柔顺机构的伪刚体模型如图 5所示. M12、M34分别为模拟柔顺转动关节和柔顺球关节的扭簧所产生的力矩,F为外部环境对其沿着导轨方向的作用力.
|
图 5 RSSP柔顺机构伪刚体模型 Fig. 5 Pseudo-rigid-body Model of RSSP mechanism |
采用虚功原理,对初始构型确定的RSSP柔顺机构进行分析,根据已经建立好的伪刚体模型,机构系统中主动力所做的虚功δW可以表示为
| $ {\rm{ \mathsf{ δ} }}W = {\mathit{\boldsymbol{M}}_{12}} \cdot {\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{\theta }} + {\mathit{\boldsymbol{M}}_{34}} \cdot {\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{\alpha }} + \mathit{\boldsymbol{F}} \cdot {\rm{ \mathsf{ δ} }}s. $ | (10) |
式中:δ为变量任意微小增量.在参考坐标系O-XYZ下,扭簧所产生的力矩和外部作用力可以分别写成以下形式:
| $ {\mathit{\boldsymbol{M}}_{12}} = \left( {\begin{array}{*{20}{c}} 0\\ 0\\ 1 \end{array}} \right){M_{12}},{\mathit{\boldsymbol{M}}_{34}} = \left( {\begin{array}{*{20}{c}} {{e_{ax}}}\\ {{e_{ay}}}\\ {{e_{az}}} \end{array}} \right){M_{34}},\mathit{\boldsymbol{F}} = \left( {\begin{array}{*{20}{c}} 0\\ {\sin \xi }\\ {\cos \xi } \end{array}} \right)F. $ | (11) |
M12和M34的大小分别为:
| $ \begin{array}{l} {M_{12}} = \left( {\theta - {\theta _{\rm{c}}}} \right){k_{12}},\\ {M_{34}} = {k_{34}}\alpha . \end{array} $ | (12) |
式中:k12和k34为扭簧的刚度.对应的虚位移也可以写成以下形式:
| $ {\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{\theta = }}\left( {\begin{array}{*{20}{c}} 0\\ 0\\ 1 \end{array}} \right){\rm{ \mathsf{ δ} }}\theta ,{\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{s = }}\left( {\begin{array}{*{20}{c}} 0\\ {\sin \xi }\\ {\cos \xi } \end{array}} \right){\rm{ \mathsf{ δ} }}s,{\rm{ \mathsf{ δ} }}\mathit{\boldsymbol{\alpha = }}\left( {\begin{array}{*{20}{c}} {{e_{ax}}}\\ {{e_{ay}}}\\ {{e_{az}}} \end{array}} \right){\rm{ \mathsf{ δ} }}\alpha . $ | (13) |
式子(3)两边同时对s求导数后得到
| $ \frac{{{\rm{ \mathsf{ δ} }}\theta }}{{{\rm{ \mathsf{ δ} }}s}} = \frac{{{\rm{d}}\theta }}{{{\rm{d}}s}} = \frac{\mathit{\mathit{\Delta}} }{{{a_3}}}. $ | (14) |
式中:
| $ {\rm{ \mathsf{ δ} }}\alpha = D{\rm{ \mathsf{ δ} }}s. $ | (15) |
式中:
| $ \begin{array}{l} D = \frac{1}{{\sin \alpha }}\left[ {\left( {{r_1}\cos {\theta _{\rm{c}}} - {r_3}} \right){r_1}\sin \theta \frac{\mathit{\mathit{\Delta}} }{{{a_3}}} + \left( {{r_1}\sin {\theta _{\rm{c}}} - } \right.} \right.\\ \left. {{s_{\rm{c}}}\sin \xi } \right) \times \left( {\frac{{\sin \xi }}{{{a_3}}} - {r_1}\cos \theta \frac{\mathit{\mathit{\Delta}} }{{{a_3}}}} \right) + \left( {{r_2} - {s_{\rm{c}}}\cos \xi } \right)\\ \left. {\frac{{\cos \xi }}{{{a_3}}}} \right]. \end{array} $ | (16) |
由以上的关系,输出力大小得出
| $ F = - {k_{12}}\left( {\theta - {\theta _{\rm{c}}}} \right)\frac{\mathit{\mathit{\Delta}}}{{{a_3}}} - {k_{34}}\alpha D. $ | (17) |
注意式(17)中含有的非无量纲化参数,引进无量纲化参数K=k34/k12进行处理后,可以得到
| $ \left. \begin{array}{l} F = \frac{{{k_{12}}}}{{{a_3}}}\mathit{\Phi },\\ \mathit{\Phi } = \left( {{\theta _{\rm{c}}} - \theta } \right) \cdot \mathit{\Delta} - \frac{{\alpha K \cdot \mathit{\Delta} }}{{\sin \alpha }}\left[ {r_1^2\cos {\theta _{\rm{c}}}\sin \theta - } \right.\\ {r_1}{r_3}\sin \theta + \frac{{{r_1}\sin {\theta _{\rm{c}}}\sin \xi }}{\mathit{\Delta} } - r_1^2\sin {\theta _{\rm{c}}}\cos \theta - \\ \left. {\frac{{{s_{\rm{c}}}}}{\mathit{\Delta} } + {r_1}{s_{\rm{c}}}\sin \xi \cos \theta + \frac{{{r_2}\cos \xi }}{\mathit{\Delta} }} \right],\\ \mathit{\Delta} = \frac{{\left( {{r_1}\sin \xi \sin \theta + {r_2}\cos \xi } \right) - \frac{s}{{{a_3}}}}}{{{r_1}{r_3}\sin \theta - \frac{s}{{{a_3}}}{r_1}\sin \xi \cos \theta }},\\ {s_{\rm{c}}} = \left( {{r_1}\sin \xi \sin \theta + {r_2}\cos \xi } \right) + \left[ {{{\left( {{r_1}\sin \xi \sin \theta } \right)}^2} + } \right.\\ {\left( {{r_2}\cos \xi } \right)^2} + 2{r_1}{r_2}\sin \xi \cos \xi \sin \theta - r_1^2 - \\ {\left. {r_2^2 + 1 + 2{r_1}{r_3}\cos \theta - r_3^2} \right]^{1/2}}. \end{array} \right\} $ | (18) |
从式(18)可以看出,RSSP柔顺常力机构与外部环境接触力F大小依赖于参数k12, a3, Φ,k12, a3为给定的设计参数,以此当Φ在机构位形变化时保持常值,则接触力F为常力.
3 目标函数的建立Φ依赖于3个无量纲化的结构参数和柔顺关节刚度的比值,分别为
| $ {r_1} = \frac{{{a_2}}}{{{a_3}}},{r_2} = \frac{f}{{{a_3}}},{r_3} = \frac{p}{{{a_3}}},K = \frac{{{k_{34}}}}{{{k_{12}}}}. $ | (19) |
当θ取n个离散值时,Φ随θ变化的波动特征的目标函数为
| $ {\rm{mb}}\left( x \right) = \sum\limits_{i = 1}^n {\left| {\mathit{\Phi }\left( i \right) - \mathit{\Phi }\left( {i + 1} \right)} \right|} . $ | (20) |
式中:x为待优化参数的集合,Φ(i)为对应着θ=θi(i=1, 2, ..., n)离散点的函数值.优化过程中的复杂约束条件是式(4)中的Λ的大小必须为正.将复杂约束条件转变成多目标优化函数后,则本文建立的含有柔顺关节的空间单自由度常力机构的结构参数优化问题可以定义如下:
| $ \begin{array}{l} {\rm{mb}}\left( x \right) = \min \left\{ {\sum\limits_{i = 1}^n {{\rm{abs}}\left( {\mathit{\Phi }\left( i \right) - \mathit{\Phi }\left( {i + 1} \right)} \right)} + \sum\limits_{i = 1}^n {\max } } \right.\\ \left. {\left( {0, - \mathit{\Lambda }\left( i \right)} \right)} \right\}.\\ {\rm{s}}.\;{\rm{t}}{\rm{.}}\;\;\;\;{r_1} \in \left[ {0.1,0.85} \right],\\ \;\;\;\;\;\;\;\;{r_2} \in \left[ {0.1,5} \right],\\ \;\;\;\;\;\;\;\;{r_3} \in \left[ {0.1,5} \right],\\ \;\;\;\;\;\;\;\;K \in \left[ {0.1,10} \right],\\ \;\;\;\;\;\;\;\;x = {\left[ {{r_1},{r_2},{r_3},K} \right]^{\rm{T}}}. \end{array} $ |
当式子(4)中的符号取正,即
| $ \mathit{\boldsymbol{\theta }} = \left[ {0,\frac{{\rm{ \mathsf{ π} }}}{{48}},\frac{{{\rm{2 \mathsf{ π} }}}}{{48}},\frac{{{\rm{3 \mathsf{ π} }}}}{{48}},\frac{{{\rm{4 \mathsf{ π} }}}}{{48}},\frac{{{\rm{5 \mathsf{ π} }}}}{{48}},\frac{{{\rm{6 \mathsf{ π} }}}}{{48}},\frac{{{\rm{7 \mathsf{ π} }}}}{{48}}} \right]. $ |
利用粒子群优化算法,所得的优化结果如表 1所示.在常力机构中,通常是以输出端与环境的最大与最小接触力Fmax/Fmin的比值大小作为评价指标,来衡量机构保持常力的性能,本文也使用λ=Fmax/Fmin=Φmax/Φmin作为指标评价机构保持常力的能力.由于结构参数较多,目标函数的取值具有耦合性,存在得到多组解的可能.下表只列出了部分解.如表 2~5所示为采用类似方法得到的优化结果.
| 表 1 当θc=π/6,ξ=π/2时结构参数优化结果 Table 1 Optimization results of structural parameters at θc=π/6, ξ=π/2 |
| 表 2 当θc=π/4,ξ=π/2时结构参数优化结果 Table 2 Optimization results of structural parameters at θc=π/4, ξ=π/2 |
| 表 3 当θc=π/3,ξ=π/2时结构参数优化结果 Table 3 Optimization results of structural parameters at θc=π/3, ξ=π/2 |
| 表 4 当θc=π/3, ξ=π/3时结构参数的优化结果 Table 4 Optimization results of structural parameters at θc=π/3, ξ=π/3 |
| 表 5 当θc=π/3,ξ=π/4时结构参数的优化结果 Table 5 Optimization results of structural parameters at θc=π/3, ξ=π/3 |
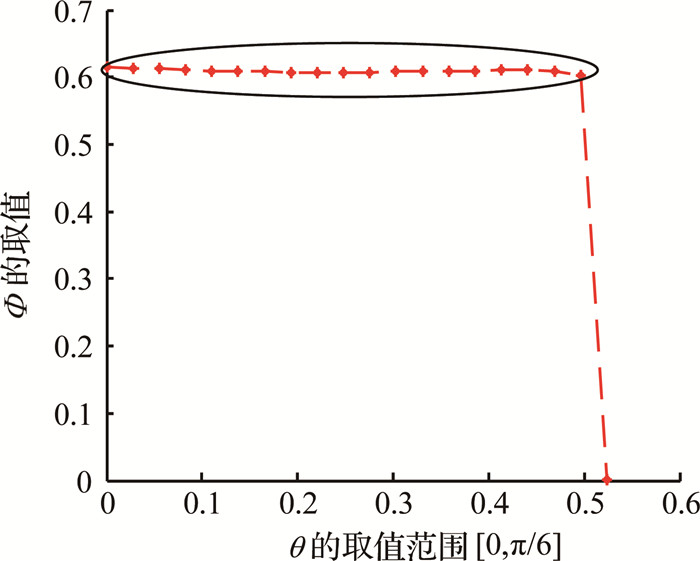
为避免离散点选取的偶然性,本文从优化结果中任取出一组,使θ在其变化区间上均匀地取20个点,观察Φ的输出是否能够保持常值,以此验证上述建模以及优化方法的有效性.如图 6所示为表 1中第1组优化数据的Φ值输出图.表 1~5中任选出的结构参数组的Φ值输出图与图 6类似,波动程度是可以从表中的mb和λ的大小可以看出来.
比较表 1至5中的优化结果的数据,并观察Φ值的输出图,可以总结如下:对于RSSP空间柔顺常力机构,θc和ξ对优化结果的影响比较大,即对常力机构保持常力的性能影响比较大.θc和ξ设计值发生变化,优化所得的参数数据的以及λ的值会发生变化.在ξ=π/2(表 1~3)时所能得到的优化结果要比ξ≠π/2(表 4~5)时的优化结果中λ的大小明显要小,证明保持常力的性能要好.同时从图 6中可以看出,RSSP空间柔顺常力机构在初始位形确定的情况下,柔顺单元不发生变形的情况下,机构的Φ输出值为零,说明在柔顺关节初始小变形的情况下,容易偏离期望的常力值.
5 实验假如以表 1中的第2组数据为参数设计常力机构.若令杆a3=500 mm,则a2=425 mm, p=763.7 mm f=202 mm,θc=π/6,ξ=π/2.若单自由度柔顺关节和三自由度柔顺关节采用的材料为高级弹簧钢60Si2CrVA,它的弹性模量为E=200 GPa.短臂柔顺转动关节的刚度公式为k=EI/l,I为与柔顺关节矩形几何截面相关的惯性矩,h为矩形截面高度,b为矩形截面宽度,l为短臂的长度.先给定柔顺单自由度转动关节的尺寸参数,然后按照K=k34/k12=I34l12/(I12l34)=1.442 1参数,进行柔顺三自由度球关节的参数设计.在设计参数确定的前提下,制造装配出RSSP空间柔顺常力机构的实验装置.在2次实验中柔顺关节使用的柔性材料主要尺寸参数如表 6所示, 表中d为柔顺球关节的直径l12, L34分别为机构中柔顺转动关节短臂的长度.
| 表 6 2组实验用弹簧片的尺寸参数 Table 6 Size parameters of spring piece in two group experiments |
在实验时,如图 7所示在机构初始位形下,用测力计接触机构输出端,沿着导轨推动滑块移动,记录下滑动的位移及力的变化.实验1时,理论的接触力相关函数Φ基本保持不变Φ≈0.61,理论接触力也变化不大,约为F≈68.5 N.实验2时,理论的力相关函数理论为Φ≈0.615,理论末端接触力为F≈20.5 N.

|
图 7 输出力测量实验 Fig. 7 Measurement experiment of output force |
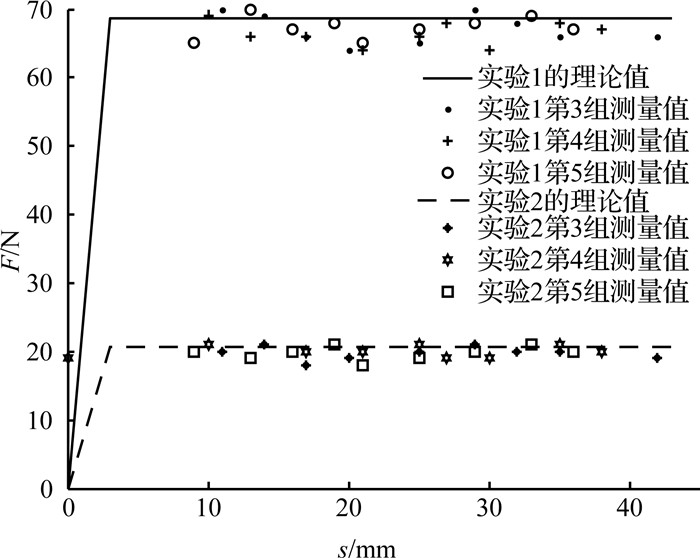
实验1和2所测得的末端接触力F与位移s绘制成末端接触力的输出图,如图 8所示.在实验预先所设计的40 mm的变形导程范围内,实验1各组测量数据的均值稳定在66~67 N之间.实验2自组测量数据的均值稳定在19.5~20 N之间,所测得的数据围绕在理论值附近百分之五以内的波动.引起波动的主要原因可能为:实验中的RSSP空间柔顺机构加工、装配误差,以及滑块导轨上存在的摩擦力以及测量数据时存在的偶然误差.
|
图 8 实验测得的末端接触力的输出 Fig. 8 End contact force output measured in experiment |
RSSP柔顺常力机构可以用于单自由度抛光工具头以及两指常力手爪的设计,其两指常力手爪的概念设计示意图,如图 9所示.

|
图 9 两指常力手爪设计示意图 Fig. 9 Design schematic diagram of gripper with two fingers |
本文推导了初始位形下各杆件不在同一个平面下的空间RSSP机构的输出力表达式.并以输出力采样点相邻差值和的方法表示输出力波动大小的特征,从而建立起表示输出力波动的目标函数,且将复杂的约束条件转化为多目标函数.优化的结果和输出力函数验证表明,以上的建模方法是有效的.柔顺转动关节初始θc和机构导路方向角ξ对优化结果的影响比较大,即对常力机构保持常力的性能影响比较大.在ξ=π/2时所能得到的优化结果要比ξ≠π/2时的优化结果保持常力的性能要好.初始位形不在同一个平面下的RSSP空间柔顺常力在设计实际机构时受到的限制比较少,具有更多的实际工程参考意义.
| [1] |
赵文宏. 纳米级超精密抛光机控制系统研制[D]. 杭州: 浙江大学, 2003. ZhAO Wen-hong. Development of the control system for nano-scale ultra precision polishing machine[D]. Hangzhou: Zhejiang University, 2003. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y513421 |
| [2] |
史素敏. 模具抛光柔顺执行机构的接触力控制研究[D]. 成都: 西华大学, 2013. SHI Su-min. Research on contact force control of compliant actuator for mold polishing[D]. Chengdu: Xihua University, 2013. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D345868 |
| [3] |
王新涛. 复杂曲面研磨抛光机器人力控制研究[D]. 沈阳: 东北大学, 2012. WANG Xin-tao. Research of force control of a grinding and polishing robot based on complex curved surface[D]. . Shenyang: Northeastern University, 2012. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=J0122108 |
| [4] |
BOYLEC L. A closed-form dynamic model of the compliant constant force mechanism using the pseudo-rigid-body model[D]. Provo: Brigham Young University, USA, 2001. http://www.researchgate.net/publication/249889625_A_CLOSED-FORM_DYNAMIC_MODEL_OF_THE_COMPLIANT_CONSTANT-FORCE_MECHANISM_USING_THE_PSEUDO-RIGID-BODY_MODEL
|
| [5] |
MIDHA A, MURPHY M D, HOWELL L L. Compliant constant-force mechanism and devices formed therewith: United States, US5649454[P]. 1997. http://www.freepatentsonline.com/5649454.html
|
| [6] |
PEDERSEN C B W, FLECK N A, ANANTHASURESH G K. Design of a compliant mechanism to modify an actuator characteristic to deliver a constant output force[J]. Journal of Mechanical Design, 2006, 128(5): 1101-1112. DOI:10.1115/1.2218883 |
| [7] |
MEADERS J C, MATTSON C A. Optimization of near-constant force springs subject to mating uncertainty[J]. Structural & Multidisciplinary Optimization, 2009, 41(1): 1-15. |
| [8] |
RAHMAN M U, ZHOU H. Design of constant force compliant mechanisms[J]. International Journal of Engineering Research and Technology, 2014, 3(7): 14-19. |
| [9] |
LAN C C, WANG J H, CHENY H. A compliant constant-force mechanism for adaptive robot end-effector operations[C]//Robotics and Automation (ICRA), IEEE International Conference on. Anchorage, AK, USA: [s. n. ], 2010: 2131-2136. http://ieeexplore.ieee.org/document/5509928/
|
| [10] |
CHEN Y H, LAN C C. An adjustable constant-force mechanism for adaptive end-effector operations[J]. Journal of Mechanical Design, 2012, 134(3): 031005. DOI:10.1115/1.4005865 |
| [11] |
PRAKASHAH H N, ZHOU H. Synthesis of constant torque compliant mechanisms[J]. Journal of Mechanisms and Robotics, 2016, 8: 064503-1. DOI:10.1115/1.4034885 |
| [12] |
TANIK E, PARLAKTAŞ V. A new type of compliant spatial four-bar (RSSR) mechanism[J]. Mechanism and Machine Theory, 2011, 46(5): 593-606. |
| [13] |
PARLAKTAŞ V, TANIK E. Partially compliant spatial slider-crank (RSSP) mechanism[J]. Mechanism and Machine Theory, 2011, 46(11): 1707-1718. |
| [14] |
PARLAKTAŞ V. Spatial compliant constant-force mechanism[J]. Mechanism and Machine Theory, 2013, 67: 152-165. |
| [15] |
PARLAKTAŞ V, TANIK E. Single piece compliant spatial slider-crank mechanism[J]. Mechanism and Machine Theory, 2014, 81: 1-10. |