宏观世界中所有机械摩擦副之间的接触都是粗糙表面间的接触,真实金属表面是由一系列微凸体构成,接触表面之间微凸体的相互作用影响着接触面的变形量与接触动刚度[1-3].粗糙表面接触动刚度反映着接触物体表面变形的趋势、引起振动和噪声的概率和零件或结构磨损的程度等,因此,对粗糙表面接触刚度的研究至关重要[4-6].粗糙表面接触刚度的计算依赖于粗糙表面模型的假设.经典Hertz接触理论适用于2个光滑曲面之间的弹性接触分析[7],用于描述接触面的法向接触力与变形关系、接触面积以及压力分布特征.但是该理论没有考虑到实际接触面积与表观面积的差异,导致结果与实际情况不匹配.GW模型[8]有效地弥补了Hertz理论的不足,它首次将表面形貌高度看成是服从正态分布随机变量,运用概率统计的办法建立了粗糙表面与光滑平面之间的模型.Greenwood等[9]在GW粗糙表面接触模型的基础上,进行随机粗糙表面间的弹性接触分析,得到表面粗糙度对接触特性的影响规律.Whitehouse等[10]认为,微凸体高度和峰顶曲率半径都是随机变量,表面轮廓的自相关函数为指数形式,接触分析结果与GW模型基本一致.
在粗糙表面模型假设的基础上,国内外众多学者对粗糙表面接触刚度进行研究.Majumdar等[11]假设粗糙表面存在自相似性,利用分形理论,提出了MB模型,然而该模型存在粗糙表面上的接触刚度不连续的问题.在MB模型的基础上,张学良等[12-13]提出了粗糙表面接触刚度分形模型,并且对MB模型进行修正.李小彭等[14-15]基于分形理论研究粗糙表面切向刚度(及切向阻尼)与载荷、分形维数等的关系.李玲等[16]研究发现两接触面无论材料是否相同,结合面的切向接触刚度均与法向载荷呈正相关.杨红平等[17]运用接触力学与分形几何建立机械结合面的法向刚度计算模型,研究不同塑性指数下接触刚度与接触载荷的关系,并与实验结果有较好的吻合.刘鹏等[18]建立了粗糙球面切向接触刚度分形模型,研究接触载荷,摩擦因数等对切向接触刚度的影响.Polycarpou等[19]研究弹性接触与弹塑性接触2种不同假设下粗糙表面微凸体模型建立的方法.尤晋闽等[20]研究了微凸体高度在不同随机分布下接触刚度的变化.Wu[21]假设粗糙表面的微凸体是曲率半径相同的半球体,高度服从正态分布,提出粗糙表面微凸体个数的统计方法,但该模型假设过于理想化.微凸体曲率半径的不同会对接触刚度产生不同程度的影响.师俊平等[22]假设微凸体为椭圆抛物体,接触面长短半轴服从二维正态分布的椭圆接触面,运用概率统计学研究了切向接触刚度.
本文针对过于理想化的曲率半径相同的微凸体模型,考虑粗糙表面的微凸体的接触半径和高度服从正态分布,建立粗糙表面切向接触刚度概率模型,对相关影响因素进行数值计算,并将计算结果与分形模型的计算结果对比.
1 粗糙表面切向接触刚度概率模型根据Hertz接触理论和GW接触模型,2粗糙表面的接触可以看成一个粗糙表面与一个理想刚性平面间的接触,取微凸体研究模型为半球体,接触截面为圆形,且接触面间不存在相互滑动.
单个微凸体的接触刚度[23]为
| $ {k_{\rm{t}}} = \frac{{{\rm{d}}{F_{\rm{T}}}}}{{{\rm{d}}t}} = \frac{{8Gr}}{{2 - \nu }}{\left( {1 - \frac{{{F_{\rm{T}}}}}{{f{F_{\rm{N}}}}}} \right)^{1/3}}. $ | (1) |
式中:FT为作用在微凸体上的总切向力,t为微凸体的切向变形,FN为作用在微凸体上的总法向力,f为接触面的静摩擦系数,且FT < fFN,G为当量切变模量,r为微凸体半径,ν为接触面当量泊松比,G与ν有如下关系[24]:
| $ G = \frac{E}{{2\left( {1 + \nu } \right)}}. $ | (2) |
式中:E为接触面的弹性模量,且有
| $ \frac{1}{E} = \frac{{1 - \nu _1^2}}{{{E_1}}} + \frac{{1 - \nu _2^2}}{{{E_2}}}. $ | (3) |
| $ \nu = {V_1}{\nu _1} + {V_2}{\nu _2}. $ | (4) |
式中:E1、E2分别为2种接触材料的弹性模量;ν1、ν2分别为2种接触材料的泊松比;V1、V2分别为上、下微凸体体积所占比例,其取值区间为(0,1),且V1+V2=1.
宏观接触面由一系列微凸体堆积而成,因此接触面的切向刚度必然由微凸体的切向刚度决定.
微凸体接触半径与高度均服从正态分布,其概率密度函数分别为
| $ \varphi \left( r \right) = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} \sigma }}\exp \left( { - \frac{{{{\left( {r - u} \right)}^2}}}{{2{\sigma ^2}}}} \right). $ | (5) |
| $ \varphi \left( {{r_1}} \right) = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} {\sigma _1}}}\exp \left( { - \frac{{{{\left( {r - {u_1}} \right)}^2}}}{{2\sigma _1^2}}} \right). $ | (6) |
式中:u为微凸体半径均值,σ为微凸体半径标准差, u1为微凸体高度均值,σ1为微凸体高度标准差.
得出接触面总切向刚度为
| $ \begin{array}{l} K = {N_L}\int_0^{{r_{\max }}} {{k_{\rm{t}}}\varphi \left( r \right){\rm{d}}r} \\ \;\;\;\;\; = {N_L}\int_0^{{r_{\max }}} {{k_{\rm{t}}}} \times \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} \sigma }}\exp \left( { - \frac{{{{\left( {r - u} \right)}^2}}}{{2{\sigma ^2}}}} \right){\rm{d}}r. \end{array} $ | (7) |
式中:rmax为微凸体接触半径的最大值,NL为接触平面长度为L测量高度为h时所检测到的微凸体的最少个数[21],NL计算方法如下:
| $ {N_L} = \frac{{L\rho }}{{2{\rm{ \mathsf{ π} }}b{{\left( {1 - {\rho ^2}} \right)}^{1/2}}}}\exp \left( { - \frac{{{h^2}}}{{\sigma _1^2\left( {1 + \rho } \right)}}} \right). $ | (8) |
| $ \rho = \exp \left( { - \frac{s}{b}} \right). $ | (9) |
式中:L为接触平面的总长度, h为测量高度, ρ为自相关系数, s和b分别为测量间距和Markov过程距离参数.
将式(1)和(8)代入式(7),得出接触面切向接触刚度为
| $ \begin{array}{l} K = {\left( {1 - \frac{{{F_{\rm{T}}}}}{{f{F_{\rm{N}}}}}} \right)^{1/3}} \times \\ \left[ {\frac{{0.116GL\rho \sigma \times \exp \left( { - \frac{{{u^2}}}{{4{\sigma ^2}}}} \right) \times \left( {1 - \exp \left( {\frac{{r_{\max }^2}}{{4{\sigma ^2}}} - \frac{{{r_{\max }}u}}{{2{\sigma ^2}}}} \right)} \right)}}{{b\exp \left( {\frac{{{h^2}}}{{\sigma _1^2\left( {\rho + 1} \right)}}} \right) \times {{\left( {1 - {\rho ^2}} \right)}^{1/2}}\left( {2 - \nu } \right)}}} \right]. \end{array} $ | (10) |
为方便后续研究计算,定义常值刚度[22]为
| $ \begin{array}{l} {K_0} = \\ \frac{{0.116GL\rho \sigma \times \exp \left( { - \frac{{{u^2}}}{{4{\sigma ^2}}}} \right) \times \left( {1 - \exp \left( {\frac{{r_{\max }^2}}{{4{\sigma ^2}}} - \frac{{{r_{\max }}u}}{{2{\sigma ^2}}}} \right)} \right)}}{{b\exp \left( {\frac{{{h^2}}}{{\sigma _1^2\left( {\rho + 1} \right)}}} \right) \times {{\left( {1 - {\rho ^2}} \right)}^{1/2}}\left( {2 - \nu } \right)}}. \end{array} $ | (11) |
由式(11)可见,常值刚度仅与材料本身的性质和统计参数有关,而与外界载荷无关.其含义是当外界切向力为零时,接触面的切向接触刚度.
2 概率模型的数值计算及结果分析 2.1 外因对切向刚度概率模型影响分析运用分形预估模型来验证概率模型的正确性.根据分形理论[14],考虑接触点的面积分布情况来计算接触面的总切向接触刚度,接触点面积分布函数为
| $ n\left( a \right) = \frac{D}{2}\frac{{a_{\max }^{0.5D}}}{{{a^{0.5D + 1}}}} \times {\psi ^{1 - 0.5D}}. $ | (12) |
式中:D为分形维数;ψ为扩展系数;amax为最大接触面积;a为接触面积;所以,接触面切向接触刚度的分形预估模型[24]为
| $ K = \int_{{a_{\rm{c}}}}^{{a_{\max }}} {{k_t}n\left( a \right){\rm{d}}a} . $ | (13) |
式中:ac为临界接触面积;可取值[14]为
| $ {a_{\rm{c}}} = 0.01{a_{\max }}. $ | (14) |
将式(1)和(12)代入式(13),所以得到切向接触刚度为
| $ \begin{array}{*{20}{c}} {K = {{\left( {1 - \frac{{{F_{\rm{T}}}}}{{f{F_{\rm{N}}}}}} \right)}^{1/3}} \times \frac{{4.64DG{\psi ^{1 - 0.5D}}}}{{\left( {D - 1} \right)\left( {\nu - 2} \right)}} \times }\\ {a_{\max }^{D/2}\left( {a_{\max }^{\left( {1 - D} \right)/2} - a_{\rm{c}}^{\left( {1 - D} \right)/2}} \right).} \end{array} $ | (15) |
对模型的验证以控制变量的方式进行.分别取切向力,法向力和摩擦系数为单一变量,其余2项为常量进行分析,变量与常量数值设置如表 1所示.两摩擦材料均是铸铁,其弹性模量为E=100 GPa,加工方式为铣削[26],此时铸铁的表面粗糙度为2.47 μm,概率模型测量参数与材料属性设置如表 2所示.分形模型测量参数与材料属性设置如表 3所示
| 表 1 单一变量及常量数值 Table 1 Single variable and constant value |
| 表 2 概率模型测量参数与材料属性 Table 2 Probability model measurement parameters and material properties |
| 表 3 分形模型测量参数与材料属性 Table 3 Fractal model measurement parameter and material properties |
按照表 1和2的参量设置,分别绘出切向接触刚度与摩擦系数f、法向力FN和切向力FT的关系曲线,如图 1~3所示.
|
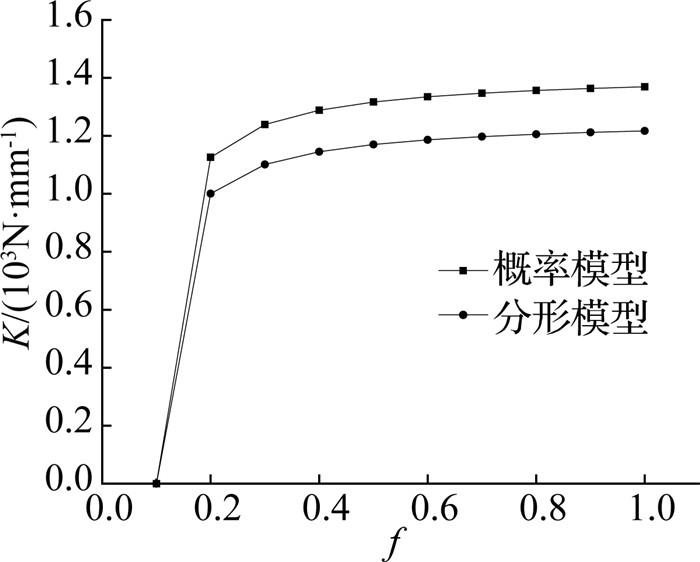
图 1 接触面切向刚度与摩擦系数关系曲线 Fig. 1 Curve of tangent stiffness and friction coefficient of contact surface |
|
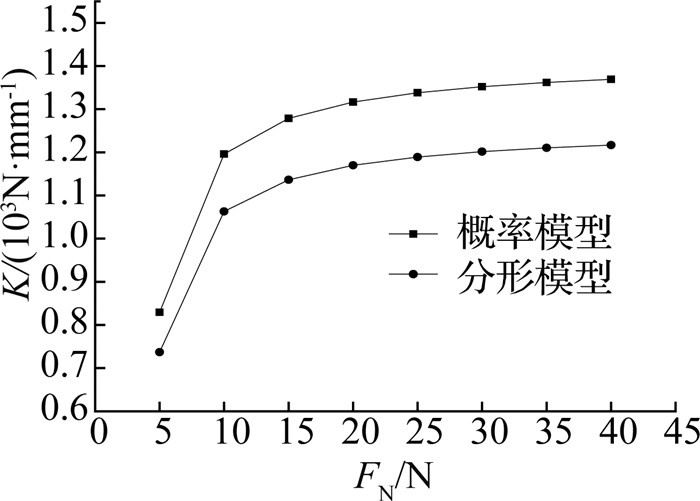
图 2 接触面切向刚度与法向载荷关系曲线 Fig. 2 Curve of tangential stiffness and normal load of contact surface |
|
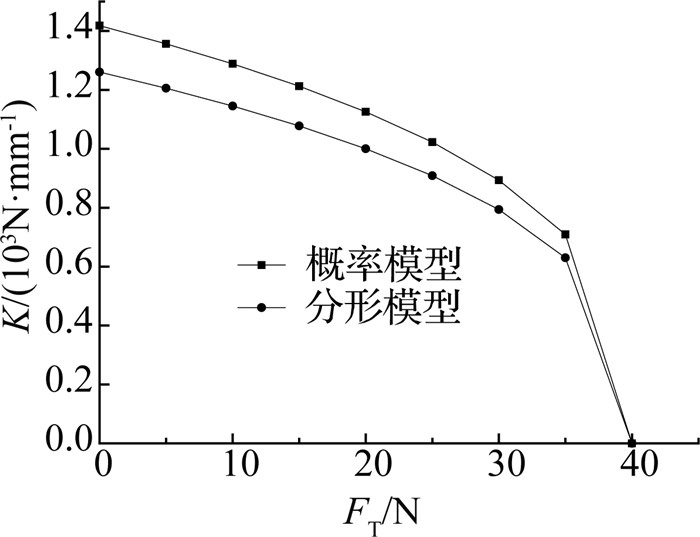
图 3 接触面切向刚度与切向载荷关系曲线 Fig. 3 Curve of tangential stiffness and normal load of contact surface |
图 1表明:接触面的切向刚度K与摩擦系数f呈正相关但非线性,在摩擦系数较小时,随着摩擦系数的增大,切向刚度迅速增大;然而,当摩擦系数较大时,静摩擦系数的增大对切向刚度的影响逐渐变小,切向刚度增长缓慢.静摩擦系数越大,则可承受的切向力就越大,表面微凸体抵抗变形的能力就越强,因而会使得切向接触刚度增大.
图 2表明:法向载荷FN的增加有利于增加接触面切向刚度K,二者成正相关;这与接触时间对切向接触刚度的影响原理相同[27],法向载荷的增大使上下接触面的微凸体接触更加紧密,一定程度上增大了静摩擦系数,因此使得切向接触刚度增大.然而,图 3却反映出切向载荷FT的作用与法向载荷相反,切向载荷越大,使得切向接触刚度K越小,当切向载荷增加到一定程度时会使切向接触刚度缩减至0.这可以用预位移原理[27]来解释,所谓的预位移即微凸体的变形,根据预位移原理,切向载荷越大,预位移越大,接触面切向刚度越小.
从图 1、2、3可知,分形模型与概率模型求出的切向刚度与各个变量之间的关系图的趋势都相同,只是对应刚度值大小上稍有差异,这在理论上验证了概率模型正确性.实验验证方面,发现上述切向接触刚度随载荷的变化趋势与实验结果[26]中所对应的变化趋势相同,进一步验证了所建立概率模型正确性.
2.2 统计参量对切向接触刚度影响分析 2.2.1 切向接触刚度与测量高度的关系将测量高度h设为变量,其余参量维持表 1中概率模型的设置,并且法向力FN=20 N, 切向力FT=2 N, 摩擦系数f=0.5.此时的切向接触刚度与测量高度h的关系曲线如图 4所示.
|
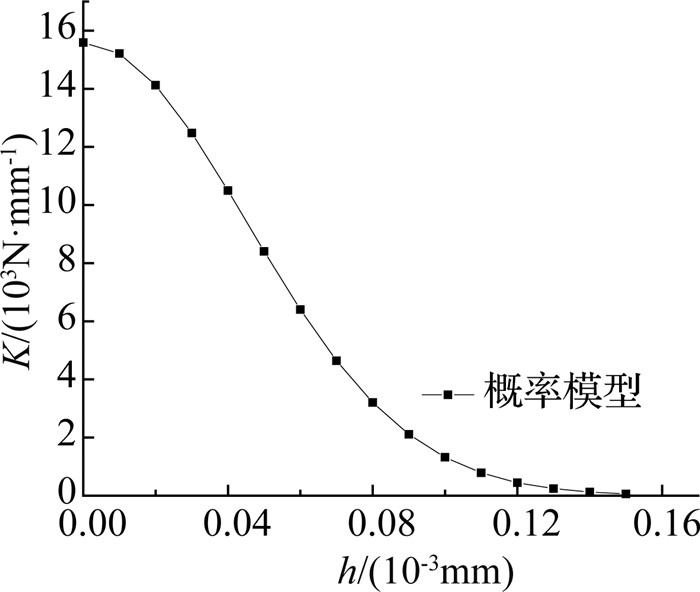
图 4 切向接触刚度与测量高度关系曲线 Fig. 4 Relationship between tangential contact stiffness and measured height |
图 4表明:测量高度h的增加会造成切向接触刚度的非线性降低,且在测量高度较小时,切向接触刚度降低幅度尤为明显.这是因为随着测量高度的增加,能够检测到的微凸体个数越来越少,总体切向接触刚度逐渐变小,在文中所应用的工况中,测量高度高于0.000 16 mm时,微凸体已经很难再被检测到,因此切向接触刚度趋近于0.
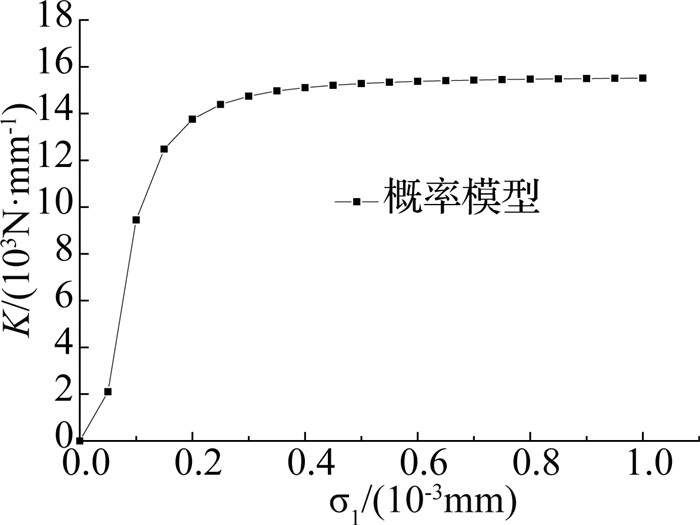
2.2.2 切向接触刚度与微凸体高度标准差的关系切向接触刚度与微凸体高度标准差关系曲线如图 5所示,从图 5中可以看出,铸铁的切向接触刚度K整体与微凸体高度标准差σ1成正相关.σ1=0.003 mm是一个分界,当0≤σ1≤0.003 mm时,随着σ1的增加,K迅速增加;当σ1≥0.003 mm时,K增加缓慢,几乎保持不变.这说明在工程中,微凸体高度的差别越小,对切向接触刚度大小的影响越大,微凸体高度差别很大时,几乎不能对切向接触刚度造成太大影响.
|
图 5 切向接触刚度与微凸体高度标准差关系曲线 Fig. 5 Relationship between tangential contact stiffness and height standard deviation of asperity |
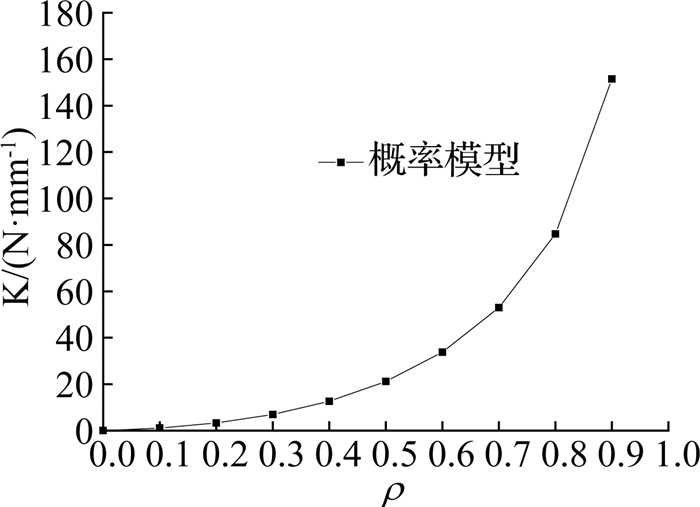
切向接触刚度与自相关系数关系曲线如图 6所示,图 6表明:切向接触刚度K与自相关系数ρ成正相关.自相关系数的大小取决于实际测量参数.测量间距s越大,Markov过程距离b越小,则自相关系数ρ越小,可测量到的微凸体越少,切向接触刚度越小.
|
图 6 切向接触刚度与自相关系数关系曲线 Fig. 6 Relationship between tangential contact stiffness and autocorrelation coefficient |
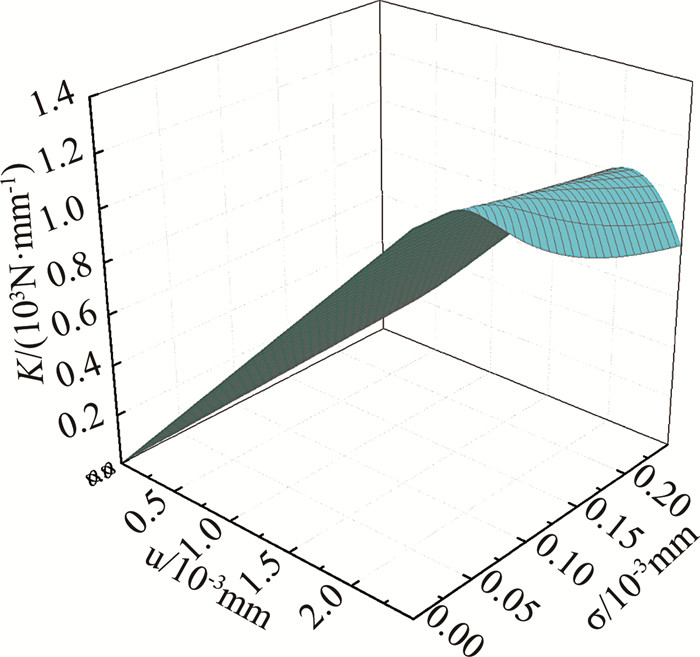
微凸体接触半径r~φ(u, σ2),即将期望u和标准差σ看成2个变量,最大接触半径rmax=2.605×10-3 mm,其余不发生改变,此时切向接触刚度K与微凸体接触半径的关系如图 7所示,当微凸体接触半径期望值较大和标准差值较小时,即表面微凸体接触半径大小相似性高时,切向接触刚度较大,且变化迅速;当接触半径标准差较大时,各个微凸体之间差别明显,切向接触刚度小.这与分形理论中的分形维数D对切向接触刚度的影响类似.
|
图 7 切向接触刚度与微凸体接触半径关系曲线图 Fig. 7 Relationship between tangential contact stiffness and asperity radius |
(1) 在经典Hertz理论和GW模型的基础上,考虑摩擦因素的影响,建立接触面切向刚度的概率模型并与切向接触刚度的分形模型进行了对比,发现二者得到的结果相似,且概率模型能够通过表面粗糙度而直接反映出微凸体的大小,更加直观,为接触面切向刚度的研究提供了新思路.
(2) 切向接触刚度概率模型反映出接触面的切向接触刚度与摩擦系数、法向载荷和切向载荷息息相关.切向刚度随着摩擦系数的增大而增大,但只在一定范围内增大明显;接触面的切向刚度与法向载荷呈正相关,法向载荷的增大有利于切向刚度的增大;接触面的切向刚度与切向载荷呈负相关,切向载荷增大到一定程度会使得切向刚度为零.
(3) 定义了常值刚度,然后由公式知常值刚度只和接触材料本身的性质和统计参量有关,而与外界载荷无关.同时利用控制变量法,研究了概率模型中统计参量对粗糙表面切向接触刚度的影响,为寻找最佳统计参量提供了依据.
| [1] |
雷海东, 段芳莉, 仇和兵, 等. 纳米级粗糙表面接触行为的分子动力学模拟[J]. 中国表面工程, 2010, 23(5): 27-34. LEI Hai-dong, DUAN Fang-li, QIU He-bing, et al. Molecular dynamics simulation of contact mechanics between nanoscale rough surfaces[J]. China Surface Engineering, 2010, 23(5): 27-34. |
| [2] |
BEHESHTI A, KHONSARI M M. Asperity micro-contact models as applied to the deformation of rough line contact[J]. Tribology International, 2012, 52(3): 61-74. |
| [3] |
李万钟, 徐颖强, 孙戬, 等. 粗糙表面弹塑性加卸载多级接触模型[J]. 中国表面工程, 2015, 28(4): 39-46. LI Wan-zhong, XU Ying-qiang, SUN Jian, et al. Multilevel contact model of elastic-plastic loading and unloading on rough surfaces[J]. China Surface Engineering, 2015, 28(4): 39-46. DOI:10.11933/j.issn.1007-9289.2015.04.005 |
| [4] |
IBRAHIM R A, PETTIT C L. Uncertainties and dynamic problems of bolted joints and other fasteners[J]. Journal of Sound and Vibration, 2005, 279(3/5): 857-936. |
| [5] |
李辉光, 刘恒, 虞烈. 考虑接触刚度的燃气轮机拉杆转子动力特性研究[J]. 振动与冲击, 2012, 31(7): 4-8. LI Hui-guang, LIU Heng, YU Lie. Dynamic characteristics of a rod fastening rotor for gas turbine considering contact stiffness[J]. Journal of Vibration and Shock, 2012, 31(7): 4-8. |
| [6] |
MAO K M, LI B, WU J, et al. Stiffness influential factors-based dynamic modeling and its parameter identification method of fixed joints in machine tools[J]. International Journal of Machine Tools and Manufacture, 2010, 50(2): 156-164. DOI:10.1016/j.ijmachtools.2009.10.017 |
| [7] |
余同希, [澳]卢国兴, 著. 华云龙, 译. 材料与结构的能量吸收: 耐撞性·包装·安全防护[M]. 北京: 化学工业出版社, 2005: 137-145.
|
| [8] |
GREENWOOD J A, WILLIAMSON J B P. Contact of nominally flat surfaces[J]. Proceedings of the Royal Society of London, 1966, 295(1442): 300-319. DOI:10.1098/rspa.1966.0242 |
| [9] |
GREENWOOD J A, TRIPP J H. The elastic contact of rough spheres[J]. Journal of Applied Mechanics, 1967, 34(1): 153-159. DOI:10.1115/1.3607616 |
| [10] |
WHITEHOUSE D J, ARCHARD J F. The properties of random surfaces of significance in their contact[J]. Proceedings of the Royal Society of London Series A, 1971, 316(1524): 97-121. |
| [11] |
MAJUMDAR A, BHUSHAN B. Fractal model of elastic-plastic contact between rough surfaces[J]. Journal of Tribology, 1991, 113(1): 1-11. DOI:10.1115/1.2920588 |
| [12] |
张学良, 温淑花, 徐格宁, 等. 结合部切向接触刚度分形模型研究[J]. 应用力学学报, 2003, 20(1): 70-72. ZHANG Xue-liang, WEN Shu-hua, XU Ge-ning, et al. Fractal model of the tangential contact stiffness of machined surfaces in contact[J]. Chinese Journal of Applied Mechanics, 2003, 20(1): 70-72. |
| [13] |
王南山, 张学良, 兰国生, 等. 临界接触参数连续的粗糙表面法向接触刚度弹塑性分形模型[J]. 振动与冲击, 2014, 33(9): 71-77. WANG Nan-shan, ZHANG Xue-liang, LAN Guo-sheng, et al. Elastoplastic fractal model for normal contact stiffness of rough surfaces with continuous critical contact parameters[J]. Journal of Vibration and Shock, 2014, 33(9): 72-77. |
| [14] |
李小彭, 鞠行, 赵光辉, 等. 考虑摩擦因素的结合面切向接触刚度分形预估模型及其仿真分析[J]. 摩擦学学报, 2013, 33(5): 463-468. LI Xiao-peng, JU Xing, ZHAO Guang-hui, et al. Fractal prediction model for tangential contact stiffness of joint surface considering friction factors and its simulation analysis[J]. Tribology, 2013, 33(5): 463-468. |
| [15] |
李小彭, 王伟, 赵米鹊, 等. 考虑摩擦因素影响的结合面切向接触阻尼分形预估模型及其仿真[J]. 机械工程学报, 2012, 48(23): 46-50. LI Xiao-peng, WANG Wei, ZHAO Mi-que, et al. Fractal prediction model for tangential contact damping of joint surface considering friction factors and its simulation[J]. Journal of Mechanical Engineering, 2012, 48(23): 46-50. |
| [16] |
李玲, 蔡力钢, 蔡安江, 等. 固定结合面切向接触刚度通用性建模方法[J]. 计算机集成制造系统, 2015, 21(8): 2108-2115. LI Ling, CAI Li-gang, CAI An-jiang, et al. Universal modeling method for tangential stiffness of fixed joint interfaces[J]. Computer Integrated Manufacturing Systems, 2015, 21(8): 2108-2115. |
| [17] |
杨红平, 傅卫平, 王雯, 等. 基于分形几何与接触力学理论的结合面法向接触刚度计算模型[J]. 机械工程学报, 2013, 49(1). YANG Hong-ping, FU Wei-ping, WANG Wen, et al. Calculation model of the normal contact stiffness of joints based on the fractal geometry and contact theory[J]. Journal of Mechanical Engineering, 2013, 49(1). |
| [18] |
刘鹏, 陈奇, 樊浩, 等. 考虑摩擦的球面切向接触刚度分形模型研究[J]. 中国机械工程, 2016, 27(20): 2773-2778. LIU Peng, CHEN Qi, FAN Hao, et al. Research on fractal model of TCS between spherical surfaces considering friction factors[J]. China Mechanical Engineering, 2016, 27(20): 2773-2778. DOI:10.3969/j.issn.1004-132X.2016.20.014 |
| [19] |
POLYCARPOU A, ETSION I. Analytical approximations in modeling contacting rough surfaces[J]. Journal of Tribology, 1999, 121(1): 234-239. |
| [20] |
尤晋闽, 陈天宁. 结合面静态接触参数的统计模型研究[J]. 振动与冲击, 2010, 29(11): 47-50. YOU Jin-min, CHEN Tian-ning. Statistical model for static contact parameters of joint surfaces[J]. Journal of Vibration and Shock, 2010, 29(11): 47-50. DOI:10.3969/j.issn.1000-3835.2010.11.011 |
| [21] |
WU J J. The properties of asperities of real surfaces[J]. Journal of Tribology, 2001, 123(4): 872-883. DOI:10.1115/1.1353179 |
| [22] |
师俊平, 朱红, 曹小杉, 等. 结合面切向接触刚度的概率统计模型[J]. 工程力学, 2010, 31(6): 226-231. SHI Jun-ping, ZHU Hong, CAO Xiao-shan, et al. Profitability and statistic model of tangent contact stiffness of joint surfaces[J]. Engineering Mechanics, 2010, 31(6): 226-231. |
| [23] |
张学良. 机械接触面动态特性及应用[M]. 北京: 中国科学技术出版社, 2002, 35-38.
|
| [24] |
党会鸿. 机械结合面接触刚度研究[D]. 大连: 大连理工大学, 2015. DANG Hui-hong. The research on contact stiffness of joint surface[D]. Dalian: Dalian University of Technology, 2015. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2823069 |
| [25] |
田红亮, 陈从平, 方子帆, 等. 应用改进分形几何理论的结合部切向刚度模型[J]. 西安交通大学学报, 2014, 48(7): 46-51. TIAN Hong-liang, CHEN Cong-ping, FANG Zi-fan, et al. Tangential stiffness model for joint interface adopting the revised fractal geometric theory[J]. Journal of Xi'an Jiaotong University, 2014, 48(7): 46-51. DOI:10.7652/xjtuxb201407009 |
| [26] |
JIANG Shuyun, ZHENG Yunjian, ZHU Hua. A contact stiffness model of machined plane joint based on fractal theory[J]. Journal of Tribology, 2010, 132(0114011): 1-7. |
| [27] |
温诗铸, 黄平. 摩擦学原理[M]. 北京: 清华大学出版社, 2008, 271-274.
|



