2. 中南大学 机电工程学院, 湖南 长沙 410083;
3. 中国铁建重工集团有限公司, 湖南 长沙 410100
2. College of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China;
3. China Railway Construction Heavy Industry Co. Ltd., Changsha 410083, China
全断面隧道掘进机(tunnel boring machine, TBM)是硬岩隧道施工中的关键掘进装备,在铁路、公路、水利、市政等隧道施工中发挥了重要的作用[1-2].由主梁、鞍架、撑靴等部件组成的支撑推进系统是TBM的骨架.掘进过程中,刀盘承受巨大的波动载荷[3],并通过主轴承、主驱动等传递至主梁、鞍架、撑靴等,引起支撑推进系统的整机振动.一方面,剧烈的整机振动会造成包括支撑推进系统关键部件的动应力过大和液压设备的不正常运转,由此造成零部件失效和停机事故,影响施工进度[4].另一方面,振动幅度过大会导致TBM在支撑时易出现被撑洞壁岩石失效,撑靴打滑的现象,直接影响掘进过程的稳定性与安全性.如何保证TBM撑靴的有效支撑是TBM工程的关键之一,也是目前业内研究的热点.
目前在TBM载荷和振动特性研究方面,国内外学者的研究主要集中刀盘刀具和主驱动.Festa等[5]研究了刀盘推力和扭矩的影响因素,并建立了相应的刀盘推力扭矩及倾覆力矩等外载的计算公式.凌静秀等[6]建立了TBM刀盘系统的平移-扭转-倾覆多自由度耦合动力学模型,研究了刀盘系统参数对固有频率的影响及敏感度问题.Sun等[7]利用广义分层建模方法建立TBM刀盘驱动系统的完全动态模型,探究了耦合参数对刀盘驱动系统动态响应的影响规律.在TBM支撑推进系统动力学传递和响应方面,国内外学者也做了一些研究.Hassanpour等[8]研究了变地质条件下TBM推进系统的动力学特性,得到了刀盘转速、推进力和推进速度之间的关系.谢启江等[9]基于并联机构理论研究TBM推进系统的力传递特性,讨论了与撑靴岩石接触界面刚度与刀盘载荷波动之间的耦合关系.余海东等[10]在考虑岩石隧道表面粗糙度,岩石力学特性、撑靴数量以及复合岩层等工况下,分析了不同参数下撑靴载荷与法向接触刚度之间的关系.
目前国内外学者对TBM支撑推进系统的动力学研究集中在力学传递和机构刚度变化上.本文以吉林引松工程用TBM为研究对象,利用动力学仿真软件建立仿真模型,研究了支撑推进系统的振动特性,并对TBM工程现场进行测试,对比仿真结果与工程测试结果,确定TBM支撑推进系统的动态特性.
1 动力学模型的建立 1.1 实体建模将TBM系统适当简化,并将其与建立的岩石模型14(为方便表示其他零部件,仅显示岩石的剖面图)装配,如图 1所示,图中x方向代表水平方向,y方向代表竖直方向,z方向代表掘进方向.TBM系统由刀盘系统和推进支撑系统组成.其中刀盘系统包括刀盘1;主轴承2;主驱动3;护盾4(下护盾未显示); 支撑推进系统包括主梁一5,推进液压缸6,撑靴7,扭矩液压缸8,撑靴液压缸9,鞍架10,主梁二11,后支撑12,主梁三13.其中刀盘直径为7.93 m,主梁一长7.45 m,主梁二长8 m.TBM系统各部件主要为钢结构件,其密度为7 850 kg/m3,杨氏弹性模量为210 GPa,泊松比为0.29.

|
图 1 TBM系统岩石相互作用模型 Fig. 1 TBM system-rock assembly model |
按照滚刀安装半径的不同,将刀盘上的滚刀分为中心滚刀群(1~8号刀)、正面滚刀群(9~40号滚刀)以及边缘滚刀群(41~51号滚刀),使用有限元分析软件LS-DYNA分别对中心滚刀、正滚刀和边滚刀切削岩体的过程进行仿真,岩石材料参数选用吉林引松工程中实测岩石参数,如表 1所示,ρ为密度,E为弹性模量,R为单轴抗压强度,Rm为抗拉强度.
| 表 1 岩石主要物理力学参数 Table 1 The main physical and mechanical parameters of rock |
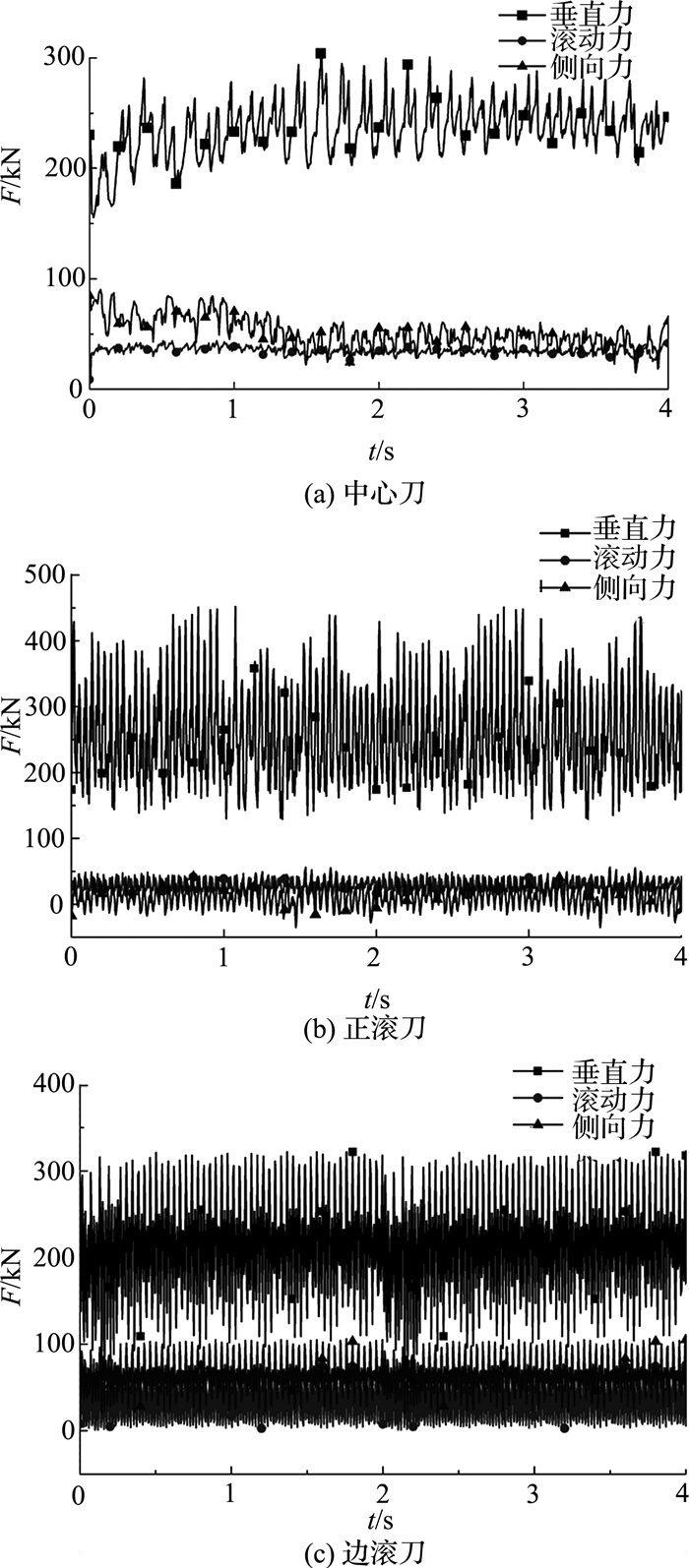
滚刀的切入深度统一为8 mm,回转速度为5 r/min,切削时间为4 s,仿真结果如图 2所示,图中F为滚刀力,t为时间.得到3种不同区域滚刀的三向力变化曲线,然后取3个循环的三向载荷数据,即12 s的数据导入到仿真软件中.
|
图 2 滚刀三向载荷曲线 Fig. 2 Curves of disc cutter three-dimension load |
如表 2所示,为模型添加运动副,同时为刀盘和主轴承间的转动副添加驱动,设置刀盘转速为5 r/min.
| 表 2 模型运动副列表 Table 2 List of model joints |
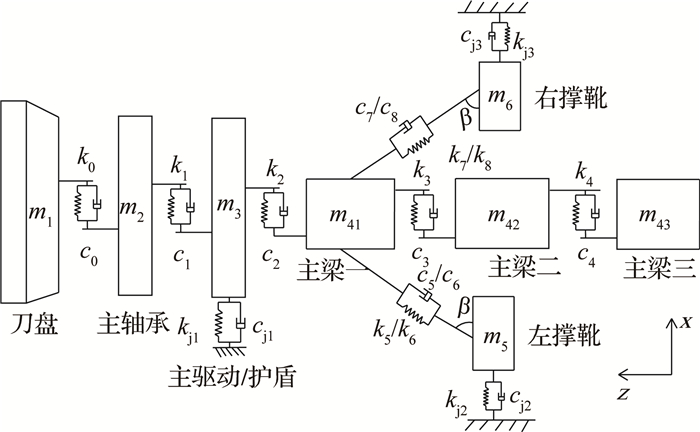
如图 3和4所示,分别为主机等效弹簧阻尼系统整体示意图和鞍架-撑靴等效弹簧阻尼系统示意图.图中k0、k1、k2、k3、k4分别为刀盘、主轴承、主驱动(包括护盾)、主梁一、主梁二的刚度,k5、k6、k7、k8分别为4个推进油缸的刚度,k9、k10分别为4个撑靴油缸的刚度,k11、k12、k13、k14分别为4个扭矩油缸的刚度,c0、c1、c2、c3、c4分别为刀盘、主轴承、主驱动(包括护盾)、主梁一、主梁二的阻尼,c5、c6、c7、c8分别为4个推进油缸的阻尼,c9、c10分别为2个撑靴油缸的阻尼,c11、c12、c13、c14分别为4个扭矩油缸的阻尼.由于刀盘和主轴承之间已经添加了转动副,无法再添加柔性连接力,这时需要将刀盘的等效刚度k0、等效阻尼c0与主轴承的等效刚度k1、等效阻尼c1串联添加到主轴承和主驱动之间的柔性连接力中.
|
图 3 主机等效弹簧阻尼系统整体示意图 Fig. 3 Overall diagram of host equivalent spring damping system |

|
图 4 鞍架-撑靴等效弹簧阻尼系统示意图 Fig. 4 Diagram of saddle-gripper equivalent spring damping system |
对刀盘、主驱动、主梁等大型复杂结构非标准件采用有限元的方法计算等效刚度和阻尼.以刀盘轴向等效刚度与阻尼的计算为例,对刀盘进行静力学受载模拟分析:首先对与法兰连接的主轴承内圈后表面实施全约,然后在刀盘上每把刀具上施加轴向推力.最后在分析结果中提取刀盘在掘进方向的最大变形量,采用胡克定律求得刀盘的轴向等效刚度,而刀盘轴向方向的等效阻尼参数,可由公式计算:
| $ c=2\xi \sqrt{{{m}_{\text{e}}}{{k}_{\text{e}}}}. $ | (1) |
式中:c为结构件的阻尼,ξ为阻尼比,钢结构在弹性阶段一般为0.02~0.05,取为0.02;me、ke分别为部件的质量和等效刚度.
主轴承刚度主要为滚子与内外圈接触区的接触刚度,接触区滚子的弹性变形量δ可按照经验公式[11-12]计算,接触载荷对弹性变形量δ求导,然后再乘以滚子数量即可得到主轴承刚度:
| $ \left. \begin{align} &\delta =3.84\times {{10}^{-6}}\frac{{{F}_{\text{Q}}}^{0.9}}{{{L}_{\text{we}}}^{0.8}}, \\ &{{k}_{1}}=Z\frac{\text{d}{{F}_{\text{Q}}}}{\text{d}\delta }=2.894\times {{10}^{5}}Z{{L}_{\text{we}}}0.8{{F}_{\text{Q}}}^{0.1}, \\ &{{F}_{\text{Q}}}=\frac{{{F}_{1}}}{Z}. \\ \end{align} \right\} $ | (2) |
式中:δ为滚子的弹性变形量,Lwe为滚子的有效长度,单位为mm,FQ为接触载荷,Z为滚子数量,F1为主轴承所受载荷.
由式(2)可见,主轴承刚度随所受载荷变化,以主轴承轴向刚度计算为例,当主轴承轴向载荷从1×104 kN变化到2×104 kN时,主轴承轴向刚度从2.73×109 N/m变化到2.93×109 N/m,变化不大,可认为主轴承轴向刚度为定值,取为2.83×109 N/m.主轴承质量为2.04×104 kg,将刚度和质量代入式(1)中,求得主轴承轴向阻尼为1.52×105 N·s/m.
在TBM掘进过程中,液压缸(包括4个推进液压缸,2个撑靴液压缸和4个扭矩液压缸)的刚度主要来自于液压油的刚度.而液压油的等效刚度随活塞的轴向位移的变化而变化,计算式[13-14]如下:
| $ k\left( x \right)={{\beta }_{\text{e}}}{{A}_{1}}\left[\frac{a}{{{L}_{1}}+x}+\frac{b{{A}_{2}}}{{{A}_{1}}\left( {{L}_{2}}+L-x \right)\text{ }} \right]. $ | (3) |
式中:βe为液压油体积弹性模量,取1.4 GPa,L为液压缸有效行程,L1为进油腔当量初位移,L2为回油腔当量终位移;A1为无杆腔横截面积,A2为有杆腔横截面积,x为活塞的轴向位移,a,b为工况选择参数,根据相关文献[15]液压缸黏性阻尼系数c取为1.5×105 N·s/m.
如图 3所示,护盾与岩石,撑靴与岩石还分别建立了等效接触碰撞模型,其刚度根据Hertz接触理论计算:
| $ \left. \begin{align} &{{k}_{j}}=\frac{4}{3\left( {{h}_{1}}+{{h}_{2}} \right)}\left[\frac{{{R}_{1}}{{R}_{2}}}{~{{R}_{1}}+{{R}_{2}}} \right]^{{1/2}}; \\ &{{h}_{i}}=\text{ }\frac{1-{{\sigma }_{i}}^{2}}{{{E}_{i}}}, \text{ }i=1, 2. \\ \end{align} \right\} $ | (4) |
式中:kj为碰撞接触刚度,h1、h2无特殊含义的连接前后2个公式,R1、R2分别为两碰撞物体碰撞处的半径,σi为材料的泊松比,Ei为材料的杨氏模量.阻尼值取刚度值大小的0.5%.
2 仿真结果分析 2.1 TBM支撑推进系统振动响应分析经过仿真分析,得到TBM支撑推进系统各部件的振动加速度,主要包括主梁一、主梁二、鞍架、撑靴,选取其中一个部件主梁二进行时域和频域分析.如图 5所示为主梁二振动加速度时域图.

|
图 5 主梁二振动加速度 Fig. 5 Vibration acceleration of the second main beam |
由图 5(a)知主梁二x方向振动加速度ax2最大数值达到8.30 m/s2, 主要变化范围为-4~4 m/s2,由图 5(b)可知主梁二y方向振动加速度ay2最大数值达到7.88 m/s2,主要变化范围为-4~4 m/s2,由图 5(c)可知主梁二z方向振动加速度az2最大数值达到11.80 m/s2,主要变化范围为-6~6 m/s2.
如图 6所示为主梁二振动加速度频谱图,由6(a)可知,主梁二x方向振动频率fx主要分布在20~30 Hz和46~56 Hz这2个范围内,x方向振动峰值出现在24.5 Hz,此处振动幅值amx达到0.67 m/s2.由图 6(b)可知,主梁二y方向振动频率fy主要分布范围与x方向相同,但y方向振动峰值出现在51 Hz,此处振动幅值amy达到1.00 m/s2,同时在24.4 Hz处的振动幅值也很大,达到了0.97 m/s2.由图 6(c)可知,主梁二z方向振动频率主要分布范围与x、y方向相同,z方向的振动峰值fz出现在24.5 Hz处,而且此处的振动幅值amz远远大于x、y方向的振动峰值,达到了3.88 m/s2.综上,主梁二的振动主要集中在低频,这一规律在支撑推进系统其他部件也同样存在.

|
图 6 主梁二振动加速度频谱图 Fig. 6 Frequency spectrum of second main beam's vibration acceleration |
如图 7所示为TBM支撑推进系统各部件振动加速度有效值aRMS折线图,折线图的横坐标是按照各个部件质心距离刀盘质心的距离依次排列的.比较部件不同方向的振动加速度有效值可以发现,鞍架、主梁二、撑靴都是z方向的振动加速度有效值最大,主梁一振动加速度有效值则是x方向最大,但由图 7可知,主梁一z方向比x方向加速度有效值也仅小10.5%.由此可见,TBM支撑推进系统振动加速度主要集中在z掘进方向.比较不同部件同一方向的振动加速度有效值可以发现,在x方向和z方向上,加速度有效值由大到小排列顺序为主梁一>鞍架>主梁二>撑靴,即部件距离刀盘质心越远,振动加速度有效值越小,在y方向,振动加速度有效值随部件距离刀盘的距离先缓慢增大后急剧减小.综合比较不同部件3个方向的加速度有效值可以发现,加速度有效值由大到小排列顺序为主梁一>鞍架>主梁二>撑靴,其中撑靴的加速度有效值远远小于其他3个部件.

|
图 7 推进支撑系统各部件振动加速度有效值 Fig. 7 Vibration accelerations RMS of supporting-thrusting system components |
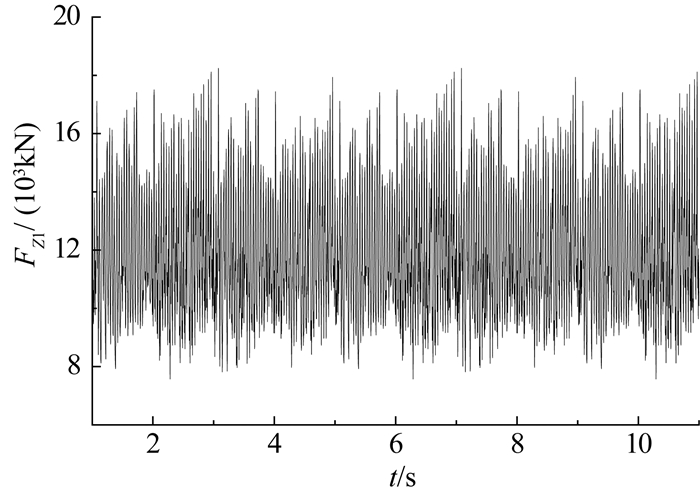
由2.2可知TBM支撑推进系统振动主要集中z方向,而载荷是引起振动的直接原因,因此需要对支撑推进系统z掘进方向的载荷进行分析,如图 8、9所示,Fz1, Fz2分别为刀盘z方向输入载荷和主梁z方向输入载荷.由图 9可知刀盘z方向输入载荷变化范围是7 00 kN到18 300 kN,均值为11 891 kN.由图 9可知主梁一输入载荷变化趋势与刀盘输入载荷变化趋势基本相同,都呈现出一定的阶跃性,主梁一z方向输入载荷变化范围是4 700 kN到9 200 kN,均值为6 814 kN,掘进方向的载荷从刀盘传递到主梁一变化幅度减小了58.3%,均值减小了42.7%,这是因为刀盘的输入载荷和能量有一部分通过护盾传递到了围岩.主梁二z方向输入载荷变化范围主要在-720 kN到195 kN,均值为-223 kN,主梁二z方向输入载荷主要为负值,即载荷方向与主梁一相反,且变化幅度很小,这是因为连接主梁一和撑靴的推进液压缸已经完全承载了来自主梁一掘进方向的载荷,而主梁一对主梁二的作用力则用来克服鞍架对主梁二的摩擦力.
|
图 8 刀盘掘进方向输入载荷 Fig. 8 Input load of cutterhead in tunneling direction |

|
图 9 主梁掘进方向输入载荷 Fig. 9 Input loads of main beam in tunneling direction |
为了验证仿真结果,对吉林引松工程的TBM支撑推进系统进行了现场振动测试.测试期间岩石以花岗岩为主,具体物理力学参数见表 1,TBM推力变化范围为9 300~13 800 kN,与图 9中仿真得到的刀盘输入载荷变化范围基本一致.振动测试系统使用型号为INV9821的ICP集成压电式三向加速度传感器,采用型号为INV3060A的信号采集仪.采样频率为400 Hz,每次采样时间取12 s,主要对主梁二、撑靴等部件进行测试,如图 10所示为现场测试传感器布置图.

|
图 10 传感器布置图 Fig. 10 Diagram of sensor placement |
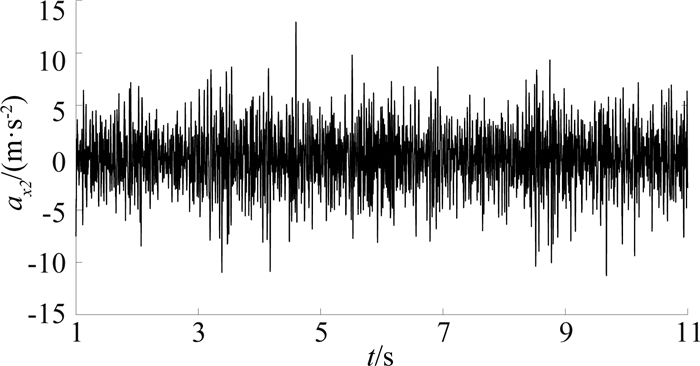
按照上述方案进行测试,主梁二x方向振动加速度值ax2如图 11所示,为了便于对比,和仿真一样只取1~11 s的数据,可见主梁二x方向振动加速度主要变化范围为-4~4 m/s2,这与仿真值是相一致的,测试结果最大值达到了12.9 m/s2,大于仿真的加速度最大值,这是因为在实际工程中岩石地质不稳定,导致几个时间点的振动测试值比较大.在主梁二其他方向和撑靴的测试结果中也出现了加速度变化范围一致,但测试的加速度最大值大于仿真值的现象.
|
图 11 主梁二x方向振动加速度测试值 Fig. 11 X-direction acceleration test value of second main beam |
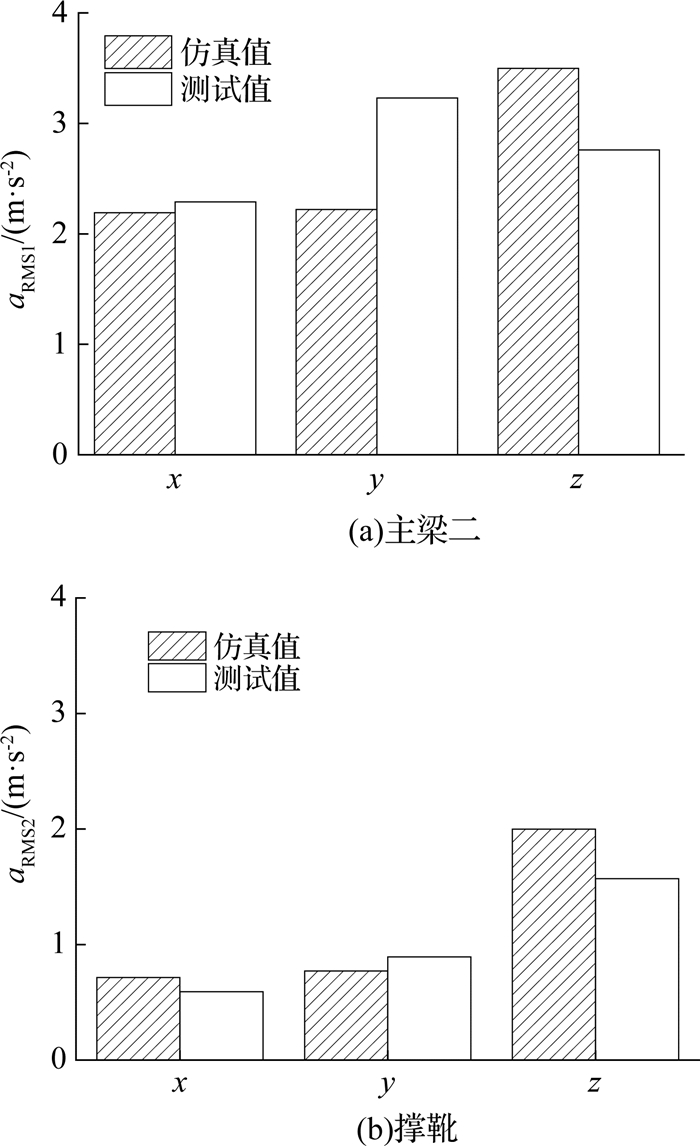
如图 12所示为主梁二和撑靴振动加速度有效值的仿真和测试对比图,图中aRMS1, aRMS2分别为主梁二和撑靴振动加速度,可见仿真值和测试值的相对误差基本都在30%以内,只有主梁二y方向的相对误差达到了31.2%,这个误差的原因主要来源于测试方法,对主梁二进行测试时,为了测试方便,测点布置在了主梁二上表面的耳板,而仿真时得到的主梁二的振动加速度是主梁二质心处的加速度.观察测试值,对比不同部件加速度可以发现,撑靴3个方向的加速度有效值都远小于主梁二,这和仿真也是相一致的.综上所述,工程测试在一定程度上验证了仿真结果.
|
图 12 仿真值与测试值对比 Fig. 12 Comparison between simulation and test value |
以吉林引松工程用TBM为对象,基于多体动力学仿真软件建立了TBM的动力学仿真模型,研究支撑推进系统各部件的振动加速度和支撑推进系统载荷传递规律,并对吉林引松工程的TBM支撑推进系统进行了现场测试,研究结果如下:
(1) 主梁二在z掘进方向的加速度最大,主梁二z方向振动加速度最大数值达到11.80 m/s2,主要变化范围为-6~6 m/s2.
(2) TBM支撑推进系统的振动以低频为主,其中主梁二的振动频率主要集中在20~30 Hz和46~56 Hz这2个范围内,z方向的振动峰值频率处的振动幅值远大于x、y方向.
(3) TBM支撑推进系统振动加速度主要集中在z掘进方向,且部件距离刀盘质心越远,振动加速度有效值越小,其中撑靴的加速度有效值远远小于其他3个部件.
(4) 掘进方向的载荷从刀盘传递到主梁一变化幅度减小了58.3%,均值减小了42.7%,主梁二z方向输入载荷主要为负值,即输入载荷方向与主梁一相反,且变化幅度很小.
(5) 对比仿真值和测试值,加速度变化范围一致,加速度有效值的相对误差基本都在30%以内,工程测试一定程度上验证了仿真结果.
| [1] |
刘统, 龚国芳, 彭左, 等. 基于液压变压器的TBM刀盘混合驱动系统[J]. 浙江大学学报:工学版, 2016, 50(3): 419-427. LIU Tong, GONG Guo-fang, PENG Zuo, et al. Hybrid cuttehead driving system for TBM based on hydraulic transformer[J]. Journal of Zhejiang University:Engineering Science, 2016, 50(3): 419-427. |
| [2] |
CHO S H, KIM J, WON J, et al. Effects of jack force and construction steps on the change of lining stresses in a TBM tunnel[J]. KSCE Journal of Civil Engineering, 2017, 21(4): 1-12. |
| [3] |
韩美东, 曲传咏, 蔡宗熙, 等. TBM刀盘掘进过程动态仿真[J]. 哈尔滨工程大学学报, 2015, 36(8): 1098-1102. HAN Hei-dong, QU Chuan-yong, CAI Zong-xi, et al. Dynamic numerical simulation of tunneling by the TBM cutter head[J]. Journal of Harbin Engineering University, 2015, 36(8): 1098-1102. |
| [4] |
李献, 邹晓阳, 徐海, 等. 硬岩掘进机的动力吸振方案优化研究[J]. 噪声与振动控制, 2015, 35(3): 189-194. LI Xian, ZOU Xiao-yang, Xu Hai, et al. Optimization of dynamic absorbers of tunnel boring machines[J]. Noise and Vibration Control, 2015, 35(3): 189-194. |
| [5] |
FESTA D, BROERE W, BOSCH J W. An investigation into the forces acting on a TBM during driving-Mining the TBM logged data[J]. Tunnelling and Underground Space Technology, 2012, 32: 143-157. DOI:10.1016/j.tust.2012.06.006 |
| [6] |
凌静秀, 孙伟, 霍军周, 等. TBM刀盘系统多自由度耦合固有特性及敏感度[J]. 东北大学学报:自然科学版, 2015, 37(4): 546-550. LING Jing-xiu, SUN Wei, HUO Jun-zhou, et al. Natural characteristics and sensitivity of TBM cutterhead system with multi-degree-of-freedom coupling[J]. Journal of Northeastern University:Nantural Science, 2015, 37(4): 546-550. |
| [7] |
SUN W, DING X, WEI J, et al. Hierarchical modeling method and dynamic characteristics of cutter head driving system in tunneling boring machine[J]. Tunnelling and Underground Space Technology, 2016, 52: 99-110. DOI:10.1016/j.tust.2015.11.022 |
| [8] |
HASSANPOUR J, ROSTAMI J, ZHAO J. A new hard rock TBM performance prediction model for project planning[J]. Tunnelling and Underground Space Technology, 2011, 26(5): 595-603. DOI:10.1016/j.tust.2011.04.004 |
| [9] |
谢启江, 余海东. 硬岩掘进机刀盘载荷与撑靴接触界面刚度的耦合关系[J]. 上海交通大学学报, 2015, 49(9): 1269-1275. XIE Qi-jiang, YU Hai-dong. Coupling ralationship between loads on cutterhead of tunnel boring machine and contact stiffness of gripper shoes and rocks[J]. Journal of Shanghai Jiaotong University, 2015, 49(9): 1269-1275. |
| [10] |
余海东, 郝培, 赵勇, 等. 硬岩掘进装备支撑系统界面接触刚度非线性特性[J]. 机械工程学报, 2014, 50(21): 54-59. YU Hai-dong, HAO Pei, ZHAO Yong, et al. Non-linear behavior of normal contact stiffness of tunnel surface and supporting system of tunnel boring machines[J]. Journal of Mechanical Engineering, 2014, 50(21): 54-59. |
| [11] |
陈於学, 王冠兵, 杨曙年. 圆柱滚子轴承的动态刚度分析[J]. 轴承, 2008(4): 1-5. CHEN Yu-xue, WANG Guan-bing, YANG Shu-nian. Analysis of dynamic stiffness of cylindrical roller bearings[J]. Bearing, 2008(4): 1-5. |
| [12] |
GAO S H, MENG G, LONG X H. Study of milling stability with Hertz contact stiffness of ball bearings[J]. Archive of Applied Mechanics, 2011, 81(8): 1141-1151. DOI:10.1007/s00419-010-0475-y |
| [13] |
王林鸿, 吴波, 杜润, 等. 液压缸运动的非线性动态特征[J]. 机械工程学报, 2007, 43(12): 12-19. WANG Lin-hong, WU Bo, DU Run, et al. Nonlinear dynamic characteristics of moving hydraulic cylinder[J]. Journal of Mechanical Engineering, 2007, 43(12): 12-19. DOI:10.3321/j.issn:0577-6686.2007.12.003 |
| [14] |
PARK Y, LEE H, PARK K, et al. Practical behavior of advanced non-linear hydraulic servo system model for a mold oscillating mechanism depending on line volume[J]. Journal of Mechanical Science and Technology, 2016, 30(3): 975-982. DOI:10.1007/s12206-016-0201-y |
| [15] |
彭欢, 张怀亮, 邹伟, 等. 硬岩掘进机推进液压缸结构参数优化[J]. 机械工程学报, 2014, 50(21): 76-83. PENG Huan, ZHANG Huai-liang, ZOU Wei, et al. Structure parameters optimization of thrust hydraulic cylinder under foundation vibration[J]. Journal of Mechanical Engineering, 2014, 50(21): 76-83. |


