飞机装配包括零组件定位、钻铆加工和连接等过程[1].按照装配层级可以分为组件-部件-大部件-整机装配阶段.在大部件装配过程中,部件对接区域的配合面间隙较小,装配误差容易累积,会产生干涉问题.为防止干涉事故的发生,可以利用飞机数字化装配系统中的测量设备对待装配产品实际状态进行信息采集,达到对装配过程进行仿真计算和预测装配结果的目的.
同时针对翼身对接过程中制造误差和装配误差积累导致机翼实际形状与理论模型不一致的现象,可以选取机翼上特定关键点并对位置进行控制,以消除误差对产品质量的影响.为保证翼身交点接头位置准确度和机翼水平测量点的高差要求,许多学者对位姿评价算法进行了研究.张斌等[2]通过引入形位误差评定当中的“最小条件”原则,提出一种基于鞍点规划理论的机翼水平位姿评估方法.梁琴[3]提出一种基于分步求解策略的水平姿态调整方法,先考虑翼身交点孔位置,再满足水平测量点高差要求.王青等[4]提出一种基于容差约束的机翼位姿评价及优化算法,在综合评价函数中同时引入翼身交点的三维相对偏差和水平测量点的相对高差.上述研究成果将翼身交点接头的配合问题转化为特征点的匹配问题,简化了求解,而且满足位置和同轴度要求[5],实现了较好的配合效果.但上述文献未对叉耳配合中翼身交点接头存在局部变形的情况进行分析,此变形虽不影响位置准确度,但会导致干涉的发生.因此在机翼的位姿评价中有必要对目标位姿下的翼身交点接头进行干涉检测.
干涉检测中涉及到的物理量分离距离与穿透深度[6]分别是指连接2个分离点集A、B间最短线段的长度和分离2个相交点集A、B需平移的最小长度.工程中,需保证叉耳接头间距在适当范围内,以避免发生干涉,即对叉耳接头的分离距离做了要求.当叉耳接头发生干涉时,需要获得穿透深度以指导相应的修正.
空间几何体的干涉检测方法包括空间分解法[7-8]、层次包围法[9-10]、分离平面法[11]、基于图像空间的算法[12-13]和距离算法[14-16].但前4种方法往往存在以下问题:只能得出是否干涉的二元结论,无法计算分离距离和穿透深度;计算过程较复杂,耗费时间多;计算准确度有待提高.综合以上分析,本文采用特定的距离检查方法对飞机装配中叉耳接头干涉进行研究.并根据测量翼身对接前叉耳接头关键点的坐标,计算出在机翼的目标位姿下的叉耳接头的分离距离或穿透深度(本文统称为最小距离),以判断翼身对接后翼身交点接头干涉可能性和提供机翼位姿修正方案.
1 问题描述由于制造误差和装配变形的影响,叉耳接头的实际形状和位姿都可能与理论值不一致(如图 1所示).叉耳接头是精加工零件,尺寸精度高,且材料刚度大,外形尺寸小,自身不容易产生变形,因而在对接干涉评价过程中可以假设叉耳接头形状与设计数模一致,重点关注因装配变形而产生的实际位姿与理论位姿不一致问题.翼身对接过程中,机身位姿先调整好,然后调整机翼位姿实现对接.因此,叉型接头位姿不再改变,而耳型接头位姿可以随着机翼位姿的调整而调整.
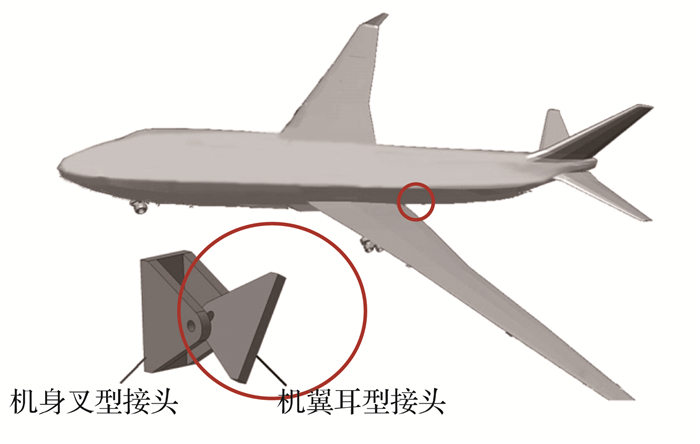
|
图 1 叉耳接头配合图 Fig. 1 Connection of fork-ear joint |
求叉耳接头之间的最小距离,实际上就是求出2组叉耳对应面(如图 2所示中的面A与面B,面C与面D)的最小距离(允许最小距离为负,代表穿透深度).为方便求解,同时方便后续对间距进行调整,所求叉耳对应面的距离都是指耳型接头面(下称耳面)到叉型接头面(下称叉面)的垂直距离.需要说明的是,本文只考虑投影点在叉面外边界以内的点,如图 2中的a、b点,而c点排除.另外,将面中的圆孔部分忽略,即认为叉面和耳面都不包含圆孔.
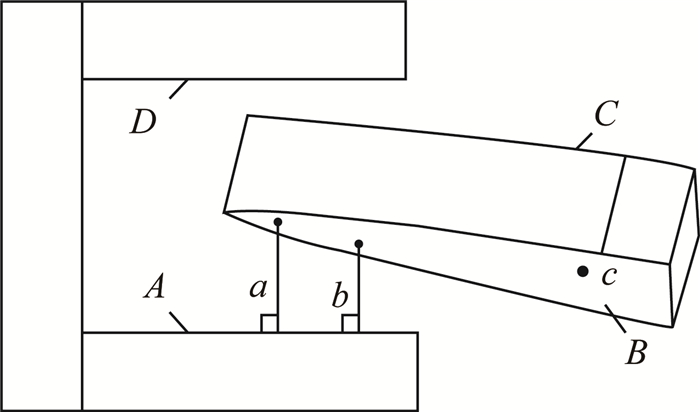
|
图 2 叉耳接头间的最小距离 Fig. 2 Minimum distance of fork-ear joint |
接头侧截面投影如图 3所示,其几何外形由直线段LA1A2, LA2A3, LA1A4以及圆弧CA3A4组成.若给定圆心A0和底部的A1、A2点的三维坐标,且根据已知r值,可求得该接头侧截面及几何边界尺寸的空间表达式.但在实际工程应用中,A0、A1、A2点的空间坐标难以直接测定,一般通过测量LA2A3, LA1A4上任意两点P2, P3和P1, P4的坐标值,通过计算求解获得接头侧截面及几何边界的空间函数表达式.首先采用数字化测量技术对上述四点位置进行测量:将激光测量所需靶球置于LA2A3及LA1A4线内任意2个测量点中;利用激光跟踪仪测得各靶球球心坐标并拟合得出球心所组成的平面法矢方向,结合已知靶球尺寸,对球心坐标进行补偿,即得到4个测量点P1, P2, P3, P4的坐标.由于接头侧截面与4个靶球球心所组成的平面平行,即接头侧截面的法矢方向同样可知.
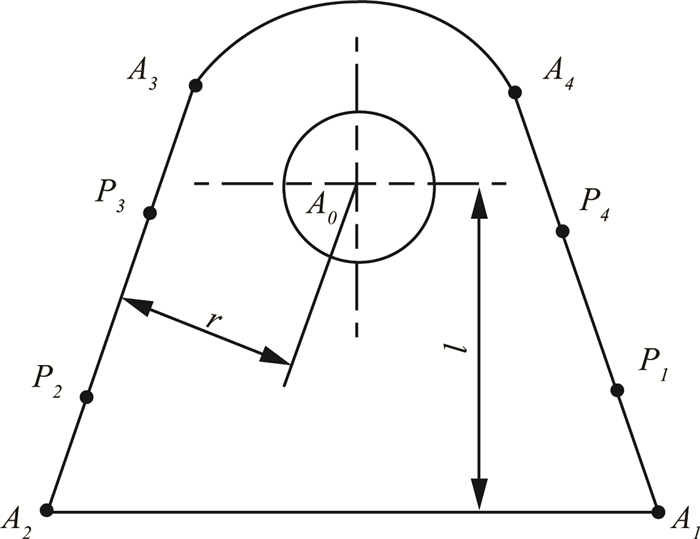
|
图 3 接头侧截面几何形状 Fig. 3 Side shape of joint |
通过测量和计算可以分别得到叉面和耳面的初始状态几何尺寸的空间函数表达式,并采用机翼最优位姿算法[4],以叉面和耳面的相应理论位置为调姿目标,计算得出机翼调姿所需的齐次变换矩阵T,并获得实际装配形位下叉耳面的几何空间函数表达式,从而计算得出叉耳面间的最小距离.
2 求解方法 2.1 坐标系建立对于笛卡尔坐标系{O},空间中任意一点qi的位置可以用齐次坐标表示:
| $ {}^O{\mathit{\boldsymbol{q}}_i} = {\left[ {{\mathit{\boldsymbol{q}}_{\mathit{\boldsymbol{ix}}}},{\mathit{\boldsymbol{q}}_{\mathit{\boldsymbol{iy}}}},{\mathit{\boldsymbol{q}}_{\mathit{\boldsymbol{iz}}}},1} \right]^{\rm{T}}}. $ | (1) |
对于点qi,如图 4所示,OGXGYGZG是全局坐标系{G}, OLXLYLZL是部件坐标系{L}.其部件坐标和全局坐标分别为Lqi和Gqi则
| $ \left. \begin{array}{l} {}^G{\mathit{\boldsymbol{q}}_i} = {}_L^G\mathit{\boldsymbol{T}} \cdot {}^L{\mathit{\boldsymbol{q}}_i},\\ {}^L{\mathit{\boldsymbol{q}}_i} = {}_G^L\mathit{\boldsymbol{T}} \cdot {}^G{\mathit{\boldsymbol{q}}_i}. \end{array} \right\} $ | (2) |
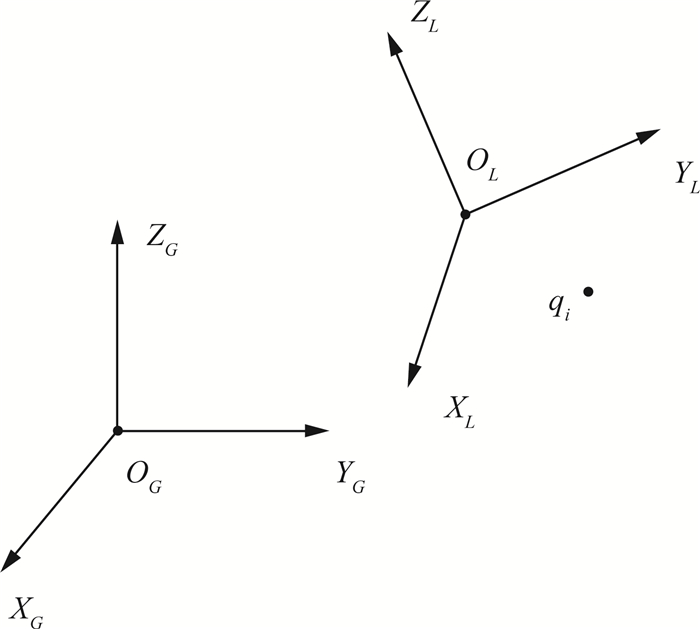
|
图 4 坐标变换关系 Fig. 4 Coordinate transformation relationship |
式中:LGT为{L}到{G}的齐次变换矩阵,GLT为{G}到{L}的齐次变换矩阵,GLT=(LGT)-1.若在{G}中,与OLXL,OLYL,OLZL同向的单位向量分别为nx=[nxx, nxy, nxz, 0]T,ny=[nyx, nyy, nyz, 0]T,nz=[nzx, nzy, nzz, 0]T,OL的坐标为[xL, yL, zL, 1]T.则齐次变换矩阵为
| $ {}_L^G\mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {{n_{xx}}}&{{n_{yx}}}&{{n_{zx}}}&{{x_L}}\\ {{n_{xy}}}&{{n_{yy}}}&{{n_{zy}}}&{{y_L}}\\ {{n_{xz}}}&{{n_{yz}}}&{{n_{zz}}}&{{z_L}}\\ 0&0&0&1 \end{array}} \right]. $ | (3) |
叉耳对接过程如图 5所示,初始状态下叉面B上的某个点Bi在全局坐标系{G}中的坐标为GBi.装配最终形位下,面B位置移动至B′,点Bi移动至B′i位置,其中点B′i坐标为
| $ {}^G{{\mathit{\boldsymbol{B'}}}_i} = {\mathit{\boldsymbol{T}}_{{\rm{Align}}}} \cdot {}^G{\mathit{\boldsymbol{B}}_i}. $ | (4) |
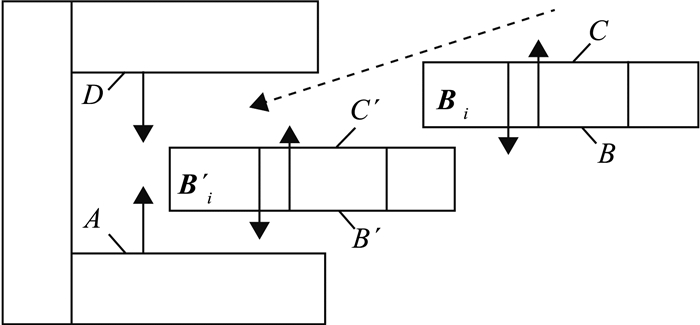
|
图 5 叉耳对接过程示意图 Fig. 5 Process of joint connection |
式中:TAlign为采用机翼最优位姿算法计算得出的齐次变换矩阵.若刚体先绕x,y,z轴分别旋转α,β,γ角,再按照x,y,z轴分别平移tx,ty,tz,相应的齐次变换矩阵为
| $ \begin{array}{l} {\mathit{\boldsymbol{T}}_{{\rm{Align}}}} = \\ \left[ {\begin{array}{*{20}{c}} {c\gamma c\beta }&{ - s\gamma c\alpha + c\gamma s\beta s\alpha }&{s\alpha s\gamma + c\gamma s\beta c\alpha }&{{t_x}}\\ {s\gamma c\beta }&{c\gamma c\alpha + s\gamma s\beta s\alpha }&{ - c\gamma s\alpha + s\gamma s\beta c\alpha }&{{t_y}}\\ { - s\beta }&{c\beta s\alpha }&{c\beta c\alpha }&{{t_z}}\\ 0&0&0&1 \end{array}} \right]. \end{array} $ | (5) |
式中:cα=cos α,sα=sin α,其余类似.
耳面A(简称为A)与叉面B(简称为B)的部件坐标系{A}{B}建立方式如图 6所示.坐标系{A}以A0为原心;X轴与耳面对称轴平行,Y轴正向指向弧形边界;Z轴方向垂直于耳面,Z轴正向指向同一耳型接头的另一个耳面(如图 5中实线箭头所示);Z轴由右手定则可得.由于假设耳接头实际形状与理论形状相同,因此可确定在{A}中点A0、A1、A2、A3、A4的坐标;坐标系{B}的定义与{A}类似.
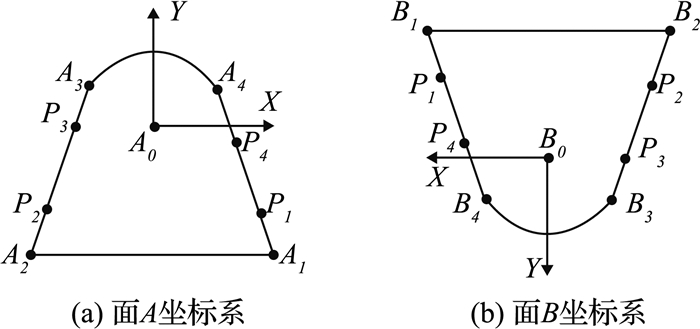
|
图 6 部件坐标系定义 Fig. 6 Definition of component coordinate system |
通过激光跟踪仪对实际装配位置的耳面上点P1,P2,P3,P4进行测量,如图 6(a)所示,获得其在坐标系{G}中的坐标.根据测量值,计算{A}到{G}的齐次变换矩阵为
| $ {}_L^G\mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {{n_{xx}}}&{{n_{yx}}}&{{n_{zx}}}&{{x_A}}\\ {{n_{xy}}}&{{n_{yy}}}&{{n_{zy}}}&{{y_A}}\\ {{n_{xz}}}&{{n_{yz}}}&{{n_{zz}}}&{{z_A}}\\ 0&0&0&1 \end{array}} \right]. $ | (6) |
则需计算A0坐标与坐标轴单位向量nx,ny,nz.由单位向量nz与P2P3、P1P4垂直,可知
| $ {\mathit{\boldsymbol{n}}_z} = \frac{{{\mathit{\boldsymbol{P}}_2}{\mathit{\boldsymbol{P}}_3} \times {\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{P}}_4}}}{{\left| {{\mathit{\boldsymbol{P}}_2}{\mathit{\boldsymbol{P}}_3} \times {\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{P}}_4}} \right|}}. $ | (7) |
由点A0到LP2P3和LP1P4的距离均为r,可得
| $ \left. \begin{array}{l} r \cdot {\mathit{\boldsymbol{n}}_z} = \frac{{{\mathit{\boldsymbol{P}}_3}{\mathit{\boldsymbol{A}}_0} \times {\mathit{\boldsymbol{P}}_2}{\mathit{\boldsymbol{P}}_3}}}{{\left| {{\mathit{\boldsymbol{P}}_2}{\mathit{\boldsymbol{P}}_3}} \right|}},\\ r \cdot {\mathit{\boldsymbol{n}}_z} = \frac{{{\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{P}}_4} \times {\mathit{\boldsymbol{P}}_4}{\mathit{\boldsymbol{A}}_0}}}{{\left| {{\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{P}}_4}} \right|}},\\ {\mathit{\boldsymbol{P}}_3}{\mathit{\boldsymbol{A}}_0} \cdot {\mathit{\boldsymbol{n}}_z} = 0. \end{array} \right\} $ | (8) |
由ny与LP1P4和LP2P3的夹角相同,可得
| $ \left. {\begin{array}{*{20}{c}} {\frac{{{\mathit{\boldsymbol{n}}_y} \cdot {\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{P}}_4}}}{{\left| {{\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{P}}_4}} \right|}} = \frac{{{\mathit{\boldsymbol{n}}_y} \cdot {\mathit{\boldsymbol{P}}_2}{\mathit{\boldsymbol{P}}_3}}}{{\left| {{\mathit{\boldsymbol{P}}_2}{\mathit{\boldsymbol{P}}_3}} \right|}},}\\ {{\mathit{\boldsymbol{n}}_y} \cdot {\mathit{\boldsymbol{n}}_z} = 0,}\\ {{\mathit{\boldsymbol{n}}_y} \cdot {\mathit{\boldsymbol{P}}_1}{\mathit{\boldsymbol{P}}_4} > 0,}\\ {\left| {{\mathit{\boldsymbol{n}}_y}} \right| = 1.} \end{array}} \right\} $ | (9) |
最后nx由右手定则算出,
| $ \left. {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{n}}_x} = {\mathit{\boldsymbol{n}}_y} \times {\mathit{\boldsymbol{n}}_z},}\\ {\left| {{\mathit{\boldsymbol{n}}_x}} \right| = 1.} \end{array}} \right\} $ | (10) |
BGT的求解与AGT求解过程类似.
2.2.2 投影方程将面B′向A所在的平面投影,得到面B″,如图 7所示.现计算{B}中任意一点Bi对应的B″i在{A}中的坐标AB″i.
| $ {}^\mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{B''}}}_i} = {\rm{diag}}\left( {1,1,0,1} \right) \cdot {}^\mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{B'}}}_i} $ | (11) |
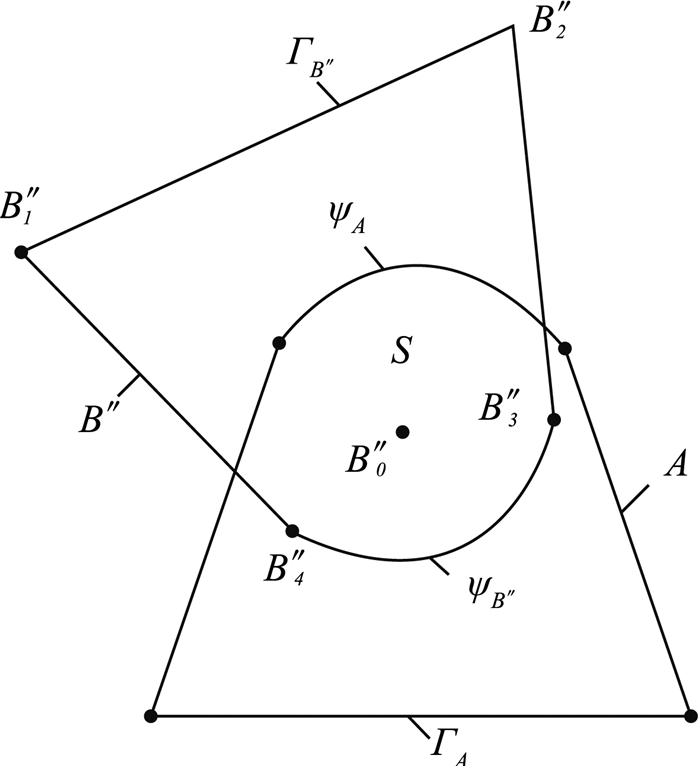
|
图 7 B′向A投影 Fig. 7 Projection from B′ to A |
式中:diag (1,1,0,1)为对角矩阵
| $ \begin{array}{*{20}{c}} {{}^\mathit{\boldsymbol{A}}{{\mathit{\boldsymbol{B'}}}_i} = {}_G^A\mathit{\boldsymbol{T}} \cdot {}^G{{\mathit{\boldsymbol{B'}}}_i} = }\\ {{}_G^A\mathit{\boldsymbol{T}} \cdot {\mathit{\boldsymbol{T}}_{{\rm{Align}}}} \cdot {}^G{\mathit{\boldsymbol{B}}_i} = }\\ {{}_G^A\mathit{\boldsymbol{T}} \cdot {\mathit{\boldsymbol{T}}_{{\rm{Align}}}} \cdot {}_B^G\mathit{\boldsymbol{T}} \cdot {}^B{\mathit{\boldsymbol{B}}_i}.} \end{array} $ | (12) |
例如,AB′0=GAT·TAlign·GB0
记面B″和面A的边界分别为ΓB”和ΓA.ΓB”由直线段LB″1B″2,LB″2B″3,LB″1B″4以及椭圆弧CB″3B″4组成,其中ΓB”包含的直线段在{A}中的表达式可由两端点确定.
由于在{B}中圆弧CB3B4的表达式为
| $ {\left[ {\begin{array}{*{20}{c}} {r\cos \theta ,}&{r\sin \theta ,}&{0,}&1 \end{array}} \right]^{\rm{T}}}. $ | (13) |
式中:(α≤θ≤π-α),α为{B}中B0B4与x轴的夹角.由式(11)、(12)、(13),得在{A}中椭圆弧CB″3B″4的表达式为
| $ \begin{array}{*{20}{c}} {{\rm{diag}}\left( {1,1,0,1} \right) \cdot {}_G^A\mathit{\boldsymbol{T}} \cdot {\mathit{\boldsymbol{T}}_{{\rm{Align}}}} \cdot {}_B^G\mathit{\boldsymbol{T}} \times }\\ {{{\left[ {\begin{array}{*{20}{c}} {r\cos \theta ,}&{r\sin \theta ,}&{0,}&1 \end{array}} \right]}^{\rm{T}}}.} \end{array} $ | (14) |
式中:ΓA在{A}中的表达式求法类似,不予赘述.
2.2.3 最小距离考虑A与B″的重叠部分S.如图 7所示,令ΓB”在A中的部分为ΨB″,ΓA在B″中的部分为ΨA,即ΨB″和ΨA组成了S的边界.在工程实际中,由于A与B″只会发生少量重叠,因此ΨB″为由直线段LB″1B″4、LB″2B″3以及椭圆弧CB″3B″4的部分或全部组成的一条连续曲线段,且不包含LB″1B″2.ΨA的情况类似.
这样,求A与B′间的最小距离d,就是求B′中到A的投影在S内的所有点的最小投影距离.即
| $ d = \min {}^\mathit{A}{{\mathit{\boldsymbol{B'}}}_{iz}},\left\{ {{}^\mathit{A}{{\mathit{\boldsymbol{B''}}}_i} \in S} \right\}. $ | (15) |
式中:AB′iz为B′i在{A}中的z轴坐标.
由AB′0和法矢AnB′, AnB′=GAT·TAlign·BGT·[0, 0, 1, 0]T,可得B′所属的平面在{A}中的表达式:
| $ Ax + By + Cz = D. $ | (16) |
由式(15)、(16)可得,最小距离d的求法如下:
| $ \left. \begin{array}{l} d = \min z,\\ {\rm{s}}.\;{\rm{t}}.\;\;Ax + By + Cz = D,\\ {\left[ {x,y,0,1} \right]^{\rm{T}}} \in S. \end{array} \right\} $ | (17) |
当d为正值时,代表分离距离,否则代表穿透深度.
2.2.4 求解对于坐标空间中的任意一条线段EF,如图 8所示,在XOY面上的投影为E′ F′.Pi为线段EF上任意一点,对应的投影为P′i.已知Piz=f(P′i),f为点P′i与Pi的Z轴坐标的对应函数,由min (Ez, Fz) ≤Piz,可得
| $ \min \left( {f\left( {E'} \right),f\left( {F'} \right)} \right) \le f\left( {{{P'}_i}} \right). $ | (18) |
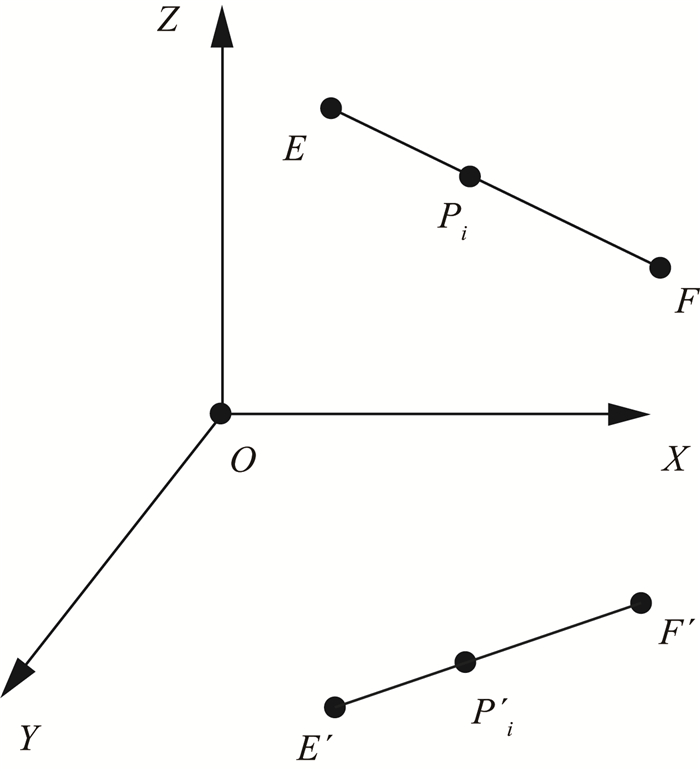
|
图 8 空间点及其投影对应关系图 Fig. 8 Space point and its projection correspondence diagram |
假设B′中的点ξB′与其在A中的投影点ξA的距离等于最小距离d.有以下3个结论:
1) 在S的边界上能找到ξA,即∃ξA∈ΨA∪ΨB″.
若ξA∈ΨA∪ΨB″,则结论直接得证.假设ξA为S内部的点(不包括边界),则作过ξA的直线交边界于两点E′、F′,由式(18)可得min (f(E′), f(F′))≤f(ξA)=d,因此可取E′、F′中某点为ξA,结论得证.
2) 若∃ξA∈ΨB″,则ξA为ΨB″所包含的直线段端点、曲线段投影距离极小值点之一.
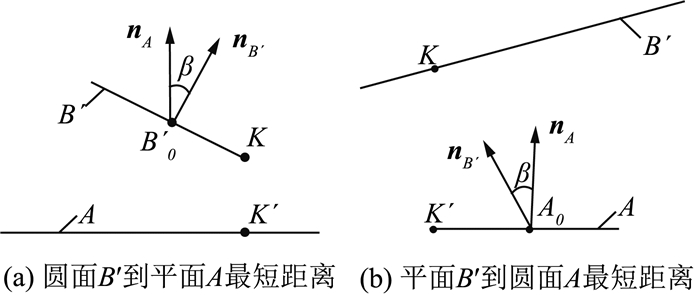
若ΨB″包含直线段,由引理可知直线段两端点为ξA可能点.若ΨB″包含曲线段,显然曲线段中的投影距离极小值点为ξA可能点.现求曲线段投影距离极小值点.该曲线段是空间中一段圆弧的投影.如图 9(a)所示,假设此时B′一个圆面,A为无穷大的平面,K为B′到A中距离最小的点,对应投影为K′.
| $ {}^A{{\mathit{\boldsymbol{B'}}}_0}\mathit{\boldsymbol{K}} = \left( {{}^A{\mathit{\boldsymbol{n}}_{B'}} \cdot \cos \beta - {}^A{\mathit{\boldsymbol{n}}_A}} \right) \cdot r/\sin \beta . $ | (19) |
|
图 9 空间圆的极值点求法 Fig. 9 Calculating extreme point of space circle |
式中:AnB′=GAT·TAlignBGT [0, 0, 1, 0]T,AnA=[0, 0, 1, 0]T,cos β=dot (AnB′, AnA),
| $ {}^A\mathit{\boldsymbol{K'}} = {\rm{diag}}\left( {1,1,0,1} \right)\left( {{}^A{{\mathit{\boldsymbol{B'}}}_0}\mathit{\boldsymbol{K + }}{}^A{{\mathit{\boldsymbol{B'}}}_0}} \right). $ | (20) |
当K′在曲线段内时,曲线段投影距离极小值点为K′;当K′不在曲线段内时,曲线段投影距离极小值点为曲线段的两端点之一.
3) 若∃ξA∈ΨA,ξA为ΨA所包含的直线段端点、曲线段投影距离极小值点之一.
与上种情况同理,但此时的极小值点求法有所不同.如图 9(b),假设此时A为一个圆面,B′为无穷大的平面,K为B′到A中垂直距离最小的点,对应投影为K′.
| $ {}^A{\mathit{\boldsymbol{A}}_0}\mathit{\boldsymbol{K'}} = \left( {{}^A{\mathit{\boldsymbol{n}}_{B'}} - {}^A{\mathit{\boldsymbol{n}}_A}\cos \beta } \right)r/\sin \beta . $ | (21) |
| $ {}^A\mathit{\boldsymbol{K'}} = {}^A{\mathit{\boldsymbol{A}}_0}\mathit{\boldsymbol{K'}}. $ | (22) |
当K′在曲线段内时,曲线段投影距离极小值点为K′;当K′不在曲线段内时,曲线段投影距离极小值点为曲线段的两端点之一.
综合1)、2)和3),面A与B′间的最小距离求法如下:求得S的边界ΨA和ΨB″的表达式,考查ΨA和ΨB″所包含的直线段端点、曲线段投影距离极小值点,分别代入式(16),算出的z值中最小一个即为d.
3 位姿修正对于部分叉型接头因位姿偏离理论值较大(位姿变形)而引起干涉的问题,优先采用位姿调整(改变机翼的调姿齐次变换矩阵)解决,其次考虑局部修配.
不同飞机的叉耳接头的布局方式常常会不同,本文讨论叉耳接头在几种常见的布局方式下的干涉检测和位姿修正方法.
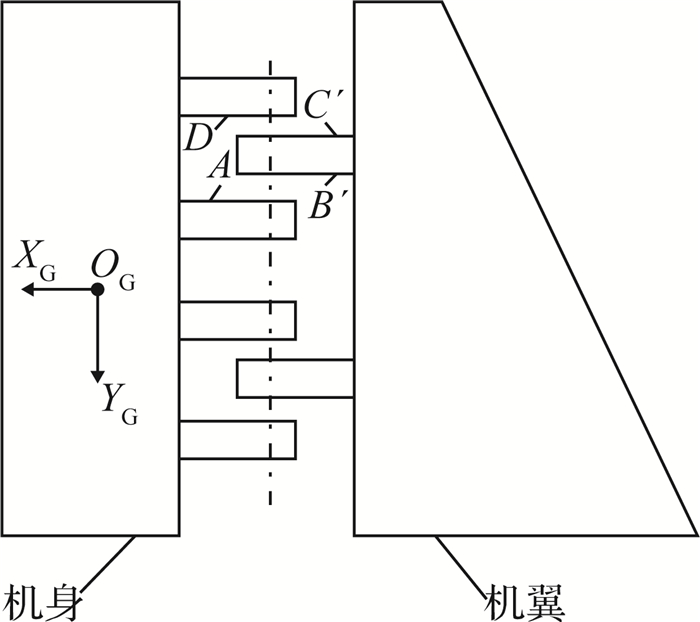
3.1 布局方式一第1种叉耳接头的布局方式如图 10所示,全局坐标系{G}的y轴方向与航向平行,且与所有机身叉面的法向平行.图中机翼的位姿为按照最优位姿算法调姿所得最终形位.若发生叉耳接头干涉,只需将机翼沿y轴方向平移进行微调;此时若对机翼整体进行旋转调姿,会影响大部分叉耳接头的同轴度或机翼水平测量点高差,计算较复杂,因此不考虑.
|
图 10 情况1机翼最终形位图 Fig. 10 Final position and orientation of wing on case 1 |
考察图 10中的A、B′、C′、D这4个面,设右机翼共有n个耳型接头,B′面和C′面对应于第k个耳型接头.假设已用上文方法求得面C′与面D间的最小距离dC′D=dk1,面B′与面A的最小距离dB′A=dk2,为防止干涉,要求叉耳面间最小距离为δ.则为防止第k组叉耳接头干涉,当前位姿下的机翼在y向上的平移距离Δyk应满足
| $ \left. \begin{array}{l} \Delta {y_k} + {d_{k1}} \ge \delta ,\\ {d_{k2}} - \Delta {y_k} \ge \delta . \end{array} \right\} $ | (23) |
同时,为了不影响翼身交点接头位置准确度,需要保证平移后不超过容差
| $ \left| {\Delta {y_k} - {\varepsilon _{yk}}} \right| \le \varepsilon _y^0. $ | (24) |
式中:εyk为第k个耳型接头对应的制造特征点的y向偏差,由该制造特征点y坐标的理论值减测量值所得,εy0为相应的容差要求.由式(23)、(24)可得
| $ \Delta {y_k} \in \left[ {{a_k},{b_k}} \right]. $ | (25) |
同理可求得所有Δyi,i∈{1, 2, …, n}.对所有Δyi求交集得Δy,以下通过对Δy的取值情况讨论说明是否存在干涉,以及如何调整位姿变换矩阵TAlign.
1) Δy∈[a, b]≠∅.
若a≤0≤b,此时不存在干涉,不需要调整;若a≤b < 0,此时存在干涉危险,为使对TAlign的影响最小,Δy=b;若0 < a≤b,此时存在干涉危险,Δy=a.调整后
| $ \begin{array}{l} {{\mathit{\boldsymbol{T'}}}_{{\rm{Align}}}} = \\ \left[ {\begin{array}{*{20}{c}} {c\gamma c\beta }&{ - s\gamma c\alpha + c\gamma s\beta s\alpha }&{s\alpha s\gamma + c\gamma s\beta c\alpha }&{{t_x}}\\ {s\gamma c\beta }&{c\gamma c\alpha + s\gamma s\beta s\alpha }&{ - c\gamma s\alpha + s\gamma s\beta c\alpha }&{{t_y} + \Delta y}\\ { - s\beta }&{c\beta s\alpha }&{c\beta c\alpha }&{{t_z}}\\ 0&0&0&1 \end{array}} \right]. \end{array} $ | (26) |
2) Δy=∅.
此时存在干涉危险,且无法通过y向平移消除.可以考虑放宽容差限制或进行修配.
放宽限制,即增大式(24)中的容差要求εy0或者忽略式(24)的限制,对得到的新的Δy进行讨论.若Δy仍然为∅,则只能进行修配.
修配方案的确立准则是,在保证不发生干涉的前提下,修配最少数量的耳型接头.具体而言,就是考虑所有Δyi,以重叠最多的区间作为参考范围,对所有不包含该参考范围的耳型接头进行修配.修配后需重新进行姿态评价.
综上,干涉检测与位姿修正流程如图 11所示.需要说明的是,以上计算的假设前提为,机身上的叉型接头位姿和理论模型一致.实际上,机身上的叉型接头也有可能发生微量位姿变形,但对Δy所在区间[a, b]的计算影响不大.为了保证调整的结果的正确性,可取最终的Δy为[a, b]中某个偏离端点的值.

|
图 11 干涉检测与位姿修正流程图 Fig. 11 Flow chart of interference detection and alignment of position and orientation |
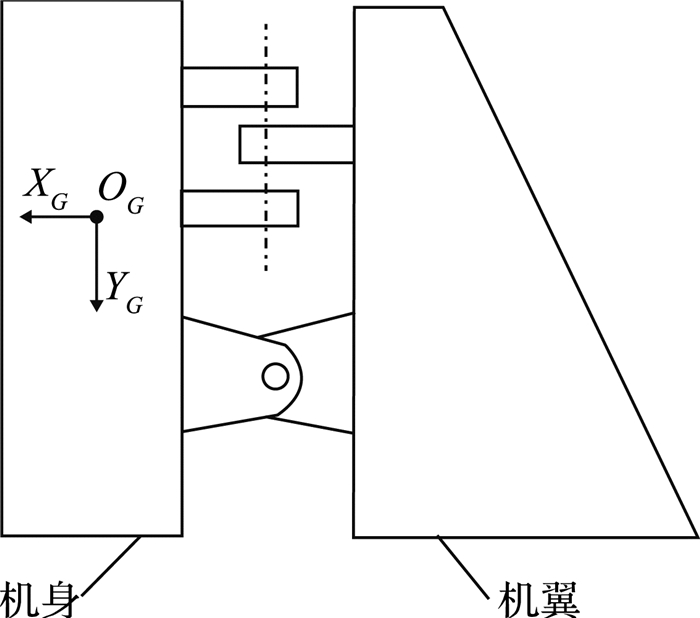
第2种叉耳接头的布局方式如图 12所示,部分叉面法矢量平行于{G}的z轴方向, 部分叉面法矢量平行于{G}的y轴方向.此时需要同时考虑这2个方向的平移微调.
|
图 12 情况2机翼最终形位图 Fig. 12 Final position and orientation of wing on case 2 |
对于法矢量平行于z轴的叉耳,为避免干涉,在z向上的平移距离Δzk应满足
| $ \left. \begin{array}{l} \Delta {y_k} + {d_{k1}} \ge \delta ,\\ {d_{k2}} - \Delta {z_k} \ge \delta . \end{array} \right\} $ | (27) |
为保证平移后不超过容差,需要
| $ \left. \begin{array}{l} \left| {\Delta {z_k} - {\varepsilon _{zk}}} \right| \le \varepsilon _z^0,\\ \left| {\Delta {y_k} - {\varepsilon _{yk}}} \right| \le \varepsilon _y^0. \end{array} \right\} $ | (28) |
对于法矢量平行于y轴的叉耳,为避免干涉,在y向上的平移距离Δyk应满足
| $ \left. \begin{array}{l} \Delta {y_k} + {d_{k1}} \ge \delta ,\\ {d_{k2}} - \Delta {y_k} \ge \delta . \end{array} \right\} $ | (29) |
为保证平移后不超过容差,需要
| $ \left. \begin{array}{l} \left| {\Delta {z_k} - {\varepsilon _{zk}}} \right| \le \varepsilon _z^0,\\ \left| {\Delta {y_k} - {\varepsilon _{yk}}} \right| \le \varepsilon _y^0. \end{array} \right\} $ | (30) |
求出Δyi和Δzi,i∈{1, 2, …, n},得到Δy和Δz的取值范围,后续再做与3.1中同样的分析即可,不予赘述.
3.3 布局方式三第3种叉耳接头的布局方式如图 13所示,所有叉面法矢量平行于任意方向n.若发生叉耳接头干涉,显然应将机翼沿n向做平移来微调.

|
图 13 情况3机翼最终形位图 Fig. 13 Final position and orientation of wing on case 3 |
令n=(cos α, cos β, cos γ), 且n与y轴正向夹角不超过90°,即cos β≥0.为避免干涉,在n向上的平移距离Δnk应满足
| $ \left. \begin{array}{l} \Delta {n_k} + {d_{k1}} \ge \delta ,\\ {d_{k2}} - \Delta {n_k} \ge \delta . \end{array} \right\} $ | (31) |
为保证平移后不超过容差,需要
| $ \left. \begin{array}{l} \left| {\Delta {n_k}\cos \alpha - {\varepsilon _{xk}}} \right| \le \varepsilon _x^0,\\ \left| {\Delta {n_k}\cos \beta - {\varepsilon _{yk}}} \right| \le \varepsilon _y^0,\\ \left| {\Delta {n_k}\cos \gamma - {\varepsilon _{zk}}} \right| \le \varepsilon _z^0. \end{array} \right\} $ | (32) |
求出Δni,i∈{1, 2, …, n},得到Δn的取值范围,后续再做与3.1中同样的分析.最后在x,y,z方向的平移量Δx, Δy, Δz分别为Δncos α, Δncos β, Δncos γ.
4 算例分析该算例基于容差约束的位姿评价算法和测量数据的干涉检测算法实现机翼干涉检测及位姿修正的目标.由于姿态评价不是本文算法涉及范畴,为方便计算,引用文献数据[4]包括机翼制造特征点和协调特征点的理论坐标值和实测坐标值,其中实测坐标值为:绕x,y,z轴正向各平移100 mm,并对各坐标值加正态分布的噪声.由于本文采用的调整方法不会对水平测量点高差造成影响,于是不必要考虑协调特征点,只需要考虑制造特征点,其值如表 1所示.经姿态评价所得的机翼的齐次变换矩阵T相关数据如表 2所示,制造特征点的y向偏差如表 3所示.
| 表 1 制造特征点理论坐标和实测坐标 Table 1 Theoretical coordinate values and measured coordinate values of manufacture feature points |
| 表 2 齐次变换矩阵T相关数据 Table 2 Homogeneous transformation matrix T |
| 表 3 制造特征点的y向偏差 Table 3 Y-direction deviations of manufacturing feature points |
进行干涉检测需已知各接头侧面上的4个测量点的实测坐标值.为方便计算,假设该机翼上所有机身叉面法矢量平行于航向,并且直接提供各叉耳面的部件坐标系信息(即省去2.2.1中的计算,直接提供AGT和BGT),如表 4所示.需说明的是,耳面部件坐标系相关数据是根据制造特征点的实测坐标值,对耳型接头进行微量位姿变形来构造得到.
| 表 4 部件坐标系数据 Table 4 Component coordinate system data |
叉耳面间最小距离要求δ=0.1 mm,各向容差εx0,εy0,εz0均为0.5 mm.文中的最小距离算法以及位姿修正算法在Matlab环境中实现,结果如表 5所示.
| 表 5 最小距离及调整区间 Table 5 Minimum distances and adjustment intervals |
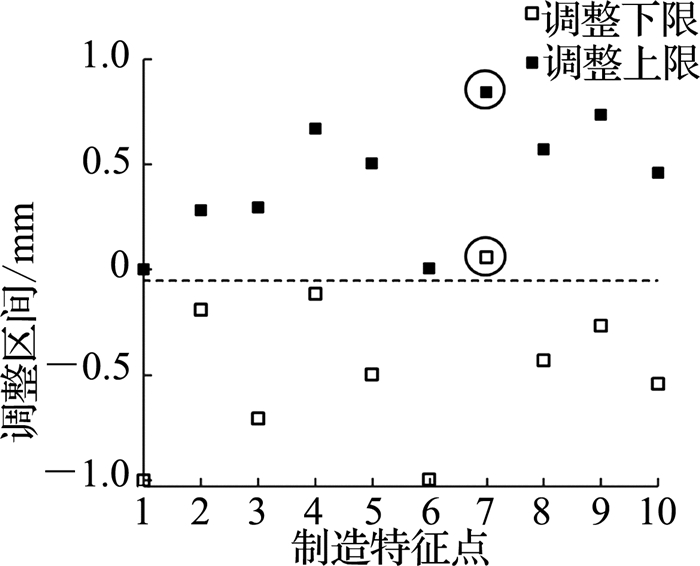
表 5中,各带容差约束的调整区间没有公共区间,即Δy=∅.此时存在干涉危险,且无法通过y向平移消除.可以考虑放宽容差限制或进行修配.
若直接进行修配,现在考虑所有Δyi,找出重叠最多的区间.所有Δyi区间如图 14所示,除了第7组叉耳以外,另外9组有重叠区间,为[-0.117,0.00].因此需对第7组叉耳的耳型接头进行修配.
|
图 14 带容差的调整区间 Fig. 14 Adjustment intervals with tolerance |
现考虑放宽容差限制进行位姿修正.各叉耳不带容差约束的调整区间如表 5所示.经计算,可调整区间为[0.059,0.100].因此,取Δy=0.059.修正后的叉耳距离和齐次变换矩阵如表 6和7所示.表 6中,叉耳距离均不小于最小距离要求δ,这表明了修正方法能有效避免干涉.
| 表 6 修正后的最小距离 Table 6 Modified minimum distances |
| 表 7 修正后的齐次变换矩阵T相关数据 Table 7 Modified homogeneous transformation matrix T |
(1) 根据现场实测数据,计算叉耳接头间的坐标变换关系,通过证明归纳出几个固定的极值点,求出接头间最小距离,得出干涉结果和机翼位姿调整方案,并运用仿真算例验证了该方法的有效性.
(2) 本文提出的基于现场实测数据的干涉检测方法不仅可以应用于飞机装配领域,也适用于所有包含叉耳等规则连接结构的对象间的干涉求解;采用的建立坐标关系,归纳极值点的求解思路可应用于其它干涉距离求解问题中.
(3) 实际过程中叉耳接头会发生微量变形,并且可能会出现仅通过平移调整无法达到要求而需要增加旋转调整的情况,这将是下一步研究的重点.
| [1] |
王云渤, 张关康. 飞机装配工艺学[M]. 北京: 国防工业出版社, 1990, 20-21.
|
| [2] |
张斌, 姚宝国, 柯映林. 基于鞍点规划理论的机翼水平位姿评估方法[J]. 浙江大学学报:工学版, 2009, 43(10): 1761-1765. ZHANG Bin, YAO Bao-guo, KE Ying-lin. Saddle point programming based level-posture evaluation method for aircraft wings[J]. Journal of Zhejiang University:Engineering Science, 2009, 43(10): 1761-1765. |
| [3] |
梁琴. 飞机数字化装配机翼位姿评价及水平姿态调整方法研究[D]. 杭州: 浙江大学, 2013. LIANG Qin. Research on Estimation and alignment of wing position and orientation for aircraft digital assembly[D]. Hangzhou: Zhejiang University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10335-1013303589.htm |
| [4] |
王青, 程亮, 程志彬, 等. 基于容差约束的机翼最优位姿评价算法[J]. 机械工程学报, 2015, 51(19): 124-130. WANG Qing, CHENG Liang, CHENG Zhi-bin, et al. Optimized position and orientation evaluation of wing based on tolerance constraints in aircraft assembly[J]. Journal of Mechanical Engineering, 2015, 51(19): 124-130. |
| [5] |
WEBER T, MOTAVALLI S, FALLAHI B, et al. A unified approach to form error evaluation[J]. Precision Engineering, 2002, 26(3): 269-278. DOI:10.1016/S0141-6359(02)00105-8 |
| [6] |
O'ROURKE J, GOODMAN J E. Handbook of Discrete and Computational Geometry[M]. Florida: CRC press, 2004, 530-543.
|
| [7] |
SAMET H. Applications of spatial data structures[M]. Boston: Addison-Wesley, 1990, 194-207.
|
| [8] |
ZHOU S, JONES C B. Design and Implementation of Multi-scale Databases[J]. Lecture Notes in Computer Science, 2001, 2121: 365-384. DOI:10.1007/3-540-47724-1 |
| [9] |
REDON S, LIN M C, MANOCHA D, et al. Fast continuous collision detection for articulated models[J]. Journal of Computing & Information Science in Engineering, 2005, 5(2): 126-137. |
| [10] |
FANG Z, JIANG J, JIE X. Efficient collision detection using a dual k-dop-sphere bounding volume hierarchy[C]//International Forum on Information Technology and Applications. Washington: IEEE, 2010: 185-189.
|
| [11] |
李学庆, 孟祥旭, 汪嘉业, 等. 基于启发式搜索分离向量的凸多面体碰撞检测[J]. 计算机学报, 2003, 26(7): 837-847. LI Xue-Qing, Meng Xiang-xu, Wang Jia-ye, et al. Detecting collision of polytopes using a heuristic search for separating vectors[J]. Chinese Journal of Computers, 2003, 26(7): 837-847. |
| [12] |
MYSZKOWSKI K, OKUNEV O G, KUNⅡ T L. Fast collision detection between complex solids using rasterizing graphics hardware[J]. The Visual Computer, 1995, 11(9): 497-511. DOI:10.1007/BF02439645 |
| [13] |
于海军, 马纯永, 张涛, 等. 基于图像空间的快速碰撞检测算法[J]. 计算机应用, 2013, 33(2): 530-533. YU Hai-jun, MA Chun-yong, ZHANG Tao, et al. Fast collision detection algorithm based on image space[J]. Journal of Computer Applications, 2013, 33(2): 530-533. |
| [14] |
MIRTICH B. V-Clip:fast and robust polyhedral collision detection[J]. Acm Transactions on Graphics, 1998, 17(3): 177-208. DOI:10.1145/285857.285860 |
| [15] |
朱向阳, 丁汉, 熊有伦. 凸多面体之间的伪最小平移距离——Ⅰ.定义及其性质[J]. 中国科学:技术科学, 2001, 31(2): 128-136. ZHU Xiang-yang, DING Hang, XIONG You-lun. Pseudo minimum translation distance between convex polyhedrons-Ⅰ. Definition and its nature[J]. Science in China:Series E, 2001, 31(2): 128-136. |
| [16] |
陈友东, 晏亮, 谷平平. 双机器人系统的碰撞检测算法[J]. 北京航空航天大学学报, 2013, 39(12): 1644-1648. CHEN You-dong, YAN Liang, GU Ping-ping. Detection collision algorithm for two-manipulator system[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(12): 1644-1648. |


