近年来,人们对海洋的探索越来越深入[1],但由于水下的成像环境复杂,拍摄的水下图像往往有着严重的退化现象,比如色彩失真和图像模糊[2],这导致后续的图像处理过程会受到极大的影响,因此水下图像处理成为越来越热门的研究课题.
水下环境图像退化的原因主要有以下2个.1)水体本身对光的吸收率较高[3],使得光在水中的传播过程中被吸收了大部分能量,并且水对光的吸收率与光的波长有着直接的关系,波长越长,吸收率越高[4],这导致了水下图像的色彩失真现象;2)水中的微粒会对光有散射作用,散射光会影响成像的清晰度.
为了解决这些问题,Schettini等[5]提出很多改进水下图像质量的方法.这些方法可以分为以下两大类.1)不考虑水下图像的成像原理,只对图像的直方图和对比度进行调整,该方法被称为水下图像增强[6].2)建立水下图像的成像模型,根据先验知识和合理的假设,求取模型中的参数,根据模型复原出退化前的图像,该方法被称为水下图像复原.
目前,对于水下图像处理的算法主要如下.Ancuti等[7]提出基于图像融合的水下图像增强算法;Galdran等[8]提出自动红通道水下图像复原算法,针对红色光在水下吸收率最高的特点,对红色通道的成像模型进行改进;Chiang等[9]提出基于波长补偿的水下图像清晰化算法,针对不同波长在水中吸收率不同的特点,对图像的3个通道进行补偿,从而得到复原的图像;Serikawa等[10]提出基于联合三角滤波的水下图像清晰化算法;Li等[11]提出基于最小信息损失和直方图先验的水下图像增强算法,建立图像复原时的图像信息损失函数,通过最优化该函数达到图像增强的目的;Chen等[12]提出基于区域特化的非均匀照明下的水下图像复原算法,将水下图像分割为人工照明区域和非人工照明区域,对人工照明区域进行补偿,达到去除人工光干扰的目的;Ghani等[13]提出基于瑞利分布色彩模型的水下图像增强算法,该算法假设各色彩通道的直方图分布为瑞利分布,对各通道进行拉伸.
本文算法基于水下图像成像模型,对于非深海水域图像,若图像包含水体部分,则通过提取图像中的水体部分,动态地计算图像3个通道透射率之间的关系;若不包含水体部分,则通过图像3个通道直方图的分布,计算透射率之间的关系.对于深海拍摄的图像,采用改进的模型进行处理.实验结果表明,采用本文算法可以较好地提高水下图像的清晰度.
1 水下图像成像模型水下图像退化的原因主要是水体对光的吸收以及水中微粒对光的散射,水下图像的背景光主要来自于从水面上进入水下的光,水下图像的成像模型可以用下式[8]表达:
| $ \begin{array}{*{20}{c}} {{I_\lambda }\left( x \right) = {J_\lambda }\left( x \right) \cdot \exp \left( { - {p_\lambda }d\left( x \right)} \right) \cdot \exp \left( { - {s_\lambda }d\left( x \right)} \right) + }\\ {{A_\lambda }\left[ {1 - \exp \left( { - {p_\lambda }d\left( x \right)} \right) \cdot \exp \left( { - {s_\lambda }d\left( x \right)} \right)} \right].} \end{array} $ | (1) |
式中:Iλ(x)为图像中位于x处且波长为λ的光的强度,Jλ(x)为Iλ(x)所对应的实际场景中的点所反射的波长为λ的光的强度,pλ为水对波长为λ的光的吸收率,sλ为水中微粒对波长为λ的光的散射率,Aλ为波长为λ的背景光强度.从式(1)可以看出,相机拍摄的图像上每一点的光照强度由以下两部分构成.1)第一部分是物体反射的光经过水的吸收和微粒的散射到达相机的部分,由于水对光的吸收率远大于空气对光的吸收率,导致水下图像亮度一般偏低;水对不同波长的色光吸收率差距较大,导致了水下图像的色彩失真现象[14].2)第二部分是背景光经过水的吸收和微粒的散射到达相机的部分,由于这一部分不是物体反射的光,反映到图像上是图像的模糊不清.令tλ=exp(-pλd(x))·exp(-sλd(x)),称tλ为波长为λ的光的透射率,则式(1)可以简化为
| $ {I_\lambda }\left( x \right) = {J_\lambda }\left( x \right){t_\lambda } + {A_\lambda }\left( {1 - {t_\lambda }} \right). $ | (2) |
由于拍摄的图像是以RGB三通道图像的形式保存的,令λ∈{R, G, B},则IR、IG、IB是已知的.只要能够求得对应的t和A,就可以通过式(2)求出JR、JG、JB,从而得到复原后的图像,因此提出的算法是围绕如何求解t和A展开的.
2 水下图像复原算法本文的算法包括以下两部分:1)对图像进行白平衡的调整,将图像分为非深海图像和深海图像,白平衡调整采用的算法是改进的灰度世界白平衡算法.2)根据水下图像成像的模型,复原出因水的作用而变得模糊的图像,这一部分的核心问题是如何得到背景光强度A和透射率t.为了解决该问题,需要用到He等[15]的暗通道先验理论.首先给出暗通道的定义:
| $ {J^{{\rm{dark}}}} = \mathop {\min }\limits_{y \in \mathit{\Omega }\left( x \right)} \left( {\mathop {\min }\limits_{C \in \left\{ {R,G,B} \right\}} {J^C}\left( y \right)} \right). $ | (3) |
式中:JC为彩色图像的每个通道,Ω(x)为以x为中心的窗口区域.根据暗通道先验理论可知,对于室外的无雾图像,非天空区域的暗通道值趋于0,即
| $ {J^{{\rm{dark}}}} \to 0. $ | (4) |
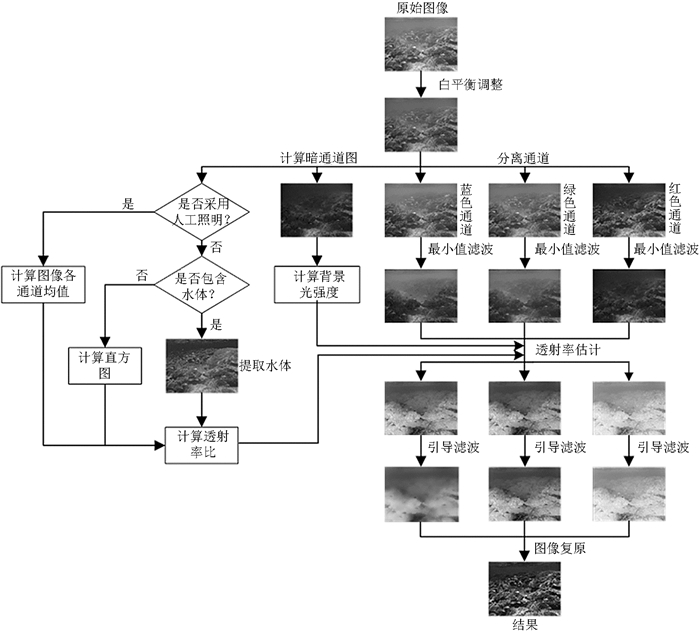
为了将暗通道先验理论用于水下图像,需要对该理论进行一些修改.由于水对红色光的吸收率远大于蓝色光和绿色光,水下图像的红色通道值很低.如果采用传统算法计算暗通道图,那么部分图像的暗通道图会出现几乎全黑的情况.为了避免该问题,只利用图像的蓝色通道和绿色通道进行暗通道图的计算,然后根据暗通道图中最亮的部分像素点,计算背景光强度;在计算背景光强度后,可以通过暗通道先验原理进行透射率的计算,由于每个通道有不一样的透射率,需要求解3个通道透射率之间的关系,以此计算出3个通道的透射率,针对不同的图像拍摄情况,采取不同的方法计算各通道透射率的关系.在计算背景光强度和各通道的透射率后,可以进行图像的复原,本文的算法流程如图 1所示.
|
图 1 基于自适应透射率比的水下图像复原算法流程图 Fig. 1 Underwater image restoration algorithm based on adaptive transmission ratio flow chart |
由于水体对不同色光的吸收率不同,导致水下图像一般都有严重的色彩失真问题,为了纠正色彩的失真,采取改进的灰度世界算法对水下图像的白平衡进行调整.为了避免传统灰度世界算法造成的红色通道过度拉伸,该算法只对蓝色和绿色通道进行调整,步骤如下.
1) 确定
| $ \overline {{\rm{Gray}}} = \frac{1}{3}\left( {\bar R + \bar G + \bar B} \right). $ | (5) |
2) 计算R、G、B 3个通道的增益系数:
| $ {k_R} = 1,{k_G} = \frac{{\overline {{\rm{Gray}}} }}{{\bar G}},{k_B} = \frac{{\overline {{\rm{Gray}}} }}{{\bar B}}. $ | (6) |
3) 对图像中的每个像素C,调整R、G、B分量:
| $ \left. \begin{array}{l} C\left( {R'} \right) = C\left( R \right){k_R},\\ C\left( {G'} \right) = C\left( G \right){k_G},\\ C\left( {B'} \right) = C\left( B \right){k_B}. \end{array} \right\} $ | (7) |
为了通过式(2)对水下图像进行复原,首先需要求出背景光强度A.He等[15]提出单幅图像去雾算法,首先计算图像的暗通道图,然后找出暗通道图里最亮的0.1%的像素所对应的原图里的像素,用其中亮度最高的点的像素作为背景光强度.该方法对于水下图像不适合,因为水下图像由于大多红色通道的像素很低,按照传统方法计算暗通道图会使暗通道图出现大面积的像素为0的区域.在利用式(3)计算暗通道图时,只针对蓝色通道和绿色通道的像素进行计算.在得到图像的暗通道图后,需要进行背景光强度的计算,本文根据水下图像的特点对He等[15]的方法进行调整.设Idark(x)为暗通道图中最亮的前0.1%像素点所对应的输入图中的像素点,IRdark(x)、IGdark(x)、IBdark(x)是3个通道分量,令
| $ D\left( x \right) = \max \left\{ {I_G^{{\rm{dark}}}\left( x \right),I_B^{{\rm{dark}}}\left( x \right)} \right\} - I_R^{{\rm{dark}}}\left( x \right). $ | (8) |
式中:D(x)为Idark(x)中蓝绿分量的最大值与红色分量的差值,则背景光强度为D(x)中的最大值对应的像素,即
| $ A = {I^{{\rm{dark}}}}\left[ {\mathop {\arg }\limits_x \max \left( {D\left( x \right)} \right)} \right]. $ | (9) |
为了通过式(2)对图像进行复原,除了A外,还需要求出透射率t.由于在水下R、G、B 3种色光的透射率存在差异,必须求出各通道透射率的关系,才能通过暗通道先验的假设求出3个通道的透射率.设tR、tG、tB为R、G、B 3个通道的透射率,令
| $ {K_{BG}} = \frac{{\ln {t_B}}}{{\ln {t_G}}},{K_{BR}} = \frac{{\ln {t_B}}}{{\ln {t_R}}},{K_{GR}} = \frac{{\ln {t_G}}}{{\ln {t_R}}}. $ | (10) |
Chiang等[9]通过不同清澈度的水体中的光的透射率测量结果作为计算各通道透射率关系的根据,但该方法无法适应复杂多变的水下场景.本文提出通过提取图像中的水体,动态地计算3个通道之间透射率比的方法.
对于水下拍摄的图像,水体部分有2个特点:1)水体部分比较平坦,很少有突兀的变化,即梯度很小;2)蓝色通道和绿色通道的像素大于红色通道.本文基于这两个特点,对非深海图像进行水体提取.为了提取图像的梯度信息,采用Sobel算子对图像进行处理.设Iinput为原图经过白平衡调整后的图像,Isobel为经过Sobel算子处理后的图像,即Isobel=Sobel(Iinput),Isobel中存储的是Iinput中各点的梯度.设IRinput(x)、IGinput(x)、IBinput(x)是Iinput中x位置处3个通道的像素,Igradsobel(x)是对应的x位置的梯度,令D(x)=max{IGdark(x), IBdark(x)}-IRdark(x),表示x位置, 蓝绿通道的最大值和红色通道的差值.本文采用如下策略进行水体部分的提取:
| $ \left\{ \begin{array}{l} D\left( x \right) > \mu \& I_{{\rm{grad}}}^{{\rm{sobel}}}\left( x \right) < \delta ,\;\;x\;属于水体部分;\\ 其他,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x\;不属于水体部分. \end{array} \right. $ | (11) |
式中:μ为蓝绿通道与红色通道差值的判定阈值,本文经过大量实验,建议μ取50~100;δ为梯度的阈值, 本文建议取5~10.水体提取的部分实验结果如图 2所示.如图 2(a)~(e)所示为输入图像,如图 2(f)~(j)所示为水体提取的结果.

|
图 2 水体提取结果图 Fig. 2 Result of water body extract |
在提取出水下图像中的水体部分后,可以计算3个通道透射率之间的关系.设Ωwater(x)为Iinput中的水体部分,IRavg、IGavg、IBavg为水体部分3个通道的均值,则有
| $ \left. \begin{array}{l} I_R^{{\rm{avg}}} = \mathop {{\rm{avg}}\left( {I_R^{{\rm{input}}}\left( x \right)} \right)}\limits_{x \in {\mathit{\Omega }_{{\rm{water}}}}\left( x \right)} ,I_G^{{\rm{avg}}} = \mathop {{\rm{avg}}\left( {I_G^{{\rm{input}}}\left( x \right)} \right)}\limits_{x \in {\mathit{\Omega }_{{\rm{water}}}}\left( x \right)} ,\\ I_B^{{\rm{avg}}} = \mathop {{\rm{avg}}\left( {I_B^{{\rm{input}}}\left( x \right)} \right)}\limits_{x \in {\mathit{\Omega }_{{\rm{water}}}}\left( x \right)} . \end{array} \right\} $ | (12) |
设Davg为图像中的水体与水面的平均距离,davg为水体与成像平面的平均距离,Rinit、Ginit、Binit为进入水面的红、绿、蓝色光的亮度, pR、pG、pB为水对3种色光的吸收率,sR、sG、sB为水对3种色光的散射率,由于图像中水体部分的光照强度是水面上的光经过Davg+davg的距离的衰减和散射后到达成像平面的光的强度,可得
| $ \begin{array}{l} I_R^{{\rm{avg}}} = {R_{{\rm{init}}}}\exp \left( { - {p_R}\left( {{D_{{\rm{avg}}}} + {d_{{\rm{avg}}}}} \right)} \right)\exp \left( { - {s_R}\left( {{D_{{\rm{avg}}}} + {d_{{\rm{avg}}}}} \right)} \right) = \\ \;\;\;\;\;{R_{{\rm{init}}}}\exp \left( { - \left( {{p_R} + {s_R}} \right)\left( {{D_{{\rm{avg}}}} + {d_{{\rm{avg}}}}} \right)} \right), \end{array} $ | (13) |
| $ \begin{array}{l} I_G^{{\rm{avg}}} = {G_{{\rm{init}}}}\exp \left( { - {p_G}\left( {{D_{{\rm{avg}}}} + {d_{{\rm{avg}}}}} \right)} \right)\exp \left( { - {s_G}\left( {{D_{{\rm{avg}}}} + } \right.} \right.\\ \;\;\;\;\;\left. {\left. {{d_{{\rm{avg}}}}} \right)} \right) = {G_{{\rm{init}}}}\exp \left( { - \left( {{p_G} + {s_G}} \right)\left( {{D_{{\rm{avg}}}} + {d_{{\rm{avg}}}}} \right)} \right), \end{array} $ | (14) |
| $ \begin{array}{l} I_B^{{\rm{avg}}} = {B_{{\rm{init}}}}\exp \left( { - {p_B}\left( {{D_{{\rm{avg}}}} + {d_{{\rm{avg}}}}} \right)} \right)\exp \left( { - {s_B}\left( {{D_{{\rm{avg}}}} + {d_{{\rm{avg}}}}} \right)} \right) = \\ \;\;\;\;\;{B_{{\rm{init}}}}\exp \left( { - \left( {{p_B} + {s_B}} \right)\left( {{D_{{\rm{avg}}}} + {d_{{\rm{avg}}}}} \right)} \right). \end{array} $ | (15) |
对式(13)~(15)进行变换和取对数操作,可得
| $ ln\left( {\frac{{I_R^{{\rm{avg}}}}}{{{R_{{\rm{init}}}}}}} \right) = - \left( {{p_R} + {s_R}} \right)\left( {{D_{{\rm{avg}}}} + {d_{{\rm{avg}}}}} \right), $ | (16) |
| $ ln\left( {\frac{{I_G^{{\rm{avg}}}}}{{{G_{{\rm{init}}}}}}} \right) = - \left( {{p_G} + {s_G}} \right)\left( {{D_{{\rm{avg}}}} + {d_{{\rm{avg}}}}} \right), $ | (17) |
| $ ln\left( {\frac{{I_B^{{\rm{avg}}}}}{{{B_{{\rm{init}}}}}}} \right) = - \left( {{p_B} + {s_B}} \right)\left( {{D_{{\rm{avg}}}} + {d_{{\rm{avg}}}}} \right). $ | (18) |
根据透射率的定义,可得
| $ {t_R} = \exp \left[ { - \left( {{p_R} + {s_R}} \right)d\left( x \right)} \right], $ | (19) |
| $ {t_G} = \exp \left[ { - \left( {{p_G} + {s_G}} \right)d\left( x \right)} \right], $ | (20) |
| $ {t_B} = \exp \left[ { - \left( {{p_B} + {s_B}} \right)d\left( x \right)} \right]. $ | (21) |
综合式(16)~(21),可得
| $ {K_{BG}} = \frac{{\ln {t_R}}}{{\ln {t_G}}} = \ln \left( {\frac{{I_B^{{\rm{avg}}}}}{{{B_{{\rm{init}}}}}}} \right)/\ln \left( {\frac{{I_G^{{\rm{avg}}}}}{{{G_{{\rm{init}}}}}}} \right). $ | (22) |
| $ {K_{BR}} = \frac{{\ln {t_B}}}{{\ln {t_R}}} = \ln \left( {\frac{{I_B^{{\rm{avg}}}}}{{{B_{{\rm{init}}}}}}} \right)/\ln \left( {\frac{{I_R^{{\rm{avg}}}}}{{{R_{{\rm{init}}}}}}} \right). $ | (23) |
| $ {K_{GR}} = \frac{{\ln {t_G}}}{{\ln {t_R}}} = \ln \left( {\frac{{I_G^{{\rm{avg}}}}}{{{G_{{\rm{init}}}}}}} \right)/\ln \left( {\frac{{I_R^{{\rm{avg}}}}}{{{R_{{\rm{init}}}}}}} \right). $ | (24) |
由于水下摄像姿态多变,部分拍摄出的图像不包含水体部分,此时无法进行水体的提取.为了解决该问题,通过图像的直方图计算透射率比.设VhistC为图像C通道的直方图,VhistC(i)为像素i处的直方图大小,VCavg(i-Δw, i+Δw)为直方图在(i-Δw, i+Δw)内的均值,即
| $ V_C^{{\rm{avg}}}\left( {i - \Delta w,i + \Delta w} \right) = \frac{1}{{2\Delta w}}\sum\limits_{i - \Delta w}^{i + \Delta w} {V_{{\rm{hist}}}^C\left( i \right)} . $ | (25) |
式中:Δw为像素值的取值半区间,本文取Δw=5.设VB、VG、VR分别为VBavg、VGavg、VRavg取最大值时对应的i,在式(22)~(24)中,分别将IBavg、IGavg、IRavg替换成VB、VG、VR,即可在图像中不包含水体的情况下,计算KBG、KBR、KGR.
2.5 透射率估计与细化在求出红、绿、蓝3个通道透射率之间的关系后,可以求解透射率.本文求解的方法基于He等[15]提出的暗通道先验原理,针对水下图像进行修改.首先将式(3)、(4)变形为
| $ {J^{{\rm{dark}}}} = \mathop {\min }\limits_{C \in \left\{ {R,G,B} \right\}} \left( {\mathop {\min }\limits_{y \in \mathit{\Omega }\left( x \right)} {J^C}\left( y \right)} \right) \to 0. $ | (26) |
根据式(2),可得
| $ {I_C}\left( x \right) = {J_C}\left( x \right){t_C} + {A_C}\left( {1 - {t_C}} \right). $ | (27) |
式中:C∈{R, G, B},AC为背景光强度的C通道分量.对式(27)等号两边同时取最小值,其中Ω(x)是以x为中心的一小块区域,可得
| $ \mathop {\min \left( {{I_C}\left( y \right)} \right)}\limits_{y \in \mathit{\Omega }\left( x \right)} = {t_C}\mathop {\min \left( {{J_C}\left( y \right)} \right)}\limits_{y \in \mathit{\Omega }\left( x \right)} + {A_C}\left( {1 - {t_C}} \right). $ | (28) |
假设M是R、G、B三个通道中miny∈Ω(x)(JC(y))最小的通道,即
| $ \mathop {\min }\limits_{C \in \left\{ {R,G,B} \right\}} \left( {\mathop {\min \left( {{I_C}\left( y \right)} \right)}\limits_{y \in \mathit{\Omega }\left( x \right)} } \right) = \mathop {\min \left( {{I_M}\left( y \right)} \right)}\limits_{y \in \mathit{\Omega }\left( x \right)} . $ | (29) |
根据式(26)可知,
| $ {t_M} = 1 - \frac{{\mathop {\min \left( {{I_M}\left( y \right)} \right)}\limits_{y \in \mathit{\Omega }\left( x \right)} }}{{{A_M}}}. $ | (30) |
由于水对红色光过高的吸收率,导致水下图像的红色通道分量过低,水下图像的红色通道分量无法正确反映物体本来的颜色,而水对蓝色光和绿色光的吸收率很低且相差不大,因此可以认为水下图像的蓝色通道分量和绿色通道分量可以反映物体本来的颜色.式(26)~(30)中,将C和M的取值修改为C∈{G, B},M∈{G, B}.为了判断M的值,需要判断
| $ \mathop {\min \left( {{J_G}\left( y \right)} \right)}\limits_{y \in \mathit{\Omega }\left( x \right)} = \frac{{\mathop {\min \left( {{I_G}\left( y \right)} \right)}\limits_{y \in \mathit{\Omega }\left( x \right)} - {A_G}}}{{{t_G}}} + {A_G}, $ | (31) |
| $ \mathop {\min \left( {{J_B}\left( y \right)} \right)}\limits_{y \in \mathit{\Omega }\left( x \right)} = \frac{{\mathop {\min \left( {{I_B}\left( y \right)} \right)}\limits_{y \in \mathit{\Omega }\left( x \right)} - {A_B}}}{{{t_B}}} + {A_B}. $ | (32) |
令
| $ {\Delta _{BG}} = \mathop {\min \left( {{J_G}\left( y \right)} \right)}\limits_{y \in \mathit{\Omega }\left( x \right)} - \mathop {\min \left( {{J_B}\left( y \right)} \right)}\limits_{y \in \mathit{\Omega }\left( x \right)} , $ |
用式(31)减去式(32),根据式(10),可得
| $ \begin{array}{*{20}{c}} {{\Delta _{BG}} = \left( {\frac{{\mathop {\min \left( {{I_G}\left( y \right)} \right)}\limits_{y \in \mathit{\Omega }\left( x \right)} - {A_G}}}{{{t_G}}} - \frac{{\mathop {\min \left( {{I_B}\left( y \right)} \right)}\limits_{y \in \mathit{\Omega }\left( x \right)} - {A_B}}}{{t_G^{{K_{BG}}}}}} \right) + }\\ {\left( {{A_G} - {A_B}} \right).} \end{array} $ | (33) |
根据式(26)~(33),计算透射率的流程如下:
1) 假设M=G, 令tG=1-ω×
2) 将tG代入式(33),求解ΔBG.
3) 若ΔBG≥0,则假设成立,根据式(10)计算tB和tR;若ΔBG < 0,则假设不成立,令
| $ M = B,{t_B} = 1 - \omega \cdot \frac{{\mathop {\min \left( {{I_B}\left( y \right)} \right)}\limits_{y \in \mathit{\Omega }\left( x \right)} }}{{{A_B}}}, $ |
根据式(10)计算tR和tG.
在流程中,ω是调整系数,一般取值为0.8~0.95.由于在计算透射率之前对图像进行了最小值滤波,计算出的透射率是粗糙的估计值.为了细化透射率,需要一种可以在保持原图边缘信息的同时,保留透射率图的纹理的滤波器.引导滤波器具有该特点,因此本文在计算出透射率后对透射率图进行引导滤波,以细化透射率图.
2.6 水下图像复原在计算出透射率和背景光强度后,可以根据式(27)复原出图像,但是为了避免因透射率t过低导致的计算溢出, 需要给t一个下界t0, 通常t0取0.10~0.20.于是,可以得到图像的复原公式:
| $ {J_C}\left( x \right) = \frac{{{I_C}\left( x \right) - {A_C}}}{{\max \left\{ {{t_C},{t_0}} \right\}}} + {A_C}. $ | (34) |
图 3给出部分水下图像的复原结果,其中图 3(a)~(e)为原始图像,图(f)~(j)为复原的结果.从图 3可以看出,图像的清晰度得到了很大的提升,色彩得到了一定的恢复.

|
图 3 水下图像的复原结果 Fig. 3 Result of underwater images restoration |
对于深海区域的图像,由于水面的光线无法到达,只能采用人工照明的方式.此时,图像的成像方式与自然光有区别.设Cλ为人工光源的光强,λ∈{R, G, B},pλ为水对波长为λ的光的吸收率,sλ为水中微粒对波长为λ的光的散射率,ρλ(x)为x处物体对波长λ的光的反射率,d(x)为光源与物体的距离,Iλ(x)为图像中位于x处且波长为λ的光的强度,Bλ为人工光照射到水中反射回来的背景光强度,则
| $ \begin{array}{*{20}{c}} {{I_\lambda }\left( x \right) = {C_\lambda }{{\left[ {\exp \left( { - {p_\lambda }d\left( x \right)} \right)\exp \left( { - {s_\lambda }d\left( x \right)} \right)} \right]}^2}{\rho _\lambda }\left( x \right) + }\\ {{B_\lambda }\left[ {1 - \exp \left( { - {p_\lambda }d\left( x \right)} \right)\exp \left( { - {s_\lambda }d\left( x \right)} \right)} \right].} \end{array} $ | (35) |
简化后可得
| $ {I_\lambda }\left( x \right) = {J_\lambda }\left( x \right)t_\lambda ^2\left( x \right) + {B_\lambda }\left( {1 - {t_\lambda }} \right). $ | (36) |
tλ2(x)的出现是因为光源的光经过了来、回两次传递过程,衰减比自然光照明下更大.由于深海区域的图像整体色调偏灰暗,难以区分背景与物体,计算整幅图像3个通道的均值,用3个通道均值的比值计算KBG、KBR、KGR,即
| $ {K_{BG}} = \frac{{I_B^{{\rm{avg}}}}}{{I_G^{{\rm{avg}}}}},{K_{BR}} = \frac{{I_B^{{\rm{avg}}}}}{{I_R^{{\rm{avg}}}}},{K_{GR}} = \frac{{I_G^{{\rm{avg}}}}}{{I_R^{{\rm{avg}}}}}. $ | (37) |
式中:IRavg、IGavg、IBavg为图像3个通道的均值.在计算出透射率和背景光强度后,代入式(37),可得复原后的图像.部分深海区域图像的处理效果如图 4所示,其中图 4(a)~(d)为原图,图 4(e)~(h)为处理后的图像.

|
图 4 深海水下图像复原结果 Fig. 4 Result of deep sea underwater images restoration |
为了评价本文算法的处理效果,选取其他几种水下图像处理算法进行对比.利用Hautiere等[16]的图像评价指标,计算e、r和σ,定量地评估本文算法和其他算法对水下图像清晰度复原的效果.其中,e为复原后图像的视觉边缘的数量的增加量与原图像视觉边缘数量的比值,r为复原后的图像像素点梯度的平均值,σ为像素完全变黑或者完全变白的百分比.e和r越大,表示复原后的图像视觉效果更好;σ越小,表示复原后的图像既没有饱和,也没有模糊视觉边缘.本文算法与其他算法的对比如图 5所示.可以看出,利用本文算法得到的图像与其他算法相比,清晰度和对比度更高,没有出现色彩失真和过度曝光的问题.

|
图 5 本文算法与其他算法视觉增强效果对比 Fig. 5 Comparison of visual enhancement effect between proposed algorithm and other algorithms |
本文算法和其他算法的定量比较如表 1、2所示.可以看出,本文算法在4张图的定量对比中,e均高于其他算法,r均为第二位,并与第一位相差不大,表明本文算法具有较好的视觉增强效果.
| 表 1 本文算法和其他算法在视觉增强效果上的对比 Table 1 Comparison of visual enhancement effect between proposed algorithm and other algorithms |
| 表 2 本文算法和其他算法视觉增强效果对比 Table 2 Comparison of visual enhancement effect between proposed algorithm and other algorithms |
分析水下图像成像的光学原理,针对图像包含水体和不包含水体、有人工光和没有人工光这几种情况进行不同的处理.对于在非人工光照明下的包含水体的图像,提出通过提取图像中的水体,动态地计算红、绿、蓝3种色光在水中的透射率之间关系的算法.利用暗通道先验的原理,计算图像的背景光强度和3个通道的透射率,采用改进的复原算法实现对水下图像的复原.对于不包含水体和人工光照明下的图像,采用修正的方法进行处理.实验结果表明,利用该算法可以提升水下图像的清晰度,在主观效果和客观评价指标上都优于对比算法.
| [1] |
DREWS P, NASCIMENTO E R, CAMPOS M F M, et al. Automatic restoration of underwater monocular sequences of images[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Hamburg:IEEE, 2015:1058-1064. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=7353501
|
| [2] |
ZHAO X W, JIN T, QU S. Deriving inherent optical properties from background color and underwater image enhancement[J]. Ocean Engineering, 2015, 94(1): 163-172. |
| [3] |
HONG S J, LIU P J, LIN J S. Improving the contrast enhancement of oceanic images using modified dark channel prior[C]//International Symposium on Computer, Consumer and Control. Xi'an:IEEE, 2016:801-804. http://ieeexplore.ieee.org/document/7545314/
|
| [4] |
LIU H, CHAU L P. Underwater image color correction based on surface reflectance statistics[C]//Pacific Signal and Information Processing Association Annual Summit and Conference. Hong Kong:IEEE, 2015:996-999. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=7415421
|
| [5] |
SCHETTINI R, CORCHS S. Underwater image processing:state of the art of restoration and image enhancement methods[J]. Advances in Signal Processing, 2010, 2010(1): 1-14. |
| [6] |
赵欣慰. 水下成像与图像增强及相关应用研究[D]. 杭州: 浙江大学, 2015: 3. ZHAO Xin-wei. Theresearch on underwater imaging, underwater image enhancement and relevant applications[D]. Hangzhou:Zhejiang University, 2015:3. http://cdmd.cnki.com.cn/Article/CDMD-10335-1015558771.htm |
| [7] |
ANCUTI C, ANCUTI C O, HABER T, et al. Enhancing underwater images and videos by fusion[C]//Computer Vision and Pattern Recognition. Rhode island:IEEE, 2012:81-88. https://www.computer.org/csdl/proceedings/cvpr/2012/1226/00/011P1A11-abs.html
|
| [8] |
GALDRAN A, PARDO D, PICON A, et al. Automatic red-channel underwater image restoration[J]. Visual Communication and Image Representation, 2015, 26(1): 132-145. |
| [9] |
CHIANG J Y, CHEN Y C. Underwater image enhancement by wavelength compensation and dehazing[J]. IEEE Transactions on Image Processing, 2012, 21(4): 1755-1769. |
| [10] |
SERIKAWA S, LU H. Underwater image dehazing using joint trilateral filter[J]. Computers and Electrical Engineering, 2014, 40(1): 41-50. DOI:10.1016/j.compeleceng.2013.10.016 |
| [11] |
LI C Y, GUO J C, CONG R M, et al. Underwater image enhancement by Dehazing with minimum information loss and histogram distribution prior[J]. IEEE Transactions on Image Processing, 2016, 25(12): 5664-5677. DOI:10.1109/TIP.2016.2612882 |
| [12] |
CHEN Z, WANG H B, SHEN J, et al. Region-specialized underwater image restoration in inhomogeneous optical environments[J]. Optik-International Journal for Light and Electron Optics, 2014, 125(9): 2090-2098. DOI:10.1016/j.ijleo.2013.10.038 |
| [13] |
GHANI A S A, ISA N A N. Underwater image quality enhancement through integrated color model with Rayleigh distribution[J]. Applied Soft Computing, 2015, 27(1): 219-230. |
| [14] |
王子韬. 基于暗原色方法的水下图像增强[D]. 青岛: 中国海洋大学, 2014: 5. WANG Zi-tao. Underwater dark channel prior method of underwater image enhance[D]. Qingdao:Ocean University of China, 2014:5. http://cdmd.cnki.com.cn/article/cdmd-10423-1014328991.htm |
| [15] |
HE K M, SUN J, TANG X O. Single image haze removal using dark channel prior[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(12): 2341-2353. DOI:10.1109/TPAMI.2010.168 |
| [16] |
HAUTIERE N, TAREL J P, AUBERT D. Blind contrast enhancement assessment by gradient rationing at visible edges[J]. Image Analysis and Stereology, 2008, 27(2): 87-95. |
| [17] |
BIANCO N C, MOHAN A, EUSTICE R M. Initial results in underwater single image dehazing[J]. Oceans, 2010, 27(3): 1-8. |



