海量轨迹数据包含了丰富的时空特征信息，记录了人、物或事件的移动轨迹信息，体现了各类移动对象的位置变化，正在深刻地影响着人们的日常生活，在城市规划、智能交通等领域发挥了极大的作用^[1-2].时空查询技术作为位置信息服务的重要技术支撑之一，已经在实际应用中发挥了重要作用，典型的k近邻查询^[3]是时空数据领域广泛应用的查询类型之一，一直是学术界与工业界共同关注的研究热点^[4].

面向移动对象的k近邻查询算法旨在查找距离给定位置或对象最近的k个移动对象.连续k近邻查询是将k近邻算法应用到动态实时环境下，对移动对象进行连续查询以实现实时动态更新.笔者等^[5]面向不确定移动对象，提出针对不确定移动对象的连续k近邻查询处理方法，利用最近一段时间的位置数据预测移动对象在未来Ⅰ时间区间内的可能区域，采用距离区间表示查询对象与可能区域的距离，利用基于模糊可能度判定的排序方法查找k近邻.在面向海量用户查询的实际应用系统中，需要应对高并发量的查询请求需求，串行算法所带来的延迟往往是不能忍受的.另外，针对当前常用计算平台的性能配置，传统单线程查询方案难以充分利用多核处理器的计算优势.基于多核多线程的不确定移动对象连续k近邻查询处理是当前解决这一问题的主要方法.

在实际环境下常常存在一部分邻近的用户同时查询附近的移动对象，这使得查询对象在地理位置上具有较大的空间相关性.将相距较近的查询对象分到相同组别，组内其他用户的查询请求结果往往与邻近用户的结果一致.利用空间相关性对邻近查询对象的结果进行有效复用，可以提升大规模并发查询请求时的处理效率.

在确定数据下的k近邻查询方面，已有较多的研究工作^[6-15].目前，针对确定数据的并行k近邻查询算法已经有所发展^[13-15].赵亮等^[14-15]结合多核多线程技术，提出在道路网下的移动对象连续k近邻查询算法，使用任务并行和数据并行的方法优化连续查询过程，该算法实现了1.51~1.7的加速比.上述算法都是针对确定的移动对象数据，查询的是当前时刻下的k近邻，针对未来一小段时间内的预测问题，没有相应的解决方案.

在不确定数据下的k近邻查询方面，Huang等^[16]考虑不确定速度的移动对象连续k近邻查询问题，提出有效代价的P²KNN (probability-based possible-KNN)算法，在给定的查询时间区间内找出每个时刻上的k近邻对象. Fan等^[21]提出基于道路网的模糊连续k近邻查询算法，处理速度不确定的移动对象查询问题；该方法考虑了移动对象的运动状态，利用基于路网的距离区间模型计算移动对象与查询对象间的最大和最小距离，采用vague模糊集计算k近邻.在传统的单线程环境下，对于大量位置邻近的查询请求都进行k近邻的计算，会造成重复查询，导致响应延迟问题.

本文针对不确定移动对象，提出高效的基于多核多线程的连续k近邻并行查询处理方法.本文的主要贡献如下：1)提出面向不确定移动对象的k近邻查询复用方法，根据临近查询对象之间的运动速度与相对位置确定是否采用查询复用，并确定两查询对象采用复用时的距离边界. 2)提出基于密度网格扩展的多线程负载均衡数据分发方法，利用网格密度对查询请求进行划分, 解决多线程并行条件下的负载均衡问题；将空间位置相邻的查询请求尽量划分到同一线程，提高查询复用率. 3)实现了多线程间的内存共享机制，对计算过移动对象的预测区域通过建立内存共享区来避免重复计算，以实现计算复用. 4)采用Oldenburg城市上模拟的大规模交通数据集，设计综合实验评估，验证了所提算法的有效性与查询性能.

1 问题定义

给出一些重要的定义和表示，对不确定数据的连续k近邻并行查询问题进行描述.

定义1(移动对象)  一个移动对象由唯一的标识符表示，记为o_i.o_i的移动轨迹数据是一个多维时空位置点序列，每个位置点为五元组(t, x, y, v_x, v_y)表示，其中t为采样时间，x、y分别为o_i在t时刻的位置坐标，v_x、v_y分别为o_i在该位置时x和y方向上的速度分量.

对于采样频率不固定的移动对象o_i，轨迹数据可以表示为轨迹序列s_i= {(t₁, x₁, y₁, v_x1, v_y1), (t_j, x_j, y_j, v_xj, v_yj), …(t_k, x_k, y_k, v_xk, v_yk)}.其中，s_{i, j}为移动目标o_i在时刻t_j时的位置，相应地，用s_{i, (j, k)}表示o_i从时刻t_j到时刻t_k区间上所采集的轨迹序列.包含n个移动对象的集合表示为DB_o= {o₁, o₂, …, o_n}，不确定轨迹数据集表示为S={s₁, s₂, …, s_n}.

采用基于时间的滑动窗口W来处理移动对象实时的位置数据，窗口长度标记为w，将最小的时间刻度单位定义为一个时间点，则W包含的时间点数|W| = w.

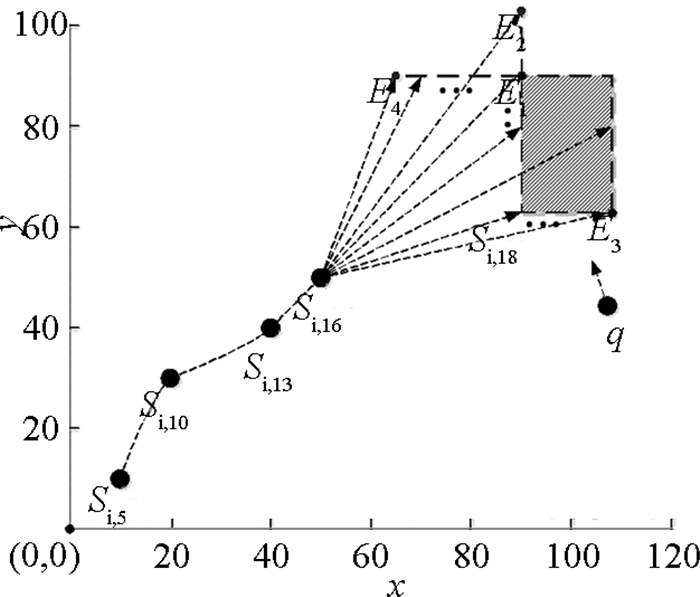
针对基于时间的滑动窗口W的不确定k近邻查询Query(q, I)，于彦伟等^[5]提出基于速度变化率的k近邻预测查询方法Rate，给定一个查询点q，通过预测周围移动对象在I时间区间内可能到达的区域，然后结合vague模糊集对q在下一时刻的k近邻进行排序.如图 1所示，s_i为移动对象o_i的轨迹数据，包含4个位置点.当q查询预测t=18(当前时间t_c=17，I=1)时的k近邻时，首先根据下式预测o_i在t=18时可能到达的区域s_{i, 18}.

$ \left. \begin{array}{l} {s_{i, {\rm{ }}{t_{\rm{c}}} + I}} = {s_{i, {t_j}}} + {v_{i, j}}(I + {t_{\rm{c}}} - {t_j}) + \frac{1}{2}a{(I + {t_{\rm{c}}} - {t_j})^2}, \\ {a_{i, j}} = \frac{{\Delta v}}{{\Delta t}} = {\rm{ }}{v_{i, j + 1}} - {v_{i, j}}{t_{j + 1}} - {t_j}. \end{array} \right\} $

(1)

当采用与当前时间临近的多个以往时间点上的速率变化时，可得一块可能到达的区域，如图 1的阴影部分所示. Rate方法既考虑了最近一个时刻的位置与速度的权重，又考虑了最近一段时间速度与采样时刻的变化情况.采用多速率变化的Rate方法获取的可能到达区域有效刻画了不确定移动对象在t_c+I区间内可能存在的位置.

使用最近距离与最远距离的区间[d, D]为查询对象到移动对象间的距离.对于查询对象q到两个移动对象o₁、o₂的距离区间，分别设为[d₁, D₁]和[d₂, D₂].若要获得q的k近邻，则需要比较q到不同移动对象的距离区间，Rate采用vague模糊集方法，利用模糊可能度判定的方法排序k近邻.如性质1所述，若q到o₁距离相比q到o₂的距离更近的概率p(o₁＜o₂)大于等于0.5，则满足D₂-d₁≥ D₁-d₂.通过验证D₂-d₁≥ D₁-d₂是否成立，可以判断查询对象q到o₁是否更近于o₂.若o₁与除o₁之外的移动对象o_i都计算一遍p(o₁＜o_i)，则可以确定o₁是查询对象q的第几近邻.对所有移动对象检查一遍，可以获取到查询对象q的k近邻.与Huang等^[16]提出的P²KNN方法相比，Rate方法的查询正确率平均提高18%，效率平均提升66%.

性质1  p(o₁＜o₂) ≥ 0.5当且仅当D₂-d₁≥ D₁-d₂.

问题定义(不确定移动对象k近邻多线程查询Multi-Query(Q, I)).给定移动对象集合DB_o、不确定轨迹数据序列S、时间窗口W、当前查询时刻t_c、查询请求集合Q、近邻数量k和线程数M，Multi-Query(Q, I)查询从M个线程并行返回Q中所有查询对象q在接下来时间I内最可能的k个最近邻移动对象.

涉及到的符号及相应含义如表 1所示.

2 基于多线程的k近邻并行查询算法 2.1 多线程k近邻并行查询框架

针对不确定移动对象，给出基于多核多线程的连续k近邻并行查询Multi-Query(Q, I)算法的框架，如算法1所示.

算法1  Multi-Query(Q, I)

Inputs：DB_o, S, W, Q, k, M;

Outputs：k-NNs for each query object in Q;

01：Q_i=1, ..._{, M} gridPartition(Q, M);

02：FOR i← 1 to M PAR-DO

03：QueryThread(Q_i, I).

采用基于密度网格扩展的多线程数据分发方法，将查询请求根据地理空间划分成数量大致相等的M份；M个线程并行执行使用数据复用优化的k近邻查询算法来获取查询对象的前k近邻. 2.2与2.3节将分别介绍查询复用优化和基于密度网格扩展的数据分发方法.

2.2 邻近查询对象间的查询复用

考虑到用户在进行k近邻查询时当前位置是已知的并且查询的是在未来很小一段时间I内的大致位置，使用匀速运动方式对查询对象在I时间区间的位置进行预测.

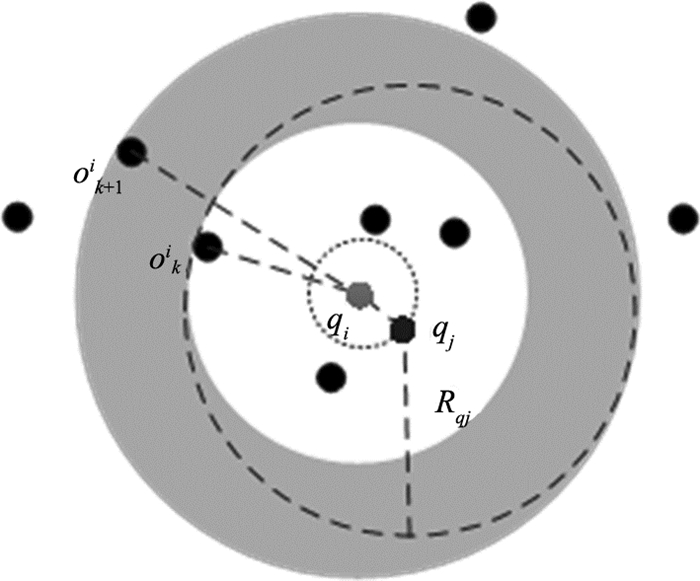
对于同一时刻发起请求的多个查询对象，若相距较近，则考虑是否可以复用已查询到的结果来减少冗余的k近邻查询过程.如图 2所示，设定已对q_i查询完毕，并返回q_i的k近邻集合O_kⁱ.当q_j进行查询时，为了能够复用q_i的查询结果，需要考虑q_j与q_i之间的距离d(q_i, q_j)可以直接复用q_i的查询结果时的条件.若使得q_j的k近邻刚好为q_i的k近邻，如图 2的虚线圆圈，即q_j的第k近邻刚好覆盖到o_kⁱ，不超出o_k+1ⁱ，则需要满足2R_qj+d(q_i, o_k+1ⁱ) -d (q_i, o_kⁱ)=2d (q_i, o_k+1ⁱ).R_qj=d(q_i, q_j) +d(q_i, o_kⁱ)，可以得出d(q_i, q_j)=[d(q_i, o_k+1ⁱ)-d (q_i, o_kⁱ)]/2.为了使得q_j的k近邻刚好包含o_kⁱ, 而不包括o_k+1ⁱ，所以d(q_i, q_j)应该满足[0, (d (q_i, o_k+1ⁱ)-d (q_i, o_kⁱ))/2), 才能直接复用q_i的计算结果.

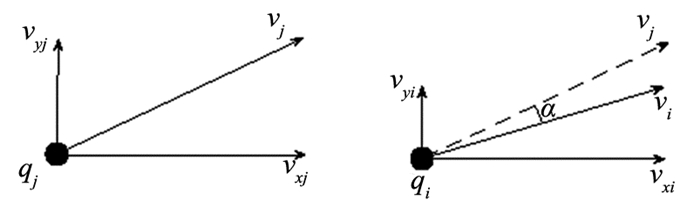
针对移动对象的k近邻查询预测问题，在复用查询结果时需要考虑查询对象之间的速度方向关系.比如两个查询对象相背而行，则在未来I时刻内对查询结果进行复用，将会导致查询准确率降低.利用两查询对象的余弦相似度来判定是否采用查询复用.如图 3所示，设定当前q_i已经查询完毕，继续对q_j进行查询，根据式(2)的余弦相似度，利用两查询对象的速度向量 v _i与 v _j计算相似度sim(q_i, q_j).在实际情况下，同向运动的查询对象之间的距离较近较小，相似度越高，因此考虑速度方向夹角α∈[0, π/6]时对查询点进行查询复用，即当余弦相似度区间满足[$\sqrt 3 $ /2, 1]时考虑查询复用.

$ {\rm{sim}}({q_i}, {q_j}) = {\rm{cos}}\alpha = \frac{{\mathit{\boldsymbol{v}}{_i}\cdot{\rm{ }}\mathit{\boldsymbol{v}}{_j}}}{{\left| {{\rm{ }}\mathit{\boldsymbol{v}}{_i}} \right||\mathit{\boldsymbol{v}}{_j}|}}. $

(2)

算法2   QueryThread(Q, I)

Inputs：DB_o, S, W, Q, k;

Outputs：k-NNs for each query object in Q;

01：FOR q_i∈Q DO

02：IF QRs= $\phi $ THEN

03：Can_i←PR-Tree(S, MAX_HITS, q_i);

04：ELSE

05：index ← reuseQuery(q_i, QRs);

06：IF index ≥ 0 THEN

07：QR_i ← QRs.get(index);

08：QR_i.isReuse ← TRUE; Goto line 12;

09：ELSE

10：Can_i←PR-Tree(S, MAX_HITS, q_i);

11：QR_i←Query(q_i, Can_i, I);

12：QRs←QRs ∪ QR_i;

13：RETURN QRs;

reuseQuery(q_i, QRs)

14：FOR QR_j in QRs DO

15：IF!QR_j. isReuse THEN

16：IF sim(q_i, q_j)∈[ $\sqrt 3 $ /2, 1] AND

d (q_i, q_j) < (d(q_j, o_k+1) -d(q_j, o_k))/2

17：THEN RETURN j;

18：RETURN -1;

Query(q_i, Can_i, I)

19：mutex ← 1;

20：FOR o_j∈ Can_i DO

21：s_j ←get(S, o_j);

22：IFs_{j, tc+I} $ \notin $ MS_tc+I THEN

23：P(mutex);

24：compute s_{j, tc+I};

25：MS_tc+I ←MS_tc+I ∪ {s_{j, tc}+I};

26：V(mutex);

27：QR_i←queryKNN(q_i, S_{{Can}i, tc+I});

28：RETURN QR_i;

算法2描述多线程下考虑查询复用时的k近邻查询算法.若当前查询为第一个查询对象q_i(i=1)，则采用PRTree索引获取在当前时刻t_c下q_i周围MAX_HITS个移动对象集合Can_i作为q_i的k近邻的候选项集合. 04~09行描述的是对查询点q_i检查是否可以采用查询复用的过程.使用reuseQuery()函数从已查询过的查询点中检查是否满足复用条件，即速度相似度与距离是否在复用范围以内；如果满足条件，则返回复用结果，否则，回退到最原始的计算方法，即对查询点的临近对象使用PR-Tree进行过滤(第10行).为了避免查询复用的漂移，每次查询复用只针对真实计算过的k近邻查询，不会对复用结果再次复用，因此使用QR.isReuse进行区分，如第15行所示.第11行表示采用不确定k近邻查询方法Rate返回q_i的前k近邻.为了共享已经计算的移动对象区域预测结果，建立内存共享区MS_tc+I用于暂存已经计算过的s_{j, tc+I}的信息，如第20~27行所示.对于q_i的每个候选邻近对象o_j，首先在共享内存区MS_tc+I中查找在t_c+I时刻的预测区域s_{j, tc+I}，若不存在，则计算出o_j在t_c+I时刻的预测区域s_{j, tc+I}.第27行描述的是针对q_i对已经计算出的候选区域集合S_{{Cani}, tc+I}查找q_i的前k近邻.有关MS_tc+I共享内存区的计算复用详细实现方法见2.3节的计算复用.考虑到多线程操作，因此采用加锁操作，避免重复计算(第23、26行).

2.3 负载均衡的多线程k近邻查询

针对多线程并行k近邻查询，对移动对象计算过的预测区域进行共享是需要考虑的关键问题.为了使得更多相邻查询对象复用查询的计算结果，需要对查询对象集合Q在地理空间上进行划分.引入计算复用与密度网格扩展划分的概念来解决以上两个关键问题.

计算复用.在同一线程内，只有当两查询对象满足复用距离时才能直接复用查询结果.针对不确定移动对象的k近邻查询，对查询对象周围的移动对象可能到达区域的计算占据较大的时间开销.对于互相之间距离较近的查询对象，查询范围通常存在较大的重叠区域，因此，在满足复用条件的前提下，可以直接共享已完成的移动对象可能到达区域的计算结果.在多线程并行计算时，不同线程上的查询对象的查询所涉及到的相关移动对象集合往往存在重叠区域.为了使得不同线程上查询对象能够共享已完成的移动对象可能到达区域的计算结果，实现多线程内存共享将有效加大查询过程中的计算复用.为了避免重复计算，通过建立计算结果内存共享区MS_future来暂存已计算的移动对象集合在未来时间future = t_c+I时刻可能到达的区域，以实现计算复用.

密度网格扩展划分.在实际应用中，大部分查询对象的分布是不均匀，例如在城市中，人口密集区域、商场商业区以及交通站点等位置查询请求往往过于密集，住宅区、公园、工厂等区域查询比较稀少.在多线程数据分发时，采用随机方式虽然能够保证负载均衡，但会导致查询对象间的数据复用率降低.网格划分是目前为止公认较高效的空间划分方法.为了提升算法整体效率，即尽量增加查询复用率，又保证负载均衡，本文结合查询对象在位置上的相关性，提出基于密度网格扩展的数据分发策略.

为了方便描述，定义查询对象集合Q = {q_i | i = 1, 2, …, n }，划分集合为Q_M = {Q_i | i = 1, 2, …, M }，| ${\bar Q}$ | =|Q|/M，ρ_{j, k}表示网格中对应单元格< j, k>(第j行第k列)的密度，即所包含查询对象的数量.首先，对Q集合所在区域进行网格划分，将查询对象在空间位置上映射到相应网格内，根据每个网格包含的查询对象数量计算网格密度ρ_{j, k}并按照降序排序得到网格密度列表L_grid.然后，从L_grid的第一个网格开始，执行扩展操作，直至得到M个划分.若当前网格密度ρ_{j, k} < |${\bar Q}$ |，则使网格< j, k>向周围未划分的网格进行扩展，扩展方式按以下原则进行.1)若当前网格周围的临近网格未被其他网格扩展，则当前网格向周围网格扩展，直到网格< j, k>及扩展网格所包含的查询对象数量刚好不小于1.2 ${\bar Q}$结束(根据经验可知, 将0.8 ${\bar Q}$ ~1.2${\bar Q}$视为负载平衡状态). 2)若当前网格周围的临近网格已被扩展或临近网格不包含任何查询对象，则不再对当前网格进行扩展.在扩展操作完毕后，将会得到M个划分，接下来继续执行平衡操作.若存在|Q_i| < 0.8|${\bar Q}$ |，首先将未划分的网格归入到Q_i中，使得满足0.8|${\bar Q}$ |≤ |Q_i| ≤1.2|${\bar Q}$|.若已不存在未划分的网格, 则循环选择Q_j=max{|Q_j| | j = 1, 2, …, M}，并将Q_j所包含的查询对象按以下平衡原则分配到Q_i.1)若Q_j是由高密度网格扩展获得，则选择某扩展网格的查询对象分配到Q_i. 2)若Q_j仅包含一个高密度网格，则随机选取Q_j中的(|Q_j|-Q_i)/2个查询对象到Q_i.该密度网格的划分方法优先将密集区域及相邻网格划分在同一线程，提高了数据复用率；考虑了每个划分包含数量相近的查询对象，进而实现了多线程间的负载均衡.

算法3. gridPartition(Q, M)

Inputs：Q, M;

Outputs：Q_M = {Q_i | i = 1, 2, …, M};

01：G← mapping(Q); /^*Mapping Q into Grid^*/

02：L_grid←density(G);

03：WHILE |L_grid|≠0 DO

04：g←L_grid.getfirst();

05：Q_i←expendCell(g); i++;

06：IF i = M THEN break;

07：Q←fetchQ_i(Q, L_grid);

08：Q←balanceMParts(Q);

09：RETURN Q;

balanceMParts(Q)

10：FOR i ← M to 1 DO

11：IF |Q_i| < 0.8${\bar Q}$ THEN

12：Q_j=max{|Q_j| | j=1, 2, …, M};

13：move q from Q_j to Q_i;

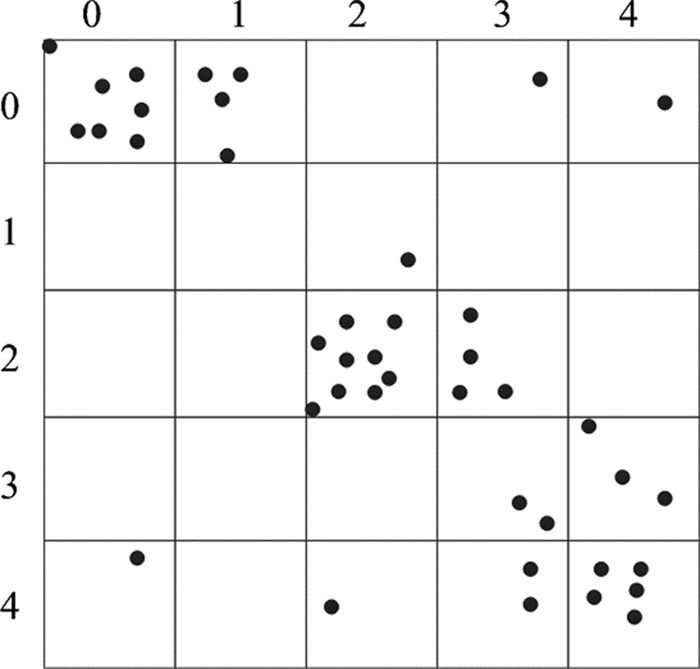
算法3描述了基于密度网扩展的数据分发策略.首先将所有查询对象映射到网格，得到按照网格密度降序排列的列表L_grid，如01、02行所示.然后循环从L_grid取出第一个网格，对该网格进行扩展，直到获取M个划分(如03~06行所示).扩展过程按照所述的2点扩展原则进行扩展，每次扩展后网格从L_grid中删除.之后，将剩余L_grid分配到较少的划分中(第07行).最后，根据M个划分的查询数量，使用平衡原则对Q的M个划分进行平衡操作，如balanceMParts(Q)函数.

如图 4所示，假设当前线程数M=4，|Q|=40，此时每个线程应当大致分得${\bar Q}$ =40/4=10个查询点.首先将查询点所覆盖的区域划分成5×5网格，并将查询点映射到相应网格，按照网格密度降序排列得到列表L_grid= {ρ_{2, 2}=9, ρ_{0, 0}=7, ρ_{4, 4}=5, ρ_{0, 1}=4, ρ_{2, 3}=4, ρ_{3, 4}=3, ρ_{3, 3}=2, ρ_{4, 3}=2, ρ_{0, 3}=1, ρ_{0, 4}=1, ρ_{1, 2}=1, ρ_{4, 0}=1, ρ_{4, 2}=1}.第一步首先得到ρ_{2, 2}=9 < 1.2 |${\bar Q}$|，因此对网格< 2, 2>进行扩展，当扩展到{ < 2, 2>, < 2, 3>, < 1, 2>}后得到划分|Q₁|=14, 以满足|Q₁|>1.2 |${\bar Q}$|.此时，L_grid={ρ_{0, 0}, ρ_{4, 4}, ρ_{0, 1}, ρ_{3, 4}, ρ_{3, 3}, ρ_{4, 3}, ρ_{0, 3}, ρ_{0, 4}, ρ_{4, 0}, ρ_{4, 2}}.继续计算Q₂，由于ρ_{0, 0} < |${\bar Q}$|，从单元格<0, 0>向周围扩展；当扩展至{ < 0, 0>, < 0, 1>}后，周围不再有包含查询点的网格，停止扩展.此时，Q₂所包含的查询对象数量为|Q₂|=11. L_grid={ρ_{4, 4}, ρ_{3, 4}, ρ_{3, 3}, ρ_{4, 3}, ρ_{0, 3}, ρ_{0, 4}, ρ_{4, 0}, ρ_{4, 2}}.继续计算Q₃，对ρ_{4, 4}扩展得到单元格{ < 4, 4>, < 3, 3>, < 3, 4>, < 4, 3>}，对应划分|Q₃| =12.此时，L_grid={ρ_{0, 3}, ρ_{0, 4}, ρ_{4, 0}, ρ_{4, 2}}，对应最后一个划分|Q₄|=4.划分阶段结束，由于存在|Q₄| < 0.8 |${\bar Q}$|，进入平衡阶段，通过选择Q₁ = max{|Q_j| | j = 1, 2, 3, 4}对Q₁进行再分配.由于Q₁是由高密度网格{ < 2, 2>, < 2, 3>, < 1, 2>}得到，将单元格< 2, 3>对应的查询点分配给Q₄，刚好得到|Q₄|=8.此时，所有划分都满足平衡状态，最终基于密度网格扩张的划分结果为|Q₁|=10，|Q₂|=11，|Q₃|=12，|Q₄|=8.

3 实验与结果 3.1 实验数据与测试方法

实验平台采用Intel Xeon E5-2660处理器，8核，48 GB内存，Windows Server 2012操作系统，所有算法全部由Java实现.

实验数据.数据集Oldenburg由Thomas Brinkhoff实现的基于网络的移动对象生成器，该生成器可以生成德国奥尔登堡城市的交通数据^[23].使用的数据包含5 000个移动对象、905 000个位置采样点；根据生成器的参数设置，生成的移动对象的速度类型包含6类(类似于行人、自行车、机动车等不同的速度).为了模拟不确定数据，将该数据集分为3个版本，分别为全部数据Full、随机删除10%采样点的数据集Full-10%以及随机删除20%采样点的数据Full-20%.

评估方法.采用准确率评估方法，Precision=(R∩D)/R，其中D为查询时刻从完整数据中查询的真实k近邻结果，R为所提算法在删除数据之后获得的k近邻预测结果.对于效率评估，通过变化各重要参数，测量单次查询所执行的CPU时间来评估算法的性能.

对比方法.对提出优化方法的组合策略及Rate方法进行综合对比分析.组合方案如下：不考虑数据复用、随机分发查询请求、无共享内存的多线程查询方法(basic random no-shared memory, BRN)；不考虑数据复用、随机分发查询、共享内存的多线程查询方法(basic random shared memory, BRS)；考虑数据复用、随机分发查询、共享内存的多线程查询方法(optimized random shared memory, ORS); 考虑数据复用、密度网格分发查询、共享内存的多线程查询处理方法(optimized grid shared memory, OGS).所有方法的实现都采用PR-Tree索引^[24].

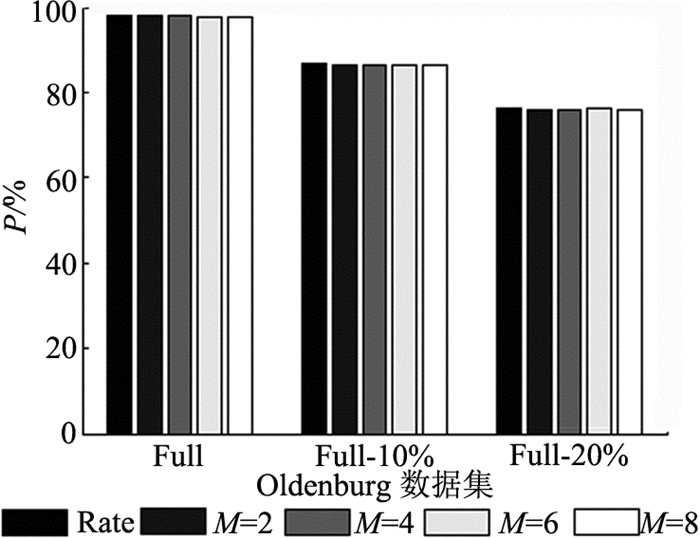
3.2 实验和结果

正确性评估.首先，在Oldenburg三组数据集上验证了所提方法的正确率，并与串行算法Rate进行对比分析.参数设置如下：W=10，查询对象数量Q=1 500，I=1，查询时间间隔Δt=2，k=40.如图 5所示为Rate与OGS方法分别在2、4、6、8个线程上并行查询的正确率P.图中, Full为所有样本，Full-10%表示在原有数据的基础上删除了10%，Full-20%表示在原有数据的基础上删除了20%.可以看出，在3个数据集上，OGS方法在多个线程上的并发查询结果几乎都与Rate方法的查询结果完全一致，验证了OGS方法的有效性.随着删除数据的增多，不确定移动对象的数量增加，导致所有算法的正确率都下降，但在Full-20%数据集上仍能达到近80%的正确率.

性能评估.下面在Full-20%数据集上评估重要参数对所提算法查询效率的影响.在没有明确指定参数变化下的默认参数设置如下：W=10，查询请求数量Q=500，I=1，查询时间间隔Δt=2，k=40，线程数M=8.

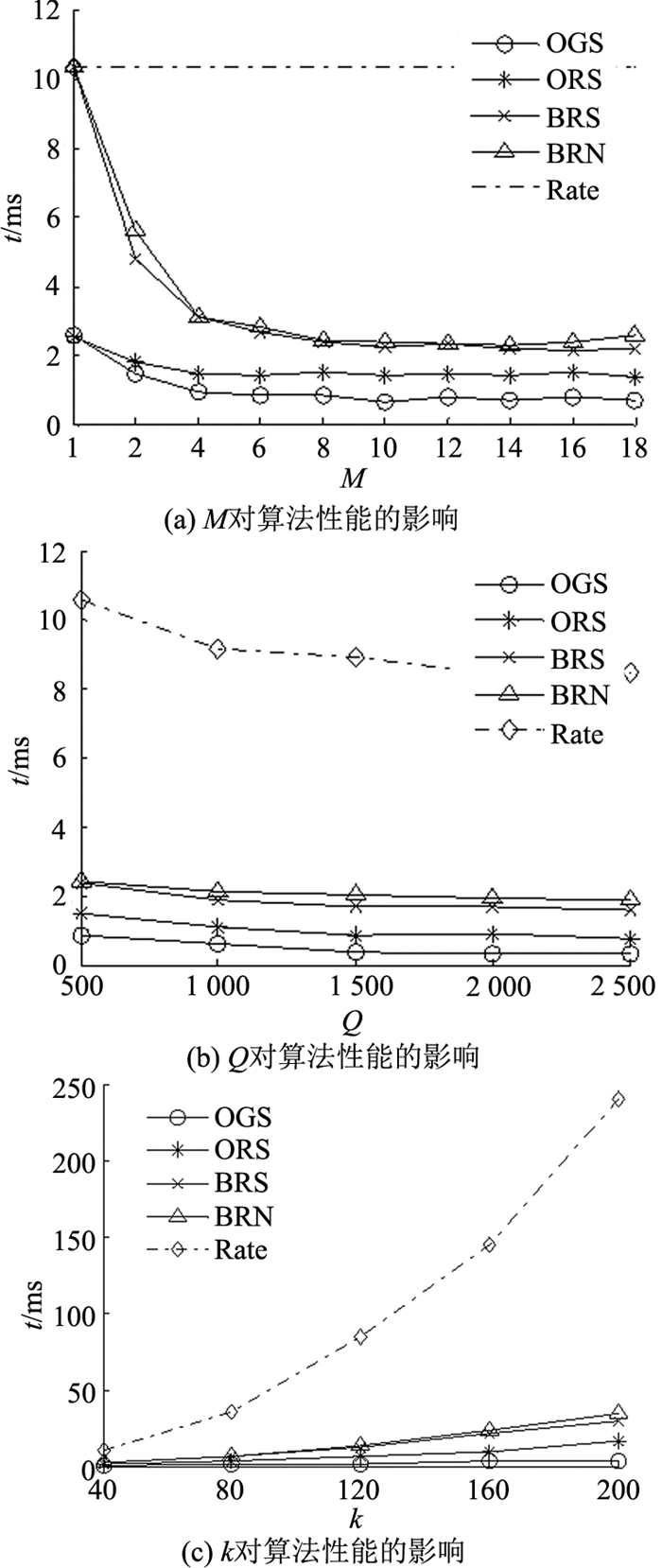
首先，通过变化M评估并行线程数量对4种组合算法性能的影响.如图 6(a)所示，采用数据复用与密度网格分发的OGS方法所消耗的时间最少，采用数据复用与随机分发的ORS次之，BRN使用最多的CPU时间.随着M的增加，单次查询的平均时间不断降低，但是当M≥10以后，所有算法趋于平稳.这是由于该实验平台CPU为八核，当线程数超过该数量后，不能进一步提升并行度；当线程过多时，单核上线程之间的切换将带来一定的开销.当M=10时，OGS方法相对于串行Rate的加速比已达16.59.通过对比OGS、ORS与BRS、BRN方法可以发现，采用查询复用方法对算法效率有很大的提升.通过对比OGS与ORS方法可以发现，利用密度网格分发策略进一步提升了数据复用率.

图 6(b)描述了Q对算法性能的影响.随着Q的不断增加，虽然算法消耗的总时间是上升的，但是单次查询的平均时间呈下降趋势.这是因为Q越多，相近的查询请求越多，数据复用率越高.同样，OGS方法使用了最少的CPU时间，当Q=2 500时，OGS方法的效率相比于BRN提高了5.27倍.这证明了所提的OGS方法相对于Q具有较高的可扩展性.

图 6(c)描述了参数k对算法效率的影响，当k增大时，单次查询的平均消耗时间都上升，这是因为当增大k时，PRTree索引需要搜索的临近移动对象数量相应增加，需要计算的可能到达的区域与排序邻居数量增加，导致平均消耗时间增加.从总体上来看，OGS消耗最少的时间，并且增长缓慢.与BRN、BRS和ORS相比，OGS分别平均提升了536%、481%和200%的效率.这验证了OGS相对参数k具有较好的可扩展性.

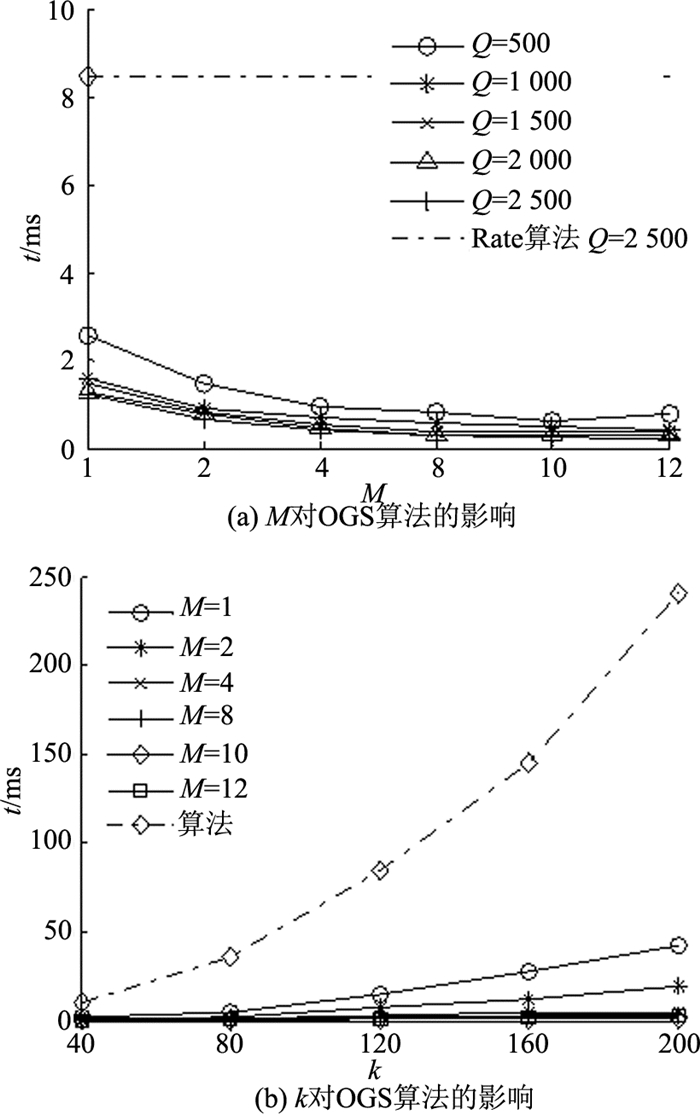
为了进一步考查OGS算法的扩展性能，分别通过变化M、k、Q对算法进行评估.首先，评估了M对不同查询请求数量下OGS算法性能的影响.如图 7(a)所示，当增大M时，OGS算法处理每次查询请求所消耗的时间不断降低，当线程数达到10之后算法性能趋于平稳，这是由硬件平台的限制导致的.当Q增多时，单次查询请求的平均消耗时间降低.与Rate算法相比，当M=8，Q=2 500时，并行后的加速比最高可达28.27.

图 7(b)给出参数k对各线程数下OGS算法效率的影响.可以发现：相对于参数k，OGS算法在多线程环境下展现了更好的扩展性.随着k的增大，单次查询的平均响应时间都上升，但线程数越多，上升越缓慢.这说明所提的复用策略在多线程下有效提升了算法效率.当M=8时，与Rate算法相比，效率平均提升了37倍.

4 结语

本文提出多核多线程环境下面向不确定移动对象的连续k近邻并行查询算法.针对不确定移动对象已计算的可能到达区域，设置内存共享区用于不同线程之间的计算复用.针对空间位置邻近的查询请求，设计查询复用的方法，确定了复用条件.利用密度网格扩展的方法，实现了负载均衡的多线程数据分发.实验结果表明，提出的多线程方法与串行算法相比，加速比达到16.5以上.下一步将考虑引入路网和城市兴趣点，进一步研究有效的不确定移动对象连续k近邻并行查询策略.