2. 山东高速股份有限公司, 山东 济南 250000
2. Shandong High-Speed Group Company, Jinan 250000, China
传统的环形交叉口一般采用无信号的让行规则控制方法.实践证明,当交通流负荷度为较低或中等水平时,无信号控制环形交叉口具有比普通平面交叉口更加安全、高效的特点[1].随着我国城市建设的高速发展,机动车保有量逐年增加,城市关键环形交叉口车流趋于密集,因而车辆进出环道的难度加大,由此导致的运行效率降低、交通事故频发等问题日益凸显.在交通流运行高峰时段,将环形交叉口的交通控制等级由无信号的让行规则控制提升至交通信号控制,已成为环形交叉口研究的必然趋势[2].
目前,国内外学者在对环形交叉口交通信号控制方法的研究中,按照控制类型主要分为2类:1)单重信号控制,这种方法起源于20世纪70年代,由Millard等[3-4]最先提出,随后在各国广泛应用,单重信号控制主要采用两相位或四相位形式,只对入环车辆进行定时控制,在一定程度上控制了环内交通量,避免环内拥堵.2)为了避免环内左转流与直行车流冲突, Yang等[5-7]分别提出并改进左转二次停车控制方法,基本原理是在环道上设置第2条停车线,分离左转车辆与入环车辆之间的冲突.该方法虽然在一定程度上增大了环形交叉口的通行能力,但增加了左转车辆停车次数;在左转交通量大的情况下,环内的二次控制易导致排队车辆溢出至上游出入口处,阻塞出环车流,造成严重的环内“死锁”.
现有的环形交叉口信号控制方法主要集中于解决高峰时期普通四路环形交叉口信号控制问题,鲜有讨论五路及以上的多支路环交的控制问题.该类环形交叉口在城市交通运行中承担着更重要的作用,一方面,环形交叉的形式可以减少多条支路相交时交通流运行的冲突点,避免复杂的相位设置,提高交叉口车流运行的安全性和高效性;另一方面,多支路环形交叉口的交通流量相对较大,环内交通组织更复杂,为了提高运行效率,合理的信号控制方法更重要.为了应对现有研究的局限性,本文提出基于模型预测控制(model predictive control, MPC)的环形交叉口轮放式控制方法,旨在为城市环形交叉口,尤其是五路以上的多支路环交信号配时方法提供理论依据.
本文主要从相位结构设计、配时方案设计、相位搭接规则3个方面,研究基于MPC的环形交叉口轮放式信号配时方法,为环形交叉口的信号控制提供理论依据和实施方法.
1 相位结构设计相位显示顺序是相位结构设计的集中表现形式,它根据环形交叉口道路空间的几何条件、交通流需求特征以及信号控制设备的技术条件,按照一定的原则,为不同行驶方向的交通流赋予相应的通行权利,即定义不同流向的交通流通行权的传承顺序,实现通行时空资源的合理分配[8].在分析环形交叉口交通流放行特点的基础上,设计顺时针轮放式的相位结构.
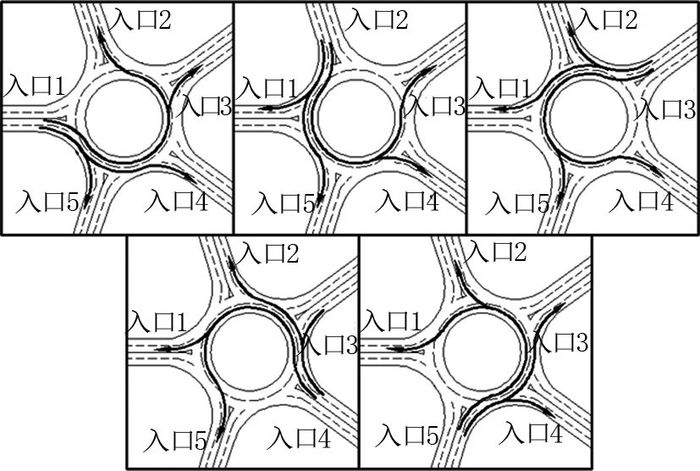
以一个五路环形交叉口为例,采用如图 1所示的顺时针轮流放行模式.按照顺时针顺序,依次为环形交叉口各个入口的机动车相位赋予通行权.这种车流逆时针绕环行驶、相位显示顺序顺时针更迭的控制方式,可以从空间上减小相位更迭时下一相位驶入环道的车流与上一相位未驶出环道车流的冲突和交织,从而提升环形交叉口的运行效率.
|
图 1 环形交叉口顺时针轮放模式相位次序图 Fig. 1 Clockwise phase sequence pattern of roundabouts |
以图 1中相位一和相位二的更迭为例,环形交叉口入口1绿灯相位结束,入口2绿灯相位开始时,驶入环道的车流在前1/5环道内不会遇到冲突车流,并且当头车驶近入口1时,上一相位的末车已驶离入口1附近环道.这种相位显示顺序从空间上减少了车流的交织和冲突,在时间上节约了车辆清尾时间,合理利用了环形交叉口时空资源,交叉口的运行更加安全、高效.
设计的轮放式相位结构只表示相位更迭的次序,不限制同一时刻放行车流的入口数,即同一时刻可以出现多进口多股车流同时放行的情况,这些情况将在2、3章中作具体说明.
2 配时方案设计提出基于MPC理论[9]的环形交叉口入口信号配时参数的计算方法,采用动态环形交叉口交通流模型作为过程预测模型,以系统总运行时间为控制目标进行最优化控制.在反馈调节机理下,滚动优化各控制周期各个入口的绿信比,达到系统最优控制的目的.
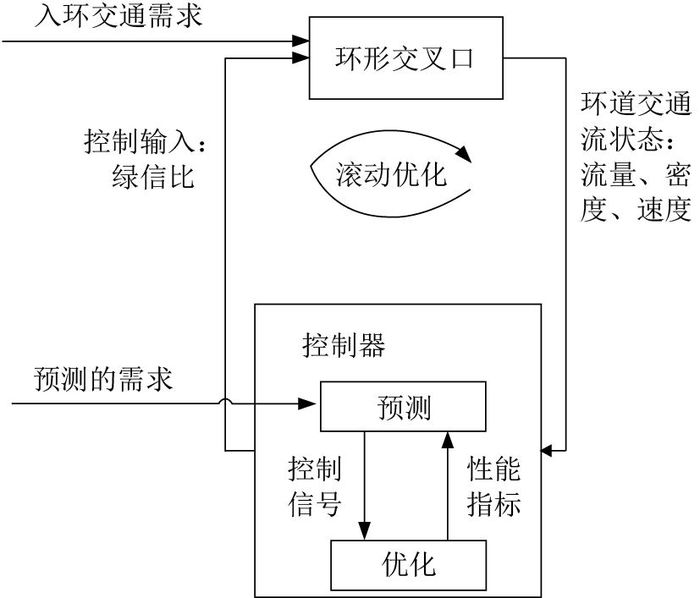
2.1 MPC研究环境及参数定义将MPC理论应用于环形交叉口得到的在线控制方法的基本原理如图 2所示.该基本原理可以概括为:在系统采样的每一个时刻,通过预测模型对环形交叉口未来的行为进行预测,基于性能指标进行优化,求解优化目标函数得到控制参数(绿信比)后作用于环形交叉口;将预测时域向前推进一步,并不断重复该过程[10].模型预测控制采用多步预测、滚动优化及反馈调节等控制思想,主要的操作步骤如下.
|
图 2 模型预测控制方法的原理图 Fig. 2 Principle of model predictive control method |
1) 建立一个预测模型,预测环形交叉口在给定控制信号情况下的交通流运行状态变化.
2) 选择一个性能指标作为目标函数,求解该目标函数最优化时的最佳信号配时参数,并将该配时参数作用于环形交叉口.
3) 在每个滚动周期,控制器根据实时检测的交通流数据确定环形交叉口的当前状态,重新进行信号配时参数的优化计算.在优化计算过程中, 预测时长包含很多个滚动周期,以考虑控制在今后相当长时间内的影响.优化得到的最优信号配时参数只作用于预测时长内的第一个滚动周期.在下一个滚动周期, 控制器根据实测的交通数据更新系统状态, 重新执行优化计算[11].
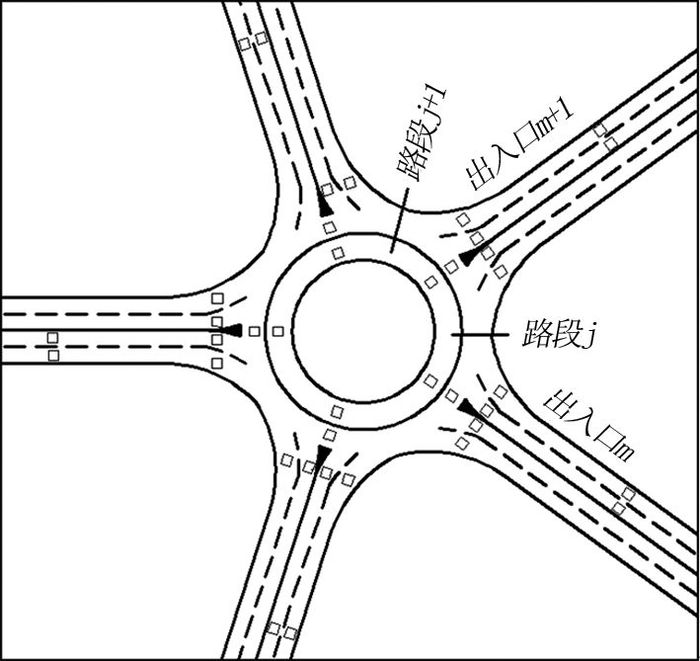
对MPC模型的主要参数进行如下定义:在一个滚动优化时域内,如图 3所示,定义一个预测范围Np,每一次滚动优化的任务为在预测范围[kaΔT, (k+Np)aΔT]内目标函数最优,此处ΔT为预测模型取样周期.为了方便计算,将预测模型取样周期的整数倍aΔT,作为控制信号更新的周期,即环形交叉口的信号周期.
|
图 3 环形交叉口路段划分及检测器布设方法 Fig. 3 Road segment and detector layout of roundabouts |
为了简化目标函数最优化的计算,定义一个控制范围Nc(Nc≤Np),即在求解目标函数最优的过程中,只在控制范围[kaΔT, (k+Nc)aΔT]内采用变化的入口绿信比,之后绿信比保持不变,于是可以有效地减小计算的复杂性.在每一个滚动优化时域内,会求得控制范围Nc内所有信号周期的绿信比,只将第一个配时参数作用于环形交叉口,滚动时域向前移动一个信号周期时长,进行新一轮的目标函数求解.
2.2 过程预测模型建立过程预测模型的功能是根据环形交叉口交通流状态历史信息和未来的输入信息预测未来的交通流状态.预测结果用于求解优化目标函数的最优值,所以过程预测模型的预测参数选择非常重要.对于环形交叉口,入口处的绿灯时间取决于环道交通流状态和入口排队长度[12],所以建立环道交通流密度、速度、流量以及入口排队长度等状态参数的过程预测模型.过程预测模型依靠线圈检测器采集输入参数,检测器的布设方法如下.
如图 3所示为以一个典型的五路环形交叉口为例的检测器布设图.出入口编号用m{m=1, 2, …, 5}表示,环道内检测器将环道划分为5个路段,路段编号用j{j=1, 2, …, 5}表示,出入口和路段编号均按照逆时针方向增大,m与j的关系如图 3所示.需要布设4类检测器:1)在环形交叉口进口道上游布设单线圈检测器,它在采样间隔内采集到的车辆数记为N1m;2)在环形交叉口入口布设单线圈检测器,它在采样间隔内采集到的车辆数记为N2m;3)在环形交叉口出口布设单线圈检测器,它在采样间隔内采集到的车辆数记为N3m;4)在环形交叉口内部布设双线圈检测器[13],它在采样间隔内采集到的车辆数记为Nj,前、后线圈的脉冲起跳沿的时间之差为Δti,两个线圈之间的距离为D;检测器将脉冲信息传给处理器,可以计算得到ρj、vj、Dm、wm、qoff, m等预测模型所需的初始参数:
| $ {{\bar v}_j} = \frac{1}{n}\sum\limits_{i = 1}^n {{v_i}} = \frac{1}{n}\sum\limits_{i = 1}^n {\frac{D}{{\Delta {t_i}}}} , $ | (1) |
| $ {\rho _j} = \frac{{{N_{2m}} + {N_j} - {N_{3m}} - {N_{j + 1}}}}{{{{\bar v}_j}}}, $ | (2) |
| $ {D_m} = {N_{1m}}, $ | (3) |
| $ {w_m} = {N_{1m}} - {N_{2m}}, $ | (4) |
| $ {q_{{\rm{off}},m}} = {N_{3m}}. $ | (5) |
1) 环道交通流状态预测模型.描述环道交通流状态的参数包括流量、密度、速度,下面建立基本参数的预测模型:
| $ {\rho _j}\left( {l + 1} \right) = {\rho _j}\left( l \right) + \frac{{\Delta T}}{{{n_j}{L_j}}}\left[ {{q_{{\rm{in}},j}}\left( l \right) - {q_{{\rm{out}},j}}\left( l \right)} \right], $ | (6) |
| $ {q_{{\rm{in}},j}}\left( l \right) = {q_{{\rm{on}},m}}\left( l \right) + {\rho _{j - 1}}\left( l \right){v_{j - 1}}\left( l \right){n_{j - 1}}, $ | (7) |
| $ {q_{{\rm{out}},j}}\left( l \right) = {q_{{\rm{off}},m + 1}}\left( l \right) + {\rho _j}\left( l \right){v_j}\left( l \right){n_j}. $ | (8) |
式(6)为交通守恒方程,即路段j在第l+1个采样步长与第l个采样步长间的密度差等于l采样步长内流入该路段和流出该路段的流量差,乘以从流量转换成密度的系数ΔT/(njLj), 其中nj代表路段j的车道数,Lj为路段j的长度.式(7)表示流入j路段的流量qin, j(l),包括两部分:入口流入流量qon, m(l)和上游j-1路段流入的交通流量ρj-1(l)vj-1(l)nj-1.式(8)表示流出j路段的流量qout, j(l),包括两部分:出口流出流量qoff, m(l)和流入下游的流量ρj(l)vj(l)nj.
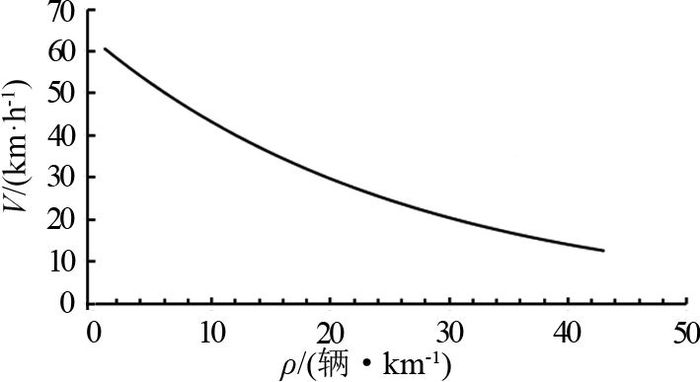
根据图 4可知,vj(l)的预测原则为速度vj收敛于速度-密度基本图中的稳态速度曲线V[ρj(l)],即vj→V[ρj(l)].考虑到收敛的时间响应因素,速度预测方程为
|
图 4 稳态速度-密度关系曲线 Fig. 4 Relation curve of steady speed-density |
| $ {v_j}\left( {l + 1} \right) = {v_j}\left( l \right) + \frac{{\Delta T}}{\tau }\left[ {V\left[ {{\rho _j}\left( l \right)} \right] - {v_j}\left( l \right)} \right]. $ | (9) |
式中:vj(l+1)为在第l+1个采样步长内编号为j的路段的交通流平均速度;τ为时间相关常数;ΔT/τ为时间响应系数;V[ρj(l)]为稳态速度,即道路的速度-密度基本图中当密度=ρj(l)时所对应的速度,根据经典Underwood模型可知,
| $ V\left[ {{\rho _j}\left( l \right)} \right] = {v_{\rm{f}}}\exp \left( { - \frac{{{\rho _j}\left( l \right)}}{{{\rho _{{\rm{cr}},j}}}}} \right). $ | (10) |
式中:vf为环道自由流速度,ρcr, j为路段j的临界密度.
2) 入口排队长度预测模型.建立环形交叉口各个入口处排队车辆数的预测模型,在一个采样步长内,当环形交叉口入口处的交通流需求流量Dm(l)超过入环通行流量qon, m(l)时,会在入口处出现排队现象.排队长度的预测模型如下:
| $ {w_m}\left( {l + 1} \right) = {w_m}\left( l \right) + \Delta T\left( {{D_m}\left( l \right) - {q_{{\rm{on}},m}}\left( l \right)} \right). $ | (11) |
qon, m(l)取决于环形交叉口入口处排队长度和入口通行能力的最小值,
| $ \begin{array}{l} {q_{{\rm{on}},m}}\left( l \right) = \\ \min \left\{ {{D_m}\left( l \right) + \frac{{{w_m}\left( l \right)}}{{\Delta T}},\frac{{{Q_m}\Delta T}}{{3600}}{r_m}\left( l \right)\min \left( {1,\frac{{{\rho _{\max ,j}} - {\rho _j}\left( l \right)}}{{{\rho _{\max ,j}} - {\rho _{{\rm{cr}},j}}}}} \right)} \right\}. \end{array} $ | (12) |
式中:Qm为环形交叉口单个入口处的通行能力;ρmax, j为环交入口对应的下游环道路段的阻塞密度;rm(l)为环形交叉口入口信号绿信比,该绿信比取值为[rmin, 1],即环形交叉口每个入口处的绿灯时间不小于预先设置的最小绿灯显示时间,并且不超过交叉口信号周期时长.
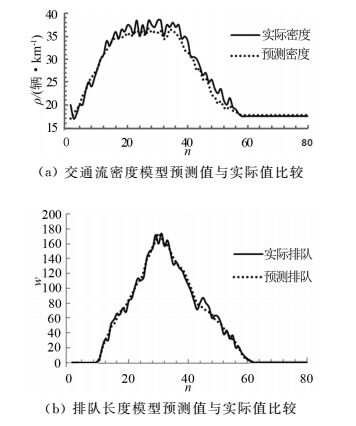
3) 模型预测效果评价.为了评价所建立的模型的预测效果,将Vissim平台采集到的实际交通流密度、实际排队长度数据与预测模型计算出的预测密度和预测排队长度数据进行对比分析,对比结果如图 5所示.
|
图 5 交通流参数模型预测结果图 Fig. 5 Prediction effect evaluation of traffic flow parameters |
图 5中,实线为实际交通流数据,虚线为预测序列,n为采样和预测的周期数,ρ为交通流密度,w为排队长度.预测结果能够很好地反映交通流状态的变化,为控制参数求解提供依据.
2.3 目标函数及约束条件目标函数是控制的结果,即采用该控制方法的目的是使整个系统的某一性能达到最优.在交通系统中,通常采用“系统总运行时间”(total time spend, TTS)这一性能指标作为最优控制问题的目标函数.这一指标既能够反映环形交叉口内部车辆总的运行时间,又包含入口处车辆的排队时间.为了保证控制方案能够很好地协调环形交叉口通行能力和入口车辆的排队等待时间,将环形交叉口总的运行时间作为最优控制的目标函数,求解目标函数的最小值,得到环形交叉口各个入口的绿信比.目标函数的表达式为
| $ J\left( {{k_0}} \right) = \sum\limits_{m = 1}^{{R_m}} {\sum\limits_{k = {k_0}}^{{k_0} + {N_{\rm{p}}} - 1} {\left[ {\alpha \sum {{\rho _j}\left( k \right){l_j}{n_j}} + \beta \sum {{w_m}\left( k \right)} } \right]\Delta T} } . $ | (13) |
式中:Rm为入口的数量.目标函数分为两部分:环道车流运行总时间和入口排队总时间,即J(k0)中前一项表示车辆在环形交叉口环道中的总运行时间,后一项表示环形交叉口入口处的总排队等候时间.按照预期控制效果,可以调整各自的权重参数α和β.
2.4 信号周期计算方法环形交叉口的信号周期取决于该环岛的交通流量以及环岛的半径.按照传统的信号周期HCM计算方法[14],可得
| $ \begin{array}{l} {C_m} = L + \frac{{{q_1}{C_m}}}{{{S_1}}} + \frac{{{q_2}{C_m}}}{{{S_2}}} + \cdots + \frac{{{q_n}{C_m}}}{{{S_n}}} = \\ \mu \cdot \frac{{2{\rm{ \mathsf{ π} }}R}}{u} + \frac{{{q_1}{C_m}}}{{{S_1}}} + \frac{{{q_2}{C_m}}}{{{S_2}}} + \cdots + \frac{{{q_n}{C_m}}}{{{S_n}}}. \end{array} $ | (14) |
式中:R为环岛半径,u为车辆绕环行驶的平均速度,μ为转向比例系数,Cm为信号周期.Cm应刚好等于一个周期内关键车流总的绿灯损失时间L,加上对应到达车辆q以各自进口道饱和流量S放行通过交叉口所需时间之和.此处的L应按照车辆绕环岛行驶所需要的时间计算.式(14)整理后,可得
| $ {C_m} = \frac{L}{{1 - Y}} = \mu \cdot \frac{{2{\rm{ \mathsf{ π} }}R}}{{u\left( {1 - Y} \right)}}. $ | (15) |
式中:Y为全部关键车流总的交通流量比.
在该方法中,信号周期时长只是配时方案的更新周期,对信号控制的影响不大.为了简化控制的过程,将按照高峰时期的流量比计算出的信号周期作为该环交的固定信号配时周期,控制过程依靠绿信比和相位搭接规则来完成.
3 相位搭接规则按照2章计算出的环形交叉口各个入口处的绿信比rm(l)会出现
相位搭接的概念如图 6所示.按照各入口排队长度占环形交叉口总排队长度的权重进行各个相位搭接时间的分配,各相位的搭接时间为

|
图 6 相位搭接概念图 Fig. 6 Concepts of phase overlapping |
| $ {t_m}\left( l \right) = C\left( {\sum\limits_{m = 1}^{{R_m}} {{r_m}\left( l \right) - 1} } \right)\frac{{{w_m}\left( l \right)}}{{\sum\limits_{m = 1}^{{R_m}} {{w_m}\left( l \right)} }}. $ | (16) |
式中:tm(l)指编号为m的入口的相位搭接时间,即上一入口相位结束前tm(l)时刻,下一入口转换为绿灯相位.式(16)表示将各个相位显示绿灯时间之和超过信号周期时长的那部分,按照各自入口排队长度赋予权重,分配到每一个入口相位上进行搭接.
按照上述的相位搭接规则可知,当环形交叉口某一入口rm(l)=1时,表明该入口一直处于绿灯放行状态;当环形交叉口所有入口都出现rm(l)=1的情况时,表明环形交叉口各个入口都处于绿灯放行状态,相当于无信号控制方式,这种情况多出现于交通流低峰时期.
4 仿真实验分析 4.1 仿真平台搭建仿真试验平台及所用的语言如下所示.
仿真工具:Vissim仿真软件.
开发语言:C++语言.
在Vissim仿真平台基础上进行二次开发,外接MPC控制中的预测模型和控制参数求解的COM接口程序,实现在线动态仿真过程.
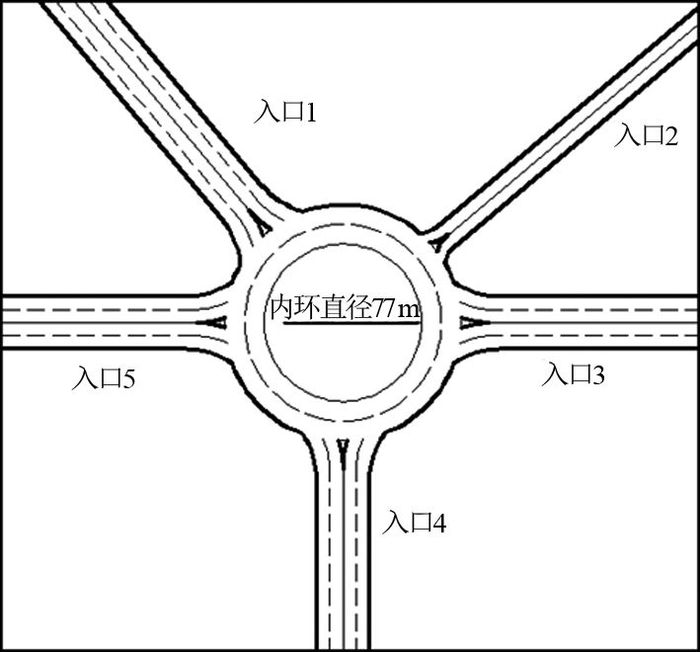
4.2 仿真场景建立建立的测试环形交叉口如图 7所示.内环直径为77 m,环道宽度为4 m,入口车道宽度为3.75 m,入口流量分布如表 1所示.
| 表 1 环交各入口交通量分布表 Table 1 Traffic flow at each entry of roundabout |
|
图 7 环形交叉口Vissim仿真场景构建图 Fig. 7 Scenario building of roundabout in Vissim simulation |
仿真参数设置如下.仿真时长取2.5 h,采样周期ΔT取5 s,信号周期时长按照式(8)计算后取整为160 s,模型预测控制的预测步长Np取10 min,控制步长Nc取5 min.
交通流预测模型参数的标定如表 2所示.
| 表 2 交通流预测模型参数标定 Table 2 Parameters calibration traffic flow prediction model |
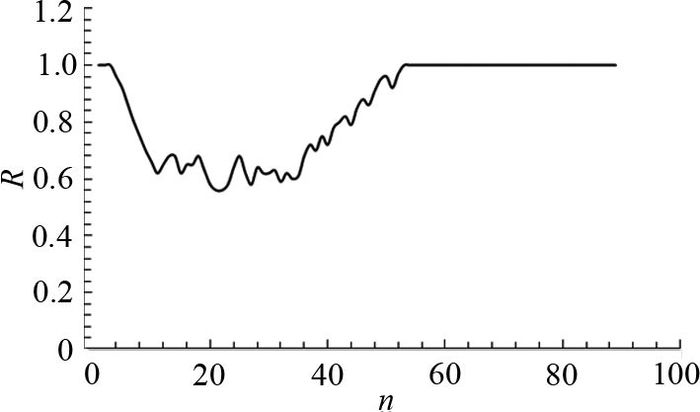
以入口1的绿信比求解结果为例,如图 8所示,R为不同周期该入口的绿信比,在前10个周期内,交通流密度较低,环形交叉口各个入口的绿信比均为1,相当于无信号控制;随着交通负荷度的不断增加,环内交通流逐渐趋于饱和,各个入口处的绿信比逐渐降低,图 8显示入口1的绿信比在0.55左右波动,在第50个周期时,交通流密度再次降低回低峰状态,环形交叉口再次呈现无信号状态.
|
图 8 目标环形交叉口入口1绿信比求解结果 Fig. 8 Green ratio at entry 1 of target roundabout |
以仿真的第25个周期为例,对相位搭接规则进行说明.该周期时长C25=160 s,其他参数如表 3所示.
| 表 3 仿真第25个周期环交信号配时参数 Table 3 Parameters of signal timing in 25th cycle of simulation |
按照相位搭接规则计算各个入口tm,如表 4所示.
| 表 4 环交各个入口相位搭接时间计算值 Table 4 Phase overlapping time of each entry in roundabout |
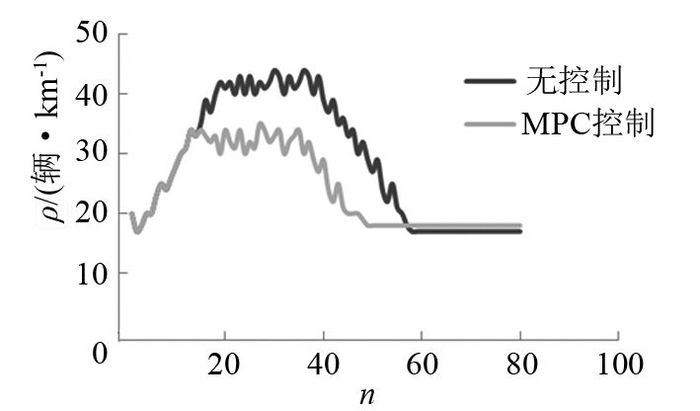
针对上述路网,给出环形交叉口在传统无信号的让行规则控制和采用MPC控制的仿真结果,如图 9所示.
|
图 9 无控制与MPC控制条件下交通流密度仿真对比结果 Fig. 9 Comparison of simulation results of traffic flow density between condition of MPC control and no control |
根据无信号控制方式和采用MPC控制方式的仿真结果对比,可以得出如下结论.
1) 从图 9可知,在无控制策略下,环道交通流密度较大,严重超出临界密度,车流运行速度缓慢,很容易出现交通拥堵现象,严重影响通行效率;在MPC控制方式下,环道内车流的密度较低,最大密度维持在不超过临界密度5%的范围以内,虽然减小了入环处车流的放行速率,但是环内车流运行相对流畅,基本不会出现“死锁”现象,所以MPC控制方式有更好的保证交叉口环流畅通的效果.
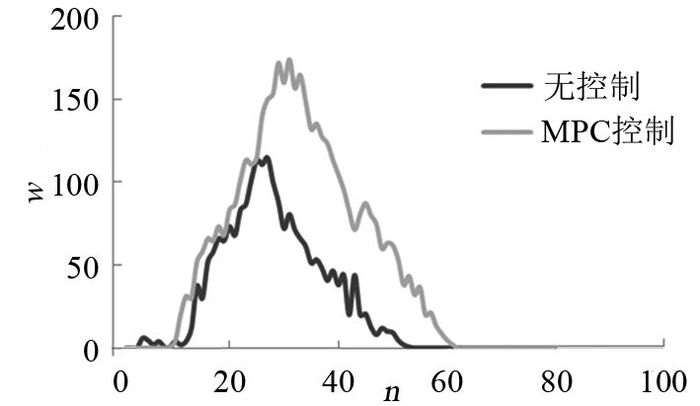
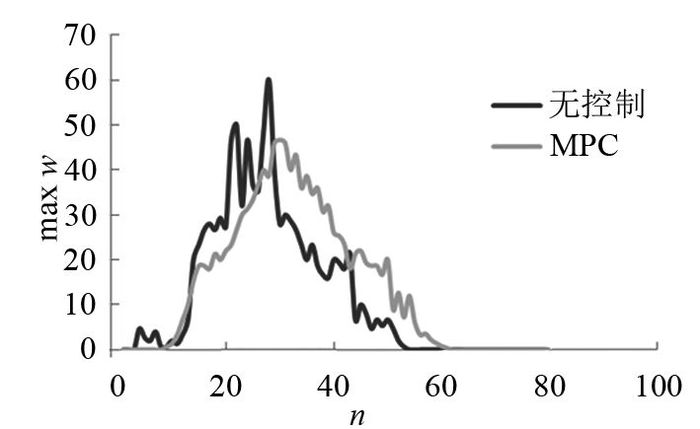
2) 根据图 10环形交叉口入口排队长度w的仿真对比结果可以看出,与无信号控制方式相比,在模型预测控制方式下,环形交叉口入口处的平均排队长度增加,这是由于MPC控制方式在保障环内交通流畅通的前提下寻求最优解,在交通需求不变的情况下,环内交通流密度降低,入口处的排队长度相对增大;图 11中,在MPC控制方式下,入口处最大排队长度max w明显减少,排队消散速度较快,这表示MPC控制方式对入口排队的优化体现在MPC控制方法使各个入口排队长度更加均衡,交通流放行速度更加平稳,交叉口整体运行效率更优.
|
图 10 无控制与MPC控制条件下入口总排队长度仿真对比结果 Fig. 10 Comparison of simulation results of queue length between condition of MPC control and no control |
|
图 11 无控制与MPC控制条件下最大排队长度仿真对比结果 Fig. 11 Comparison of simulation results of maximum queue length between condition of MPC control and no control |
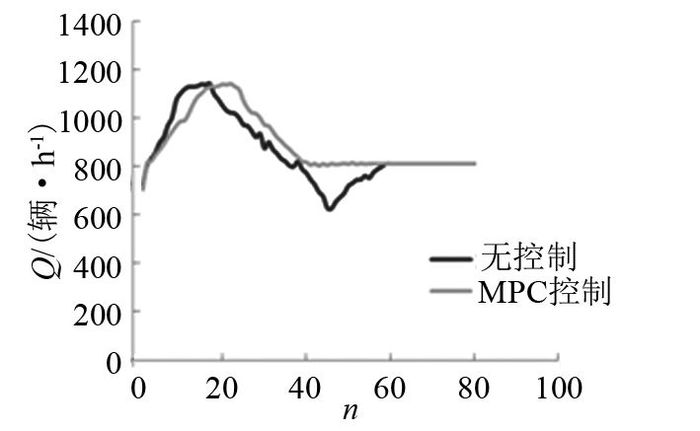
3) 为了更好地理解MPC控制方式对环形交叉口的改善作用,图 12对比了在有无MPC控制的两种情况下环形交叉口每个信号周期的总出口流量Q(转化成小时交通量).可以看出,在无控制方式下出口流量虽然很快达到约1 200辆/h的最大值,但随即出现交通拥堵,总出口流量急剧减小,出现了很大的波动性.在MPC控制方式下,出口流量变化平稳,并且在仿真的20~40个周期内,MPC控制方式使环形交叉口多驶出89辆车,与无控制的情况相比,这部分车辆一方面更早地驶出了环形交叉口,自身的出行时间减少;另一方面避免了对其他车辆的干扰,使得后续车辆的行程时间减少.整个环形交叉口的总的TTS得到了改善,由无信号控制条件下的1 125.575辆/h减小为1 034.237辆/h,TTS改善率为8.11%.
|
图 12 无控制与MPC控制条件下通行效率的仿真对比结果 Fig. 12 Comparison of simulation results of traffic efficiency between condition of MPC control and no control |
本文探索了基于模型预测控制的环形交叉口轮放式信号配时方法,提出环形交叉口动态预测模型和最优控制模型.在顺时针相序设计和相位搭接规则的辅助下,自适应地为环形交叉口入口赋予信号配时方案,更加合理地利用了环形交叉口的时空资源.仿真实验结果显示,对于包括多路畸形环交在内的各种环形交叉口,提出的基于模型预测控制的环形交叉口入口轮放式信号配时方法更加科学有效,环形交叉口的总的TTS显著提高.
| [1] |
RAUTIO J, KUMPULAINEN H, HEIMBACH T, et al. Prodrugs:design and clinical applications[J]. Nature Reviews Drug Discovery, 2008, 7(3): 255-270. DOI:10.1038/nrd2468 |
| [2] |
BRABANDER B D, VEREECK L. Safety effects of roundabouts in Flanders:signal type, speed limits and vulnerable road users[J]. Accident Analysis and Prevention, 2007, 3(3): 591-599. |
| [3] |
YANG X, LI X, XUE K. A new traffic-signal control for modern roundabouts:method and application[J]. IEEE Transactions on Intelligent Transportation Systems, 2004, 5(4): 282-287. DOI:10.1109/TITS.2004.838181 |
| [4] |
KIDD T, BROSE K, MITCHELL K J, et al. Roundabout controls axon crossing of the CNS midline and defines a novel subfamily of evolutionarily conserved guidance receptors[J]. Cell, 1998, 92(2): 205-215. DOI:10.1016/S0092-8674(00)80915-0 |
| [5] |
YANG X, LI X, XUE K. A new traffic-signal control for modern roundabouts:method and application[J]. IEEE Transactions on Intelligent Transportation Systems, 2004, 5(4): 282-287. DOI:10.1109/TITS.2004.838181 |
| [6] |
薛昆, 杨晓光, 白玉. 给定周期条件下环型交叉口优化控制方法研究[J]. 公路交通科技, 2004, 21(5): 83-87. XUE Kun, YANG Xiao-guang, BAI Yu. Optimization of control method for roundabout at fixed cycle[J]. Journal of Highway and Transportation Research and Development, 2004, 21(5): 83-87. |
| [7] |
敖谷昌, 赵宪尧, 胡光明. 剖圆环形灯控交叉口的理论与实践[J]. 天津城市建设学院学报, 2003, 9(3): 163-167. AO Gu-chang, ZHAO Xian-yao, HU Guang-ming. Theory and application of signalized roundabout crossings[J]. Journal of Tianjin Institute of Urban Construction, 2003, 9(3): 163-167. |
| [8] |
LI X, REN Z, FAUTRELLE Y. Phase distribution and phase structure control through a high gradient magnetic field during the solidification process[J]. Materials and Design, 2008, 29(9): 1796-1801. DOI:10.1016/j.matdes.2008.03.012 |
| [9] |
BELLEMANS T, SCHUTTER B D, MOOR B D. Model predictive control for ramp metering of motorway traffic:a case study[J]. Control Engineering Practice, 2006, 14(7): 757-767. DOI:10.1016/j.conengprac.2005.03.010 |
| [10] |
ANDREAS H, BART D S, HANS H. Model predictive control for optimal coordination of ramp metering and variable speed limits[J]. Transportation Research Part C-Emerging Technologies, 2005, 13(3): 185-209. DOI:10.1016/j.trc.2004.08.001 |
| [11] |
PAPAGEORGIOU M, PAPAMICHAIL I, MESSMER A, et al. Traffic simulation with METANET[M]//Fundamentals of traffic simulation. New York:Springer, 2010:399-430. https://link.springer.com/chapter/10.1007/978-1-4419-6142-6_11/fulltext.html
|
| [12] |
赵伟明, 王殿海, 朱文韬, 等. 基于改进NJW算法的交通控制时段划分[J]. 浙江大学学报:工学版, 2014, 48(12): 2259-2265. ZHAO Wei-ming, WANG Dian-hai, ZHU Wen-tao, et al. Short-time traffic flow prediction based on KSOM-BP neural network[J]. Journal of Zhejiang University:Engineering Science, 2014, 48(12): 2259-2265. |
| [13] |
金盛, 徐程, 王殿海. 城市路网交叉口检测器均衡布设优化方法[J]. 浙江大学学报:工学版, 2013, 47(03): 515-521. JIN Sheng, XU Cheng, WANG Dian-hai. Optimal traffic detector locations for equal distribution at urban network intersections[J]. Journal of Zhejiang University:Engineering Science, 2013, 47(03): 515-521. |
| [14] |
蔡云, 杨晓光, 王浩. 一种灵活的在线交通信号相位切换结构[J]. 城市交通, 2009, 7(3): 80-85. CAI Yun, YANG Xiao-guang, WANG Hao. A flexible on-line transition structure of traffic signal phases[J]. Urban Transport of China, 2009, 7(3): 80-85. |
| [15] |
ZHENG Z. Recent developments and research needs in modeling lane changing[J]. Transportation Research Part B Methodological, 2014, 60(1): 16-32. |



