随着人民生活水平的提高,人们对于快速、准点的出行需求不断增长,轨道交通快速发展.如何使高速列车变得更加高效、安全、舒适、便捷、节能,成为很多科研工作者的研究方向.在目前的研究成果中,多是单车运行以及多车同速运行的能耗优化,随着铁路网规模的扩大,将不可避免地会出现跨线列车[1];从2011年7月起,我国高速铁路开始采用新的运输组织模式,即:高中速列车混跑[2].高、中速列车的混合运行必然会造成铁路运输能力的减弱,引入快车的越行可以提高快车的运行效率,因此在不同速度列车混合运行的前提下开展运行安全及能耗的研究非常必要.
单列车运行能耗主要取决于列车的运行控制模式.列车运行有牵引、巡航、惰行、制动4种控制模式,在给定的运行时间之下,确定一条能够使列车在站间运行能耗最小的列车运行曲线,是列车节能控制的问题[3].国内外学者对列车的节能控制进行大量的研究,优化方法层出不穷.Milroy[4]通过控制牵引力、制动力来减少能耗,构建了控制模型.随后,大家在各自的研究基础上,先后证明节能运行策略应该包括最大牵引、巡航、惰行、最大制动4个运行工况,决定能耗用量的关键为4个工况的持续时间.学者们改进模型,引入天气、坡道、弯道等实际线路的影响因素,如Howlett等[5]在单列车节能控制策略的基础上考虑了连续坡道变化的因素.Li等[6-7]考虑气候、车辆特性等不确定因素的影响,基于随机优化理论建立最小化平均能耗的最优控制模型.随着信息技术的高速发展,智能控制理论被应用于求解列车优化运行控制问题.冯晓云[8]将模糊控制应用到列车控制模型,构建多目标决策模型.王成莉[9]提出基于遗传算法,结合全线优化控制及惰行优化控制的列车节能优化控制方法.
在多列车运行的情况下,能耗的降低来源于两部分:一部分是单车运行曲线的优化,另一部分是多车之间能量交互利用率的优化;后者主要是通过再生制动能量来进行能耗节省.关于再生制动的研究,始于Kokotovic等[10]提出的考虑再生制动能量的机动车控制策略.Gordon等[11]首先提出通过协调多列车的牵引、惰行、停车和发车时间来减少总的牵引能耗.Albrecht[12]采用遗传算法求解节能时刻表的最优运行时间,使得再生能量利用率最大.Chen等[13]利用遗传算法优化列车的停站时间,更节能地分配列车的牵引、制动功率,通过高雄地铁的案例分析验证了算法的正确性.Kim等[14]通过建立数学模型,调整每辆车的发车间隔,探讨发车间隔对系统能耗的影响.PEÑA-ALCARAZ等[15]通过建立数学规划模型同步相邻列车的制动、牵引时间段来最大化再生制动能量.Nasri等[16]考虑再生制动能量在牵引网中的流动情况,建立简单的牵引供电系统模型,探讨发车间隔和停站时间对能耗的影响.赵莹莹[17]根据时刻表的组成要素,选取列车间的发车间隔、上下行同步时间、列车停站时间以及站间运行时间4个时间因素,分析多列车节能运行.赵乐[18]基于再生制动能量利用方式分析相邻列车的相对位置及运行状态,建立地铁列车时刻表优化模型并采用模拟退火算法进行求解.Yang等[19]通过优化前、后列车的牵引时间、制动时间、发车间隔及停站时间,以重叠时间为目标建立多车协同控制模型,以北京地铁亦庄线为例来验证该模型的正确性.丁奕[20]从区间运行节能和匹配再生制动能的角度出发,建立节能时刻表模型,以北京地铁昌平线为例来验证优化时刻表的节能效果,但未考虑列车混行情况下的能耗优化和巡航阶段再生能的利用.
由于列车调度可以控制多车之间的能量交互,而列车的运行控制能够指导单车的具体运行过程[21],从而控制单车自身的能耗.通过再生制动的纽带,将两者结合,把能量优化从单车扩展到多车,可以大大提升能源利用率.分析既有的列车运行-调度一体化优化方法的不足如下.1)线路上的前、后列车均同速,优化研究适用范围较窄.2)现有的多车协同优化方法虽然考虑到列车站间的运行能耗优化,但对站间列车运行因素的分析较单一.3)现有的再生制动能量利用方法只局限于列车之间牵引—制动两种工况的相互利用.本文在传统的一体化优化模型基础上,引入列车混行,提出较全面的考虑列车追踪、越行及再生制动能量回收的运行-调度一体化优化方法,扩大了再生制动能量的利用范围,在优化各列车运行曲线的同时,优化出各列车的时刻表.
1 列车运行-调度一体化优化模型 1.1 单列车运行能耗计算考虑的列车均为电力机车,电力机车耗电量通常由3部分组成,包括牵引运行时的耗电量Qy、惰行、制动以及停站时的自用电量Q0和出入段及途中作业耗电量Qt.为了简化该模型,只考虑列车在线路上的运行过程,暂不考虑列车的出入段及途中作业耗电量,相应在计算列车运行能耗时将省去这一项.
牵引运行耗电量Qy分为最高负荷牵引运行量Qy1和部分负荷牵引运行量Qy2,
| $ {Q_{{\rm{y1}}}} = \frac{{{U_{\rm{w}}}\left[ {\sum\limits_{i = 1}^K {\left( {{I_{{\rm{p1}}}}{\lambda _{\rm{y}}} * \Delta {t_i}} \right)} + {I_{{\rm{p0}}}}\sum\limits_{i = 1}^K {\Delta {t_i}} } \right]}}{{3600 \times 1000}}. $ | (1) |
| $ {Q_{{\rm{y2}}}} = \frac{{{U_{\rm{w}}}\left[ {\sum\limits_{i = 1}^K {\left( {{I_{{\rm{p2}}}} * \Delta {t_1}} \right)} + {I_{{\rm{p0}}}}\sum\limits_{i = 1}^K {\Delta {t_i}} } \right]}}{{3600 \times 1000}}. $ | (2) |
式中:Uw为受电弓处电压;Ip1为最高负荷平均有功电流;Ip2为部分负荷平均有功电流,两者与列车速度相关.根据《列车牵引计算规程》的规定可知,部分负荷的Ip2不得大于同速度Ip1λy,其中λy为机车牵引力使用系数,取值为0.9;Ip0为自用有功电流,牵引运行时,4轴或6轴机车Ip0取6 A,8轴机车取7.5 A;Δti为计算相应工况能耗时所取的步长;K与每个工况时长相关.分母是将单位焦耳转换成了kW·h.
惰行、制动及停站耗电量为
| $ {Q_{\rm{0}}} = \frac{{{U_{\rm{w}}}\left[ {\sum\limits_{i = 1}^K {\left( {{I_{{\rm{p0}}}}\Delta {t_i}} \right)} } \right]}}{{3600 \times 1000}}. $ | (3) |
当列车处于惰行、空气制动、停站时,Ip0取2 A.
目前,列车速度的控制序列多数按照最大牵引-部分牵引-惰行-制动4个阶段进行,其中部分牵引表示列车速度不变,匀速行驶,即巡航状态,所以单列车总运行能耗为
| $ Q = \frac{{{U_{\rm{w}}}\left[ {\sum\limits_{i = 1}^{{K_1}} {\left( {{I_{{\rm{p1}}}}{\lambda _{\rm{y}}}\Delta {t_i}} \right)} + {I_{{\rm{p0}}}}\sum\limits_{i = 1}^{{K_1}} {\Delta {t_i}} + \sum\limits_{i = 1}^{{K_2}} {\left( {{I_{{\rm{p2}}}}\Delta {t_i}} \right)} + {I_{{\rm{p0}}}}\sum\limits_{i = 1}^{{K_2}} {\Delta {t_i}} + {I_{{\rm{p0}}}}\sum\limits_{i = 1}^{{K_3}} {\Delta {t_i}} + {I_{{\rm{p0}}}}\sum\limits_{i = 1}^{{K_4}} {\Delta {t_i}} } \right]}}{{3600 \times 1000}}. $ | (4) |
本文使用的再生制动能量利用方法属于再生制动能量能馈式利用方式,原理在于当列车制动时,制动能量通过逆变装置返回到电网,若此刻与其位于同一供电区间的其他列车处于牵引吸能状态,再生能量通过接触网直接传递给牵引列车使用.相邻列车在时间和空间上会发生两次再生制动能量利用:前向列车到达站台,并且停站时间结束,即将牵引,后向列车即将到达同一站台,开始制动,前车可以利用后车的制动能量进行牵引;前向列车即将到达下一站台,准备制动,后向列车在上一站台停站时间已过,准备牵引,若这两站台属于同一供电区间,则后车可以利用前车的制动能量进行牵引.
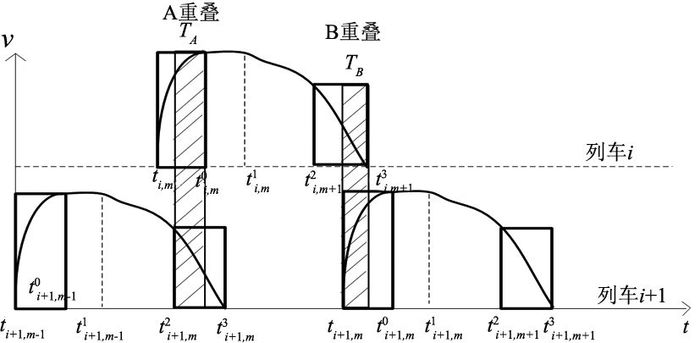
原理如图 1所示,假设相邻列车的型号、速度等级相同,在线路上的运行行为相同.黑色矩形框框出了列车各自的牵引、制动时间范围,显示了利用值的一个上限,阴影部分表示重叠可利用时间段,A重叠的阴影部分时间长度表示为TA,B重叠的阴影部分时间长度表示为TB.
|
图 1 列车再生制动能量利用原理图 Fig. 1 Schematic diagram utilization principle of trains'regenerative energy |
根据相邻列车运行情况的不同,两车在同一站台时的重叠时间的大小分为以下4类:列车i已经牵引结束,列车i+1开始制动,重叠时间为0;列车i的牵引结束时刻处于列车i+1的制动区间内,重叠时间为列车i的牵引结束时刻与列车i+1的制动开始时刻的时间差和列车i的总牵引时间的取小值;列车i+1的制动结束时刻处于列车i的牵引区间内,重叠时间为列车i+1的制动结束时刻与列车i的牵引开始时刻的时间差和列车i+1的总制动时间的取小值;列车i+1制动结束,列车i开始牵引,重叠时间为0;同理可以得到不同站台时的重叠时间情况,即图 1中的B重叠.根据4种情况写出重叠时间表达式如下:
| $ {T_{\rm{A}}} = \left\{ \begin{array}{l} 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t_{i,m}^0 < t_{i + 1,m}^2,\\ \min \left\{ {\Delta t_{i,m}^1,\left( {t_{i,m}^0 - t_{i + 1,m}^2} \right)} \right\},\;\;\;\;\;\;t_{i + 1,m}^2 < t_{i,m}^0 < t_{i + 1,m}^3;\\ \min \left\{ {\Delta t_{i + 1,m}^4,\left( {t_{i + 1,m}^3 - {t_{i,m}}} \right)} \right\},\;\;\;\;{t_{i,m}} < t_{i + 1,m}^3 < t_{i,m}^0;\\ 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t_{i + 1,m}^3 < {t_{i,m}}. \end{array} \right. $ | (5) |
| $ {T_{\rm{B}}} = \left\{ \begin{array}{l} 0,\;\;\;\;t_{i + 1,m}^0 < t_{i,m + 1}^2;\\ \min \left\{ {\Delta t_{i + 1,m}^1,\left( {t_{i + 1,m}^0 - t_{i,m + 1}^2} \right)} \right\},\;\;\;\;\;\;t_{i,m + 1}^2 < t_{i + 1,m}^0 < t_{i,m + 1}^3;\\ \min \left\{ {\Delta t_{i,m + 1}^4,\left( {t_{i,m + 1}^3 - {t_{i + 1,m}}} \right)} \right\},\;\;\;\;{t_{i + 1,m}} < t_{i,m + 1}^3 < t_{i + 1,m}^0;\\ 0,\;\;\;\;t_{i,m + 1}^3 < {t_{i + 1,m}}. \end{array} \right. $ | (6) |
式中:ti, m为列车i离开m站的时刻;ti, m0为列车i从m站出发最高牵引结束的时刻,ti, m0=ti, m+Δti, m1,Δti, m1为第i辆列车在第m站台与第m+1站台之间的牵引持续时间;ti, m1为列车i从m站出发巡航结束的时刻,ti, m1=ti, m+Δti, m1+Δti, m2,其中Δti, m2为第i辆列车在第m站台与第m+1站台之间的巡航持续时间;ti, m+12为列车i到达m+1站之前制动的时刻,ti, m+12=ti, m+13-Δti, m+14=ti, m+Δti, m1+Δti, m2+Δ ti, m+13,其中Δti, m3和Δti, m4分别为第i辆列车在第m站台与第m+1站台之间的惰行和制动持续时间;ti, m+13为列车i到达m+1站时刻,xm+1=ti, m+1-ti, m+13;xm+1为列车i在第m+1站台的停站时间;tm为列车在第m站与第m+1站之间的运行时间,tm=ti, m+13-ti, m.
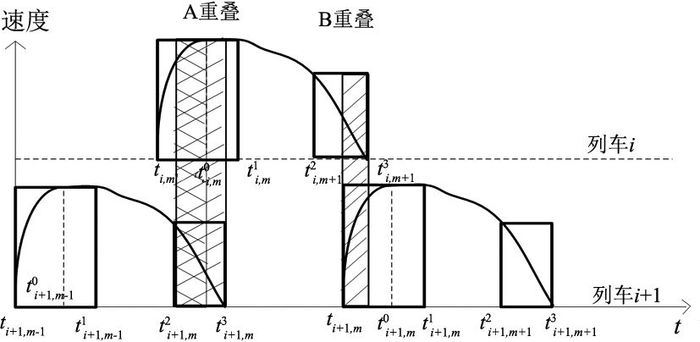
1.2.2 改进后再生制动能量计算方法常规的再生制动能量利用只考虑列车之间牵引、制动重叠时间内的利用,但很多时候会出现后车开始制动,但前车牵引时间已过开始巡航,即1.2.1节所介绍的重叠时间的第一种情况.根据常规利用方法可知,这部分的再生制动能量将产生浪费,因此考虑将吸能列车的范围扩展到牵引+巡航阶段,原理如图 2所示.可以发现,吸能列车的范围扩展到牵引+巡航时间段后,图 2所展现的A重叠时间从原本的交叉斜线部分扩大到整个单斜线部分,增加了巡航时期对再生制动能量的利用.
|
图 2 改进后列车再生制动能量利用原理图 Fig. 2 Improved schematic diagram utilization principle of trains' regenerative energy |
再生制动能量的表示方法如下:1)计算列车牵引和制动重叠时间[19],通过重叠时间来表示再生制动能量利用值;2)计算在这段重叠时间内所利用的能量[18].由于扩大利用范围,增加了巡航阶段,牵引、巡航两阶段的特性有差异,直接利用制动力做功计算再生制动能量,表达式如下:
| $ {W_A} = \left\{ \begin{array}{l} 0,\;\;\;t_{i,m}^1 < t_{i + 1,m}^2;\\ \min \left\{ {\int_{{t_{i,m}}}^{t_{i,m}^1} {F\left( v \right){v_{i,m}}\left( \tau \right){\rm{d}}\tau } ,\int_{t_{i + 1,m}^2}^{t_{i,m}^1} {B\left( v \right){v_{i + 1,m}}\left( \tau \right){\rm{d}}\tau } } \right\},\\ \;\;\;\;\;\;\;t_{i + 1,m}^2 < t_{i,m}^1 < t_{i + 1,m}^3;\\ \min \left\{ {\int_{t_{i + 1,m}^2}^{t_{i + 1,m}^3} {B\left( v \right){v_{i + 1,m}}\left( \tau \right){\rm{d}}\tau } ,\int_{{t_{i,m}}}^{t_{i + 1,m}^3} {B\left( v \right){v_{i + 1,m}}\left( \tau \right){\rm{d}}\tau } } \right\},\\ \;\;\;\;\;\;\;{t_{i,m}} < t_{i + 1,m}^3 < t_{i,m}^1;\\ 0,\;\;\;\;\;t_{i + 1,m}^3 < {t_{i,m}}. \end{array} \right. $ | (7) |
| $ {W_B} = \left\{ \begin{array}{l} 0,\;\;\;t_{i + 1,m}^1 < t_{i,m + 1}^2;\\ \min \left\{ {\int_{{t_{i + 1,m}}}^{t_{i + 1,m}^1} {F\left( v \right){v_{i + 1,m}}\left( \tau \right){\rm{d}}\tau } ,\int_{t_{i,m + 1}^2}^{t_{i + 1,m}^1} {B\left( v \right){v_{i,m}}\left( \tau \right){\rm{d}}\tau } } \right\},\\ \;\;\;\;\;\;\;t_{i,m + 1}^2 < t_{i + 1,m}^1 < t_{i,m + 1}^3;\\ \min \left\{ {\int_{t_{i,m + 1}^2}^{t_{i,m + 1}^3} {B\left( v \right){v_{i,m}}\left( \tau \right){\rm{d}}\tau } ,\int_{{t_{i + 1,m}}}^{t_{i,m + 1}^3} {B\left( v \right){v_{i,m}}\left( \tau \right){\rm{d}}\tau } } \right\},\\ \;\;\;\;\;\;\;{t_{i + 1,m}} < t_{i,m + 1}^3 < t_{i + 1,m}^1;\\ 0,\;\;\;\;\;t_{i,m + 1}^3 < {t_{i + 1,m}}. \end{array} \right. $ | (8) |
式中:F和B分别为列车的牵引力和制动力,与速度相关;vi, m表示第i辆慢车从第m站出发后的速度.
1.3 列车运行-调度一体化模型的建立 1.3.1 列车运行-调度关联性说明从节能角度来讲,通过控制列车的速度曲线可以实现列车低能耗驾驶,通过调度调节多车之间牵引-制动的重叠时间,修改列车的时刻表可以达到节能的目的,因此通过再生制动能量的利用,可以将两者紧密联系起来,实现运行-调度一体化优化.
引入再生制动能量之后,本文的调度模型以再生能利用量为优化目标,通过控制相邻列车的发车间隔、停站时间、运行时间、牵引及制动时间的长短来实现再生制动能量利用最大化.本文的速度控制模型通过调节列车4个运行阶段的时间长短来降低运行能耗,因此列车运行曲线所决定的区间加速时间、制动时间是列车调度模型的关键参数,调度模型所输出的列车时刻表中的运行时间是列车速度控制模型的基本约束,因此两者相互联系、相互制约,可以一体化优化.
1.3.2 模型建立该模型假设M个站点,c个越行站,Ⅰ辆列车按快慢车1:1比例发出,再生制动能量利用发生在相同速度等级的列车之间,以列车在整条线路上的能耗最少为目标,道路的限速、列车的追踪间隔、运行时间及等待时间为约束条件,目标函数如下:
| $ \min E = {E_1} + {E_2} - W. $ | (9) |
| $ \begin{array}{l} {E_1} = \sum\limits_{i = 1}^{I/2} {\sum\limits_{m = 1}^{M - 1} {{U_w}\left[ {\sum\limits_{k = 1}^{{K_{1,m}}} {\left( {{I_{{\rm{pl}}}}{\lambda _y}\Delta t_{i,m}^k} \right)} + {I_{{\rm{p0}}}}\sum\limits_{k = 1}^{{K_{1,m}}} {\Delta t_{i,m}^k} + } \right.} } \\ \left. {\sum\limits_{k = 1}^{{K_{2,m}}} {\left( {{I_{{\rm{p2}}}}\Delta t_{i,m}^k} \right)} + {I_{{\rm{p0}}}}\sum\limits_{k = 1}^{{K_{2,m}}} {\Delta t_{i,m}^k} + {I_{{\rm{p0}}}}\sum\limits_{k = 1}^{{K_{3,m + 1}}} {\Delta t_{i,m}^k} + {I_{{\rm{p0}}}}\sum\limits_{k = 1}^{{K_{4,m + 1}}} {\Delta t_{i,m}^k} } \right]/\\ \left( {3600 \times 1000} \right). \end{array} $ | (10) |
| $ \begin{array}{l} {E_2} = \sum\limits_{i = 1}^{I/2} {\sum\limits_{m = 1}^{M - 1 - c} {{{U'}_{\rm{w}}}\left[ {\sum\limits_{k = 1}^{{{K'}_{1,m}}} {\left( {{{I'}_{{\rm{pl}}}}{\lambda _y}\Delta t_{i,m}^{'k}} \right)} + {{I'}_{{\rm{p0}}}}\sum\limits_{k = 1}^{{{K'}_{1,m}}} {\Delta t_{i,m}^{'k}} + } \right.} } \\ \left. {\sum\limits_{k = 1}^{{{K'}_{2,m}}} {\left( {{{I'}_{{\rm{p2}}}}\Delta t_{i,m}^{'k}} \right)} + {{I'}_{{\rm{p0}}}}\sum\limits_{k = 1}^{{{K'}_{2,m}}} {\Delta t_{i,m}^{'k}} + {{I'}_{{\rm{p0}}}}\sum\limits_{k = 1}^{{{K'}_{3,m + 1}}} {\Delta t_{i,m}^{'k}} + {{I'}_{{\rm{p0}}}}\sum\limits_{k = 1}^{{{K'}_{4,m + 1}}} {\Delta t_{i,m}^{'k}} } \right]/\\ \left( {3600 \times 1000} \right). \end{array} $ | (11) |
| $ \begin{array}{l} W = \sum\limits_{i = 1}^{1/2} {\sum\limits_{m = 1}^{M - 1} {\left( {{W_{\rm{A}}} + \lambda \left( {m - 1,m} \right){W_{\rm{B}}}} \right)} } + \sum\limits_{i = 1}^{I/2} {\sum\limits_{m = 1}^{M - 1 - c} {\left( {{{W'}_{\rm{A}}} + } \right.} } \\ \left. {\lambda \left( {m - 1,m} \right){{W'}_{\rm{B}}}} \right). \end{array} $ | (12) |
式中:I为列车个数,M为站台个数,c为越行站个数,K1, m、K2, m、K3, m、K4, m分别为慢车在第m站台与第m+1站台之间的牵引、巡航、惰行和制动阶段单位计算步长的Δti, mk,间接表示了相应工况的总时长;K′1, m、K′2, m、K′3, m、K′4, m分别为快车在第m站台与第m+1站台之间的牵引、巡航、惰行和制动阶段单位计算步长Δti, m′k的数量;U′w为快车受弓处电压;I′p1为快车最高负荷平均有功电流;I′p0为快车自用有功电流;I′p2为快车部分牵引平均有功电流.
目标函数(9)表示所有列车在整条线路上的总能耗,为列车的总运行能耗扣除掉再生制动利用的能量,单位均统一为kW·h.由于快车和慢车的牵引特性、制动特性均不一样,列车的总运行能耗分成了两部分:慢车运行能耗E1和快车运行能耗E2.E1和E2均由4部分组成:列车的最高牵引能耗、巡航时间段能耗、惰行能耗和制动能耗,分别为式(10)、(11).
减去的部分为再生制动能量W,模型假设再生制动能量只发生在相同速度等级的列车之间,因此W分成了两部分,分别为慢车和快车的再生制动能量利用,WA为相邻慢车在同一站台的再生制动能量使用值,WB为相邻慢车在不同站台的再生制动能量使用值,λ(m-1, m)为0-1变量,判断第m-1站和第m站是否在同一供电段,0表示不在同一供电段,1表示在同一供电段;W′A为相邻快车在同一站台的再生制动能量使用值,W′B为相邻快车在不同站台的再生制动能量使用值,具体的计算公式在1.3.3节介绍.
列车的限速条件如下:
| $ \begin{array}{l} \sum\limits_{k = 1}^{{K_{1,m}}} {\Delta t_{i,m}^k} + \sum\limits_{k = 1}^{{K_{2,m}}} {\Delta t_{i,m}^k} + \sum\limits_{k = 1}^{{K_{3,m + 1}}} {\Delta t_{i,m}^k} + \sum\limits_{k = 1}^{{K_{4,m + 1}}} {\Delta t_{i,m}^k} \ge t_{i,m}^{\min };\\ m = 1,2, \cdots ,M; \end{array} $ | (13) |
| $ \begin{array}{l} \sum\limits_{k = 1}^{{{K'}_{1,m}}} {\Delta t_{i,m}^{'k}} + \sum\limits_{k = 1}^{{{K'}_{2,m}}} {\Delta t_{i,m}^{'k}} + \sum\limits_{k = 1}^{{{K'}_{3,m + 1}}} {\Delta t_{i,m}^{'k}} + \\ \sum\limits_{k = 1}^{{{K'}_{4,m + 1}}} {\Delta t_{i,m}^{'k}} \ge t_{i,m}^{'\min };m = 1,2, \cdots ,M\;且\;m \ne k. \end{array} $ | (14) |
将限速转化为运行时间的约束,运行时间由4个工况的持续时间组成.由于慢车运行距离为短间距,快车是长间距,制定了两类运行时间边界值.按列车运行方向,从1开始依次给所有站台标号,k为所有越行站站台标号的集合.ti, mmin为第i辆列车在第m站与m+1站之间的最小运行时间;ti, m′min表示快车发生越行,即跨站后第i辆快车在第m站与m+1站之间的最小运行时间.
站台到达的约束条件如下:
| $ \begin{array}{l} \int_0^{\left( {\sum\limits_{k = 1}^{{K_{1,m}}} {\Delta t_{i,m}^k} + \sum\limits_{k = 1}^{{K_{2,m}}} {\Delta t_{i,m}^k} + \sum\limits_{k = 1}^{{K_{3,m + 1}}} {\Delta t_{i,m}^k} + \sum\limits_{k = 1}^{{K_{4,m + 1}}} {\Delta t_{i,m}^k} } \right)} {{v_{i,m}}\left( t \right){\rm{d}}t} = {s_m};\\ m = 1,2, \cdots ,M \end{array} $ | (15) |
| $ \begin{array}{l} \int_0^{\left( {\sum\limits_{k = 1}^{{{K'}_{1,m}}} {\Delta t_{i,m}^{'k}} + \sum\limits_{k = 1}^{{{K'}_{2,m}}} {\Delta t_{i,m}^{'k}} + \sum\limits_{k = 1}^{{{K'}_{3,m + 1}}} {\Delta t_{i,m}^{'k}} + \sum\limits_{k = 1}^{{{K'}_{4,m + 1}}} {\Delta t_{i,m}^{'k}} } \right)} {{{v'}_{i,m}}\left( t \right){\rm{d}}t} = {{s'}_m};\\ m = 1,2, \cdots ,M\;且\;m \ne k. \end{array} $ | (16) |
m=1, 2, …, M且m≠k.(16)
对列车还没到达站台就停车的情况进行约束.对站间速度进行积分求得实时距离.Sm为第m站与第m+1站之间的距离;S′m为根据越行站位置计算得到的快车所运行的站间距离;vi, m为第i辆慢车从第m站出发后的速度;v′i, m表示第i辆快车从第m站出发后的速度.按列车运行方向,从1开始依次给所有站台标号,k为所有越行站站台标号的集合.
列车在整条线路上总运行时间的约束如下:
| $ \begin{array}{l} 0 \le \sum\limits_{m = 1}^{M - 1} {\left( {\sum\limits_{k = 1}^{{K_{1,m}}} {\Delta t_{i,m}^k} + \sum\limits_{k = 1}^{{K_{2,m}}} {\Delta t_{i,m}^k} + \sum\limits_{k = 1}^{{K_{3,m + 1}}} {\Delta t_{i,m}^k} + } \right.} \\ \left. {\sum\limits_{k = 1}^{{K_{4,m + 1}}} {\Delta t_{i,m}^k} } \right) \le T. \end{array} $ | (17) |
| $ \begin{array}{l} 0 \le \sum\limits_{m = 1}^{M - 1 - c} {\left( {\sum\limits_{k = 1}^{{{K'}_{1,m}}} {\Delta t_{i,m}^{'k}} + \sum\limits_{k = 1}^{{{K'}_{2,m}}} {\Delta t_{i,m}^{'k}} + \sum\limits_{k = 1}^{{{K'}_{3,m + 1}}} {\Delta t_{i,m}^{'k}} + } \right.} \\ \left. {\sum\limits_{k = 1}^{{{K'}_{4,m + 1}}} {\Delta t_{i,m}^{'k}} } \right) \le T'. \end{array} $ | (18) |
式中:T为整条线路慢车最大总运行时间,T′为整条线路快车最大总运行时间.
为了保证效率,并且与当前时刻表的总运行时间偏差不能过大,总运行时间不能过长,用当前时刻表总运行时间增加2 min作为上限.
快车能够发生越行的安全约束如下:
| $ \int_{{t_{i + 1,k - 1}}}^{t_{i,k}^3} {{{v'}_{i + 1,k - 1}}{\rm{d}}t} < {s_{k - 1}}, $ | (19) |
| $ {s_{k - 1}} < \int_{{t_{i + 1,k - 1}}}^{t_{i + 1,k + 1}^3} {{{v'}_{i + 1,k - 1}}{\rm{d}}t} . $ | (20) |
列车间追踪间隔约束如下:
| $ \begin{array}{l} {L_{i,m}} = {s_{i - 1 - 2p}} - {s_i} = \int_0^t {{v_{i - 1 - 2p,m}}\left( \tau \right){\rm{d}}\tau } - \\ \int_0^t {{{v'}_{i,m}}\left( \tau \right){\rm{d}}\tau } > {L_{\min }};\;\;\;p = 0,1,2,3, \cdots ,c. \end{array} $ | (21) |
式(21)保证了列车的安全行驶.按列车运行方向,从1开始依次给所有越行站独立标号,p为所有越行站独立标号的集合;Si为第i辆列车的实时位移;Li, m为第i辆列车与前向列车的实时追踪间隔;Lmin为相邻列车最小追踪间隔.
发车间隔和停站时间的范围约束如下:
| $ \left. \begin{array}{l} {T_{\min }} < {h_1} < {U_{\rm{n}}},\\ {T_{\min }} < {h_2} < {U_{\rm{n}}},\\ {U_{\min }} < {x_m} < {U_{\max }},\\ {U_{\min }} < {{x'}_m} < {U_{\max }}. \end{array} \right\} $ | (22) |
式中:xm为慢车在第m站台的停站时间,x′m为快车在第m站台的停站时间,Tmin、Un分别为发车间隔的下限与上限,Umin、Umax分别为各站台停站时间的下限与上限.模型发车间隔分为慢-快发车间隔h1和快-慢发车间隔h2.
1.3.3 引入快慢车的再生制动能量部分计算根据1.2.2节介绍的再生制动能量利用原理可得再生制动能量表达式.在该模型下,快慢车按1:1发车,并且快车会在相应的越行站进行越行,线路上列车次序随着快车的越行而变化,每辆列车的相邻列车也不固定,因此假设再生制动能量只发生在同等速度等级的列车之间,慢车与慢车利用,快车与快车利用,这样次序不会因越行而改变.快慢车都各自与次邻列车利用,根据式(7)、(8)得到慢车再生制动能量如下:
| $ {W_{\rm{A}}} = \left\{ \begin{array}{l} 0,\;\;\;t_{i,m}^1 < t_{i + 2,m}^2;\\ \min \left\{ {\int_{{t_{i,m}}}^{t_{i,m}^1} {F\left( v \right){v_{i,m}}\left( \tau \right){\rm{d}}\tau } ,\int_{t_{i,m}^1}^{t_{i + 2,m}^2} {B\left( v \right){v_{i + 2,m}}\left( \tau \right){\rm{d}}\tau } } \right\},\\ \;\;\;\;\;\;\;t_{i + 2,m}^2 < t_{i,m}^1 < t_{i + 2,m}^3;\\ \min \left\{ {\int_{t_{i + 2,m}^2}^{t_{i + 2,m}^3} {B\left( v \right){v_{i + 2,m}}\left( \tau \right){\rm{d}}\tau } ,\int_{{t_{i,m}}}^{t_{i + 2,m}^3} {B\left( v \right){v_{i + 2,m}}\left( \tau \right){\rm{d}}\tau } } \right\},\\ \;\;\;\;\;\;\;{t_{i,m}} < t_{i + 2,m}^3 < t_{i,m}^1;\\ 0,\;\;\;\;\;t_{i + 2,m}^3 < {t_{i,m}}. \end{array} \right. $ | (23) |
| $ {W_{\rm{B}}} = \left\{ \begin{array}{l} 0,\;\;\;t_{i + 2,m}^1 < t_{i,m + 1}^2;\\ \min \left\{ {\int_{{t_{i + 2,m}}}^{t_{i + 2,m}^1} {F\left( v \right){v_{i + 2,m}}\left( \tau \right){\rm{d}}\tau } ,\int_{t_{i,m + 1}^2}^{t_{i + 2,m}^1} {B\left( v \right){v_{i,m}}\left( \tau \right){\rm{d}}\tau } } \right\},\\ \;\;\;\;\;\;\;t_{i,m + 1}^2 < t_{i + 2,m}^1 < t_{i,m + 1}^3;\\ \min \left\{ {\int_{t_{i,m + 1}^2}^{t_{i,m + 1}^3} {B\left( v \right){v_{i,m}}\left( \tau \right){\rm{d}}\tau } ,\int_{{t_{i + 2,m}}}^{t_{i,m + 1}^3} {B\left( v \right){v_{i,m}}\left( \tau \right){\rm{d}}\tau } } \right\},\\ \;\;\;\;\;\;\;{t_{i + 2,m}} < t_{i,m + 1}^3 < t_{i + 2,m}^1;\\ 0,\;\;\;\;\;t_{i,m + 1}^3 < {t_{i + 2,m}}. \end{array} \right. $ | (24) |
同理,快车再生制动能量如下:
| $ {{W'}_{\rm{A}}} = \left\{ \begin{array}{l} 0,\;\;\;t_{i,m}^1 < t_{i + 2,m}^2;\\ \min \left\{ {\int_{{t_{i,m}}}^{t_{i,m}^1} {F'\left( v \right){v_{i,m}}\left( \tau \right){\rm{d}}\tau } ,\int_{t_{i,m}^1}^{t_{i + 2,m}^2} {B'\left( v \right){v_{i + 2,m}}\left( \tau \right){\rm{d}}\tau } } \right\},\\ \;\;\;\;\;\;\;t_{i + 2,m}^2 < t_{i,m}^1 < t_{i + 2,m}^3;\\ \min \left\{ {\int_{t_{i + 2,m}^2}^{t_{i + 2,m}^3} {B'\left( v \right){v_{i + 2,m}}\left( \tau \right){\rm{d}}\tau } ,\int_{{t_{i,m}}}^{t_{i + 2,m}^3} {B'\left( v \right){v_{i + 2,m}}\left( \tau \right){\rm{d}}\tau } } \right\},\\ \;\;\;\;\;\;\;{t_{i,m}} < t_{i + 2,m}^3 < t_{i,m}^1;\\ 0,\;\;\;\;\;t_{i + 2,m}^3 < {t_{i,m}}. \end{array} \right. $ | (25) |
| $ {{W'}_{\rm{B}}} = \left\{ \begin{array}{l} 0,\;\;\;t_{i + 2,m}^1 < t_{i,m + 1}^2;\\ \min \left\{ {\int_{{t_{i + 2,m}}}^{t_{i + 2,m}^1} {F'\left( v \right){v_{i + 2,m}}\left( \tau \right){\rm{d}}\tau } ,\int_{t_{i,m + 1}^2}^{t_{i + 2,m}^1} {B'\left( v \right){v_{i,m}}\left( \tau \right){\rm{d}}\tau } } \right\},\\ \;\;\;\;\;\;\;t_{i,m + 1}^2 < t_{i + 2,m}^1 < t_{i,m + 1}^3;\\ \min \left\{ {\int_{t_{i,m + 1}^2}^{t_{i,m + 1}^3} {B'\left( v \right){v_{i,m}}\left( \tau \right){\rm{d}}\tau } ,\int_{{t_{i + 2,m}}}^{t_{i,m + 1}^3} {B'\left( v \right){v_{i,m}}\left( \tau \right){\rm{d}}\tau } } \right\},\\ \;\;\;\;\;\;\;{t_{i + 2,m}} < t_{i,m + 1}^3 < t_{i + 2,m}^1;\\ 0,\;\;\;\;\;t_{i,m + 1}^3 < {t_{i + 2,m}}. \end{array} \right. $ | (26) |
在优化过程中,需要根据实时速度计算实时距离,进行到站判断.实时速度根据列车在站间的4个运行工况分别计算,表达式为
| $ {v_{i,m}}\left( t \right) = \left\{ \begin{array}{l} \int_{{t_{i,m}}}^t {a_{i,m}^0{\rm{d}}t} ,{t_{i,m}} \le t < t_{i,m}^0\left( {最高牵引} \right);\\ \int_{{t_{i,m}}}^{t_{i,m}^0} {a_{i,m}^0{\rm{d}}t} ,t_{i,m}^0 \le t < t_{i,m}^1\left( {巡航} \right);\\ \int_{{t_{i,m}}}^{t_{i,m}^0} {a_{i,m}^0{\rm{d}}t} - \int_{t_{i,m}^1}^t {a_{i,m}^1{\rm{d}}t} ,\;\;t_{i,m}^1 \le t < \\ \;\;\;\;\;\;\;t_{i,m + 1}^2\left( {惰行} \right);\\ \int_{{t_{i,m}}}^{t_{i,m}^0} {a_{i,m}^0{\rm{d}}t} - \int_{t_{i,m}^1}^{t_{i,m}^2} {a_{i,m}^1{\rm{d}}t} - \int_{t_{i,m}^2}^t {a_{i,m}^2{\rm{d}}t} ,\\ \;\;\;\;\;\;\;t_{i,m}^2 \le t < t_{i,m + 1}^3\left( {制动} \right). \end{array} \right. $ | (27) |
| $ \left. \begin{array}{l} a_{i,m}^0 = \frac{{F\left( v \right) - f\left( v \right) - 附加阻力\left( {道路因素} \right)}}{{{M_{\rm{g}}} + \sum n }},\\ a_{i,m}^1 = \frac{{f\left( v \right) + 附加阻力\left( {道路因素} \right)}}{{{M_{\rm{g}}} + \sum n }},\\ a_{i,m}^2 = \frac{{B\left( v \right) + f\left( v \right) + 附加阻力\left( {道路因素} \right)}}{{{M_{\rm{g}}} + \sum n }}. \end{array} \right\} $ | (28) |
式中:ai, m0、ai, m1、ai, m2分别为列车i在第m站台与第m+1站台之间的最高牵引、惰行、制动时的加速度;Mg+∑n为列车及乘客的总重量;n为乘客数量;f(v)为列车的运行阻力,运行阻力根据列车型号的不同,表达也不同.巡航工况的速度是一个常数,大小与第m车站第i辆列车的牵引时间长度ti, m0相关,因为巡航工况表示的是匀速行驶阶段,速度不变,且取决于前一段加速时间.牵引力和制动力分别是与速度相关的函数,根据列车型号可以拟合出快慢列车的牵引力和制动力的表达式.附加阻力描述的是道路因素所带来的影响,包含坡道附加阻力、曲线附加阻力和隧道附加阻力.
在求解过程中,设置时间步长来求解列车的实时速度,将前一时间步长所求的速度代入当前时间步长中的加速度公式中,进而求出当前速度.
1.5 最小追踪间隔表达由于不同速度的列车混行,为了保证安全,需要实时监控相邻列车的追踪间隔,但由于快车越行行为的存在,同一辆列车的相邻列车不固定,因此引入根据越行站的分布将线路分段计算追踪间隔的方法,并且只要使得每辆快车每时每刻与前方慢车保持安全间隔.模型设定线路共有c个越行站,快慢车发车比例为1:1,除了始发的前c辆快车越行次数小于c次,其余每辆列车均进行c次越行,在第一个越行站之前,第i辆快车须与第i-1辆慢车保持安全间隔;在第一次越行后,第i辆快车须与第i-3辆慢车保持安全间隔,以此类推,第i辆快车在第p与第p+1越行站之间的相邻列车追踪距离表达式为
| $ \begin{array}{l} {L_{i,m}} = {S_{i - 1 - 2p}} - {S_i} = \int_0^t {{v_{i - 1 - 2p,m}}\left( \tau \right){\rm{d}}\tau } - \\ \int_0^t {{{v'}_{i,m}}\left( \tau \right){\rm{d}}\tau } > {L_{\min }};\;\;\;p = 0,1,2,3, \cdots ,c. \end{array} $ | (29) |
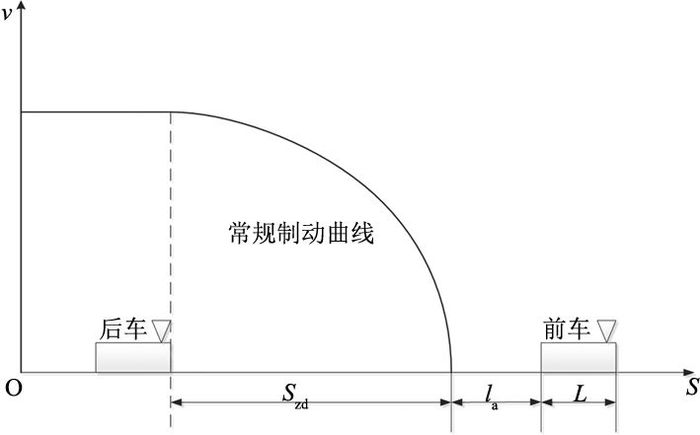
式中:p为0,表示未越行前.然后按列车运行方向,从1开始依次给越行站独立标号,p为所有越行站独立标号的集合;在追踪间隔约束条件中,涉及到最小追踪间隔Lmin;当考虑列车在区间的追踪间隔时,通常有两种方式,即绝对制动距离方式和相对制动距离方式.采用基于移动闭塞的绝对制动方式条件下的最小追踪间隔的表达式.该方式不考虑前方列车的速度,只考虑前方列车的位置,原理如图 3所示,表达式[22]为
|
图 3 最小追踪间隔示意图 Fig. 3 Minimal tracking intervals schematic diagram |
| $ {L_{\min }} = {S_{{\rm{zd}}}} + {l_{\rm{a}}} + L. $ | (30) |
式(30)由3部分组成:后车的常规制动距离Szd、一定的安全预留距离la和前车的车身长度L.
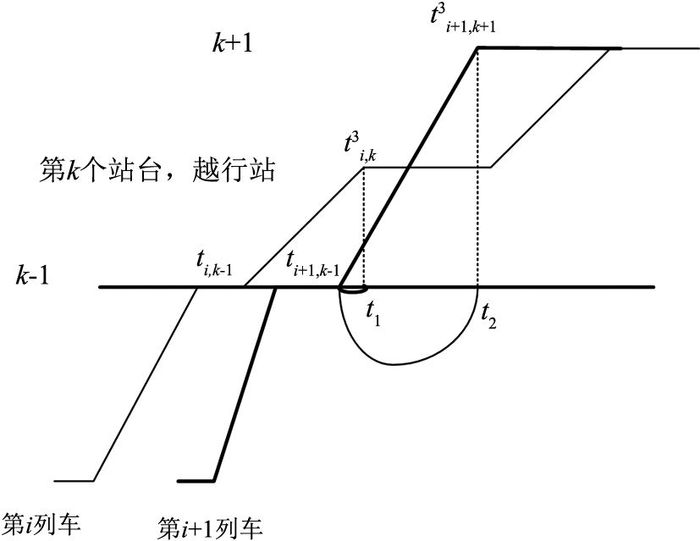
1.6 快车越行状态表达如图 4所示为第i辆列车与第i+1辆列车的距离运行图.假设在第k个站台快车发生越行,防止列车发生碰撞,则快车的距离曲线必须从慢车在第k个站台的停站区间穿过.即使列车在t1间点行驶的距离小于k-1和k之间的站间距离sk-1,在t2时间点行驶距离大于sk-1,具体的约束表达式为
|
图 4 列车越行限制表达 Fig. 4 Limit description of trains' overtaking |
| $ \int_{{t_{i + 1,k - 1}}}^{t_{i,k}^3} {{{v'}_{i + 1,k - 1}}{\rm{d}}t} < {s_{k - 1}},{s_{k - 1}} < \int_{{t_{i + 1,k - 1}}}^{t_{i + 1,k + 1}^3} {{{v'}_{i + 1,k - 1}}{\rm{d}}t} . $ | (31) |
由于列车的运行-调度问题比较复杂,约束条件多,是典型的np难问题.很多学者在研究这类问题时都会采用人工智能算法,包括:遗传算法、蚁群算法、模拟退火和粒子群算法等,所以采用粒子群算法,求解步骤如下.
1) 距离判断控制模式模块.根据列车的牵引、制动距离和与各个站间距离比较划分控制模式;设定了3种模式,若站间距离小于列车的牵引、制动距离和,则控制模式为牵引-制动;若站间距离大于列车的牵引、制动距离和,且小于2倍的牵引、制动距离和,则控制模式为牵引-惰行-制动;若站间距离大于2倍的牵引、制动距离和,则控制模式为牵引-巡航-惰行-制动.根据该模块来确定下一步粒子初始化的维度.
2) 粒子群初始化.粒子群初始化包括初始化粒子种群规模、每个粒子的初始速度、初始位置、粒子更新的最大速度、最大迭代次数和惯性权重,粒子的初始值由数据库中原来的运行曲线和时刻表定义;由于决策变量都是时间,并且约束条件中有关于它们的约束,初始化时,定义各站间运行时间、线路总运行时间、发车间隔和各站停站时间的范围,约束粒子更新的区域.
3) 适应度函数计算.适应度函数采用模型的目标函数.
4) 个体极值和群体极值更新.
5) 粒子速度更新及位置更新.在粒子位置更新完成后,检查该粒子是否满足各种约束条件.在进行约束条件判断时,需要计算出所有列车在线路上的速度、距离曲线及时刻表,然后判断列车是否满足限速及到站约束;在计算追踪间隔过程中,须查询线路上越行站的分布情况及个数,然后按越行情况分布讨论并计算不同时间段的相邻列车的追踪间隔,根据计算出的结果,判断追踪间隔是否满足最小间隔约束以及快车在越行站的越行条件约束.
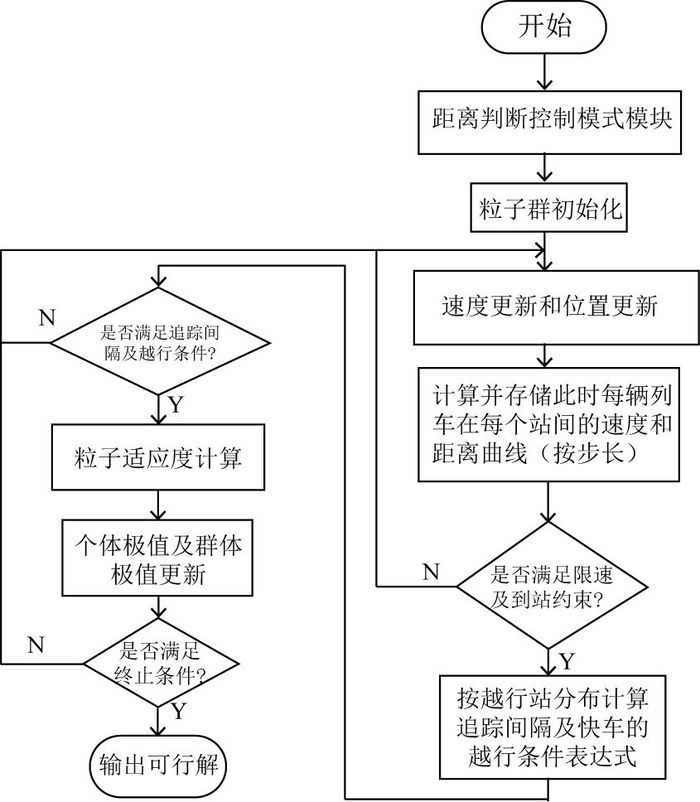
6) 终止条件判断.若达到最大迭代次数,则停止寻优.求解步骤如图 5所示.
|
图 5 粒子群算法的求解步骤 Fig. 5 Solving steps of particle swarm optimization algorithm |
以杭州东到上海虹桥的D3208次动车、G7336次高铁为例进行仿真测试,以两者按1:1发车情况下优化后的能耗与当前实际能耗进行对比,两者平均时速分别为125和138 km/h,最高运营速度分别为250和300 km/h.D3208次动车和G7336次高铁型号分别为CRH2_200和CRH380A.根据技术文件,拟合它们的牵引特性曲线和制动特性曲线.D3208和G7336的运行阻力分别如下:
| $ {f_1} = 8.63 + 0.07295v + 0.00112{v^2}, $ | (32) |
| $ {f_2} = 0.000755mg + 120.344\left( {v + {\rm{d}}v} \right) + 7.84{\left( {v + {\rm{d}}v} \right)^2}. $ | (33) |
慢车的牵引特性和制动特性如下:
| $ {F_1} = \left\{ \begin{array}{l} - 0.3612v + 175.8,\;\;\;0 \le v \le 122{\rm{km/h;}}\\ {\rm{0}}{\rm{.00264}}{v^2} - 1.5v + 274.3,\\ \;\;\;\;\;\;122{\rm{km/h}} < v < 250{\rm{km/h}}. \end{array} \right. $ | (34) |
| $ {B_1} = \left\{ \begin{array}{l} 124.8,\;\;\;\;\;0 \le v \le 70{\rm{km/h}};\\ 0.00297{v^2} - 1.28v + 198.1,\\ \;\;\;\;\;\;70\;{\rm{km/h}} < v < 200\;{\rm{km/h}}{\rm{.}} \end{array} \right. $ | (35) |
快车的牵引特性和制动特性如下:
| $ {F_2} = \left\{ \begin{array}{l} - 0.29v + 300,\;\;\;0 \le v \le 119{\rm{km/h;}}\\ {\rm{0}}{\rm{.003}}{v^2} - 2.1v + 476,\\ \;\;\;\;\;\;119{\rm{km/h}} < v < 350{\rm{km/h}}. \end{array} \right. $ | (36) |
| $ {B_2} = \left\{ \begin{array}{l} 60v,\;\;\;\;\;0 \le v \le 5{\rm{km/h}};\\ - 0.29v + 300.5,5\;{\rm{km/h}} < v \le 106{\rm{km/h}};\\ 0.0024{v^2} - 1.96v + 450.8,\\ \;\;\;\;\;\;106\;{\rm{km/h}} < v \le 350\;{\rm{km/h}}{\rm{.}} \end{array} \right. $ | (37) |
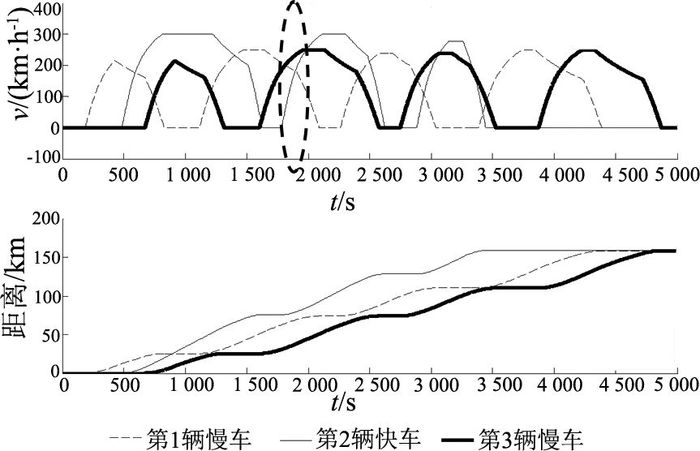
如图 6所示为采用改进后的再生制动能量利用方法所优化出的能耗最低时的列车速度曲线和距离曲线.发车比例为1:1,3辆车按发车次序分别为D3208、G7336和D3208.慢车D3208次列车经历杭州东-海宁西-嘉兴南-金山北-上海虹桥5个站点,总长度为159 km;G7336次列车经历杭州东-嘉兴南-金山北-上海虹桥4个站点,总长度为159 km;D3208次列车在海宁西站的停站时间较长,并且在该站之后,G7336次列车比D3208次列车先到达嘉兴南站,说明在海宁西站G7336次列车发生一次越行.从图 6的速度曲线可以看出,当第1辆列车处于制动/牵引状态时,第3辆列车被匹配到牵引/制动状态.从图 6可以看出,在距离较短的站间,列车没有匀速阶段,也没有加速到最大速度,这是本文优化算法优化的一部分内容:根据站间距离长短,优化列车在该站间的控制模式次序;若距离较短,则会优化出只有牵引—制动两个阶段的控制次序.根据快车的制动距离及车身长,设定最小追踪间隔为5 km.
|
图 6 能耗最低时的列车运行曲线和距离曲线 Fig. 6 Train operation curve and its distance curve of lowest energy consumption |
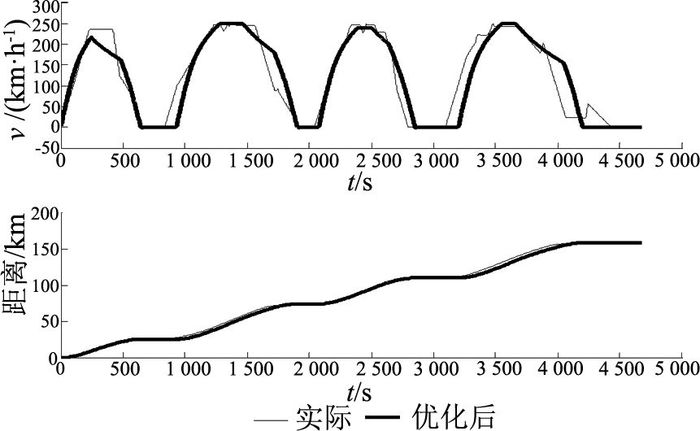
如表 1、2所示分别为D3208优化前、后的时刻表,优化后的时刻表比当前时刻表快167 s.如图 7所示为优化后的D3208次列车站间运行曲线与实际运行曲线的对比.根据D3208当前运行曲线,计算得到D3208列车在杭州东到上海虹桥这段线路上的总运行能耗为2 823 kW·h,优化后运行能耗为2 574 kW·h,运行能耗节省8.8%.
| 表 1 D3208优化前的时刻表 Table 1 Timetable of D3208 before optimization |
| 表 2 D3208优化后的时刻表 Table 2 Timetable of D3208 after optimization |
|
图 7 D3208优化前、后的运行曲线和距离曲线 Fig. 7 Train operation curve and its distance curve of D3208 after improvement |
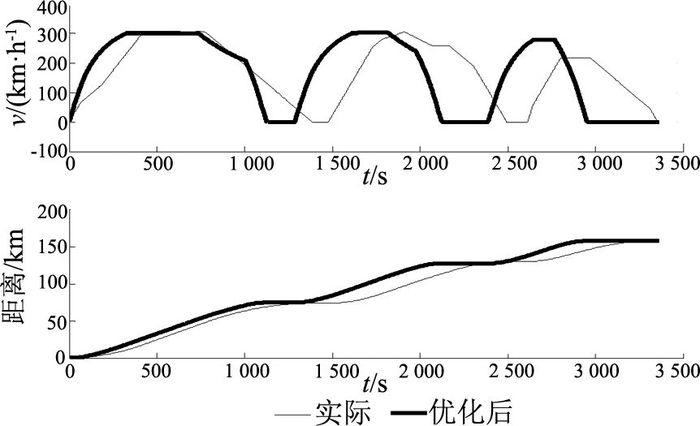
如表 3、4所示分别为G7336优化前、后的时刻表,优化后的时刻表比当前时刻表快435 s.如图 8所示为优化后的G7336次列车站间运行曲线与实际运行曲线的对比.根据G7336当前运行曲线计算可得,在杭州东到上海虹桥这段线路上的总运行能耗为5 786 kW·h,优化后运行能耗为5 040 kW·h,运行能耗节省12.9%.
| 表 3 G7336优化前的时刻表 Table 3 Timetable of G7336 before optimization |
| 表 4 G7336优化后时刻表 Table 4 Timetable of G7336 after optimization |
|
图 8 G7336优化前、后的运行曲线和距离曲线 Fig. 8 Train operation curve and its distance curve of G7336 after improvement |
优化前,D3208、G7336和D5432三辆列车的运行总能耗为11 268 kW·h,优化前3辆列车型号均不相同,未使用再生制动能量;优化后,按两种型号的列车1:1发车,运行能耗为10 188 kW·h,运行能耗节省9.6%.列车1、3之间利用到的再生制动能量为1491 kW·h,再生制动能量利用达到13.2%,扣除再生制动能量利用量,优化后的实际能耗为8 697 kW·h,整个线路总能耗节省22.8%,每辆车平均节省7.6%.如表 5、6所示分别为第3辆列车优化前、后的时刻表对比.在实际运营中,每辆列车的停站方案均不相同,这使得列车再生制动能量在同一站台的使用率较低,因此根据优化模型的1:1发车假设条件,使线路上只存在两种型号的列车;两种停站方案可以在很大程度上提高再生制动能量的利用率.可以发现,优化后的列车时刻表比当前提前100 s,不仅提升了列车运行速度,而且提高了列车之间再生制动能量的利用率.
| 表 5 第3辆列车优化前时刻表 Table 5 Timetable of third train before optimization |
| 表 6 第3辆列车优化后时刻表 Table 6 Timetable of third train after optimization |
根据常规再生制动能量利用方法优化该算例,再生制动能量利用值为1323 kW·h;将再生制动能量利用范围扩大至牵引—巡航阶段后,利用值提升至1 491 kW·h,再生能利用提高了12.7%.这部分的提升主要体现在图 6中虚线椭圆所圈出的部分,该部分描述的是第一辆列车制动时,第二辆列车大部分处于巡航阶段,改进前这部分制动能量不予利用,改进后扩大利用范围,没有造成这部分能量的浪费.由于该算例的站台较少,并且列车不是每个站台都存在巡航阶段,若扩大线路规模,且站台距离增长,则这部分能量的提升将更加明显.
4 结语本文对已有的再生制动能量利用方法进行改进,扩大利用范围,提升再生制动能量利用率;分析运行与调度之间的耦合关系,建立基于列车混行的运行-调度一体化优化模型.以杭州东到上海虹桥的D3208次动车和G7336次高铁为例,开展算例求解,得出优化后的速度曲线和时刻表.通过结果分析可以看出,利用本文建立的一体化优化方法,不仅可以降低各列车在区间内的运行能耗,还可以大大提升列车之间的再生制动能量的使用;本文改进后的再生能利用方法可以将能量利用在常规方法的基础上提升12.7%,使得线路上总能耗达到总体最优.考虑了列车混行的背景,计算列车的追踪间隔,确保列车行车安全;考虑快车的站台越行行为,提升了线路的运输能力,具有实际意义.
本文建立的优化模型尚有不足,为了简化问题,只考虑同等速度等级列车之间的再生制动能量利用,在快车越行之前,相邻列车利用率为0,只有次邻列车之间的利用;接下来将克服越行所带来的列车次序变化的复杂度,将模型更改,推广至整条线路及所有相邻的列车.
| [1] |
韩瑛. 不同速度等级列车混行对高速铁路通过能力的影响研究[D]. 兰州: 兰州交通大学, 2013. HAN Ying. Study on influence of mixed traffic with different speed grade on high-speed railway carrying capacity[D]. Lanzhou:Lanzhou Jiaotong University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10732-1013352939.htm |
| [2] |
董霄. 不同速度等级列车混跑对高速铁路运输能力的影响研究[D]. 北京: 北京交通大学, 2012. DONG Xiao. Study on theinfluence of mixed traffic on high-speed railway transport capacity[D]. Beijing:Beijing Jiaotong University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10004-1012357289.htm |
| [3] |
陈尔超. 城市轨道交通调度与控制一体化方法的研究[D]. 北京: 北京交通大学, 2015. CHEN Er-chao. Study on integrated method of scheduling and control in urban rail transit[D]. Beijing:Beijing Jiaotong University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10004-1015558170.htm |
| [4] |
MILROY I P. Aspect of automatic train control[D]. Leicestershire:Loughborough University, 1980. https://core.ac.uk/display/9690129
|
| [5] |
HOWLETT P G, PUDNEY P J, XUAN V. Local energy minimization in optimal train control[J]. Automatica, 2009, 45(11): 2692-2698. DOI:10.1016/j.automatica.2009.07.028 |
| [6] |
LI X, LI L, GAO Z, et al. Train energy-efficient operation with stochastic resistance coefficient[J]. International Journal of Innovative Computing, Information and Control, 2013, 9(8): 3471-3483. |
| [7] |
LI X, GAO Z, SUN W. Existence of an optimal strategy for stochastic train energy-efficient operation problem[J]. Soft Computing, 2013, 17(4): 651-657. DOI:10.1007/s00500-012-0938-x |
| [8] |
冯晓云. 模糊预测控制及其在列车自动驾驶中的应用研究[D]. 成都: 西南交通大学, 2001. FENG Xiao-yun. Fuzzy predictive control and its application in the automatic train operation[D]. Chengdu:Southwest Jiaotong University, 2001. http://d.wanfangdata.com.cn/Thesis/Y430825 |
| [9] |
王成莉. 基于遗传算法的高速列车节能运行控制研究[D]. 北京: 北京交通大学, 2016. WANG Cheng-li. Research on high speed train energy-saving control methods based on genetic algorithm[D]. Beijing:Beijing Jiaotong University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10004-1016120726.htm |
| [10] |
KOKOTOVIC P, SINGH G. Minimum-energy control of a traction motor[J]. IEEE Transactions on Automatic Control, 1972, 17(1): 92-95. DOI:10.1109/TAC.1972.1099870 |
| [11] |
GORDON S P, LEHRER D G. Coordinated train control and energy management control strategies[C]//Proceedings of the 1998 ASME/IEEE Joint Railroad Conference. Philadelphia:IEEE, 1998:165-176. https://digital.library.unt.edu/ark:/67531/metadc710984/
|
| [12] |
ALBRECHT T. Reducing power peaks and energy consumption in rail transit systems by simultaneous train running time control[J]. Computers in Railways, 2004, 74(3): 885-894. |
| [13] |
CHEN J F, LIN R L, LIU Y C. Optimization of an MRT train schedule:reducing maximum traction power by using genetic algorithms[J]. IEEE Transactions on Power Systems, 2005, 20(3): 1366-1372. DOI:10.1109/TPWRS.2005.851939 |
| [14] |
KIM K M, KIM K T, HAN M S. A model and approaches for synchronized energy saving in timetable[C]//9th World Congress of Railway Research. France:[s. n.], 2011:22-26.
|
| [15] |
PEÑA-ALCARAZ M, FERNÁNDEZ A, CUCALA A P, et al. Optimal underground timetable design based on power flow for maximizing the use of regenerative-braking energy[J]. Part F:Journal of Rail and Rapid Transit, 2011, 226(4): 397-408. |
| [16] |
NASRI A, MOGHADAM M F, MOKHATARI H. Timetable optimization for maxmun usage of regenerative energy of braking in electrical railway system[C]//2010 International Symposium on Power Electronics Electrical Drives Automation and Motion (SPEEDAM). Pisa:IEEE, 2010:1218-1221.
|
| [17] |
赵莹莹. 考虑再生制动能量利用的城轨交通多列车节能运行研究[D]. 北京: 北京交通大学, 2015. ZHAO Ying-ying. Research of multiple train operation for maximum usage of regenerative energy[D]. Beijing:Beijing Jiaotong University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10004-1015545465.htm |
| [18] |
赵乐. 基于再生制动的地铁列车时刻表优化模型与算法研究[D]. 北京: 北京交通大学, 2014. ZHAO Le. Research on metro timetable optimization model and algorithm based on regenerative braking[D]. Beijing:Beijing Jiaotong University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10004-1014177939.htm |
| [19] |
YANG X, LI X, GAO Z, et al. A cooperative scheduling model for timetable optimization in subway systems[J]. IEEE Transactions on Intelligence Transportation System, 2013, 14(1): 438-447. DOI:10.1109/TITS.2012.2219620 |
| [20] |
丁奕. 基于列车节能的时刻表制定方法的研究[D]. 北京: 北京交通大学, 2013. DING Yi. The study of timetable design based on the train energy saving[D]. Beijing:Beijing Jiaotong University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10004-1013279416.htm |
| [21] |
孙亚华. 高速列车运行控制与调度一体化研究[D]. 北京: 北京交通大学, 2015. SUN Ya-hua. The integration study of high-speed train operation control and scheduling[D]. Beijing:Beijing Jiaotong University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10004-1015558193.htm |
| [22] |
路飞. 移动闭塞条件下地铁列车的运行优化[D]. 济南: 山东大学, 2007. LU Fei. Operation optimization of the subway train under moving block system[D]. Jinan:Shandong University, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10422-2007088773.htm |



