钢筋锈蚀是导致混凝土结构性能退化的主要原因之一[1].我国大部分小跨径的预应力混凝土桥梁采用先张法施工.这种先张预应力混凝土结构中的钢绞线与混凝土直接接触,没有波纹管的保护,容易发生锈蚀.锈蚀产物的膨胀会对周围混凝土产生锈胀力,进而导致混凝土的开裂.混凝土的开裂为锈蚀溶液的流通提供了通道,会进一步加快钢筋的锈蚀[2-3].混凝土开裂是评估既有结构正常使用寿命的关键指标[4].
锈蚀产物在裂缝内的填充是锈胀开裂研究的主要内容之一.早期研究认为保护层开裂前,锈蚀产物会完全填充内部裂缝[5-6],Zhao等[7]研究认为保护层开裂前锈蚀产物不会填充混凝土裂缝,Lu等[8]认为锈蚀产物只会部分填充混凝土裂缝.以往研究主要针对于保护层开裂前锈蚀产物的填充情况,保护层开裂后,锈蚀产物随时间逐渐填充混凝土裂缝[9].Jaffer等[10]对锈蚀产物在开裂混凝土内的分布进行观测.现有研究尚不能明确锈蚀产物在裂缝内的填充规律,锈蚀产物的填充与锈蚀程度、钢筋类型及保护层厚度等多种因素有关,如何量化锈蚀产物在裂缝内的填充有待进一步研究[11].
根据锈蚀率预测裂缝宽度是锈胀开裂研究的另一个关键问题.Torres-Acosta等[12]基于试验数据,建立裂缝宽度和锈蚀率之间的关系.Li等[13]考虑钢筋锈蚀和外加荷载的耦合效应,提出裂缝宽度预测模型.Khan等[14]通过既有混凝土梁的裂缝宽度,对钢筋的锈蚀程度进行预测.以上文献主要研究了钢筋锈蚀引起的混凝土开裂,钢绞线由多根钢丝捻制而成,其截面呈梅花状,钢绞线锈蚀引起的混凝土开裂可能与普通钢筋锈蚀引起的情况存在差异.Dai等[15]假定锈蚀产物的填充为常值,建立预应力混凝土锈胀开裂预测模型.如何合理地考虑锈蚀产物填充对混凝土锈胀开裂的影响有待进一步研究.
本文通过试验研究钢绞线锈蚀产物在开裂混凝土内的填充情况,基于试验结果,考虑锈蚀产物填充和钢绞线捻制形状等因素,建立裂缝宽度预测模型.
1 试验方案 1.1 构件设计设计制作了12根混凝土梁,梁长1 200 mm,横断面尺寸为150 mm×150 mm.为了研究箍筋对混凝土开裂的影响,将试验梁分成S组(无箍筋)和RS组(有箍筋),每组各6根.梁内布置有一根直径为15.2 mm的7丝钢绞线,RS组四周各有一根直径为10 mm的HRB335变形钢筋.箍筋采用直径为8 mm的R235光圆钢筋,间距为100 mm.在端部布置一根聚氯乙烯(PVC)管,以防止锈蚀溶液从梁端溢出.钢绞线与普通钢筋的保护层厚度分别为67.4和30 mm.
混凝土采用32.5级的硅酸盐水泥,水灰比为0.43,配合比如下:水泥质量浓度为417 kg/m3,细骨料质量浓度为676 kg/m3,粗骨料质量浓度为1 026 kg/m3.S组和RS组混凝土28 d抗压强度分别为32.5和35.5 MPa.试件的详细尺寸如图 1所示.

|
图 1 混凝土构件的尺寸 Fig. 1 Details of concrete beams |
采用人工通电方法对构件进行快速锈蚀,为了单独研究钢绞线锈蚀对混凝土开裂的影响,使用环氧树脂对普通钢筋进行防锈处理.构件浸泡在质量分数为5%的NaCl溶液中,钢绞线作为阳极,不锈钢板作为阴极;在电流作用下,阳极钢绞线释放出电子被氧化发生锈蚀.锈蚀电流为0.3 A,电流密度为270 μA/cm2,加速锈蚀装置如图 2所示.

|
图 2 加速锈蚀装置 Fig. 2 Accelerated corrosion device |
加速锈蚀后,混凝土表面出现纵向裂缝,采用精度为0.01 mm的便携式显微镜对纵向裂缝宽度进行观测.为了研究横断面径向裂缝的分布及裂缝内锈蚀产物的填充,将每根锈蚀构件切割成4个15 mm厚的切块,依次编号为A~D,切块总数为48个,如图 1所示.以构件S6为例,切块分别命名为S6A、S6B、S6C和S6D.试验采用开裂角度来描述横断面径向裂缝的开展情况.由于锈蚀产物在不同位置处的填充有差异,将切块沿最大裂缝位置破除,进而观察锈蚀产物在裂缝内的填充,采用平均铁锈填充深度来反映裂缝内锈蚀产物的填充情况.
在试验过程中,选取最大裂缝进行开裂角度的测量.测量步骤如下:首先,绘制出径向裂缝轮廓示意图;然后,将裂缝示意图扫描至计算机,将裂缝的夹角定义为开裂角度;最后,利用辅助绘图程序计算开裂角度,更详细的介绍见文献[16].铁锈填充深度采用相同的方法进行测量.
研究表明,裂缝宽度与质量损失具有良好的线性关系[14].本文试验研究发现,由于钢绞线直径较大,轻微的锈蚀会造成混凝土保护层开裂.本文以每10 mm的平均质量损失来评估不同位置钢绞线的锈蚀率.
钢绞线质量损失的测量步骤如下.首先,破除混凝土保护层取出锈蚀钢绞线;然后,使用质量分数为12%的盐酸溶液对钢绞线进行除锈处理,再用碱液中和;最后,对每10 mm钢绞线的平均质量损失率进行测定.
2 锈蚀形态和裂缝发展 2.1 钢绞线锈蚀形态采用数字显微镜对钢绞线的锈蚀形态进行观测.图 3给出钢绞线的锈蚀形态,钢绞线表面存在坑锈和缝隙锈蚀,锈坑多为椭圆形,体积较小,深度较浅.此外,钢绞线内丝与外丝之间的缝隙为锈蚀溶液的流动提供了通道,这会进一步加快钢绞线的锈蚀速率.由于钢绞线几何形状和缝隙锈蚀的共同作用,单位长度钢绞线的锈蚀损失会比普通钢筋的大.

|
图 3 钢绞线锈蚀形态 Fig. 3 Corrosion morphology of strand |
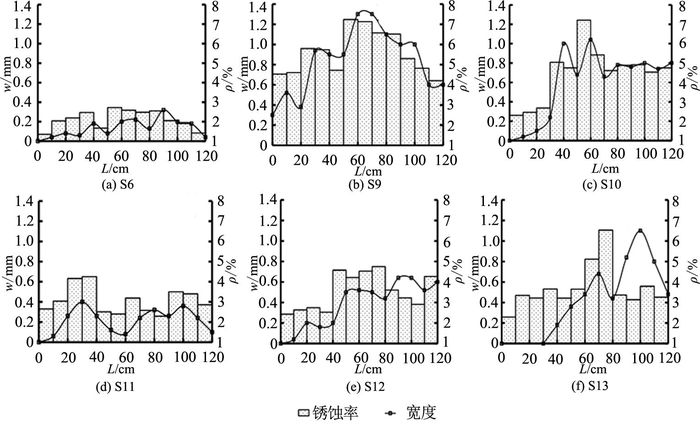
预测钢绞线锈蚀是评估既有结构性能退化的重要环节之一.Khan等[14]认为裂缝宽度与平均质量锈蚀率具有良好的线性关系.该试验根据裂缝宽度来评估钢绞线的锈蚀,对每10 mm位置处的裂缝宽度和质量损失率进行测量,如图 4、5所示.
|
图 4 S组裂缝宽度和锈蚀率 Fig. 4 Crack width and corrosion loss (group S) |
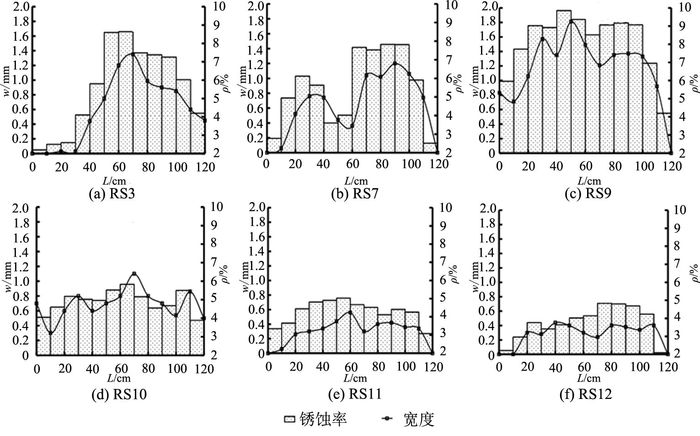
|
图 5 RS组裂缝宽度和锈蚀率 Fig. 5 Crack width and corrosion loss (group RS) |
由图 4、5可知,锈裂宽度随锈蚀率的增加而增大.跨中位置的裂缝比梁端位置的裂缝宽度大,出现这种现象的原因是跨中梁段在整个锈蚀期间一直沉浸在NaCl溶液中,跨中位置钢绞线的锈蚀程度较高,进而裂缝宽度较大.箍筋可以抑制混凝土的锈胀开裂.在相同锈蚀率下,S组的裂缝宽度比RS组裂缝宽度大.箍筋能够承担钢绞线锈蚀产物的膨胀力,进而减小锈胀裂缝宽度.
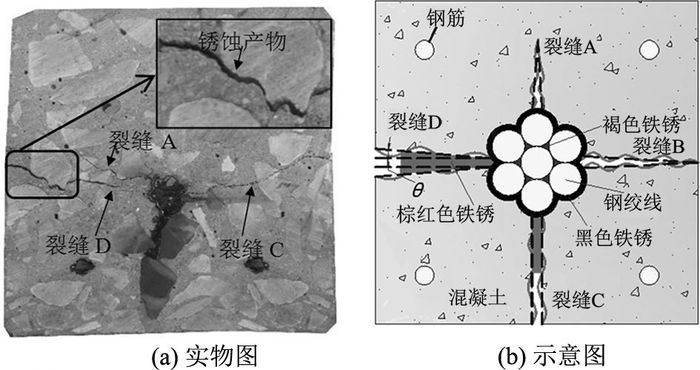
2.3 锈胀裂缝扩展混凝土裂缝在横断面的分布形态是研究锈胀开裂的一个关键问题,混凝土内部裂缝的分布通常难以观察.为了研究横断面径向裂缝的分布形态,将试件切割成厚度为15 mm的混凝土切块.图 6给出切块的横断面示意图,断面存在3条裂缝,分别命名为裂缝A、裂缝C和裂缝D.
裂缝A未开裂到混凝土表面,裂缝C和裂缝D发展到混凝土表面.裂缝C沿径向方向基本具有相同宽度,裂缝D沿半径方向逐渐变宽,是3条裂缝中最宽的一条.
|
图 6 横断面裂缝分布 Fig. 6 Crack propagation of cross-section |
混凝土裂缝宽度与锈蚀程度有关,图 6(b)给出裂缝扩展的示意图,裂缝不同阶段的发展呈现出不同的形状:三角形、矩形和梯形.在保护层开裂前,内部裂缝多呈三角形,与裂缝A类似.随着锈蚀程度的增加,内部裂缝开展到混凝土表面,裂缝形状为三角形,与裂缝B相似.当裂缝开展到混凝土表面后,裂缝宽度随着锈蚀率的增加而增大,形状类似于矩形,与裂缝C类似.随着锈蚀程度的进一步增加,裂缝宽度沿径向开展,形状变为梯形,与裂缝D近似.综上可知,随着锈蚀程度的增加,混凝土锈胀裂缝在横断面的形状由三角形逐渐向梯形发展,这一现象与文献[5]的观测结果类似.
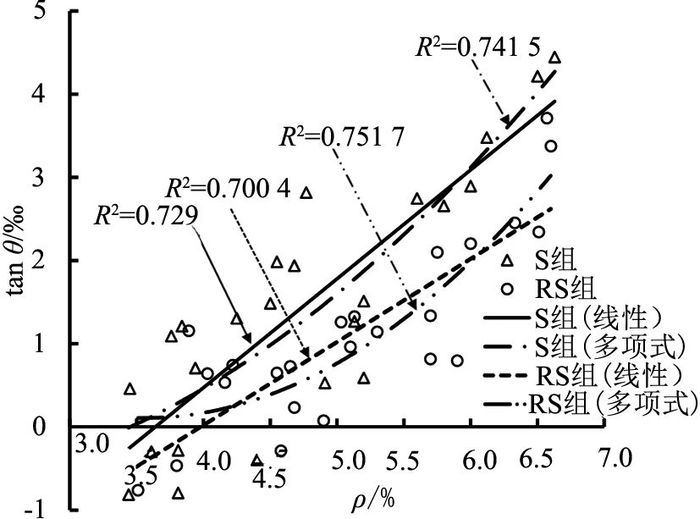
构件共切割成48个15 mm厚的切块.利用图 6(b)的开裂角θ来表示径向裂缝宽度的变化.当裂缝沿半径方向逐渐变窄时,θ<0°;当径向裂缝宽度保持为常值时,θ=0°;当裂缝沿径向逐渐变宽时,θ>0°.图 7给出tan θ与锈蚀率之间的线性和多项式关系.
|
图 7 开裂角正切值与锈蚀率之间的关系 Fig. 7 Tangent of cracking angle and corrosion loss |
开裂角的正切值随锈蚀程度的增加而增大.由图 7可知,线性回归与多项式回归的精度接近,故tan θ与锈蚀率ρ的关系采用线性回归,表达式如下:
| $ \tan \theta = a\rho - b. $ | (1) |
其中:θ为开裂角;a、b为常量,对于S组试件:a=0.130 9,b=0.004 8,对于RS组试件:a=0.099 9,b=0.004 0.
3 锈蚀产物在裂缝内的填充 3.1 锈蚀产物组成相关研究表明,锈蚀产物的组成成分与混凝土含碱、供氧和含水量等因素有关.通过该试验观测到混凝土横断面不同位置处的锈蚀产物存在不同的颜色,即黑色、棕红色和褐色3种颜色.
钢绞线-混凝土交界面存在黑色铁锈,如图 8所示.锈蚀产物的主要成分为氧化亚铁(FeO)和四氧化三铁(Fe3O4),两者均为黑色.FeO在空气中不稳定,极易氧化生成Fe3O4;因此,黑色铁锈的主要成分可以认为是Fe3O4.

|
图 8 钢绞线混凝土界面处的黑色铁锈 Fig. 8 Black rust at strand-concrete interface |
混凝土裂缝内存在棕红色铁锈,如图 9所示.裂缝为氧气进入混凝土内部提供了通道,因此锈蚀过程中有大量氧气参与反应,氧化铁(Fe2O3)是棕红色铁锈的主要成分.

|
图 9 锈蚀产物在裂缝内的填充情况 Fig. 9 Filling of corrosion products in cracks |
褐色铁锈存在于钢绞线内丝和外丝的间隙之间,如图 3所示.氧气随着流动的锈蚀溶液进入内丝和外丝的间隙内,进而与铁发生反应,间隙内氧气的质量分数低于裂缝内氧气的质量分数,但比钢绞线-混凝土界面区氧气的质量分数高.间隙内的铁锈颜色介于黑色与棕红色之间.
3.2 锈蚀产物的填充情况在加速锈蚀过程中可以观察到部分锈蚀产物从混凝土表面的纵向裂缝中溢出.将切块沿最大裂缝位置破除,进而观察锈蚀产物在裂缝内的填充.如图 9所示为切片S6B、S9A和S9C的剖面.锈蚀产物在不同位置处的填充有差别,锈蚀产物主要填充于最大裂缝内,其他细小裂缝中只能观测到少量锈蚀产物,这一观测结果与Šavija等[9]采用CT扫描监测到的试验现象一致.
图 9中,3个切块的最大裂缝宽度分别为0.08、0.39、0.91 mm,锈蚀产物的填充深度随裂缝宽度的增加而增大.在试验过程中,无法直接测量锈蚀产物的体积,但填充深度较易测量,通过几何公式变换,可以由铁锈填充深度得到锈蚀产物的体积.该试验采用铁锈填充深度来描述铁锈填充率,铁锈填充率定义为平均填充深度与保护层的比值,表达式为
| $ f = \frac{{{R_{\rm{i}}}}}{C}. $ | (2) |
式中:f为铁锈填充率,Ri为铁锈平均填充深度,C为保护层厚度.
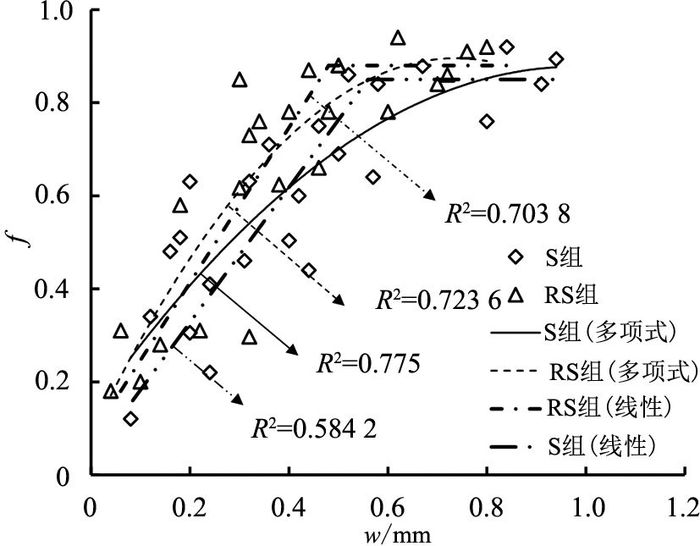
试验观察表明,即使是在开裂相当严重的情况下,锈蚀产物也不能完全填满裂缝,即铁锈填充率小于1.图 10给出铁锈填充率与裂缝宽度的线性和多项式回归,当裂缝宽度较小时,铁锈填充率随裂缝宽度的增加而增大;当裂缝宽度超过某一临界值后,铁锈填充率基本保持为常数,即最大铁锈填充率.S组和RS组的最大铁锈填充率分别为0.85和0.88,该值对应的临界裂缝宽度分别为0.79和0.63 mm.
|
图 10 铁锈填充率与宽度的回归线 Fig. 10 Rust-filling ratio and crack width |
由图 10可知,RS组铁锈填充率的增长速度比S组快.箍筋可以承受锈胀力,进而减小裂缝宽度,从而导致RS组的铁锈填充率比S组的大.多项式回归精度比线性回归高,故采用多项式对裂缝宽度和铁锈填充率的关系进行回归,表达式分别为
| $ {f_{\rm{s}}} = \left\{ \begin{array}{l} - 0.773w_{\rm{s}}^2 + 1.515{w_{\rm{s}}} + 0.1353,{w_{\rm{s}}} \le 0.79{\rm{mm;}}\\ 0.85,{w_{\rm{s}}} > 0.79{\rm{mm}}{\rm{.}} \end{array} \right. $ | (3a) |
| $ {f_{\rm{r}}} = \left\{ \begin{array}{l} - 1.4938w_{\rm{r}}^2 + 2.2011{w_{\rm{r}}} + 0.085,{w_{\rm{r}}} \le 0.63{\rm{mm;}}\\ 0.88,{w_{\rm{r}}} > 0.63{\rm{mm}}{\rm{.}} \end{array} \right. $ | (3b) |
式中:fs和fr为S组和RS组的铁锈填充率, ws和wr为S组和RS组的裂缝宽度.
4 锈胀开裂预测模型采用厚壁圆筒理论对混凝土的锈胀开裂过程进行模拟,原因有以下两点:首先,钢绞线捻制梅花形肋深相对钢绞线直径和混凝土保护层厚度较小,可以忽略钢绞线捻制形状的影响,将钢绞线锈蚀产生的膨胀力等效为环向应力;其次,已有学者将厚壁圆筒理论应用于钢绞线的应力传递长度和黏结性能的分析计算[17-18].在锈蚀过程中,锈蚀产物首先填充钢绞线-混凝土交界面,随之产生膨胀力,进而渗透到锈胀裂缝中.根据锈蚀产物体积相等的原则,可以得到裂缝宽度和锈蚀率之间的关系.
4.1 微裂缝形成时的锈蚀产物在锈蚀过程中,锈蚀产物在钢绞线-混凝土交界面累积,并逐渐产生膨胀力,当膨胀力产生的切应力达到混凝土抗拉强度时,混凝土微裂缝形成.根据钢绞线-混凝土界面的径向变形,可得微裂缝形成时锈蚀产物的体积.
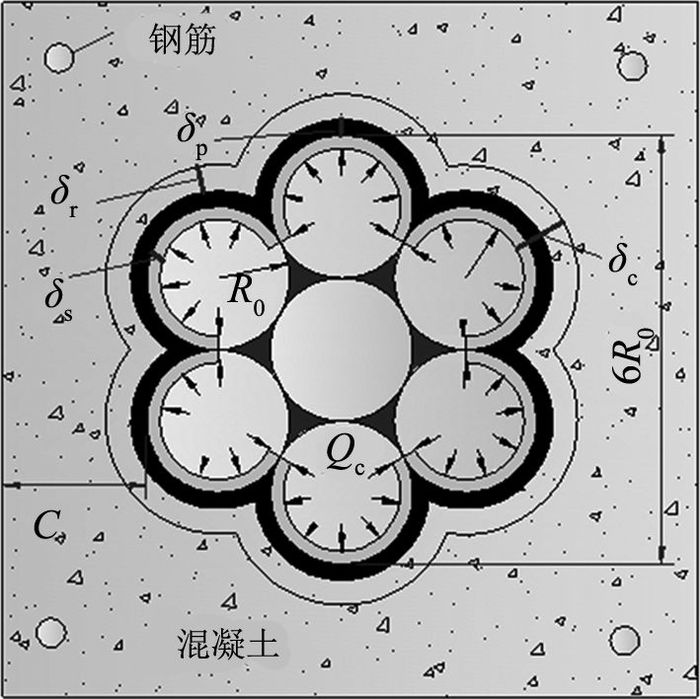
钢绞线直径一般较大,轻微的锈蚀会导致保护层开裂.当锈蚀程度较低时,锈蚀产物在钢绞线表面一般均匀分布,周围混凝土受到均匀锈胀力,如图 11所示为钢绞线-混凝土界面的变形.
|
图 11 钢绞线混凝土界面的变形 Fig. 11 Deformation at strand-concrete interface |
混凝土的锈胀开裂过程可以考虑为均匀受压的轴对称平面应力问题,利用厚壁圆筒理论进行模拟,径向应力平衡方程为
| $ \frac{{{\rm{d}}{\sigma _r}}}{{{\rm{d}}r}} + \frac{{{\sigma _r} - {\sigma _\theta }}}{r} = 0. $ | (4) |
式中:σr和σθ分别为径向应力和切向应力,r为任意半径.
在对称平面应力问题中,应变与位移关系为
| $ {\varepsilon _r} = \frac{{{\rm{d}}u}}{{{\rm{d}}r}}, $ | (5a) |
| $ {\varepsilon _\theta } = \frac{u}{r}. $ | (5b) |
式中:εr、εθ和u分别为径向应变、切向应变和径向位移.
混凝土的应力与应变关系为
| $ {\sigma _r} = \frac{{{E_{\rm{c}}}}}{{1 - \nu _{\rm{c}}^2}}\left( {{\varepsilon _r} + {\nu _{\rm{c}}}{\varepsilon _\theta }} \right), $ | (6a) |
| $ {\sigma _\theta } = \frac{{{E_{\rm{c}}}}}{{1 - \nu _{\rm{c}}^2}}\left( {{\varepsilon _\theta } + {\nu _{\rm{c}}}{\varepsilon _r}} \right). $ | (6b) |
式中:Ec为混凝土的弹性模量,νc为混凝土的泊松比.
混凝土是一种非均质材料,所以钢绞线-混凝土界面周围存在多孔区,锈蚀产物首先填充这些多孔区[19].随着锈蚀程度的增加,锈蚀产物的锈胀力会导致混凝土发生变形.联立式(4)~(6),可得混凝土的变形:
| $ {\delta _{\rm{r}}} = \frac{{\left( {{R_0} + {\delta _{\rm{p}}}} \right)}}{{{E_{\rm{c}}}}}\left( {1 + k + {\nu _{\rm{c}}}} \right){Q_{\rm{c}}}. $ | (7) |
式中:k为常量,k=2(R0+δp) 2/[C2+2C(R0+δp)];Qc为膨胀力;R0为钢丝半径;C为保护层厚度;δp为多孔区厚度,取值为10~20 μm[5].
通过几何关系的变化,可以得到单位长度内,填充微裂缝的锈蚀产物体积Vm,为
| $ {V_{\rm{m}}} = \frac{{4{\rm{ \mathsf{ π} }}n}}{{n - 1}}\left[ {{{\left( {{R_0} + {\delta _0} - {\delta _{\rm{s}}}} \right)}^2} - R_0^2} \right]. $ | (8) |
式中:n为铁锈膨胀率,可取n=2~4[5];δs为锈蚀钢丝的损失半径;δc为锈蚀产物厚度,δc=δs+δp+δr.
由于R0的单位为mm,δp+δr的单位为μm,δp+δr远小于R0.为了简化分析,计算过程中(δp+δr)2忽略不计,式(8)可以简化为
| $ {V_{\rm{m}}} = \frac{{4{\rm{ \mathsf{ π} }}n{R_0}}}{{n - 1}}\left( {{\delta _{\rm{p}}} + {\delta _{\rm{r}}}} \right). $ | (9) |
联立式(7)、(9),Qc可以表示为
| $ {Q_{\rm{c}}} = \frac{{{E_{\rm{c}}}}}{{\left( {1 + k + {\nu _{\rm{c}}}} \right)\left( {{R_0} + {\delta _{\rm{p}}}} \right)}}\left( {\frac{{\left( {n - 1} \right){V_{\rm{m}}}}}{{4{\rm{ \mathsf{ π} }}n{R_0}}} - {\delta _{\rm{p}}}} \right). $ | (10) |
当锈蚀产物膨胀产生的切应力超过混凝土抗拉强度后出现微裂缝,Dai等[15]通过弹性力学轴对称应力解得到相应的切应力,进而得到了微裂缝产生时的最大膨胀力:
| $ {Q_{{\rm{cmax}}}} = \left( {0.225 + 0.075\frac{C}{{{R_0}}}} \right){f_{\rm{t}}}. $ | (11) |
式中:ft为混凝土抗拉强度.
联立式(10)、(11),可得微裂缝产生时锈蚀产物的体积为
| $ \begin{array}{l} {V_{\rm{m}}} = \frac{{{\rm{ \mathsf{ π} }}n{R_0}}}{{\left( {n - 1} \right){E_{\rm{c}}}}}\left[ {\left( {0.9 + 0.3\frac{C}{{{R_0}}}} \right){f_{\rm{t}}}\left( {1 + k + {\nu _{\rm{c}}}} \right) \times } \right.\\ \;\;\;\;\;\;\left. {\left( {{R_0} + {\delta _{\rm{p}}}} \right) + {E_{\rm{c}}}{\delta _{\rm{p}}}} \right]. \end{array} $ | (12) |
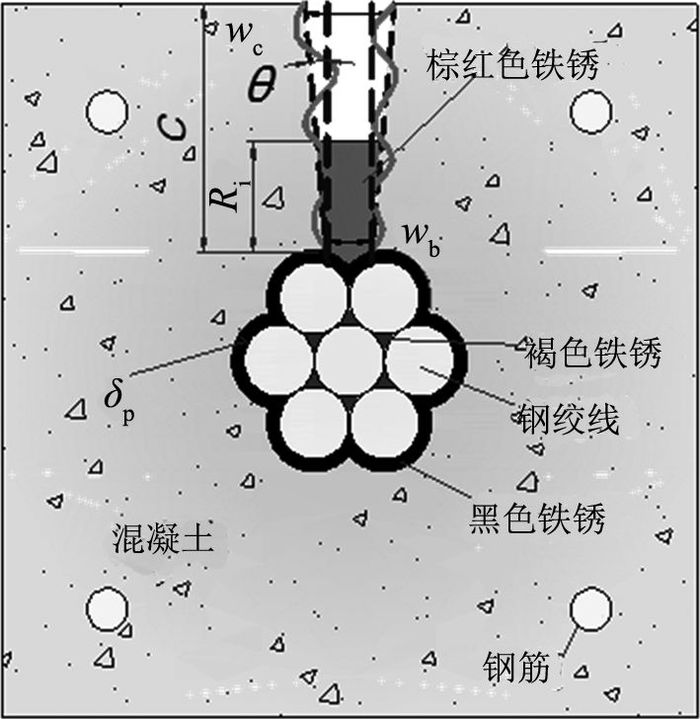
在保护层开裂后,混凝土表面出现可见裂缝.由上文试验可知,锈蚀产物主要填充于最大裂缝内,在微小裂缝内的填充极少,本文忽略了微小裂缝内锈蚀产物的填充,进而选取横截面最大裂缝为研究对象,如图 12所示.
|
图 12 简化锈胀裂缝示意图 Fig. 12 Simplified schematic diagram of crack |
试验表明,锈蚀产物的填充与裂缝宽度有关,裂缝宽度与开裂角度相关,本文采用开裂角度来计算裂缝中锈蚀产物的体积.根据锈蚀产物填充率和开裂角度之间的关系,得到裂缝中锈蚀产物的体积:
| $ {V_{\rm{p}}} = \left[ {{w_{\rm{c}}} + C\left( {f - 2} \right)\tan \theta } \right] \times {R_{\rm{i}}}. $ | (13) |
式中:wc为混凝土表面的裂缝宽度.
根据几何关系可知,锈蚀产物的总体积为
| $ {V_{\rm{c}}} = n\rho {V_{\rm{s}}}. $ | (14) |
式中:Vs为单位长度钢绞线的锈蚀损失体积.
根据锈蚀产物体积相等的原则可知,Vc=Vm+Vp.联立式(1)、(12)~(14),可得混凝土表面裂缝宽度:
| $ \begin{array}{l} {w_{\rm{c}}} = C\left( {f - 2} \right)\left( {b - a\rho } \right) + \frac{{n{V_{\rm{s}}}\rho }}{{Cf}} - \\ \;\;\;\;\;\;{\rm{ \mathsf{ π} }}n{R_0}\left[ {\left( {0.9 + 0.3\frac{C}{{{R_0}}}} \right){f_{\rm{t}}}\left( {1 + k + {\nu _{\rm{c}}}} \right) \times } \right.\\ \;\;\;\;\;\;\left. {\left( {{R_0} + {\delta _{\rm{p}}}} \right) + {E_{\rm{c}}}{\delta _{\rm{p}}}} \right]/\left[ {\left( {n - 1} \right){E_{\rm{c}}}Cf} \right]. \end{array} $ | (15) |
裂缝宽度和铁锈填充率之间的关系可由式(3)计算得到,进而联立式(3)、(15),即可通过钢绞线锈蚀率计算得到裂缝宽度.计算公式表明,锈蚀产物的填充、保护层厚度、铁锈膨胀率、混凝土抗拉强度和钢绞线的几何形状等因素都会影响混凝土的锈胀开裂.进行锈胀开裂预测时须综合考虑以上因素的影响.
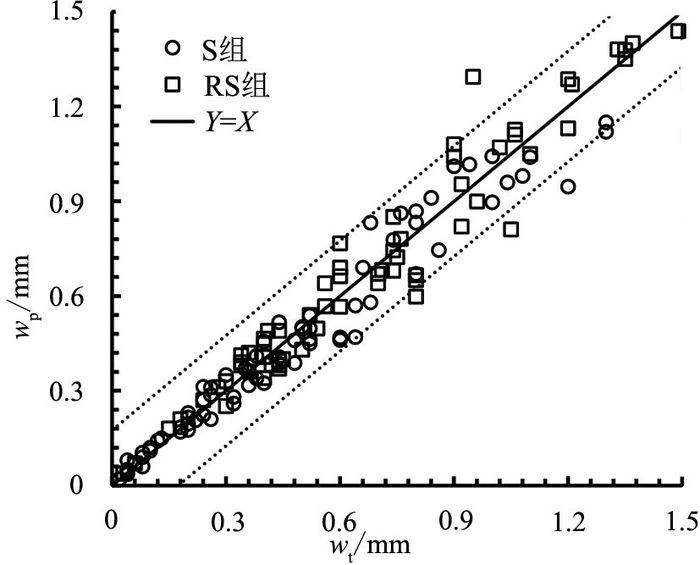
4.3 预测模型的验证利用提出的预测模型,对试验结果进行验证.预测模型的部分参数选取如下:铁锈膨胀率和多孔区厚度分别取3和15 μm.图 13给出裂缝宽度的预测值wp和试验值wt,S组和RS组的预测误差分别为13.56%和11.79%,平均误差为12.68%.
|
图 13 裂缝宽度预测结果和试验结果 Fig. 13 Predicted and testresults of crack widths |
预测值与试验值较吻合,预测误差在可接受范围内.造成预测误差的原因主要包括:裂缝宽度、锈蚀率和开裂角测量过程中的不确定性;预测模型中忽略了微小裂缝内的锈蚀产物填充;混凝土材料的不均匀性和变异性等.
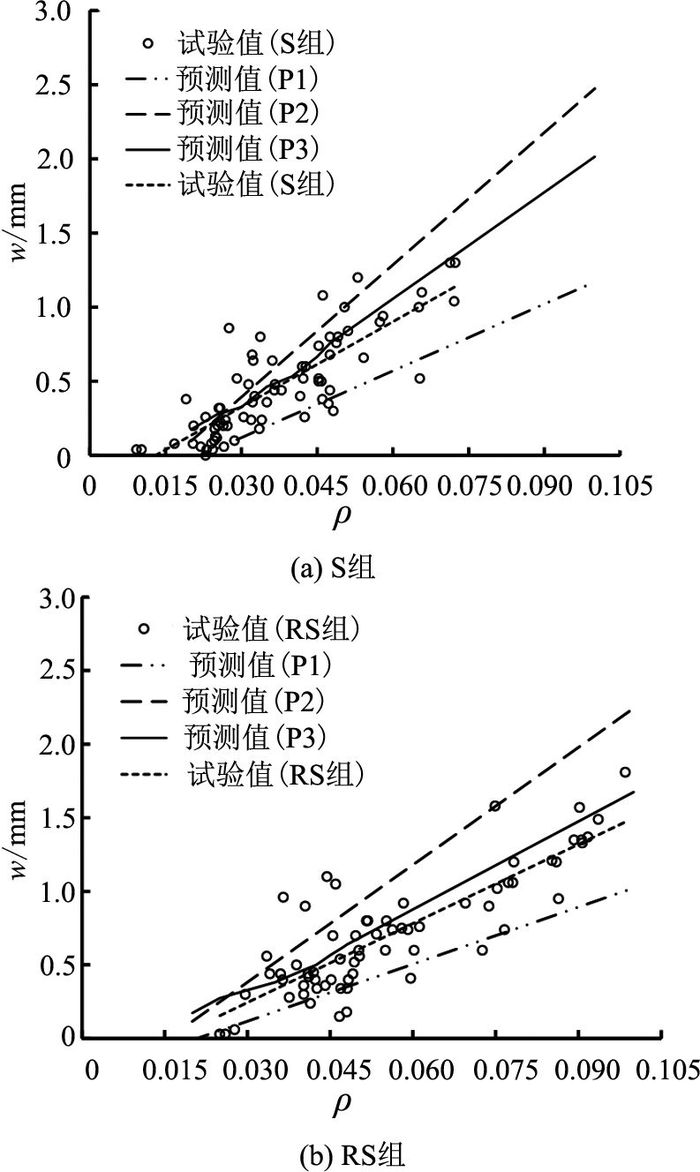
为了明确锈蚀产物填充对锈胀开裂预测模型的影响,图 14给出不同铁锈填充率下的预测结果.图中,P1和P2分别选取铁锈填充率为1和0.5常值时的预测结果,P3为使用该模型得到的预测结果.由图 14可知,P1的预测值小于试验值,P2的预测值大于试验结果,P3的预测值与试验结果较吻合.由此可知,铁锈填充率是预测模型的一个重要参数,为了提高锈胀裂缝宽度的预测精度,必须合理地考虑锈蚀产物在裂缝中的填充情况.
|
图 14 不同铁锈填充率下的预测裂缝宽度 Fig. 14 Predicted crack widths under various rust-filling ratios |
(1) 锈蚀产物的填充随裂缝宽度的发展而改变.当裂缝较小时,铁锈填充率随裂缝的发展而增大;当裂缝宽度超过临界值时,锈蚀产物的填充基本维持为常值.
(2) 箍筋的使用可以有效地抑制锈胀裂缝宽度和开裂角度,开裂角度的正切值随锈蚀程度的增加而增大.
(3) 利用提出的模型可以合理地预测混凝土锈胀裂缝宽度.铁锈填充率是预测模型的一个重要参数,为了提高锈胀裂缝宽度的预测精度,必须合理考虑锈蚀产物在裂缝中的填充.
该试验采用电化学方法进行快速锈蚀,加速锈蚀导致的混凝土开裂可能与自然锈蚀环境下的情况不同;此外,保护层厚度会对铁锈填充率产生影响.以上因素对裂缝内锈蚀产物填充的影响有待进一步的研究.
| [1] |
毛江鸿, 陈佳芸, 崔磊, 等. 氯盐侵蚀钢筋混凝土锈胀开裂监测及预测方法[J]. 建筑材料学报, 2016, 19(1): 59-64. MAO Jiang-hong, CHEN Jia-yun, CUI Lei, et al. Monitoring and predicting method for reinforced concrete expansion and cracking induced by chloride erosion[J]. Journal of Building Materials, 2016, 19(1): 59-64. |
| [2] |
王晓舟, 金伟良, 延永东. 混凝土结构锈胀开裂预测的路径概率模型[J]. 浙江大学学报:工学版, 2010, 44(6): 1191-1196. WANG Xiao-zhou, JIN Wei-liang, YAN Yong-dong. Path probability model of corrosion-crack assessment for existing reinforced concrete structures[J]. Journal of Zhejiang University:Engineering Science, 2010, 44(6): 1191-1196. |
| [3] |
LI Fu-min, YUAN Ying-shu, LI C Q. Corrosion propagation of prestressing steel strands in concrete subject to chloride attack[J]. Construction and Building Materials, 2011, 25(10): 3878-3885. DOI:10.1016/j.conbuildmat.2011.04.011 |
| [4] |
王治, 金贤玉, 付传清, 等. 基于损伤的钢筋混凝土锈胀开裂模型[J]. 建筑结构学报, 2014, 35(9): 115-122. WANG Zhi, JIN Xian-yu, FU Chuan-qing, et al. Concrete cracking model for rust expansion based on damage[J]. Journal of Building Structures, 2014, 35(9): 115-122. |
| [5] |
ZHAO Yu-xi, JIN Wei-liang. Modeling the amount of steel corrosion at the cracking of concrete cover[J]. Advance in Structural Engineering, 2006, 9(5): 687-696. DOI:10.1260/136943306778827556 |
| [6] |
BAZANT Z. Physical model for steel corrosion in concrete sea structures:theory[J]. Journal of the Structural Division, 1979, 105(6): 1155-1166. |
| [7] |
ZHAO Yu-xi, YU Jiang, HU Bing-yan, et al. Crack shape and rust distribution in corrosion-induced cracking concrete[J]. Corrosion Science, 2012, 55: 385-393. DOI:10.1016/j.corsci.2011.11.002 |
| [8] |
LU Chun-hua, JIN Wei-liang, LIU Rong-gui. Reinforcement corrosion-induced cover cracking and its time prediction for reinforced concrete structures[J]. Corrosion Science, 2011, 53(4): 1337-1347. DOI:10.1016/j.corsci.2010.12.026 |
| [9] |
ŠAVIJA B, LUKOVIC M, HOSSEINI S, et al. Corrosion induced cover cracking studied by X-ray computed tomography, nanoindentation, and energy dispersive X-ray spectrometry (EDS)[J]. Materials and Structures, 2015, 48(7): 2043-2062. DOI:10.1617/s11527-014-0292-9 |
| [10] |
JAFFER S J, HANSSON C M. Chloride-induced corrosion products of steel in cracked-concrete subjected to different loading conditions[J]. Cement and Concrete Research, 2009, 39(2): 116-125. DOI:10.1016/j.cemconres.2008.11.001 |
| [11] |
吴灵杰, 寇新建, 周拥军, 等. 既有钢筋混凝土码头保护层锈胀开裂计算时长对比[J]. 哈尔滨工业大学学报, 2016, 48(12): 51-55. WU Ling-jie, KOU Xin-jian, ZHOU Yong-jun, et al. Propagation assessment of existing concrete dock based on concrete cover corrosion-crack[J]. Journal of Harbin Institute of Technology, 2016, 48(12): 51-55. DOI:10.11918/j.issn.0367-6234.2016.12.006 |
| [12] |
TORRES-ACOSTA A A, NAVARRO-GUTIERREZ S, TERAN-GUILLEN J. Residual flexure capacity of corroded reinforced concrete beams[J]. Engineering Structures, 2007, 29(6): 1145-1152. DOI:10.1016/j.engstruct.2006.07.018 |
| [13] |
LI C Q, YANG S T. Prediction of concrete crack width under combined reinforcement corrosion and applied load[J]. Journal of Engineering Mechanics, 2011, 137(11): 722-731. DOI:10.1061/(ASCE)EM.1943-7889.0000289 |
| [14] |
KHAN I, FRANCOIS R, CASTEL A. Prediction of reinforcement corrosion using corrosion induced cracks width in corroded reinforced concrete beams[J]. Cement and Concrete Research, 2014, 56: 84-96. DOI:10.1016/j.cemconres.2013.11.006 |
| [15] |
DAI Li-zhao, WANG Lei, ZHANG Jian-ren, et al. A global model for corrosion-induced cracking in prestressed concrete structures[J]. Engineering Failure and Analysis, 2016, 62: 263-275. DOI:10.1016/j.engfailanal.2016.01.013 |
| [16] |
FARROW W C, HIGGINS C. Tests of reinforced concrete beams with corrosiondamaged stirrups[J]. ACI Structural Journal, 2006, 103(1): 133-141. |
| [17] |
OH B H, KIM E S, CHOI Y C. Theoretical analysis of transfer lengths in pretensioned prestressed concrete members[J]. Journal of Engineering Mechanics, 2006, 132(10): 1057-1066. DOI:10.1061/(ASCE)0733-9399(2006)132:10(1057) |
| [18] |
ALBERTO T R, CANH N D, HALE W M, et al. A higher-order equation for modeling strand bond in pretensioned concrete beams[J]. Engineering Structures, 2017, 131: 345-361. DOI:10.1016/j.engstruct.2016.10.050 |
| [19] |
MAADDAWY T E, SOUDKI K. A model for prediction of time from corrosion initiation[J]. Cement and Concrete Composites, 2007, 29(3): 168-175. DOI:10.1016/j.cemconcomp.2006.11.004 |



