2. 扬州大学 建筑科学与工程学院, 江苏 扬州 225127
2. College of Civil Science and Engineering, Yangzhou University, Yangzhou 225127, China
荷载引起的钢材失效分为单调荷载下的延性破坏和循环荷载下的疲劳破坏两类.1994年,美国Northridge地震和1995年日本阪神地震中不少钢结构发生了低周或超低周疲劳破坏,引起了许多学者对地震作用下钢结构低周疲劳破坏机理的关注.Kanvinde等[1]认为超低周疲劳破坏起始是复杂的断裂-疲劳相互作用,引起了材料延性裂纹的萌生;Nip等[2]研究碳钢和不锈钢的破坏断面得出,失效机理与加载应变幅有关,当应变幅较高时表现为延性失效,应变幅较低时表现为疲劳失效,当应变幅介于两者之间时表现为混合失效模式;Liu等[3]根据SM490YA钢T型焊接接头的疲劳试验结果,发现当循环应变介于疲劳断裂和延性断裂之间时会出现延性-疲劳过渡断裂模式.
另一方面,低周疲劳寿命预测通常采用Coffin-Manson公式,但一些学者认为Coffin-Manson公式对超低周疲劳寿命的预测值偏大,提出新的疲劳寿命预测模型,如Kuroda[4]提出考虑循环加载时延性耗尽的超低周疲劳寿命预测模型;Tateishi等[5]提出同时考虑韧性损伤和疲劳损伤的修正Coffin-Manson公式;Xue[6]通过引入指数函数以及附加的材料参数,提出适用于低周、超低周疲劳寿命预测的统一表达式.为了评价地震荷载作用下低周疲劳破坏性能,Ge等[7-9]基于Coffin-Manson公式和Miner准则,验算了钢结构超低周疲劳延性裂纹的萌生强度,通过钢桥墩的低周疲劳试验进行验证;Tateishi等[10-12]通过建立不同精度的有限元模型,拟合得到墩底焊趾部位与焊趾半径有关的局部应变,结合Miner准则评价钢桥墩的超低周疲劳损伤.
尽管国内外学者对钢结构的超低周疲劳破坏机理、疲劳寿命预测以及验算方法等开展了一系列试验研究和理论分析,但是目前对钢桥中最常用的Q345qC钢材及焊接接头的低周疲劳性能鲜有研究.游翔等[13]研究与Q345qC接近的Q345B钢材及焊接接头在应变幅为0.3%~0.7%的条件下的低周疲劳性能,利用Coffin-Manson公式拟合了疲劳寿命参数,但试验应变幅偏低,不能满足钢结构在地震荷载作用下预测超低周疲劳性能的需要.
本文以钢桥常用的Q345qC钢材为对象,首先研究初始延性损伤对钢材低周疲劳性能的影响;通过总应变为2.0%~5.0%时母材和焊接试样的低周疲劳试验和断口电镜扫描,分析母材及焊接接头的低周疲劳寿命预测公式,比较不同疲劳寿命预测模型的精度,研究焊接接头的疲劳断裂机理以及焊接缺陷对疲劳损伤的影响;最后得到母材及焊接接头的低周疲劳损伤评价公式,为钢桥地震时的低周疲劳强度验算提供依据.
1 试样尺寸及试验方法以Q345qC低碳钢为对象,钢材的力学性能如表 1所示.表中,E为弹性模量,εy为屈服应变,σy为屈服强度,σu为拉伸强度,A为断后伸长率.
| 表 1 Q345qC钢材的力学性能 Table 1 Mechanical properties of Q345qC steel |
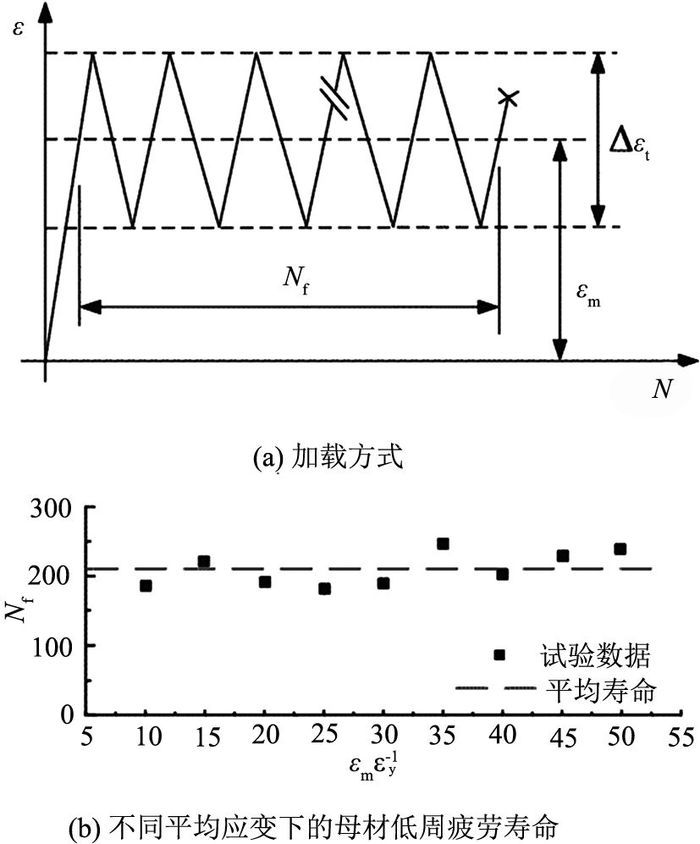
Kuroda[4]认为材料损伤包含单调拉伸损伤、循环加载延性消耗损伤和裂纹扩展损伤3部分,钢材的低周疲劳寿命由以上3种损伤模式共同决定.为了研究单调拉伸损伤对钢材低周疲劳寿命的影响,在开展母材和焊接接头低周疲劳试验之前,首先通过试验研究平均应变与材料低周疲劳寿命的关系[14].试验加载方式如图 1(a)所示,即经过一定的塑性拉伸变形后再进行反复加载.图中,ε、εm和Δεt分别为试样所受的应变、循环荷载的平均应变和总应变范围,N和Nf分别为试样经历的荷载循环次数和疲劳寿命.试样在不同εm下按20εy的总应变范围进行循环加载至断裂.如图 1(b)所示为疲劳寿命Nf与平均应变εm关系的试验结果.结果表明,在试验考虑的应变范围内,当平均应变不超过50εy时,平均应变对母材低周疲劳寿命的影响没有明显的规律,但试验数据的离散性不大,即单调拉伸应变损伤对钢材低周疲劳损伤的影响可以忽略.由于钢桥在地震作用下的平均应变一般远低于50εy,在低周疲劳试验中可以不考虑平均应变的影响.
|
图 1 平均应变对材料低周疲劳寿命的影响 Fig. 1 Effects of mean strain on low cycle fatigue life |
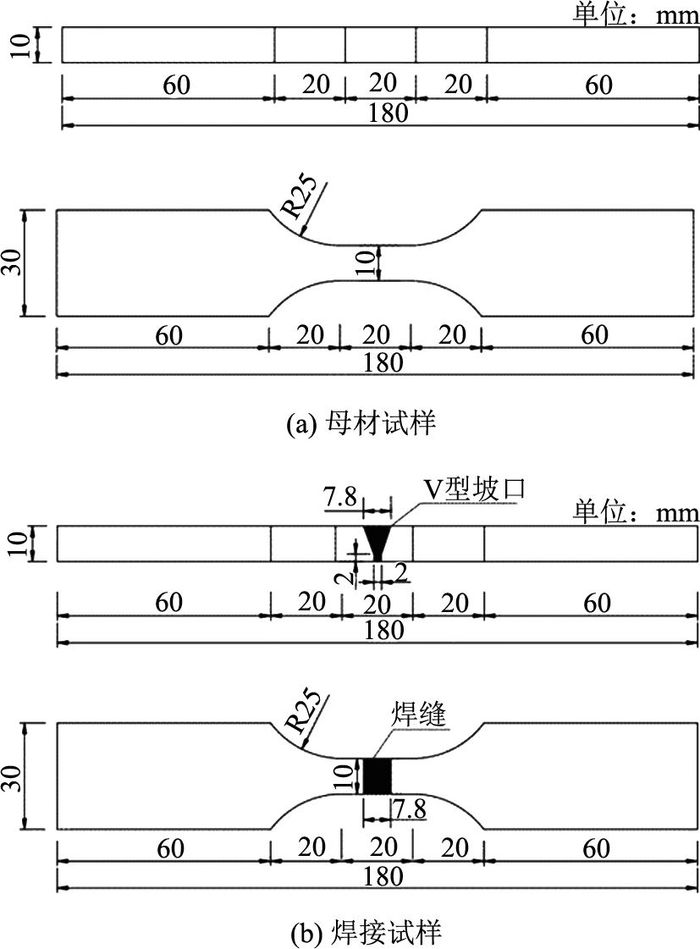
如图 2(a)、(b)所示为母材以及焊接试样的尺寸,试样标距段采用尺寸为10 mm×10 mm的矩形等截面.焊丝的型号为ATLANTIC CHW-50C6,直径为1.2 mm.焊接采用CO2气体保护电弧焊,三层施焊,焊接工艺参数如表 2所示.表中,I为焊接电流,U为电弧电压,υ为焊接速度,qV为CO2体积流量.为了消除焊接残余应力对低周疲劳性能的影响,在加工焊接试样前,采用“锤击法”对焊接后的钢板进行消除焊接残余应力处理[15];为了消除表面缺陷对低周疲劳性能的影响,对焊接试样的表面逐级打磨抛光,去除焊缝余高.
|
图 2 低周疲劳试样尺寸 Fig. 2 Dimensions for low cycle fatigue specimens |
| 表 2 焊接工艺参数 Table 2 Welding parameters |
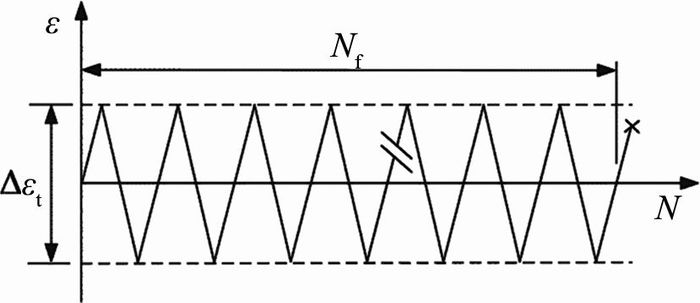
材料低周疲劳试验在INSTRON8802-100KN电液伺服疲劳试验机上实施,如图 3所示.试验方法参照《金属材料轴向等幅低循环疲劳试验方法》(GB/T15248-2008)[16]的相关规定,试验加载由试样轴向应变控制,应变比R=-1,加载频率为0.1 Hz,轴向引伸计标距为12.5 mm,加载应变范围为2.0%、3.0%、4.0%、5.0%,以试样在标距范围内断裂作为失效判据,循环波形为三角波,如图 4所示.低周疲劳试验共有24个试样,其中母材和焊接试样各12个,母材试样编号为BM01~BM12,焊接试样编号为WM01~WM12,每一加载应变幅下均进行3个试样的重复试验.其中试样BM03、BM06、BM09和BM12因试验机加载异常,试验结果无效.此外,分别对母材和焊接试样进行单调拉伸试验,母材试样编号为BM13、BM14,焊接试样编号为WM13、WM14.

|
图 3 低周疲劳试验装置 Fig. 3 Low cycle fatigue test device |
|
图 4 低周疲劳试验的加载方式 Fig. 4 Low cycle fatigue test loading mode |
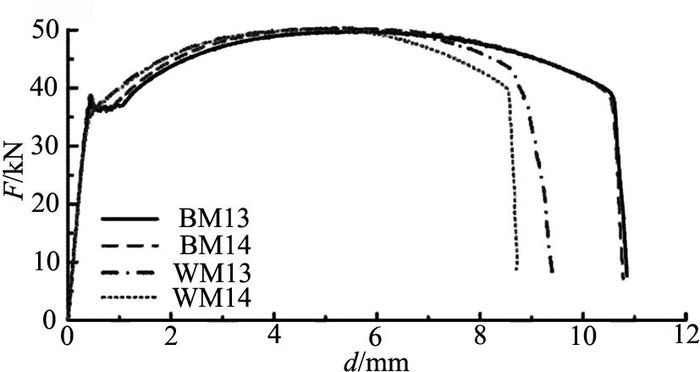
如图 5所示为母材和焊接接头的拉伸荷载-位移曲线.图中,F、d分别为试验荷载和位移.与母材对比,焊接接头的抗拉强度较接近,但是延性显著降低;由于焊接的影响,焊接接头的屈服平台缩小甚至消失,其中WM13在焊缝区断裂,WM14在热影响区断裂,WM13的抗拉强度与WM14接近,延性提高.
|
图 5 母材及焊接接头的拉伸荷载位移曲线 Fig. 5 Tensile load-displacement curves of specimens |
如表 3所示为不同应变幅下母材和焊接试样疲劳试验各参数的平均结果.表中,Δεt/2、Δεe/2和Δεp/2分别为总应变幅、弹性应变幅和塑性应变幅,Δσ/2为应力幅值,Nf, min、Nf, max分别为疲劳寿命最小值、最大值,Δεe/2、Δεp/2和Δσ/2由稳定滞回环得到.由表 3可知,焊接接头在同一总应变幅下的塑性应变低于母材,疲劳寿命仅为母材的31%~50%,但应力幅明显高于母材.另一方面,同一应变幅下不同焊接接头疲劳寿命的离散性相对母材明显增大,表明焊接质量对焊接接头的疲劳寿命影响显著.
| 表 3 母材和焊接试样疲劳试验平均结果 Table 3 Average results of fatigue tests |
根据试验焊接接头的断裂位置分析发现,当试验应变幅为1.0%、1.5%时,断裂位置既有焊缝区又有热影响区;当应变幅为2.0%、2.5%时,仅在热影响区发生断裂.可见,焊接接头的低周疲劳断裂位置与加载应变幅Δεt/2有关.
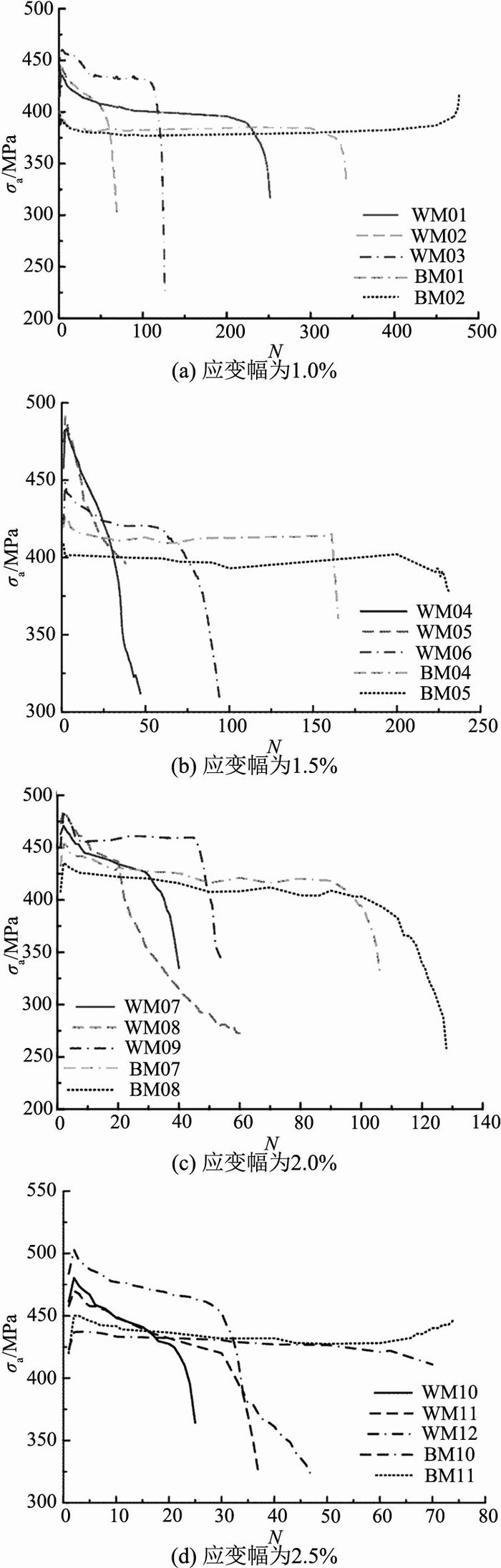
如图 6所示为不同应变幅下响应应力幅σa随循环周次N的演化曲线.可知,对于母材,当应变幅为1.0%和1.5%时,在初始阶段表现为循环软化,之后进入循环稳定,直至断裂;当应变幅为2.0%和2.5%时,在初始阶段快速循环硬化,随后表现为循环稳定,直至断裂.对于焊接接头,在各应变幅均表现为初始阶段短暂循环硬化,之后进入循环软化直至断裂.母材主要表现为循环稳定,焊接接头主要表现为循环软化.在相同应变幅度下,母材稳定状态的响应应力幅值低于焊接接头;此外,疲劳寿命试验结果有一定的离散性,且焊接接头的离散性高于母材.
|
图 6 循环响应特征曲线 Fig. 6 Cyclic stress response curves |
为了分析焊接接头的断裂机理以及焊接缺陷对疲劳损伤的影响,对部分焊接试样用扫描电镜进行断口观察.
如图 7所示为焊接试样WM02 (Δεt/2=1.0%,Nf=69)和WM03 (Δεt/2=1.0%,Nf=127)的断口形貌,两者的断裂位置均发生在焊缝区.如图 7(a)所示为断口形貌,WM02断口中心存在明显的焊接缺陷,疲劳裂纹在该处萌生并向四周扩展,裂纹狭窄且尖锐,说明该应变幅(Δεt/2=1.0%)下的断裂模式为疲劳断裂,瞬断区存在较多的焊接气孔;WM03疲劳裂纹在内部焊接缺陷处萌生,裂纹源附近较平整,扩展区凹凸不平且出现贝纹状裂纹扩展痕迹,瞬断区呈现剪切唇的形貌特征.如图 7(b)所示为两者裂纹源的微观形貌,WM02的裂纹源表面较粗糙,扩展区较平整,在裂纹源和扩展区之间存在明显的台阶;WM03的裂纹源含有较多的夹杂物,这些夹杂物在焊接过程中产生,促进了疲劳裂纹的萌生.如图 7(c)所示为试样裂纹扩展区的典型形貌,WM02的扩展区出现了轮胎压痕及二次裂纹,同时有较多微孔洞分布,微孔洞的产生与焊接有关,并可以加速疲劳裂纹的扩展,从而导致疲劳寿命降低[17];WM03扩展区有疲劳辉纹产生,并呈现断续状分布的特点.如图 7(d)所示分别为WM02扩展区微孔洞以及WM03扩展区疲劳辉纹的放大图.如图 7(e)所示为瞬断区的微观形貌,两试样的瞬断区均分布大量韧窝,说明焊接金属具有较好的延性.通过对比可知,WM02由于明显的焊接缺陷导致疲劳裂纹早期萌生,同时由于扩展区焊接微孔洞的出现加速了疲劳裂纹的扩展,疲劳寿命相对于WM03下降了45.7%.

|
图 7 焊接试样WM02和WM03断口形貌 Fig. 7 Fracture morphology of specimens WM02 and WM03 |
如图 8所示为焊接试样WM01 (Δεt/2=1.0%,Nf=252)和WM12 (Δεt/2=2.5%,Nf=47)的断口形貌,两者均在热影响区发生断裂.如图 8(a)所示为试样的断口形貌,对比可知,两者均在应力集中的截面角端萌生疲劳裂纹,并以角端为中心向截面内部扩展;WM12由于应变幅大,裂纹源和扩展区断面在拉压循环中反复研磨呈现光亮的金属面;瞬断区均出现明显的颈缩,并呈剪切型破坏.如图 8(b)所示为试样裂纹源的微观形貌,在裂纹源均存在夹杂物,夹杂物使得截面角端塑性变形能力降低,早期萌生裂纹[17].如图 8(c)所示为裂纹扩展区的微观形貌,在扩展区出现断续状分布的疲劳辉纹,且WM01在扩展区有二次裂纹产生;WM12在循环拉压应变的作用下,断面较平滑.如图 8(d)所示为试样瞬断区的微观形貌,对比可知,WM12的韧窝密度和深度均大于WM01,因此WM12瞬断区的韧性损伤更明显.

|
图 8 焊接试样WM01和WM12断口形貌 Fig. 8 Fracture morphology of specimens WM01 and WM12 |
由Ramberg-Osgood公式可知,循环应力-应变关系表示为
| $ \Delta \sigma /2 = K'{\left( {\Delta {\varepsilon _{\rm{p}}}/2} \right)^n}^\prime . $ | (1) |
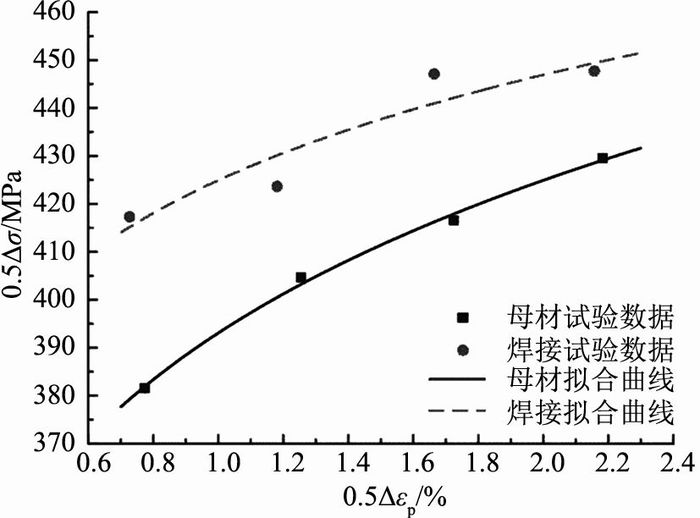
式中:K′为循环强度系数,n′为循环应变硬化指数.取各试样半寿命时的塑性应变幅和应力幅作为各加载应变幅下的稳定值,根据表 3可得,母材和焊接接头的循环应力-塑性应变关系如图 9所示.可知,母材及焊接接头的稳定应力幅均随着应变幅的增加而增加,且在相同的应变幅下,焊接接头的应力幅高于母材.
|
图 9 循环应力塑性应变曲线 Fig. 9 Cyclic stress-plastic strain curves |
根据图 9的拟合曲线,可得母材和焊接接头的循环应力-塑性应变曲线常数,如表 4所示.
| 表 4 循环应力塑性应变曲线常数 Table 4 Parameters of cyclic stress-plastic strain curves |
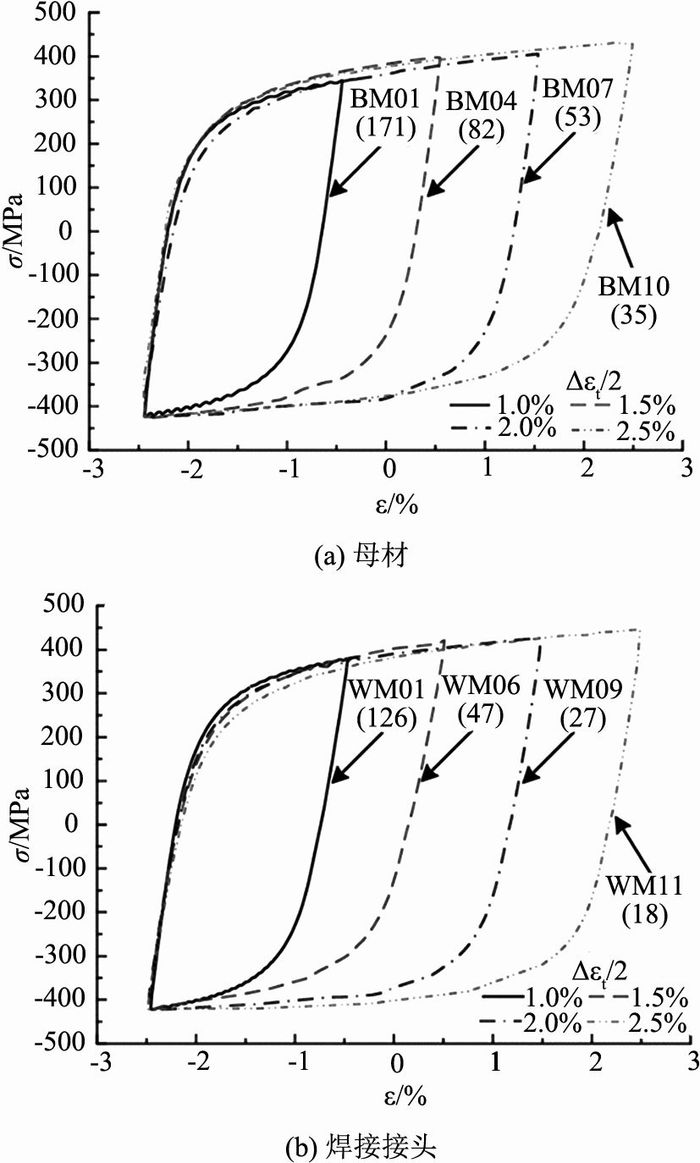
每一循环周次的应力-应变滞回围成的面积代表该循环消耗的塑性应变能,反映了材料的抗震性能.如图 10所示为母材和焊接接头在不同应变幅下最低点平移至同一点的半寿命滞回曲线,此时的滞回曲线处于稳定循环状态.图 10中标出了各滞回曲线的试样编号及半寿命循环周次.可知,应变幅越大,材料消耗的塑性应变能越大.
|
图 10 不同应变幅度下的半寿命滞回曲线 Fig. 10 Hysteresis loops at middle of fatigue life |
由图 10可知,不同应变幅滞回曲线的上半段基本重合,说明母材和焊接接头都具有Masing特性.每一循环的塑性应变能ΔWp可由下式[18]计算得到:
| $ \Delta {W_{\rm{p}}} = \left( {\frac{{1 - n'}}{{1 + n'}}} \right)\Delta \sigma /\Delta {\varepsilon _{\rm{p}}}. $ | (2) |
为了比较母材和焊接接头的耗能能力,对两种试样稳定循环状态的塑性应变能进行计算,结果如表 5所示.表中,ΔWp, t为半寿命塑性应变能试验值,ΔWp, c为半寿命塑性应变能计算值.由表 5可知,同一应变幅下母材和焊接接头的半寿命塑性应变能相差不大,表明两者的耗能能力基本相同;各试样塑性应变能的试验值和计算值较接近,误差基本在±5%以内.
| 表 5 塑性应变能试验值与计算值 Table 5 Experimental and calculated values of plastic strain energy |
钢材低周疲劳寿命一般采用Coffin-Manson公式预测.根据试样的断口形貌特征以及试验应变范围可知,试样断裂基本属于低周疲劳破坏,与韧性损伤为主的超低周疲劳破坏有差异.以下用Coffin-Manson公式预测Q345qC母材和焊接接头的低周疲劳寿命.
低周疲劳试验的总应变幅包括弹性应变幅和塑性应变幅两个部分,弹性和塑性应变幅与疲劳寿命的关系可以分别由Basquin和Coffin-Manson公式来表示:
| $ \left. \begin{array}{l} \Delta {\varepsilon _{\rm{e}}}/2 = \frac{{{{\sigma '}_{\rm{f}}}}}{E}{\left( {2{N_{\rm{f}}}} \right)^b},\\ \Delta {\varepsilon _{\rm{p}}}/2 = {{\varepsilon '}_{\rm{f}}}{\left( {2{N_{\rm{f}}}} \right)^c}. \end{array} \right\} $ | (3) |
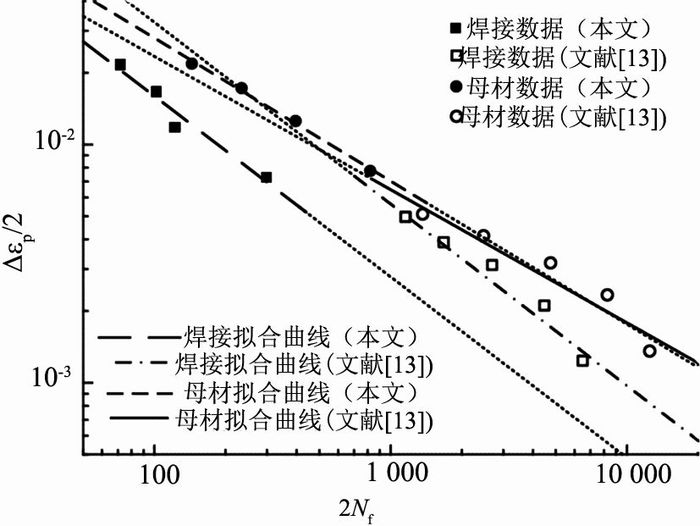
式中:σ′f为疲劳强度系数,b为疲劳强度指数,ε′f为疲劳塑性系数,c为疲劳塑性指数.根据表 3试验数据拟合得到的应变-寿命曲线疲劳参数如表 6所示.如图 11所示为母材和焊接接头的塑性应变-寿命曲线.为了与类似材料的结果进行对比,给出游翔等[13]得到的Q345B母材和焊接接头的低周疲劳寿命预测曲线.由于本文和文献[13]试样加载应变幅相差较大,为了便于对比,距离数据点较远的拟合曲线均通过延伸推算(图 11用虚线表示).
| 表 6 应变-寿命曲线疲劳参数 Table 6 Parameters of strain-life curves |
|
图 11 母材及焊接接头的塑性应变寿命曲线 Fig. 11 Plastic strain-life curves of specimens |
由图 11可以发现,Q345qC母材和焊接接头的低周疲劳寿命可以用Coffin-Manson公式较精确地预测;游翔等[13]给出的Q345B母材与本文的Q345qC母材的应变-寿命曲线较接近,焊接接头的应变-寿命曲线相差较大.这表明两种钢材的低周疲劳性能相近,焊接接头由于受焊接工艺、焊接质量等的影响较大,低周疲劳性能差异显著.
从图 11可以发现,同等应变水平下焊接接头的疲劳寿命比母材显著降低,且焊接接头的塑性应变-寿命曲线明显低于母材,这说明焊接接头的塑性相对于母材显著下降.
单调拉伸失效可以理解为一种极端情况的超低周疲劳破坏,即材料经过1/4周次循环后发生断裂,此时,塑性应变幅及失效周次分别为
| $ \left. \begin{array}{l} \Delta {\varepsilon _{\rm{p}}}/2 = {\varepsilon _{\rm{f}}},\\ {N_{\rm{f}}} = 1/4. \end{array} \right\} $ | (4) |
式中:εf为单调拉伸至断裂时的拉伸韧性.εf可由下式[2]计算得到:
| $ {\varepsilon _{\rm{f}}} = \ln \left( {\frac{{{A_0}}}{{{A_{\rm{u}}}}}} \right) \times 100\% . $ | (5) |
式中:A0为拉伸试样标距段的初始横截面积,Au为拉断后的最小横截面积,通过该试验得到的母材和焊接接头的εf分别为92.32%和43.91%.
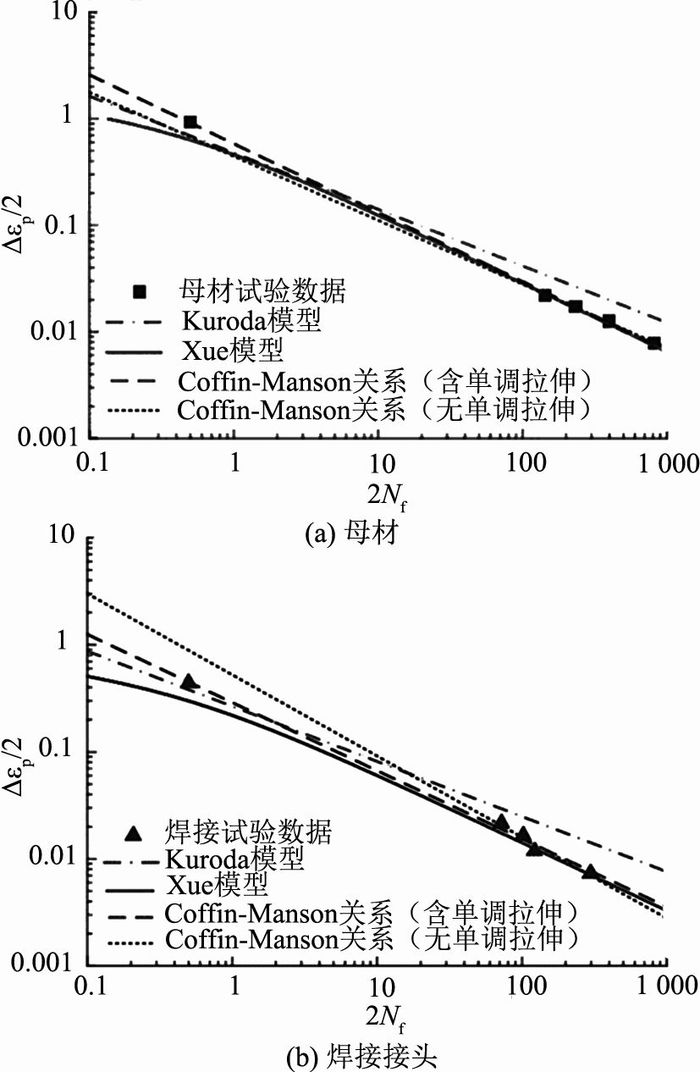
如图 12(a)、(b)所示分别为母材和焊接接头考虑单调拉伸试验数据的疲劳寿命曲线.为了比较不同疲劳寿命预测模型的预测精度,分别用Coffin-Manson公式、Kuroda[4]模型和Xue[6]模型进行预测,同时给出不考虑单调拉伸的Coffin-Manson拟合曲线.
|
图 12 不同疲劳寿命预测模型的对比 Fig. 12 Comparison of different fatigue life prediction models |
Kuroda[4]提出的疲劳寿命预测模型形式为
| $ \frac{{{\varepsilon _{{\rm{pmax}}}}}}{{{\varepsilon _{\rm{f}}}}} + 4{N_{\rm{f}}}{\left( {\frac{{\Delta {\varepsilon _{\rm{p}}}}}{{2{\varepsilon _{\rm{f}}}}}} \right)^a}^\prime + \frac{{\Delta {\varepsilon _{\rm{p}}}}}{{C'}}N_{\rm{f}}^{\alpha '} = 1. $ | (6) |
式中:εpmax为最大拉伸塑性应变,对于本文试验,εpmax=0;a′、α′和C′为材料常数,均按Kuroda[4]试验结果取值.
Xue[6]提出的同时适用于低周疲劳和超低周疲劳寿命预测模型的形式如下:
| $ 2N = \frac{{\exp \left[ {\lambda {{\left( {\frac{{\Delta {\varepsilon _{\rm{p}}}}}{{{\varepsilon _{\rm{f}}}}}} \right)}^m}} \right] - 1}}{{{{\rm{e}}^\lambda } - 1}} = 1. $ | (7) |
式中:材料常数λ、m和εf可以根据试验结果得到.母材和焊接接头的材料常数如表 7所示.
| 表 7 Xue模型材料常数 Table 7 Material parameters of Xue model |
由图 12(a)可知,无论是对于低周疲劳还是超低周疲劳,考虑单调拉伸的Coffin-Manson公式均可以精确预测母材的疲劳寿命,Xue模型仅在失效反向数2Nf>10时具有较好的预测精度,Kuroda模型的预测精度较差.由图 12(b)可知,考虑单调拉伸的Coffin-Manson公式可以精确预测焊接接头的低周和超低周疲劳寿命.由于本文的试验数据不是很充分,为了精确预测超低周疲劳的失效寿命,需要有该区段的试验数据作进一步补充.
2.5 低周疲劳损伤评价疲劳损伤一般采用Miner损伤累积准则计算,即在反复荷载下的损伤程度可以表示为如下形式:
| $ D = \sum\limits_{i = 1}^M {\frac{{{n_i}}}{{{N_{{\rm{f}}i}}}}} . $ | (8) |
式中:D为疲劳损伤指标,D=1表示材料达到损伤极限;i为疲劳荷载的等级;ni为第i等级疲劳荷载的循环次数;Nfi为第i等级疲劳荷载对应的疲劳寿命.
预测低周疲劳寿命的Coffin-Manson公式可以表示为如下形式:
| $ \Delta {\varepsilon _{\rm{p}}}N_{\rm{f}}^k = C. $ | (9) |
材料常数k、C通过单调拉伸和疲劳试验数据的拟合并对比式(3)、(9)得到,结果如表 8所示.
| 表 8 Coffin-Manson公式材料参数 Table 8 Coffin-Manson formula material parameters |
根据Coffin-Manson公式,有
| $ {N_{{\rm{f}}i}} = {\left( {\frac{C}{{\Delta {\varepsilon _{{\rm{p}}i}}}}} \right)^{1/k}}. $ | (10) |
损伤指标可以表示为
| $ D = \frac{1}{{{C^{1/k}}}}\sum\limits_{i = 1}^n {{{\left( {\Delta {\varepsilon _{{\rm{p}}i}}} \right)}^{1/k}}} . $ | (11) |
式中:Δεpi为履历响应中第i个循环荷载的塑性应变范围.
由于在地震作用下的塑性应变幅变化具有随机性,从结构地震反应分析结果中只能获得半个周期的结果,故式(11)改写为
| $ D = \frac{1}{{2{C^{1/k}}}}\sum\limits_{i = 1}^n {{{\left( {\Delta {\varepsilon _{{\rm{p}}i}}} \right)}^{1/k}}} . $ | (12) |
将表 8的材料参数k、C代入式(12),考虑到同一应变幅下母材和焊接接头疲劳寿命的离散性,可以偏安全地将母材和焊接接头的损伤指标D分别乘以系数1.5和3.0,则母材和焊接接头的低周疲劳损伤评价公式可由下式计算得到:
| $ D = 1.1841\sum\limits_{i = 1}^n {{{\left( {\Delta {\varepsilon _{{\rm{p}}i}}} \right)}^{1.5461}}} , $ | (13) |
| $ D = 7.0836\sum\limits_{i = 1}^n {{{\left( {\Delta {\varepsilon _{{\rm{p}}i}}} \right)}^{1.5701}}} . $ | (14) |
(1) 在20εy的总应变范围下(约为3.4%),当平均应变不超过50εy (约为8.5%)时,单调拉伸应变损伤对材料低周疲劳损伤的影响可以忽略.
(2) 焊接接头的低周疲劳寿命为母材的31%~50%,且疲劳寿命的离散性大于母材.母材循环响应的特征总体表现为循环稳定,焊接接头表现为循环软化.
(3) 焊接缺陷容易成为焊接接头低周疲劳破坏的裂纹萌生源,在2.0%的应变范围下有焊接缺陷焊接接头疲劳寿命仅为无焊接缺陷焊接接头的27.4%,因此确保焊接质量十分重要.
(4) 在同一应变水平下母材和焊接接头的半寿命塑性应变能相差不大,两者的耗能能力基本相同.
(5) 考虑单调拉伸的Coffin-Manson公式,对母材和焊接接头的低周、超低周疲劳寿命均可以进行较精确的预测,Kuroda模型和Xue模型的预测精度相对较低.
(6) 基于Miner损伤累积准则和Coffin-Manson公式,建立可以用于地震作用下Q345qC钢桥母材及焊接接头低周疲劳损伤评价的损伤指标计算公式.
由于试样在较大的压应变作用下易发生屈曲,本研究仅涉及母材及焊接接头总应变为2.0%~5.0%的疲劳试验结果,且试验样本有限,今后将改进试验方法,在更大的应变范围下进一步研究母材及焊接接头的超低周疲劳性能.
| [1] |
KANVINDE A, DEIERLEIN G. Cyclic void growth model to assess ductile fracture initiation in structural steels due to ultra low cycle fatigue[J]. Journal of Engineering Mechanics, 2007, 133(6): 701-712. DOI:10.1061/(ASCE)0733-9399(2007)133:6(701) |
| [2] |
NIP K H, GARDNER L, DAVIES C M, et al. Extremely low cycle fatigue tests on structural carbon steel and stainless steel[J]. Journal of Constructional Steel Research, 2010, 66(1): 96-110. DOI:10.1016/j.jcsr.2009.08.004 |
| [3] |
LIU Y, JIA L J, GE H, et al. Ductile-fatigue transition fracture mode of welded T-joints under quasi-static cyclic large plastic strain loading[J]. Engineering Fracture Mechanics, 2017, 176: 38-60. DOI:10.1016/j.engfracmech.2017.02.018 |
| [4] |
KURODA M. Extremely low cycle fatigue life prediction based on a new cumulative fatigue damage model[J]. International Journal of Fatigue, 2002, 24(6): 699-703. DOI:10.1016/S0142-1123(01)00170-0 |
| [5] |
TATEISHI K, HANJI T, MINAMI K. A prediction model for extremely low cycle fatigue strength of structural steel[J]. International Journal of Fatigue, 2007, 29(5): 887-896. DOI:10.1016/j.ijfatigue.2006.08.001 |
| [6] |
XUE L. A unified expression for low cycle fatigue and extremely low cycle fatigue and its implication for monotonic loading[J]. International Journal of Fatigue, 2008, 30(10/11): 1691-1698. |
| [7] |
GE H, KANG L. A damage index-based evaluation method for predicting the ductile crack initiation in steel structures[J]. Journal of Earthquake Engineering, 2012, 16(5): 623-643. DOI:10.1080/13632469.2012.676231 |
| [8] |
KANG L, GE H. Predicting ductile crack initiation of steel bridge structures due to extremely low-cycle fatigue using local and non-local models[J]. Journal of Earthquake Engineering, 2013, 17(3): 323-349. DOI:10.1080/13632469.2012.746211 |
| [9] |
GE H, LUO X. A seismic performance evaluation method for steel structures against local buckling and extra-low cycle fatigue[J]. Journal of Earthquake and Tsunami, 2011, 05(02): 83-99. DOI:10.1142/S1793431111001005 |
| [10] |
TATEISHI K, CHEN T, HANJI T. Extremely low cycle fatigue assessment method for unstiffened cantilever steel columns[J]. Doboku Gakkai Ronbunshuu A, 2008, 64(25): 288-296. |
| [11] |
CHEN T, TATEISHI K. Extremely low cycle fatigue assessment of thick walled steel pier using local strain approach[J]. Kozo Kogaku Ronbunshu A, 2007, 53: 485-492. |
| [12] |
TATEISHI K, CHEN T, HANJI T. A new local strainbased approach to low cycle fatigue assessment of welded joint[J]. Kou Kouzou Rombunshuu, 2006, 13(52): 73-81. |
| [13] |
游翔, 刘永杰, 崔仕明, 等. Q345B母材及其焊接接头的低周疲劳行为[J]. 四川大学学报:工程科学版, 2015, 47(1): 112-117. YOU Xiang, LIU Yong-jie, CUI Shi-ming, et al. Low cycle fatigue behaviors of Q345B steel and welded joint[J]. Journal of Sichuan University:Engineering Science Edition, 2015, 47(1): 112-117. |
| [14] |
唐站站. 钢桥弹塑性地震反应计算方法及钢材地震损伤指标研究[D]. 杭州: 浙江大学, 2016. TANG Zhan-zhan. Research on seismic response evaluation method of steel bridges and seismic damage index of steel material[D]. Hangzhou:Zhejiang University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10335-1016264188.htm |
| [15] |
钢结构焊接规范: GB 50661-2011[S]. 北京: 中华人民共和国住房与城乡建设部, 2011. http://www.doc88.com/p-957282647690.html
|
| [16] |
GB/T 15248-2008: 金属材料轴向等幅低循环疲劳试验方法[S]. 北京: 中国国家标准化管理委员会, 2008. http://www.doc88.com/p-2532995574793.html
|
| [17] |
盛光敏, 林振邺, 樊良中, 等. 焊接对热轧H型钢高应变低周疲劳行为的影响[J]. 重庆大学学报, 2012(01): 70-75. SHENG Guang-min, LIN Zhen-ye, FAN Liang-zhong, et al. Effect of welding on high strain and low cycle fatigue behavior of hot-rolled H-beam[J]. Journal of Chongqing University, 2012(01): 70-75. |
| [18] |
CALLAGHAN M D, HUMPHRIES S R, LAW M, et al. Energy-based approach for the evaluation of low cycle fatigue behavior of 2.25Cr-1Mo steel at elevated temperature[J]. Materials Science and Engineering:A, 2010, 527(21): 5619-5623. |



