2. 山东大学 高效洁净机械制造教育部重点实验室, 山东 济南 250061
2. Key Laboratory of High-Efficiency and Clean Mechanical Manufacture, Ministry of Education, Shandong University, Jinan 250061, China
在传统的化石能源被日益消耗的同时,环境也在不断恶化[1-2].随着能源危机和环境污染问题的日益凸显,人们把目光逐渐转向海洋,海洋蕴藏着丰富的可再生能源[3-4].飞机的机翼在气流的作用下会产生升力.将空中的翼置于水中,在一定的条件下,水流的作用会使翼产生升力[5-7].
Mckinney等[8]首先提出利用翼的振荡运动捕获流体中能量的概念. Kinsey等[9-12]给出评估振荡翼能量提取性能的参数. Young等[13]研究在过渡雷诺数下不同振荡运动频率和振荡幅度的涡结构. Thiery等[14-15]采用非定常雷诺时均方程法,研究湍流模型对能量捕获性能的影响.刘臻等[16]应用Realizable k-ε湍流模型,研究水翼的绕流问题;结果表明:在一定的水翼攻角条件下,水翼振幅及振荡频率均对水翼的涡结构产生影响.
水翼在潮流中的水动力学特性受众多参数的影响(如水翼厚度、俯仰轴位置、运动频率、流速、流体黏性等),各参数之间还存在耦合关系[17-18].目前,对水翼发生振荡运动而捕获潮流能的相关研究仍然处于探索阶段[19-22].前人的研究大部分是从流场参数或单一参数角度探讨水翼的流体动力特性.
本文建立水翼的振荡运动模型,从运动、受力、能量吸收及流场等方面研究水翼运动参量、几何参数等对水翼的流体动力特性的影响规律,获得不同工况下的最优几何结构及运动参数,为水翼的设计奠定理论基础.
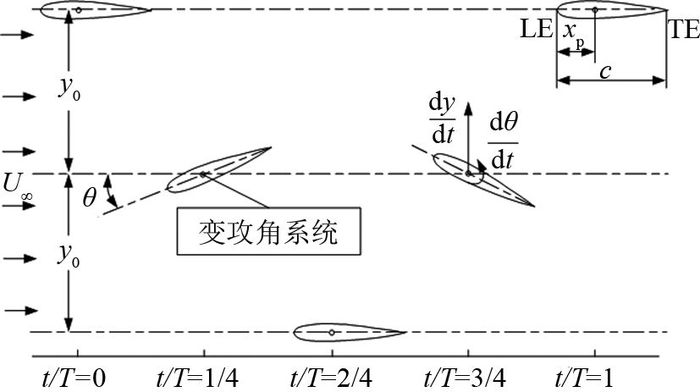
1 运动模型水翼在来流U∞作用下的运动为升沉运动yt与俯仰运动θt的耦合,如图 1所示.水翼的前缘点为LE,水翼的后缘点为TE,c为水翼弦长,xp为俯仰轴位置与前缘点LE的距离.假设水翼按简谐运动规律作俯仰运动和升沉运动,运动频率为f,俯仰振幅为θ0,升沉振幅为y0,俯仰和升沉的相位差为Φ,则水翼的运动规律可以表示为
|
图 1 水翼运动模型 Fig. 1 Motion model of hydrofoil |
| $ \theta \left( t \right) = {\theta _0}\sin \left( {\omega t} \right), $ | (1) |
| $ \psi \left( t \right) = {\rm{d}}\theta /{\rm{d}}t = {\theta _0}\omega \cos \left( {\omega t} \right), $ | (2) |
| $ y\left( t \right) = {y_0}\sin \left( {\omega t + \frac{{{\rm{ \mathsf{ π} }}\mathit{\Phi }}}{{180}}} \right), $ | (3) |
| $ v\left( t \right) = {\rm{d}}y/{\rm{d}}t = {y_0}\omega \cos \left( {\omega t + \frac{{{\rm{ \mathsf{ π} }}\mathit{\Phi }}}{{180}}} \right). $ | (4) |
式中:ω=2πf.
在水流的作用下,水翼所受的流体力为F(t),可以分解为与来流方向垂直的升力L(t)和平行于来流方向的阻力D(t),F(t)相对于俯仰轴的力矩为M(t).根据流体力学[8-11],可得
| $ {C_{\rm{L}}}\left( t \right) = \frac{{2L\left( t \right)}}{{\rho U_\infty ^2c}}, $ | (5) |
| $ {C_{\rm{D}}}\left( t \right) = \frac{{2D\left( t \right)}}{{\rho U_\infty ^2c}}, $ | (6) |
| $ {C_{\rm{M}}}\left( t \right) = \frac{{2M\left( t \right)}}{{\rho U_\infty ^2{c^2}}}, $ | (7) |
| $ P\left( t \right) = {P_{\rm{L}}}\left( t \right) + {P_{\rm{M}}}\left( t \right) = L\left( t \right)v\left( t \right) + M\left( t \right)\psi \left( t \right). $ | (8) |
式中:ρ为流体的密度,CL(t)为瞬时升力系数,CD(t)为瞬时阻力系数,CM(t)为瞬时俯仰力矩系数,PL(t)为升沉运动捕获的功率,PM(t)为俯仰运动捕获的功率,P(t)为水翼从潮流中捕获能量的总功率,P为平均捕获功率.
为了便于分析,引入水翼的瞬时功率系数CP及平均功率系数CP[8-11]:
| $ {C_{\rm{P}}}\left( t \right) = \frac{{2\left[ {{P_{\rm{L}}}\left( t \right) + {P_{\rm{M}}}\left( t \right)} \right]}}{{\rho U_\infty ^3c}}, $ | (9) |
| $ \begin{array}{*{20}{c}} {{{\bar C}_{\rm{P}}} = {{\bar C}_{{\rm{PL}}}} + {{\bar C}_{{\rm{PM}}}} = }\\ {\frac{1}{T}\int_0^T {\frac{{{C_{\rm{L}}}\left( t \right)v\left( t \right)}}{{{U_\infty }}}{\rm{d}}t} + \frac{1}{T}\int\limits_0^T {\frac{{c{C_{\rm{M}}}\left( t \right)\psi \left( t \right)}}{{{U_\infty }}}{\rm{d}}t} .} \end{array} $ | (10) |
式中:CPL、CPM分别为L(t)和M(t)的平均功率系数.
为了避免翼型变化、非定常流导致流速变化等带来的问题,引入描述f的无量纲参数-折算频率f*[8-10]如下:
| $ {f^ * } = fc/{U_\infty }. $ | (11) |
在翼型的形状和雷诺数Re一定的条件下,升力系数与攻角有关.攻角α(t)[8-11]可以表示为
| $ \alpha \left( t \right) = \arctan \left( {\frac{{ - v\left( t \right)}}{{{U_\infty }}}} \right) - \theta \left( t \right). $ | (12) |
| $ \eta = \frac{{\frac{1}{T}\int\limits_0^T {P\left( t \right){\rm{d}}t} }}{{\frac{1}{2}\rho U_\infty ^3S}} = \frac{{c{{\bar C}_{\rm{P}}}}}{H}. $ | (13) |
式中:S为水翼的扫掠面积,H为水翼在竖直方向上的运动幅值,对于二维水翼,S=H.
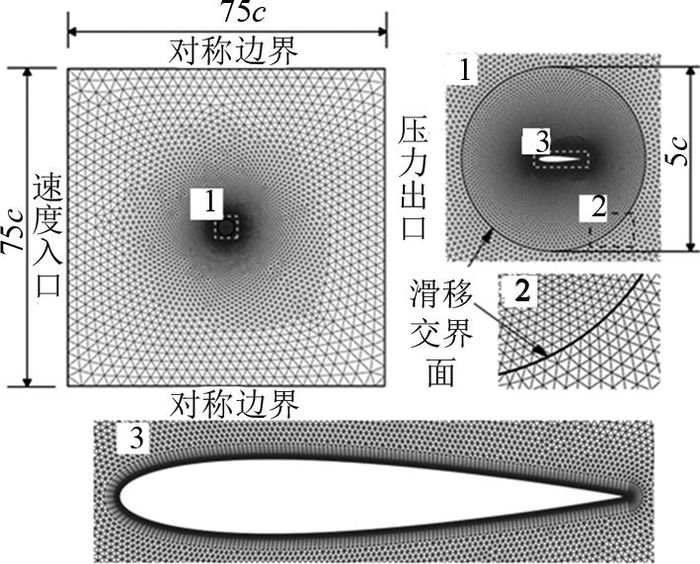
2 数值模拟与算例验证采用软件ANSYS Fluent来求解水翼发生振荡运动时的流场.水翼网格模型如图 2所示,利用滑移交界面将计算区域划分为两部分:内部圆形区域随水翼作俯仰—升沉运动;外部网格只受滑移交界面运动的影响,可以加密核心区域网格.在模拟过程中,采用动网格技术和用户自定义函数模拟水翼壁面边界振荡运动.雷诺数Re为500 000,湍流模型为Spalart-Allmaras模型,流场求解器采用基于压力的分离求解算法,压力和速度的耦合方法采用PISO格式,计算中梯度的插值方法采用基于节点的Green-Gauss方法,压力、动量、湍流黏性系数的离散格式选用二阶迎风格式,时间离散采用一阶隐式格式,continuity和velocity残差的绝对收敛标准为10-5.为了获得水翼所受的水动力特性,通过编写专门的用户自定义程序从Fluent求解器中提取数据.
|
图 2 水翼数值模拟的网格模型 Fig. 2 Mesh model of hydrofoil numerical simulation |
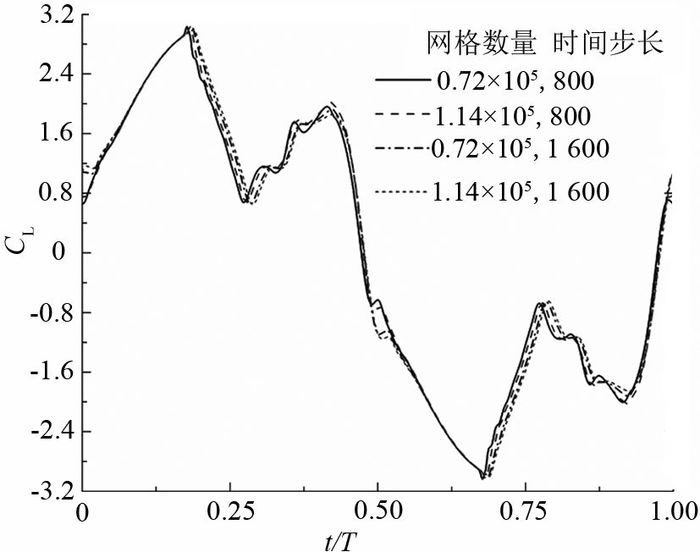
为了验证网格数量及时间步长的独立性,采用不同的网格数量及时间步长进行数值模拟计算,结果如图 3所示.结果表明,在本文所选择的参数范围内,网格的数量及时间步长对模拟结果的影响可以忽略.在确保模拟精度的前提下,为了减少计算的时间,选择的网格数量为0.72×105,时间步长为1 600步/周期.
|
图 3 网格数量及时间步长独立性验证(θ0=60°,f*=0.13, xp/c=1/3,Re=5×105,y0/c=1,Φ=90°) Fig. 3 Influence of different mesh sizes and time steps (θ0=60°, f*=0.13, xp/c=1/3, Re=5×105, y0/c=1, Φ=90°) |
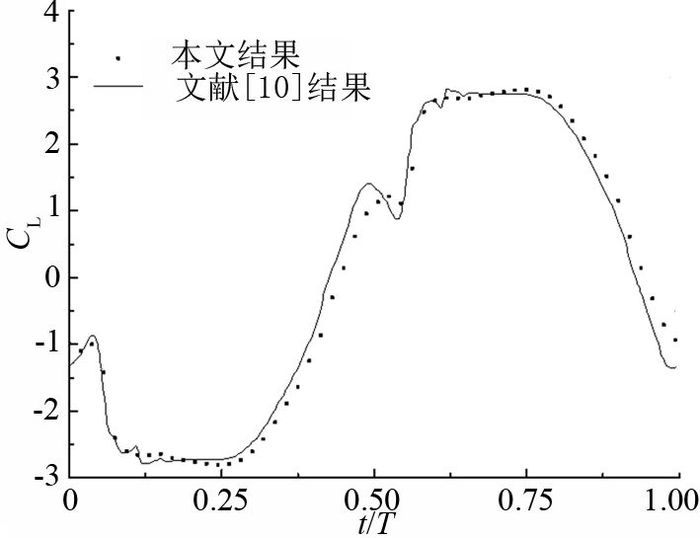
将数值模型的模拟参数设置为文献[10]的参数,获得的水翼瞬时升力系数如图 4所示[10].在一个周期内,文献[10]的CP为0.986,η为38.68%.在一个周期内,本文模型的CP为0.984,η为38.63%,与文献[10]的结果高度一致,验证了本文数值模拟模型的准确性.
|
图 4 升力系数的对比验证(θ0=75°,f*=0.14, xp/c=1/3,Re=5×105,y0/c=1,Φ=90°) Fig. 4 Comparison of numerical results of lift coefficient (θ0=75°, f*=0.14, xp/c=1/3, Re=5×105, y0/c=1, Φ=90°) |
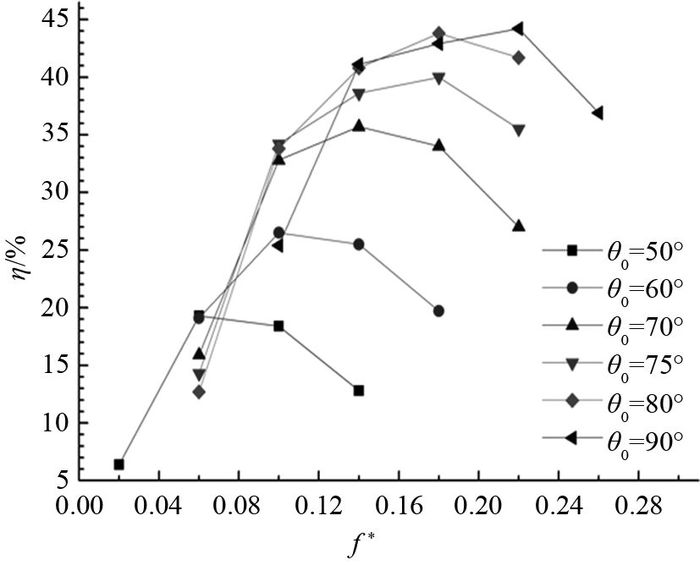
翼型NACA0015在相同的升沉振幅y0、不同俯仰振幅θ0的条件下,η随f*变化的规律如图 5所示.在较低的折算频率下(约为0.06以下),总效率随着θ0的增加出现不同程度的下降,但是随着折算频率的进一步上升,总效率开始随着俯仰振幅的增大而增大.造成这一现象的主要原因是俯仰振幅增大,导致水翼在竖直方向上的运动幅值增大的同时,增加了水翼从潮流中捕获的功率.根据式(13)可知,η与平均功率系数CP成正比,与水翼在竖直方向上的运动幅值成反比.当θ0的增量引起CP对η的贡献大于水翼在竖直方向上的运动幅值H对η的贡献时,总效率开始随俯仰振幅的增大而增大.此外,从图 5可以看出,在相同的θ0和y0的条件下,总效率随折算频率变化的过程存在拐点.在拐点处,能量捕获效率最高,如图 5所示,当θ0=50°时,最高总效率对应的折算频率为0.06;当θ0=75°时,最高总效率对应的折算频率为0.18;当θ0=90°时,最高总效率对应的折算频率为0.22.
|
图 5 效率变化规律(xp/c=1/3,Re=5×105,y0/c=1,Φ=90°) Fig. 5 Efficiency versus time (xp/c=1/3, Re=5×105, y0/c=1, Φ=90°) |
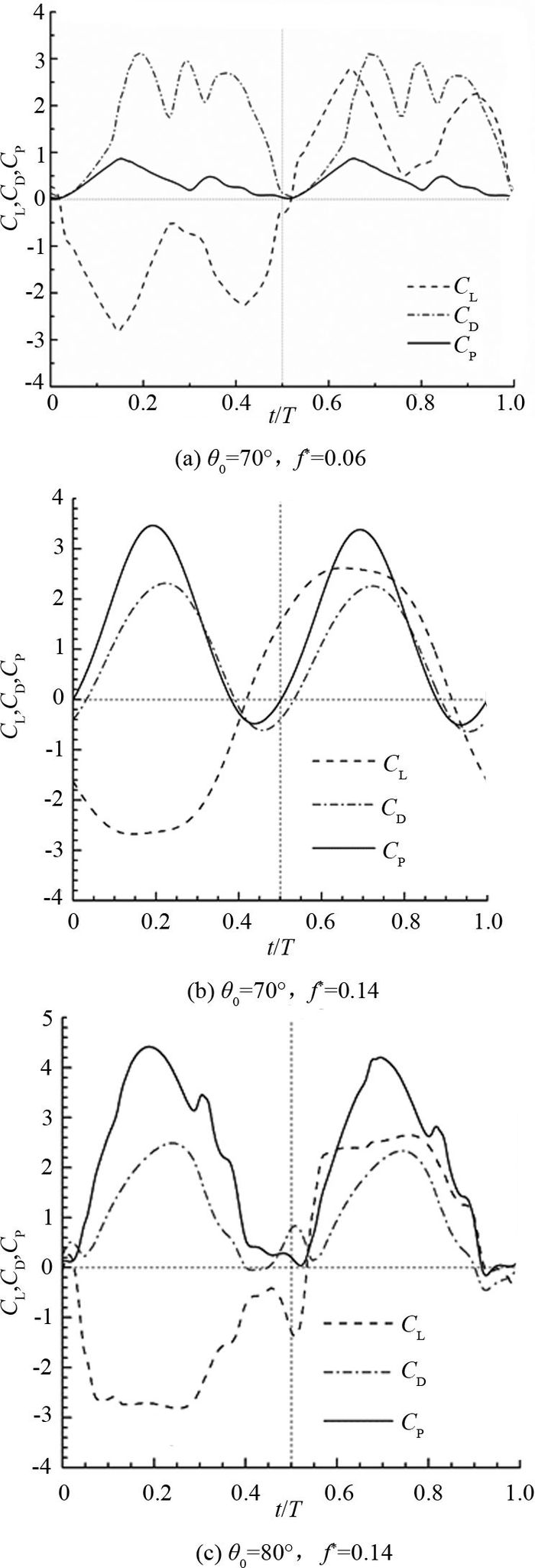
根据图 5可知,当θ0=60°时,η的最高值为26.5%.改变运动参数,当y0/c=1.5时,f*=0.07;当y0/c=0.5时,f*=0.20;获得的CP和η如表 1所示.在相同的θ0条件下,随着f*的增加,CP随着y0的减小而减小,但总效率的变化过程存在拐点.在θ0和f*一定的条件下,通过增大升沉振幅来提高系统的能量捕获效率的作用将会越来越弱,不同的水翼升沉振幅对应的扫略面积和高度不同,当升沉振幅超过某一值时,将使水翼边界层产生分离与旋涡脱落现象,从而造成总效率的剧烈下降.为了阐明运动参数变化对水翼流体动力特性的影响,须进一步分析水翼运动过程中瞬态升力、阻力和功率系数的变化规律.不同运动参数下瞬时升力、阻力和功率系数的变化曲线如图 6所示.
| 表 1 不同升沉运动参数的影响 Table 1 Effect of different heaving motion parameters |
|
图 6 不同运动参数下的升力、阻力和功率系数曲线(xp/c=1/3,Re=5×105,y0/c=1,Φ=90°) Fig. 6 Comparison of lift coefficient, drag coefficient and power coefficient between numerical simulations using different parameters (xp/c=1/3, Re=5×105, y0/c=1, Φ=90°) |
图 6(a)中,θ0=70°,f*=0.06,一个周期内,水翼瞬时升力系数运行在2以上的时间不到30%,瞬时阻力系数运行在2以上的时间超过了50%,一个周期的CP只有0.40左右. CL(t)、CD(t)、CP(t)曲线都出现了不平滑的振荡现象,局部突变较多,水翼的水动力特性较差.旋涡的脱落会引起水翼水动力性能的突变,使系统的稳定性降低.旋涡脱落的频率与运动参数有关.为了提高水翼运行的平稳性,可以通过对运动参数进行调节,避免旋涡脱落.保持水翼的俯仰振幅不变(θ0=70°),将水翼的折算频率增大,f*=0.14,CL(t)、CD(t)和CP(t)的变化曲线如图 6(b)所示,CL(t)、CD(t)、CP(t)各系数曲线不平滑的振荡突变现象消失.在一个周期内,水翼的瞬时升力系数运行在2以上的时间超过了60%,瞬时阻力系数运行在2以上的时间下降到20%左右,一个周期的CP上升为0.90.维持f*=0.14,增大俯仰振幅,θ0=80°,CLt、CD(t)和CP(t)的变化曲线如图 6(c)所示,各系数曲线出现了不平滑的振荡现象.由图 6可知,在相同的θ0和y0的条件下,将折算频率设置在最高总效率对应的运动参数下,能够减小CL(t)、CD(t)、CP(t)各系数曲线不平滑的振荡突变现象,但是,此种参数下运行的水翼平均功率输出未必是最大的,因为CP随f*的变化规律与总效率η随f*变化的规律不完全一致. CP随f*的变化情况如表 2所示.由图 5可知,当f*=0.18时,θ0=80°的总效率最高;由表 2可知,f*=0.18时的平均功率系数最高是在θ0=90°,原因是当俯仰振幅不同时,振荡水翼的扫掠高度发生了变化.在水翼运动参数的选择过程中,应当注意能量捕获总效率与平均功率系数的变化规律的不同.
| 表 2 平均功率系数的变化规律(NACA0015,xp/c=1/3,Re=5×105,y0/c=1,Φ=90°) Table 2 Changes of power cycle-averaged coefficient (NACA0015, xp/c=1/3, Re=5×105, y0/c=1, Φ=90°) |
Kinsey等[9]在流体黏性影响比较高的条件下(Re=1 100)研究俯仰轴位置、厚度对水翼工作性能的影响.实际工况下的Re远远大于1 100.本文在流体黏性影响相对较小的实际工况(Re=500 000)下,研究几何参数对水翼工作性能的影响,与文献[9]的结果进行比较分析.
1) 俯仰轴位置.俯仰轴位置的变化对水翼(NACA0018)性能的影响规律如表 3所示.改变水翼的俯仰轴位置会导致水翼表面的瞬时线加速度发生变化,与俯仰轴距离变大的点的瞬时线加速度增加,与俯仰轴距离变小的点的瞬时线加速度减小,造成水翼的旋涡流动状态发生变化,从而改变水翼附近旋涡的产生及脱落时间,最终影响水翼的水动力特性和能量捕获性能.由表 3可以看出,水翼的升力和俯仰力矩所捕获的能量随着俯仰轴位置的变化而变化.俯仰轴位置越靠近水翼的前缘,水翼升沉运动所捕获的功率系数越高,但是水翼俯仰运动所消耗功率的系数相应增加.当俯仰轴位置为c/3时,振荡水翼的能量捕获总效率η可达26.5%,高于俯仰轴位置为c/5和c/2的能量捕获效率.
| 表 3 俯仰轴位置对水翼性能的影响(θ0=60°,f*=0.10,Re=5×105,y0/c=1,Φ=90°) Table 3 Effect of pitching-center location(θ0=60°, f*=0.10, Re=5×105, y0/c=1, Φ=90°) |
Kinsey等[9]的计算结果如表 4所示.表中,工况1为f*=0.14, θ0=76.3°, 工况2为f*=0.18, θ0=60°.比较表 3、4的结果可知:在流体黏性影响相对较小的实际工况下,俯仰轴位置变化对水翼的捕能功率和效率的影响与Kinsey等[9]结果的影响趋势一致,俯仰轴位置为c/3时所获得的水翼的总效率最高.对比图 5的结果可知,相同型号的水翼在流体黏性影响相对较小的实际工况下,水翼捕能的总效率更高,如当xp/c=1/3,θ0=60°,f*=0.18时,图 5的总效率约为20%(在流体黏性影响相对较小的实际工况下),表 4的总效率只有11.4%(在流体黏性影响相对较高的条件下).
| 表 4 俯仰轴位置对水翼性能影响(Re=1 100) Table 4 Effect of pitching-center location (Re=1 100) |
2) 水翼厚度.水翼的厚度对流过水翼表面的流体的流动特性有较大的影响.为了选择合适的水翼厚度,分析不同厚度对系统的水动力特性和能量捕获性能的影响.
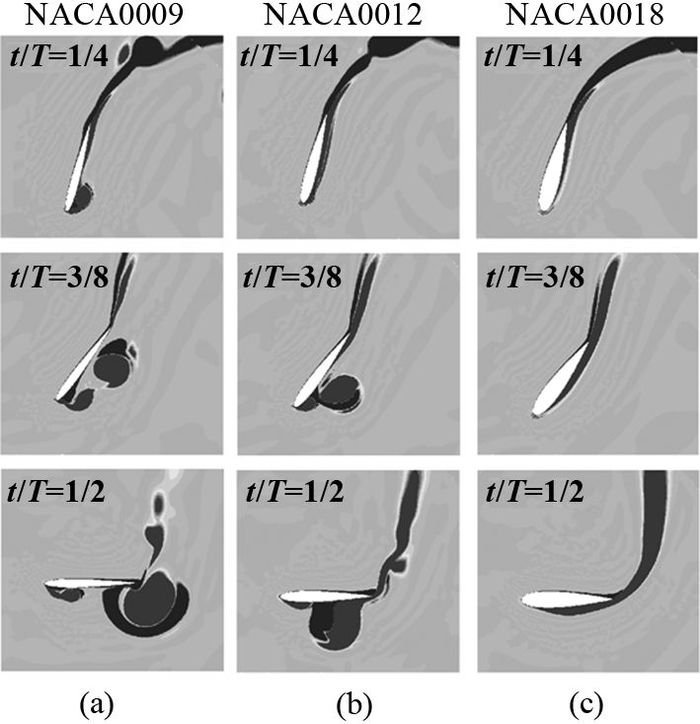
不同厚度的水翼周围流场的旋涡结构如图 7所示. 图 7(a)中,水翼的相对厚度为9%,在T/t=1/4时刻,水翼前缘下表面的边界层发生分离,出现了旋涡(记为Ⅰ).此后,随着水翼的继续运动,旋涡Ⅰ逐渐变大,并从水翼前缘点区域逐渐脱离水翼下表面.在T/t=3/8时刻,旋涡Ⅰ的主体部分已经脱离水翼前缘点区域;同时,在水翼下表面靠近前缘点的区域又出现了小旋涡(记为Ⅱ).随着水翼的进一步运动,旋涡Ⅱ沿着水翼下表面向后缘点移动并脱落. 图 7(b)中,水翼的相对厚度为12%,周围流场出现了类似的边界层分离和旋涡脱落现象. 图 7(c)的水翼相对厚度为18%,周围流场没有出现旋涡.
|
图 7 不同厚度水翼周围流场的旋涡结构(θ0=75°,f*=0.14,xp/c=1/3,Re=5×105,y0/c=1,Φ=90°) Fig. 7 Vortex contours of hydrofoils with different relative thicknesses (θ0=75°, f*=0.14, xp/c=1/3, Re=5×105, y0/c=1, Φ=90°) |
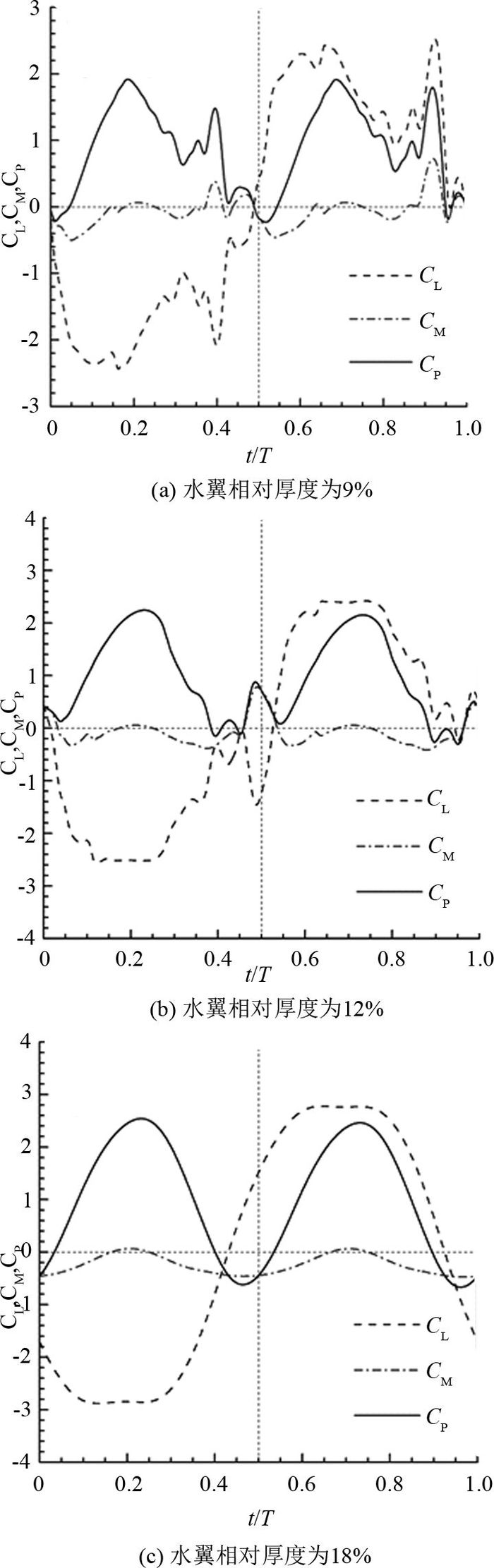
当θ0=75°, f*=0.14时,相对厚度分别为9%、12%、18%的水翼的瞬时升力、瞬时俯仰力矩和功率系数曲线如图 8所示.边界层的分离及旋涡的脱落会影响水翼周围流场的压力和速度的分布,而且旋涡的脱落会带走大量的能量,因此边界层的分离以及旋涡的脱落会引起水翼受力和瞬时功率的突变.由图 7、8可知,较薄翼型的NACA0009和NACA0012存在边界层分离和旋涡脱落的现象,NACA0009和NACA0012翼型的瞬时升力、瞬时俯仰力矩和功率系数曲线非常不平滑,局部突变较多,NACA0009的瞬时功率系数CP(t)的最大值约为2,NACA0012的瞬时功率系数的最大值约为2.15.从图 8曲线的波动程度可以推测出NACA0009翼型的旋涡脱落频率高于NACA0012翼型的旋涡脱落频率.由图 7(c)、8(c)可知,当将水翼的相对厚度增加至18%时,水翼不再出现边界层分离和旋涡的现象,水翼的瞬时升力、瞬时俯仰力矩和功率系数曲线变得平滑,CP(t)的最大值上升为2.3,与翼型NACA0009和NACA0012相比,功率系数分别增大了15%和7%,有利于提高水翼的功率输出.
|
图 8 不同厚度水翼的瞬态升力、俯仰力矩和功率系数曲线的对比(xp/c=1/3,Re=5×105,y0/c=1,Φ=90°) Fig. 8 Comparison of lift coefficient, pitch moment coefficient and power coefficient between numerical simulations using different relative thicknesses(xp/c=1/3, Re=5×105, y0/c=1, Φ=90°) |
不同的相对厚度对振荡水翼的水动力和能量捕获性能影响的计算结果如表 5所示.可知,升力贡献的时均功率系数与水翼厚度呈正相关性,俯仰力矩贡献的功率系数与水翼厚度呈负相关,能量捕获效率随着水翼厚度的增加而增加.增加水翼厚度能够增加水翼升力所捕获的能量,但也会增加俯仰运动消耗的能量,对总的能量捕获效率的影响与水翼的运动参数有关.随着水翼厚度的增加,水翼厚度对提高能量捕获效率的作用减弱.
| 表 5 水翼厚度对水翼性能的影响(θ0=75°,f*=0.14,xp/c=1/3,Re=5×105,y0/c=1,Φ=90°) Table 5 Effect of hydrofoil thickness (θ0=75°, f*=0.14, xp/c=1/3, Re=5×105, y0/c=1, Φ=90°) |
Kinsey等[9]的计算结果如表 6所示,结论是“水翼的厚度对水翼的能量捕获功率和总效率的影响十分弱”.由表 5的结果可知,水翼厚度对捕获功率和总效率的影响比较明显.通过与Kinsey等[9]的结果比较可得:在流体黏性影响相对较小的实际工况下,水翼厚度对水翼的能量捕获功率和效率的影响更大.
| 表 6 水翼厚度对水翼性能的影响(Re=1 100) Table 6 Effect of hydrofoil thickness (Re=1 100) |
(1) 将水翼的运行参数设置在最高效率点对应的参数下,能够减小瞬时升力系数、瞬时阻力系数、瞬时功率系数等各系数曲线的不平滑振荡突变现象,但是该参数设置下的水翼功率输出未必能够达到最大.在俯仰振幅和折算频率一定的条件下,通过增大升沉振幅来提高系统的能量捕获效率的作用越来越弱;当升沉振幅超过某一值时,将使水翼边界层产生分离与旋涡脱落现象,从而造成总效率下降.
(2) 在流体黏性影响相对较小的条件下,水翼的几何参数对水翼水动力性能的影响程度更大,水翼的捕能总效率更高.
(3) 在特定的流场中,选择合适的水翼,调整水翼的运动参数可以避免水翼的边界层分离现象的发生,从而使水翼的工作状态和能量提取效率都达到最优.
| [1] |
JOSLIN J. Evaluating environmental risks for marine renewable energy[J]. Sea Technology, 2016, 57(2): 73. |
| [2] |
BICER Y, DINCER I. Analysis and performance evaluation of a renewable energy based multi generation system[J]. Energy, 2016, 94: 623-632. DOI:10.1016/j.energy.2015.10.142 |
| [3] |
OUREILIDIS K O, BAKIRTZIS E A, DEMOULIAS C S. Frequency-based control of islanded microgrid with renewable energy sources and energy storage[J]. Journal of Modern Power Systems and Clean Energy, 2016, 4(1): 54-62. DOI:10.1007/s40565-015-0178-z |
| [4] |
吕沁, 李德堂, 唐文涛, 等. 基于液压传动的振荡浮子式波浪发电系统设计[J]. 浙江大学学报:工学版, 2016, 50(2): 234-240. LV Qin, LI De-tang, TANG Wen-tao, et al. Design oscillating buoy wave power generating system based on hydraulic transmission[J]. Journal of Zhejiang University:Engineering Science, 2016, 50(2): 234-240. |
| [5] |
LIU X, ZHOU L J, ESCALER X, et al. Numerical simulation of added mass effects on a hydrofoil in cavitating flow using acoustic fluid-structure interaction[J]. Journal of Fluids Engineering, 2017, 139(4): 041301. DOI:10.1115/1.4035113 |
| [6] |
GARG N, KENWAY G K W, LYU Z J, et al. High-fidelity hydrodynamic shape optimization of a 3-D hydrofoil[J]. Journal of Ship Research, 2015, 59(4): 209-226. DOI:10.5957/JOSR.59.4.150046 |
| [7] |
AKCABAY D T, YOUNG Y L. Parametric excitations and lock-in of flexible hydrofoils in two-phase flows[J]. Journal of Fluids and Structures, 2015, 57: 344-356. DOI:10.1016/j.jfluidstructs.2015.06.004 |
| [8] |
MCKINNEY W, DELAURIER J. Thewingmill:an oscillating-wing windmill[J]. Journal of Energy, 1981, 5(2): 109-115. DOI:10.2514/3.62510 |
| [9] |
KINSEY T, DUMAS G. Parametric study of an oscillating airfoil in a power-extraction regime[J]. AIAA Journal, 2008, 46(6): 1318-1330. DOI:10.2514/1.26253 |
| [10] |
KINSEY T, DUMAS G. Computational fluid dynamics analysis of a hydrokinetic turbine based on oscillating hydrofoils[J]. Journal of Fluids Engineering, 2012, 134(2): 21104. DOI:10.1115/1.4005841 |
| [11] |
AMIRALAEI M R, ALIGHANBARI H, HASHEMI S M. An investigation into the effects of unsteady parameters on the aerodynamics of a low Reynolds number pitching airfoil[J]. Journal of Fluids and Structures, 2010, 26(6): 979-993. DOI:10.1016/j.jfluidstructs.2010.06.004 |
| [12] |
AMIRALAEI M R, ALIGHANBARI H, HASHEMI S M. Flow field characteristics study of a flapping airfoil using computational fluid dynamics[J]. Journal of Fluids and Structures, 2011, 27(7): 1068-1085. DOI:10.1016/j.jfluidstructs.2011.06.005 |
| [13] |
YOUNG J, LAI J C S, PLATZER M F, et al. Oscillation frequency and amplitude effects on the wake of a plunging airfoil[J]. AIAA Journal, 2004, 42(10): 2042-2052. DOI:10.2514/1.5070 |
| [14] |
THIERY M, COUSTOLS E. URANS computations of shock-induced oscillations over 2D rigid airfoils:influence of test section geometry[J]. Flow Turbulence and Combustion, 2005, 74(4): 331-354. DOI:10.1007/s10494-005-0557-z |
| [15] |
THIERY M, COUSTOLS E. Numerical prediction of shock induced oscillations over a 2D airfoil:influence of turbulence modelling and test section walls[J]. International Journal of Heat and Fluid Flow, 2006, 27(4): 661-670. DOI:10.1016/j.ijheatfluidflow.2006.02.013 |
| [16] |
刘臻, 史宏达, 刘芸. 应用Realizable k-ε湍流模型的振荡水翼绕流数值模拟研究[J]. 哈尔滨工程大学学报, 2008, 29(6): 628-634. LIU Zhen, SHI Hong-da, LIU Yun. Numerical simulation of water flow overan oscillating hydrofoil using realizable k-ε turbulence model[J]. Journal of Harbin Engineering University, 2008, 29(6): 628-634. |
| [17] |
PENG Z, ZHU Q. Energy harvesting through flow-induced oscillations of a foil[J]. Physics of Fluids, 2009, 21(9): 1-9. |
| [18] |
XIAO Q, LIAO W, YANG S, et al. How motion trajectory affects energy extraction performance of a biomimic energy generator with an oscillating foil[J]. Renewable Energy, 2012, 37(1): 61-75. DOI:10.1016/j.renene.2011.05.029 |
| [19] |
LE T Q, KO J H. Effect of hydrofoil flexibility on the power extraction of a flapping tidal generator via two-and three-dimensional flow simulations[J]. Renewable Energy, 2015, 80: 275-285. DOI:10.1016/j.renene.2015.01.068 |
| [20] |
KARN A, SHAO S Y, ARNDT R E A, et al. Bubble coalescence and breakup in turbulent bubbly wake of a ventilated hydrofoil[J]. Experimental Thermal and Fluid Science, 2016, 70: 397-407. DOI:10.1016/j.expthermflusci.2015.10.003 |
| [21] |
CHEN Y, CHEN X, LI J, et al. Large eddy simulation and investigation on the flow structure of the cascading cavitation shedding regime around 3D twisted hydrofoil[J]. Ocean Engineering, 2017, 129: 1-19. DOI:10.1016/j.oceaneng.2016.11.012 |
| [22] |
DAVIDS S T. A computational and experimental investigation of a flutter generator[D]. Monterey:Naval Postgraduate School, 1999. http://calhoun.nps.edu/handle/10945/13500
|


