轴流式止回阀是通过改变入口流量来实现启闭件开启与关闭的一种止回阀,被广泛应用于工业管道运输系统[1].降低阀门能耗是当前国内外阀设计的一项重要指标.在工业生产中,由于轴流式止回阀存在大量不合理的结构设计,导致阀内复杂涡系产生,流阻增大,能耗增加.优化阀门内部结构,对实现流动减阻具有十分重要的研究意义.目前,李德禹等[2-5]采用实验或数值模拟方法,对轴流式止回阀内流场进行可靠分析,通过改善压降特性、壁面粗糙度等来减小流阻系数,实现流动减阻.近年来,张希恒等[6]采用源汇法对轴流式止回阀的阀芯进行流线型设计.以上减阻设计的方法或者依赖经验,或者参考流线线型,缺乏有力的理论指导,对阀内流阻的变化机理没有深入研究.为了寻求阀设计的理论指导方法,本文引入Guo等[7]提出的场协同原理.
场协同原理最早在强化换热领域中提出,现已在实验和数值模拟中得到很好的验证,并广泛应用于湍流对流换热领域[8-11].基于动量传递与热量传递之间的相似性,陈群等[12]将场协同原理推广至流动领域,推导得到层流流动场协同方程,指出流阻与流动场协同角之间的联系,结合机械能耗散最小原理,对速度分配器进行优化设计.此外,Zhang等[13]推导可压缩层流流动场协同方程,并将该方程应用于变截面空气管道内的减阻设计.吕金升[14]基于雷诺平均应力模型,利用流动场协同原理对喷射器结构进行优化设计.
基于流动场协同原理在减阻设计中的可行性,本文首先将该原理从层流推广至湍流,对推导公式进行验证.利用Fluent软件对2种不同型号(优化前、后)阀门的内流场进行数值模拟和流动场协同分析,得到压降、流速分布、流动场协同角余弦值分布和有效黏性系数等.本文研究流动场协同程度、有效黏性系数对流阻的影响.从增大流动场协同角、降低机械能耗散量两方面分别提出减阻优化的设计思路.
1 数值模型与几何模型 1.1 湍流流动场协同原理对于层流流动,在整个流动区域Ω内,对动量方程进行积分[12]可得
| $ - \frac{D}{{\rho u_{{\rm{in}}}^2}}\int_\mathit{\Omega } {\frac{{\partial p}}{{\partial {x_i}}}{\rm{d}}\bar V} = - \frac{\mu }{{\rho {u_{{\rm{in}}}}D}}\int_\mathit{\Gamma } {\nabla \overline {{u_i}} \cdot \mathit{\boldsymbol{n}}{\rm{d}}\bar S} + \int_\mathit{\Omega } {\mathit{\boldsymbol{\bar U}} \cdot \nabla \overline {{u_i}} {\rm{d}}\bar V} . $ | (1) |
式中:Γ为流体流动区域的外边界,S为流体流动区域外边界表面积,n为外边界的单位外法向矢量,上标“-”表示无量纲变量.
对于稳态、无体积力作用的不可压缩湍流流动过程,动量方程为
| $ \rho {u_j}\frac{{\partial {u_i}}}{{\partial {x_j}}} = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left[ {{\mu _{{\rm{eff}}}}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \frac{2}{3}\rho k{\delta _{ij}}} \right]. $ | (2) |
式中:ρ为流体介质的密度;p为压力;μeff为包括层流黏性系数和湍流黏性系数在内的有效黏性系数,μeff=μl+μt,其中ui、uj分别为速度矢量在i、j方向上的分量;k为湍动能系数;δij为单位二阶张量在(i, j)上的分量,在整个流动区域Ω内对式(2)进行积分,可得
| $ \begin{array}{l} \int_\mathit{\Omega } {\rho {u_j}\frac{{\partial {u_i}}}{{\partial {x_j}}}{\rm{d}}V} = - \int_\mathit{\Omega } {\frac{{\partial p}}{{\partial {x_i}}}{\rm{d}}V} + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\int_\mathit{\Omega } {\frac{\partial }{{\partial {x_j}}}\left[ {{\mu _{{\rm{eff}}}}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \frac{2}{3}\rho k{\delta _{ij}}} \right]{\rm{d}}V} . \end{array} $ | (3) |
式中:V为流体流动区域的体积.将式(3)右边第二项进行拆分,可得
| $ \begin{array}{l} \int_\mathit{\Omega } {\frac{\partial }{{\partial {x_j}}}\left[ {{\mu _{{\rm{eff}}}}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \frac{2}{3}\rho k{\delta _{ij}}} \right]{\rm{d}}V} = \\ \;\;\;\int_\mathit{\Omega } {\frac{\partial }{{\partial {x_j}}}\left( {{\mu _{{\rm{eff}}}}\frac{{\partial {u_i}}}{{\partial {x_j}}} - \frac{2}{3}\rho k{\delta _{ij}}} \right){\rm{d}}V} + \int_\mathit{\Omega } {\frac{\partial }{{\partial {x_j}}}\left( {{\mu _{{\rm{eff}}}}\frac{{\partial {u_j}}}{{\partial {x_i}}}} \right){\rm{d}}V} . \end{array} $ | (4) |
拆分后的第一项通过格林公式转化为面积积分:
| $ \begin{array}{l} \int_\mathit{\Omega } {\frac{\partial }{{\partial {x_j}}}\left( {{\mu _{{\rm{eff}}}}\frac{{\partial {u_i}}}{{\partial {x_j}}} - \frac{2}{3}\rho k{\delta _{ij}}} \right){\rm{d}}V} = \int_\mathit{\Gamma } {\left( {{\mu _{{\rm{eff}}}}\frac{{\partial {u_i}}}{{\partial {x_j}}} - \frac{2}{3}\rho k{\delta _{ij}}} \right) \cdot } \\ \mathit{\boldsymbol{n}}{\rm{d}}S. \end{array} $ | (5) |
在不可压缩流体中,
| $ \frac{\partial }{{\partial {x_j}}}\left( {\frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) = \frac{\partial }{{\partial {x_i}}}\left( {\frac{{\partial {u_j}}}{{\partial {x_j}}}} \right) = 0, $ |
拆分后的第二项可以化为
| $ \begin{array}{l} \int_\mathit{\Omega } {\frac{\partial }{{\partial {x_j}}}\left( {{\mu _{{\rm{eff}}}}\frac{{\partial {u_j}}}{{\partial {x_i}}}} \right){\rm{d}}V} = \int_\mathit{\Omega } {\frac{{\partial {\mu _{{\rm{eff}}}}}}{{\partial {x_j}}}\frac{{\partial {u_j}}}{{\partial {x_i}}}{\rm{d}}V} + \\ \;\;\;\;\int_\mathit{\Omega } {{\mu _{{\rm{eff}}}}\frac{\partial }{{\partial {x_j}}}\left( {\frac{{\partial {u_j}}}{{\partial {x_i}}}} \right){\rm{d}}V} = \int_\mathit{\Omega } {\frac{{\partial {\mu _{{\rm{eff}}}}}}{{\partial {x_j}}}\frac{{\partial {u_j}}}{{\partial {x_i}}}{\rm{d}}V} . \end{array} $ | (6) |
将式(5)、(6)代入式(3),有
| $ \begin{array}{l} \int_\mathit{\Omega } {\rho {u_j}\frac{{\partial {u_i}}}{{\partial {x_j}}}{\rm{d}}V} = - \int_\mathit{\Omega } {\frac{{\partial p}}{{\partial {x_i}}}{\rm{d}}V} + \int_\mathit{\Gamma } {\left( {{\mu _{{\rm{eff}}}}\frac{{\partial {u_i}}}{{\partial {x_j}}} - \frac{2}{3}\rho k{\delta _{ij}}} \right) \times } \\ \;\;\;\mathit{\boldsymbol{n}}{\rm{d}}S + \int_\mathit{\Omega } {\frac{{\partial {\mu _{{\rm{eff}}}}}}{{\partial {x_j}}}\frac{{\partial {u_j}}}{{\partial {x_i}}}{\rm{d}}V} . \end{array} $ | (7) |
定义D=V/S为特征长度,引入下列无量纲变量:
| $ \overline {{u_i}} = \frac{{{u_i}}}{{{u_{{\rm{in}}}}}},\overline {{u_j}} = \frac{{{u_j}}}{{{u_{{\rm{in}}}}}},\nabla \overline {{u_i}} = \frac{{\nabla {u_i}}}{{{u_{{\rm{in}}}}/D}},{\rm{d}}\bar V = \frac{{{\rm{d}}V}}{V},{\rm{d}}\bar S = \frac{{{\rm{d}}S}}{S}, $ |
则式(7)可以写为
| $ \begin{array}{l} - \frac{D}{{\rho u_{{\rm{in}}}^2}}\int_\mathit{\Omega } {\frac{{\partial p}}{{\partial {x_i}}}{\rm{d}}\bar V} = - \frac{1}{{\rho {u_{{\rm{in}}}}D}}\int_\mathit{\Gamma } {\left( {{\mu _{{\rm{eff}}}}\nabla \overline {{u_i}} - \frac{{2D}}{{3{u_{{\rm{in}}}}}}\rho k{\delta _{ij}}} \right) \times } \\ \;\;\;\mathit{\boldsymbol{n}}{\rm{d}}\bar S + \int_\mathit{\Omega } {\mathit{\boldsymbol{\bar U}} \cdot \nabla \overline {{u_i}} {\rm{d}}\bar V} - \frac{D}{{\rho {u_{{\rm{in}}}}}}\int_\mathit{\Omega } {\frac{{\partial {\mu _{{\rm{eff}}}}}}{{\partial {x_j}}}\frac{{\partial \overline {{u_j}} }}{{\partial {x_i}}}{\rm{d}}V} . \end{array} $ | (8) |
式(8)左边表示xi方向的无量纲压力梯度:
| $ {\rm{D}}{{\rm{C}}_i} = - \frac{D}{{\rho {u_{{\rm{in}}}}}}\int_\mathit{\Omega } {\frac{{\partial p}}{{\partial {x_i}}}{\rm{d}}\bar V} . $ | (9) |
式(8)右边第二项为无量纲速度矢量和速度分量ui的无量纲梯度矢量之间的点积在整个流动区域内的积分:
| $ {\rm{F}}{{\rm{S}}_m} = \int_\mathit{\Omega } {\mathit{\boldsymbol{\bar U}} \cdot \nabla \overline {{u_i}} {\rm{d}}\bar V} = \int_\mathit{\Omega } {\left| {\mathit{\boldsymbol{\bar U}}} \right|\left| {\nabla \overline {{u_i}} } \right|{\rm{cos}}{\beta _{\rm{m}}}{\rm{d}}\bar V} . $ | (10) |
式中:βm为速度矢量和速度分量ui梯度矢量之间的夹角.湍流场流动协同数FSm的表达式与层流流动场协同原理中一致,FSm不仅与速度和速度梯度有关,而且与βm有关,βm越大,则FSm越小,表示速度场和速度梯度场的协同程度越差.
由式(8)可知,无量纲压力梯度与FSm有关,当流体入口边界条件一定时,速度场和速度梯度场在整个流动区域中的协同程度越差,则流体的流动阻力越小.此外,无量纲压力梯度与
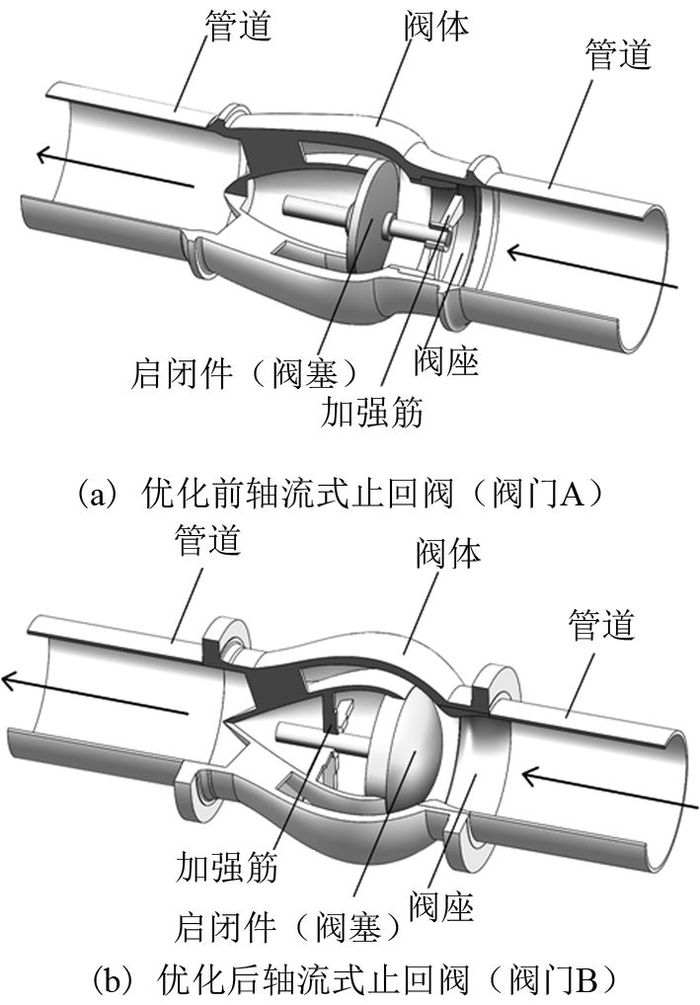
轴流式止回阀的三维模型来自于某阀门公司产品,有2种类型:阀门A是优化前的轴流式止回阀,阀门B是优化后的轴流式止回阀.根据该公司提供的特殊阀门规格书可知,当止回阀正常工作时,为常开启状态,如图 1所示.
|
图 1 2种不同型号轴流式止回阀三维示意图 Fig. 1 Two different types of non-slam check valve |
对比图 1(a)、(b)可以发现,优化前、后阀门结构的主要区别如下:1)阀芯结构,阀芯优化为流线型的液滴状;2)加强筋设置,连接启闭件的加强筋由外置改为内置.已知连通这2种不同型号阀门的管道直径为685 mm.
为了使研究流体有充分发展的空间,选取阀门入口管道为5倍管径长度,出口管道为10倍管径长度,利用SolidWorks软件对几何模型进行简化,通过ANSYS-ICEM软件对几何模型进行网格划分.
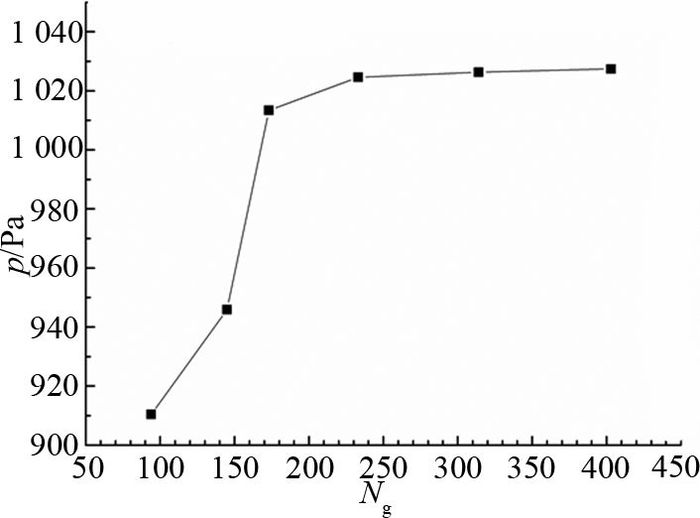
2 轴流式止回阀的流场模拟 2.1 网格无关性验证由于阀门内部结构的复杂性,流体介质区域采用非结构网格,通过网格质量检查可知,网格质量满足计算要求.在数值计算之前,为了验证计算结果与网格数量无关,对计算模型的网格数量无关性进行验证.本文阀门流阻研究的主要评判标准之一是压降,因此选取优化后阀门为例,观察比较不同流体网格密度(从94万增加至403万)下的总压力损失,结果如图 2所示.图中,Ng为网络数,p为压降.当网格数达到233万时,压降基本趋于稳定;当网格数大于233万时,计算量会大幅增大,为了在减少计算时间的同时确保计算精度,优化后阀门模型的网格数选用233万.优化前、后的阀门在结构与尺寸上有一定的相似性,因此在网格划分时使用同样的网格最大尺寸,得到217万网格数的优化前阀门模型.
|
图 2 网格数对压降的影响 Fig. 2 Influence of mesh number on pressure drop |
2种型号轴流式止回阀内的流体介质为丙烯,在工作温度为351.79 K,工作压力为1.994 MPa的工况下,丙烯呈气态,密度为38.19 kg/m3,动力黏性系数为10-5 Pa·s.当阀门正常工作时,丙烯气体的质量流量为381 293.69 kg/h,计算可得雷诺数远远大于4 000,属于高雷诺数范畴,因此选用k-ε模型.根据雷诺数计算阀门A、B内的湍流强度为1.96%.由该特殊阀规格书可得阀内介质的入口流量范畴,在该范畴内分别选取7个成等差数列分布的流量,根据流量与入口直径分别计算得到入口速度:6.396 691 m/s、6.772 967 m/s、7.149 243 m/s、7.525 519 m/s、7.901 795 m/s、8.278 071 m/s、8.654 347 m/s;出口压力与工作压力相等,因此选用速度入口边界条件与压力出口边界条件.此外,阀芯内壁面的粗糙度厚度为0.05 mm.在计算过程中,压力与速度的解耦采用SIMPLEC算法,压力项采用标准格式离散;在控制方程中,动量项和其他系数项均采用二阶迎风差分格式离散.
1) 在流体流动过程中,所受的阻力主要来源于黏性耗散导致的机械能损失Φ,表达式为
| $ \begin{array}{l} \mathit{\Phi = }{\mu _{{\rm{eff}}}}\left[ {2{{\left( {\frac{{\partial u}}{{\partial x}}} \right)}^2} + 2{{\left( {\frac{{\partial v}}{{\partial y}}} \right)}^2} + 2{{\left( {\frac{{\partial w}}{{\partial z}}} \right)}^2} + {{\left( {\frac{{\partial u}}{{\partial y}} + \frac{{\partial v}}{{\partial x}}} \right)}^2} + } \right.\\ \;\;\;\;\;\left. {{{\left( {\frac{{\partial u}}{{\partial z}} + \frac{{\partial w}}{{\partial x}}} \right)}^2} + {{\left( {\frac{{\partial v}}{{\partial z}} + \frac{{\partial w}}{{\partial y}}} \right)}^2}} \right]. \end{array} $ | (11) |
黏性耗散在整个区域内的体积积分是流体流动所需要耗散的机械能总量.在Fluent软件中,利用用户自定义函数(user-defined function,UDF)对每个单元黏性耗散和单元体积的乘积循环求和计算得到.
| $ {J_\mathit{\Phi }} = \int_\mathit{\Omega } {\mathit{\Phi }{\rm{d}}V} = \sum\limits_{i = 1}^n {{\mathit{\Phi }_i}{V_i}} . $ | (12) |
2) 场协同角余弦值的计算式为
| $ {\rm{cos}}{\beta _{\rm{m}}} = \frac{{\left| {\mathit{\boldsymbol{\bar U}} \cdot \nabla {u_i}} \right|}}{{\left| {\mathit{\boldsymbol{\bar U}}} \right|\left| {\nabla {u_i}} \right|}}. $ | (13) |
式(8)中,βm包含了3个方向的夹角,本文研究的主要是在x方向上的压降,因此式(13)的i取1,即速度矢量与x方向速度梯度矢量的夹角.采用用户自定义内存(user-defined memory,UDM)来存储计算域中各个网格单元处的场协同角余弦值.
3) 为了考察
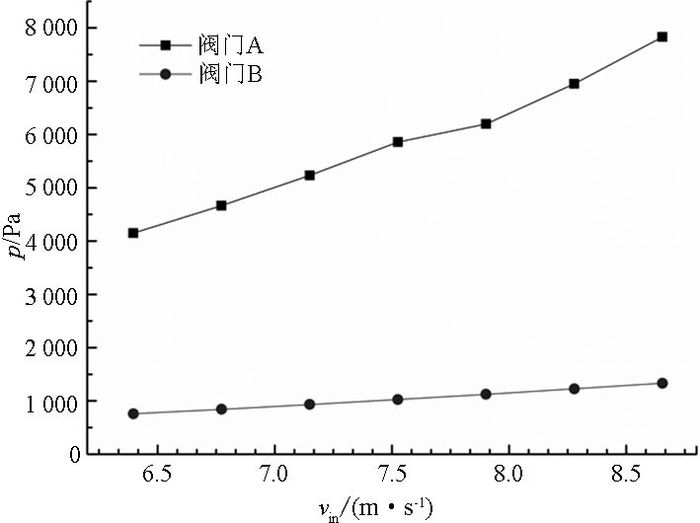
流体压降、流体质量加权平均流速和流阻系数是评价阀门流阻性能的3个重要参数[2].如图 3、4所示为2种不同型号阀门流体压降和平均流速va随入口速度vin的变化.从图 3可以看出,阀门B内流体压降远小于阀门A内流体压降,且符合该特殊阀规格书上对该轴流式止回阀压降小于3 000 Pa的要求.随着入口速度的增加,阀门B的压降增加速度比阀门A慢且稳定.由此说明,阀门B的结构在流阻性能上比阀门A的结构优化很多.
|
图 3 优化前、后阀门压降特性曲线图 Fig. 3 Pressure drop characteristic curves of valves before and afteroptimized |

|
图 4 优化前、后阀门内流体平均流速与入口速度关系 Fig. 4 Relationship between average velocity and inlet velocity of valve flow before and after optimized |
从图 4可以看出,阀门A内湍流流体的平均流速大于阀门B,但是差距不大,这可能与管道直径有关,阀门A内的流道更复杂,过流面积更小,导致平均流速更大.
已知阀门流阻系数的表达式为K=2Δp/(ρva2),其中K为阀门的流阻系数,Δp为对应阀门的压力损失,ρ为流体密度.经过计算发现,流阻系数随流量的变化基本不变,通过计算所得的流阻系数平均值分别为4.447 3和0.920 3,这一规律与大多数文献一致[5],证明了数值计算结果的可靠性.流阻系数小的管道系统可以有效地节约经济支出,因此在减阻节能方面,阀门B的结构设计更加有优势.为了进一步分析研究阀门的流阻性能与流动场协同之间的联系,探究不同阀门结构对流动场协同程度的影响,取正常工作流量(381 293.69 kg/h,对应的流速为7.525 519 m/s)时的流动情况进行讨论.
3.2 湍流场协同角分析Zhu等[15]指出通过直接求解流场内平均场协同角余弦值的方法来评估目标量不够严谨,对于研究壁面结构对目标量的影响没有实质意义.选择考察场协同角在整个流动区域内的分布情况.由于轴流式止回阀在各个面呈现的流动状态是基本对称的,选其中一个轴截面为例.
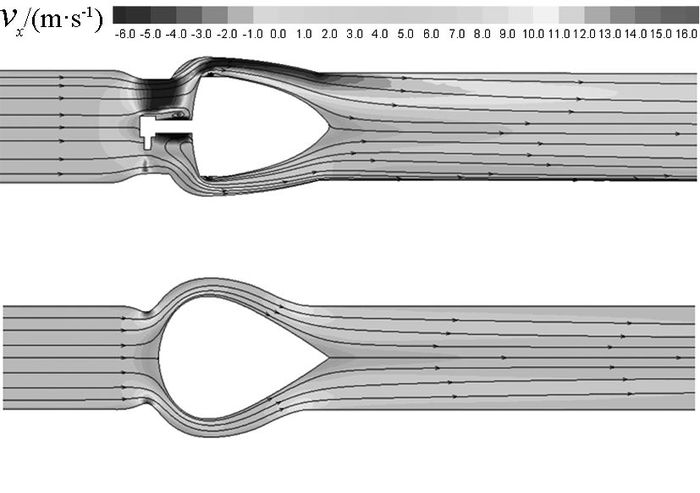
如图 5所示为2种不同型号阀门的速度分布和流线分布.图中,vx为x方向的流体速度.如图 6所示为利用UDM存储,再经Tecplot软件后处理得到的流动场协同角余弦值分布.根据式(8)可知,流域中流体的流阻与速度、速度梯度的模以及场协同角余弦值正相关;吕金升[14]提出可以把速度和速度梯度模的乘积看成是流阻对余弦的加权,乘积越大,余弦值对流动场协同数的影响越大.流动场协同数值越大,说明速度场和速度梯度场在整个流动区域内的协同程度越好,导致流动阻力越大,越不利于流动.
|
图 5 优化前、后阀门内流体速度和流线分布图 Fig. 5 Velocity and streamline diagram of valve flow before and after optimized |
|
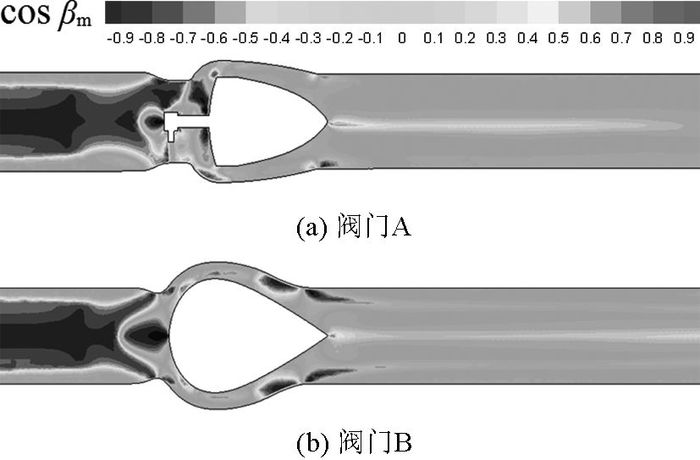
图 6 优化前、后阀门内流体场协同角余弦值分布图 Fig. 6 Cosine of field synergy angles diagram of valve flow before and after optimized |
首先对比图 6(a)和(b),从定性角度来看,阀门B中流体流动场协同角余弦值小于-0.7的部分比阀门A占比更大;阀门B整体上流体速度和流速变化都更小,阀门B内流动场协同程度更差,流阻更小,压降更小,结构设计更合理.这与3.1节的结论分析一致,验证了流动场协同原理的有效性.
对阀门A内流场进行场协同分析.从图 6(a)的流动场协同角余弦值分布情况来看,该值大于0.7的部分主要集中在入口管道区域.结合图 5(a)的流速分布情况可知,入口管道区域速度梯度很小,因此流动场协同数不大.事实上,入口管道区域内流阻小,压降小,说明即使在流动场协同角余弦值大的区域,流动场协同数不一定大,流阻并非都很大.从流阻产生的原因来看,入口管道区域的流阻仅来源于圆柱形管道壁面边界层的黏性作用,机械能耗散相对较小,说明上述分析符合实际情况.在出口管道区域,流动场协同角余弦值趋于0,出口管道区域流阻相应很小.由上述可知,流阻主要集中在阀门内流道区域,下面进行具体分析.根据图 5(a)可知,在阀门启闭件前方区域,流体流速先急剧增加,后急剧减小,说明此处速度和速度梯度的模都很大,速度梯度方向先是沿着x正方向,后沿着x负方向,因此场协同角余弦值前半区域接近于1,后半区域接近于-1,这与图 6(a)吻合,说明该区域的流阻先增大后减小,且变化显著,该区域的压力先减小后增大.在启闭件前端阀杆的正下方,流体速度小于0,出现回流.由于该回流是绕轴运动,轴壁面对流体运动起到减速作用,因此从图 5(a)可以发现,速度梯度方向沿轴心向外壁面的方向,与速度方向成90°夹角,即此处的场协同角余弦值趋于0,流阻很小,压力不减反增,这说明即使在回流区域,也可能出现流阻小的情况.在流体绕过启闭件后,首先经过一个拐角,发现此处的流体速度在轴向上明显增加,小范围内出现速度与速度梯度的夹角趋于0°,场协同角余弦值接近于1,使得此处的流阻很大,压力快速减小,同时还有回流,说明该区域在结构设计上极不合理.随后,流体流过阀芯与阀体间的流道,随着流道坡度的增加,在受到外壁面边界层的影响下,流体沿着径向表现出明显的速度变化;观察图 5(a)可知,该区域的速度梯度与速度方向的夹角趋近于90°,即场协同角余弦值为0,故此处流阻很小,压力变化不大.
对阀门B内流场进行场协同分析.从图 5(b)、6(b)可以看出,阀门B启闭件正前方区域由于流速迅速从约7 m/s减至0 m/s,速度方向和速度减小的方向相同,即场协同角为180°,场协同数接近于-1,流阻减小,压力不减反增.对比图 6(a)发现,该减阻区域范围比阀门A大,这是由于将加强筋由外置改为内置造成的,使得阀门B的结构设计更符合流动减阻的要求.当流体在阀芯与阀体间的流道流过时,阀门B流道截面积梯度比阀门A的更小,流速主要沿着径向(非轴向)有比较明显的变化,这使得速度方向与速度梯度方向更容易在一条直线上,流动场协同角基本上只能在180°和0°两者中变化.从图 6(b)可以发现,该区域的场协同角余弦值先为-1后为1再为-1,造成流阻的增减变化显著,压力变化非常大.阀门B在该区域的结构设计需要改进.
3.3 机械能耗散分析图 7、8分别给出2种不同型号阀门内流体机械能耗散量分布和有效黏性系数分布.机械能耗散量是评价阀门节能性能高低的重要指标之一,同时在场协同分析中,在给定约束条件下求机械能耗散总量的最小值是获得完全场协同最佳速度场的重要途径之一,即最小机械能原理.研究机械能耗散量及其分布情况对流动场协同分析具有一定的指导作用.通过UDF方法得到计算结果,在正常流速下,阀门A内流体的机械能耗散总量为11 028.5 W,阀门B内流体的机械能耗散总量为1 904.61 W,证明了阀门B的结构更优.对比图 7、8可以发现,在有效黏性系数大的区域内,流体机械能耗散总量更大;机械能耗散总量的表达式包含了有效黏性系数项,说明数值模拟结果与数学表达式是吻合的.黏性耗散量大和有效黏性系数大的部分都主要集中在远离壁面的区域.另外,阀门A中涡流和逆流存在的区域,黏性耗散显著增加,说明两者存在一定的联系.由此可得,减小阀内流体的有效黏性系数平均值,减小涡流或逆流的存在,可以有效地降低阀内流体的机械能耗散总量.有效黏性系数的平均值是衡量流动场协同程度的评判标准之一.经计算可知,阀门A内流体的有效黏性系数μeff平均值为0.463 2 Pa·s,阀门B内流体的有效黏性系数μeff平均值为0.281 6 Pa·s.从数值上来看,阀门A内流体的有效黏性系数略大于阀门B,即说明阀门B中的流场更接近最佳速度场的分布情况.

|
图 7 优化前、后阀门内流体黏性耗散分布图 Fig. 7 Viscous dissipation diagram of valve flow before and after optimized |
|
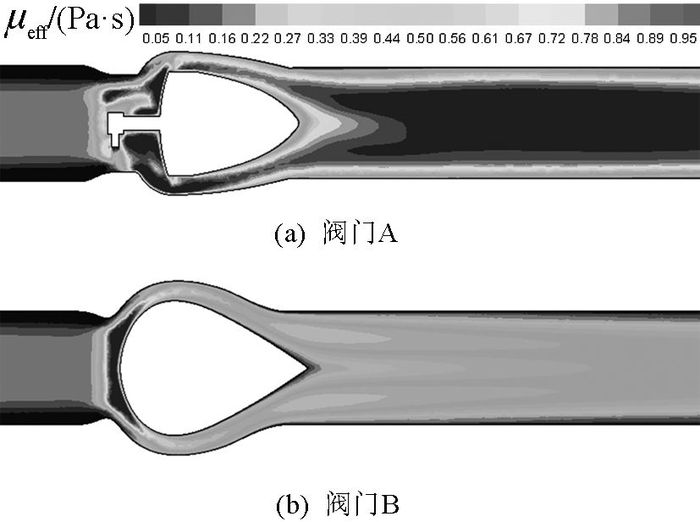
图 8 优化前、后阀门内流体有效黏性系数分布图 Fig. 8 Effective viscosity coefficient diagram of valve flow before and after optimized |
针对阀门内流体流阻的分布情况,考察阀门流阻最集中的流通通道区域.观察图 8(a)、(b)可知,该区域阀门B内流体的有效黏性系数梯度远大于阀门A.根据式(8)可知,
流动场协同角不仅能够通过整体特征体现阀门总压降和阀门结构设计的优劣,还能够揭示流阻在阀门局部范围内的变化机理,从而得到阀门内需要改进的目标位置.流动场协同分析在以机械能耗散最小为目标的评价基础上,可以有效地获得阀门内流体需要改进的目标参数.本文提出阀门减阻设计的思路.
1) 减小流动场协同角余弦值.由3.2节可知,流体在拐角、转弯等区域,不仅速度会发生剧烈变化,而且流动场协同角余弦值在一定范围内会显著变化,该值的正负对流阻的影响起决定性作用.对于流动场协同角余弦值小于0的区域,场协同数为负值,流阻减小,不需要进行结构改进;对于流动场协同角余弦值大于0的区域,流阻增大,为需要进行结构改进的目标位置.接下来应讨论需要改进的目标参数.若流动场协同角余弦值小于0.7,说明流动场协同角对场协同数的影响不占主导地位,主要分析该区域速度和速度梯度对场协同数的影响,尽可能地减小速度并增加流场速度的均匀性;若流动场协同角余弦值大于0.7,则需要重点考察几何结构对速度方向和速度梯度方向的影响,并进行优化.对比优化前、后的阀门结构可以得到以下3个有效方法:a)把加强筋由外置改为内置,既减少回流,又增大流动场协同角;b)增加阀门流道坡度,使流道截面积梯度变大,加强壁面边界层的黏性作用,从而改变速度矢量与速度梯度的夹角;c)拐角处采用平缓过渡的流线型,减少速度矢量变化剧烈的区域.
2) 减小机械能耗散量.由3.3节可知,减小平均有效黏性系数,可以有效地减小机械能耗散量.由式(8)可知,增加有效黏性系数梯度,可以减小流动阻力和压力降,也可以减小机械能耗散量.有效黏性系数与梯度可以作为衡量机械能耗散量大小的评价标准之一.在湍流流动中,有效黏性系数不是物性参数,取决于流动状态,在k-ε模型中,与湍动能系数和耗散率相关.从陈群等[12]的经验来看,目前可以尝试的方法有:利用机械能最小原理,在质量守恒、k方程和ε方程的约束条件下建立拉格朗日方程,考虑在μeff与坐标位置有关的前提下,推导湍流流动完全场协同方程,进而求得流场最优解.由于k-ε模型是双方程模型,建立完全湍流场协同模型的过程比较复杂,此处不作详细论述.
4 结论(1) 对稳态、无体积力作用的不可压缩湍流动量方程进行积分变换,从而得出湍流流动场协同原理,即流动阻力不仅与流动场协同数FSm项相关,而且与有效黏性系数μeff有一定关系.
(2) 优化前、后阀门的压降分别为5 857.1、1 024.6 Pa;优化前、后阀门的机械能耗散总量分别为11 028.5、1 904.61 W.这证明优化后的阀门流阻和能耗大大降低.
(3) 优化后阀门的流动场协同角余弦值小于-0.7部分的占比更大,流动场协同程度更差,流动场协同数FSm更小,因此流动减阻效果更明显.可以通过增加速度矢量和速度梯度矢量间夹角的方法进行流动减阻.具体方法如下:1)加强筋由外置改为内置;2)适当增加阀内渐宽流道坡度;3)拐角处改用平缓过渡的流线型.
(4) 优化前、后阀门内流体的有效黏性系数μeff平均值分别为0.463 2、0.281 6 Pa·s.流体有效黏性系数μeff平均值可以作为评价流动场协同程度的标准之一.减小流体的有效黏性系数平均值,增大有效黏性系数梯度都能够有效地实现流动减阻.
| [1] |
张宝江. 轴流式止回阀的应用[J]. 石油化工设计, 2011, 28(2): 45-46. ZHANG Bao-jiang. Application of non-slam check valve[J]. Petro-Chemical Design, 2011, 28(2): 45-46. |
| [2] |
李德禹. 阀门节能的重要途径——降低流阻系数[J]. 流体机械, 1984(1): 56-59. LI De-yu. An important way to save energy of valve:reduce flow resistance coefficient[J]. Fluid Machinery, 1984(1): 56-59. |
| [3] |
SIBILLA S, GALLATI M. Hydrodynamic characterization of a nozzle check valve by numerical simulation[J]. Journal of Fluids Engineering, 2008, 130(12): 121101-121112. DOI:10.1115/1.3001065 |
| [4] |
LAI Z, KARNEY B, YANG S, et al. Transient performance of a dual disc check valve during the opening period[J]. Annals of Nuclear Energy, 2017, 101: 15-22. DOI:10.1016/j.anucene.2016.10.010 |
| [5] |
伍国果. 轴流式止回阀动态特性的数值模拟[D]. 兰州: 兰州理工大学, 2013. WU Guo-guo. Numerical simulation for dynamic characteristics of axial flow check valve[D]. Lanzhou:Lanzhou University of Technology, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10731-1013251534.htm |
| [6] |
张希恒, 吴佳宝, 段峰波, 等. 基于源汇法和数学解析法的轴流式止回阀阀芯流线型设计及流阻系数分析[J]. 石油化工设备, 2013, 42(4): 23-26. ZHANG Xi-heng, WU Jia-bao, DUAN Feng-bo, et al. Streamlined design of axial check valve spool and analysis of flow resistance coefficient base on singularity distribution method and mathematical analytic method[J]. Petro-Chemical Equipment, 2013, 42(4): 23-26. |
| [7] |
GUO Z Y, TAO W Q, SHAH R K. The field synergy (coordination) principle and its applications in enhancing single phase convective heat transfer[J]. International Journal of Heat and Mass Transfer, 2005, 48(9): 1797-1807. DOI:10.1016/j.ijheatmasstransfer.2004.11.007 |
| [8] |
MENG J A, LIANG X G, LI Z X. Field synergy optimization and enhanced heat transfer by multi-longitudinal vortexes flow in tube[J]. International Journal of Heat and Mass Transfer, 2005, 48(16): 3331-3337. DOI:10.1016/j.ijheatmasstransfer.2005.02.035 |
| [9] |
CHEN Q, REN J, MENG J A. Field synergy equation for turbulent heat transfer and its application[J]. International Journal of Heat and Mass Transfer, 2007, 50(25): 5334-5339. |
| [10] |
HAMID M O A, ZHANG B, YANG L. Application of field synergy principle for optimization fluid flow and convective heat transfer in a tube bundle of a pre-heater[J]. Energy, 2014, 76(76): 241-253. |
| [11] |
ZHAI Y, LI Z, WANG H, et al. Analysis of field synergy principle and the relationship between secondary flow and heat transfer in double-layered microchannels with cavities and ribs[J]. International Journal of Heat and Mass Transfer, 2016, 101: 190-197. DOI:10.1016/j.ijheatmasstransfer.2016.05.025 |
| [12] |
陈群, 任建勋, 过增元. 流体流动场协同原理及其在减阻中的应用[J]. 科学通报, 2008, 53(4): 489-492. CHEN Qun, REN Jian-xun, GUO Zeng-yuan. A study of synergy principle on fluid flow field and its application in resistance reduction[J]. Chinese Science Bulletin, 2008, 53(4): 489-492. |
| [13] |
ZHANG B, LV J, ZUO J. Compressible fluid flow field synergy principle and its application to drag reduction in variable-cross-section pipeline[J]. International Journal of Heat and Mass Transfer, 2014, 77: 1095-1101. DOI:10.1016/j.ijheatmasstransfer.2014.06.027 |
| [14] |
吕金升. 场协同流动分析模型基础研究[D]. 大连: 大连理工大学, 2014. LV Jin-sheng. Fundamental study on the fluid flow analysis using field synergy principle[D]. Dalian:Dalian University of Technology, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10141-1015571985.htm |
| [15] |
ZHU X W, ZHAO J Q. Improvement in field synergy principle:more rigorous application, better results[J]. International Journal of Heat and Mass Transfer, 2016, 100: 347-354. DOI:10.1016/j.ijheatmasstransfer.2016.05.003 |



