串联型机器人以工作效率高、重复定位精度高等优点在工业领域中被广泛运用,诸如搬运、焊接、装配和喷涂.在实际加工中,由于制造、装配及长时间机械磨损等原因造成机械本体产生误差,主要包括连杆尺寸变化和关节间隙,由此引起机器人末端的实际轨迹与理想路径之间的偏差,加剧关节冲击甚至引起运动失效[1-5].在机器人的运动过程中,考虑机器人自身的本体误差,机器人的实际末端位置满足定位精度要求的概率称为可靠性[6].
针对上述问题,宋月娥等[7]假设关节间隙随机性满足某种分布,利用概率论建立机器人末端点位置误差的概率密度函数,通过积分得到累计分布函数,从而计算机器人运动可靠性,不足之处在于没有考虑连杆尺寸的偏差影响.Rao等[6]利用Monte Carlo模拟(Monte Carlo simulations, MCS),研究机器人末端位置满足一定精度要求下连杆尺寸偏差和关节间隙的优化方法,解决了机器人本体的设计问题,但是需要处理大量的数据并且计算效率低.Kim等[8]通过一阶可靠性方法(the first order reliability method, FORM)研究六自由度串联型机器人的本体误差对末端位姿精度的影响,通过假设所有的连杆尺寸偏差和关节间隙组成的随机变量满足正态分布,分别建立末端位置和姿态的6个功能函数,得到机器人系统的可靠性指标.Wang等[9]基于多维度混合抑制方法,对运动系统位置误差的均值和方差进行估计,建立正态分布模型,该方法主要应用在曲柄滑块结构.
针对目前常用方法计算效率低,且计算精度有限的不足,本文考虑机器人本体误差对运动稳定性和可靠性的影响,建立含本体误差的机器人运动学模型,研究离散点的位置误差极值分布与整个路径可靠性之间的关系.将路径点位置误差极值作为随机变量,得到机器人系统的功能函数,利用四阶矩估计法(the fourth-moment reliability method, FMRM)计算机器人运动的可靠性.
1 机器人建模 1.1 运动学针对6自由度串联型机器人,采用Denavit-Hartenberg(D-H)方法对如图 1所示的PUMA560型机器人建立运动学模型.
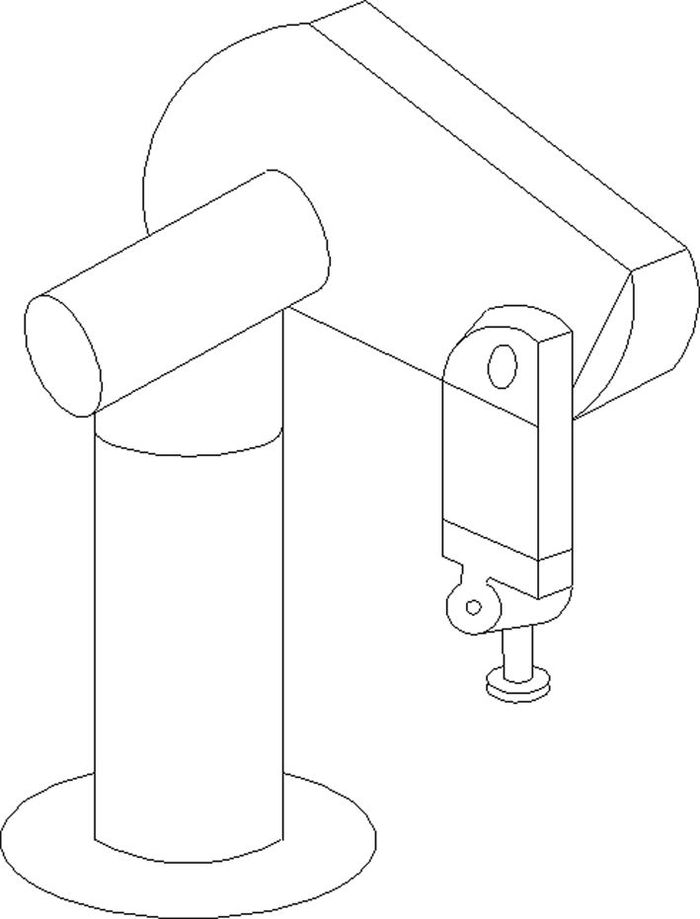
|
图 1 PUMA560机器人 Fig. 1 PUMA560 robot |
任意相邻连杆之间的位置可以通过一个4×4矩阵描述[10]:
| $ A_i^{i - 1} = \left[ {\begin{array}{*{20}{c}} {{\rm{C}}{\theta _i}}&{ - {\rm{S}}{\theta _i}{\rm{C}}{\alpha _i}}&{{\rm{S}}{\theta _i}{\rm{S}}{\alpha _i}}&{{a_i}{\rm{C}}{\theta _i}}\\ {{\rm{S}}{\theta _i}}&{{\rm{C}}{\theta _i}{\rm{C}}{\alpha _i}}&{ - {\rm{C}}{\theta _i}{\rm{S}}{\alpha _i}}&{{a_i}{\rm{S}}{\theta _i}}\\ 0&{{\rm{S}}{\alpha _i}}&{{\rm{C}}{\alpha _i}}&{{d_i}}\\ 0&0&0&1 \end{array}} \right]. $ | (1) |
式中:C为cos, S为sin, ai为连杆长度, di为连杆偏矩, αi为连杆扭转角, θi为关节角.
如图 2所示,其中将局部坐标系oi-1-xi-1yi-1zi-1绕zi-1轴旋转θi使得xi-1与xi轴平行,并沿zi-1轴平移di得到坐标oi′-xi′yi′zi′,zi′与zi之间的公垂线距离为ai,夹角为αi.
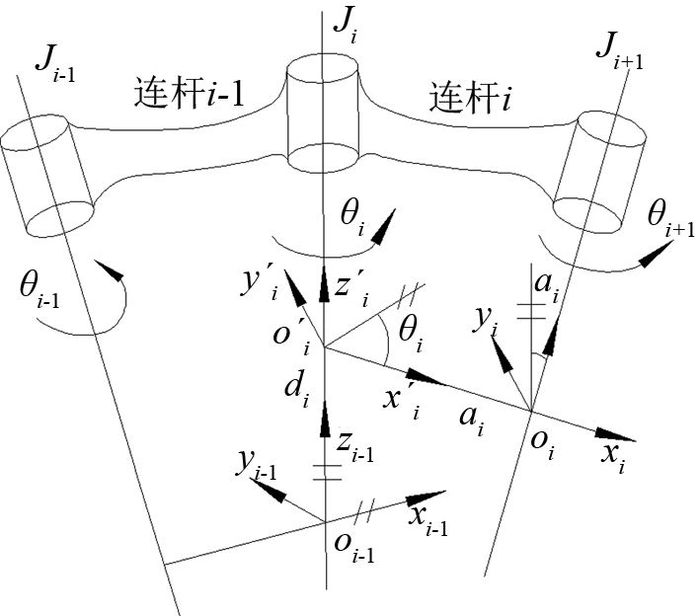
|
图 2 连杆坐标系 Fig. 2 Link coordinate of robot |
根据D-H建模方法,可以建立PUMA560型机器人的连杆坐标系如图 3所示,相应的D-H参数如表 1所示.
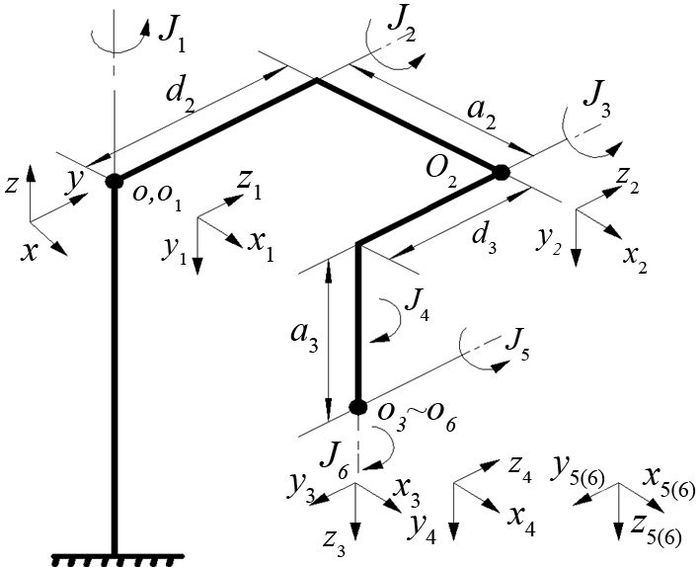
|
图 3 运动学模型 Fig. 3 Kinematic model of robot |
| 表 1 机器人D-H参数 Table 1 D-H parameters of robot |
通过机器人的连杆坐标系可以得到末端点在基座标系中的位姿矩阵:
| $ A_n^0 = \prod\limits_{i = 1}^n {A_i^{i - 1}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{R}}&\mathit{\boldsymbol{P}}\\ 0&1 \end{array}} \right]. $ | (2) |
式中:R为机器人末端法兰盘中心在基座标系中的姿态矩阵;P为位置矢量,P=[Px, Py, Pz].
1.2 机器人本体误差分析加工、装配及磨损等原因会使得机器人的本体存在误差,主要表现为连杆尺寸偏差和关节间隙,因此机器人的上述参数可以看成是满足某种分布类型的随机变量[11], 关节转角在间隙的影响下会存在角度误差.假设关节转角θ1~θ6的误差均为均匀分布的随机变量,是[-0.1°, 0.1°],则实际转角和理论转角的关系为
| $ {\theta _i} = {{\bar \theta }_i} + {\Delta _i}. $ | (3) |
式中:θi为第i关节的理论转角,θi为第i关节的实际转角,Δi为服从均匀分布的间隙误差.
连杆长度和连杆偏距的分布类型如表 2所示.
| 表 2 随机变量概率分布类型 Table 2 Probability distributions of random variables |
多个随机变量组成的系统,其静态和动态的可靠性能取决于系统在随机变量范围内的极值分布情况.对于n维随机变量X=[x1, x2, …, xn],最大值为Xmax,则有如下结论[12]成立:
| $ {\rm{Pr}}\left\{ {\bigcap\limits_{i = 1}^n {\left( {{x_i} < k} \right)} } \right\} = \Pr \left\{ {{X_{\max }} < k} \right\}. $ | (4) |
式中:
在运动过程中,机器人末端轨迹通常离散成N个插补点,因此机器人的可靠性可以进一步分为单个插补点的可靠性和沿整个路径运动的可靠性(运动可靠性).Zhang等[10, 13]主要针对机器人的单个路径点可靠性进行研究,采用的方法包括一阶可靠性方法和直接线性法等.
定义机器人在第i个插补点的位置误差为
| $ {\varepsilon _i} = \left\| {{{\mathit{\boldsymbol{P'}}}_i} - {\mathit{\boldsymbol{P}}_i}} \right\|. $ | (5) |
向量Pi=[Pxi, Pyi, Pzi]为机器人末端的理论位置坐标, 向量Pi′=[Pxi′, Pyi′, Pzi′]为实际位置坐标.
给定末端点的位置精度或误差边界为hf,以(Pxi, Pyi, Pzi)为圆心,hf为半径的球形区域构成该点的可靠区域,内部的点为可靠点,外部的点为失效点,实际位置(Pxi′, Pyi′, Pzi′)落在球形区域内部的概率称为单个路径点的可靠性,具体示意图如图 4所示.

|
图 4 单个路径点的可靠性 Fig. 4 Reliability at point in trajectory |
实际中,机器人的任务路径常由一系列复杂轨迹组成,如沿着工件表面喷涂、焊接等,机器人满足某一个局部点的精度要求并不能实现整个加工过程,因此研究机器人在整个路径中的可靠性具有更重要的实际价值.定义机器人的有效路径如下:所有插补点均满足精度hf要求的路径,反之则为失效路径,如图 5所示.
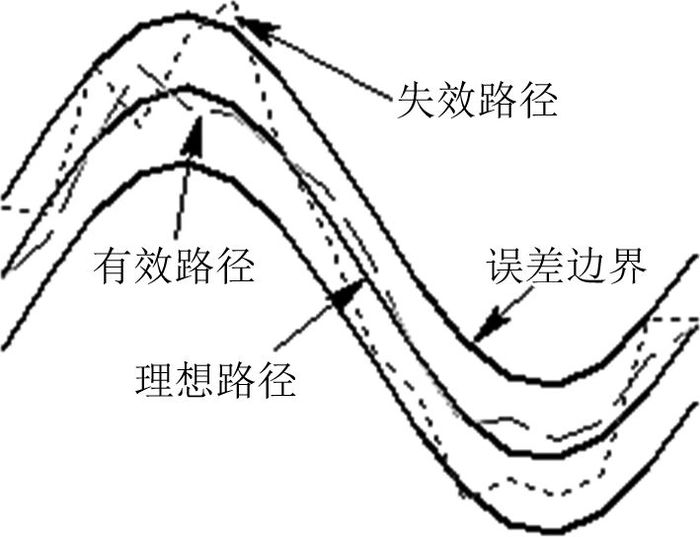
|
图 5 机器人末端运动路径 Fig. 5 Trajectory of manipulators' end-effector |
机器人的运动可靠性为
| $ P_{\rm{r}}^{\rm{s}} = \Pr \left\{ {\bigcap\limits_{i = 1}^N {\left( {{\varepsilon _i} < {h_{\rm{f}}}} \right)} } \right\}. $ | (6) |
机器人的运动失效概率为
| $ P_{\rm{f}}^{\rm{s}} = 1 - P_{\rm{r}}^{\rm{s}}. $ | (7) |
定义变量γ表示路径中所有插补点位置误差的最大值:
| $ \gamma = {\rm{max}}\left\{ {{\varepsilon _1},{\varepsilon _2}, \cdots ,{\varepsilon _N}} \right\}. $ | (8) |
定义机器人系统的功能函数:
| $ Z = g\left( \gamma \right) = {h_{\rm{f}}} - \gamma . $ | (9) |
机器人运动的失效概率进一步转换成如下表达式:
| $ P_{\rm{f}}^{\rm{s}} = \Pr \left\{ {Z \le 0} \right\}. $ | (10) |
求取机器人的可靠性问题等价于求取系统功能函数Z的概率密度函数.机器人的实际轨迹为有效路径的前提是每一个插补点的位置误差均在精度范围之内.系统的极值分布与可靠性之间的关系表明,机器人的运动可靠性仅取决于所有离散点中位置误差最大的插补点满足精度要求的概率,因此可以将整个路径所有插补点的计算进一步转换成对位置误差最大的单个点的研究.
3 矩估计方法 3.1 一阶可靠性法及一次二阶矩法对于n维随机变量X=[x1, x2, …, xn]组成的系统,结构的功能函数为Z=g(X).传统的一阶可靠性方法以基本随机变量的概率分布为基础,利用随机变量的一阶矩(均值)和二阶矩(方差)对功能函数的均值及方差进行估计.通过一阶可靠性方法计算系统的可靠性等价为如下约束优化问题[8]:
| $ \left. {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {\min }\\ {{\rm{s}}{\rm{.}}\;{\rm{t}}{\rm{.}}} \end{array}}&{\begin{array}{*{20}{c}} {\beta = {{\left( {{\mathit{\boldsymbol{U}}^{\rm{T}}}\mathit{\boldsymbol{U}}} \right)}^{1/2}},}\\ {g\left( \mathit{\boldsymbol{X}} \right) = 0.} \end{array}} \end{array}} \right\} $ | (11) |
式中:U为随机变量X通过变换后的标准随机变量,β为可靠性指标.
机器人的运动失效概率为
| $ P_{\rm{f}}^{\rm{s}} = \phi \left( { - \beta } \right). $ | (12) |
式中:φ(*)为标准正态累计分布函数.
一次二阶矩法(the first-order second-moment method, FOSM)主要通过将功能函数在系统参数的均值点μX进行一阶泰勒级数展开:
| $ Z = g\left( {{\mu _X}} \right) + \sum\limits_{i = 1}^n {{g_i}\left( {{x_i} - {\mu _i}} \right)} . $ | (13) |
式中:gi=∂g(μi)/∂Xi.利用式(13)求解出系统的均值μZ及方差σZ,结合可靠性指标定义:
| $ \beta = {\mu _Z}/{\sigma _Z}. $ | (14) |
利用式(13)可以获得系统的失效概率[9].
3.2 四阶矩估计传统的方法忽略了随机变量的其他统计特征,例如包括描述随机变量概率密度函数陡峭程度的峰度信息和反映概率密度函数对称特性的偏度信息.对于诸如原子能反应堆、航空航天结构以及机器人运动控制等高可靠性指标问题,概率密度函数曲线的尾部形状对计算结果的精度具有重要影响[14-15].
一阶可靠性方法及一次二阶矩法的计算过程简洁,但精度有限,主要运用在对计算精度要求不高的工程领域,原因如下.基于一阶可靠性分析法或一次二阶矩法均需要以系统的输出结果严格满足正态分布为前提(假设偏差),若系统存在高度非线性或不满足正态分布假设,则计算结果将出现较大偏差,甚至失效[6, 8-9].高于四阶的矩估计需要基于Pearson系统进行描述,计算过程复杂,难以满足实际运用.本文采用四阶矩估计法,在保证算法效率的前提下,可以得到较高的计算精度,不会大幅度增加计算的复杂程度.
四阶矩估计法主要是通过求取基本随机变量的前四阶矩,利用该方法进一步获得系统功能函数的前四阶矩,计算系统的可靠性.四阶矩估计不仅包括了随机变量的均值和方差,而且考虑了峰度和偏度的统计信息,因此可以得到更加准确的概率密度函数方程,能够避免传统方法的假设偏差(假设系统输出严格服从正态分布),最终提高计算精度.
定义随机变量x的前四阶原点矩为
| $ {\upsilon _{Xi}} = E\left( {{x^i}} \right) = \int\limits_X {{x^i}{f_X}\left( x \right){\rm{d}}x} . $ | (15) |
式中:E为期望,fX(x)为概率密度函数, i=0, 1, …, 4,当i=1时,υX1为均值.
定义随机变量x的前四阶中心矩为
| $ {\mu _{Xi}} = E\left\{ {{{\left( {x - {\mu _X}} \right)}^i}} \right\} = \int\limits_X {{{\left( {x - {\mu _X}} \right)}^i}{f_X}\left( x \right){\rm{d}}x} . $ | (16) |
式中:μX=υX1为均值,i=0, 1, …, 4,当i=2时,μX2为方差,记为σX2.
将系统的功能函数Z=g(X)在随机变量X的均值点μX=[μX11, μX21, …, μXn1]处进行一阶泰勒级数展开.利用随机变量X的均值和前四阶矩,通过式(13)可以获得功能函数Z的均值及前四阶中心矩.
4 基于最大熵的概率分布Shannon在1948年将热力学熵的概念引入到信息研究理论中,从统计学角度对事件的不确定进行度量,对系统功能函数Z的Shannon熵定义如下:
| $ H\left[ {{f_Z}} \right] = - \int\limits_z {{f_Z}\left( z \right)\ln \left[ {{f_Z}\left( z \right)} \right]{\rm{d}}z} . $ | (17) |
式中:fZ(z)为功能函数Z的概率密度函数.
Jaynes[16]提出最大熵原理,指出:给定外在条件,针对随机变量存在多个可能的概率分布,符合已知的约束条件并使随机变量的熵取得最大值的分布是最佳概率分布.
考虑将功能函数Z的前四阶原点矩作为约束条件,使得式(17)取得最大值,可得Z的概率密度函数表达式,由此将求解过程转换为带约束条件的优化问题.通过Lagrange乘子法构造Lagrange函数如下:
| $ \begin{array}{*{20}{c}} {L = - \int_z {{f_Z}\left( z \right)\ln \left[ {{f_Z}\left( z \right)} \right]{\rm{d}}z} - }\\ {\sum\limits_{i = 0}^4 {{\lambda _i}\left[ {\int_z {{z^i}{f_Z}\left( z \right){\rm{d}}z} - {\upsilon _{Zi}}} \right]} .} \end{array} $ | (18) |
式中:i=0, 1, …, 4, λ=(λ0, λ1, …, λ4)为Lagrange系数.
为了简化计算,将随机变量Z转换成均值为0、方差为1的标准随机变量Y:
| $ Y = \frac{{Z - {\mu _Z}}}{{{\sigma _Z}}}. $ | (19) |
构造仅含λi的方程组,解出Lagrange系数λ=[λ0, λ1, …, λ4].
机器人的运动失效概率进一步表示为
| $ \begin{array}{l} P_{\rm{f}}^{\rm{s}} = \Pr \left\{ {Z \le 0} \right\} = \Pr \left\{ {Y \le \frac{{ - {\mu _Z}}}{{{\sigma _Z}}}} \right\} = \\ \int\limits_{ - \infty }^{ - {\mu _Z}/{\sigma _Z}} {\exp \left( { - \sum\limits_{i = 0}^4 {{\lambda _i}{y^i}} } \right){\rm{d}}y} . \end{array} $ | (20) |
以PUMA560机器人为模型,运用四阶矩估计法(FMRM)对机器人的运动可靠性进行计算.分别基于Monte Carlo模拟(MCS)、一阶可靠性方法(FORM)及一次二阶矩法(FOSM)进行仿真,作为对比分析.
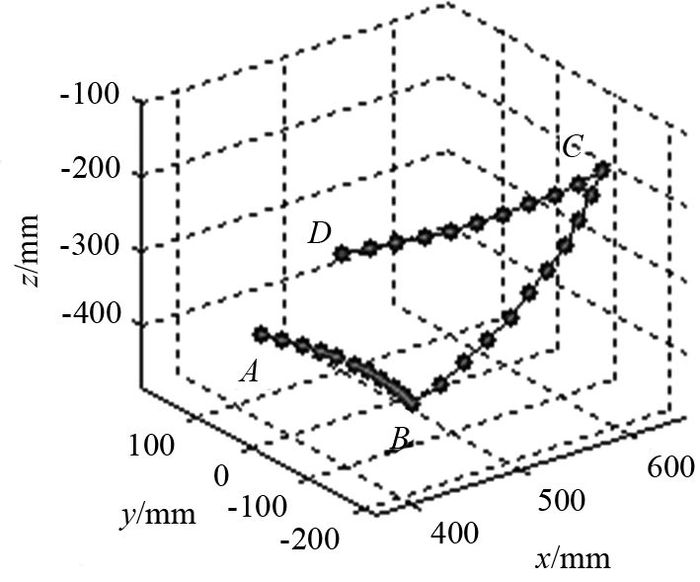
在机器人笛卡尔空间中,任意规划一条轨迹作为运动路径,控制机器人的各关节依次运动一定角度,如表 3所示.得到机器人理想的末端轨迹ABCD如图 6所示,将轨迹ABCD作为模拟运动路径.
| 表 3 关节角度变化范围 Table 3 Ranges of joint angle |
|
图 6 含关节间隙的仿真路径 Fig. 6 Trajectory of simulations with joint clearance |
Monte Carlo模拟(MCS)作为系统可靠性测量最重要的方法之一,能够在模型未知的情况下精确求解系统可靠性[6, 10].通过MCS计算机器人的运动可靠性为
| $ P_{\rm{f}}^{\rm{s}} = \frac{{{N_{\rm{f}}}}}{{{N_{\rm{t}}}}}. $ | (21) |
式中:Nt为总的模拟次数,Nf为失效的次数.
在表 2所示的连杆尺寸偏差和关节间隙的影响下,模拟机器人沿路径ABCD运动.每沿路径运动一次,可以获得一个单次路径中的位置误差最大的极值点.
模拟路径运动105次,作为MCS计算的样本.将MCS计算的结果作为标准值,模拟500次作为一阶可靠性方法(FORM)、一次二阶矩法(FOSM)及四阶矩估计法(FMRM)的样本.
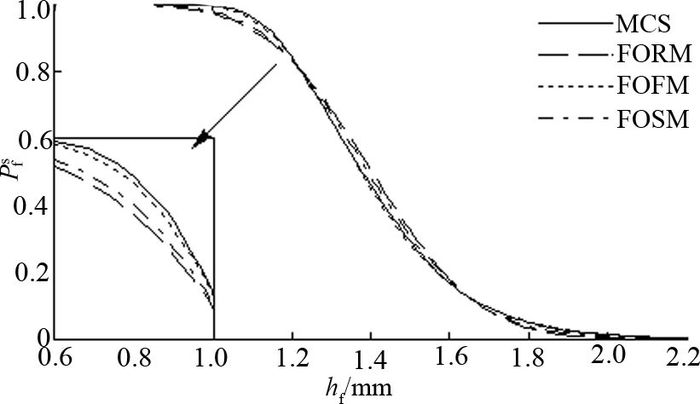
机器人的末端精度hf为0 ~ 2.2 mm,则运动的失效概率Pfs与末端位置精度hf之间的关系如图 7所示.
|
图 7 运动失效概率 Fig. 7 Probability of failure |
定义相对于MCS的估计偏差为
| $ \xi = \tilde P_{\rm{f}}^{\rm{s}} - P_{\rm{f}}^{\rm{s}}. $ | (22) |
式中:
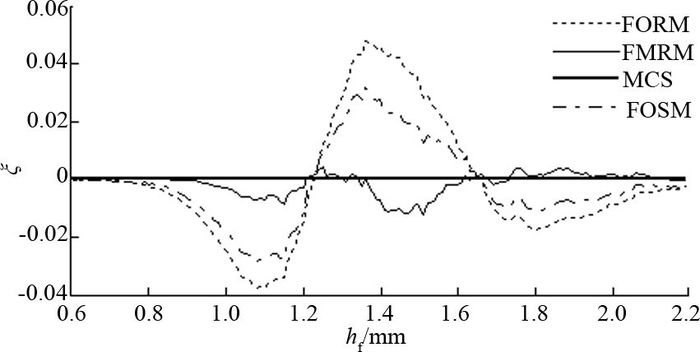
估计的偏差如图 8所示.
|
图 8 各矩估计法相对于MCS的估计偏差 Fig. 8 Estimation error of each moment estimation method relative to MCS |
从图 7、8可以看出,四阶矩估计法和MCS计算的结果非常接近,一阶可靠性方法和一次二阶矩法出现了较大的估计偏差.通过曲线的变化趋势可以看出,随着用户期望的精度降低,即hf不断增大,机器人沿目标路径运动的实际轨迹失效的概率降低.
从图 8可以得到,一阶可靠性方法的最大估计误差为0.046 3,一次二阶矩法的最大误差为0.032,四阶矩估计法的最大误差仅为0.012 0,因此提出的方法可以将结果的准确性最大提高3.0~4.0倍.
仿真采用的CPU为Intel core i5,计算主要包括采集样本和统计分析两个步骤.3种方法计算所需的时间以及各步骤占总时间的比例分别如表 4、5所示.
| 表 4 各步骤仿真时间 Table 4 Simulation time of each step |
| 表 5 各步骤仿真时间的比例 Table 5 Ratio of simulation time of each step |
表 4中,Ts为获取样本所需的时间,Tc为对样本统计分析所需的时间,Tt为总消耗时间,其中
| $ {T_{\rm{t}}} = {T_{\rm{s}}} + {T_{\rm{c}}}. $ | (23) |
表 5中,ωs为获取样本时间占总时间的比例,ωc为统计分析时间占总时间比例,
| $ {\omega _{\rm{s}}} = \frac{{{T_{\rm{s}}}}}{{{T_{\rm{t}}}}} \times 100\% , $ | (24) |
| $ {\omega _{\rm{c}}} = \frac{{{T_{\rm{c}}}}}{{{T_{\rm{t}}}}} \times 100\% . $ | (25) |
通过表 4可以看出,由于MCS方法需要基于大量的样本才能获得比较准确的计算结果,整个过程非常耗时,所需总时间最长, 效率最低.所有算法中效率最高的为一阶可靠性分析方法,两者的效率相差约150倍.
在样本采集阶段,MCS所需时间占总时间的比例远高于其他3种基于矩估计的统计方法,主要在于仿真样本规模较大,需要采集105次,其他方法仅需500次.
在样本分析阶段,MCS无需对样本进行各阶矩的信息分析,因而计算时间非常短.基于矩估计的方法需要通过对样本进行分析,提取反映随机变量统计特性的各阶矩信息,进而推测出随机变量的内在分布规律.其中一阶可靠性法及一次二阶矩法主要利用了均值(一阶矩)和方差(二阶矩),一次二阶矩法在分析过程中需要对功能函数进行泰勒展开,求一阶偏导数,因此比一阶可靠性法的用时稍长.一阶可靠性法多适用于结构简单的线性系统,针对复杂的机器人系统,计算精度最低; 一次二阶矩采用泰勒级数展开,一定程度上可以增加功能函数的非线性程度,减少降维带来的误差,结果比一阶可靠性法更准确,但是由于仅考虑了随机变量的前两阶矩,估计结果会存在较多的偏差,精度低于四阶矩估计法.四阶矩估计进一步计算了偏度(三阶矩)及峰度(四阶矩),计算精度最高,同时四阶矩估计方法在样本分析阶段所需的时间最多,所占的时间比例最高.此外,基于样本的进一步统计分析是矩估计方法可以在保证精度的前提下,有效减小所需的样本规模的根本原因.
基于四阶矩估计法求解得到的Lagrange系数λ=[λ0, λ1, …, λ4]分别为:[0.020 67, 0.165 11, 0.523 18, -0.430 76, 0.890 07].
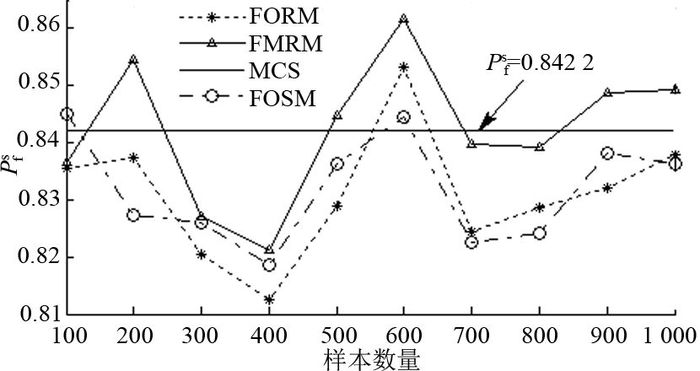
矩估计方法是基于一定数量样本进行的计算分析,因此样本的规模对矩估计方法的计算结果存在影响.考虑当末端位置精度hf=1.2 mm时,将样本数量从100变化到1 000,分别利用一阶可靠性方法、一次二阶距法及四阶矩估计法进行计算,将MCS计算的失效概率0.842 2作为标准值, 则样本数量对计算结果的影响如图 9所示.
|
图 9 样本数量对结果的影响 Fig. 9 Effect of sample size to results |
从图 9可以看出,随着样本数量的增加,三者的结果都逐渐接近标准值.在较小的样本数量下,四阶矩估计法比一阶可靠性方法及一次二阶距法计算的结果更加准确,估计的偏差更小.
6 结论(1) 在一定的轨迹精度要求下,机器人运动的可靠性主要取决于路径中位置误差最大的插补点的可靠性.
(2) 基于大量的样本,MCS能够获得比较准确的结果,精度最高,但效率最低.四阶矩估计法的效率接近于一阶可靠性法和一次二阶距法,但仅需较少的样本,同时计算精度较高,在综合考虑效率及精度的情况下,四阶矩估计方法具有较明显的优势.
(3) 传统的一阶可靠性法和一次二阶距法主要针对结构简单并且输出满足正态分布的系统;四阶矩估计方法可以适用于任意分布类型的系统,能够避免传统估计方法中的假设偏差,进一步拓展应用的领域.
| [1] |
LAI X, HE H, LAI Q, et al. Computational prediction and experimental validation of revolute joint clearance wear in the low-velocity planar mechanism[J]. Mechanical Systems and Signal Processing, 2017, 85(5): 963-976. |
| [2] |
LIAN B, SUN T, SONG Y. Parameter sensitivity analysis of a 5-DoF parallel manipulator[J]. Robotics and Computer-Integrated Manufacturing, 2017, 46(14): 1-14. |
| [3] |
LI Y, CHEN G, SUN D, et al. Dynamic analysis and optimization design of a planar slider-crank mechanism with flexible components and two clearance joints[J]. Mechanism and Machine Theory, 2016, 99(10): 37-57. |
| [4] |
GENG X, WANG X, WANG L, et al. Non-probabilistic time-dependent kinematic reliability assessment for function generation mechanisms with joint clearances[J]. Mechanism and Machine Theory, 2016, 104(6): 202-221. |
| [5] |
ERKAYA S. Investigation of joint clearance effects on welding robot manipulators[J]. Robotics and Computer-Integrated Manufacturing, 2012, 28(4): 449-457. DOI:10.1016/j.rcim.2012.02.001 |
| [6] |
RAO S S, BHATTI P K. Probabilistic approach to manipulator kinematics and dynamics[J]. Reliability Engineering and System Safety, 2001, 72(1): 47-58. DOI:10.1016/S0951-8320(00)00106-X |
| [7] |
宋月娥, 吴林, 戴明. 机器人关节间隙误差分析[J]. 机械工程学报, 2003, 39(4): 11-14. SONG Yue-e, WU Lin, DAI Ming. Error analysis of robot joint clearance[J]. Chinese Journal of Mechanical Engineering, 2003, 39(4): 11-14. |
| [8] |
KIM J, SONG W, KANG B. Stochastic approach to kinematic reliability of open-loop mechanism with dimensional tolerance[J]. Applied Mathematical Modelling, 2010, 34(5): 1225-1237. DOI:10.1016/j.apm.2009.08.009 |
| [9] |
WANG J, ZANG J, DU X. Hybrid dimension reduction for mechanism reliability analysis with random joint clearances[J]. Mechanism and Machine Theory, 2011, 46(10): 1396-1410. DOI:10.1016/j.mechmachtheory.2011.05.008 |
| [10] |
HAFEZIPOUR M, KHODAYGAN S. An uncertainty analysis method for error reduction in end-effector of spatial robots with joint clearances and link dimension deviations[J]. International Journal of Computer Integrated Manufacturing, 2016, 30(8): 1-11. |
| [11] |
BOWLING A P, RENUAD J E, NEWKIRK J T, et al. Reliability-based design optimization of robotic system dynamic performance[J]. IEEE/RSJ International Conference on Intelligence, 2007, 129(4): 3611-3617. |
| [12] |
LI J, CHEN J, FAN W. The equivalent extreme-value event and evaluation of the structural system reliability[J]. Structural Safety, 2007, 29(2): 112-131. DOI:10.1016/j.strusafe.2006.03.002 |
| [13] |
ZHANG Z, XU L, FLORES P, et al. A Kriging model for dynamics of mechanical systems with revolute joint clearances[J]. Journal of Computational and Nonlinear Dynamics, 2014, 9(3): 1-13. |
| [14] |
王锋, 陈凯, 陈小平. 一种含间隙机械臂的在线校准方法[J]. 机器人, 2013, 35(5): 521-526. WANG Feng, CHEN Kai, CHEN Xiao-ping. An online calibration method for manipulator with joint clearance[J]. Robot, 2013, 35(5): 521-526. |
| [15] |
李云贵, 赵国藩. 结构可靠度的四阶矩分析法[J]. 大连理工大学学报, 1992, 18(4): 455-459. LI Yun-gui, ZHAO Guo-fan. Reliability analysis of structures based on maximum entropy theory[J]. Journal of Dalian University of Technology, 1992, 18(4): 455-459. |
| [16] |
JAYNES E T. Information theory and statistical mechanics[J]. Physical Review, 1957, 106(4): 171-190. |



