微纳卫星具有体积小、重量轻、研制周期短、成本低等优点, 在军事和民用领域均可广泛应用, 成为近年来的研究热点[1-2].随着任务需求的提高, 微纳卫星的结构与功能愈加复杂, 也为姿态控制系统的设计带来新的挑战.一方面, 卫星任务对姿态控制精度的要求更为严苛;另一方面, 星上高密度集成多组载荷及平台分系统导致剩磁环境复杂, 不同工作模式下剩磁波动数量级大, 对姿态控制精度产生不利影响.
卫星剩磁由材料剩磁、感磁、电流系统所产生的磁场共同叠加形成[3].受剩磁影响, 磁强计不能准确测量地磁场信息, 影响姿态确定精度.整星剩磁与地磁场相互作用产生剩磁距, 对姿态控制产生干扰[4].
针对剩磁对微纳卫星姿态控制系统的负面影响, 传统的地面手段主要有2种:消磁和地面标定[5].消磁是在整星结构布局时充分考虑各分系统的电磁特性, 通过合理布局布线、后期静态磁场补偿, 尽量减小整星剩磁[3].这种方法操作复杂, 且消除剩磁的程度有限.以整星剩磁地面标定结果为参考, 在轨通过软件进行剩磁补偿在工程中也十分常用.但由于卫星在轨与地面标定存在环境差异, 卫星实际剩磁数值发生变化, 补偿效果并不理想.
剩磁在轨标定技术作为一种提高姿态控制精度的有效手段, 近年来受到研究人员的关注.目前已发表的研究成果大部分集中在对固定剩磁偏差或剩磁距的在轨估计方面, 主要依据地磁场模型计算值标定磁强计偏置[5-9], 或将卫星姿态动力学模型引入系统状态方程中标定整星剩磁矩[7, 10-13].文献[6]实现了磁强计固定偏置、刻度因子、非正交矩阵以及MEMS陀螺漂移的同时在轨标定, 计算效率高.文献[11]基于磁测结合磁控和偏置动量控制的方案, 提出了一种在单磁强计条件下完成剩磁距的在轨辨识、利用磁力距器实现剩磁距主动补偿的新方法.该方法所需器件少, 不依赖地面辅助, 主动补偿效果良好.但上述研究均未考虑多系统多任务模式切换所带来的动态剩磁影响, 难以满足实际执行复杂任务时期的姿态测量精度要求.
本文提出一种结合卫星各分系统切换过程中剩磁变化的地面标定数据, 基于太阳敏感器、陀螺、磁强计的采样信息和卫星姿态运动学模型, 采用EKF算法实现姿态四元数、陀螺漂移和磁强计偏置同时在轨标定的方法.针对剩磁波动造成的模型失真问题, 系统噪声协方差阵采用变参数设计, 并以地面标定结果的数量级为参数选取依据, 有效改善了标定算法的动态跟踪性能, 提高了卫星的定姿精度.
1 卫星剩磁分析及建模卫星剩磁来自于各部件的剩磁、感磁及环电流, 与各部件的空间分布相关[3].将每个部件剩磁都简化为分布于卫星的各处的偶极子模型[10, 14], 则整星剩磁造成磁强计的测量偏差为各部件剩磁干扰量的叠加:
| $ {\mathit{\boldsymbol{B}}_{\rm{m}}} = \sum\limits_{i = 1}^n {\left( {\frac{{{\mu _0}}}{{4{\rm{ \mathsf{ π} }}l_i^3}}{\mathit{\boldsymbol{m}}_i}} \right)} . $ | (1) |
式中:μ0为真空磁导率, n为部件总数, li为部件i的磁偶极子中心到磁强计距离, mi为部件i的剩磁距.
当卫星各项设备工作状态稳定时, 可将卫星剩磁距视为常量;但星载设备众多, 受部件开关机状态影响, 卫星剩磁数值在不同工作模式下不尽相同;此外, 不同工况和外部磁场条件下, 星上感磁材料也会产生不可预估的磁干扰.
由式(1)可得, Bm与剩磁本身呈正相关, 整星剩磁造成磁强计偏差的模型可进一步简化为
| $ {\mathit{\boldsymbol{B}}_{\rm{m}}} = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{b}}_{{\rm{m1}}}},}\\ {{\mathit{\boldsymbol{b}}_{{\rm{m2}}}},}\\ {{\mathit{\boldsymbol{b}}_{{\rm{m3}}}},}\\ \vdots \\ {{\mathit{\boldsymbol{b}}_{{\rm{mn}}}},} \end{array}}&{\begin{array}{*{20}{c}} {工作模式1;}\\ {工作模式2;}\\ {工作模式3;}\\ \vdots \\ {工作模式\;n.} \end{array}} \end{array}} \right. $ | (2) |
式中:bmj(j=1, 2, …, n)为定值.
由于微纳卫星体积小、功能密度集中, 整星剩磁环境复杂, 不同工作模式磁强计剩磁偏置的差值可达几十nT到几千nT不等, 由于近地轨道的地磁感应强度仅有104nT量级, 可见剩磁波动对地磁场测量的影响严重.
以浙江大学皮星二号卫星为例, 地面标定结果显示最小工况下磁强计剩磁偏置为[8 237, -2 781, -12 896]nT, 其他工况如表 1所示.表 1中, Δbm为磁强计剩磁偏置的增量.由表 1可得, 卫星工作状态切换造成剩磁偏置的变量最小为10nT左右, 最大达到4 000nT左右.该卫星在轨运行时磁强计的部分采样数据如图 1所示, 图中Bx、By、Bz分别为磁强计的三轴采样数据, t为时间.图 1显示了载荷试验带来的剩磁波动使磁强计三轴采样值分别跳跃1 800nT、1 300nT、1 100nT, 对地磁场测量产生显著干扰.
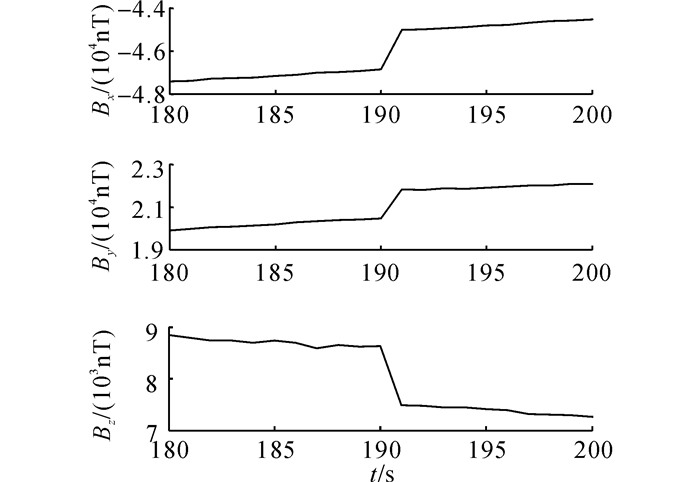
|
图 1 浙江大学皮星二号磁强计在轨采样数据 Fig. 1 On-orbit sampled data of magnetometer on ZDPS-2 |
| 表 1 浙江大学皮星二号磁强计剩磁偏置地面标定结果 Table 1 Ground calibration data of magnetometer bias from residual magnetism on ZDPS-2 |
基于微纳卫星常用的磁强计、太阳敏感器和MEMS陀螺的姿态测量系统配置方案, 变参数EKF快速跟踪算法采用磁强计和太阳敏感器的测量信息, 同时估计姿态四元数、陀螺漂移和磁强计偏置的在轨数值, 并针对剩磁波动进行系统参数优化.
由卫星姿态运动学方程和陀螺测量模型[15-16], 得到姿态误差四元数导数的线性化方程:
| $ \Delta {{\mathit{\boldsymbol{\dot {\tilde q}}}}_{{\rm{bi}}}} = - \left[ {{{\mathit{\boldsymbol{\hat \omega }}}_{{\rm{bi\_b}}}} \times } \right]\Delta {{\mathit{\boldsymbol{\tilde q}}}_{{\rm{bi}}}} - \frac{1}{2}\Delta {\mathit{\boldsymbol{b}}_g} - \frac{1}{2}{\mathit{\boldsymbol{v}}_{\rm{g}}}. $ | (3) |
式中:
考虑陀螺和磁强计的测量模型:
| $ \Delta {{\mathit{\boldsymbol{\dot b}}}_g} = {\mathit{\boldsymbol{v}}_{\rm{u}}},\Delta {{\mathit{\boldsymbol{\dot b}}}_{\rm{m}}} = {\bf{0}}. $ | (4) |
式中:bg为陀螺漂移, vu为陀螺角速度随机游走白噪声, bm为整星静态剩磁引入的磁强计偏置.式(3)~(4)组合成系统状态方程.
用太阳敏感器和磁强计的测量结果组建误差量测方程:
| $ \Delta {\mathit{\boldsymbol{B}}_{\rm{b}}} = {\mathit{\boldsymbol{B}}_{\rm{b}}} - \mathit{\boldsymbol{A}}\left( {{\mathit{\boldsymbol{q}}_{{\rm{bi}}}}} \right) \cdot {\mathit{\boldsymbol{B}}_i} = 2\left[ {{{\mathit{\boldsymbol{\hat B}}}_{\rm{b}}} \times } \right]\Delta {{\mathit{\boldsymbol{\tilde q}}}_{{\rm{bi}}}} + \Delta {\mathit{\boldsymbol{b}}_{\rm{m}}} + {\mathit{\boldsymbol{v}}_{\rm{b}}}, $ | (5) |
| $ \Delta {\mathit{\boldsymbol{S}}_{\rm{b}}} = {\mathit{\boldsymbol{S}}_{\rm{b}}} - \mathit{\boldsymbol{A}}\left( {{\mathit{\boldsymbol{q}}_{{\rm{bi}}}}} \right) \cdot {\mathit{\boldsymbol{S}}_i} = 2\left[ {{{\mathit{\boldsymbol{\hat S}}}_{\rm{b}}} \times } \right]\Delta {{\mathit{\boldsymbol{\tilde q}}}_{{\rm{bi}}}} + {\mathit{\boldsymbol{v}}_{\rm{s}}}. $ | (6) |
式中:A(qbi)为惯性坐标系到本体坐标系的姿态矩阵, Bb为磁强计测量结果在本体坐标系下的矢量, Bi为惯性坐标系下的地磁场矢量,
系统状态变量为
| $ \Delta \mathit{\boldsymbol{x}} = {\left[ {\begin{array}{*{20}{c}} {\Delta {{\mathit{\boldsymbol{\dot {\tilde q}}}}_{{\rm{bi}}}}}&{\Delta \mathit{\boldsymbol{b}}_{\rm{g}}^{\rm{T}}}&{\Delta \mathit{\boldsymbol{b}}_{\rm{m}}^{\rm{T}}} \end{array}} \right]^{\rm{T}}}, $ |
测量变量为
| $ \Delta \mathit{\boldsymbol{y}} = {\left[ {\begin{array}{*{20}{c}} {\Delta \mathit{\boldsymbol{B}}_{\rm{b}}^{\rm{T}}}&{\Delta \mathit{\boldsymbol{S}}_{\rm{b}}^{\rm{T}}} \end{array}} \right]^{\rm{T}}}, $ |
对应的EKF滤波器的模型为
| $ \Delta \mathit{\boldsymbol{\dot x}}\left( t \right) = \mathit{\boldsymbol{F}}\left( t \right)\Delta \mathit{\boldsymbol{x}}\left( t \right) + \mathit{\boldsymbol{G}}\left( t \right)\mathit{\boldsymbol{W}}. $ | (7) |
| $ \Delta \mathit{\boldsymbol{y}}\left( t \right) = \mathit{\boldsymbol{H}}\left( t \right)\Delta \mathit{\boldsymbol{x}}\left( t \right) + \mathit{\boldsymbol{V}}. $ | (8) |
将系统状态方程和测量方程带入上述模型, 并参照更新计算公式(9)~(13)[17], 即可进行EKF滤波计算(该组公式中, 下标“k+1|k”表示由第k时刻得到的第k+1时刻预测值, 下标“k|k”表示第k时刻的更新值).
1) 状态预测:
| $ \Delta {{\mathit{\boldsymbol{\hat x}}}_{k + 1\left| k \right.}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_k}\Delta {{\mathit{\boldsymbol{\hat x}}}_{k\left| k \right.}}. $ | (9) |
式中:Φk=I9×9+F(t)T, T为递推时间间隔, I9×9为9×9的单位矩阵.
2) 误差协方差阵预测:
| $ {\mathit{\boldsymbol{P}}_{k + 1\left| k \right.}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_k}{\mathit{\boldsymbol{P}}_{k\left| k \right.}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_k^{\rm{T}} + {\mathit{\boldsymbol{G}}_k}{\mathit{\boldsymbol{Q}}_k}\mathit{\boldsymbol{G}}_k^{\rm{T}}. $ | (10) |
式中:
| $ {\mathit{\boldsymbol{Q}}_k} = {\left[ {\begin{array}{*{20}{c}} {\sigma _{\rm{g}}^2{\mathit{\boldsymbol{I}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}\\ {{{\bf{0}}_{3 \times 3}}}&{\sigma _{\rm{u}}^2{\mathit{\boldsymbol{I}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}\\ {{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{\sigma _{{\rm{bias}}}^2{\mathit{\boldsymbol{I}}_{3 \times 3}}} \end{array}} \right]_{9 \times 9}}, $ |
为W协方差阵;σg2为陀螺角度随机游走白噪声方差;σu2为陀螺角速度随机游走白噪声方差;σbias为引入剩磁偏置的估计误差, 方便滤波器调整参数.
3) 卡尔曼增益矩阵计算:
| $ {\mathit{\boldsymbol{K}}_{k + 1}} = {\mathit{\boldsymbol{P}}_{k + 1\left| k \right.}}\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}}{\left( {{\mathit{\boldsymbol{K}}_{k + 1}}{\mathit{\boldsymbol{P}}_{k + 1\left| k \right.}}\mathit{\boldsymbol{H}}_{k + 1}^{\rm{T}} + {\mathit{\boldsymbol{R}}_{k + 1}}} \right)^{ - 1}}. $ | (11) |
式中:
| $ {\mathit{\boldsymbol{R}}_{k + 1}} = {\left[ {\begin{array}{*{20}{c}} {\sigma _{\rm{b}}^2{\mathit{\boldsymbol{I}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}\\ {{{\bf{0}}_{3 \times 3}}}&{\sigma _{\rm{s}}^2{\mathit{\boldsymbol{I}}_{3 \times 3}}} \end{array}} \right]_{6 \times 6}}, $ |
为V协方差阵;σb2和σs2分别为磁强计与太阳敏感器测量噪声方差.
4) 状态估计值更新:
| $ \Delta {{\mathit{\boldsymbol{\hat x}}}_{k + 1\left| {k + 1} \right.}} = {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_k}\Delta {{\mathit{\boldsymbol{\hat x}}}_k} + {\mathit{\boldsymbol{K}}_{k + 1}}\left[ {\Delta {\mathit{\boldsymbol{y}}_{k + 1}} - {\mathit{\boldsymbol{K}}_{k + 1}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_k}\Delta {{\mathit{\boldsymbol{\hat x}}}_{k\left| k \right.}}} \right]. $ | (12) |
5) 误差协方差阵更新:
| $ {\mathit{\boldsymbol{P}}_{k + 1\left| {k + 1} \right.}} = \left( {\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_{k + 1}}{\mathit{\boldsymbol{H}}_{k + 1}}} \right){\mathit{\boldsymbol{P}}_{k + 1\left| k \right.}}. $ | (13) |
在EKF更新计算公式中, Q是系统噪声矩阵, 其数值大小决定了该时刻的滤波结果中, 递推结果所占比重[18].针对于磁强计剩磁偏置的估计过程, σbias数值越小, 系统模型递推在滤波算法中的置信度越高.
在稳定工作状态下, 剩磁造成的磁偏波动不大, 系统方程中
为此, 本文在定常滤波法的基础上采用变参数设计, 在卫星工作模式切换时增大σbias数值, 针对剩磁波动减少系统模型递推结果的影响, 提高敏感器量测信息在滤波估计中的比重, 兼顾算法的估计精度和快速跟踪性能.
在工程实际应用中, 卫星在轨剩磁变化的确切数据未知, 且工况众多, 为每个工况选取σbias参数难度较大.本文按照磁强计剩磁偏置增量的标定值量级将各个工况划分等级, 每个等级设置一个σbias参数, 参数值与磁偏增量正相关.稳定状态下, σbias参数使用默认值;卫星切换工况后, 通常情况下,σbias选取稳定状态下的参数值进行运算;卫星切换工况后,算法代入相应等级的σbias参数进行运算.
以浙江大学皮星二号的地面标定数据为例, 将磁强计单轴偏置最大波动值在10nT量级的工况归于等级1, 在102nT量级的工况归于等级2, 在103nT量级的工况归于等级3.选取σbias默认值为1 nT, 对该卫星各个工况进行仿真, 选取不同等级对应的σbias参数值, 具体如表 2所示.表 2中, tc为磁偏估计值的收敛时间.仿真结果显示, 工况切换条件下算法收敛时间均少于250 s.该操作方法降低了参数选取的工作量和星上代码的复杂度, 同时保证了算法的普适性和动态跟踪性能.
| 表 2 浙江大学皮星二号各工况下的仿真结果 Table 2 Simulation results of ZDPS-2 under different conditions |
基于浙江大学皮星二号的剩磁标定结果和σbias参数值设置, 每个等级选取一组工况展开仿真验证, 如表 3所示.表 3中, t0为工况开启时间, bm为磁强计剩磁偏置.
| 表 3 磁强计剩磁偏置期望值 Table 3 Expected value of magnetometer bias from residual magnetism |
卫星轨道为524 km的太阳同步轨道, 设置敏感器性能参数:陀螺角度随机游走0.03°/s1/2, 角速度随机游走0.000 1°/s3/2, 初始偏置[-0.10, -0.02, 0.20]°/s;太阳敏感器噪声1°(1σ);三轴磁强计噪声10nT(1σ).
选取系统状态初值:
| $ {x_0} = \left[ {\begin{array}{*{20}{c}} {{q_0}}\\ {{b_0}}\\ {{b_{{\rm{m}}0}}} \end{array}} \right] = {\left[ {\begin{array}{*{20}{c}} {{{\left[ {\begin{array}{*{20}{c}} 0&0&0&1 \end{array}} \right]}^{\rm{T}}}}\\ {{{\left[ {\begin{array}{*{20}{c}} 0&0&0 \end{array}} \right]}^{\rm{T}}}}\\ {{{\left[ {\begin{array}{*{20}{c}} 0&0&0 \end{array}} \right]}^{\rm{T}}}} \end{array}} \right]^{\rm{T}}}, $ |
初始误差协方差阵:
| $ {P_0} = \left[ {\begin{array}{*{20}{c}} {0.1{\mathit{\boldsymbol{I}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}\\ {{{\bf{0}}_{3 \times 3}}}&{5 \times {{10}^{ - 3}}{\mathit{\boldsymbol{I}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}\\ {{{\bf{0}}_{3 \times 3}}}&{{{\bf{0}}_{3 \times 3}}}&{5 \times {{10}^{ - 6}}{\mathit{\boldsymbol{I}}_{3 \times 3}}} \end{array}} \right]. $ |
σbias依据等级划分采用分段设计:
| $ {\sigma _{{\rm{bias}}}} = \left\{ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {1{\rm{nT}}}\\ {10{\rm{nT}}}\\ {60{\rm{nT}}}\\ {100{\rm{nT}}} \end{array}}&{\begin{array}{*{20}{c}} {稳定状态,}\\ {工况1前50{\rm{s,}}}\\ {工况2前50{\rm{s,}}}\\ {工况3前50{\rm{s}}{\rm{.}}} \end{array}} \end{array}} \right. $ |
如图 2所示为全流程仿真过程中磁强计剩磁偏置bm的标定结果.从图 2可以看出, 仿真约2 000 s后算法收敛, 剩磁偏置标定值在卫星稳定工作状态下波动不大, 在卫星切换工作状态时随之快速调整, 与预期相符.
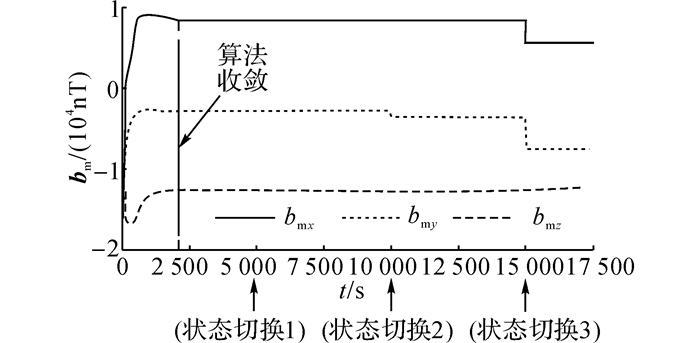
|
图 2 磁强计剩磁偏置标定结果 Fig. 2 Calibration curve of magnetometer bias fromresidual magnetism |
为对比该标定方法的有效性, 设置σbias为定值进行仿真.2种方法剩磁偏置实时标定结果在三次工作模式切换过程中的细节图分别如图 3所示.图中, 快速跟踪法标定值为本文提出的变参数动态标定算法的结果, 定常滤波法标定值为设置σbias恒为1nT的仿真计算结果;bmx、bmy、bmz分别为剩磁偏置在卫星本体坐标系下的三轴分量.从图 3可以看出, 相较于定常滤波法, 本文提出的方法在工作状态发生变化时, 磁强计剩磁偏置标定值调整更加迅速, 动态响应效果较好.

|
图 3 磁强计剩磁偏置标定结果局部放大图 Fig. 3 Calibration curve magnification of magnetometer bias resulting from residual magnetism |
定常滤波法和本文方法对磁强计动态剩磁偏置的标定结果如表 4所示.表 4中, σb为磁强计剩磁偏置的静态估计标准差.从表中可以看出, 本文方法在3种量级剩磁波动下的收敛时间均少于200 s, 相对于定常滤波法按照剩磁波动量级不同, 缩短时间从550 s到1 850 s不等.这2种算法的剩磁偏置的静态估计标准差相近, Y轴的估计标准差分别为20nT和25nT, X轴与Z轴的估计标准差均为4nT~6nT左右.这是因为剩磁偏置标准差与剩磁稳定状态下估计过程相关, 而2种算法在此过程中采用σbias值相同.此外, 由于被测地磁场的Y轴分量变化范围较小, 该轴磁偏标定过程中引入量测信息的比重较大, 造成其标定结果的稳定性更差.
| 表 4 剩磁偏置标定结果 Table 4 Calibration value of magnetometer bias resulting from residual magnetism |
这2种标定方法在剩磁波动时定姿误差的曲线如图 4所示, 具体数值如表 5所示.图 4中, ϕ为滚动角, θ为俯仰角, ψ为偏航角.表 5中, δatt为算法的静态定姿误差, δatt1、δatt2、δatt3分别为状态切换1、状态切换2、状态切换3时的算法定姿误差.从图 4可以看出, 2种方法在工作状态稳定时定姿精度相近, 但剩磁波动时, 定常滤波法的定姿误差显著增大, 且误差的幅值与剩磁波动的大小正相关.本文提出的方法在剩磁波动时, 定姿误差约为0.6°, 与静态剩磁状态下定姿精度相差不大;在百nT和千nT量级的剩磁波动下与定常滤波法相比, 定姿精度分别提高了1°和5°左右.
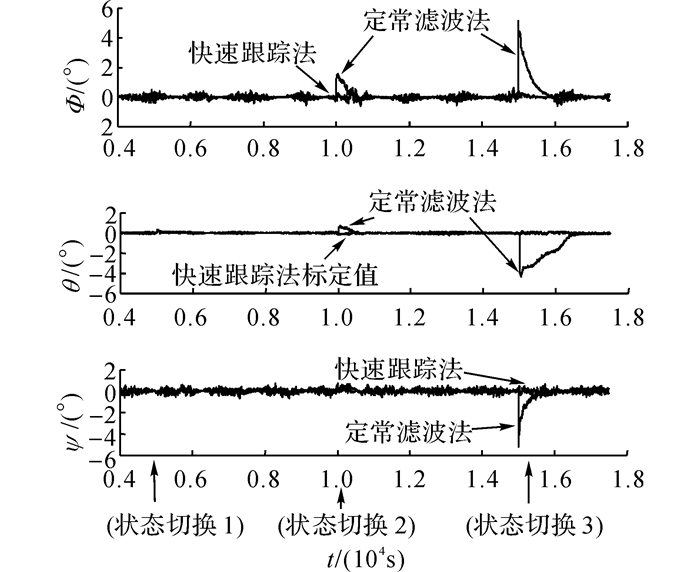
|
图 4 快速跟踪法和定常滤波法的定姿误差曲线 Fig. 4 Attitude determination error curve of fast-tracking algorithm and fixed constant filtering algorithm |
| 表 5 快速跟踪法和定常滤波法的三轴定姿误差 Table 5 Attitude determination error in three axis |
本文提出了一种结合地面剩磁标定数据、采用变参数改进EKF算法对磁强计偏置进行在轨动态标定的方法.该算法基于太阳敏感器、陀螺和磁强计的实测信息, 使用变参数设计系统噪声协方差阵, 兼顾算法的准确性和动态跟踪性能.以浙江大学皮星二号实测数据为应用背景的仿真结果表明, 该算法在剩磁波动条件下收敛时间小于250 s, 估计结果稳定性优于20nT(1σ);与定常滤波法相比, 收敛时间缩短了约1 850 s, 姿态确定精度提高了5°, 有效消除了剩磁波动对微纳卫星姿态确定的影响.本研究给出了常规工况下的参数选取依据, 对于微纳卫星波动剩磁在轨标定的工程应用具有一定的借鉴价值.
| [1] |
詹亚锋, 马正新. 现代微小卫星技术及发展趋势[J].
电子学报, 2000, 28(7): 102–106.
ZHAN Ya-feng, MA Zheng-xin. Technology of modern micro satellite and its development direction[J]. Acta Electronica Sinica, 2000, 28(7): 102–106. |
| [2] |
高彬. 小卫星技术的发展现状及其军事应用前景[J].
天津通信技术, 2003(2): 6–9.
GAO Bin. Developing actuality tactic and militaryapplication foreground of small satellite technology[J]. Tianjin Communications Technology, 2003(2): 6–9. |
| [3] |
周斌, 王劲东. 卫星磁部件分布对梯度法消除剩磁的影响分析[J].
中国空间科学技术, 2013, 33(5): 29–34.
ZHOU Bin, WANG Jin-dong. Influence of magnetic component distribution of satellite on eliminating remanant magnetic field by gradient method[J]. Chinese Space Science and Technology, 2013, 33(5): 29–34. DOI:10.3780/j.issn.1000-758X.2013.05.005 |
| [4] |
李杨, 涂歆滢. 星体剩磁矩对姿控系统影响的仿真研究[J].
系统仿真学报, 2002, 14(2): 215–218.
LI Yang, TU Xin-ying. Simulation of the remanence moment influencing on satellite attitude control system[J]. Journal of System Simulation, 2002, 14(2): 215–218. |
| [5] | HAN K, WANG H, XIANG T, et al. Magneto-meter compensation scheme and experimental results on ZDPS-1A pico-satellite[J]. Chinese Journal of Aeronautics, 2012, 25(3): 430–436. DOI:10.1016/S1000-9361(11)60407-X |
| [6] |
向甜, 王昊, 蒙涛, 等. 三轴磁强计与MEMS陀螺的在轨实时标定方法[J].
浙江大学学报:工学版, 2014, 48(3): 541–547.
XIANG Tian, WANG Hao, MENG Tao, et al. Real-time on-orbit calibration method for three-axis magnetometer and MEMS gyroscope[J]. Journal of Zhejiang University:Engineering Science, 2014, 48(3): 541–547. |
| [7] | INAMORI T, SAKO N, NAKASUKA S. Magnetic dipole moment estimation and compensation for an accurate attitude control in nano-satellite missions[J]. Acta Astronautica, 2011, 68(11): 2038–2046. |
| [8] | CRASSIDIS J I, LAI K L, HARMAN R R. Real-time attitude-independent gyro calibration from three-axis magnetometer measurements[C]//AIAA/AAS Astrodynamics Specialist Confe-rence and Exhibit. Providence:AIAA, 2004:1-11. https://arc.aiaa.org/doi/abs/10.2514/6.2004-4855 |
| [9] |
段方, 刘建业, 李丹. 微小卫星太阳敏感器/磁强计实时标定算法研究[J].
航空学报, 2007, 28(1): 173–176.
DUAN Fang, LIU Jian-ye, LI Dan. Real-time sun-sensor/magnetometer calibration algorithm for micro-satellite[J]. Acta Aeronautica et Astro-nautica Sinica, 2007, 28(1): 173–176. |
| [10] |
郁丰, 刘建业, 熊智, 等. 微小卫星剩磁在轨标定技术研究[J].
航空学报, 2007, 28(5): 1142–1145.
YU Feng, LIU Jian-ye, XIONG Zhi, et al. Research on remanence on-orbit calibration for micro-satellites[J]. Acta Aeronautica et Astronautica Sinica, 2007, 28(5): 1142–1145. |
| [11] |
李烨, 郁丰, 王群仰, 等. 立方星剩磁在轨辨识与主动补偿技术[J].
中国惯性技术学报, 2016, 24(3): 342–348.
LI Ye, YU Feng, WANG Qun-yang, et al. On-orbit estimation and compensation for CubeSats reman-ence[J]. Journal of Chinese Inertial Technology, 2016, 24(3): 342–348. |
| [12] |
郁丰, 刘建业, 熊智, 等. 微小卫星姿态确定系统多信息融合滤波技术[J].
上海交通大学学报, 2008, 42(5): 831–835.
YU Feng, LIU Jian-ye, XIONG Zhi, et al. Multi-information fusion method of micro satellite attitude determination system[J]. Journal of Shanghai Jiao Tong University, 2008, 42(5): 831–835. |
| [13] | SAKAI S I, FUKUSHIMA Y, SAITO H. Design and on-orbit evaluation of magnetic attitude control system for the "REIMEI" microsatellite[C]//IEEE International Workshop on Advanced Motion Control. Trento:IEEE, 2008:584-589. http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=4516132 |
| [14] |
黄琳, 荆武兴. 关于剩磁对卫星姿态确定与控制影响的研究[J].
航空学报, 2006, 27(3): 390–394.
HUANG Lin, JING Wu-xing. Effects of remanence on attitude determination and control of satellites[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(3): 390–394. |
| [15] | RONG S, MU R, CUI N. A fault tolerant filter applied on magnetometer-based autonomous satellite navigation[C]//International Symposium on Systems and Control in Aerospace and Astronautics. Harbin:ISSCAA, 2006:597-600. http://ieeexplore.ieee.org/xpl/abstractKeywords.jsp?arnumber=1627408 |
| [16] | 章仁为. 卫星轨道姿态动力学与控制[M]. 北京: 北京航空航天大学出版社, 1998: 340-345. |
| [17] | CHUI C K, CHEN G. Kalman filtering with real-time applications[M]. Springer-Verlag, 1987:232-234. |
| [18] | CRASSIDIS J L, Lai K L, HARMAN R R. Real-time attitude-independent three-axis magnetometer calibration[J]. Journal of Guidance Control and Dynamics, 2005, 28(1): 115–120. DOI:10.2514/1.6278 |



