微网可将多种间歇式新能源和负荷联系起来, 对电网表现为可控单元, 具有灵活、便捷、就地消纳等优点, 已成为分布式新能源的重要组织利用形式.由于微网存在大量间歇式电源, 并采用电力电子装置接入主馈线, 惯性为零, 抗扰动能力弱.同时, 由于微网的容量有限, 分布式发电(distributed generation, DG)的波动、负荷的波动、离并网过程都会对馈线产生较大的影响.因此, 相对于大电网, 微网交流馈线的电压闪变和暂降更加频繁剧烈.如果不能检测并有效治理, 闪变和暂降将进一步导致DG解列、负载馈线脱离, 致使敏感用电设备工作失常, 甚至网络崩溃[1-3].
在大电网中可以采用动态电压恢复器(dynamic voltage regulator, DVR)[4]、静止无功发生器(static var generator, SVG)[5]、有源电力滤波器(active power filter, APF)[6]等电能质量治理设备来应对电压暂降等问题.以上设备由于体积、速度、成本和自动化程度等问题, 不适合微网使用.因此, 本文开发一种新型的电能质量综合控制器(new power quality conditioner, NPQC), 控制的前提是快速检测.融合希尔伯特-黄变换(Hilbert-Huang transform, HHT)和最小方差(least error squares, LES)滤波算法的微网电压暂降快速检测方法可解决该问题.该算法利用短时HHT算法对采样窗口进行自适应变化采样, 改进型LES滤波算法用于计算电压暂降的时间、幅值和相位跳变特征值.该组合算法计算量少, 可快速精确地检测出电压暂降的时间、幅值和相位, 从而提高NPQC设备对微网电压暂降的补偿效果.
1 HHT-LES算法在电压暂降检测中的应用 1.1 HHT-LES算法的流程HHT-LES算法由两部分组成:自适应HHT采样算法和改进型LES算法.自适应HHT采样算法利用短时HHT算法实时跟踪信号带宽, 采样时间间隔由电压暂降信号瞬时带宽决定, 采样后数据再送入改进型LES算法计算.最终可快速、准确地检测交流微电网电压暂降的时间、幅值和相位, 其控制系统结构如图 1所示.其中,U为最终得到的信号幅值,θ为相位角,t为采样时刻.

|
图 1 HHT-LES组合算法流程图 Fig. 1 Flow chart of HHT-LES combination algorithm |
在应用中检测得到的电压暂降信号往往与其他干扰信号混叠在一起, 存在干扰和噪声, 影响信号的检测精度.过多使用低通滤波环节会导致系统响应速度变慢.同时, 固定采样频率下所采集的数据有一定偏差, 要精确测量这些参数, 减少电压波动导致的测量误差, 就需要自动改变测量频率.HHT算法由于能够同时提供信号时域和频域局部信息, 在信号处理领域得到了广泛应用.HHT算法具有固有的端点效应和模态混叠问题[7-8], 为此, 提出一种基于改进型HHT算法的自适应采样算法, 以得到准确的瞬时幅值和瞬时频率.
根据Hilbert-Huang变换方法, 先对交流微电网电压暂降信号进行经验模态分解(empirical mode decomposition, EMD), 得到信号的本征模态函数(intrinsic mode function, IMF)[9];再对本征模态函数进行Hilbert变换, 从而进一步得到该信号的Hilbert谱、时频能量谱等;最后对信号进行分析可得到瞬时频率和瞬时幅值, 从而得到信号的Hilbert谱.最终得到的Hilbert谱表示了信号完整的幅值和频率分布, 计算公式[7]为
| $ X\left( t \right) = \sum\limits_{i = 1}^n {{c_i}\left( t \right) + {r_n}\left( t \right)} . $ | (1) |
式中:ci(t)为信号第i个IMF, rn(t)为残余函数.每个IMF分量的瞬时频率为
| $ {f_i}\left( t \right) = \frac{1}{{2{\rm{ \mathsf{ π} }}}}\frac{{{\rm{d}}{\mathit{\Phi }_i}\left( t \right)}}{{{\rm{d}}t}}. $ | (2) |
式中:Фi(t)为瞬时相位函数.
由HHT变换最终得到的Hilbert频谱为
| $ X\left( t \right) = {a_i}\left( t \right)\exp \left( {j2{\rm{ \mathsf{ π} }}\int {{f_i}\left( t \right){\rm{d}}t} } \right). $ | (3) |
式中:ai(t)为瞬时振幅函数.
针对EMD的端点效应问题, 许多专家学者提出了不同的延拓方法, 如:极值点镜像延拓、包络线延拓、局部波形延拓、波形匹配度延拓、支持向量机延拓、神经网络延拓等[7].这些方法既需要大量的计算时间, 又不能完全消除端点效应.本文使用多项式拟合方法以提高EMD精度.通过最小二乘法二范数取2次近似多项式拟合电压暂降信号:
| $ \left\| {x - y} \right\| = {\left( {\sum\limits_{i = 1}^n {{{\left| {{x_i} - {y_i}} \right|}^2}} } \right)^{1/2}}. $ | (4) |
对于模态混叠问题, 通过集成EMD(ensemble EMD, EEMD)的方法解决.基本过程是:在原始信号中加入白噪声, 对新形成信号进行EMD分解得到各阶IMF.再加入新的白噪声重复上以上步骤, 通过多次重复分解后, 将以上几次分解的结果进行平均处理, 即可得到最终的IMF.由于白噪声在多次平均后会相互抵消, 不仅不会造成误差,还可以削弱模态混叠效应, 平均结果就是最终的IMF.
电压暂降信号经HHT变换后, Hilbert频谱中的瞬时频率将决定下一周期的采样频率.连续电压信号[10]可表示为
| $ X\left( t \right) = f\left[ {\Gamma \left( t \right)} \right]. $ | (5) |
式中:f(t)为限带信号.
| $ \Gamma \left( t \right) = \int_0^t {\varphi \left( \tau \right){\rm{d}}\tau ,\varphi \left( \tau \right) > 0} . $ | (6) |
对连续电压信号进行非均匀采样:
| $ X\left( t \right) = f\left[ {\Gamma \left( t \right)} \right] = f\left[ {\Gamma \left( t \right)} \right]\sum\limits_{k = - \infty }^{ + \infty } {\delta \left[ {t - {\Gamma ^{ - 1}}\left( {k{T_{\rm{s}}}} \right)} \right]} . $ | (7) |
式中:k为采样次数, Ts为采样时间常数.
自适应采样的时间间隔由信号HHT变换的瞬时频率来决定[11]:
| $ \Delta t = {\Gamma ^{ - 1}}\left( {\left( {k + 1} \right){T_{\rm{s}}}} \right) - {\Gamma ^{ - 1}}\left( {k{T_{\rm{s}}}} \right) \approx \frac{{{T_{\rm{s}}}}}{{{f_i}\left( t \right)}}. $ | (8) |
由式(8)可知, Δt与瞬时频率fi(t)成反比.自适应采样时间间隔将根据信号瞬时频率按式(8)进行实时跟踪, 以提高检测精度.
1.3 改进型LES算法LES滤波器又称最小方差滤波器, 可方便快速地提取电压信号各基波分量和谐波分量.为便于分析推导, 对于微电网电压信号, 本文假设不考虑信号的直流分量.以A相为例, 数学表达式[12]为
| $ {u_{\rm{a}}}\left( t \right) = \sum\limits_{n = 1}^\infty {\left( {{k_{{\rm{a}}n}}\sin \left( {n{\omega _0}t + {\theta _{{\rm{a}}n}}} \right)} \right)} . $ | (9) |
式中:ua(t)为电网A相的相电压;n为谐波次数;kan为各次分量对应的电压峰值;ω0为基波角频率;θan为各次分量对应的初始角度.
为方便公式推导, 本文提取信号的基波分量用于推导, 以A相为例, 式(9)可展开为
| $ {u_{\rm{a}}}\left( t \right) = {k_{\rm{a}}}\cos \left( {{\theta _{\rm{a}}}} \right)\sin \left( {{\omega _0}t} \right) + {k_{\rm{a}}}\sin \left( {{\theta _{\rm{a}}}} \right)\cos \left( {{\omega _0}t} \right). $ | (10) |
式(10)总共含有2个未知量ka和θa.对电压信号进行N次采样, 采样时间间隔为Δt, 采样结果记为
| $ {\mathit{\boldsymbol{U}}_{\rm{a}}} = {\left[ {\begin{array}{*{20}{c}} {u\left( t \right)u\left( {t - \Delta t} \right)}& \cdots &{u\left( {t - \left( {N - 1} \right)\Delta t} \right)} \end{array}} \right]^{\rm{T}}}. $ | (11) |
定义
| $ \begin{array}{l} \mathit{\boldsymbol{A = }}\\ {\left[ {\begin{array}{*{20}{c}} {\cos \left( {N{\omega _0}\Delta t} \right)}&{\cos \left( {\left( {N - 1} \right){\omega _0}\Delta t} \right)}& \cdots &{\cos \left( {{\omega _0}\Delta t} \right)}\\ {\sin \left( {N{\omega _0}\Delta t} \right)}&{\sin \left( {\left( {N - 1} \right){\omega _0}\Delta t} \right)}& \cdots &{\sin \left( {{\omega _0}\Delta t} \right)} \end{array}} \right]^{\rm{T}}}. \end{array} $ | (12) |
| $ \mathit{\boldsymbol{X}} = {\left[ {\begin{array}{*{20}{c}} {{k_{\rm{a}}}\sin \left( {{\theta _{\rm{a}}}} \right)}&{{k_{\rm{a}}}\cos \left( {{\theta _{\rm{a}}}} \right)} \end{array}} \right]^{\rm{T}}} = {\left[ {\begin{array}{*{20}{c}} {{X_1}}&{{X_2}} \end{array}} \right]^{\rm{T}}}. $ | (13) |
可得
| $ {\mathit{\boldsymbol{U}}_{\rm{a}}} = \mathit{\boldsymbol{A}} \times \mathit{\boldsymbol{X}}. $ | (14) |
式中:矩阵A的数据固定, 不需要实时进行计算.输入采样得到的数据U, 即可得到矩阵X数值.但对于每次采样U来说, 新采样数据放在第一行, 矩阵A数据保持不变, 要重新得到矩阵X必须重做2N次加法和2N次乘法运算.LES新型算法通过减少计算次数, 以降低计算数据量, 从而提高LES算法的实时检测效果.
根据式(14)可得
| $ X = {\left[ {{A^{\rm{T}}}A} \right]^{ - 1}}{A^{\rm{T}}}{\mathit{\boldsymbol{U}}_{\rm{a}}}. $ | (15) |
令
| $ D = {\left[ {{A^{\rm{T}}}A} \right]^{ - 1}} = \left[ {\begin{array}{*{20}{c}} {{D_{11}}}&{{D_{12}}}\\ {{D_{21}}}&{{D_{22}}} \end{array}} \right], $ | (16) |
| $ F = {A^{\rm{T}}}{\mathit{\boldsymbol{U}}_{\rm{a}}}. $ | (17) |
将式(16)和(17)代入式(11)和(12)可得
| $ \begin{array}{l} \mathit{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{c}} {\sum\limits_{i = 1}^N {u\left[ {t - \left( {i - 1} \right)\Delta t} \right]\cos \left[ {N - \left( {i - 1} \right)} \right]{\omega _0}\Delta t} }\\ {\sum\limits_{i = 1}^N {u\left[ {t - \left( {i - 1} \right)\Delta t} \right]\sin \left[ {N - \left( {i - 1} \right)} \right]{\omega _0}\Delta t} } \end{array}} \right] = \\ \;\;\;\;\;\;{\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_1}}&{{\mathit{\boldsymbol{F}}_2}} \end{array}} \right]^{\rm{T}}}. \end{array} $ | (18) |
联立式(13)、(15)~(18)可得
| $ {X_1} = {D_{11}} \times {\mathit{\boldsymbol{F}}_1} + {D_{12}} \times {\mathit{\boldsymbol{F}}_2}, $ | (19) |
| $ {X_2} = {D_{21}} \times {\mathit{\boldsymbol{F}}_1} + {D_{22}} \times {\mathit{\boldsymbol{F}}_2}. $ | (20) |
对比第k和k+1次递归过程, 矩阵F产生的变化量为
| $ \begin{array}{l} {\mathit{\boldsymbol{F}}_1}\left( {k + 1} \right) = {\mathit{\boldsymbol{F}}_1}\left( k \right) + u\left( t \right)\cos \left[ {\left( {N + k} \right){\omega _0}\Delta t} \right] - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;u\left( {t - N\Delta t} \right)\cos \left( {k{\omega _0}\Delta t} \right), \end{array} $ | (21) |
| $ \begin{array}{l} {\mathit{\boldsymbol{F}}_2}\left( {k + 1} \right) = {\mathit{\boldsymbol{F}}_2}\left( k \right) + u\left( t \right)\sin \left[ {\left( {N + k} \right){\omega _0}\Delta t} \right] - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;u\left( {t - N\Delta t} \right)\sin \left( {k{\omega _0}\Delta t} \right). \end{array} $ | (22) |
式中:u(t)和u(tNΔt)分别是t和t-NΔt时刻的采样数据.
分析式(19)~(22)可得, D11、D12、D21、D22、cos [(N+k)ω0Δt]、cos (kω0Δt)、sin [(N+k)ω0Δt]、sin (kω0Δt)的数值在每次计算中均保持不变, 可预先算出以固定数据的形式保存于DSP内部.对于每次新的采样, 需要重新计算的仅为F1和F2的数值, 再次得到X1和X2仅需重新进行部分乘法和加法运算.相比以前每次计算都要重做2N次加法和2N次乘法运算, 可大幅度减少DSP计算的负担, 以减少延时时间, 达到快速提高系统的响应速度的目的.
根据LES算法, 通过求得的X1和X2可最终计算出基波分量的幅值和瞬时相位[13-14]:
| $ {k_{\rm{a}}} = \sqrt {\mathit{\boldsymbol{X}}_1^2 + \mathit{\boldsymbol{X}}_2^2} , $ | (23) |
| $ {\theta _{\rm{a}}} = \arctan \left( {{\mathit{\boldsymbol{X}}_1}/{\mathit{\boldsymbol{X}}_2}} \right). $ | (24) |
改进型LES算法利用式(23)和(24)可提取该时刻电压信号(基波和谐波)的幅值和瞬时相位角, 从而实现对微电网电压的暂降幅值、起始时刻和相位跳变的快速检测.结合短时HHT自适应采样和改进LES组合算法可以有效去除干扰信号, 并精确分离出电压暂降信号, 该组合算法可快速精确地检测微电网电压暂降的时间、幅值和相位.
2 仿真与实验分析 2.1 仿真分析在Matlab/Simulink上对新型算法进行仿真验证.仿真分信号带宽跟踪、三相暂降和带相位跳变的三相暂降进行.将HHT-LES算法与其他2种方法(传统d-q法和HHT法)在检测动态响应和精度方面作对比分析, 以验证本文方法的有效性.仿真参数如下:初始电压有效值为220 V, 频率为50 Hz, 信号在t=0.015~0.085 s时发生幅值为0.5 pu的暂降.
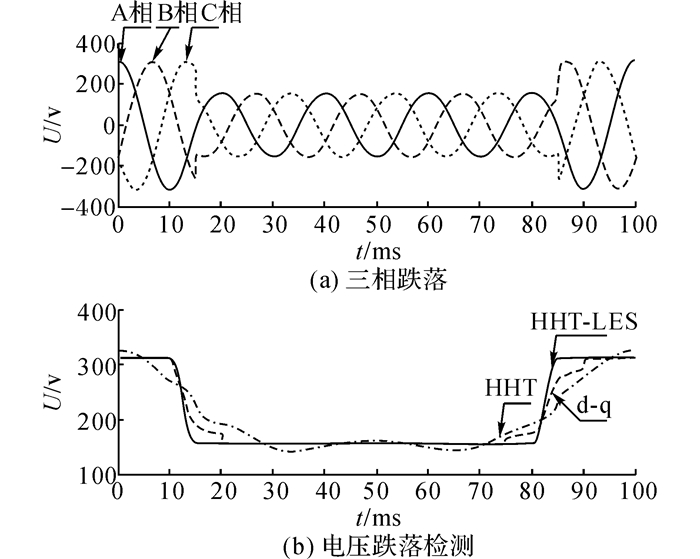
在线性负载下, 网侧电压谐波含量很少, 微电网母线电压(A、B和C三相)同时从15.0~85.0 ms发生深度为0.5 pu的电压暂降.利用3种不同方法检测到的仿真结果如图 2所示.暂降发生后, 3种方法均可检测到电压暂降信号.HHT方法速度最快, 但是检测结果的稳定性不如其他2种算法.传统的d-q方法虽然可以反映暂降的深度, 但是最终检测的结果要比其他2种算法慢.改进后的HHT-LES算法能在5.1 ms内检测到电压由1 pu暂降至0.5 pu, 检测时出现一定延迟.在幅值检测精度方面, d-q变换算法和HHT方法的检测结果出现了波动, 影响最终输出精度.d-q法的最终检测精度小于5.01%, HHT方法的最终检测精度小于4.10%, 而HHT-LES方法的检测精度小于2.05%.
|
图 2 线性负载下三相电压暂降的检测 Fig. 2 Linear loads of three-phase voltage sag detection |
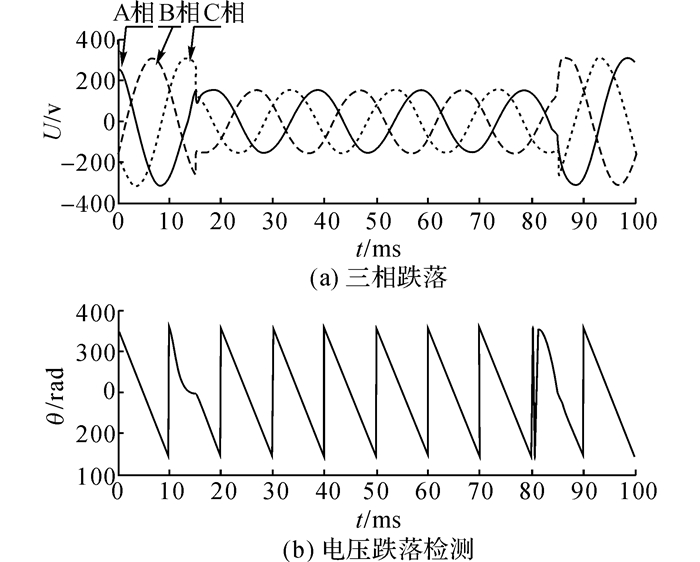
图 3为模拟非线性负载条件下, 微网三相母线电压同时发生幅值0.5 pu的暂降, 且相位跳变90 °时, 采用以上3种检测方法的对比效果.当发生相位跳变后, 采用HHT-LES法检测得到的电压波形虽发生明显的波动, 但经短暂波动后在5.2 ms内准确检测到微网的电压暂降.说明电网电压的相位跳变对检测过程有一定干扰和影响.HHT-LES算法在电网电压相位发生变化时, 依然具有良好的跟踪性.如图 4所示为采用HHT-LES算法检测得到的信号相位波形图.当相位发生跳变后, 在5.2 ms内检测出相位变化, 相位检测过程非常迅速和准确, 表明该算法可快速跟踪信号的相位变化.

|
图 3 非线性负载下三相电压暂降(带相位跳变)的检测 Fig. 3 Detection of three-phase voltage drop (with phase jump) in nonlinear load |
|
图 4 HHT-LES法对非线性负载下电压相位跳变的检测 Fig. 4 HHT-LES method for nonlinear loads voltage and phase jump detection |
为验证算法的有效性, 搭建三相20 kVA最大补偿能力为0.4 pu的硬件检测平台, 如图 5所示.包含三相逆变IGBT驱动、数据采集模块、DSP处理器、电抗器、滤波器和辅助电源组成.采用艾普斯电源(ACST-S-33100T)作为模拟电网输入, 直流支撑使用台湾Chroma公司的程控直流电源(62012P-600-8).电压暂降检测使用泰克公司的高压差分探头P5200A, 并采用安捷伦DSO-X 3034A示波器观察波形.

|
图 5 基于NPQC的电压暂降试验系统 Fig. 5 Voltage transient test system based on NPQC |
实验采用TI的DSP芯片TMS320F28335作为处理器.交流微网电压信号经电压互感器采样后, 通过运放电路输入到DSP的A/D采样口.A/D采样初始频率设定为10 kHz, 采样窗口宽度M=100.电压信号经HHT变换可得到瞬时角频率和瞬时幅值.自适应采样系统以瞬时信号频率的5倍进行采样.经式(8)计算可得到新的采样时间间隔, 用于下一批次采样.对于后续计算, 利用式(19)~(22)仅需重新做8次乘法和6次加法运算.实验平台开发环境使用CCS6.0, 并安装GUI Composer插件用于观察3种不同算法的对比检测输出结果.
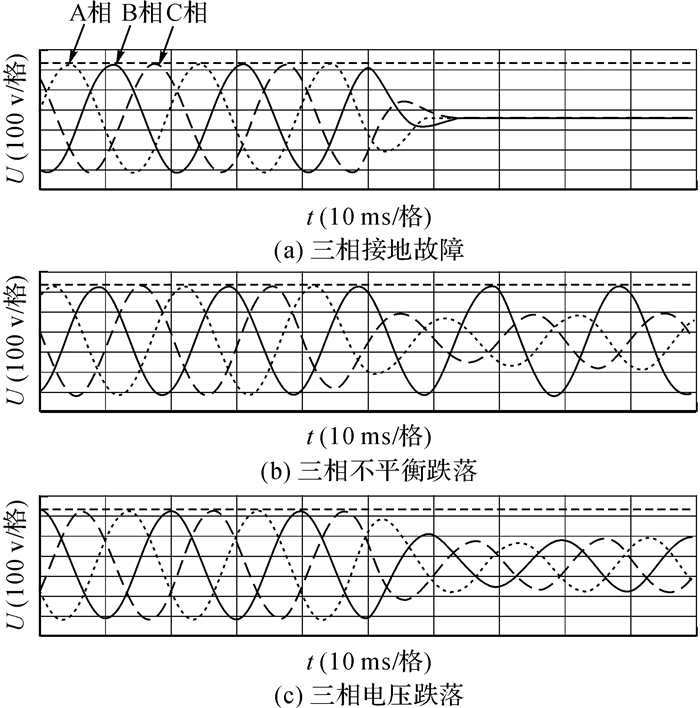
如图 6和7所示分别为艾普斯电源输入的电压暂降信号和不同算法在DSP中检测到的暂降信号.由于艾普斯电源设置中无法产生电压相位跳变, 实验平台仅仅试验三相接地故障、三相不平衡暂降和三相电压暂降3种情况, 其中三相不平衡暂降和三相电压暂降深度均为0.5 pu.
|
图 6 示波器检测到的实验平台输入波形 Fig. 6 Input waveform of experimental platformdetected by oscilloscope |
|
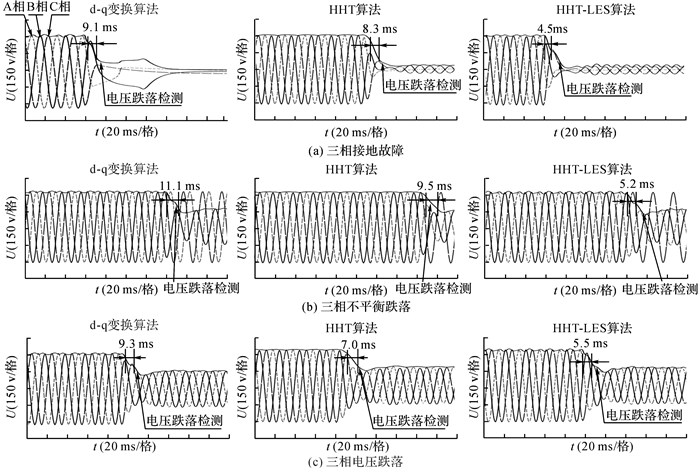
图 7 不同算法在NPQC试验平台中检测电压暂降的输出波形 Fig. 7 Output waveform of voltage drop in NPQC test plat form detected by different algorithms |
图 7中, 当微网出现电压暂降, DSP分别经过d-q变换算法、HHT算法和HHT-LES算法检测计算后, 输出检测到的暂降电压.通过对比分析发现:d-q变换算法响应时间在9.1~11.2 ms, 暂降幅值检测误差<5.50%.HHT法响应时间在7.0~9.1 ms, 暂降幅值检测误差<5.08%.而HHT-LES新算法的响应时间在4.5~5.5 ms, 暂降幅值检测误差<2.11%.
实验结果表明, 基于HHT-LES算法的交流微网电压暂降检测新算法可有效提高系统响应速度和检测精度.
3 结语微网电压暂降检测是微电网电能质量治理的前提, 本文提出了一种基于HHT-LES算法的微网电压快速暂降检测新方法.通过使用短时HHT变换跟踪信号瞬时带宽的算法, 有效解决采样精度与检测速度矛盾的问题.同时使用改进算法的LES滤波新算法, 可使系统计算时间减少, 有效提高电压暂降的检测速度.仿真和实验表明, 改进后的检测方法对各种不同情况的三相电压暂降和带相位跳变的暂降故障均能实现快速准确检测.电压暂降的检测时间少于5.2 ms, 误差小于2.11%.该方法计算量少, 并易于在实际工程中应用, 能较好地实现交流微电网电压暂降的快速检测.
| [1] | AHMADIAN A, SEDGHI M, ALIAKBAR-GOLKAR M, et al. Two-layer optimization methodology for wind distributed generation planning considering plug-in electric vehicles uncertainty:a flexible active-reactive power approach[J]. Energy Conversion and Management, 2016, 124: 231–246. DOI:10.1016/j.enconman.2016.07.025 |
| [2] | RAHMANI-ANDEBILI M. Distributed generation placement planning modeling feeder's failure rate and customer's load type[J]. IEEE Transactions on Industrial Electronics, 2016, 63(3): 1598–1606. DOI:10.1109/TIE.2015.2498902 |
| [3] | AHMED N R, CORTES J, MARTINEZ S. Distributed control and estimation of robotic vehicle networks:anoverview of part 2[J]. IEEE Control Systems, 2016, 36(4): 18–21. DOI:10.1109/MCS.2016.2558398 |
| [4] | NABIPOUR M, RAZAZ M, SEIFOSSADAT S G H, et al. A novel adaptive fuzzy membership function tuning algorithm for robust control of a PV-based dynamic voltage restorer (DVR)[J]. Engineering Applications ofArtificial Intelligence, 2016, 53: 155–175. DOI:10.1016/j.engappai.2016.04.007 |
| [5] | WANG S K. Coordinated parameter design of power system stabilizers and static synchronous compensator using gradual hybrid differential evaluation[J]. Interna-tional Journal of Electrical Power and Energy Systems, 2016, 81: 165–174. DOI:10.1016/j.ijepes.2016.02.016 |
| [6] | HE J, LI Y W, WANG R, et al. A measurement method to solve a problem of using DG interfacing converters for selective load harmonic filtering[J]. IEEE Transactions on Power Electronics, 2016, 31(3): 1852–1856. DOI:10.1109/TPEL.2015.2479116 |
| [7] |
雷亚国. 基于改进Hilbert-Huang变换的机械故障诊断[J].
机械工程学报, 2011, 47(5): 71–77.
LEI Ya-guo. Machinery fault diagnosis based onimproved Hilbert-Huang transform[J]. Journal ofmechanical Engineering, 2011, 47(5): 71–77. |
| [8] |
宋海军, 黄传金, 刘宏超, 等. 基于改进LMD的电能质量扰动检测新方法[J].
中国电机工程学报, 2014, 34(10): 1700–1708.
SONG Hai-jun, HUANG Chuan-jin, LIU Hong-chao, et al. A new power quality disturbance detection method based on the improved LMD[J]. Proceedings of the CSEE, 2014, 34(10): 1700–1708. |
| [9] |
黄正梁, 胡雨晨, 王靖岱, 等. 基于希尔伯特-黄变换测量搅拌釜临界分散转速[J].
浙江大学学报:工学版, 2012, 46(9): 1685–1691.
HUANG Zheng-liang, HU Yu-chen, WANG Jing-dai, et al. Measurement of critical dispersion speed in stirred tank based on Hilbert-Huang transform[J]. Journal of Zhejiang University:Engineering Science, 2012, 46(9): 1685–1691. |
| [10] | BARMUTA P, AVOLIO G, FERRANTI F, et al. Hybrid nonlinear modeling using adaptive sampling[J]. IEEE Transactions on Microwave Theory and Techniques, 2015, 63(12): 4501–4510. DOI:10.1109/TMTT.2015.2495124 |
| [11] | REN Y, ZHAO Y, ZHAO Z, et al. A novel adaptive sampling method for interpolation/extrapolation in time and frequency domains[J]. Journal of Electromagnetic Waves and Applications, 2014, 28(10): 1167–1174. DOI:10.1080/09205071.2014.906328 |
| [12] |
陈国栋, 朱淼, 蔡旭, 等. 一种软件锁相环和电压跌落检测新算法[J].
中国电机工程学报, 2014, 34(25): 4385–4394.
CHEN Guo-dong, ZHU Miao, CAI Xu, et al. A new algorithm for software phase locked loop and voltage drop detection[J]. Proceedings of the CSEE, 2014, 34(25): 4385–4394. |
| [13] | EBRAHIMZADEH E, FARHANGI S, IMAN-EINI H, et al. Improved phasor estimation method fordynamic voltage restorer applications[J]. IEEE Tran-sactions on Power Delivery, 2015, 30(3): 1467–1477. DOI:10.1109/TPWRD.2014.2366241 |
| [14] | ZADEH R A, GHOSH A, LEDWICH G. Combination of Kalman filter and least-error square techniques in power system[J]. IEEE Transactions on PowerDelivery, 2010, 25(4): 2868–2880. |



