内置式永磁同步电机(interior permanent magnet synchronous motor, IPMSM)具有高效率、高转矩电流比、高功率密度以及结构简单等优点, 被广泛应用于风力发电、电动汽车等领域[1-2].在IPMSM的有关控制算法中, 直接转矩控制(direct torque control, DTC)以动态响应速度快、参数敏感性低以及控制结构简单等优点, 在20世纪80年代一经提出就受到广泛关注[3-4].
根据电机输出的转矩误差、磁链误差以及当前定子磁链矢量所处的位置, 传统DTC方案从开关表中选择可施加在电机端的电压矢量[5].对于由两电平电压型逆变器供电的电机驱动系统, 只有6个非零矢量和2个零矢量可供选择.在电压矢量的选择过程中, 传统DTC方案未考虑转矩误差和磁链误差的大小, 使得电机输出中存在很大的转矩脉动和磁链脉动.此外, 滞环控制器的使用导致逆变器的开关频率不固定[6].针对上述问题, 为了能生成更多电压矢量, 学者们提出了很多改进方案:离散空间电压矢量调制算法[7-8]、多电平逆变器[9]以及矩阵逆变器[10]等方法.然而, 可利用的电压矢量越多, 需要构建的开关表就越复杂.
在多数情况下所选电压矢量并不需要施加一整个开关周期, 有学者提出了占空比调制技术.Kang等[11~13]根据转矩和定子磁链的微分方程, 按照不同的控制目标来计算所选电压矢量的占空比.将此类算法应用于IPMSM驱动系统时比较复杂, 参数敏感性较强.Zhang等[14]通过调节2个与转矩误差和磁链误差相关的增益系数来计算电压矢量的占空比, 但是该方案需要通过反复尝试来确定系统的增益系数.
空间电压矢量调制(space vector modulation, SVM)算法能够生成足够多的电压矢量, 并且开关频率固定, 可用SVM来代替开关表, 实现对转矩误差和磁链误差的精确补偿.此时, 控制系统的主要任务是通过各种算法来计算系统所需要的参考电压矢量.Tang等[15]利用一个PI控制器来调节系统的转矩误差.由于转矩控制环PI控制器的存在, 不合适的PI参数会在电机的转矩输出中产生超调, 甚至会影响整个系统的稳定.Xu等[16]提出了一种变结构控制器来调节系统的转矩输出.该方案需要通过大量计算才能确定保证系统稳定运行所需的控制律.Zhang等[17]利用2个与转矩误差和磁链误差相关的增益系数分别来调节参考电压矢量的幅值和相位, 发现需要经过反复尝试才能选出合适的增益系数.Zhu等[18]根据转矩的微分方程提出了一种改进的预测转矩控制算法, 将该算法应用于IPMSM时同样很复杂.
以上分析发现, 除了PI-SVM DTC方案[15]外, 当具有较低转矩脉动输出的DTC方案在IPMSM驱动系统中实施时, 算法的复杂程度都会大大增加.对于PI-SVM DTC方案来说, 系统的动态性能又严重依赖于PI控制器的参数设计.
本研究提出一种定子磁链矢量控制方案来改善系统的动静态性能.首先推导基于静止坐标系的定子磁链微分方程, 构建以定子磁链为状态变量的IPMSM离散域状态空间模型, 在两相静止坐标系下省去解耦环节, 实现对定子磁链矢量的直接控制.构建一个无差拍全阶状态观测器, 实现对定子磁链的闭环观测, 提高作为反馈变量的定子磁链的观测精度[19], 改善系统的稳态性能.在定子磁链矢量控制方案中, 转矩控制环被移除, 利用定子磁链控制环来调节系统的转矩输出以改善系统的动态性能.将速度控制环的输出作为转矩角的给定值δ*, 简化定子磁链矢量期望值的计算过程.根据定子磁链控制环的极点位置来调节系统的前向增益矩阵, 计算参考电压矢量.
1 IPMSM的数学模型 1.1 IPMSM的连续域数学模型两相旋转d-q坐标系下的IPMSM电压方程为
| $ \left. \begin{array}{l} {u_{d{\rm{s}}}} = {R_{\rm{s}}}{i_{ds}} + \frac{{{\rm{d}}{\psi _{d{\rm{s}}}}}}{{{\rm{d}}t}} - {\omega _{\rm{r}}}{\psi _{q{\rm{s}}}},\\ {u_{q{\rm{s}}}} = {R_{\rm{s}}}{i_{qs}} + \frac{{{\rm{d}}{\psi _{q{\rm{s}}}}}}{{{\rm{d}}t}} + {\omega _{\rm{r}}}{\psi _{d{\rm{s}}}}. \end{array} \right\} $ | (1) |
式中:uds、uqs分别为定子电压的d、q轴分量, ids、iqs分别为定子电流的d、q轴分量, ψds、ψqs分别为定子磁链的d、q轴分量, Rs为定子电阻, ωr为电机电角速度.
两相旋转d-q坐标系下的定子磁链表达式为
| $ {\psi _{d{\rm{s}}}} = {L_d}{i_{d{\rm{s}}}} + {\psi _{\rm{f}}},{\psi _{q{\rm{s}}}} = {L_q}{i_{q{\rm{s}}}}. $ | (2) |
式中:Ld、Lq分别为IPMSM的d、q轴电感, ψf为永磁体磁通量.
根据式(2), 消去式(1)中的电流分量, 通过坐标旋转逆变换, 将式(1)变换到两相静止α-β坐标下, 得如下定子磁链的微分方程:
| $ \left[ {\begin{array}{*{20}{c}} {\frac{{{\rm{d}}{\psi _{\alpha {\rm{s}}}}}}{{{\rm{d}}t}}}\\ {\frac{{{\rm{d}}{\psi _{\beta {\rm{s}}}}}}{{{\rm{d}}t}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{R_{\rm{s}}}X}&{{R_{\rm{s}}}M}\\ {{R_{\rm{s}}}M}&{ - {R_{\rm{s}}}Y} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\psi _{\alpha {\rm{s}}}}}\\ {{\psi _{\beta {\rm{s}}}}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\cos {\theta _{\rm{r}}}}\\ {\sin {\theta _{\rm{r}}}} \end{array}} \right]\frac{{{R_{\rm{s}}}}}{{{L_d}}}{\psi _{\rm{f}}} + \left[ {\begin{array}{*{20}{c}} {{u_{\alpha {\rm{s}}}}}\\ {{u_{\beta {\rm{s}}}}} \end{array}} \right]. $ | (3) |
式中:ψαs、ψβs分别为定子磁链的α、β轴分量, uαs、uβs分别为定子电压的α、β 轴分量, θr为转子位置电角度,
| $ \begin{array}{l} X = \frac{{\left( {{L_d} - {L_q}} \right)\cos 2{\theta _{\rm{r}}} - {L_d} - {L_q}}}{{2{L_d}{L_q}}},\\ Y = \frac{{\left( {{L_d} - {L_q}} \right)\cos 2{\theta _{\rm{r}}} + {L_d} + {L_q}}}{{2{L_d}{L_q}}},\\ M = \frac{{\left( {{L_d} - {L_q}} \right)\sin 2{\theta _{\rm{r}}}}}{{2{L_d}{L_q}}}. \end{array} $ | (4) |
根据式(2), 定子电流可以表示为
| $ \left[ {\begin{array}{*{20}{c}} {{i_{\alpha {\rm{s}}}}}\\ {{i_{\beta {\rm{s}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - X}&{ - M}\\ { - M}&Y \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\psi _{\alpha {\rm{s}}}}}\\ {{\psi _{\beta {\rm{s}}}}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {\cos {\theta _{\rm{r}}}}\\ {\sin {\theta _{\rm{r}}}} \end{array}} \right]\frac{{{\psi _{\rm{f}}}}}{{{L_d}}}. $ | (5) |
式中:iαs、iβs分别为定子电流的α、β轴分量.
IPMSM输出的转矩可以表示为
| $ \begin{array}{l} {\mathit{\boldsymbol{T}}_{\rm{e}}} = \frac{3}{2}p\left( {{\psi _{d{\rm{s}}}}{i_{q{\rm{s}}}} - {\psi _{q{\rm{s}}}}{i_{d{\rm{s}}}}} \right) = \\ \frac{{3p\left| {{\mathit{\boldsymbol{\psi }}_{\rm{s}}}} \right|}}{{4{L_d}{L_q}}}\left[ {2{\psi _{\rm{f}}}{L_q}\sin \delta + \left| {{\mathit{\boldsymbol{\psi }}_{\rm{s}}}} \right|\left( {{L_d} - {L_q}} \right)\sin \left( {2\delta } \right)} \right]. \end{array} $ | (6) |
式中:|ψs|为定子磁链幅值;δ为转矩角, 即定转子磁链矢量之间的夹角.
转矩Te关于转矩角δ的导数可以表示为
| $ \begin{array}{l} {k_{T{\rm{e}}}} = \frac{{{\rm{d}}{T_{\rm{e}}}}}{{{\rm{d}}\delta }} = \frac{{3p\left| {{\mathit{\boldsymbol{\psi }}_{\rm{s}}}} \right|}}{{2{L_d}{L_q}}} \times \\ \;\;\;\;\;\;\;\;\;\;\left[ {{\psi _{\rm{f}}}{L_q}\cos \delta + \left| {{\mathit{\boldsymbol{\psi }}_{\rm{s}}}} \right|\left( {{L_d} - {L_q}} \right)\cos \left( {2\delta } \right)} \right]. \end{array} $ | (7) |
在IPMSM的状态空间模型中, 分别选择定子磁链矢量的α、β轴分量作为状态变量, 定子电压为输入变量, 定子电流为输出变量.根据式(3)和(5),对永磁体产生的分量进行补偿后,IPMSM的状态方程可以表示为
| $ \mathit{\boldsymbol{\dot x}}\left( t \right) = \mathit{\boldsymbol{A}}\left( t \right)\mathit{\boldsymbol{x}}\left( t \right) + \mathit{\boldsymbol{Bu}}\left( t \right). $ | (8) |
输出方程为
| $ \mathit{\boldsymbol{y}}\left( t \right) = \mathit{\boldsymbol{C}}\left( t \right)\mathit{\boldsymbol{x}}\left( t \right). $ | (9) |
式中:状态变量x(t)=[ψαs ψβs]T, 输出变量y(t)=[iαs iβs]T, 输入变量u(t)=[uαs uβs]T,
| $ \mathit{\boldsymbol{A}}\left( t \right) = \left[ {\begin{array}{*{20}{c}} {{R_{\rm{s}}}X}&{{R_{\rm{s}}}M}\\ {{R_{\rm{s}}}M}&{ - {R_{\rm{s}}}Y} \end{array}} \right],\mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} 1&0\\ 0&1 \end{array}} \right], $ |
| $ \mathit{\boldsymbol{C}}\left( t \right) = \left[ {\begin{array}{*{20}{c}} { - X}&{ - M}\\ { - M}&Y \end{array}} \right]. $ |
为便于数字实现, 令k代表第k次采样的时刻, 则系统矩阵G(k), 输入矩阵H可分别表示为
| $ \mathit{\boldsymbol{G}}\left( k \right) \approx \mathit{\boldsymbol{I + A}}\left( k \right){T_{\rm{s}}} = \left[ {\begin{array}{*{20}{c}} {1 + {T_{\rm{s}}}{R_{\rm{s}}}X}&{{T_{\rm{s}}}{R_{\rm{s}}}M}\\ {{T_{\rm{s}}}{R_{\rm{s}}}M}&{1 - {T_{\rm{s}}}{R_{\rm{s}}}Y} \end{array}} \right], $ | (10) |
| $ \mathit{\boldsymbol{H}} \approx {T_{\rm{s}}}\mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} {{T_{\rm{s}}}}&0\\ 0&{{T_{\rm{s}}}} \end{array}} \right]. $ | (11) |
式中:I为单位矩阵, Ts为采样周期, A(k)和G(k)分别为相关矩阵在第kTs时刻的瞬时值.
根据式(8)和(9), IPMSM的离散域状态空间模型可以表示成
| $ \mathit{\boldsymbol{x}}\left( {k + 1} \right) = \mathit{\boldsymbol{G}}\left( k \right)\mathit{\boldsymbol{x}}\left( k \right) + \mathit{\boldsymbol{Hu}}\left( k \right), $ | (12) |
| $ \mathit{\boldsymbol{y}}\left( k \right) = \mathit{\boldsymbol{C}}\left( k \right)\mathit{\boldsymbol{x}}\left( k \right). $ | (13) |
离散域IPMSM状态空间模型的结构框图如图 1所示.图中,Δx(k)、Δy(k)分别为由永磁体在状态变量和输出变量中引入的补偿分量:
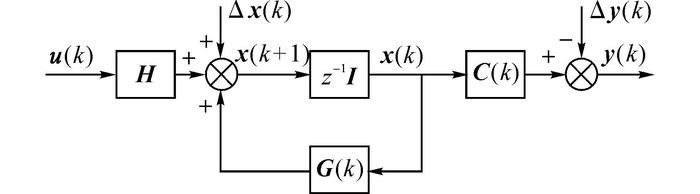
|
图 1 离散域IPMSM状态空间模型的结构框图 Fig. 1 Block diagram of discrete-time IPMSM model in state space |
| $ \left. \begin{array}{l} \Delta \mathit{\boldsymbol{x}}\left( k \right) = {\left[ {\begin{array}{*{20}{c}} {{T_{\rm{s}}}\frac{{{R_{\rm{s}}}}}{{{L_d}}}{\psi _{\rm{f}}}\cos {\theta _{\rm{r}}}}&{{T_{\rm{s}}}\frac{{{R_{\rm{s}}}}}{{{L_d}}}{\psi _{\rm{f}}}\sin {\theta _{\rm{r}}}} \end{array}} \right]^{\rm{T}}},\\ \Delta \mathit{\boldsymbol{y}}\left( k \right) = {\left[ {\begin{array}{*{20}{c}} {\frac{{{\psi _{\rm{f}}}}}{{{L_d}}}\cos {\theta _{\rm{r}}}}&{\frac{{{\psi _{\rm{f}}}}}{{{L_d}}}\sin {\theta _{\rm{r}}}} \end{array}} \right]^{\rm{T}}}. \end{array} \right\} $ | (14) |
定子磁链矢量控制方案的原理图如图 2所示.图 2中, n*和|ψs|*分别为转速和定子磁链幅值的给定值, Δus为定子电阻上的压降, is为定子电流矢量,
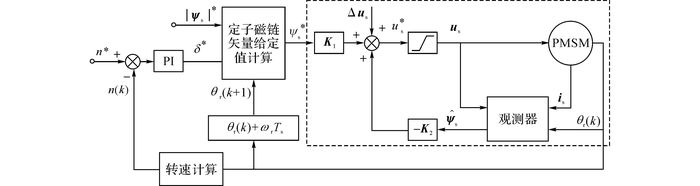
|
图 2 IPMSM定子磁链矢量控制算法原理图 Fig. 2 Schematic diagram of stator flux vector control strategy for IPMSM |
与PI-SVM DTC相比, 定子磁链矢量控制方案没有转矩控制环, 直接通过定子磁链控制环来实现对IPMSM输出转矩的控制.参考定子磁链矢量计算模块, 可以获得定子磁链矢量的期望值ψs*, 并且在此过程中不需要提取定子磁链的幅值和相位角.定子磁链矢量控制方案利用一个无差拍全阶状态观测器来估算定子磁链矢量以改善系统的稳态性能.在参考电压矢量us*的计算过程中, 根据定子磁链环的极点位置, 即状态反馈增益矩阵K2, 来调节系统的前向增益矩阵K1.
2.1 定子磁链矢量期望值的计算离散域内定转子磁链矢量之间的位置关系如图 3所示, 图中带s下标的量为定子参数, 带r下标的量为转子参数.定义转子磁链矢量ψr=ψf exp (jθr), 在k时刻, 定子磁链矢量ψs(k)的电角位置为θs(k), 转子磁链矢量ψr(k)的电角位置为θr(k).
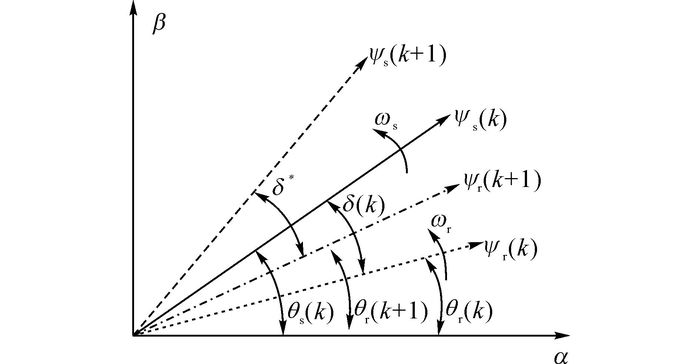
|
图 3 离散域定转子磁链矢量之间的位置关系图 Fig. 3 Position relationship between stator and rotor flux vectors in discrete-time |
在已知电机电角速度ωr的前提下, 预测转子电角位置在k+1时刻的值为
| $ {\theta _{\rm{r}}}\left( {k + 1} \right) = {\theta _{\rm{r}}}\left( k \right) + {\omega _{\rm{r}}}{T_{\rm{s}}}, $ | (15) |
根据图 3的定转子磁链矢量之间的位置关系, 预测定子磁链矢量在k+1时刻的位置角θs(k+1)为
| $ \begin{array}{*{20}{c}} {{\theta _{\rm{s}}}\left( {k + 1} \right) = {\theta _{\rm{r}}}\left( {k + 1} \right) + \delta \left( {k + 1} \right) = }\\ {{\theta _{\rm{r}}}\left( k \right) + {\omega _{\rm{r}}}{T_{\rm{s}}} + {\delta ^ * }.} \end{array} $ | (16) |
为保证IPMSM的正常起动, 根据文献[5], 将定子磁链幅值的给定值|ψs|*设置为ψf, 因此在两相静止坐标系下, 定子磁链矢量的期望值可表示为
| $ \begin{array}{l} \mathit{\boldsymbol{\psi }}_{\rm{s}}^ * = {\mathit{\boldsymbol{\psi }}_{\rm{s}}}\left( {k + 1} \right) = {\left[ {\begin{array}{*{20}{c}} {{\psi _{\alpha {\rm{s}}}}\left( {k + 1} \right)}&{{\psi _{\beta {\rm{s}}}}\left( {k + 1} \right)} \end{array}} \right]^{\rm{T}}} = \\ \;\;\;\;{\left[ {\begin{array}{*{20}{c}} {{{\left| {{\psi _{\rm{s}}}} \right|}^ * }\cos \left( {{\theta _{\rm{s}}}\left( {k + 1} \right)} \right)}&{{{\left| {{\psi _{\rm{s}}}} \right|}^ * }\sin \left( {{\theta _{\rm{s}}}\left( {k + 1} \right)} \right)} \end{array}} \right]^{\rm{T}}}. \end{array} $ | (17) |
为了改善系统的稳态性能, 作为反馈变量的定子磁链需要具备足够的精度.由于定子磁链不能被直接测量, 构建一个无差拍全阶状态观测器来实现对定子磁链的闭环观测, 基本原理如图 4所示.图 4中:Ke为观测器反馈增益矩阵,
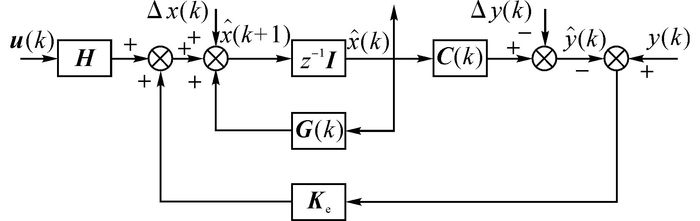
|
图 4 无差拍全阶定子磁链观测器结构图 Fig. 4 Schematic diagram of dead-beat full-order stator flux observer |
在观测器设计之前, 需先检测系统的能观性:
| $ tank\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{C}}\left( k \right)\mathit{\boldsymbol{G}}\left( k \right)}\\ {\mathit{\boldsymbol{C}}\left( k \right)} \end{array}} \right] = 2. $ | (18) |
可见, 该能观性矩阵的秩等于系统的阶数, 因此该系统完全能观, 即可以通过选择Ke将矩阵G(k)-KeC(k)的特征根放置在任意位置上.根据图 4, 观测器的状态方程可以表示为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat x}}\left( {k + 1} \right) = \mathit{\boldsymbol{G}}\left( k \right)\mathit{\boldsymbol{\hat x}}\left( k \right) + \mathit{\boldsymbol{Hu}}\left( k \right) + \Delta \mathit{\boldsymbol{x}}\left( k \right) + }\\ {{\mathit{\boldsymbol{K}}_{\rm{e}}}\left[ {\mathit{\boldsymbol{y}}\left( k \right) - \mathit{\boldsymbol{\hat y}}\left( k \right)} \right].} \end{array} $ | (19) |
估算的输出变量为
| $ \mathit{\boldsymbol{\hat y}}\left( k \right) = \mathit{\boldsymbol{C}}\left( k \right)\mathit{\boldsymbol{\hat x}}\left( k \right) - \Delta \mathit{\boldsymbol{y}}\left( k \right). $ | (20) |
将式(20)代入式(19)中, 修正观测器的状态方程为
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat x}}\left( {k + 1} \right) = \left[ {\mathit{\boldsymbol{G}}\left( k \right) - {\mathit{\boldsymbol{K}}_{\rm{e}}}\mathit{\boldsymbol{C}}\left( k \right)} \right]\mathit{\boldsymbol{\hat x}}\left( k \right) + \mathit{\boldsymbol{Hu}}\left( k \right) + }\\ {\Delta \mathit{\boldsymbol{x}}\left( k \right) + {\mathit{\boldsymbol{K}}_{\rm{e}}}\mathit{\boldsymbol{y}}\left( k \right) + {\mathit{\boldsymbol{K}}_{\rm{e}}}\Delta \mathit{\boldsymbol{y}}\left( k \right).} \end{array} $ | (21) |
用式(12)减去式(21), 得到状态观测器的误差方程:
| $ \begin{array}{l} \mathit{\boldsymbol{x}}\left( {k + 1} \right) - \mathit{\boldsymbol{\hat x}}\left( {k + 1} \right) = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\mathit{\boldsymbol{G}}\left( k \right) - {\mathit{\boldsymbol{K}}_{\rm{e}}}\mathit{\boldsymbol{C}}\left( k \right)} \right]\left[ {\mathit{\boldsymbol{x}}\left( k \right) - \mathit{\boldsymbol{\hat x}}\left( k \right)} \right]. \end{array} $ | (22) |
定义误差矢量
| $ \mathit{\boldsymbol{e}}\left( {k + 1} \right) = \left[ {\mathit{\boldsymbol{G}}\left( k \right) - {\mathit{\boldsymbol{K}}_{\rm{e}}}\mathit{\boldsymbol{C}}\left( k \right)} \right]\mathit{\boldsymbol{e}}\left( k \right). $ | (23) |
由式(23)可知, 误差信号的动态性能由矩阵G(k)-KeC(k)的特征根决定, 因此可以通过选择合适的观测器反馈增益矩阵Ke来实现观测误差的快速衰减.根据式(21), 观测器的特征方程为
| $ \left| {z\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{G}}\left( k \right) + {\mathit{\boldsymbol{K}}_{\rm{e}}}\mathit{\boldsymbol{C}}\left( k \right)} \right| = 0. $ | (24) |
将Ke按如下形式来选择:
| $ {\mathit{\boldsymbol{K}}_{\rm{e}}} = \left[ {\begin{array}{*{20}{c}} {{k_1}}&{{k_2}}\\ { - {k_2}}&{{k_1}} \end{array}} \right]. $ | (25) |
为了实现无差拍响应, 令观测器的特征方程为z2=0, 矩阵Ke中的未知参数需满足如下条件:
| $ \left. \begin{array}{l} {k_1} = \frac{{2{L_d}{L_q}}}{{{L_d} + {L_q}}} - {T_{\rm{s}}}{R_{\rm{s}}},\\ {k_2} = \pm \frac{{{L_q} - {L_d}}}{{{L_q} + {L_d}}}\sqrt {{L_d}{L_q}} . \end{array} \right\} $ | (26) |
忽略无差拍定子磁链观测器在反馈回路中引入的延时环节, 定子磁链控制回路如图 2中虚线框部分所示.可以看出, 在参考电压矢量的计算过程中, 需要确定增益矩阵K1和K2的取值.
在两相静止坐标系下, 定子磁链与定子电压之间的关系为
| $ \left[ {\begin{array}{*{20}{c}} {{u_{\alpha {\rm{s}}}}}\\ {{u_{\beta {\rm{s}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{R_{\rm{s}}}{i_{\alpha {\rm{s}}}}}\\ {{R_{\rm{s}}}{i_{\beta {\rm{s}}}}} \end{array}} \right] + {\left[ {\begin{array}{*{20}{c}} {\frac{{d{\psi _{a{\rm{s}}}}}}{{{\rm{d}}t}}}&{\frac{{d{\psi _{\beta {\rm{s}}}}}}{{{\rm{d}}t}}} \end{array}} \right]^{\rm{T}}}. $ | (27) |
根据式(27), 图 2中的定子电压补偿矢量Δus可以表示为[Rsiαs Rsiβs]T, 可令增益矩阵K1= K2.
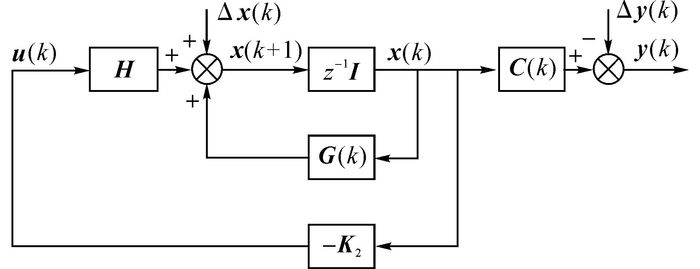
假设实际的定子磁链等于估算的定子磁链, 则定子磁链闭环控制回路的结构框图如图 5所示.通过选择合适的状态反馈增益矩阵K2, 可以将定子磁链闭环控制回路的极点放置在期望的位置上.
|
图 5 离散域状态反馈控制系统结构图 Fig. 5 State feedback control system in discrete-time |
在进行极点配置之前, 需要检测系统的能控性:
| $ {\rm{rank}}\left[ {\mathit{\boldsymbol{H}} \vdots \mathit{\boldsymbol{G}}\left( k \right)\mathit{\boldsymbol{H}}} \right] = 2. $ | (28) |
由于该能控性矩阵的秩等于系统的阶数, 该系统是完全能控的.式(12)所示的开环系统的特征方程为
| $ \left| {z\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{G}}\left( k \right)} \right| = \left( {z + \frac{{{T_{\rm{s}}}{R_{\rm{s}}}}}{{{L_d}}} - 1} \right)\left( {z + \frac{{{T_{\rm{s}}}{R_{\rm{s}}}}}{{{L_q}}} - 1} \right) = 0. $ | (29) |
如图 5所示, 令输入变量u(k)=-K2x(k), 可实现定子磁链闭环控制.状态反馈增益矩阵K2的选择通常需要综合考虑误差矢量的衰减速度以及系统的抗扰动能力.为了便于调试, 令
| $ {\mathit{\boldsymbol{K}}_2} = \left[ {\begin{array}{*{20}{c}} {m/{T_{\rm{s}}}}&0\\ 0&{m/{T_{\rm{s}}}} \end{array}} \right], $ |
在K2中预留一个未知数m, 调节闭环系统的性能:
| $ \begin{array}{l} \left| {z\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{G}}\left( k \right) + \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{K}}_2}} \right| = \\ \;\;\;\left( {z + \frac{{{T_{\rm{s}}}{R_{\rm{s}}}}}{{{L_d}}} - 1 + m} \right)\left( {z + \frac{{{T_{\rm{s}}}{R_{\rm{s}}}}}{{{L_q}}} - 1 + m} \right) = 0. \end{array} $ | (30) |
相比式(29), 式(30)可在一定范围内改变参数m的取值, 将矩阵G(k)-HK2的特征根沿z平面的正实轴方向移动, 实现对定子磁链控制环控制性能的调节.
传统PI-SVM DTC方案[15]直接根据式(27), 令参数m=1;将本文实验所用电机参数代入式(30)中, 可得系统的2个极点分别为:z1=-4.582e-3, z2=-3.098e-3.可见, 在传统PI-SVM DTC方案的定子磁链控制环中, 2个极点被直接放置在z平面负实轴距离原点很近的位置, 这导致系统的动态性能较差, 同时需要外部提供很高的直流母线电压来产生具有很强控制能力的输入变量[20].
根据估算的定子磁链和所选矩阵K2, 计算出参考电压矢量u(k)为
| $ \mathit{\boldsymbol{u}}_{\rm{s}}^ * = {\mathit{\boldsymbol{K}}_1}\mathit{\boldsymbol{\psi }}_{\rm{s}}^ * - {\mathit{\boldsymbol{K}}_2}{{\hat \psi }_{\rm{s}}} + \Delta {\mathit{\boldsymbol{u}}_{\rm{s}}}, $ | (31) |
| $\left[ {\begin{array}{*{20}{c}} {u_{\alpha {\rm{s}}}^*}\\ {u_{\beta {\rm{s}}}^*} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {m/{T_{\rm{s}}}}&0\\ 0&{m/{T_{\rm{s}}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {\psi _{\alpha {\rm{s}}}^* - {{\hat \psi }_{\alpha {\rm{s}}}}\left( k \right)}\\ {\psi _{\beta {\rm{s}}}^* - {{\hat \psi }_{\beta {\rm{s}}}}\left( k \right)} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{R_{\rm{s}}}{i_{\alpha {\rm{s}}}}\left( k \right)}\\ {{R_{\rm{s}}}{i_{\beta {\rm{s}}}}\left( k \right)} \end{array}} \right].$ | (32) |
为验证定子磁链矢量控制方案的有效性, 搭建一个5 kW IPMSM实验平台, 如图 6所示.利用型号为TMS320F2808的DSP执行有关控制算法.由1台7.5 kW IPMSM与1台5 kW内置式永磁同步发电机IPMSG通过联轴器直接相连, 组成相应的驱动测试平台.转子位置信息由IPMSM一侧1个10 000 p/r的增量式光电编码器通过正交编码的方式来提取.所有实验都围绕IPMSM展开, IPMSM的具体参数如表 1所示.系统的开关频率为10 kHz, 直流母线电压为500 V.实际的电机转矩输出和定子磁链的估算结果通过PCAN-USB接口从DSP中传输出来.

|
图 6 定子磁链矢量控制测试平台 Fig. 6 Test platform for direct stator flux vector control |
| 表 1 5 kW IPMSM测试平台的各项参数 Table 1 Parameters of 5 kW IPMSM test platform |
为检测如图 2所示的定子磁链控制回路的性能, IPMSG由1台安川A1000逆变器驱动, 工作在电动状态;IPMSM由搭建的实验平台供电, 运行在发电状态.整个驱动系统的运行转速由IPMSG一侧控制.为了对比定子磁链矢量控制方案与PI-SVM DTC方案的动态性能, PI-SVM DTC方案同样采用无差拍全阶状态观测器来获得定子磁链.实验中2种控制方案所用控制器的参数如表 2所示.
| 表 2 2种控制方案中的控制器参数 Table 2 Controllers' parameters for two control schemes |
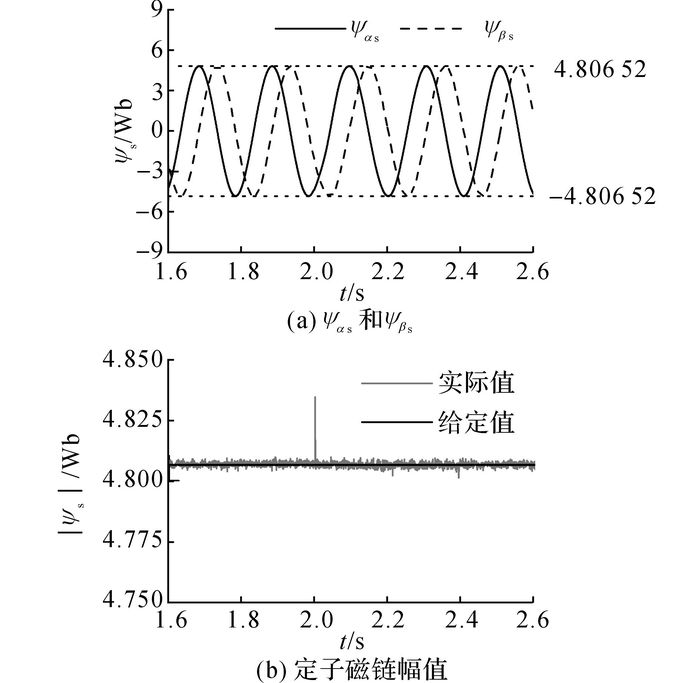
当转速为37.5 r/min时, 给定转矩角δ*在2.0 s由-0.055 003 rad阶跃至-0.091 537 rad时, 即给定转矩由-300 N·m阶跃至-500 N·m时, 定子磁链的估算结果如图 7所示.在图 7(b)中, 当给定转矩跳变时, 由于定子磁链不能突变, 在定子磁链的幅值中出现了一个很小的毛刺;在稳态中, 定子磁链幅值的实际值与给定值之间的误差很小.由此可见, 无差拍全阶状态观测器具有较高的观测精度.
|
图 7 基于无差拍全阶状态观测器对定子磁链的估算结果 Fig. 7 Estimated stator flux by dead-beat full-order state observer |
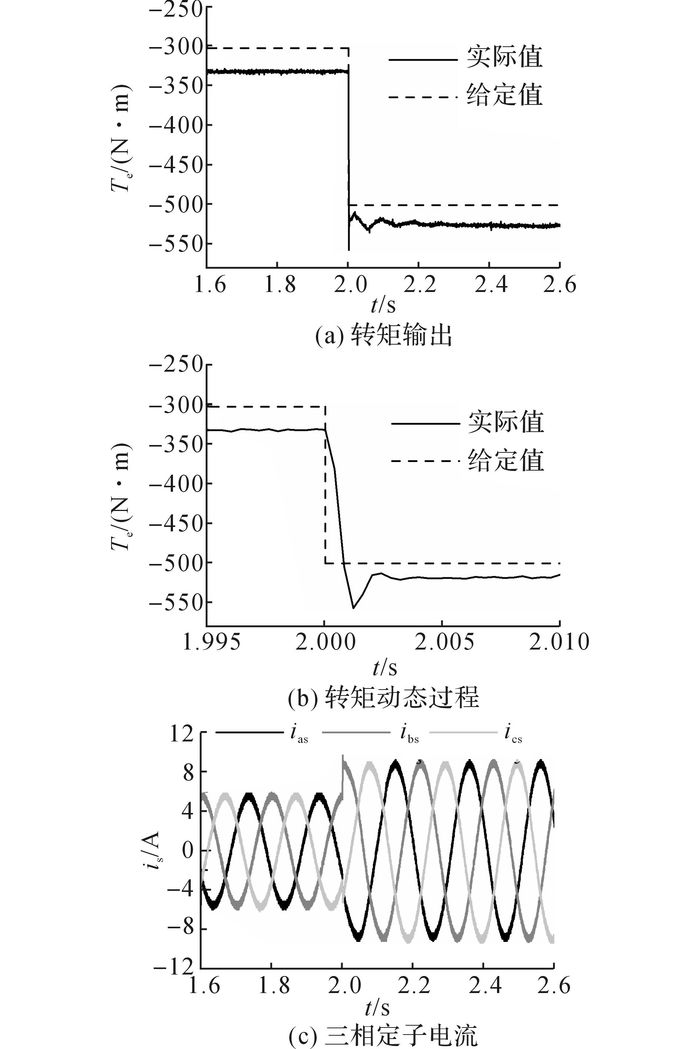
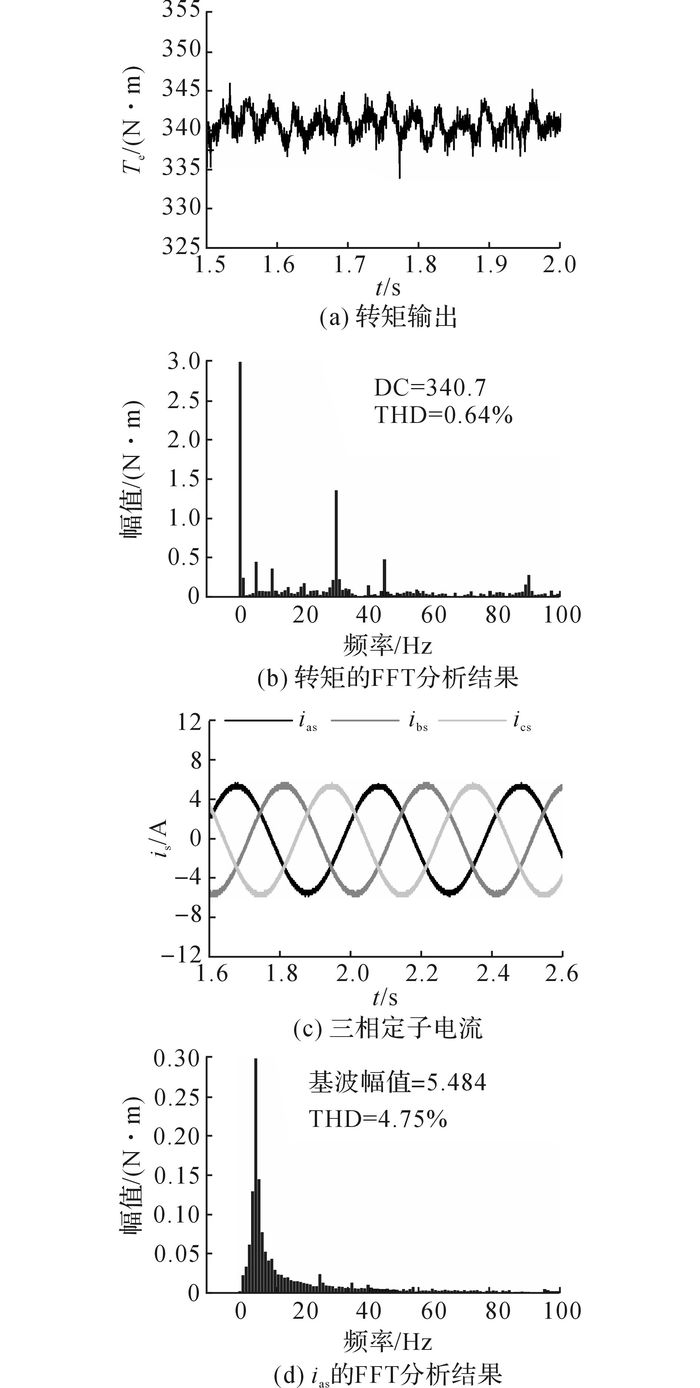
当转矩跳变时, 2种控制方案对应的转矩波形和电流波形分别如图 8和9所示.对比图 8(a)和9(a)可知,PI-SVM DTC方案的转矩输出中存在大约0.2 s的调节时间, 而定子磁链矢量控制方案中只有大约0.05 s的调节时间.对比图 8(b)和图 9(b)可知,PI-SVM DTC方案的转矩上升时间约为0.005 s, 而定子磁链矢量控制方案中转矩上升时间约为0.001 s.对比图 8(c)和图 9(c)所示的三相电流输出波形:PI-SVM DTC方案中存在明显的动态过程, 定子磁链矢量控制方案几乎是以阶跃跳变的方式变化到稳态值.

|
图 8 当给定转矩由-300 N·m阶跃至-500 N·m时PI-SVM DTC方案对应的实验结果 Fig. 8 Experimental results of PI-SVM DTC scheme when desired torque stept from -300 N·m to -500 N·m |
|
图 9 当给定转矩角由-0.055 003 rad阶跃至-0.091 537 rad时定子磁链矢量控制方案对应的实验结果 Fig. 9 Experimental results of stator flux vector control scheme when desired torque stept from -0.055 003 rad to -0.091 537 rad |
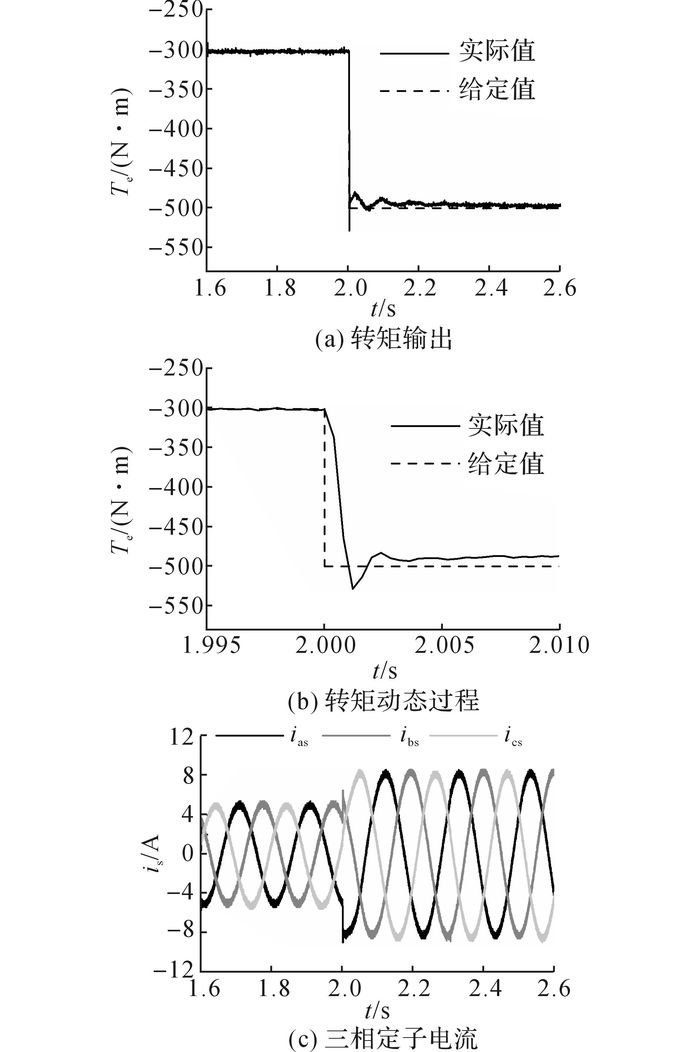
由于定子磁链矢量控制方案中不存在积分环节, IPMSM输出的转矩中存在一定的稳态误差[21].如图 9(a)所示, 在IPMSM的转矩输出中存在大约30 N·m的稳态误差.根据表 1所示的IPMSM参数, 取转矩导数kTe=5 475来简化转矩角补偿量Δδ的计算.为消除30 N·m的转矩稳态误差, 将转矩角补偿量Δδ=30/5 475= 0.005 479 452添加到转矩角的给定值中.相应的转矩输出波形和电流波形如图 10所示.
|
图 10 添加转矩角补偿的定子磁链矢量控制方案实验结果 Fig. 10 Experimental results of stator flux vector control scheme with compensatory torque angle |
从图 10(a)中可以看出, IPMSM输出的转矩基本随给定值变化, 而且对系统的动态性能基本无影响.定子磁链矢量控制系统中的转矩角给定值, 根据IPMSM的负载由速度控制环进行调节, 可忽略控制方案中的稳态误差问题.
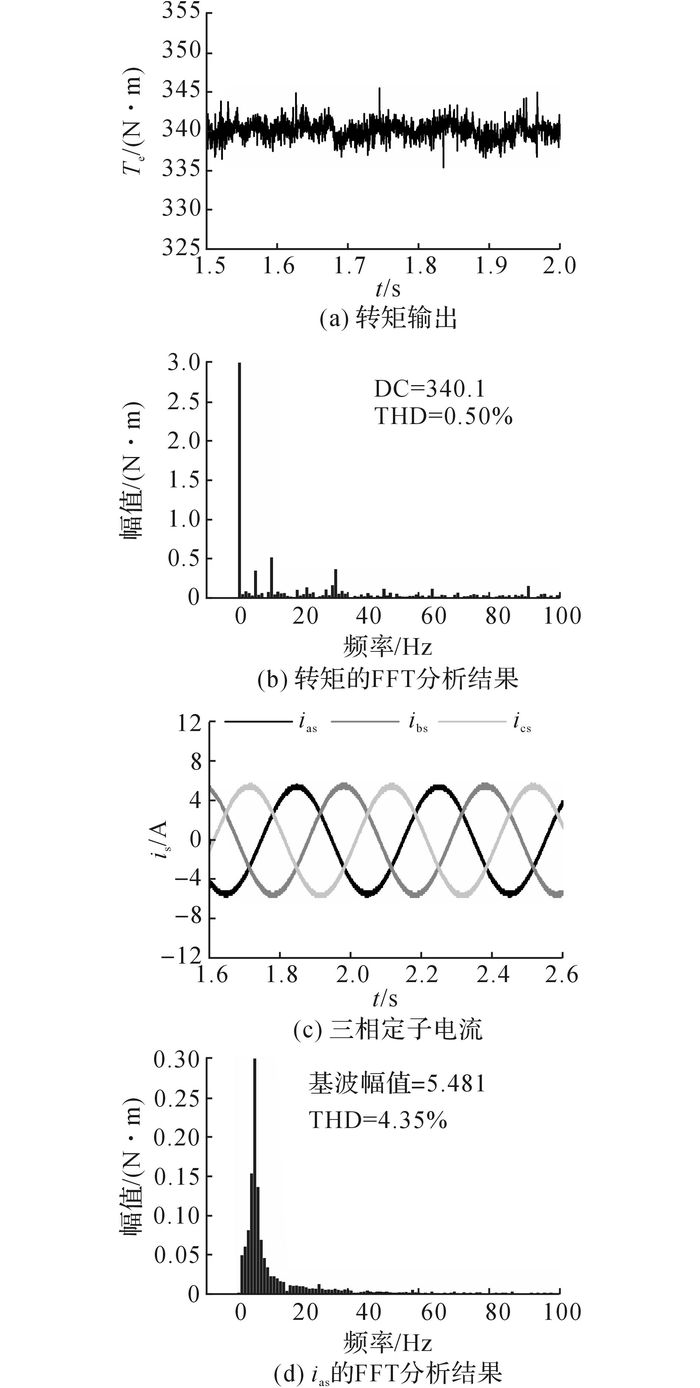
3.2 带速度外环的稳态运行测试为检测图 2中整个系统的控制性能, 在IPMSM控制系统中加入速度控制环, 通过IPMSM一侧来控制整个驱动系统的转速.在IPMSG的定子一侧连接3个9 Ω的电阻作为IPMSM的驱动负载.当转速为37.5 r/min时, 2种控制方案对应的转矩输出稳态波形和电流稳态波形分别如图 11和12所示.
|
图 11 转速为37.5 r/min时带速度控制环的PI-SVM DTC方案实验结果 Fig. 11 Experimental results of PI-SVM DTC scheme with speed outer loop control when running speed was 37.5 r/min |
|
图 12 当转速为37.5 r/min时带速度控制环的定子磁链矢量控制方案实验结果 Fig. 12 Experimental results of stator flux vector control scheme with speed outer loop control when running speed was 37.5 r/min |
对比图 11(b)和图 12(b)可知, 2种控制方案对应的转矩的基波分量基本相等;对比图 11(d)和图 12(d)可知, 2种控制方案对应的电机A相负载电流ias的基波分量也基本相等.由此可见, 速度控制环生成了定子磁链矢量控制方案所需的转矩角补偿量, 有效抑制了转矩输出中的稳态误差.此外, 对比2种控制方案的FFT(fast fourier transform)分析结果和THD(total harmonic distortion)值可以看出, 与PI-SVM DTC相比, 定子磁链矢量控制方案具有较小的转矩脉动输出和定子电流谐波.
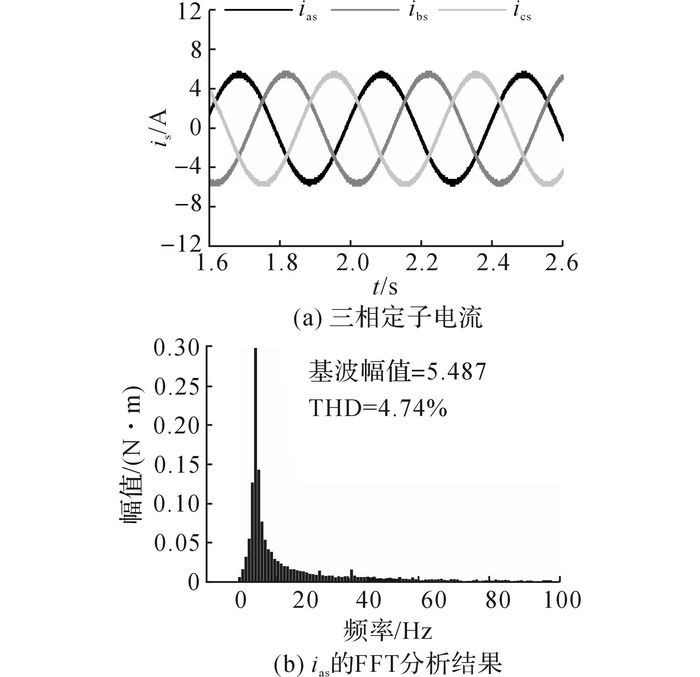
3.3 参数敏感性检测定子磁链矢量控制方案中存在大量电机参数, 将DSP中所用的IPMSM参数Rs、Ld、Lq和ψf分别增大20%, 以检验控制方案的参数鲁棒性.有关测试条件与3.2节相同, 相应的实验结果如图 13所示.
|
图 13 IPMSM参数增大20%时定子磁链矢量控制方案在转速为37.5 r/min时的实验结果 Fig. 13 Experimental results of stator flux vector control scheme at speed of 37.5 r/min when IPMSM parameters increased by 20% |
考虑到IPMSM输出的转矩是根据式(6)在DSP中计算后送出的, 当DSP中的IPMSM参数改变时, 输出量并非实际的电机转矩.因此, 这里只把通过电流探头直接测量到的IPMSM三相定子电流呈现出来, 如图 13所示.对比图 12(d)和图 13(b), 参数变化后的IPMSM A相定子电流ias的基波分量基本与参数未变化时的结果相等.由此可见, 定子磁链矢量控制方案具有较强的参数鲁棒性.
4 结语本研究提出了一种静止坐标系下适用IPMSM的定子磁链矢量控制方案.首先, 利用所构建的无差拍全阶状态观测器, 获得了较高的定子磁链的观测精度, 改善了系统的稳态性能.其次, 与PI-SVM DTC相比, 通过定子磁链矢量控制方案, 系统的动态性能得到了明显改善.为验证本文所提控制方案的有效性, 在相同的测试条件下, 分别检测PI-SVM DTC方案与本文所提控制方案的转矩动态性能和稳态性能.实验结果表明, 与PI-SVM DTC方案相比, 本文所提出的定子磁链矢量控制方案在保持较低转矩脉动输出的前提下, 获得了较高的转矩响应速度.
| [1] | GVEMES J A, IRAOLAGOITIA A M, DEL HOYO J I, e t, a l. Torque analysis in permanent-magnet synchronous motors:a comparative study[J]. IEEE Transactions on Energy Conversion, 2011, 26(1): 55–63. DOI:10.1109/TEC.2010.2053374 |
| [2] | HAQUE M E, RAHMAN M F. Incorporating control trajectories with the direct torque control scheme of interior permanent magnet synchronous motor drive[J]. IET Electric Power Applications, 2009, 3(2): 93–101. DOI:10.1049/iet-epa:20070518 |
| [3] | TAKAHASHI I, NOGUCHI T. A new quick-response and high-efficiency control strategy of an induction motor[J]. IEEE Transactions on Industry Applications, 1986(5): 820–827. |
| [4] | DEPENBROCK M. Direct self-control (DSC) of inverter-fed induction machine[J]. IEEE Transactions on Power Electronics, 1988, 3(4): 420–429. DOI:10.1109/63.17963 |
| [5] | ZHONG L, RAHMAN M F, HU W Y, et al. Analysis of direct torque control in permanent magnet synchronous motor drives[J]. IEEE Transactions on PowerElectronics, 1997, 12(3): 528–536. |
| [6] | ZAID S A, MAHGOUB O A, EL-METWALLY K A. Implementation of a new fast direct torque control algorithm for induction motor drives[J]. IET Electric Power Applications, 2010, 4(5): 305–313. DOI:10.1049/iet-epa.2009.0059 |
| [7] | CASADEI D, SERRA G, TANI K. Implementation of a direct control algorithm for induction motors based on discrete space vector modulation[J]. IEEE Transactions on Power Electronics, 2000, 15(4): 769–777. DOI:10.1109/63.849048 |
| [8] | SINGH B, JAIN S, DWIVEDI S. Torque ripple reduction technique with improved flux response for a direct torque control induction motor drive[J]. IET PowerElectronics, 2013, 6(2): 326–342. |
| [9] | BRANDO G, DANNIER A, DEL PIZZO A, et al. Generalised look-up table concept for direct torque control ininduction drives with multilevel inverters[J]. IET Electric Power Applications, 2015, 9(8): 556–567. DOI:10.1049/iet-epa.2014.0488 |
| [10] | YAN Y, ZHAO J, XIA C, et al. Direct torque control of matrix converter-fed permanent magnet synchronous motor drives based on master and slave vectors[J]. IET Power Electronics, 2015, 8(2): 288–296. DOI:10.1049/iet-pel.2014.0031 |
| [11] | KANG J K, SUL S K. New direct torque control of induction motor for minimum torque ripple and constant switching frequency[J]. IEEE Transactions on Industry Applications, 1999, 35(5): 1076–1082. DOI:10.1109/28.793368 |
| [12] | PACAS M, WEBER J. Predictive direct torque control for the PM synchronous machine[J]. IEEE Transactions on Industrial Electronics, 2005, 52(5): 1350–1356. DOI:10.1109/TIE.2005.855662 |
| [13] | NIU F, LI K, WANG Y. Direct torque control for permanent-magnet synchronous machines based onduty ratio modulation[J]. IEEE Transactions onIndustrial Electronics, 2015, 62(10): 6160–6170. DOI:10.1109/TIE.2015.2426678 |
| [14] | ZHANG Y, ZHU J. Direct torque control of permanent magnet synchronous motor with reduced torque ripple and commutation frequency[J]. IEEE Transactions on Power Electronics, 2011, 26(1): 235–248. DOI:10.1109/TPEL.2010.2059047 |
| [15] | TANG L, ZHONG L, RAHMAN M F, et al. A novel direct torque controlled interior permanent magnet synchronous machine drive with low ripple in flux and torque and fixed switching frequency[J]. IEEE Transactions on Power Electronics, 2004, 19(2): 346–354. DOI:10.1109/TPEL.2003.823170 |
| [16] | XU Z, RAHMAN M F. Direct torque and flux regulation of an IPM synchronous motor drive using variable structure control approach[J]. IEEE Transactions on Power Electronics, 2007, 22(6): 2487–2498. DOI:10.1109/TPEL.2007.909208 |
| [17] | ZHANG Y, ZHU J, XU W, et al. A simple method to reduce torque ripple in direct torque-controlled permanent-magnet synchronous motor by using vectors with variable amplitude and angle[J]. IEEE Transactions on Industrial Electronics, 2011, 58(7): 2848–2859. DOI:10.1109/TIE.2010.2076413 |
| [18] | ZHU H, XIAO X, LI Y. Torque ripple reduction of the torque predictive control scheme for permanent-magnet synchronous motors[J]. IEEE Transactions on Industrial Electronics, 2012, 59(2): 871–877. DOI:10.1109/TIE.2011.2157278 |
| [19] |
孙丹, 陈殷, 林斌. 基于集成观测器的PMSM无差拍直接转矩控制系统[J].
浙江大学学报:工学版, 2015, 49(6): 1079–1086.
SUN Dan, CHEN Yin, LIN Bin. Dead-beat direct torque control system of PMSM based on integrated observer[J]. Journal of Zhejiang University:Engineering Science, 2015, 49(6): 1079–1086. |
| [20] | 胡寿松. 自动控制原理[M]. 第5版. 北京: 科学出版社, 2007: 364-366. |
| [21] | 明尼苏达大学. 离散时间控制系统[M]. 第2版. 北京: 机械工业出版社, 2006: 405-434. |



