2. 嘉兴学院 机电工程学院, 浙江 嘉兴 314001;
3. 上海大学 应用数学与力学研究所, 上海 200072
2. College of Mechanical and Electrical Engineering, Jiaxing University, Jiaxing 314001, China;
3. Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, China
在微尺度气体流动中, 当气体分子平均自由程与气流的特征尺度相比不可忽略时, 需要考虑气流的非平衡效应, 速度滑移就是其中的重要效应之一[1].Knudsen数(Kn), 即气体分子平均自由程与气流特征尺度的比值, 是微尺度气流的重要参数.依据Kn数的大小, 将气体流动划分4个领域[2]:连续流区Kn<0.001、滑移流区0.001<Kn<0.1、过渡流区0.1<Kn<10和自由分子流区Kn>10.尽管Boltzmann方程是求解微尺度气流的基本方程[3-5], 但是由于其求解非常耗时, 尤其在滑移和近过渡流区, 利用Navier-Stokes方程加滑移边界条件的方法, 因其简洁有效, 仍然是求解微尺度气流问题的较好选择.
气固界面的速度滑移边界条件首次由英国学者Maxwell推导得到, 因此后人也称之为Maxwell速度滑移边界[6].Maxwell速度滑移边界条件为一阶形式, 为了扩展Navier-Stokes方程的适用范围, 许多学者基于不同的作用机理, 提出了速度滑移边界条件的二阶形式[6-15]或者对其一阶形式进行修正[16-17].Zhang等[18]对微尺度气流速度滑移边界模型进行了综述.
本文的内容安排如下:第一, 给出文献中典型的速度滑移边界模型, 指出其中滑移系数保持不变的特点;第二, 给出线性无量纲R13矩方程组及其求解的边界条件;第三, 基于微尺度气流Knudsen层外热通量为零, 理论推导扩展的速度滑移边界条件;第四, 以微尺度Poiseuille流为例, 验证扩展的速度滑移边界条件的有效性.
1 典型的速度滑移边界模型通常, 微尺度气流速度滑移边界条件[19]写成:
| $ {u_{\rm{s}}} = \frac{{2 - \alpha }}{\alpha }{A_1}\lambda \frac{{\partial u}}{{\partial n}} - {A_2}{\lambda ^2}\frac{{{\partial ^2}u}}{{\partial {n^2}}}. $ | (1) |
式中:∂u/∂n表示壁面附近气流沿壁面法向的速度梯度, A1、A2为滑移系数, α为壁面动量适应系数, λ为气体分子平均自由程.
基于不同的物理机制, 研究人员提出了各种不同的速度滑移边界形式, 归根到底在于滑移系数的不同.为了便于比较说明, 将文献中典型滑移边界条件的滑移系数列在表 1.可以看出, 目前文献中的速度滑移边界条件的滑移系数不随Kn数的变化而变化, 即, 与气体非平衡程度是无关的.针对相同的气体分子模型, 滑移边界中的滑移系数是否会随Kn数的变化而变化, 值得商榷.本文从R13矩方程[20]出发, 寻求一扩展的速度滑移边界条件, 其滑移系数不是固定的, 而是随Kn数的变化而变化.
| 表 1 典型速度滑移边界条件的滑移系数 Table 1 Slip coefficients of typical velocity slip boundaryconditions |
矩方法, 又称Grad矩方法[21], 由美国学者Grad首次提出, 作为求解Boltzmann方程的近似方法.与Chapman-Enskog展开[22]相比, Grad矩方法具有良好的线性稳定性.但是当激波的马赫数大于1.65时, Grad13矩方程组不能给出光滑的激波结构, 这一问题导致矩方法多年来发展缓慢[23].近年来, 不少学者对矩方法进行深入研究, 加以改进, 给出了正则化的R13矩方程组[20, 24]和完整的壁面边界条件[25-26], 使得矩方法重新引起人们的关注.关于矩方法及其改进的理论[20, 27-31], 这里不再详述.下面省略具体的推导过程, 直接给出等温情形下线性无量纲的R13方程组:
| $ \frac{{\partial \bar \rho }}{{\partial \bar t}} + \frac{{\partial {{\bar u}_i}}}{{\partial {{\bar x}_i}}} = 0, $ | (2) |
| $ \frac{{\partial {{\bar u}_i}}}{{\partial \bar t}} + \frac{{\partial \bar \rho }}{{\partial {{\bar x}_i}}} + \frac{2}{3}\frac{{\partial {{\bar \sigma }_{ij}}}}{{\partial {{\bar x}_j}}} = 0, $ | (3) |
| $ \frac{{\partial \bar T}}{{\partial \bar t}} + \frac{2}{3}\frac{{\partial {{\bar q}_i}}}{{\partial {{\bar x}_i}}} + \frac{2}{3}\frac{{\partial {{\bar u}_i}}}{{\partial {{\bar x}_i}}} = 0, $ | (4) |
| $ \frac{{\partial {{\bar \sigma }_{ij}}}}{{\partial \bar t}} + \frac{{\partial {{\bar m}_{ijk}}}}{{\partial {{\bar x}_k}}} = - \frac{{{{\bar \sigma }_{ij}}}}{{{\rm{Kn'}}}} - 2\frac{{\partial {{\bar u}_{\left\langle i \right.}}}}{{\partial {{\bar x}_{\left. j \right\rangle }}}} - \frac{4}{5}\frac{{\partial {{\bar q}_{\left\langle i \right.}}}}{{\partial {{\bar x}_{\left. j \right\rangle }}}}, $ | (5) |
| $ \frac{{\partial {{\bar q}_i}}}{{\partial \bar t}} + \frac{1}{2}\frac{{\partial {{\bar R}_{ij}}}}{{\partial {{\bar x}_j}}} = - \frac{2}{3}\frac{{{{\bar q}_i}}}{{{\rm{Kn'}}}} - \frac{{\partial {{\bar \sigma }_{ik}}}}{{\partial {{\bar x}_k}}} - \frac{1}{6}\frac{{\partial \Delta }}{{\partial {{\bar x}_i}}}. $ | (6) |
式中:ρ、ui、T、σij、qi、t分别为无量纲的气流质量密度、速度、温度、剪切应力、热通量和时间, i, j, k∈1, 2, 3, 且满足Einstein求和约定[32];下标旁的角括号表示张量的对称偏量部分;
| $ {\rm{Kn'}} = \frac{{\mu \sqrt {{T_0}} }}{{{p_0}L}},{\rm{Kn'}} = \sqrt {\frac{2}{{\rm{ \mathsf{ π} }}}} {\rm{Kn,}} $ |
p0、T0分别为平衡态时气流的压力、温度, μ为气体的黏度, L为气流的特征尺度;另外, 高阶矩量mijk、Rj、Δ分别为
| $ {{\bar m}_{ijk}} = - 2{\rm{Kn'}}\frac{{\partial {{\bar \sigma }_{\left\langle {ij} \right.}}}}{{\partial {x_{\left. k \right\rangle }}}},{{\bar R}_{ij}} = - \frac{{24}}{5}{\rm{Kn'}}\frac{{\partial {{\bar q}_{\left\langle i \right.}}}}{{\partial {{\bar x}_{\left. k \right\rangle }}}}, $ |
| $ \bar \Delta = - 12{\rm{Kn'}}\frac{{\partial {{\bar q}_k}}}{{\partial {{\bar x}_k}}}. $ |
R13矩方程组的求解, 需要一套合适的壁面边界条件, 仍然需要通过对Boltzmann方程的边界条件求矩得到.具体的推导过程参见文献, 这里直接给出与线性无量纲R13矩方程对应的壁面边界条件:
| $ {{\bar \sigma }_{{\rm{ \mathsf{ τ} n}}}} = - \frac{\alpha }{{2 - \alpha }}\sqrt {\frac{2}{{\rm{ \mathsf{ π} }}}} \left( {{{\bar u}_{\rm{s}}} + \frac{1}{5}{{\bar q}_\tau } + \frac{1}{2}{{\bar m}_{{\rm{ \mathsf{ τ} nm}}}}} \right), $ | (7) |
| $ {{\bar q}_n} = \frac{\alpha }{{2 - \alpha }}\sqrt {\frac{2}{{\rm{ \mathsf{ π} }}}} \left( { - 2{{\bar T}_{\rm{s}}} - \frac{1}{2}{{\bar \sigma }_{{\rm{nn}}}} - \frac{1}{{15}}\bar \Delta - \frac{5}{{28}}{{\bar R}_{{\rm{nn}}}}} \right), $ | (8) |
| $ {{\bar m}_{{\rm{nnn}}}} = - \frac{\alpha }{{2 - \alpha }}\sqrt {\frac{2}{{\rm{ \mathsf{ π} }}}} \left( { - \frac{2}{5}{{\bar T}_{\rm{s}}} + \frac{7}{5}{{\bar \sigma }_{{\rm{nn}}}} - \frac{1}{{75}}\bar \Delta + \frac{1}{{14}}{{\bar R}_{{\rm{nn}}}}} \right), $ | (9) |
| $ {{\bar m}_{{\rm{ \mathsf{ τ} \mathsf{ τ} n}}}} = \frac{\alpha }{{2 - \alpha }}\sqrt {\frac{2}{{\rm{ \mathsf{ π} }}}} \left( { - \frac{1}{5}{{\bar T}_{\rm{s}}} - {{\bar \sigma }_{{\rm{ \mathsf{ τ} \mathsf{ τ} }}}} + \frac{1}{5}{{\bar \sigma }_{{\rm{nn}}}} - \frac{1}{{150}}\bar \Delta - \frac{1}{{14}}{{\bar R}_{{\rm{ \mathsf{ τ} \mathsf{ τ} }}}}} \right), $ | (10) |
| $ {{\bar R}_{{\rm{ \mathsf{ τ} n}}}} = - \frac{\alpha }{{2 - \alpha }}\sqrt {\frac{2}{{\rm{ \mathsf{ π} }}}} \left( { - {{\bar u}_{\rm{s}}} + \frac{{11}}{5}{{\bar q}_{\rm{ \mathsf{ τ} }}} + \frac{1}{2}{{\bar m}_{{\rm{ \mathsf{ τ} nn}}}}} \right). $ | (11) |
式中:us=uτ-uτw, Ts=T-Tw分别为壁面附近气流的速度滑移和温度跳跃;uτw为壁面的速度, Tw为壁面的温度, 下标n和τ分别表示气流壁面的法向和切向.
3 扩展的速度滑移边界条件的推导不失一般性, 从半空间气体流动情形来推导扩展的速度滑移边界条件.半空间气流如图 1所示, 壁面静止, 且壁面温度与气流相同, 即等温情形.气流Knudsen层的厚度为L, Ωλ的位置在Knudsen层外, 且Ωλ>L.

|
图 1 半空间气体流动示意图 Fig. 1 Diagram of half space gas flows |
仅考虑一维情形的气体流动, 则线性无量纲R13矩方程写为
| $ \frac{{\partial {{\bar \sigma }_{xy}}}}{{\partial \bar y}} = - \frac{{\partial \bar p}}{{\partial \bar x}}. $ | (12) |
| $ \frac{{\partial {{\bar m}_{xyy}}}}{{\partial \bar y}} = - \frac{{{{\bar \sigma }_{xy}}}}{{{\rm{Kn'}}}} - \frac{{\partial {{\bar u}_x}}}{{\partial \bar y}} - \frac{2}{5}\frac{{\partial {{\bar q}_x}}}{{\partial \bar y}}, $ | (13) |
| $ \frac{1}{2}\frac{{\partial {{\bar R}_{xy}}}}{{\partial \bar y}} = - \frac{2}{3}\frac{{{{\bar q}_x}}}{{{\rm{Kn'}}}} - \frac{{\partial {{\bar \sigma }_{xy}}}}{{\partial \bar y}}. $ | (14) |
相应的壁面边界条件写为
| $ {{\bar u}_x} = - \beta {{\bar R}_{xy}} - \frac{1}{2}{{\bar m}_{xyy}} - \frac{1}{5}{{\bar q}_x}, $ | (15) |
| $ {{\bar q}_x} = - \frac{5}{{18}}\beta \left( {7{{\bar \sigma }_{xyy}} + {{\bar R}_{xy}}} \right) - \frac{5}{3}{{\bar u}_x} - \frac{{10}}{9}{{\bar m}_{xyy}}. $ | (16) |
式中:
| $ {{\bar m}_{xyy}} = - \frac{{16}}{{15}}{\rm{Kn'}}\frac{{\partial {{\bar \sigma }_{xy}}}}{{\partial \bar y}},\beta = \frac{{2 - \alpha }}{\alpha }\sqrt {\frac{{\rm{ \mathsf{ π} }}}{2}} ,{{\bar R}_{xy}} = - \frac{{12}}{5}{\rm{Kn'}}\frac{{\partial {{\bar q}_x}}}{{\partial \bar y}}. $ |
将Rxy带入式(14), 联立式(12), 有
| $ \frac{6}{5}{\rm{Kn'}}\frac{{{\partial ^2}{{\bar q}_x}}}{{\partial {{\bar y}^2}}} = \frac{2}{3}\frac{{{{\bar q}_x}}}{{{\rm{Kn'}}}} - \frac{{\partial \bar p}}{{\partial \bar x}}. $ | (17) |
式(17)是关于qx的二阶微分方程, 其中∂p/∂x作为常数项.对于二阶常微分方程, 根据高等数学常微分方程的求解方法, 不难得到其解:
| $ {{\bar q}_x} = {C_1}\sinh \left( {\frac{{\sqrt 5 }}{{3{\rm{Kn'}}}}\bar y} \right) + {C_2}\cosh \left( {\frac{{\sqrt 5 }}{{3{\rm{Kn'}}}}\bar y} \right) + \frac{3}{2}{\rm{Kn'}}\frac{{\partial \bar p}}{{\partial \bar x}}. $ | (18) |
其中, C1、C2为积分常数.式(18)表明, 气流的热通量包括两部分:一部分与气流压力有关, 另一部分则与气流Knudsen层的修正有关, 即式(18)中下划线的部分.
将式(15)代入式(16), 有
| $ {{\bar q}_x} = - \frac{5}{{12}}\beta \left( {{{\bar \sigma }_{xy}} + {{\bar R}_{xy}}} \right) - \frac{5}{{12}}{{\bar m}_{xyy}}. $ | (19) |
将mxyy、Rxy代入式(19), 有
| $ {{\bar q}_x} = - \frac{5}{{12}}\beta {{\bar \sigma }_{xy}} + \beta {\rm{Kn'}}\frac{{\partial {{\bar q}_x}}}{{\partial \bar y}} + \frac{4}{9}{\rm{Kn'}}\frac{{\partial {{\bar \sigma }_{xy}}}}{{\partial \bar y}}. $ | (20) |
根据气体动理论, 等温情形下, 在气流Knudsen层外, Knudsen层的修正效应将非常小, 近似为0, 即式(18)中下划线部分为0.因此, 当y=Ω时,
| $ {{\bar q}_x} = \frac{3}{2}{\rm{Kn'}}\frac{{\partial \bar p}}{{\partial \bar x}}. $ | (21) |
联立式(20)和(21), 有
| $ \begin{array}{l} - \frac{{\sqrt 5 }}{3}\beta {C_1}\cosh \left( {\frac{{\sqrt 5 }}{{3{\rm{Kn'}}}}\mathit{\Omega }} \right) - \frac{{\sqrt 5 }}{3}\beta {C_2}\sinh \left( {\frac{{\sqrt 5 }}{{3{\rm{Kn'}}}}\mathit{\Omega }} \right) = \\ - \frac{5}{{12}}\beta {{\bar \sigma }_{xy}} - \frac{3}{2}{\rm{Kn'}}\frac{{\partial \bar p}}{{\partial \bar x}} + \frac{4}{9}{\rm{Kn'}}\frac{{\partial {{\bar \sigma }_{xy}}}}{{\partial \bar y}}. \end{array} $ | (22) |
同理, 当y=0时, 联立式(18)和(20), 有
| $ - {C_1}\beta \frac{{\sqrt 5 }}{3} + {C_2} = - \frac{5}{{12}}\beta {{\bar \sigma }_{xy}} - \frac{3}{2}{\rm{Kn'}}\frac{{\partial \bar p}}{{\partial \bar x}} + \frac{4}{9}{\rm{Kn'}}\frac{{\partial {{\bar \sigma }_{xy}}}}{{\partial \bar y}}. $ | (23) |
最后, 联立式(22)和(23), 求出积分常数:
| $ \begin{array}{l} {C_1} = - \left[ {\frac{3}{{\sqrt 5 \beta }} + \sinh \left( {\frac{{\sqrt 5 }}{{3{\rm{Kn'}}}}\mathit{\Omega }} \right)} \right] \times \\ \frac{{ - \frac{5}{{12}}\beta {{\bar \sigma }_{xy}} - \frac{3}{2}{\rm{Kn'}}\frac{{\partial \bar p}}{{\partial \bar x}} + \frac{4}{9}{\rm{Kn'}}\frac{{\partial {{\bar \sigma }_{xy}}}}{{\partial \bar y}}}}{{\cosh \left( {\frac{{\sqrt 5 }}{{3{\rm{Kn'}}}}\mathit{\Omega }} \right) + \frac{{\sqrt 5 }}{3}\beta \sinh \left( {\frac{{\sqrt 5 }}{{3{\rm{Kn'}}}}\mathit{\Omega }} \right)}}, \end{array} $ |
| $ \begin{array}{l} {C_2} = \left[ {\cosh \left( {\frac{{\sqrt 5 }}{{3{\rm{Kn'}}}}\mathit{\Omega }} \right) - 1} \right] \times \\ \;\;\;\;\;\;\;\;\frac{{ - \frac{5}{{12}}\beta {{\bar \sigma }_{xy}} - \frac{3}{2}{\rm{Kn'}}\frac{{\partial \bar p}}{{\partial \bar x}} + \frac{4}{9}{\rm{Kn'}}\frac{{\partial {{\bar \sigma }_{xy}}}}{{\partial \bar y}}}}{{\cosh \left( {\frac{{\sqrt 5 }}{{3{\rm{Kn'}}}}\mathit{\Omega }} \right) + \frac{{\sqrt 5 }}{3}\beta \sinh \left( {\frac{{\sqrt 5 }}{{3{\rm{Kn'}}}}\mathit{\Omega }} \right)}}. \end{array} $ |
将式(18)再代入式(15), 有
| $ \begin{array}{l} {{\bar u}_x} = - \beta {{\bar \sigma }_{xy}} - \frac{1}{2}{{\bar m}_{xyy}} - \frac{1}{5}{{\bar q}_x} = \\ \;\;\;\;\;\; - \beta {{\bar \sigma }_{xy}} - \frac{8}{{15}}{\rm{Kn'}}\frac{{\partial {{\bar \sigma }_{xy}}}}{{\partial \bar y}} - \frac{3}{{10}}{\rm{Kn'}}\frac{{\partial \bar p}}{{\partial \bar x}} - \\ \;\;\;\;\;\;\frac{1}{5}\left[ {{C_1}\sinh \left( {\frac{{\sqrt 5 }}{{3{\rm{Kn'}}}}\bar y} \right) + {C_2}\cosh \left( {\frac{{\sqrt 5 }}{{3{\rm{Kn'}}}}\bar y} \right)} \right]. \end{array} $ | (24) |
将积分常数C1、C2代入式(24), 且令y=0,有
| $ \begin{array}{l} {{\bar u}_x} = - \beta {{\bar \sigma }_{xy}} + \frac{8}{{15}}{\rm{Kn'}}\frac{{\partial {{\bar \sigma }_{xy}}}}{{\partial \bar y}} - \frac{3}{{10}}{\rm{Kn'}}\frac{{\partial \bar p}}{{\partial \bar x}} - \\ \;\;\;\;\;\;\;\left( { - \frac{1}{{12}}\beta {{\bar \sigma }_{xy}} + \frac{4}{{45}}{\rm{Kn'}}\frac{{\partial {{\bar \sigma }_{xy}}}}{{\partial \bar y}} - \frac{3}{{10}}{\rm{Kn'}}\frac{{\partial \bar p}}{{\partial \bar x}}} \right)a = \\ \;\;\;\;\;\;\; - \left( {1 - \frac{a}{{12}}} \right)\beta {{\bar \sigma }_{xy}} + \left( {\frac{8}{{15}} - \frac{4}{{45}}a} \right){\rm{Kn'}}\frac{{\partial {{\bar \sigma }_{xy}}}}{{\partial \bar y}} - \\ \;\;\;\;\;\;\;\frac{3}{{10}}\left( {1 - a} \right){\rm{Kn'}}\frac{{\partial \bar p}}{{\partial \bar x}}. \end{array} $ |
简化后, 即得到壁面的速度滑移:
| $ {{\bar u}_x} = - \left( {1 - \frac{a}{{12}}} \right)\beta {{\bar \sigma }_{xy}} + \left( {\frac{5}{6} - \frac{7}{{18}}a} \right)\frac{{\partial {{\bar \sigma }_{xy}}}}{{\partial \bar y}}. $ | (25) |
其中,
| $ a = \frac{{\cosh \left( {\frac{{\sqrt 5 }}{{3{\rm{Kn'}}}}\mathit{\Omega }} \right) - 1}}{{\cosh \left( {\frac{{\sqrt 5 }}{{3{\rm{Kn'}}}}\mathit{\Omega }} \right) + \frac{{\sqrt 5 }}{3}\beta \sinh \left( {\frac{{\sqrt 5 }}{{3{\rm{Kn'}}}}\mathit{\Omega }} \right)}} $ |
式(25)为无量纲形式.为了与文献中的速度滑移边界条件比较, 利用
| $ {u_x} = \sqrt {R{T_0}} {{\bar u}_x},{\sigma _{xy}} = {\rho _0}{\rm{R}}{T_0}{{\bar \sigma }_{xy}},\lambda = \frac{\mu }{{{p_0}}}\sqrt {\frac{{{\rm{ \mathsf{ π} R}}{T_0}}}{2}} , $ |
| $ {p_0} = {\rho _0}{\rm{R}}{T_0},{\sigma _{xy}} = - \mu \frac{{\partial {u_x}}}{{\partial y}}, $ |
R为气体常数, 将式(25)改写成有量纲形式:
| $ {u_x} = \frac{{2 - \alpha }}{\alpha }\left( {1 - \frac{a}{{12}}} \right)\lambda \frac{{\partial u}}{{\partial y}} - \left( {\frac{5}{6} - \frac{7}{{18}}a} \right){\lambda ^2}\frac{{{\partial ^2}u}}{{\partial {y^2}}}, $ | (26) |
即为扩展的速度滑移边界条件.
可以看出, 式(26)与式(1)具有相同的形式, 且滑移系数不是固定的:
| $ {A_1} = 1 - \frac{a}{{12}},{A_2} = \frac{5}{6} - \frac{{7a}}{{18}}. $ |
以微尺度Poiseuille流为例, 如图 2所示, 则简化后的Navier-Stokes方程为

|
图 2 二维Poiseuille流 Fig. 2 Two-dimensional Poiseuille flows |
| $ \frac{{{\rm{d}}p}}{{{\rm{d}}{x_1}}} = \mu \frac{{{{\rm{d}}^2}{u_1}}}{{{\rm{d}}x_3^2}}. $ | (27) |
根据扩展的速度滑移边界条件, 可得式(27)的解:
| $ \begin{array}{l} {u_1} = - \frac{1}{{2\mu }}\frac{{{\rm{d}}p}}{{{\rm{d}}{x_1}}}\left[ {\left( {\frac{5}{6} - \frac{{7a}}{{18}}} \right){\lambda ^2} + } \right.\\ \;\;\;\;\;\;\;\left. {\frac{{2 - \alpha }}{\alpha }\left( {1 - \frac{a}{{12}}} \right)L\lambda + L{x_3} - x_3^2} \right]. \end{array} $ | (28) |
沿流道断面对式(28)积分, 得到质量流率为
| $ \begin{array}{l} Q = \int_0^L {\rho {u_1}{\rm{d}}{x_3}} = - \frac{\rho }{{2\mu }}\frac{{{\rm{d}}p}}{{{\rm{d}}{x_1}}}\left[ {\frac{{{L^3}}}{6} + \frac{{2 - \alpha }}{\alpha }\left( {1 - \frac{a}{{12}}} \right){L^2}\lambda + } \right.\\ \;\;\;\;\;\;\left. {\left( {\frac{5}{6} - \frac{{7a}}{{18}}} \right)L{\lambda ^2}} \right]. \end{array} $ | (29) |
为了便于比较, 将质量流率无量纲化, 有
| $ \begin{array}{l} \bar Q = \frac{Q}{{ - {L^2}\frac{{{\rm{d}}p}}{{{\rm{d}}{x_1}}}/\sqrt {2{\rm{R}}T} }} = \\ \;\;\;\frac{\pi }{2} + \frac{{2 - \alpha }}{\alpha }\left( {1 - \frac{a}{{12}}} \right)\frac{{\sqrt 2 }}{{12{\rm{Kn'}}}} + \left( {\frac{5}{6} - \frac{{7a}}{{18}}} \right)\frac{{{\rm{ \mathsf{ π} Kn'}}}}{{2\sqrt 2 }}. \end{array} $ | (30) |
为了验证扩展的速度滑移边界条件的有效性, 将不同速度滑移边界条件下的质量流率进行比较, 如图 3所示.实际计算中, 扩展的速度滑移边界条件中的参数取值:α=1.0, Ω=10.分析可知, 在近过渡流区扩展的速度滑移边界条件情形的质量流率与Cercignani and Lorenzani模型[11]和文献[13]中的滑移模型的结果非常接近, 两者与FK模型[33]的结果均匀较大偏差.尽管FK模型也是基于线性Boltzmann方程推导、计算得到的, 但是FK模型是基于Boltzmann-BGK模型方程[34], 而Cercignani & Lorenzani模型是基于线性Boltzmann硬球分子模型, 这是两者产生差别的原因.

|
图 3 不同速度滑移边界条件的Poiseuille流质量流率 Fig. 3 Mass flow rate of Poiseuille flow for differentvelocity slip boundary conditions |
另外, 由于文献[13]中的滑移模型中引入带有修正函数的有效分子平均自由程, 其分析结果在整个过渡流区与基于线性Boltzmann硬球分子模型的结果均非常接近.其他的速度滑移边界条件下的质量流率与基于线性Boltzmann硬球分子模型的分析结果相差较大.
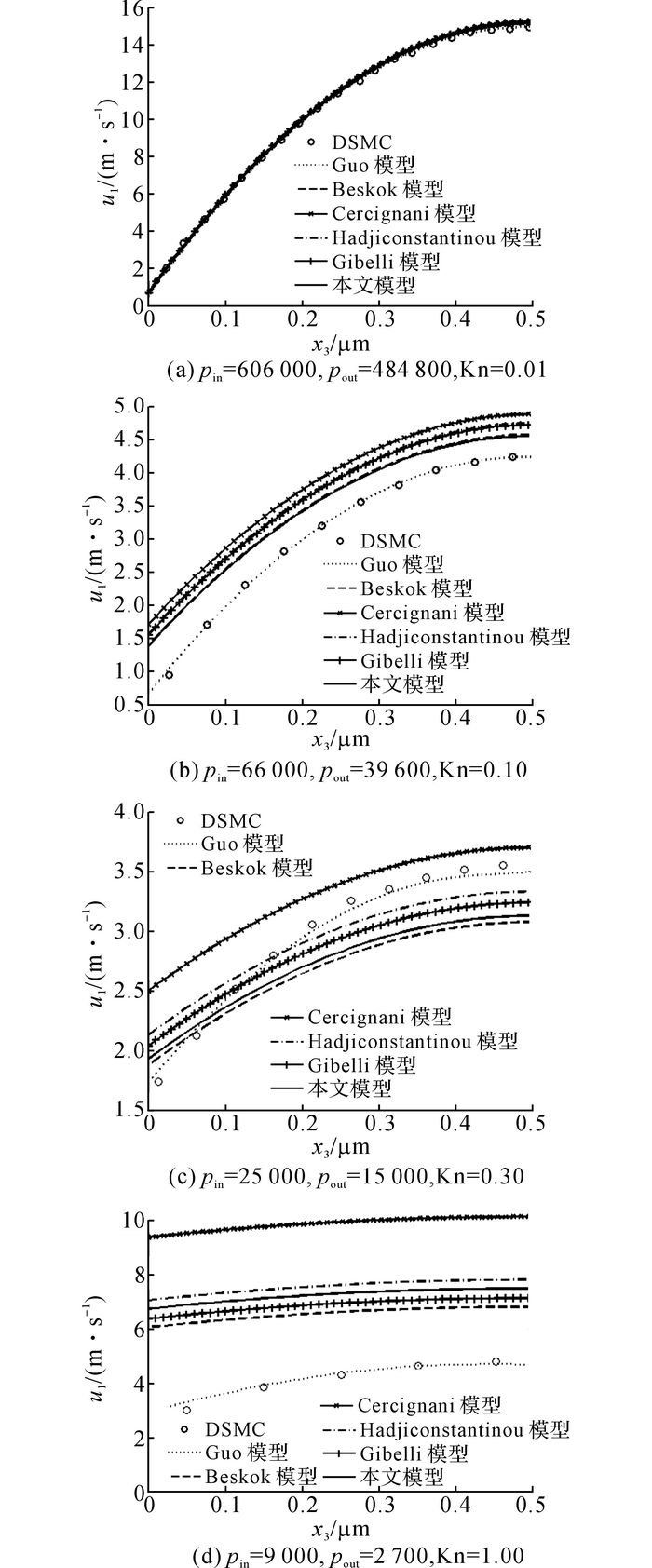
下面具体量化比较微槽道流的速度分布.为便于比较, 微槽道流的尺寸及两端压力参数选取文献[19]中的数据, 即微通道流的长度为50 μm, 高度为1 μm, 流动介质为氩气(Ar), 计算结果如图 4所示, 其中, pin为进口压力, pout为出口压力.
|
图 4 不同滑移边界条件下的微槽道流速度比较 Fig. 4 Comparison of micro channel flow velocitiesunder different velocity slip boundary conditions |
当Kn=0.01时(图 4(a)), 气流处于滑移流区, 不同速度滑移边界条件的结果均与直接模拟Monte Carlo (DSMC)[35]模拟吻合较好.当Kn=0.10时(图 4(b)), 气流处于滑移流区和过渡流区的交界处, 扩展的速度滑移边界条件情形下的气流速度与DSMC模拟结果更接近, 优于其他的速度滑移边界条件.当Kn=0.30时(图 4(c)), 气流处于过渡流区, 此时包括扩展的速度滑移边界条件在内, 各速度滑移边界情形下的结果明显偏离DSMC模拟结果.当Kn=1.00时(图 4(d)), 气流处于典型的过渡流区, 所有的速度滑移边界情形下的结果与DSMC模拟结果偏差较大, 已不能预测微槽道气流的速度.
另外, 基于Guo等[13]提出的速度滑移边界的分析结果始终与DSMC模拟结果较接近, 原因在于文献[13]的速度滑移边界模型中引入了复杂修正函数对分子平均自由程进行了修正.
5 结论(1) 该扩展的速度滑移边界优于现有文献中的速度滑移边界模型, 这是由于该滑移模型的滑移系数是变化的, 其大小取决于气流努森数和壁面适应系数, 这是本文最重要的结论;
(2) 气体动理论中, Boltzmann矩方程的形式与气体分子模型有关, 因此不同气体分子模型对应的扩展的速度滑移边界模型将存在差别, 这是课题组进一步研究的课题;
(3) 该扩展的速度滑移边界是基于气流和壁面等温情形得到的.对于不等温的情形, Boltzmann矩方程的数目将增加, 建模的复杂度随之增加, 如何构建扩展的速度滑移边界模型, 需要深入分析.
| [1] |
樊菁, 沈青. 微尺度气体流动[J].
力学进展, 2002, 32(3): 321–336.
FAN Jing, SHEN Qing. Micro-scale gas flows[J]. Advances in Mechanics, 2002, 32(3): 321–336. DOI:10.6052/1000-0992-2002-3-J2002-009 |
| [2] | 沈青. 稀薄气体动力学[M]. 北京: 国防工业出版社, 2003: 1-6. |
| [3] |
李志辉, 张涵信. 基于Boltzmann模型方程的气体运动论统一算法研究[J].
力学进展, 2005, 35(4): 559–576.
LI Zhi-hui, ZHANG Han-xin. Study on gas kinetic numerical algorithm using Boltzmann model equation[J]. Advances in Mechanics, 2005, 35(4): 559–576. DOI:10.6052/1000-0992-2005-4-J2004-072 |
| [4] |
李志辉, 张涵信, 符松. 用于Poiseuille等微槽道流的Boltzmann模型方程算法研究[J].
中国科学G辑, 2005, 35(3): 271–291.
LI Zhi-hui, ZHANG Han-xin, FU Song. Study on Boltzmann model equation algorithm applied in micro channel flows[J]. Science in China Serial G Physics, Mechanics and Astronomy, 2005, 35(3): 271–291. |
| [5] |
李志辉, 蒋新宇, 吴俊林, 等. 转动非平衡玻尔兹曼模型方程统一算法与全流域绕流计算应用[J].
力学学报, 2014, 46(3): 336–351.
LI Zhi-hui, JIANG Xin-yu, WU JUN-lin, et al. Gas-kinetic unified algorithm for Boltzmann model equation in rotational nonequilibrium and its application to the whole range flow regimes[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(3): 336–351. DOI:10.6052/0459-1879-13-246 |
| [6] | MAXWELL J C. On stresses in rarified gases arising from inequalities of temperature[J]. Philosophical Transactions of the Royal Society of London, 1879, 170: 231–256. DOI:10.1098/rstl.1879.0067 |
| [7] | CERCIGNANI C. Higher order slip according to the linearized Boltzmann equation[R]. Institute of Engineering Research Report AS-64-19, Berkeley:University of California, 1964. |
| [8] | DEISSLER R G. An analysis of second-order slip flow and temperature jump boundary conditions for rarefied gases[J]. International Journal of Heat and Mass Transfer, 1964, 7: 681–694. DOI:10.1016/0017-9310(64)90161-9 |
| [9] | HSIA Y T, DOMOTO G A. An experimental investigation of molecular rarefaction effects in gas lubricated bearings at ultra-low clearances[J]. Journal of Lubrication Technology, 1983, 105(1): 120–130. DOI:10.1115/1.3254526 |
| [10] | BESKOK A, KARNIADAKIS G E. A model for flows in channels, pipes and ducts at micro and nano scales[J]. Microscale Thermophysics Engineering, 1999, 3(1): 43–77. DOI:10.1080/108939599199864 |
| [11] | CERCIGNANI C, LORENZANI S. Variational derivation of second-order slip coefficients on the basis of the Boltzmann equation for hard-sphere molecules[J]. Physics of Fluids, 2010, 22: 062004. DOI:10.1063/1.3435343 |
| [12] | GIBELLI L. Velocity slip coefficients based on the hard-sphere Boltzmann equation[J]. Physics ofFluids, 2012, 24: 022001. DOI:10.1063/1.3680873 |
| [13] | GUO Z, QIN J, SHI B. Generalized second-order slip boundary condition for nonequilibrium gas flows[J]. Physical Review E, 2014, 89: 013021. DOI:10.1103/PhysRevE.89.013021 |
| [14] |
郭照立, 郑楚光, 施保昌. 微尺度流动的扩展二阶滑移边界条[J].
工程热物理学报, 2009, 30(8): 1383–1385.
GUO Zhao-li, ZHENG Chu-guang, SHI Bao-chang. An extended second order slip boundary condition for micro flows[J]. Journal of Engineering Thermophysics, 2009, 30(8): 1383–1385. |
| [15] | SCHAMBERG R. The fundamental differential equations and the boundary conditions for high speed slip flow and their application to several specific problems[D]. Pasadena:California Institute of Technology, 1947. http://www.openthesis.org/documents/fundamental-differential-equations-boundary-conditions-273231.html |
| [16] | SHEN S, CHEN G. A kinetic-theory based first order slip boundary condition for gas flow[J]. Physics of Fluids, 2007, 19(8): 086101. DOI:10.1063/1.2754373 |
| [17] |
张海军, 祝长生, 杨琴, 等. 广义的Maxwell速度滑移边界模型[J].
中国科学:物理学, 力学和天文学, 2013, 43: 662–669.
ZHANG Hai-jun, ZHU Chang-sheng, YANG Qin, et al. Generalized Maxwell velocity slip boundary model[J]. Science in China Serial G Physics, Mechanics & Astronomy, 2013, 43: 662–669. |
| [18] | ZHANG W M, MENG G, WEI X Y. A review on slip models for gas microflows[J]. Microfluidics and Nanofluidics, 2012, 13: 845–882. DOI:10.1007/s10404-012-1012-9 |
| [19] |
谢翀, 樊菁. Navier-Stokes方程二阶速度滑移边界条件的检验[J].
力学学报, 2007, 39(1): 1–6.
XIE Chong, FAN Jing. Assessment of second-order velocity slip boundary conditions of the Navier-Stokesequations[J]. Chinese Journal of Theoretical and Applied Mechanics, 2007, 39(1): 1–6. |
| [20] | STRUCHTRUP H. Macroscopic transport equations for rarefied gas flows[M]. Berlin: Springer, 2005. |
| [21] | GRAD H. On the kinetic theory of rarefied gases[J]. Communications on Pure and Applied Mathematics, 1949, 2: 331–407. DOI:10.1002/(ISSN)1097-0312 |
| [22] | 查普曼S, 考林TG. 非均匀气体的数学理论[M]. 北京: 科学出版社, 1985: 149-160. |
| [23] |
蔡振宁. 气体动理学中数值矩方法的算法研究与应用[D]. 北京: 北京大学, 2013.
CAI Zhen-ning. Investigations and applications of the numerical moment method in the kinetic theory of gases[D]. Beijing:Peking University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10001-1013024356.htm |
| [24] | STRUCHTRUP H, TORRIHON M. Regularization of Grad's 13 moment equations:derivation and linearanalysis[J]. Physics of Fluids, 2003, 15: 2668–2880. DOI:10.1063/1.1597472 |
| [25] | GU X J, EMERSON D R. A computational strategy for the regularized 13 moment equations with enhanced wall-boundary conditions[J]. Journal of Computational Physics, 2007, 225: 263–283. DOI:10.1016/j.jcp.2006.11.032 |
| [26] | TORRIHON M, STRUCHTRUP H. Boundary conditions for regularized 13-moment-equations for micro-channel-flows[J]. Journal of Computational Physics, 2008, 227: 1982–2011. DOI:10.1016/j.jcp.2007.10.006 |
| [27] | GUPTA V K, TORRIHON M. Higher order moment equations for rarefied gas mixtures[J]. Proceedings of the Royal Society A:Mathematical, Physical & Engineering Sciences, 2015, 471: 20150159. |
| [28] | RAHIMI B, STRUCHTRUP H. Capturing non-equilibrium phenomena in rarefied polyatomic gases:a high-order macroscopic model[J]. Physics of Fluids, 2014, 26: 052001. DOI:10.1063/1.4873577 |
| [29] | CAI Z N, FAN Y W, LI R. Globally hyperbolic regularization of Grad's moment system[J]. Communications on Pure and Applied Mathematics, 2014, 67(3): 464–518. DOI:10.1002/cpa.21472 |
| [30] | TANG G H, ZHAI G X, TAO W Q, et al. Extended thermodynamic approach for non-equilibrium gas flow[J]. Communications in Computational Physics, 2013, 13(5): 1330–1356. DOI:10.4208/cicp.301011.180512a |
| [31] | STRUCHTRUP H, TORRIHON M. Regularized 13 moment equations for hard sphere molecules:Linear bulk equations[J]. Physics of Fluids, 2013, 25: 052001. DOI:10.1063/1.4802041 |
| [32] | 吴望一. 流体力学[M]. 北京: 北京大学出版社, 1982: 52-56. |
| [33] | FUKUI S, KANEKO R. Analysis of ultra-thin gas film lubrication based on linearized Boltzmann equation:first report-derivation of a generalized lubrication equation including thermal creep flow[J]. Journal of Tribology, Transactions of the ASME, 1988, 110(2): 253–262. DOI:10.1115/1.3261594 |
| [34] | BHATNAGAR P L, GROSS E P, KROOK M. A model for collision processes in gases. I. small amplitude processes in charged and neutral one-component systems[J]. Physical Review, 1954, 94(3): 511–525. DOI:10.1103/PhysRev.94.511 |
| [35] | BIRD G A. Molecular gas dynamics and the direct simulation of gas flows[M]. New York: Oxford University Press, 1994: 208-216. |


