2. 大连理工大学 工业装备结构分析国家重点实验室, 辽宁 大连 116024;
3. 哈尔滨工程大学 船舶工程学院, 黑龙江 哈尔滨 150001
2. State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian 116024, China;
3. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China
随着绿色船舶[1]、节能减排[2]等环境保护要求的提出, 使用液化天然气(liquefied natural gas, LNG)作为燃料逐渐成为航运业的主流.双燃料主机以及配套的LNG加注设施应运而生.在LNG的加注方式中, 专用LNG加注船以其方便灵活、投资节省、极少占用码头资源等众多优势成为一个具有很强竞争力的LNG产业装备选择[3].但是, 不管LNG加注船的液舱还是作为燃料贮存的LNG燃料罐, 工作条件导致的晃荡问题无法避免, 晃荡载荷也是围护系统的一个重要设计载荷[4-5].
晃荡现象从根本上说是由自由液面运动引起的.当外界激励的频率接近液体固有频率时, 会产生非常剧烈的液体运动, 对液舱的结构产生较大的冲击, 同时产生的力矩会影响船舶的稳定性[6].在单自由度激励情况下, 共振现象一般在最低阶固有频率附近会产生较大的液体晃荡及对液舱顶部的冲击, 而随着共振阶数上升, 液体的自由液面变化非线性加剧, 产生的晃荡力会大幅减小[7].因此, 准确得出液舱内液体共振频率十分必要[8].Faltinsen等[9]基于线性势流理论, 对于不同形状液舱的固有频率进行理论推导, 求解出二维矩形、三维方形、直立圆柱形等形状液舱中液体固有频率的解析式.潘利剑等[10]采用瑞利-里兹法对圆柱形液舱进行模态分析, 利用商业软件ADINA进行验证, 拓展了算法的应用范围.Takahara等[11]利用平移及转动的激励方式, 研究环形立式圆柱液舱的频率响应, 试验发现环形立式圆柱液舱的非线性特性比普通立式圆柱液舱更加明显.
有学者研究发现, 液体晃荡出现共振时的频率并非理论固有频率, 而是略有偏差.Bouscasse等[12-13]发现在低液位时, 晃荡产生的最大抨击载荷发生在略低于固有频率的激励频率下.蒋梅荣等[14-15]研究了刚性方形舱的固有频率与共振频率的关系, 得出结论:当液深较浅时, 固有频率比共振频率约小5%;而当液深变深时, 理论值反而比试验值大5%~10%.卫志军等[16]研究了薄膜型液舱的晃荡固有频率, 发现虽然改进了固有频率的计算公式, 但理论固有频率与实际共振频率仍有偏差, 表现为:低液位时理论值偏大, 高液位时理论值偏小, 该研究将产生偏差的原因归结为模型的特殊性.
成本低廉、技术成熟的LNG独立C型液舱通常被应用于LNG加注船的货舱或LNG燃料储罐, 但针对其晃荡及固有频率的研究相对较少.本研究以中海油能源发展服务有限公司的研究课题“1 000 m3 LNG加注船液货系统国产化技术研究及试验”为背景, 以独立C型货舱为模型, 通过试验及数值分析研究自由震荡下固有频率及受迫振动下的共振频率, 对该形式液舱的共振现象进行描述.利用统计值结合不同的载液高度定量分析理论固有频率与共振频率的关系.
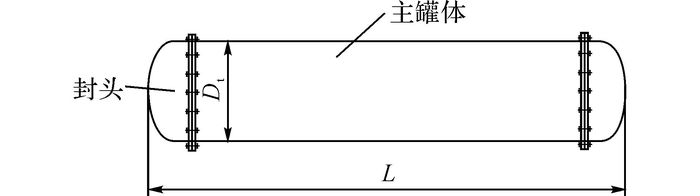
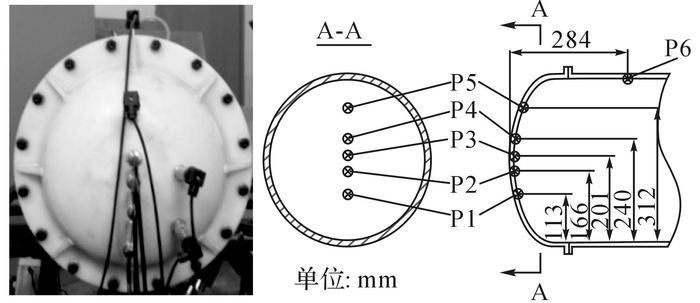
1 试验准备 1.1 液舱模型与试验介质液舱模型[17]由1 000 m3加注船的储液舱按照比例尺17.8︰1等比例缩小.液舱模型的总长度L=1.910 m, 外径Dt=0.400 m, 内径Di=0.380 m, 厚度为10 mm.根据LNG独立C型液舱的一般结构, 液舱模型由主罐体及2个封头组成(如图 1所示), 封头的型号为EHB 390×10 PMMA JB/T4746[18], 封头与主罐体通过螺栓进行连接.其中, 封头由聚氯乙烯(polyvinyl chloride, PVC)材料制成, 主罐体由有机玻璃制成.为了测量晃荡载荷, 在一端的封头及液舱顶部设置8个孔用于安装压力传感器, 各测量点的位置如图 2所示.
|
图 1 物理试验液舱模型 Fig. 1 Tank model of physical test |
|
图 2 压力传感器监测点在封头处的布置图 Fig. 2 Arrangement diagram of monitor points for pressure senor on head of test model tank |
根据文献[7]中不同形状液舱内液体固有频率的解析式可知, 液体固有频率仅与液舱形状、液体高度等有关, 液体本身属性并不影响其固有频率.因此, 试验中使用水作为试验介质, 对LNG液体进行模拟.为了使自由液面更加容易区分, 在水中滴入了大约5 mL的红墨水.
1.2 试验装置试验采用六自由度运动平台模拟晃荡运动, 如图 3(a)所示.运动平台的参数如表 1所示.其中, Ap为最大激励幅值, 单位为mm(平移运动)或°(摇摆运动);vcenter为相对于平台中心点的速度, 单位为mm/s(平移运动)或°/s(摇摆运动).平台通过6个电动缸的往复运动产生相应的激励, 由控制柜控制, 如图 3(b)所示, 控制指令由电脑中的软件发送.另外, 液舱模型采用实际LNG独立C型舱的固定形式安装在平台上.为了消除平台起振时的影响, 平台利用20 s的时间使激励稳步达到最大幅值.整个激励方式可以表示为

|
图 3 晃荡试验的激励及采集装置 Fig. 3 Excitation and acquisition devices in sloshingexperiment |
| 表 1 六自由度运动平台参数 Table 1 Parameters of six degree of freedom motion platform |
| $\theta \left( t \right) = \left\{ {\begin{array}{*{20}{l}} {\frac{{{\theta _{\rm{A}}}t}}{{20}}{\rm{sin}}\left( {2{\rm{ \mathit{ π} }}ft} \right),{\rm{ }}0 \leqslant t \leqslant 20;} \\ {{\theta _{\rm{A}}}{\rm{sin}}\left( {2{\rm{ \mathit{ π} }}ft} \right),{\rm{ }}t \geqslant 20.} \end{array}} \right.$ | (1) |
式中:θ为运动角度,θA为激励幅值,f为试验的激励频率,t为运动时间.
试验中使用齐平膜式传感器配合PLC采集模块采集晃荡引起的压力, 如图 3(c)所示, 其测量范围为0~10 KPa, 精度为0.2% FS(full scale, 满量程).此外, 晃荡引起的自由液面变化通过JVC高速摄像机捕捉, 如图 3(d)所示, 录制速度为50帧/s.
2 数值计算方法及模型本研究基于有限元离散方法, 进行液舱模型的模态分析, 其控制方程为
| $\mathit{\boldsymbol{M}}\ddot u + \mathit{\boldsymbol{C}}\dot u + \mathit{\boldsymbol{K}}u = - \mathit{\boldsymbol{M}}{\mathit{\boldsymbol{d}}_k}{a_k}\left( t \right).$ | (2) |
式中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;dk是方向矢量;ak为外界加速度, 当进行固有频率分析时, 假设整个待分析系统受到连续的重力加速度作用;u为待分析系统相对于地面的位移.
液舱模型中的流体介质借助势流体单元进行模拟.该流体单元是基于无旋、无黏、彼此间无热交换且流体边界只有小位移的势流理论假设, 即在流场内速度势φ满足拉普拉斯方程:
| ${\nabla ^2}\varphi = \frac{{{\partial ^2}\varphi }}{{\partial {x^2}}} + \frac{{{\partial ^2}\varphi }}{{\partial {y^2}}} + \frac{{{\partial ^2}\varphi }}{{\partial {z^2}}} = 0.$ | (3) |
势流体单元在壁面上需要满足的条件为
| $\partial \varphi /\partial n = 0.$ | (4) |
三维势流体单元的自由液面上动力学边界条件[9]为
| $\frac{{\partial \varphi }}{{\partial n}} + \frac{1}{2}{\left( {\nabla \varphi } \right)^2} - {\mathit{\boldsymbol{v}}_b} \cdot \nabla \varphi - g \cdot \mathit{\boldsymbol{r}} = 0.$ | (5) |
式中:φ为速度势, n为边界外法向, vb为液舱运动速度矢量, g为重力加速度, r为位置矢量.
通过引入势流体单元, 控制方程中的特征值问题通过下式进行求解:
| $\begin{gathered} \left( { - \omega _j^2\left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{M}}&0 \\ 0&{{\mathit{\boldsymbol{M}}_{{\rm{FF}}}}} \end{array}} \right] - {\omega _J}\left[ {\begin{array}{*{20}{c}} 0&{\mathit{\boldsymbol{C}}_{{\rm{FU}}}^{\rm{T}}} \\ {{\mathit{\boldsymbol{C}}_{{\rm{FU}}}}}&0 \end{array}} \right] + } \right. \hfill \\ \quad \left. {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{K}} + {{\left( {{\mathit{\boldsymbol{K}}_{{\rm{UU}}}}} \right)}_S}}&0 \\ 0&{{\mathit{\boldsymbol{K}}_{{\rm{FF}}}}} \end{array}} \right]} \right) \times \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{U}}^{\left( j \right)}}} \\ {{\mathit{\boldsymbol{F}}^{\left( j \right)}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 0 \\ 0 \end{array}} \right]. \hfill \\ \end{gathered} $ | (6) |
式中:F(j)=-iφ(j),
采用数值方法计算液舱模型的固有频率.由于没有外界激励, 该固有频率为液舱模型在自由振荡下的自然频率, 称为理论固有频率.利用试验系统, 结合FFT, 对晃荡载荷进行频谱分析, 验证计算结果.
3.1 数值计算结果对舱壁及液体建模, 划分4节点网格.将有机玻璃及PVC属性分别赋予液舱的主罐体及舱壁, 将水的材料属性赋予势流体单元.使用行列式搜索法(determinate search)分析液舱模型的固有频率.选定0.25Di、0.40Di和0.60Di 三个载液高度工况, 分别计算前3阶的纵向理论固有频率, 结果如表 2所示.
| 表 2 不同载液高度下的纵向理论固有频率 Table 2 Longitudinal theoretical natural frequency underdifferent filling levels |
利用试验系统对液舱模型内的液体, 在纵向自由振荡的条件下, 分析固有频率.通过六自由度运动平台激励液舱模型内液体使其达到一定的速度后, 静止液舱模型, 使用FFT对封头捕捉到的压力时历曲线进行频域变换, 根据能量谱峰值, 得到对应阶数的液体频率, 即纵向理论固有频率.
比较1阶、2阶、3阶纵向固有频率试验结果与数值计算结果, 并引入文献[19]中1阶圆筒型自然振动频率计算结果, 计算公式如下:
| ${T_n} = \frac{1}{{{f_n}}} = a\sqrt {\frac{l}{{g\,{\rm{tanh}}\left( {{\rm{ \mathsf{ π} }}h/l} \right)}}} .$ | (7) |
式中:fn为纵向理论固有频率,l为液舱长度, h为载液高度;D为液舱直径,
| $a = 1.8\sqrt {1 - \frac{h}{D}} + 2.5.$ |
比较结果如表 3所示, fexp为试验所得理论固有频率, ffor为文献公式所得理论固有频率;σexp为数值计算结果与试验及文献公式结果的相对误差;σfor为数值计算结果与公式计算结果的相对误差.通过与试验结果及文献公式结果的比较发现, 数值计算结果在1阶、2阶、3阶纵向模态下的固有频率分析中均具有较高的精度.
| 表 3 自由振荡工况下理论固有频率计算结果比较 Table 3 Comparison of computational results of theoreticalnatural frequencies under condition of free oscillation |
基于数值计算确定的液舱模型的理论固有频率, 利用试验系统分析受迫振动下的共振频率.选取3种不同载液高度工况, 分别进行局部扫频试验, 即在理论固有频率附近加密激励频率, 通过分析对比自由液面的变化及晃荡载荷大小, 确定共振频率.由于运动平台的精度限制, 最小增大的激励频率步长为0.01 Hz.试验激励方式为纵摇, 激励的幅值为3°.试验所用激励频率如表 4所示, fe为激励频率, Mfn为激励频率与理论固有频率的倍数.
| 表 4 受迫振动的晃荡试验工况 Table 4 Sloshing test condition with forced excitation |
当载液高度为0.25Di时, 激励频率达到0.59fn(0.13 Hz)时, 自由液面随激励运动, 如图 4(a)所示.由于激励频率过于远离固有频率, 液体表现出来的是在一侧封头的缓慢“堆积”现象.随着激励频率的升高, 液体将会沿封头曲面翻卷而下, 液面呈现出行波状态, 如图 4(b)所示.在激励频率超过固有频率, 达到1.50fn(0.33 Hz)时, 液体在过快的频率下, 无法进行“完全”地翻卷, 如图 4(c)所示.当激励频率继续增高至1.59fn(0.35 Hz)时, 液体呈现出驻波形式, 无法形成流动的自由液面.

|
图 4 0.25Di载液高度时不同激励频率下的舱内自由液面变化 Fig. 4 Deformation of free surface in tank under different excitation frequencies with filling level of 0.25Di |
当液位上升至0.40Di, 激励频率达到0.52fn(0.15 Hz)时, 液舱模型内液体开始晃动, 液面随激励上下抖动, 主要呈现驻波形式, 如图 5(a)所示.当激励频率达到0.59fn(0.17 Hz)之后, 液面出现行波状态, 在到达封头后翻卷.随着激励频率的不断升高, 自由液面翻卷幅度变大, 一部分液体快速到达封头上端后与其碰撞, 自由液面破碎, 形成飞溅的液滴, 如图 5(b)所示.当激励频率变为1.24fn(0.36 Hz)后, 一部分液体沿封头运动后飞溅而出, 而剩余被激励的液体则触壁反向运动, 如图 5(c)所示.当激励频率达到1.46fn(0.41 Hz)时, 快速的激励使液面恢复至驻波状态.

|
图 5 0.40Di载液高度时不同激励频率下的舱内自由液面变化 Fig. 5 Deformation of free surface in tank under different excitation frequency with filling level of 0.40Di |
当液位达到0.60Di, 激励频率为0.6fn(0.22 Hz)时, 液体开始随激励晃动, 液面呈现驻波状态.当激励频率达到0.69fn(0.25 Hz)后, 液面变为行波状态.与之前2个液位下的情况一样, 随着频率的升高, 液体行波运动速度加快, 在封头处形成翻卷, 如图 6(a)所示.但由于液位的升高, 液体翻卷的垂向空间减小, 导致液面破碎严重.当激励频率达到1.21fn(0.44 Hz)时, 受激励液体将拍击封头上端角隅处, 形成射流, 如图 6(b)所示.在该载液高度, 激励频率达到1.29fn(0.47 Hz)时, 液面恢复驻波状态.

|
图 6 0.60Di载液高度时不同激励频率下的舱内自由液面变化 Fig. 6 Deformation of free surface in tank under different excitation frequency with filling level of 0.60Di |
总体来说, 在单自由度简谐激励下, 液体晃荡开始于激励频率达到0.5fn后.当激励频率过高时, 液体会由于过快的激励频率无法晃动.终止晃荡的激励频率会随着液位的升高而下降.
4.2 晃荡载荷共振时液体会剧烈运动并给液舱结构带来较大的晃荡载荷, 因此, 基于试验工况, 提取每一工况下的晃荡载荷最大值.因为晃荡具有较强的随机性, 其体现在晃荡冲击载荷峰值的随机分布中[20], 所以晃荡载荷中的最大值可以表示出每一工况下液体的冲击程度.统计晃荡载荷的1/10最大值, 即提取载荷前1/10数量的较大值, 计算其平均值.该统计值可以表示出每一工况下整体晃荡载荷较大值的分布情况, 在一定程度上排除最大值的随机分布带来的干扰.
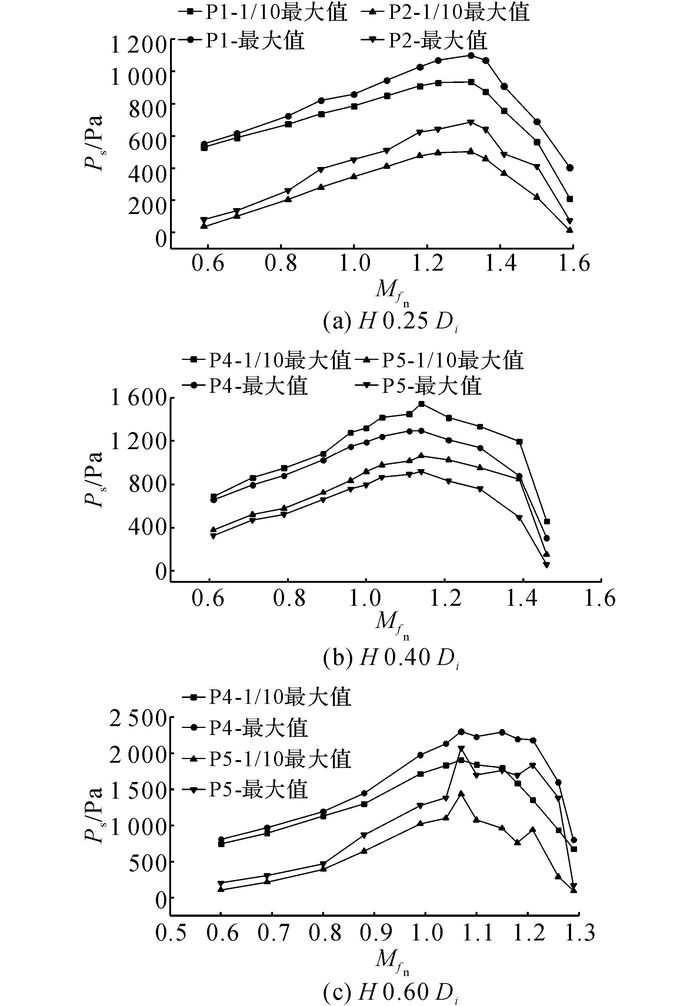
为了避免液体静压对结果的影响, 选取每个工况下自由表面处的监测点及其上部的监测点作为载荷比较对象.晃荡载荷的最大值、1/10最大值与激励频率的关系如图 7所示.Ps为晃荡载荷, 根据图 7(a)、(b)可知, 在0.25Di及0.40Di液位下, 2个监测点的载荷变化趋势基本保持一致.在0.60Di载液高度下, 监测点P5的最大值曲线变化趋势要比监测点P4剧烈, 尤其在Mfn=1.07~1.26时(见图 7(c)).原因是:自由液面上部监测点较少的受到液体静压的影响, 而在该激励频率区间, 晃荡会使液体对舱壁产生较大的冲击载荷, 凸显了载荷的最大值.
|
图 7 不同载液高度及不同工况下晃荡载荷的统计值 Fig. 7 Statistical value of sloshing pressure under different test conditions and different filling levels |
本文认为, 在不同载液高度下, 对应晃荡载的最大值与1/10最大值的激励激励频率, 即为共振频率, 如表 5所示.表中, dFL为液舱的液体深度, fr为共振频率, P1/10为晃荡载荷的1/10最大值, Pmax为晃荡载荷的最大值.通过表 5可以得出, 舱内液体的共振频率会与理论固有频率有所偏差, 这个偏差会随着dFL与L比值的增大而减小.具体来说, 在载液高度为0.25Di、0.40Di和0.60Di时, 共振频率分别比理论固有频率增大了31%、13%和7%.此外,文献[12-13]也提出了类似的结论.晃荡共振时的强非线性是造成这种偏差的主要原因.理论固有频率是液体自由震荡下的自然频率.在这种情况下, 液体自由液面的波动幅度较小, 液面形状可以得到很好的保持.从试验结果可以看到, 共振时自由液面发生旋转及破碎, 导致受迫振动下共振频率与理论固有频率的不同.
| 表 5 不同载液高度下晃荡载荷的统计分析 Table 5 Statistical analysis of sloshing pressure under different filling levels |
(1) 利用有限元离散方式结合势流理论, 计算了LNG独立C型舱的液体晃荡的理论固有频率.通过晃荡试验系统对数值算法的结果进行了验证, 同时与经验公式的计算结果进行比较, 表明数值算法有较高的精度.
(2) 利用晃荡试验系统, 使用外界激励在3种载液高度下进行了晃荡扫频试验, 当激励频率位于理论固有频率附近时, 减小激励频率间隔.通过观察分析自由液面的变化得出:在单自由度简谐激励达到0.5fn时, 液舱模型内的液体才会被激励晃荡;当激励频率过高时, 液体由于过快的激励频率而无法晃动;终止晃荡的激励频率随液位的升高而下降.
(3) 建立了不同液位下液舱模型晃荡载荷统计值与激励频率的关系, 得出了共振频率, 给出了不同载液高度与理论固有频率的对应关系, 即当载液高度为内直径的0.25、0.40和0.60时, 共振频率比理论固有频率分别增大31%、13%和7%.
| [1] | 林焰, 陈明, 王运龙, 等. 船舶设计原理[M]. 第5版. 大连: 大连理工大学出版社, 2016: 9-12. |
| [2] | LIN Y, YU Y Y, GUAN G. Research on energy efficiency design index for sea-going LNG carriers[J]. Journal of Marine Science and Application, 2014(4): 430–436. |
| [3] |
杨波, 盛苏建, 周斌. 1000 m3 LNG燃料加注船总体布置设计[J].
船海工程, 2014, 43(5): 138–141.
YANG Bo, SHENG Su-jian, ZHOU Bin. On general arrangement design of 1000 m3 LNG fuel bunker vessel[J]. Ship and Ocean Engineering, 2014, 43(5): 138–141. |
| [4] | 中国船级社. 液化天然气燃料加注船舶规范[S]. 北京, 2015: 1-30. http://www.cqvip.com/QK/95278X/201505/667666790.html |
| [5] | 中国船级社. 散装运输液化气体船舶构造与设备规范[S]. 北京: 人民交通出版社, 2006: 1-147. http://www.cqvip.com/Main/Detail.aspx?id=22880515 |
| [6] |
黄硕, 段文洋, 马庆位, 等. 液舱晃荡及其与船舶耦合运动问题的研究进展[J].
船舶力学, 2013(10): 1209–1220.
HUANG Shuo, DUAN Wen-yang, MA Qing-wei, et al. Research progress on sloshing and coupling motion of sloshing and ship[J]. Journal of Ship Mechanics, 2013(10): 1209–1220. DOI:10.3969/j.issn.1007-7294.2013.10.015 |
| [7] | JUNG J H, YOON H S, LEE C Y. Effect of natural frequency modes on sloshing phenomenon in a rectangular tank[J]. International Journal of Naval Architecture and Ocean Engineering, 2015, 7(3): 580–594. DOI:10.1515/ijnaoe-2015-0041 |
| [8] | FALTINSEN O M, TIMOKHA A N. Analytically approximate natural sloshing modes and frequencies in two-dimensional tanks[J]. European Journal ofMechanics-B/Fluids, 2014, 47: 176–187. DOI:10.1016/j.euromechflu.2014.01.005 |
| [9] | FALTINSEN O M, TIMOKHA A N. Sloshing[M]. Cambridge: Cambridge University Press, 2009: 48-192. |
| [10] |
潘利剑, 武湛君, 张博明, 等. 应用瑞利-里滋法分析储箱内液体晃动模态[J].
哈尔滨工程大学学报, 2007(1): 31–34.
PAN Li-jian, WU Zhan-jun, ZHANG Bo-ming, et al. Modal analysis of liquid filled in tank applying Rayleigh-Ritz method[J]. Journal of Harbin Engineering University, 2007(1): 31–34. |
| [11] | TAKAHARA H, KIMURA K. Frequency response of sloshing in an annular cylindrical tank subjected to pitching excitation[J]. Journal of Sound and Vibration, 2012, 331(13): 3199–3212. DOI:10.1016/j.jsv.2012.02.023 |
| [12] | BOUSCASSE B, ANTUONO M, COLAGROSSI A, et al. Numerical and experimental investigation of nonlinear shallow water sloshing[J]. International Journal of Nonlinear Sciences and Numerical Simulation, 2013, 14(2): 123–138. |
| [13] | DELORME L, COLAGROSSI A, SOUTO-IGLESIAS A, et al. A set of canonical problems in sloshing, Part Ⅰ:Pressure field in forced roll-comparison between experimental results and SPH[J]. Ocean Engineering, 2009, 36(2): 168–178. DOI:10.1016/j.oceaneng.2008.09.014 |
| [14] |
蒋梅荣, 任冰, 李小超, 等. 有限液深下弹性侧壁液舱内晃荡共振特性实验研究[J].
大连理工大学学报, 2014, 54(5): 558–567.
JIANG Mei-rong, REN Bing, LI Xiao-chao, et al. Experimental study of resonant behavior of sloshing inelastic bulkhead tanks under finite depth[J]. Journal of Dalian University of Technology, 2014, 54(5): 558–567. DOI:10.7511/dllgxb201405012 |
| [15] | JIANG M R, REN B, WANG G Y, et al. Laboratory investigation of the hydroelastic effect on liquid sloshing in rectangular tanks[J]. Journal of Hydrodynamics, Ser. B, 2014, 26(5): 751–761. DOI:10.1016/S1001-6058(14)60084-6 |
| [16] |
卫志军, 阮诗伦, 岳前进, 等. 超大型储液舱内晃荡载荷实验研究[J].
海洋工程装备与技术, 2014, 1(1): 55–61.
WEI Zhi-jun, RUAN Shi-lun, YUE Qian-jin, et al. Experimental investigation of liquid slsohing impact load in a large-scale prismatic tank[J]. Ocean Engineering equipment and Technology, 2014, 1(1): 55–61. |
| [17] | 管官, 林焰, 陈明, 等. 可变组合式C型LNG液舱晃荡模型试验装置及试验方法[P]. 201410359571. 4. 2014-07-28. |
| [18] | 中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 中华人民共和国国家标准GB/T25189-2010: 压力容器用封头[S]. 中国标准出版社, 2010: 1-64. |
| [19] |
戴经武. 全压式液化气船设计[J].
船舶, 1993(1): 1–10.
DAI Jing-wu. The design of fully pressurized carrier[J]. Ship and Boat, 1993(1): 1–10. |
| [20] | KIM S Y, KIM Y, KIM K H. Statistical analysis of sloshing-induced random impact pressures[J]. Proceedings of the Institution of Mechanical Engineers, Part M:Journal of Engineering for the Maritime Environment, 2014, 228(3): 235–248. DOI:10.1177/1475090213492807 |



