2. 中车青岛四方机车车辆股份有限公司 国家高速动车组总成工程技术研究中心, 山东 青岛 266111
2. National Engineering Research Center for High-speed EMU, CRRC Qingdao Sifang Co. Ltd, Qingdao 266111, China
目前, 一般采用风洞试验方法来研究高速列车明线运行时受到的阻力、升力及车体表面压力分布等气动特性;采用动模型试验方法对列车通过隧道、列车交会时的非定常气动特性进行研究.数值方法主要通过模型试验结果来进行考核和修正[1].
研究列车气动特性中应用最广泛的手段之一的列车模型试验, 具有试验理论和试验手段成熟、测量精密、气流参数(如:速度、压力)易于控制、天气变化基本上不受影响等优点[2].由于模型试验存在受雷诺数影响等问题, 当采用模型缩比时, 会出现试验流场雷诺数远小于真实流场雷诺数的情形.雷诺数在一定范围内会出现自模拟区[3], 此时雷诺数对列车气动力、压力等参数的影响比较小[4].对于自模拟区的范围和影响程度, 以及是否可以在实际列车中应用模型试验的结果等问题, 目前一直没有准确的结论[5].该问题已经引起专家和学者的广泛关注[6].黄志祥等[7]指出影响高速列车模型风洞试验结果的因素众多, 列车模型缩比就是其中之一.牛纪强等[8]通过风洞试验的方法研究了雷诺数效应对列车气动力的影响, 并未涉及对于列车交会压力波的研究.目前, 公开报道的国外文献多侧重于高速列车模型试验研究结果的讨论, 而鲜有关于缩比尺度变化的研究结果[9].因此, 本文通过研究不同模型缩比模型对列车气动性能的影响, 找到将模型试验结果推广到实际列车上的方法, 并进一步修正和指导数值方法的工作, 为推导实车气动参数提供指导.采用数值模拟计算的方法来研究列车交会压力波已经相对比较成熟, 现有的计算方法完全能够满足工程计算精度的要求[10].
本文通过对高速列车明线运行、明线交会、隧道通过以及隧道交会工况进行全面数值模拟, 综合研究尺度效应对高速列车气动力以及交会压力波的影响.
1 数值计算方法高速列车运行工况包括明线运行(含侧风)、明线交会、隧道通过(单车或双线隧道)以及隧道交会[11].不同的运行工况需要采用不同的计算方法[12].
对于列车明线运行工况, 当列车运行速度较低(低于350 km/h)时, 空气密度ρ的变化对流动的影响可以略去不计, 此时, 数值求解中可以采用不可压缩流动的基本控制方程, 认为空气密度为常数, ρ=1.225 kg/m3[13].不可压缩流的基本控制方程采用纳维-斯托克斯(Navier-Stokes, N-S)方程[14]:
| $\frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial {x_i}}}\left( {\rho {u_i}} \right) = 0.$ | (1) |
式中:ui为列车周围流场的速度, 代表u、v、w三个坐标方向的速度分量;xi为坐标的三分量, 分别代表x、y、z三个方向坐标.
由式(1)推导出直角坐标系下的运动方程:
| $\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \rho u}}{{\partial x}} + \frac{{\partial \rho v}}{{\partial y}} + \frac{{\partial \rho w}}{{\partial z}} = 0.$ | (2) |
数值计算就是基于由式(1)和(2)组成的不可压缩流动方程组进行求解[15].在不可压缩流动模型中, 能量方程与连续方程和运动方程不耦合, 因此, 无需引入能量方程.湍流模型根据工程经验, 采用基于RANS方法的k-ω SST两方程湍流模型.
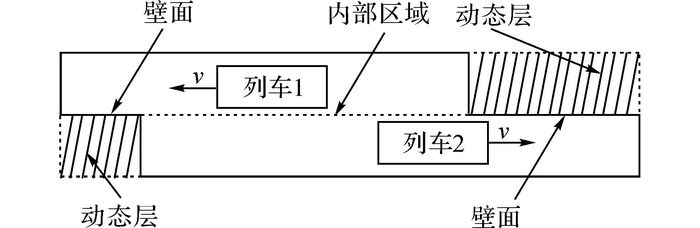
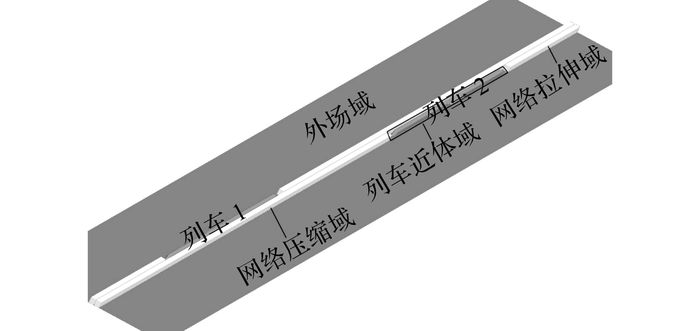
对于列车明线交会、隧道通过以及隧道交会工况, 由于在计算过程中, 列车是运动的, 需要引入动网格技术.本文所采用的动网格技术主要为动态分层法[16], 列车交会动网格示意图如图 1所示.将整个计算域的流场划分为4个子区域:列车的近体域、列车前方的网格压缩域、列车后方的网格拉伸域以及外场域[17], 如图 2所示.
|
图 1 列车交会动网格示意图 Fig. 1 Diagram of dynamic mesh for train crossing |
|
图 2 列车交会计算域分区示意图 Fig. 2 Diagram of calculation domain division for train crossing |
采用“头车+中间车+尾车”3车编组的动车组作为计算模型, 并对其进行简化处理, 不模拟受电弓及车体表面的一些细小部件, 如图 3所示.

|
图 3 动车组计算模型 Fig. 3 Electric Multiple Units calculation model |
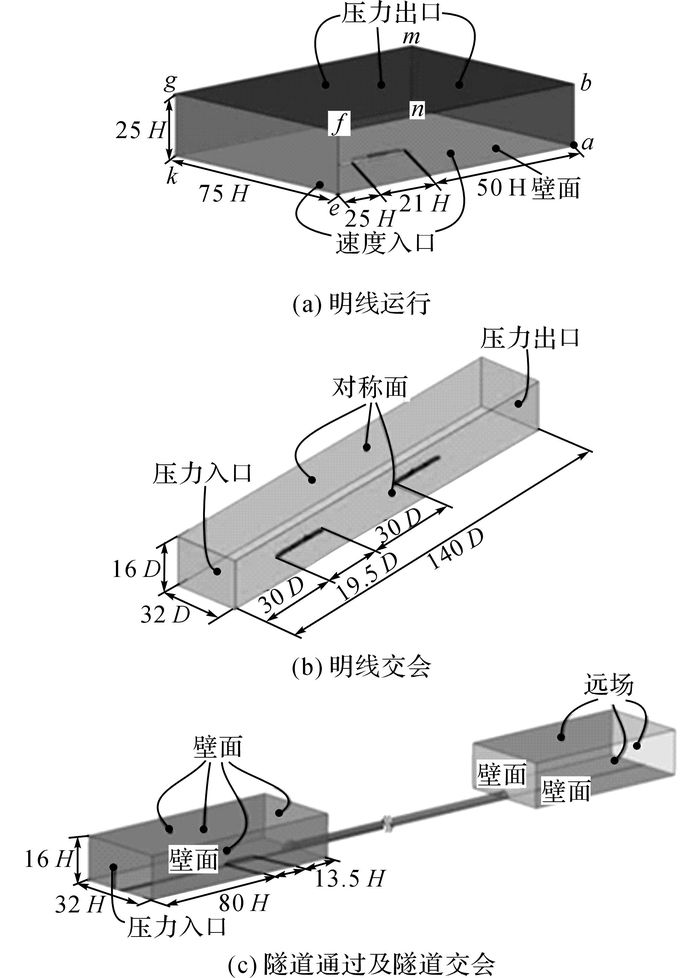
对于明线运行工况, 为了保证流场的充分发展, 避免边界条件对所关心区域流场结构的影响, 计算流域的长、宽、高分别为92.5H、75H和25H(H为列车的高度, 取H=3.7 m), 列车初始位置鼻尖点位于距入口边界条件25H处.为了避免出口边界条件对列车尾流的影响, 尾涡区域为50H.计算区域如图 4(a)所示.
|
图 4 各工况下的计算外场示意图 Fig. 4 Diagram of calculation domain under various working conditions |
列车明线交会计算区域如图 4(b)所示, 为真实模拟列车交会全过程, 在保证列车交会时列车周围流场已充分发展, 对计算结果影响不大的情况下, 设定两列车初始位置相距30D, (D为列车的特征长度, 取D=3.7 m).
列车过隧道的计算区域如图 4(c)所示, 为真实模拟列车通过隧道全过程, 在保证列车进入隧道洞口前, 列车周围流场已充分发展, 同时保证对计算结果影响不大, 选择列车初始位置距离隧道洞口13.5H处.
3 计算网格列车周围采用结构网格进行划分, 并对车身表面附近的单元进行加密处理.第一层网格厚度为0.000 5 m, 满足所选湍流模型对计算得到的壁面函数Y+值的要求, 空间体单元数量约为3.0×107.车身表面离散网格图如图 5所示.隧道入口附近处最小网格间距为0.05 m, 列车运行方向隧道上网格间距为0.10 m.整个流场体网格数不少于2 000万.

|
图 5 不同工况下的计算网格划分结果 Fig. 5 Calculation mesh divided results under different working conditions |
边界条件的参数(如:进口、固体壁面、对称位置面、出口)直接影响求解过程的效率和结果的准确性[18].
如图 4所示, 对于明线运行工况, 列车表面均设置为无滑移壁面, 入口边界为速度入口, 出口边界为压力出口.地面边界条件设置为移动壁面, 其移动速度与列车速度相同.对于明线交会、隧道通过以及隧道交会工况, 列车运行方向的流场两端的外表面的进出口采用压力边界条件, 进出口远离列车交会区域, 压力值变化亦不大, 进出口压力值设定为大气压力.
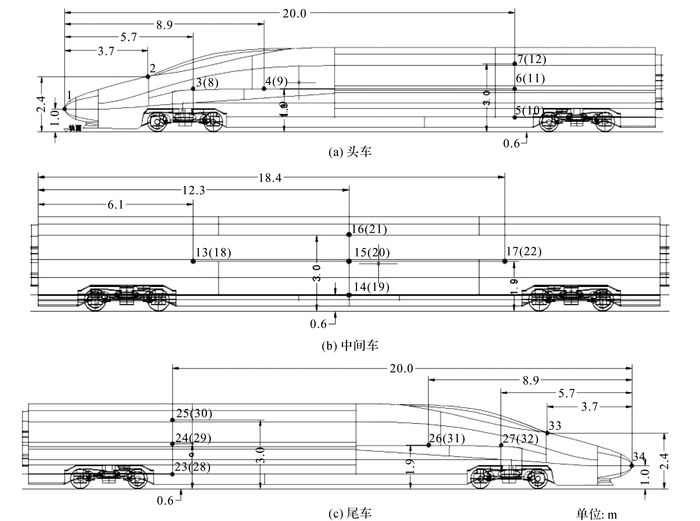
对3车编组动车组车体表面共布置34个测点:头车12个测点, 尾车12个测点, 中间车10个测点, 如图 6所示.
|
图 6 动车组(EMU)测点布置图 Fig. 6 Layout of monitor points on electric multiple units (EMU) |
计算网格的质量和数量关乎着计算结果的准确性和稳定性[19].为了验证不同计算网格对数值计算结果的影响, 在保证计算网格质量的前提下, 采用列车表面划分三棱柱的边界层网格和空间划分非结构化网格进行网格无关性验证.分别划分出粗、中、稀3套计算网格, 网格量分别为3 010万、4 240万和5 560万, 所有计算网格的第一层边界层网格的厚度均满足壁面函数的要求.
采用3套计算网格分别进行计算验证, 选取头车表面某测点的压力系数作为监测点进行验证, 计算得到的测点的压力系数值分别为0.040 0、0.039 7、0.040 2.从计算结果可以得知, 计算网格的数量对监测点的压力系数的影响并不明显, 压力系数变化很小, 误差均小于1%, 因此, 计算网格对计算结果的影响可以忽略.考虑到CFD流场计算的效率, 本文选用3 010万量级的网格.
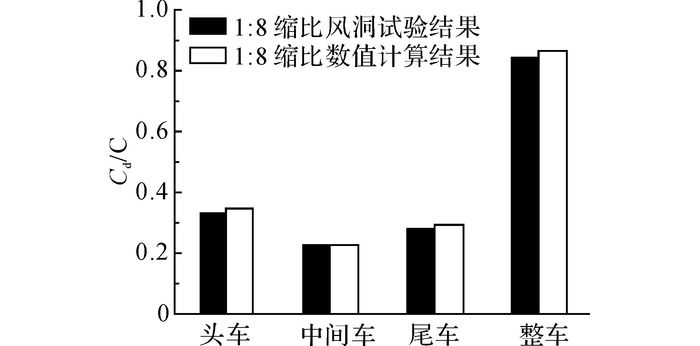
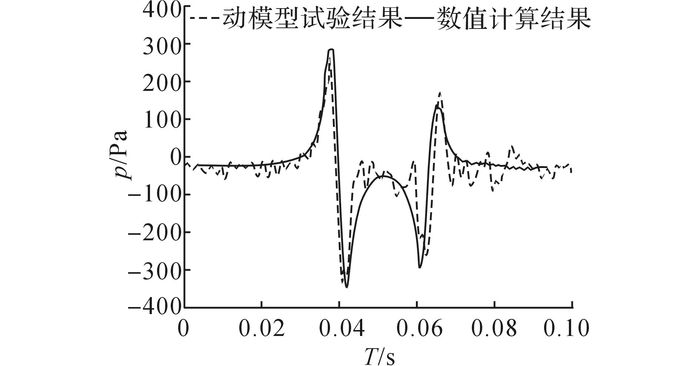
为了验证数值计算的准确性, 将模型缩比λ=1/8的数值计算的阻力系数Cd的结果与风洞试验的结果进行对比(数值计算的工况设置与风洞试验完全一致).头车、中间车、尾车及整车的阻力系数与风洞试验结果对比如图 7所示(C为某一固定常数).此外, 为了验证动网格技术计算的精度, 将数值计算的交会压力波的结果与动模型试验的结果进行对比, 如图 8所示.其中, p为列车表面的测点压力, T为两列车交会时间.由图 7、8可以看出, 数值计算的结果与风洞试验以及动模型试验的结果吻合较好, 保证了计算的精度, 数值计算的可靠性得到保证.
|
图 7 模型缩比为1/8时的数值计算的阻力系数与风洞试验结果对比 Fig. 7 Results comparison of drag coefficient from numerical calculation and wind tunnel test when train ratio is 1/8 |
|
图 8 模型缩比为1/20时的列车交会压力波数值计算结果与动模型试验结果对比 Fig. 8 Results comparison of pressure wave of train crossing from numerical calculation and moving model test when train model ratio is 1/20 |
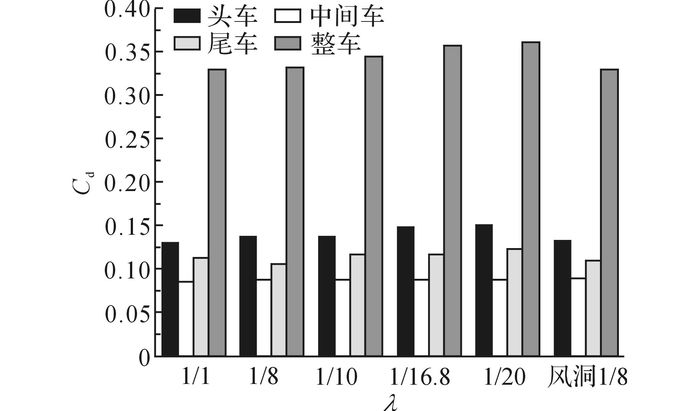
为研究尺度效应对高速列车明线运行气动力的影响, 分别对λ=1/1、1/8、1/10、1/16.8、1/20的模型进行计算分析, 来流速度为83.33 m/s, 并与风洞试验结果进行比较.计算采用的湍流模型、离散格式、网格等均一致.如图 9所示为不同模型尺度下的头车、中间车、尾车及整车的阻力系数与风洞试验结果对比图.可知,列车模型缩比越大, 整车气动阻力系数越小.当列车采用1/1全尺寸模型时, 头车阻力系数为0.131 4;而当采用1/20模型缩比计算时, 头车阻力系数为0.150 3, 阻力系数增加了14.4%.
|
图 9 不同模型缩比对阻力系数的影响 Fig. 9 Effect of different model scales on drag coefficient |
如表 1所示为λ=1/1、1/8、1/10、1/16.8、1/20的模型尺度效应对高速列车气动升力数值计算结果的影响, 来流速度为83.33 m/s.计算采用的湍流模型、离散格式、网格等均一致.由表 1可以看出, 随着缩比尺度的减小, 整车升力系数有减小的趋势.
| 表 1 尺度效应对高速列车气动升力系数的影响 Table 1 Effect of scale on aerodynamic lift coefficient of high speed train |
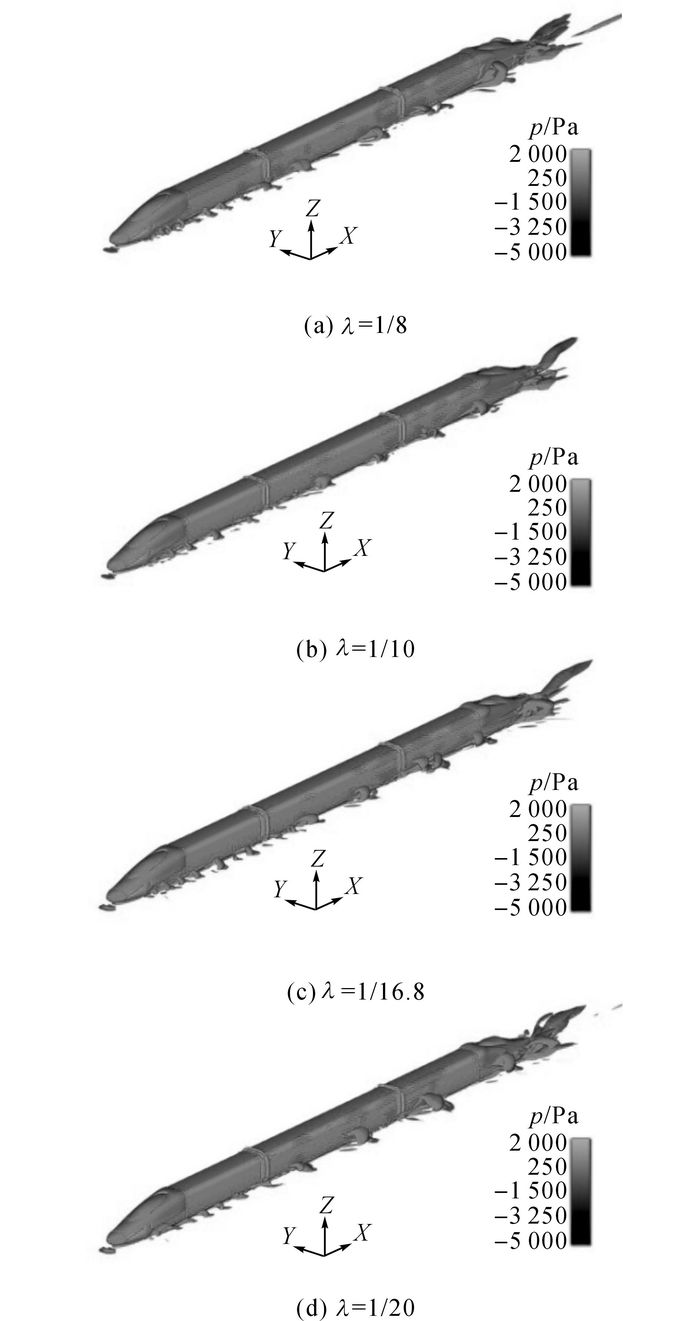
由于模型缩比增加而引起的阻力系数变化可用尾流区高度的变化[18]来解释.如图 10所示, 模型缩比较低时, 分离的尾流高度大于车体高度, 随着模型缩比增加, 尾流高度减小, 阻力系数减小.随着模型缩比的增加, 头车的阻力系数减小, 这种现象可用边界层理论[19]解释:列车气动阻力由摩擦阻力和压差阻力组成, 在无侧偏角度下, 压差阻力随模型缩比的变化并不明显, 摩擦阻力随着模型缩比的增大而减小, 使得列车气动阻力随着模型缩比的增大而减小.
|
图 10 不同模型缩比对尾涡结构的影响 Fig. 10 Effect of various model scales on tail vortex structure |
为研究尺度效应对高速列车明线交会气动性能的影响, 分别对λ=1/1、1/8、1/16.8、1/20的模型进行计算分析, 设v为列车速度, p′为加密处理的压力, x/L为各测点距离列车鼻尖点距离的系数(其中,x为各测点距离鼻失点的距离,L为列车的长度), 数值范围为0~1.
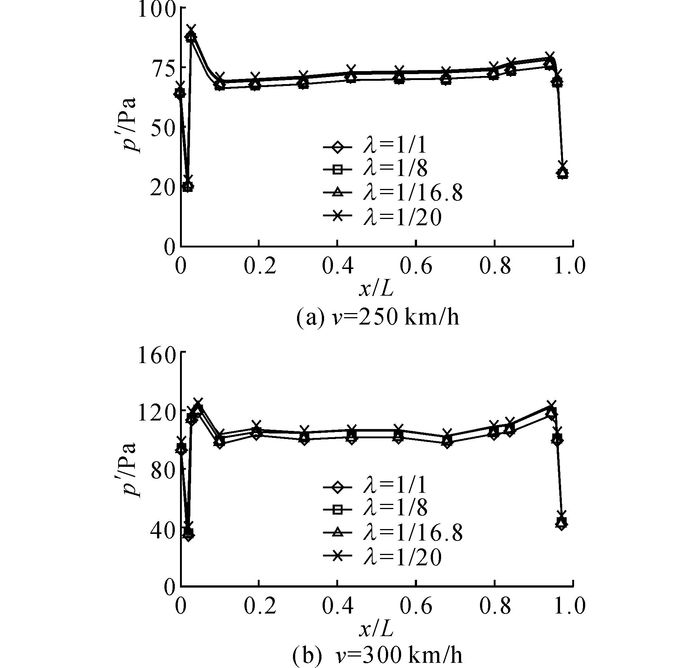
如图 11所示为不同模型缩比下, 列车分别以250 km/h等速交会和300 km/h等速交会时, 列车表面压力变化峰峰值沿车体长度方向测点分布情况的对比.由图 11(a)可以看出, 不同模型缩比的列车等速交会时, 均在头、尾流线型与列车等截面交接处压力变化较大, 头部流线型压力变化显著大于尾部流线型区域, 鼻尖驻点压力最大, 列车等截面车身段压力波动很小.不同模型缩比下, 列车表面压力变化幅值沿车体长度分布规律一致, 幅值有明显差异, 列车全尺寸交会时, 车体表面压力变化幅值相对最小.当λ=1/20时, 车体壁面压力变化幅值最大(66.8 Pa), 相对全尺寸工况(63.0 Pa), 幅值增加最大可达6%.观察图 11(b)300 km/h等速交会工况可以得到同样的规律.对比图 11(a)和图 11(b)可以看出, 随着交会速度的提高, 车体壁面压力变化幅值增大.
|
图 11 明线等速交会工况下, 不同模型缩比的列车车体表面的压力分布 Fig. 11 Pressure distribution of body surface of trains with various model scales in condition of trains passing each other on open track in same speed |
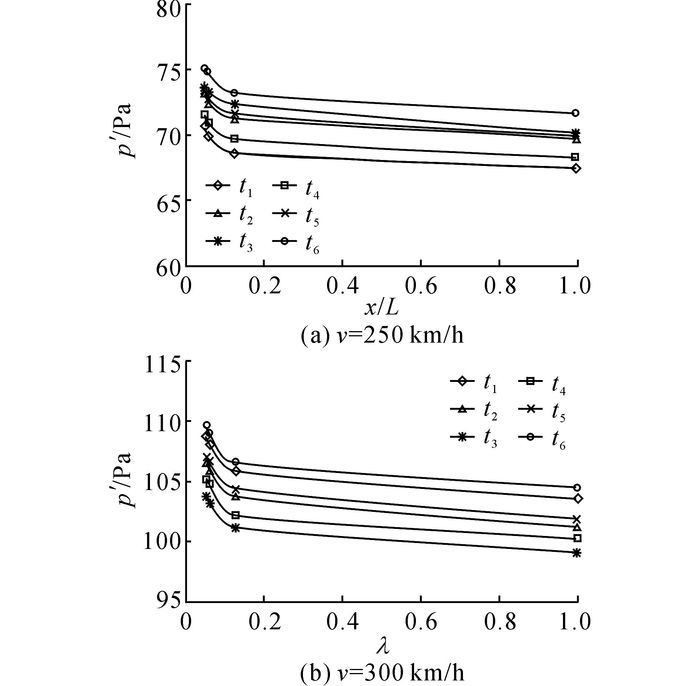
如图 12所示, t1~t6分别对应图 6中的测点编号8、9、18、19、28、29, 下同.不同模型缩比模型等速交会时, 车体表面压力变化幅值随缩比尺度增大而减小, 即模型缩比越大, 车体表面交会压力波幅值越大.模型缩比不改变列车表面压力在头尾流线型处变化较大的规律, 头部流线型压力变化显著大于尾部流线型区域, 除头尾流线型区域外, 列车车身压力相差很小.
|
图 12 列车等速交会时, 车体表面测点压力幅值随模型缩比的变化曲线 Fig. 12 Variation curve of pressure amplitude of train body surface monitor point with model scales in condition of trains passing each other in same speed |
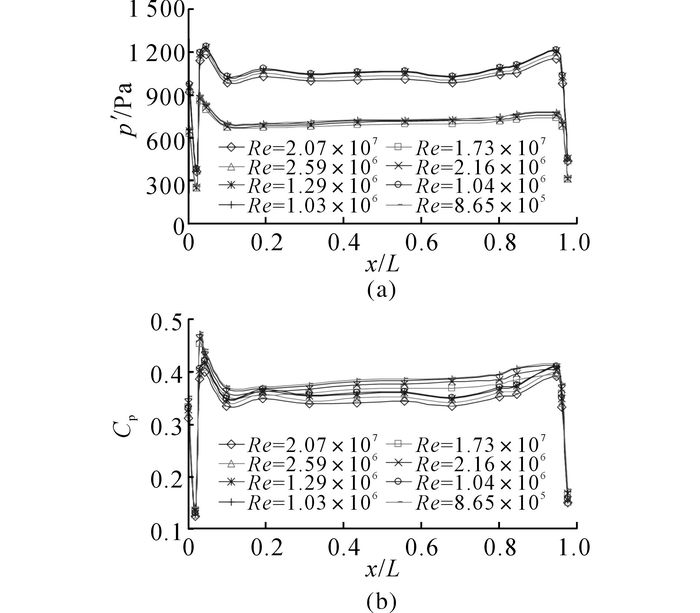
图 13中, Cp为压力系数, 可以看出, 尺度效应不改变列车表面压力系数, 在头尾流线型处变化较大, 头部流线型压力变化显著大于尾部流线型区域, 除头尾流线型区域外, 列车车身压力系数相差很小.从图 13中还可以看出, 列车表面大部分测点压力变化幅值系数具有随着模型缩比减小而增大的趋势.随着雷诺数减小, 列车明线交会车体表面压力变化幅值系数增幅在10%左右, 部分区域增幅可达20%.
|
图 13 列车等速交会时, 车体表面压力及压力系数随模型缩比的变化曲线 Fig. 13 Variation curve of body surface pressure and body surface pressure coefficient with model scales in condition of trains passing each other in same speed |
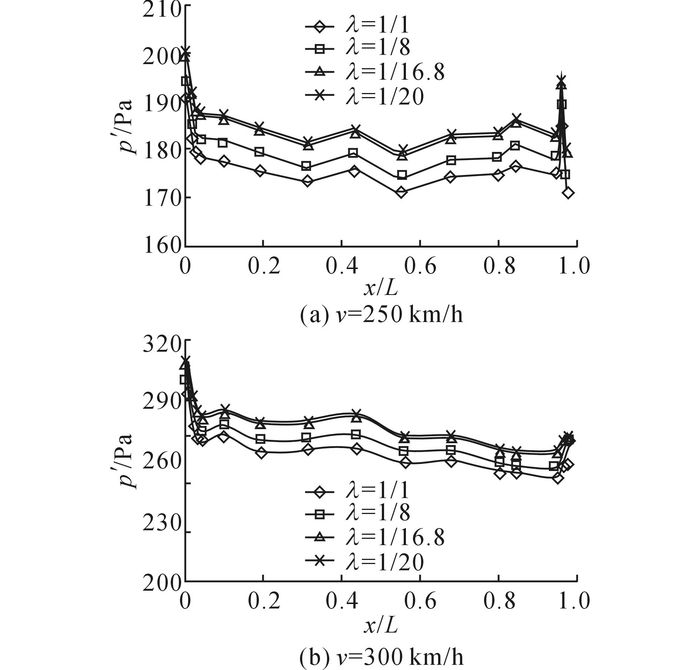
对车速分别为250 km/h和300 km/h, λ=1/1、1/8、1/16.8、1/20的列车模型单车过隧道工况进行计算分析.由于列车通过隧道的速度不同, 如图 14(a)所示, 导致隧道内压缩波和膨胀波的叠加, 在隧道内形成复杂的波系作用在车体上, 导致列车表面压力变化幅值沿车体长度方向波动明显.从沿车体长度方向压力变化幅值线型处压力变化幅值分布来看, 头部流线型和尾部流线型区域压力幅值波动剧烈, 列车等截面车身段压力波动相对较小.不同缩比尺度下,列车通过隧道时, 列车表面压力变化幅值沿车体长度分布规律一致, 幅值有明显差异, 以λ=1/1通过隧道时, 车体表面压力变化幅值相对最小.当λ=1/20时, 车体壁面压力变化幅值最大.
|
图 14 不同模型缩比的列车单车过隧道时的车体表面的压力分布 Fig. 14 Pressure distribution of body surface of trains with various model scales passing through tunnels individually |
当列车以300 km/h通过隧道时, 如图 14(b)所示, 车体表面压力变化幅值沿车体长度呈现减小趋势, 在头部流线型区域变化率最大, 这与车速为250 km/h的车体表面压力分布规律存在显著差异.这是由于列车通过隧道速度不同, 导致隧道内压缩波和膨胀波的叠加在时间和空间上产生了明显差异, 导致列车表面压力变化幅值沿车体长度方向分布规律发生改变.但是不同缩比尺度下当列车以300 km/h通过隧道时, 列车表面压力变化幅值沿车体长度分布规律一致, 幅值有明显差异, 列车全尺寸通过隧道时, 车体表面压力变化幅值相对最小.
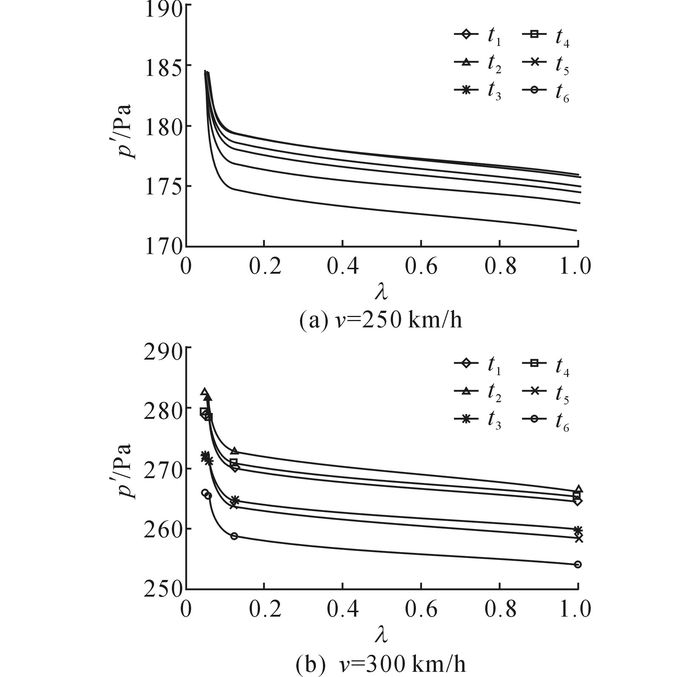
当不同缩比的列车模型以250 km/h的速度通过隧道时, 如图 15(a)所示, 车体表面压力变化幅值随缩比尺度增大而减小, 即缩比越大, 车体表面压力波幅值越大, 最大增幅可达6%.列车模型越接近全尺寸, 压力变化梯度越小.
|
图 15 单车过隧道时, 车体表面测点压力幅值随模型缩比的变化曲线 Fig. 15 Variation curve of body surface pressure and body surface pressure coefficient with model scales in condition of trains passing thorough tunnel individually |
当不同缩比的列车模型以300 km/h通过隧道时, 如图 15(b)所示, 车体表面压力变化幅值随缩比尺度增大而减小, 即缩比越大, 车体表面压力波幅值越大, 最大增幅可达6%.列车模型越接近全尺寸, 压力变化梯度越小.当λ=1/20时, 车体壁面压力变化幅值最大, 相对全尺寸工况, 幅值增加5%左右.
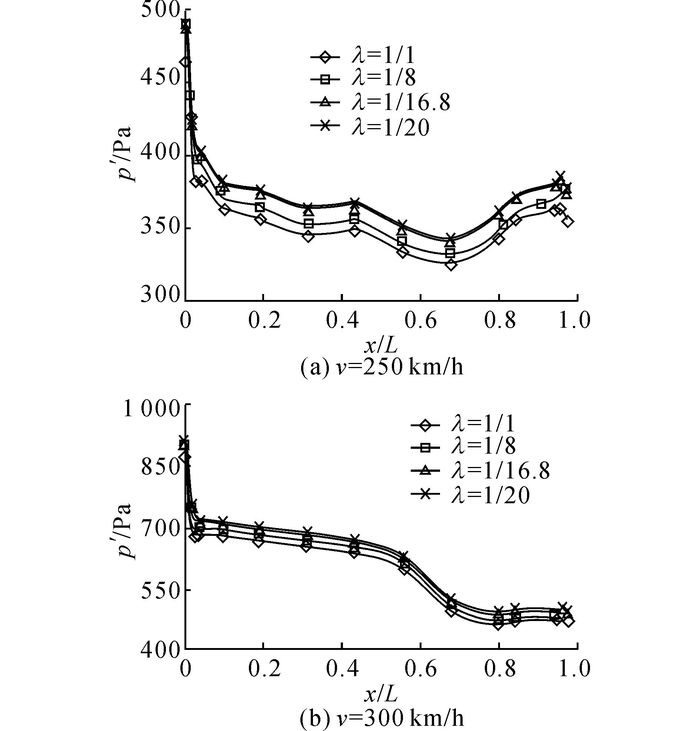
6.4 尺度效应对隧道交会压力波的影响当不同模型缩比的列车在隧道内等速交会时, 如图 16(a)所示, 均在头部区域压力变化相对较大, 其次是尾部区域, 列车等截面车身段压力变化相对较小.由于列车隧道内交会工况下, 隧道内压缩波和膨胀波的叠加会更加复杂, 列车周围流场的强非定常性、压力分布的不均匀性和强湍流状态更加突出, 导致列车表面压力变化幅值存在显著差异.但是在不同缩比尺度下,当列车隧道内等速交会时, 列车表面压力变化幅值沿车体长度分布规律一致, 幅值有明显差异, 当列车全尺寸交会时, 车体表面压力变化幅值相对最小.
|
图 16 隧道内等速交会时, 不同模型缩比下不同运行速度的车体表面的压力分布 Fig. 16 Pressure distribution of train body surface with different speeds under various model scales in condition of trains passing each other in tunnel individually |
当不同模型缩比的列车在隧道内以300 km/h等速交会时, 如图 16(b)所示, 车体表面压力变化幅值沿车体长度明显减小, 在头部流线型区域变化率最大, 这与车速为250 km/h的车体表面压力分布规律存在显著差异.这是由于列车隧道内交会速度不同, 导致隧道内压缩波和膨胀波的叠加在时间和空间上产生了明显差异, 导致列车表面压力变化幅值沿车体长度方向分布规律发生改变.但是在不同缩比尺度下,当列车内以300 km/h等速交会时, 列车表面压力变化幅值沿车体长度分布规律一致, 幅值有明线差异, 当列车全尺寸交会时, 车体表面压力变化幅值相对最小.
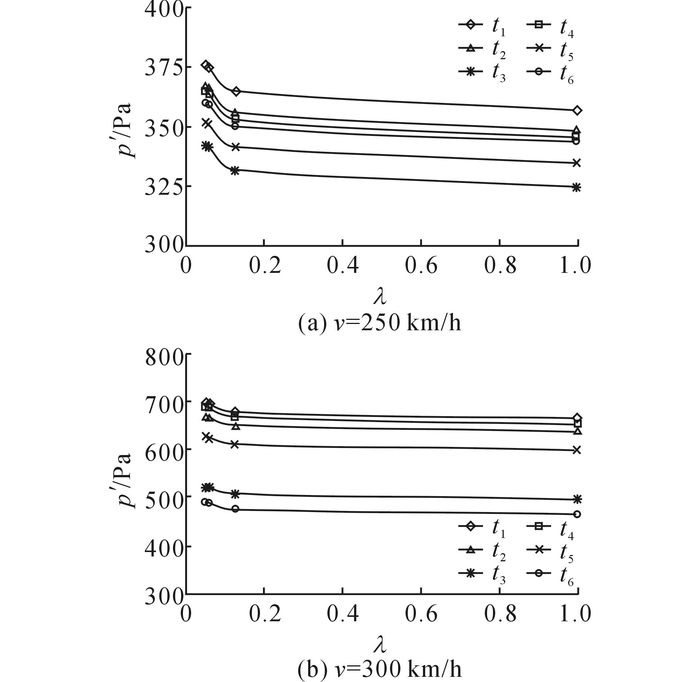
当不同缩比的列车模型以250 km/h的速度在隧道内等速交会时, 如图 17(a)所示, 车体表面压力变化幅值随缩比尺度增大而减小, 即缩比越大, 车体表面交会压力波幅值越大, 最大增幅可达6%.列车模型越接近全尺寸, 压力变化梯度越小.
|
图 17 车体表面测点压力幅值随模型缩比的变化曲线 Fig. 17 Change of pressure amplitude on train surface test points with model scales |
当不同缩比的列车模型300 km/h等速交会时, 如图 17(b)所示, 车体表面压力变化幅值随缩比尺度增大而减小, 即缩比尺度越大, 车体表面交会压力波幅值越大, 最大增幅可达6%.列车模型越接近全尺寸, 压力变化梯度越小.
明线交会(图 11)、隧道通过(图 14)以及隧道交会(图 16)各工况下压力幅值随模型缩比的曲线变化趋势一致, 但各图纵坐标幅值大小有显著差异, 隧道交会工况最恶劣, 压力波幅值最大.
7 结论(1) 对于明线运行工况, 随着运行速度的提高, 雷诺数逐渐增大, 头车及整车阻力系数逐渐减小.当雷诺数高于2.20×106时, 气动力参数受雷诺数变化的影响减弱.在保证列车运行速度不变的条件下, 模型比例和雷诺数越小, 头车及整车的阻力系数越大.
(2) 对于明线交会工况, 尺度效应不改变列车表面压力系数, 在头尾流线型处变化较大, 头部流线型区域的压力变化显著大于尾部流线型区域, 除头尾流线型区域外, 列车车身的压力系数相差很小.
(3) 对于单车过隧道工况, 尺度效应不改变列车表面压力变化幅值沿车体长度的分布规律, 当不同模型缩比的列车等速交会时, 头部区域压力变化相对较大, 其次是尾部区域, 列车等截面车身段压力变化相对较小.
(4) 对于隧道交会工况, 隧道内压缩波和膨胀波的叠加更加复杂, 列车周围流场的强非定常性、压力分布的不均匀性和强湍流状态更加突出, 导致列车表面压力变化幅值存在显著差异.在不同缩比尺度下, 当列车在隧道内等速交会时, 列车表面压力变化幅值沿车体长度分布规律一致, 幅值有明显差异;当列车全尺寸交会时, 车体表面压力变化幅值相对最小.缩比越大, 车体表面压力波幅值越大, 且列车模型越接近全尺寸, 压力变化梯度越小, 车速不改变这一规律.
基于数值计算方法研究高速列车尺度效应具有试验手段无法比拟的优势, 通过数值校验, 保证了数值计算的准确性.研究成果为模型缩比试验模型比例的选取提供参考依据, 具有重要的工程指导意义.
| [1] | 田红旗. 列车空气动力学[M]. 北京: 中国铁道出版社, 2007: 160-161. |
| [2] |
刘峰, 姚松, 刘堂红, 等. 高速铁路隧道壁面气动压力实车试验分析[J].
浙江大学学报:工学版, 2016, 50(10): 2018–2024.
LIU Feng, YAO Song, LIU Tang-hong, et al. Analysis on aerodynamic pressure of tunnel wall of high-speed railways by full-scale train test[J]. Journal of Zhejiang University:Engineering Science, 2016, 50(10): 2018–2024. |
| [3] | BELL J R, BURTON D, THOMPSON M C, et al. Moving model analysis of the slipstream and wake of a high-speed train[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012, 136(4): 127–137. |
| [4] | ZHOU D, TIAN H Q, ZHANG J, et al. Pressure transients induced by a high-speed train passing througha station[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 135(7): 1–9. |
| [5] | PAZ C, SUÁREZ E, GIL C, et al. Numerical study of the impact of windblown sand particles on a high-speed train[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 145(9): 87–93. |
| [6] | YANG N, ZHENG X K, ZHANG J, et al. Experimental and numerical studies on aerodynamic loads on anoverhead bridge due to passage of high-speed train[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 140(6): 19–33. |
| [7] |
黄志祥, 陈立, 蒋科林. 高速列车模型风洞试验数据的影响因素分析[J].
铁道学报, 2016, 38(7): 34–39.
HUANG Zhi-xiang, CHEN Li, Jiang Ke-lin. The analysis of effect factors on wind tunnel testing data of high-speed train model[J]. Journal of The China RailwaySociety, 2016, 38(7): 34–39. |
| [8] | NIU J Q, LIANG X F, ZHOU D. Experimental study on the effect of Reynolds number on aerodynamicperformance of high-speed train with and without yaw angle[J]. Journal of Wind Engineering and IndustrialAerodynamics, 2016, 157(9): 36–46. |
| [9] | BELL J R. The slipstream and wake structure of high-speed trains[D]. Melbourne:Monash University, 2016. Journal of The China RailwaySociety, 2016, 38(7): 34–39. |
| [10] |
郗艳红, 毛军, 柳润东, 等. 高速列车明线会车压力波波幅研究[J].
华南理工大学学报:自然科学版, 2016, 44(3): 118–127.
XI Yan-hong, MAO Jun, LIU Run-dong, et al. A probe into air pressure pulse amplitude of high-speed trains crossing in open air[J]. Journal of South China University of Technology:Nature Science Edition, 2016, 44(3): 118–127. |
| [11] | OGAWA T, FUJⅡ K. Numerical investigation of three-dimensional compressible flows induced by a train moving into a tunnel[J]. Computers and Fluids, 1997, 26(6): 565–585. DOI:10.1016/S0045-7930(97)00008-X |
| [12] | MOK J K, YOO J. Numerical study on high speed train and tunnel hood interaction[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(1): 17–29. DOI:10.1016/S0167-6105(00)00021-0 |
| [13] | ZHUANG Y, LU X. Numerical investigation on the aerodynamics of a simplified high-speed train undercrosswinds[J]. Theoretical and Applied Mechanics Letters, 2015, 65(5): 181–186. |
| [14] | SCHOBER M, WEISE M, ORELLANO A, et al. Wind tunnel investigation of an ICE 3 endcar on three standard ground scenarios[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98(6): 345–352. |
| [15] | ZHUANG Y, LU X. Numerical investigation on the aerodynamics of a simplified high-speed train undercrosswinds[J]. Theoretical and Applied Mechanics Letters, 2015, 266(4): 5181–186. |
| [16] | KWON H B, KIM T Y, LEE D H, et al. Numerical simulation of unsteady compressible flows induced by a high-speed train passing through a tunnel[J]. Proceedings of the Institution of Mechanical Engineers, Part F:Journal of Rail and Rapid Transit, 2003, 217(2): 111–124. DOI:10.1243/095440903765762850 |
| [17] | BAKER C. The flow around high speed trains[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010, 98(9): 277–298. |
| [18] | RICCO P, BARON A, MOLTENI P. Nature of pressure waves induced by a high-speed train travelling through a tunnel[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007, 95(8): 781–808. DOI:10.1016/j.jweia.2007.01.008 |
| [19] | YAO S B, GUO D L, SUN Z X, et al. Multi-objective optimization of the streamlined head of high-speed trains based on the Kriging model[J]. Science China:Technical Science, 2012, 55(12): 3495–3509. DOI:10.1007/s11431-012-5038-8 |



