在电子系统中, 时钟是数字逻辑电路准确处理信号的基准, 时钟的精度和稳定性直接决定了整个系统的性能.近年来, 随着微小卫星技术[1]和编队飞行技术[2]的发展, 电子系统对定时和时钟同步的要求越来越高.在定时系统和时钟同步[3]中, 需要根据时差测量模块得到的时差信息调节系统时钟的频率, 因此需要一个可以实时调节频率的时钟源.
目前电子系统中常用的时钟源有晶体振荡器、基于分频锁相环的频率合成器和直接数字频率合成器.晶体振荡器产生的时钟的频率精确度和稳定度都较高[4-5], 但是频率单一, 只能在极小的范围内微调.基于分频锁相环的频率合成器的分频倍频因子都是一定范围内的整数, 单环频率合成器的频率间隔不可能做得很小, 频率转换时间较长[6].直接数字频率合成器采用全数字的合成方法, 产生信号的频率分辨率高, 频率切换速度快, 相位连续[7-8], 被广泛应用于现代电子系统及设备的频率源设计中.但是实际应用大多采用直接数字频率合成器来产生单一频率的本振信号, 该方法并不能实时调整频率.
随着软件无线电技术的广泛应用, 电子系统正在向低成本、低功耗集成化和数字化方向发展.现场可编程门阵列(field programmable gate array, FPGA)作为一种可编程逻辑器, 具有集成度高、结构灵活以及开发周期短等优点, 在现代航空、遥控遥测、雷达、通信等电子系统中应用广泛[9].FPGA内部有专门的时钟管理模块, 具有完成时钟的相位偏移、分频、倍频等功能[10], 数字系统设计中通常采用该模块来产生整个系统所需的时钟;但是FPGA内部时钟管理模块可供选择的分频倍频因数有限, 不能生成任意频率的时钟信号[11-12], 调节不方便.
本研究提出一种可实时调节频率的全数字时钟生成方法, 该方法基于数控振荡器(numerically controlled oscillator, NCO)技术.NCO技术的频率控制精度较高, 但是单独使用NCO技术生成的时钟存在严重的边沿抖动问题.针对这一问题, 引入抖动算法和锁相环技术.抖动算法在NCO输出的数字相位上加入随机数以抑制杂散, 锁相环技术则用来降低相位噪声.NCO技术、抖动算法以及锁相环均在FPGA内部实现, 有效地利用了FPGA自带的资源, 使得系统具有集成化、小型化和低功耗的优点.通过调节NCO的频率控制字即可实时调节生成时钟信号的频率, 较为简便灵活.
1 单独NCO的时钟生成方法NCO由系统处理时钟、频率控制字寄存器、相位控制字寄存器以及相位累加器组成.在系统时钟(基准时钟)的作用下, 相位累加器对频率控制字进行累加, 得到以该频率控制字为步进的数字相位, 相位控制字寄存器输出初始相位.将输出的数字相位和初始相位之和进行相位过零检测, 得到输出时钟.NCO的频率控制字设置为2B·f0/fs, 其中f0为目标时钟的频率, fs为系统处理时钟的频率, B为频率控制字的字长, 频率控制精度为δLSB=fs/2B.以250 MHz系统处理速率, 32位字长为例, 频率控制精度可达到0.058 Hz, 增加频率控制字的字长还可以进一步提高频率控制精度.
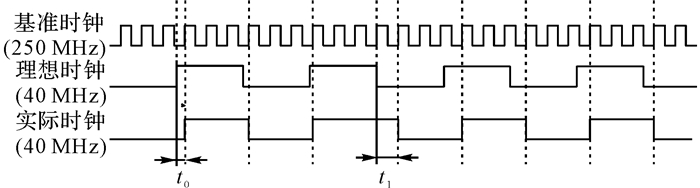
单独使用NCO产生时钟的方法存在缺陷:由于NCO为同步系统, 实际输出时钟在数字相位过零点时不一定立刻跳变, 需要等到系统时钟上升沿到来后才进行跳变.如图 1所示, 实际时钟信号的边沿相对于理想时钟发生了偏离, 以2个时钟周期为例, 偏移量分别为t0和t1, 这说明实际时钟存在较明显的边沿抖动问题.由于初始相位值和频率控制字都是固定值, 每次相位累加后的结果是确知的, 相位自然溢出后的过零点初值也是可以预测的.从时域上看, 边沿抖动并不是随机分布, 而是呈周期性变动, 一旦频率控制字确定, 该周期也确定.这种时域上周期性的边沿抖动会导致频域中产生离散的杂散信号[13].杂散信号的位置与周期有关, 具有不确定性和不易消除的特点.单独使用NCO生成时钟的方法会产生时域上严重的边沿抖动和频域上离散的杂散信号, 影响时钟信号的性能.
|
图 1 实际时钟的边沿抖动 Fig. 1 Edge jitter of actual clock |
为定量衡量相位抖动值的大小, 引入相位抖动的标准差[13-14]:
| $ {\sigma _{\theta \_{\rm{NCO}}}} = \sqrt {\frac{1}{n}{{\sum\nolimits_{j = 1}^n {\left( {\theta \left( j \right) - \frac{1}{n}\sum\nolimits_{i = 1}^n {\theta \left( i \right)} } \right)} }^2}} . $ | (1) |
式中:θ(i)为第i边沿的抖动相位, θ(j)为第j边沿的抖动相位, n为统计次数.
由于相位抖动在0~Ts周期性变化, 线性累加和自然溢出使得相位抖动服从均匀分布[14], 以时间为单位的相位抖动的标准差为
| $ {\sigma _{T\_{\rm{NCO}}}} = \sqrt {{{\left( {{T_{\rm{s}}} - 0} \right)}^2}/12} = 0.2887{T_{\rm{s}}}. $ | (2) |
式中:Ts = 1/fs.将式(2)转化为以rad为单位的形式:
| $ {\sigma _{\theta \_{\rm{NCO}}}} = 0.2887{T_{\rm{s}}} \cdot 2{\rm{ \mathsf{ π} }}/{T_0}. $ | (3) |
式中:T0=1/f0.由式(3)可知相位抖动的大小σθ_NCO与系统处理时钟的频率fs成反比, 提高系统时钟频率可以减小σθ_NCO.
时钟边沿的抖动为衡幅度的相位抖动, 将其功率[15]定义为
| $ \begin{array}{l} P = \frac{1}{{n{T_0}}}\sum\nolimits_{k = 1}^n {\left| {{A^2}{T_{{\rm{jitter}}}}} \right|} = \frac{1}{n}\sum\nolimits_{k = 1}^n {\left| {{A^2}\frac{{{T_{{\rm{jitter}}}}}}{{{T_0}}}} \right|} = \\ \;\;\;\;\;\;\frac{1}{n}{A^2}\sum\nolimits_{k = 1}^n {\left| {\frac{{{\theta _{{\rm{jitter}}}}}}{{2{\rm{ \mathsf{ π} }}}}} \right|} . \end{array} $ | (4) |
式中:A为幅度, Tjitter为每次抖动持续的时间, θjitter为每次抖动所对应的相位.由式(4)可以看出, 相位抖动功率P与相位抖动θjitter的大小成正比, 因此σθ_NCO与P成正比.由于相位抖动只是杂散的一种时域表现形式[13], 抖动的功率与杂散的功率相同, 即σθ与杂散功率成正比, 抑制杂散功率可以减小相位抖动.
由上述分析可知, 提高NCO性能的方法主要有2种.1)提高系统时钟的频率以减小σθ.因为σθ与Ts成正比, 所以系统时钟频率每提高1倍, σθ就能降低一半;但是系统时钟频率的提高会大幅增加功耗, 同时时序要求升高, 布局布线约束加强, 因此也不能采用过高的时钟频率.2)从频域内抑制杂散信号的能量, 利用杂散信号功率与相位抖动间的比例关系间接降低σθ;可从两方面入手:一是使杂散的功率均匀化分布到整个频域, 二是降低杂散的功率.杂散是由相位抖动的周期性造成的, 若能降低相位抖动的周期性, 就可以抑制杂散.
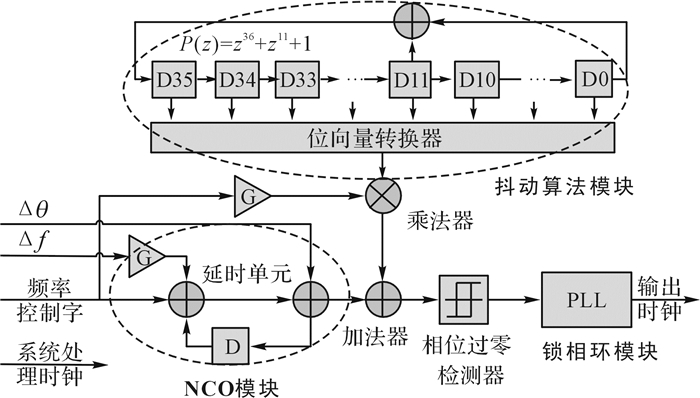
2 改进的全数字时钟生成系统基于对NCO相位抖动的分析, 设计一种改进的全数字时钟生成系统, 系统框图如图 2所示.该系统在NCO基础上引入了抖动算法模块和锁相环模块.NCO相位累加器在系统处理时钟的控制下, 对频率控制字进行累加, 输出以该频率控制字为步进的数字相位;抖动算法模块输出的随机数叠加到NCO累加相位上, 随机化相位抖动, 经相位过零检测器判决输出;锁相环模块用来跟踪信号, 降低相位噪声, 提高输出时钟的性能.Δθ为初始相位控制字, Δf为频率调节控制字, 可以根据对时钟频率和初始相位的需求来改变Δθ和Δf的值.抖动算法和锁相环技术的加入可以有效改善单独NCO生成时钟的性能.
|
图 2 全数字时钟生成系统框图 Fig. 2 System block diagram of all-digital clock generation |
在单独NCO的时钟生成方法中, 杂散是由相位抖动的周期性产生的.在累加相位上增加随机的抖动, 可以降低相位抖动的周期性, 将杂散功率平均到整个频带, 使有规律的杂散分量转化为随机的相位噪声, 从而抑制杂散.
采用抖动算法白化杂散.抖动算法的核心是产生一个范围在[0, 2Bf0/fs-1]的随机数, 并且将其添加到NCO的数字相位输出端, 使得时钟边沿随机提前, 从而减小相位抖动的周期, 白化杂散信号.该算法实现的具体过程如下.
1) 构建线性反馈移位寄存器, 产生1个具有伪随机特性的m序列, 生成多项式p(z)=z36+z11+1.该生成多项式可以生成一个周期为236-1的m序列, 由于周期很长, 可认为该序列在一定周期内为非周期性随机序列.
2) 将36个寄存器中的值组合成一个整数.由于该整数与m序列一一对应, 其循环周期为236-1, 并且该整数的范围在[0, 236-1].
3) 将频率控制字乘以增益因子1/236, 并且与2)中产生的随机数相乘, 使得随机数的数值范围归一化为[0, 2Bf0/fs-1].
4) 将3)中生成的随机数添加到NCO的数字相位输出端.
加入随机数后, 相位抖动被随机化, 周期性被削弱, 频域中杂散得到较有效的白化, 杂散信号的能量转化为噪声的能量.随机数的加入使得相位抖动的幅度范围变大, 由0~2Bf0/fs变为-2Bf0/fs~2Bf0/fs, 而且相位抖动不再服从均匀分布, 而是服从2个均匀分布之和, 其概率密度函数[14]为
| $ f\left( x \right) = \left\{ \begin{array}{l} \frac{1}{{T_{\rm{s}}^2}}x + \frac{1}{{{T_{\rm{s}}}}},\;\;\;\;\;\;\;\; - {T_{\rm{s}}} \le x \le 0;\\ - \frac{1}{{T_{\rm{s}}^2}}x + \frac{1}{{{T_{\rm{s}}}}},\;\;\;\;\;\;\;\;\;{T_{\rm{s}}} \ge x \ge 0. \end{array} \right. $ | (5) |
可以求得相位抖动的标准差[15]为
| $ {\sigma _{T\_{\rm{dither}}}} = \sqrt {\int_{ - {T_{\rm{s}}}}^{{T_{\rm{s}}}} {{x^2}f\left( x \right){\rm{d}}x} - {{\left( {\int_{ - {T_{\rm{s}}}}^{{T_{\rm{s}}}} {xf\left( x \right){\rm{d}}x} } \right)}^2}} = \frac{{{T_{\rm{s}}}}}{{\sqrt 6 }}. $ | (6) |
转化为相位为
| $ {\sigma _{\theta \_{\rm{dither}}}} = \frac{{2{\rm{ \mathsf{ π} }}{T_{\rm{s}}}}}{{\sqrt 6 {T_0}}}. $ | (7) |
对比式(3)和(7)可知, 加入抖动算法后, 抖动值增加了1倍.这种代价是值得的, 因为噪声远比杂散容易消除, 并且杂散出现位置的不确定性会影响消除的效果, 如:当杂散出现在目标频率信号近端时很难被消除.
为了白化杂散, 时钟信号的基底噪声能量会增加, 即杂散的均匀化是以基底噪声的增加为代价的.噪声的增加会降低时钟信号的频谱纯度, 使得时钟的信号质量下降.为了提高时钟信号的性能, 在抑制杂散后需要将噪声能量减小.常用的降低噪声的方法有滤波和锁相环技术.由于锁相环技术能够完整地保留方波信号的高次谐波, 并且噪声带宽较小, 本研究选用锁相环技术.
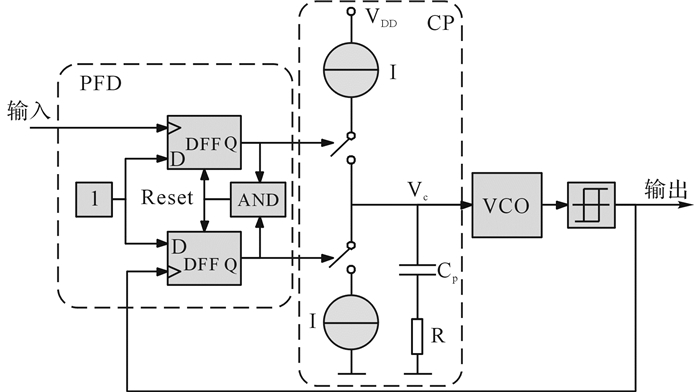
2.2 锁相环技术锁相环路是一种反馈控制电路, 利用外部输入参考信号来控制环路内部振荡信号的频率和相位[16].考虑到现在FPGA中大多数集成有片内的锁相环, 为实现系统的集成化和小型化, 采用FPGA集成的模拟锁相环.该模拟锁相环是一种电荷泵锁相环, 其原理[16-18]如图 3所示.
|
图 3 电荷泵锁相环原理框图 Fig. 3 Principle block diagram of charge pumpphase-locked loop |
电荷泵锁相环的闭环传递函数[16]为
| $ H\left( s \right) = \frac{{\frac{{I{A_0}Rs}}{{2{\rm{ \mathsf{ π} }}}} + \frac{{I{A_0}}}{{2{\rm{ \mathsf{ π} }}{C_{\rm{p}}}}}}}{{\frac{{{s^2} + I{A_0}Rs}}{{2{\rm{ \mathsf{ π} }}}} + \frac{{I{A_0}}}{{2{\rm{ \mathsf{ π} }}{C_{\rm{p}}}}}}}. $ | (8) |
式中:I、R、Cp均为原理图中对应量的数值, A0为压控振荡器(VCO)的压控灵敏度.令
| $ {w_n} = \sqrt {\frac{{I{A_0}}}{{2{\rm{ \mathsf{ π} }}{C_{\rm{p}}}}}} ,\zeta = \frac{R}{2} \cdot \sqrt {\frac{{I{C_{\rm{p}}}{A_0}}}{{2{\rm{ \mathsf{ π} }}}}} , $ |
其中, wn为锁相环的固有角频率, ε为阻尼系数, 则传递函数可以转化为
| $ H\left( s \right) = \frac{{2\zeta {w_n}s + w_n^2}}{{{s^2} + 2\zeta {w_n}s + w_n^2}}. $ | (9) |
由传递函数可以看出, 该电荷泵锁相环可以等效为含有一个理想积分滤波器的二阶锁相环.利用该传递函数的低通特性可降低时钟信号中的噪声能量.经过锁相环后, 相位抖动标准差可由下式估算[15]:
| $ \begin{array}{l} {\sigma _{\theta \_{\rm{PLL}}}} = \\ 2{\rm{ \mathsf{ π} }}\sqrt {\int_0^{ + \infty } {{S_n}\left( f \right){{\left| {H\left( {j \cdot 2{\rm{ \mathsf{ π} }}f} \right)} \right|}^2}{\rm{d}}f} } = 2{\rm{ \mathsf{ π} }}\sqrt {{N_{\rm{i}}}{B_{\rm{L}}}} . \end{array} $ | (10) |
式中:Sn(f)为杂散信号的功率谱密度, Ni为噪声功率密度, BL为单边带等效噪声带宽.针对所选锁相环有
| $ {B_{\rm{L}}} = {w_n}\left( {\varepsilon + 0.25\varepsilon } \right)/2, $ |
因此,
| $ {\sigma _{\theta \_{\rm{PLL}}}} = 2{\rm{ \mathsf{ π} }}\sqrt {0.707{f_0}{w_n}\left( {\varepsilon + 0.25\varepsilon } \right)/f_{\rm{s}}^2} . $ | (11) |
由式(11)可以看出, 本方法的性能由NCO的系统时钟频率fs、锁相环的固有角频率wn和阻尼系数ε共同决定.对于ε, 当ε=0.5时, ε+0.25ε取到最小值, 但是此时在瞬态响应中会有较大的过冲, 因此研究中取ε=0.707, ε+0.25ε=1.06, 性能损失约为3%, 以此换取更好的动态特性, 防止在时钟调节过程中出现失锁.对于fs, 需要结合具体硬件进行设计.
2.3 系统仿真在Matlab中按图 2搭建仿真模型, 设置系统时钟分别为250、450和650 MHz, 生成不同频率的目标时钟, 设置wn = 105 rad/s, ε= 0.707进行仿真.对各组时钟的初始相位抖动、加入抖动算法后的相位抖动、加入锁相环后的相位抖动和理论推算的相位抖动如表 1所示.其中, fsys为系统时钟频率, fobj为目标时钟频率.从表中的统计结果可以看到, NCO输出时钟的相位抖动标准差σθ_NCO的仿真值与由式(3)得出的理论值基本相符;加入抖动算法后, 相位抖动增加, σθ_dither仿真值与式(7)得出的理论值基本相符;加入锁相环后, 时钟的相位抖动有了明显的改善, σθ_PLL仿真值与理论值较为相符.这说明抖动算法模块和锁相环模块的加入可以显著地降低相位抖动标准差, 减小相位抖动.由于加入抖动算法后的噪声并不完全服从高斯分布, 而上述分析是按照白噪声进行的, 造成仿真值与理论值存在微小偏差.
| 表 1 相位抖动标准差的理论值与仿真值对比 Table 1 Comparison of theoretical value and simulation value for phase jitter |
采用Xilinx公司的ISE Design Suite 13.2开发环境, 在FPGA内部实现NCO和抖动算法模块, 利用FPGA自带的电荷泵锁相环完成降低时钟边沿抖动的功能.因为Spartan-6 FPGA自带锁相环的参数基本不可调节[19], 所以性能需求主要依靠合理设置来满足.综合考虑性能目标、FPGA的时序需求及功耗需求, 选用的系统时钟频率为250 MHz, 在Spartan-6 FPGA平台上进行实验验证.实验主要针对杂散抑制和噪声消除能力、频率精度与短期频率稳定度.
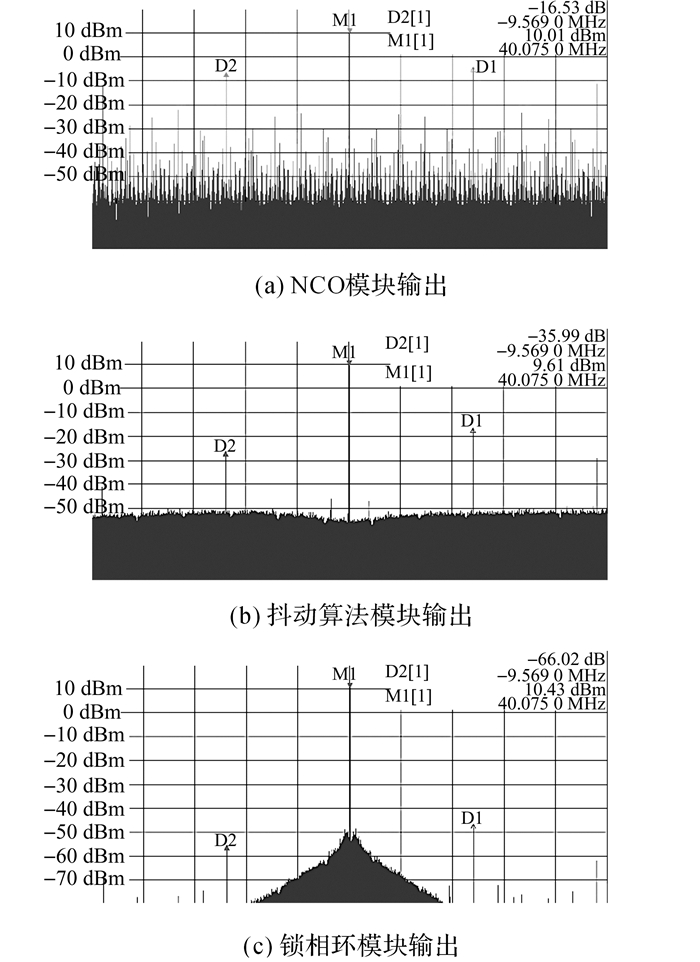
3.1 验证系统的杂散抑制能力和噪声消除能力采用频谱仪测试信号经过各模块后的频域特性, 验证系统各模块的功能.设定目标频率为40.075 MHz, 用频谱仪测试经过各模块后实际信号的频域特性如图 4所示.其中, 图 4(a)为只经过NCO模块后的信号;图 4(b)为经过引入抖动算法后的NCO模块的信号;图 4(c)为经过引入抖动算法与经锁相环技术后的NCO模块最终输出的信号.
|
图 4 各模块输出信号的频域特性 Fig. 4 Frequency domain characteristics of outputsignals after each module |
由图 4可见, 图 4(a)中信号在频域内有较多杂散, 且杂散功率较大, 最大的单根杂散为-14.15 dBc;图 4(b)中杂散功率被均匀化到整个频域中, 大部分杂散被白化, 个别较大的杂散被抑制, 最大杂散降为-26.26 dBc, 同时信号的基底噪声被抬高;图 4(c)中经过滤波, 基底噪声被降低, 原先最大杂散已降为-56.83 dBc.对比图 4(a)、(b)可知, 抖动算法可使杂散白化并抑制杂散, 使杂散功率均匀化到整个频域, 但杂散的均匀化是以基底噪声的抬高为代价的;对比图 4(b)、(c)可知, 锁相环的引入可以滤除大部分噪声和带外杂散.由此可见, 引入的抖动算法模块和锁相环模块可有效抑制杂散、降低相位噪声, 提高输出时钟信号的性能.
3.2 验证频率精度及频率稳定度频率精度和频率稳定度是衡量时钟性能的2个重要指标[15], 可以使用频率计测试信号的频率精度和60 s频率稳定度.现有方法大多是利用FPGA中的时钟管理模块来产生系统时钟.设置40 MHz附近的目标频率点:38.750、39.091、39.300、40.075、40.400和41.176 MHz, 利用研究所提出的方法和直接使用FPGA时钟管理模块的锁相环(以下简称直接锁相环方法)分别实现, 用频率计测量实际输出频率和60 s频率稳定度, 测试结果如表 2所示.其中,fobj为目标频率, f为实际频率, Δf为频率误差, s为频率稳定度.
| 表 2 时钟的频率精度与频率稳定度 Table 2 Frequency accuracy and frequency stability of clock |
从表 2中可以看出, 本研究方法与直接锁相环方法的频率稳定度相近, 但是本研究方法的频率精度有较大改善, 且对不同目标频点的频率误差相近.如:当目标频率为39.091 MHz时, 2种方法的频率稳定度都是2.47×10-9, 但是直接锁相环方法的频率误差为158.70 Hz, 而本研究方法频率误差仅为0.25 Hz.直接锁相环方法在不同目标频点的频率误差相差很大, 而本研究方法可以在一定范围内产生任意频率点.如:当目标频率为38.750 MHz时, 频率误差为42.80 Hz, 而当目标频率为40.075 MHz时, 频率误差高达75 069.20 Hz, 而利用本研究方法的2个目标频率处的频率误差分别为0.28 Hz和0.29 Hz.这是由于当采用直接锁相环方法产生时钟时, VCO输出频率为fVCO = fCLKIN·M/D, 其中,fCLKIN为基准时钟频率,乘除因子M、D为一定范围内的整数[19], 无法产生精确的目标频率.本研究方法将NCO模块、抖动算法模块和锁相环模块结合起来, NCO模块产生精准的频率, 同时锁相环模块可以显著降低相位噪声, 从而保证在频率稳定度与直接锁相环方法相近的情况下, 频率精度有较大的提高, 并且不同目标频点的频率误差相近.此外, 由表 2中数据可知, 利用本研究方法的频率误差小于0.30 Hz, 与理论分析时的频率精度极限0.058 Hz有一定差距, 这主要是由器件(如:频率源)及VCO的非理想特性造成的.然而, 0.30 Hz对应的频率精度为7.5×10-9, 这样的频率精度足以满足大部分应用的需求.在频率稳定性方面, 本研究方法生成时钟的短期频率稳定度为2.5×10-9, 考虑到系统中参考频率源本身的短期稳定度也为2.5×10-9, 可认为该方法不会引入额外的频率稳定性损失.如表 2所示, 采用该方法生成的5个频率范围在38.750 MHz~40.400 MHz的频率, 具有相似的频率精度以及频率稳定度, 可见该方法具有频率适应性.
4 结语本文将NCO技术、抖动算法和锁相环技术相结合, 设计了一种改进的全数字时钟生成方法, 并在FPGA中实现.针对NCO生成时钟边沿存在严重的周期性抖动以及频域内存在较多杂散这一缺陷, 本研究引入了抖动算法生成随机数, 使时钟边沿随机提前, 有效地破坏了时钟相位抖动的周期性, 使得频域中的杂散白化为基底噪声.使用锁相环模块跟踪生成的时钟信号, 利用其传递函数的低通特性降低时钟信号中的噪声能量.经过仿真和实际测试后, 抖动算法有效抑制了杂散, 但是同时抬高了基底噪声.通过锁相环模块锁定时钟信号, 降低了相位噪声.与现有方法相比, 该方法生成的时钟信号的频率精度和频率稳定度能够达到7.5×10-9和2.5×10-9, 并且具有频率适应性, 能够满足大部分应用的需求.在后续研究中, 若在该设计的基础上加入反馈控制环节, 可实现对时钟频率的实时调节, 从而将本设计应用于定时系统.
| [1] |
林来兴, 张小琳. 迎接"轨道革命"——微小卫星的飞速发展[J].
航天器工程, 2016, 25(2): 97–105.
LIN Lai-xing, ZHANG Xiao-lin. To meet "revolution in orbit":rapid development of micro-small satellite[J]. Spacecraft Engineering, 2016, 25(2): 97–105. |
| [2] |
李亮, 王洪, 刘良玉, 等. 微小卫星星座与编队技术发展[J].
空间电子技术, 2017(1): 1–3.
LI Liang, WANG Hong, LIU Liang-yu, et al. Development of micro-satellite constellation and formation technologies[J]. Space Electronic Technology, 2017(1): 1–3. |
| [3] |
王喜文, 朱旭东. 精确的时间同步技术[J].
现代雷达, 2008, 30(8): 91–93.
WANG Xi-wen, ZHU Xu-dong. Accurate time synchronization technology[J]. Modern Radar, 2008, 30(8): 91–93. |
| [4] | MAFFEZZONI P, ZHANG Z, DANIEL L. A study of deterministic jitter in crystal oscillators[J]. IEEE Transactions on Circuits and Systems, 2014, 61(4): 1044–1054. DOI:10.1109/TCSI.2013.2286028 |
| [5] | TIAN M, WANG Z, XU J. Design of a novel differential quadrature crystal oscillator[J]. Analog Integrated Circuits and Signal Processing, 2014, 78(3): 827–833. DOI:10.1007/s10470-013-0243-3 |
| [6] |
张献中, 张涛. 频率合成技术的发展及应用[J].
电子设计工程, 2014, 22(3): 142–145.
ZHANG Xian-zhong, ZHANG Tao. The development and application of frequency synthesis technology[J]. Electronic Design Engineering, 2014, 22(3): 142–145. |
| [7] | LIU C, JI J, QI A, et al. Design of direct digital synthesizer based on FPGA[J]. Advanced MaterialResearch, 2013, 748: 829–832. |
| [8] | SI C, XU C, CHU G. Design and optimization of microwave frequency synthesizer based on DDS[J]. Applied Mechanics and Materials, 2012, 136: 380–385. |
| [9] |
宋克非. FPGA在航天遥感器中的应用[J].
光机电信息, 2010, 27(12): 49–55.
SONG Ke-fei. Application of FPGA in aerospace remote sensing systems[J]. OME Information, 2010, 27(12): 49–55. |
| [10] |
侯伶俐. FPGA中DCM的设计研究[D]. 成都: 电子科技大学, 2012.
HOU Ling-li. The design and research of DCM inFPGA[D]. Chengdu:University of electronic science and technology of China, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10614-1013148400.htm |
| [11] |
封彦彪, 刘兴春. 基于XilinxFPGA的时钟管理设计与实现[J].
电子测量技术, 2010, 33(10): 52–55.
FENG Yan-biao, LIU Xing-chun. Design and implementation of clock management based on XilinxFPGA[J]. Electronic Measurement Technology, 2010, 33(10): 52–55. DOI:10.3969/j.issn.1002-8978.2010.10.012 |
| [12] |
贾亮, 马兴, 孙伟, 等. 基于XilinxFPGADCM的研究与设计[J].
电子测量技术, 2014, 37(10): 85–88.
JIA Liang, MA Xing, SUN Wei, et al. Research and design based on Xilinx FPGA DCM[J]. Electronic Measurement Technology, 2014, 37(10): 85–88. DOI:10.3969/j.issn.1002-7300.2014.10.020 |
| [13] |
宋屾, 焦淑红, 胡尔富. 时钟抖动和相位噪声关系的研究[J].
应用科技, 2006, 33(4): 1–6.
SONG Shen, JIAO Shu-hong, HU Er-fu. Study of the relation between the clock jitter and phase noise[J]. Application Science and Technology, 2006, 33(4): 1–6. |
| [14] | 盛骤, 谢式千, 潘承毅, 等. 概率论与数理统计[M]. 第4版. 北京: 高等教育出版社, 2008: 30-83. |
| [15] |
段宗明, 柴文乾, 代传堂. 时钟抖动和相位噪声对数据采集的影响[J].
雷达科学与技术, 2010, 8(4): 372–375.
DUAN Zong-ming, CHAI Wen-qian, DAI Chuan-tang. Effect of clock jitter and phase noise on dataacquisition[J]. Radar Science and Technology, 2010, 8(4): 372–375. |
| [16] | GARDNER, FLOYD M. Charge-pump phase-locked loops[J]. IEEE Transactions on Communication, 1980, 28(11): 1849–1858. DOI:10.1109/TCOM.1980.1094619 |
| [17] | XU X, LIU H, TAN W. Parameters design of 1.25 GHz low jitter charge pump PLL[C]. ICEICE, 2011:318-3421. http://ieeexplore.ieee.org/document/5777576/ |
| [18] |
杜云飞. 用于时钟信号发生的锁相环电路的设计[D]. 哈尔滨: 哈尔滨工业大学, 2015.
DU Yun-Fei. Design of phase-locked loops circuits for generate clock signal[D]. Harbin:Harbin institute of technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10213-1015982709.htm |
| [19] | Xilinx, Spartan-6 FPGA Clocking Resources User Guide[EB/OL].[2017-03-22]. http://china.xilinx.com/support/documentation/user_guides/ug382.pdf.html. |



