2. 南阳师范学院 软件学院, 河南 南阳 473061
2. College of Software, Nanyang Normal University, Nanyang 473061, China
揭示人脑的功能组织结构是理解人脑认知的基础, 也是实现类脑智能的前提条件.功能磁共振影像(functional magnetic resonance imaging, fMRI)因具有无创伤性和分辨率高的特点而成为目前获取脑功能神经影像数据的主流技术[1-2], 为人脑功能组织结构的研究带来了发展机遇.到目前为止, 出现了许多基于fMRI数据的人脑功能组织结构研究方法.其中, 基于人脑功能划分的研究方法是一种通过分割人脑皮层研究人脑功能特性的方法.该方法得到的人脑功能图谱不仅揭示了人脑的功能组织特征, 也为进一步研究人脑的功能提供了较为坚实可靠的基础[3].因此, 人脑功能划分方法受到脑研究者的重视, 逐渐成为人脑功能研究中的一个重要课题.在空间尺度上, 人脑功能划分可以分为全脑功能划分和局部脑区功能划分[3].由于人脑功能的复杂性和fMRI数据的高维性, 局部脑区的功能划分得到了脑研究者更多的重视.其中, 脑岛因其功能多样性而成为被广泛关注的划分对象.
脑岛位于人脑外侧裂下面、外侧沟深处, 是一个三角体岛叶, 也是人脑中的一个多功能区, 参与嗅觉、味觉处理、运动感觉、内感作用、动机和体内平衡等功能[4].近年来, 脑研究者开始基于fMRI数据对脑岛的功能划分进行探索.Kurth等[5]在BrainMap数据库上利用激活似然估计进行元分析, 揭示了脑岛的4个功能亚区, 并且将其映射到人脑的社会情感、感觉运动、嗅觉味觉和认知功能上.不过这种方法对BrainMap中收集的神经影像实验(结果)数据具有较强的依赖性.K-means算法被用于脑岛内所有体素的功能连接的聚类, 得到了3个功能亚区[6-7];但是K-means算法对初始值敏感, 需要运行多次.Cauda等[8]先通过激活似然估计建立元分析连接, 再对其实施层次聚类, 在不同粒度上揭示了脑岛的功能组织结构.尽管层次聚类以系统树状图的形式展示了聚类的整个过程, 但是需要较大的存储空间, 并且难以确定最终的划分结果.Vercelli等[4]将模糊聚类用于脑岛的功能划分, 得到了12个功能亚区.这种细粒度的划分对人脑手术具有指导作用, 然而模糊聚类在迭代过程中容易陷入局部最优.Normi等[9]利用独立成分分析将脑岛划分为4个功能亚区;该方法的优点是易于发现数据的潜在结构, 不足之处是不太稳定.总之, 这些划分方法在一定程度上揭示了脑岛的功能组织结构, 表明了脑岛在功能上可以进一步分离, 但是在划分结果的区域连续性和功能一致性上还存在不足.目前, 迫切需要更为有效的脑岛功能划分方法以满足人脑认知和人脑疾病诊断的实际需求.
作为一种常用的人脑功能划分方法, 基于GMM的功能划分方法已被用于视觉皮层、顶内沟、纹状体和全脑皮层的功能划分, 并取得了良好的效果[10-12].然而这些研究所使用的期望最大(expectation maximum, EM)算法是一种单搜索路径的梯度下降算法, 容易陷入局部最优, 并且在搜索GMM的过程中没有考虑相邻体素间的相互作用.从GMM参数和fMRI数据特点上看, GMM模型参数与结构的联合空间具有不可微、多峰值和欺骗性的特点[13];fMRI数据的信噪比较低.与梯度下降法相比, 基于群体智能的元启发式搜索算法具有自组织性、分散性和多点多路径搜索的特点, 在高维多峰空间中表现出更优的搜索性能[14], 并具有容易融入其他信息的优点.其中, 免疫克隆选择(immune clonal selection, ICS)算法是对生物体免疫系统克隆选择机理的模拟, 能够结合问题先验知识和生物免疫系统的自适应能力, 在求解复杂优化问题中表现出较高的潜力[15].
在此背景下, 本文提出一种基于动态邻域信息和ICS搜索GMM的脑岛功能划分方法(an insula functional parcellation method based on Gaussian mixture model searched by dynamic neighborhood information and immune clonal selection algorithm, NICS-GMM), 并得到更优的脑岛划分结构.所提方法的创新之处体现在:
1) 采用融入混合变异策略的ICS代替传统的EM来搜索GMM参数;
2) 针对fMRI数据信噪比低和大脑功能的区域性特点, NICS-GMM利用一种具有抗噪能力的动态邻域信息指导GMM的搜索.
1 相关内容 1.1 脑岛功能划分人脑功能划分是以功能神经影像数据为基础, 根据某种功能一致性度量策略把全脑或局部脑区分割为一定数量的互不相交的功能亚区(功能子区域).因此, 人脑功能划分具有2个特点:
1) 所有功能亚区两两互不相交;
2) 每个功能亚区具有更强的功能一致性.
在fMRI扫描中, 人脑被fMRI扫描仪中的磁场梯度分割成不同的体素, 并通过扫描仪记录每个体素在不同时间点的磁共振信号强度的变化, 最终形成体素的时间序列.因此, fMRI时间序列反映了相应体素的功能活动, 体素功能的一致性就可以由这些时间序列(或导出数据)的相似性(同步性)来表征.简单地说, 基于fMRI数据的人脑功能划分是以体素的时间序列为基本数据, 利用某种功能一致性度量策略(如:皮尔森相关)把全脑或局部脑区分割为功能一致性更强的若干个功能亚区.更直观地讲, fMRI中的人脑功能划分就是通过某种功能一致性指标度量时间序列或由其提取出的特征的相似性, 将与时间序列相对应的体素指派到不同的功能簇/功能子划分中.fMRI时间序列或其导出数据的相似性(同步性)度量就成了基于fMRI数据的功能划分的核心依据.
脑岛功能划分就是把局部脑区脑岛作为目标区域, 对其进行功能划分.相关研究表明, 人脑的基本功能是由多个相邻体素共同完成的, 呈现出区域性的特点[16].脑岛是人脑中的一个局部脑区, 其划分也应具有此特点.fMRI数据具有信噪比低和维数高的特点[17], 给脑岛功能划分方法的性能(区域连续性和功能一致性)带来了不良影响.因此, 设计出既抗噪又具有较强搜索能力的脑岛功能划分算法是提高脑岛功能划分方法性能的重要手段.
1.2 高斯混合模型(GMM)假设N个d维数据点xi(i=1, 2, …, N)服从高斯分布, 这N个数据点可被划分为K个簇(类).每个簇(类)j都服从形式已知的多元高斯概率分布, 记为ϕj(x|θj), 该分布由参数θj确定.若给出所有簇(类)的分布参数值, 那么每个数据点由各簇(类)合成的概率分布为
| $ \left. \begin{array}{l} p\left( {{\mathit{\boldsymbol{x}}_i}\left| \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right.} \right) = \sum\limits_{j = 1}^K {\left( {{\pi _j}{\phi _j}\left( {{\mathit{\boldsymbol{x}}_i}\left| {{\theta _j}} \right.} \right)} \right)} ,\\ {\phi _j}\left( {{\mathit{\boldsymbol{x}}_i}\left| {{\theta _j}} \right.} \right) = \phi \left( {{\mathit{\boldsymbol{x}}_i}\left| {{\mathit{\boldsymbol{\mu }}_j},{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_j}} \right.} \right) = \\ \;\;\;\;\;\frac{1}{{\sqrt {{{\left| {2\pi {\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_j}} \right|}^d}} }}{{\rm{e}}^{ - \left( {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{\mu }}_j}} \right)\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_j^{ - 1}\left( {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{\mu }}_j}} \right)}}. \end{array} \right\} $ | (1) |
式中:xi为某个数据点, d表示其维数, μj和Σj分别为第j个多元高斯分布的均值向量和协方差矩阵, πj为先验概率, 并满足:
| $ \sum\nolimits_{j = 1}^K {{\pi _j} = 1} . $ |
称式(1)为GMM, 完全由参数Θ决定.因此, 由K个分量组成的GMM可以简单地表示为一个三元组集:
| $ \lambda = \left\{ {\left( {{\pi _1},{\mathit{\boldsymbol{\mu }}_1},{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_1}} \right),\left( {{\pi _2},{\mathit{\boldsymbol{\mu }}_2},{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_2}} \right), \cdots ,\left( {{\pi _K},{\mathit{\boldsymbol{\mu }}_K},{\mathit{\boldsymbol{ \boldsymbol{\varSigma} }}_{\rm{K}}}} \right)} \right\}. $ |
GMM的求解过程本质上是确定分布形式已知的概率模型中参数的过程.在已知样本的情况下, 最大似然估计法是求解该问题的常用方法, 对数似然函数如下式:
| $ \begin{array}{l} log\left( {L\left( {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left| \mathit{\boldsymbol{X}} \right.} \right)} \right) = \log \prod\limits_{i = 1}^N {p\left( {{\mathit{\boldsymbol{x}}_i}\left| \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right.} \right)} = \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{i = 1}^N {\log } \sum\limits_{j = 1}^K {\left( {{\pi _j}{\phi _j}\left( {{\mathit{\boldsymbol{x}}_i}\left| {{\theta _j}} \right.} \right)} \right)} . \end{array} $ | (2) |
其中, X表示由N个d维数据点xi组成的数据集.从式(2)可以看出, 当模型参数出现在对数中, 对其直接求解是比较困难的.目前, 求解该模型比较常用的算法是EM算法, 该算法把每个数据点的簇标号作为EM算法的隐性变量.EM算法由E步和M步组成:
1) E步计算隐性变量的后验概率:
| $ p\left( {k\left| {{\mathit{\boldsymbol{x}}_i},{{\mathit{\boldsymbol{ \boldsymbol{\hat \varTheta} }}}^{\left( t \right)}}} \right.} \right) = \frac{{\hat \pi _k^{\left( t \right)}{\phi _k}\left( {{\mathit{\boldsymbol{x}}_i}\left| {\hat \theta _k^{\left( t \right)}} \right.} \right)}}{{\sum\limits_{j = 1}^K {\left( {\hat \pi _j^{\left( t \right)}{\phi _j}\left( {{\mathit{\boldsymbol{x}}_i}\left| {\hat \theta _j^{\left( t \right)}} \right.} \right)} \right)} }}; $ | (3) |
2) M步最大化似然函数的下界:
| $ \hat \pi _k^{\left( {t + 1} \right)} = \frac{1}{N}\sum\limits_{i = 1}^K {p\left( {k\left| {{\mathit{\boldsymbol{x}}_i},{{\mathit{\boldsymbol{ \boldsymbol{\hat \varTheta} }}}^{\left( t \right)}}} \right.} \right)} , $ | (4) |
| $ \hat \mu _k^{\left( {t + 1} \right)} = \frac{{\sum\limits_{i = 1}^K {\left( {{\mathit{\boldsymbol{x}}_i}p\left( {k\left| {{\mathit{\boldsymbol{x}}_i},{{\mathit{\boldsymbol{ \boldsymbol{\hat \varTheta} }}}^{\left( t \right)}}} \right.} \right)} \right)} }}{{\sum\limits_{i = 1}^K {p\left( {k\left| {{\mathit{\boldsymbol{x}}_i},{{\mathit{\boldsymbol{ \boldsymbol{\hat \varTheta} }}}^{\left( t \right)}}} \right.} \right)} }}, $ | (5) |
| $ \begin{array}{l} \mathit{\hat \Sigma }_k^{\left( {t + 1} \right)} = \\ \frac{{\sum\limits_{i = 1}^N {\left[ {p\left( {k\left| {{\mathit{\boldsymbol{x}}_i},{{\mathit{\boldsymbol{ \boldsymbol{\hat \varTheta} }}}^{\left( t \right)}}} \right.} \right)\left( {{\mathit{\boldsymbol{x}}_i} - \mathit{\boldsymbol{\hat \mu }}_k^{\left( {t + 1} \right)}} \right){{\left( {{\mathit{\boldsymbol{x}}_i} - \mathit{\boldsymbol{\hat \mu }}_k^{\left( {t + 1} \right)}} \right)}^{\rm{T}}}} \right]} }}{{\sum\limits_{i = 1}^K {p\left( {k\left| {{\mathit{\boldsymbol{x}}_i},{{\mathit{\boldsymbol{ \boldsymbol{\hat \varTheta} }}}^{\left( t \right)}}} \right.} \right)} }}. \end{array} $ | (6) |
E步和M步一起迭代运行, 直到满足终止条件为止, 从而得到最优的参数估计值.根据最大后验概率p(k| xi,
GMM具有高斯分布的优越性, 可以逼近任何分布.因此, 它具有较强的特征表达能力, 比较适合于人脑的功能划分.然而, 上述优化问题不是一个凸优化问题[18], 而搜索GMM的EM算法属于梯度下降搜索算法, 容易陷入局部最优, 并且在搜索过程中没有考虑样本点之间的关联性信息.
1.3 免疫克隆选择(ICS)算法生物免疫系统是存在于生物体内的保护性系统, 具有使生物体免受致病细菌和病毒等异物侵袭, 进而维持其正常机能的功能.Burnet等[19]提出的克隆选择学说解释了生物免疫系统的工作过程, 该学说的中心思想如下:当抗原(病毒性异物)入侵生物体时, 细胞表面的抗体选择性地与抗原反应(识别抗原), 并使识别程度较高的抗体分化和增殖, 最终消灭抗原并保持与该抗原相应的记忆.基于该学说, de Castro等[20]提出了模拟生物体内抗体克隆选择机制的ICS算法.从算法范畴上讲, ICS算法是一种基于群体的智能搜索算法, 遵守群智能算法的一般性框架.具体来说, ICS算法首先执行初始化操作, 即初始化抗体种群数量、最大迭代次数和变异概率等参数与种群;然后进入迭代搜索阶段, 该阶段由克隆抗体、变异抗体和选择抗体3个算子组成[21].ICS算法具有以下特点:1)克隆抗体、变异抗体和选择抗体分别模拟了抗体扩增、抗体分化和具有高识别能力的新抗体种群的形成, 也是ICS中的3个最主要的算子;2)从空间搜索和信息处理的角度看, 这3个算子实现了局部搜索和全局搜索, 同时也体现出了并行搜索的特点.因此, ICS算法是一种具有较强全局优化能力的搜索算法.
2 NICS-GMM算法 2.1 基本思想搜索GMM的EM算法容易陷入局部最优或早熟, 影响GMM搜索和最终的划分结果.ICS算法拥有较强的全局寻优能力.人脑的基本功能呈现出区域性的特点, fMRI数据中的噪音给GMM的搜索质量和划分结果带来了不良影响.鉴于此, 提出一种基于ICS搜索GMM的脑岛功能划分方法(NICS-GMM), 并将具有抗噪能力的动态邻域信息融入到ICS搜索GMM的过程中, 然后利用最优GMM实现对脑岛的功能划分.
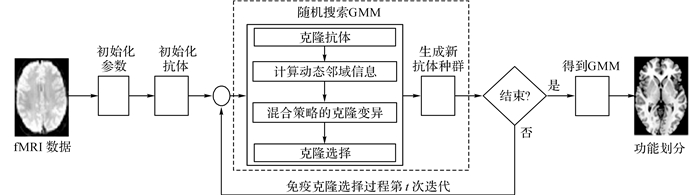
NICS-GMM的流程如图 1所示.得到脑岛的fMRI数据后, 初始化参数和所有的抗体, 并计算其适应度;利用优化的ICS搜索GMM, 包括克隆抗体、计算动态邻域信息、混合策略的克隆变异和克隆选择等主要子过程, 不断迭代直到满足停止条件, 并输出最优的GMM;根据最大后验概率(maximum a posterior, MAP), 实现对脑岛的功能划分.从图 1可以看出:GMM的搜索是NICS-GMM的核心, GMM的质量将对最终的划分结果产生决定性的影响.
|
图 1 基于免疫克隆选择算法(ICS)搜索高斯混合模型(GMM)的脑岛功能划分方法流程图 Fig. 1 Flowchart of insula functional parcellation method based on Gaussian mixture model (GMM) search byimmune clonal selection (ICS) algorithm |
在NICS-GMM中, 一个抗体被表示成一个三元组集λ(一个GMM模型), 抗原被表示为待划分的数据样本(体素的时间序列), 如图 2所示.其中, K表示GMM的成分数(划分数);D表示被划分的数据点(即抗原:被预处理后的fMRI时间序列), 其每一行对应于一个体素的(预处理后的)时间序列(也被作为该体素的特征), d和n分别表示时间序列的长度(维数)与体素数.为了便于与EM-GMM方法比较, 本文采用式(2)作为适应度函数, 其值也被称为似然分数.

|
图 2 NICS-GMM中的抗体和抗原示意图 Fig. 2 Schematic diagram of antibody and antigen in NICS-GMM |
在NICS-GMM算法中, 首先初始化抗体并计算其适应度, 然后进入迭代过程.在免疫克隆子过程中, 每个抗体被克隆, 克隆的数目由其适应度在种群中的排序位置决定.克隆的抗体将进入下面的子过程, 执行搜索.
2.3.2 计算动态邻域信息动态邻域信息是针对人脑功能的区域性特点和fMRI数据的特点而提出的.人脑中的基本功能不是由某个体素独立完成的, 而是由局部区域内的多个相邻体素协同完成的[16], 而且fMRI数据有噪音[3, 17, 22].鉴于此, 定义一种动态邻域信息并用于指导GMM的搜索.该信息借鉴了文献[23]提出的用于二维图像分割的自适应空间邻域信息策略.文献[23]定义的自适应空间邻域信息函数定义如下:
| $ {h_{ik}} = \mathop {{\rm{median}}}\limits_{{x_j} \in N\left( {{x_i}} \right)} \left\{ {p\left( {k\left| {{\mathit{\boldsymbol{x}}_j},\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \right.} \right)} \right\}. $ | (7) |
式中:N(xi)表示xi的邻居集, median{·}表示取中位数.
人脑功能图像是三维图像, 因此对人脑的功能划分是在三维空间中进行的, 需要把式(7)从二维平面推广到三维空间, 以适应人脑功能划分的需求.在此需求下, 把体素v的相邻定义为点相邻, 即如果某个体素与体素v共享相同的面、相同的边或相同的点, 那么称该体素为体素v的邻居体素.这样, 对于某个体素来说, 最多有26个相邻体素.由于时间序列依附于体素, 时间序列的相邻也据此导出.进一步地, 把由推广后的式(7)计算得到的信息称为动态邻域信息.融入了动态邻域信息的后验概率根据下式计算:
| $ {p_{{\rm{SI}}}}\left( {k\left| {{\mathit{\boldsymbol{x}}_i},{{\mathit{\boldsymbol{ \boldsymbol{\hat \varTheta} }}}^{\left( t \right)}}} \right.} \right) = \frac{{\hat \pi _k^{\left( t \right)}{h_{ik}}{\phi _k}\left( {{\mathit{\boldsymbol{x}}_i}\left| {\hat \theta _k^{\left( t \right)}} \right.} \right)}}{{\sum\limits_{j = 1}^K {\left[ {\hat \pi _j^{\left( t \right)}{h_{ik}}{\phi _j}\left( {{\mathit{\boldsymbol{x}}_i}\left| {\hat \theta _j^{\left( t \right)}} \right.} \right)} \right]} }}. $ | (8) |
式中:ϕj为GMM中第j个高斯分量,
| $ \sum\nolimits_{k = 1}^K {{p_{{\rm{SI}}}}\left( {k\left| {{\mathit{\boldsymbol{x}}_i},\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \right.} \right)} = 1. $ |
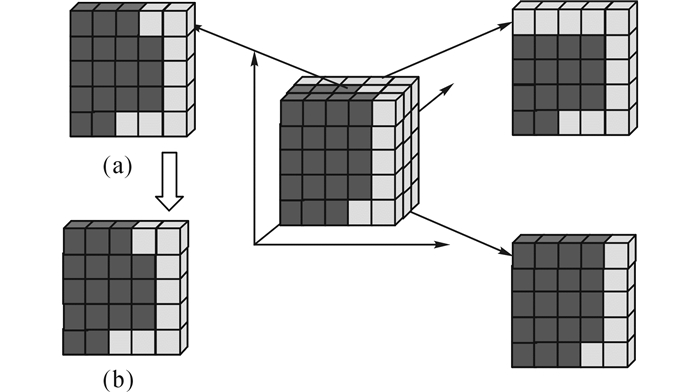
动态邻域信息反映了GMM参数搜索过程中邻居的概率划分信息的变化, 能够及时修正相应时间序列(体素)后验概率的计算, 进而指导GMM参数的搜索.图 3说明了动态邻域信息的作用, 其中不同的颜色表示不同的簇.在迭代过程中, 当一个时间序列(与体素相对应)所属的簇被另一簇包围时, 动态邻域信息会修改该点的后验概率, 指导GMM的搜索, 把该数据点(体素)“拉回”到包围它的簇中.因此, 动态邻域信息体现了人脑功能的区域性特点, 即人脑的基本功能是由相邻体素组成的区域(团块)共同完成的.由于动态邻域信息被定义为邻居信息的中间值, 能够降低fMRI数据中的噪音带来的不利影响.因此, 动态邻域信息策略较好地表达了体素功能的相邻性, 能够真实地反映人脑功能的特点, 有助于得到更好的划分结果.
|
图 3 搜索过程中体素的动态邻域信息作用示意图 Fig. 3 Function diagram of voxel's dynamic neighborhood information in searching process |
在克隆变异子过程中, 均值μj作为直接克隆变异的参数, 先验概率πj和协方差Σj矩阵由公式导出.具体分析如下:πj是先验概率, 可根据下式计算得到:
| $ \hat \pi _j^{\left( {t + 1} \right)} = \frac{1}{N}\sum\limits_{i = 1}^K {{p_{{\rm{SI}}}}\left( {j\left| {{\mathit{\boldsymbol{x}}_i},{{\mathit{\boldsymbol{ \boldsymbol{\hat \varTheta} }}}^{\left( t \right)}}} \right.} \right)} . $ | (9) |
因为fMRI数据的高维特性(时间序列的维数高), μj和Σj具有较高的维数;但是Σj的维数要比μj高得多.因此, 对μj执行直接的克隆变异, 而Σj根据下式计算得到:
| $ \begin{array}{l} \mathit{\boldsymbol{ \boldsymbol{\hat \varSigma} }}_j^{\left( {t + 1} \right)} = \\ \frac{{\sum\limits_{i = 1}^N {\left[ {{p_{{\rm{SI}}}}\left( {k\left| {{\mathit{\boldsymbol{x}}_i},{{\mathit{\boldsymbol{ \boldsymbol{\hat \varTheta} }}}^{\left( t \right)}}} \right.} \right)\left( {{\mathit{\boldsymbol{x}}_i} - \mathit{\boldsymbol{\hat \mu }}_k^{\left( {t + 1} \right)}} \right){{\left( {{\mathit{\boldsymbol{x}}_i} - \mathit{\boldsymbol{\hat \mu }}_k^{\left( {t + 1} \right)}} \right)}^{\rm{T}}}} \right]} }}{{\sum\limits_{j = 1}^K {{p_{{\rm{SI}}}}\left( {j\left| {{\mathit{\boldsymbol{x}}_j},{{\mathit{\boldsymbol{ \boldsymbol{\hat \varTheta} }}}^{\left( t \right)}}} \right.} \right)} }}. \end{array} $ | (10) |
这样操作有以下几点好处.
1) 均值搜索的随机性通过计算公式传播到相应的先验概率和协方差, 扩大了搜索路径.
2) 式(9)和(10)代表了一个较好的搜索方向, 因此用其计算先验概率和协方差矩阵是比较合理的.
3) 没有把先验概率和协方差矩阵直接作为免疫克隆选择算法的搜索对象, 这样既极大地缩小了搜索空间, 又减少了搜索的盲目性, 同时降低了算法的复杂性.原因在于:一方面, 静息态fMRI数据通常具有较高的维数, 因此每个类的协方差矩阵规模是比较大的;另一方面, 每次迭代的先验概率可以通过前一代搜索结果来估算, 没有再将其作为免疫克隆选择算法搜索对象的必要.基于ICS搜索GMM的问题也可以看成是一个最优化问题:搜索主参数均值使得相应的对数似然函数达到最大.
克隆变异是ICS中产生新抗体的算子, 对ICS的搜索能力有重要影响.因为不同的变异算子有不同的特点, 所以本文使用混合变异算子策略提高算法的搜索能力.
1) 正常情况下(当停滞代数未超过阈值时), 使用高斯变异:
| $ \mathit{\boldsymbol{\hat \mu }}_{ki}^{\left( {t + 1} \right)} = \mathit{\boldsymbol{\hat \mu }}_{ki}^t + \left( {{\rm{pro}} < {p_{\rm{m}}}} \right) * {\rm{rnd}} * \left( {\mathit{\boldsymbol{\hat \mu }}_{k\_{\rm{best}}i}^t - \mathit{\boldsymbol{\hat \mu }}_{ki}^t} \right). $ | (11) |
式中:
2) 当停滞代数超过阈值时, 对较差抗体采取突变策略:
| $ \mathit{\boldsymbol{\hat \mu }}_k^{\left( {t + 1} \right)} = \left\{ \begin{array}{l} {\rm{rand}}\;\mathit{\boldsymbol{\hat \mu }}_k^t + \left( {1 - {\rm{rand}}} \right)\mathit{\boldsymbol{a}},p > 0.5;\\ {\rm{rand}}\;\mathit{\boldsymbol{b}} + \left( {1 - {\rm{rand}}} \right)\mathit{\boldsymbol{c}},p \le 0.5. \end{array} \right. $ | (12) |
式中:rand表示0~1.0的随机数, p为程序运行中的(0,1)随机数,a、b和c表示从被划分的数据集中随机选择的数据点.式(12)可以充分利用变异的随机性, 增加变异的多向性.这种多样化的变异策略可以降低免疫克隆选择算法早熟的可能性, 增强算法的全局寻优能力.
2.4 算法描述在NICS-GMM中, 抗体首先被映射为GMM;然后执行ICS搜索GMM, 并通过在搜索过程中融入动态邻域信息降低fMRI数据中噪声带来的不利影响;最后根据MAP完成对脑岛的功能划分.NICS-GMM的伪代码如下.
Algorithm 1 : NICS-GMM
Input: a sample ROI Data D, the parcel number K.
Output: the cluster labels of voxels idx, the fitness of the best GMM fitness*.
Initialization:
Initialize the number of antibody Np, the number ofiteration T, the mutation probability pm and antibody population;
Compute fitness of antibodies with formula (3);
Record the antibody with the best fitness;
For c = 1: T
1. Clone antibodies;
2. For n=1: M
3. Compute spatial information with formula (7);
4. Calculate posterior probability of every cloned antibody with formula (8);
5. Compute prior probabilities with formula (9);
6. Perform clone variation for cloned antibodies with formula (11)~(12);
7. Update covariance of every cloned antibody with formula (10);
8. Compute the fitness of cloned antibodies with formula (3);
9. End
10. Select antibodies:
ⅰ) Detect the antibodies and balance immune density;
ⅱ) Generate new population;
11. Update the best antibody;
End
Compute posterior probability of each voxel and assign each voxel to the corresponding parcels according to MAP;
Return idx, fitness*.
可以看出, 在输入数据集D和簇数K后, NICS-GMM首先初始化相关参数和种群, 时间复杂度为O(Np);然后新算法进入迭代搜索阶段.在每一次迭代过程中, NICS-GMM先克隆抗体, 其时间复杂度为O(M), M为克隆抗体的数量;然后对克隆抗体进行如下操作:
1) 空间邻域信息的计算:针对每个抗体, 每个体素都要计算空间邻域信息, 因此时间复杂度为O(M×P), P为划分脑区中的体素数.
2) 计算后验概率:每个抗体下每个体素都有K个后验概率, 故时间复杂度为O(M×K×P).
3) 对抗体种群做克隆变异:对每个克隆抗体均执行克隆变异, 时间复杂度为O(M×(P×pm+P2)).
4) 计算抗体的适应度:每个抗体属于每个簇的高斯值都需要计算, 时间复杂度为O(M×K×P).
退出内层for循环后, 探测并平衡抗体浓度:通过相应的克隆子群更新每个抗体, 平衡抗体浓度时需要对克隆抗体按适应度排序, 时间复杂度为O(M+Np2);紧接着选择出下一代抗体种群, 这一操作需要首先计算适应度概率和浓度概率, 再利用轮盘赌选出新种群, 其时间复杂度为O(Np2).因此, 整个算法的时间复杂度为
| $ \begin{array}{l} O\left( {{N_p} + M + T \times \left( {\left( {M \times P} \right) + \left( {M \times K \times P} \right) + } \right.} \right.\\ \left. {\left. {\left( {M \times \left( {P \times {p_{\rm{m}}} + {P^2}} \right) + \left( {M \times K \times P} \right)} \right) + M + N_p^2} \right)} \right) = \\ O\left( {T \times \left( {\left( {M \times K \times P} \right) + M \times \left( {P \times {p_{\rm{m}}} + {P^2}} \right)} \right)} \right) \end{array} $ |
为了验证新算法NICS-GMM的性能, 进行大量的实验, 并将实验结果与近年来常用的K-means、基于沃德链的层次聚类(hierarchical clustering based on Ward chain, WHC)和基于稀疏表示的谱聚类(spectral cluster based on sparse representation, SSC)[24]等划分算法进行比较.
实验采用公开的fMRI数据, 以左脑岛功能划分为例.实验环境如下:Windows 7, CPU为Intel 5, 内存为4 G, 用Matlab编程实现.在NICS-GMM中, 参数设置如下:运行次数NNICS-GMM=20, T= 100, pm=0.01.由于聚类的结果就是对数据的一个划分, 因此在不影响理解的情况下聚类与划分和簇数与划分数不再区分.
3.1 实验数据及其预处理为了检验新算法在脑岛功能划分方面的效果, 从网上得到公开的fMRI数据[25].在获取该数据时, 57个被试在静息态下被扫描, 扫描时要求被试尽量放松并闭上眼睛, 但是不能睡着.结构像和功能像的扫描参数如表 1所示.其中, F.V.和S.V.分别表示功能像和结构像, S表示扫描时所用的序列, t表示扫描一个全脑所需要的时间, L表示磁场切割的slice数, F表示视野域, R表示对全脑扫描的次数.
| 表 1 fMRI数据扫描参数表 Table 1 Scanning parameters of fMRI data |
利用DPARSF[26]预处理fMRI数据, 具体处理过程如下.为了排除fMRI扫描仪和被试适应过程的影响, 删除前10个时间点;对每个脑图像做层间校正和头动校正, 使用DARTEL分割并对应到T1结构像, 回归掉滋扰变量的影响, 选择24个Friston滋扰变量, 去掉白质和脑积液;使用0.01~0.10 Hz的滤波器滤波, 得到全脑的低频波动信号;标准化到MNI空间, 并实施空间光滑(FWHM=4 mm).使用AAL模板制作脑岛的掩膜Mask, 并通过该Mask提取被试脑岛内体素的时间序列.本文实验中预处理后的每个体素的时间序列的长度为190, GMM中每个均值μi和协方差矩阵Σi的规模分别为190和190×190.由于NICS-GMM是直接对GMM进行搜索, 待搜索的参数空间为R190×K.
3.2 评价指标在实际的人脑功能划分中, 客观真实的功能划分数事先是不知道的.目前比较一致的做法是:根据某个标准, 采取试探性的方法获得较为可信的划分数(簇数).本文采用和文献[27-29]相同的方法, 即使用信息变化指数(variation of information, VI)和戴斯系数(Dice’s coefficient).信息变化是一种基于信息论的准则[29], 目前被较多地用在人脑功能划分中, 其具体形式如下:
| $ {\rm{V}}{{\rm{I}}_K}\left( {{C_1},{C_2}} \right) = {H_K}\left( {{C_1}} \right) + {H_K}\left( {{C_2}} \right) - 2{I_K}\left( {{C_1},{C_2}} \right), $ | (13) |
| $ {H_K}\left( C \right) = - \sum\limits_{i = 1}^K {\left[ {p\left( i \right) \cdot \log p\left( i \right)} \right]} , $ | (14) |
| $ {I_K}\left( {{C_1},{C_2}} \right) = \sum\limits_{i = 1}^K {\sum\limits_{j = 1}^K {\left[ {p\left( {i,j} \right)\log \frac{{p\left( {i,j} \right)}}{{p\left( i \right)p\left( j \right)}}} \right]} } . $ | (15) |
式中:K为划分数(簇数), C1和C2分别表示2组被试的划分结果, HK(C)表示划分结果的熵, IK(C1, C2)为2组划分结果间的互信息;p(i)表示一个体素属于簇i的概率, p(i, j)为一个体素既属于C1中簇i又属于C2中簇j的概率.
较小的VI值表明2个聚类结果分享了更多的信息, 两者更相似;反之亦然.聚类结果的稳定性和简约性是判断其最优性的一个准则[17], 因此使用和文献[27, 29]相似的方法定义稳定解:划分数为K的VI值与划分数为K-1时的VI值第一次在统计意义上不可区分时, K为最优划分数.
戴斯系数常被用来度量2个组分别聚类后的相似性, 即划分结果的重叠性或再现性.该系数的计算公式如下:
| $ {\rm{Dice}} = \frac{1}{K}\sum\limits_{i = 1}^K {\frac{{2\left| {{X_i} \cap {Y_i}} \right|}}{{\left| {{X_i}} \right| + \left| {{Y_i}} \right|}}} . $ | (16) |
式中:, Xi和Yi表示不同划分结果中的簇, |Xi∩Yi|为Xi和Yi这2个簇的共有个体(体素)数.
明显地, 戴斯系数的取值范围为0~1.0, 戴斯系数越大, 2个划分结果的重叠性越高, 因此, 戴斯系数常被用来度量划分结果的稳定性.
划分结果的功能一致性是评价划分方法性能的一个重要指标, 也是构建脑功能图谱的本质要求.轮廓系数(silhouette index, SI)常被用来度量划分结果的功能一致性, 其定义如下:
| $ {\rm{SI}}\left( C \right) = \frac{1}{K}\sum\limits_{k = 1}^K {\frac{{{a_k} - {b_k}}}{{\max \left\{ {{a_k},{b_k}} \right\}}}} , $ | (17) |
| $ {a_k} = \frac{1}{{{n_k}\left( {{n_k} - 1} \right)}}\sum\limits_{i,j \in {c_k},i \ne j} {s\left( {{v_i},{v_j}} \right)} , $ | (18) |
| $ {b_k} = \frac{1}{{{n_k}\left( {N - {n_k}} \right)}}\sum\limits_{i \in {c_k}} {\sum\limits_{j \ne {c_k}} {s\left( {{v_i},{v_j}} \right)} } . $ | (19) |
式中:C表示一个聚类结果, 由K个簇(划分)组成, ck表示第k个簇, nk为第k个簇中体素的个数, s(vi, vj)表示体素vi和vj的相似性.
SI度量了簇的紧致性, 从相对值的角度平均衡量了划分结果的一致性.本文中体素间的功能相似性s(vi, vj)根据皮尔森相关系数来计算.
3.3 实验比较 3.3.1 搜索能力对比为了验证新算法的搜索能力, 随机选取数据集中某个被试的fMRI数据做实验.对选择的被试做划分数为2~12的功能划分, 每个划分数运行20次,记下每次的似然分数, 计算对应于每个簇数的似然分数的平均值.为了表明动态邻域信息和ICS的有效性, 对EM-GMM、NEM-GMM(在EM-GMM中融入动态邻域信息)、ICS-GMM(仅用ICS搜索GMM, 未融入动态邻域信息)和NICS-GMM进行相同的实验.ICS-GMM的参数设置和NICS-GMM相同.实验结果如表 3所示, 其中, 似然分数表示为μ±σ的形式.
| 表 3 EM-GMM、NEM-GMM、ICS-GMM和NICS-GMM算法的似然分数 Table 3 Likelihood scores of EM-GMM, NEM-GMM, ICS-GMM and NICS-GMM algorithms |
从表 3可以看出, 与EM-GMM相比, NEM-GMM能够得到具有更高似然分数的GMM, 这意味着由NEM-GMM得到的GMM能够更好地表征fMRI数据.原因在于动态邻域信息修正了GMM参数的计算, 实时地指导参数的搜索, 较好地反映了相邻体素的相互作用和人脑基本功能的区域性特征.ICS-GMM使用了全局性的智能搜索方法ICS, 并且新的混合变异策略增强了抗体和搜索方向的多样性, 因此能够得到优于EM搜索的GMM.但是ICS-GMM的搜索结果劣于NEM-GMM, 这可能是由fMRI数据的高维特性造成的.由NICS-GMM搜索得到的GMM具有最高的似然分数;而且随着划分数的增大, NICS-GMM的优势越明显.这说明了NICS-GMM具有较强的搜索能力.主要原因是:动态邻域信息考虑了邻居的功能分布, 在迭代过程中不断地使GMM参数向着能够真实反映功能区域性的方向演化;ICS是一种多路径搜索技术, 对搜索空间具有多发探测的能力.从算法稳定性的角度看:EM-GMM算法是随机初始化, 且使用了单路径搜索的梯度下降法, 因此其稳定性较差.SEM-GMM算法加入了具有抗噪能力的动态邻域信息, 搜索性能和稳定性都有所提高;ICS-GMM是基于种群的多点多路径搜索算法, 其稳定性显著提高;加入动态邻域信息后, NICS-GMM的稳定性最强.这也表明了新算法对初始化和fMRI数据有一定的鲁棒性.
综合EM-GMM、NEM-GMM、ICS-GMM和NICS-GMM算法的实验结果可以看到:动态邻域信息和ICS都能提高GMM的搜索质量;NICS-GMM具有最强的搜索能力和稳定性, 为得到可靠的脑岛功能划分奠定了基础.
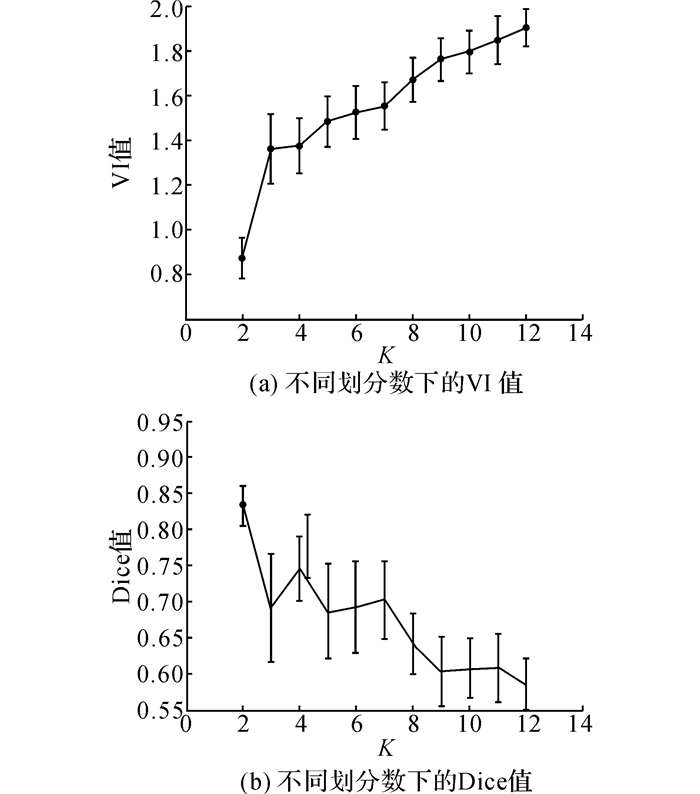
3.3.2 最优划分数的确定为了确定最优的划分数, 本文采用的方法与文献[18, 20]中的方法相似:对预处理后的56个被试运行100次, 每次随机平均分成2组, 测试了划分数为2~12的划分结果.信息变化指标VI和戴斯系数Dice随划分数变化的结果如图 4所示:K表示划分数.对运行后的VI值进行配对t检验(P<0.001), 发现K=3和K=4在统计意义下的VI均值是不可区分的, 而且在K=4时Dice值也取得了局部极大值, 因此K=4是最优的划分数.
|
图 4 不同划分数下的VI值和Dice值 Fig. 4 VI and Dice values under different parcellationnumbers |
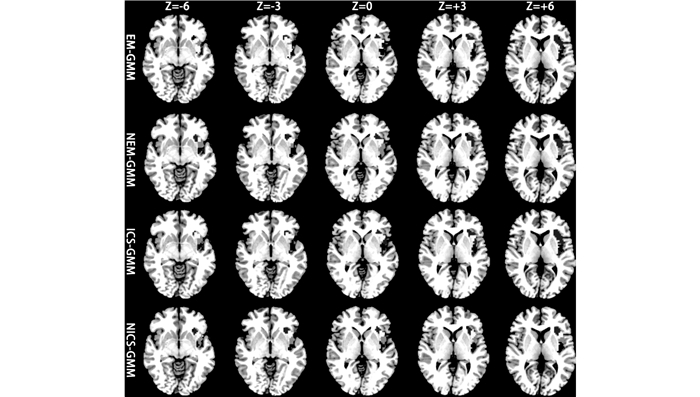
在最优划分数确定后, 选择与3.3.1节中相同的被试为实验数据, 分别运行EM-GMM、NEM-GMM、ICS-GMM和NICS-GMM四个算法, 划分结果如图 5所示.图中展示了人脑的轴状图, 列向表示不同Z坐标(原点位于将前连合处, 将前连合和后连合的连线定义为Y轴, 建立三维坐标系)的剖面图, 行向表示不同算法的划分结果.从图 5可以看到, 由NEM-GMM得到的划分结果比EM-GMM具有更强的区域性和连续性;ICS-GMM的划分结果的区域性和连续性介于EM-GMM和NEM-GMM之间;NICS-GMM取得了最好的划分结果.出现这种结果的原因是:动态邻域信息能够表征邻居体素的功能信息, 考虑了人脑功能的区域特性, 降低了fMRI数据噪音带来的不利影响, 使最终得到的GMM能够更真实地刻画脑岛的功能特征, 进而增强了划分结构的区域性;与EM相比, ICS是一种搜索能力较强的全局性搜索算法, 但是fMRI数据具有较高的维数, 影响了ICS的搜索效果.NICS-GMM既融入了能够反映功能区域性的动态邻域信息, 又利用了基于种群搜索的ICS, 可以得到能够较真实反映脑岛功能分布的GMM.
|
图 5 EM-GMM、NEM-GMM、ICS-GMM和NICS-GMM算法的划分结果 Fig. 5 Parcellation results of EM-GMM, NEM-GMM, ICS-GMM and NICS-GMM algorithms |
综合4种算法的划分结果可以看到:动态邻域信息的抗噪性和促进区域化的作用是明显的, 原因是直接对fMRI数据聚类;只有从算法搜索能力和fMRI数据两方面考虑, 才能得到较好的划分结果.
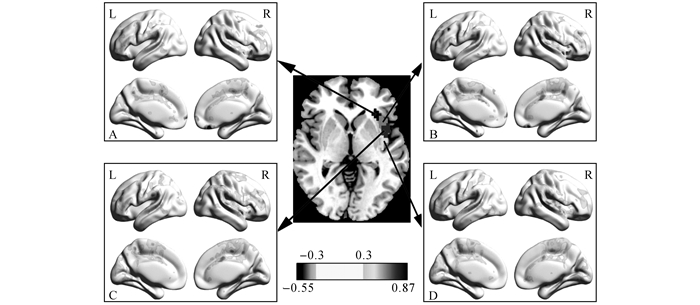
3.3.4 划分结果的连接模式为了检验划分结果的正确性, 计算由NICS-GMM得到的每个功能亚区的功能连接模式.具体过程如下:在3.3.3节的基础上, 首先计算每个亚区的平均时间序列, 然后计算其与除左脑岛之外的人脑皮层的功能连接图.考虑到fMRI数据的噪音特性, 功能相关系数的绝对值小于0.3的功能连接被排除.每个簇的功能连接如图 6所示, 图中的L和R分别表示左脑和右脑.从图 6可以看到, 这4个功能簇是脑岛背前侧、脑岛腹前侧、脑岛后侧和脑岛中部.脑岛腹前侧和内侧额叶有负连接, 同时与扣带回有较强的正连接.与脑岛腹前侧相比, 脑岛背前侧与扣带回的功能连接较弱, 而与额叶有较强的负功能连接.脑岛后侧与中央旁回内侧、内侧枕叶、后扣带回和感觉运动区有正连接;相比之下, 脑岛中部与中央旁回内侧和后扣带回有更强的正连接, 同时与额前回有负连接.实验结果表明:这些功能亚区的连接模式是不同的, 说明了新划分方法的正确性.另一方面, 不同功能亚区的功能连接模式与文献[9]中的结果相似, 这表明了新方法的有效性:NICS-GMM能够在较小的粒度上对左脑岛作出具有不同连接模式的功能划分, 较为可信地揭示了脑岛的功能特性.
|
图 6 功能亚区的连接模式(与A框对应的亚区:脑岛背前侧, 与B框对应的亚区:脑岛腹前侧, 与C框对应的亚区:脑岛中部, 与D框对应的亚区:脑岛后侧) Fig. 6 Connectivity patterns of insula functional subregions (subregion corresponding to box A: dorsal anteriorinsula, to box B: ventral anterior insula, to box C: middle insula, to box D: posterior insula) |
划分结果的功能一致性是人脑功能划分中常用的评价指标.为了充分说明NICS-GMM划分结果的功能一致性, 将其与EM-GMM、NEM-GMM、ICS-GMM进行纵向比较, 也将其与K-means、WHC和SSC进行横向比较.
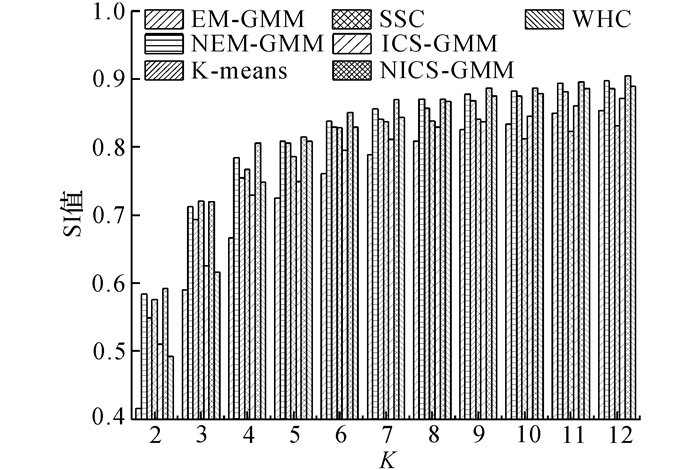
以3.3.1节中选择的被试为实验数据, 采用SI指标度量划分结果的功能一致性, 分别运行20次后平均的SI值如图 7所示:从图 7可以看到, K-means、WHC得到的划分结果的功能一致性要高于EM-GMM.主要原因在于:EM-GMM直接估计依附于体素的时间序列的后验概率, 而时间序列具有较多的噪音, 在搜索GMM的过程中没有考虑时间序列(体素)的邻域信息;K-means和WHC是对相关系数聚类.NEM-GMM结果的功能一致性高于K-means、WHC和SSC(K=3除外).这是因为动态邻域信息考虑了相邻体素在功能上相互作用的特点, 降低了噪音带来的负面影响.ICS-GMM结果的功能一致性高于EM-GMM, 但是低于NEM-GMM.出现这种结果的主要原因如下:
|
图 7 EM-GMM、NEM-GMM、K-means、SSC、ICS-GMM、NICS-GMM和WHC算法的划分结果的功能一致性比较 Fig. 7 Comparison of functional consistency of parcellation results from EM-GMM, NEM-GMM, K-means, SSC, ICS-GMM, NICS-GMM and WHC algorithms |
1) 与EM相比, ICS利用了种群多路径搜索的优势, 是一种带有较强全局性搜索能力的算法.
2) fMRI数据的维数较高且具有噪音, 这给ICS的搜索带来了困难.
3) NEM-GMM利用动态邻域信息抑制了噪音带来的不利影响, 提高了GMM的质量.
NICS-GMM结果的功能一致性是最高的, 意味着由此得到的功能亚区是比较合理的.在GMM参数搜索上, NICS-GMM采用搜索能力较强的ICS代替EM搜索, 并在搜索过程中融入了具有抗噪能力的动态邻域信息.从图 7中也可以看到, SSC的结果是不稳定的:当划分数较小时, SSC结果的功能一致性处于中间位置, 随着划分数的增大, 其结果变差.可能的原因是稀疏表示本身是有误差的, 而且在划分数较大时时间序列(体素)非常相似, 这造成了其归属不能较好地确定.
4 讨论针对EM算法搜索能力的不足和人脑功能的区域性特点, 提出了一种融合动态邻域信息和ICS的搜索GMM的脑岛功能划分方法, 并得到了具有较强功能一致性和区域性的结果.由此可以得出较为一般的结论:1)在人脑功能划分的研究中, fMRI数据低信噪比和人脑功能区域性特点应该给予充分考虑.2)从方法学的角度, 提高方法的搜索性能也是研究人脑功能划分所需要的.另外, NICS-GMM在脑疾病诊断中也有一定的应用前景:针对脑疾病被试, 执行NICS-GMM得到的脑岛功能组织结构可以为脑疾病的诊断提供神经影像学证据:1)划分后功能亚区形态的变化;2)以划分后的功能亚区为种子计算功能连接, 检查连接异常.然而, 从实验结果可以看到, NICS-GMM的实验结果优于NEM-GMM的程度并不明显, 可能的原因是:fMRI数据的高维数性导致了参数的搜索空间较大, 进而给基于ICS的搜索带来了困难.在实验过程中发现, ICS-GMM和NICS-GMM的运行时间较其他算法长, 这是新算法的不足之处.
迄今为止, 人们对脑岛有多少个功能亚区这个问题还没有统一的结论.本文从划分结果稳定性和简约性的角度, 使用了和文献[27-28]相同的指标来确定最优的划分数.在此标准下, 最优的划分数为4.这与文献[9]的划分数相同, 在一定程度上也表明了该方法的合理性.从实验结果看, 左脑岛被划分为背前侧、腹前侧、中部和后部4个功能亚区, 与文献[9]的结果相似.每个功能亚区不仅有自己的功能连接模式, 也具有较强的区域性和功能一致性,这也表明了划分结果的正确性和可信性.因此, 本文不但验证了以前的研究结果, 而且提供了一种更为有效的人脑功能划分方法.脑岛的功能划分没有形成统一的结论, 可能的原因如下:1)脑岛的功能比较复杂, 在不同的状态下有不同的变化.2)确定最优划分数的指标仅刻画了划分结果的某个方面, 没有对功能亚区的特性作出全面的刻画.3)人脑的功能复杂性和fMRI数据的高维噪音性需要表达脑区功能的模型和算法在准确性上有进一步提高.因此, 脑岛的功能划分在上述3个方面还有待深入且系统的研究.
5 结语本文从方法学的角度提出了一种基于ICS算法搜索GMM的脑岛功能划分方法.该方法利用具有较强全局搜索能力的ICS算法搜索GMM, 在搜索过程中融入了具有抗噪能力的动态邻域信息;使用最优的GMM实现对脑岛的功能划分;相关实验验证了新方法能够得到具有更强功能一致性和区域连续性的划分结构.一方面, NICS-GMM算法得到的划分结果揭示了脑岛的功能组织结构, 为脑岛认知理解和脑疾病诊断提供了帮助;另一方面, 该算法不仅可以应用到脑岛的功能划分中, 而且也可以应用到其他脑区的功能划分中, 丰富了人脑功能划分的方法学研究.下一步的工作重点是:针对fMRI数据的高维特性, 研究基于智能算法的快速有效的划分方法.
| [1] | HONNORAT N, EAVANI H, SATTERTHWAITE T D, et al. GraSP:geodesic graph-based segmentation with shape priors for the functional parcellation of the cortex[J]. Neuroimage, 2015, 106(2): 207–221. |
| [2] | MEZER A, YOVEL Y, PASTERNAK O, et al. Cluster analysis of resting-state fMRI time series[J]. Neuroimage, 2009, 45(4): 1117–1125. DOI:10.1016/j.neuroimage.2008.12.015 |
| [3] |
赵学武, 冀俊忠, 梁佩鹏. 面向fMRI数据的人脑功能划分[J].
科学通报, 2016, 61(18): 2035–2052.
ZHAO Xue-wu, JI Jun-zhong, LIANG Pei-peng. The human brain functional parcellation based on fMRI data[J]. Chinese Science Bulletin, 2016, 61(18): 2035–2052. |
| [4] | VERCELLI U, DIANO M, COSTA T, et al. Node detection using high-dimension-al fuzzy parcellation applied to the insula cortex[J]. Neural Plasticity, 2016, 2016(5-6): 1–8. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4736219/ |
| [5] | KURTH F, ZILLES K, FOX P T, et al. A linkbetween the systems:functional differentiation andintegration within the human insula revealed by meta-analysis[J]. Brain Structure and Function, 2010, 214(5-6): 519–534. DOI:10.1007/s00429-010-0255-z |
| [6] | CHANG L J, YARKONI T, KHAW M W, et al. Decoding the role of the insula in human cogntion:functional parcellation and large-scale reverse inference[J]. Cerebral Cortex, 2013, 23(3): 739–749. DOI:10.1093/cercor/bhs065 |
| [7] | BEN D, PITSKEL N B, PELPHREY K A. Three systems of insula functional connectivity identified with cluster analysis[J]. Cerebral Cortex, 2011, 21(7): 1498–1506. DOI:10.1093/cercor/bhq186 |
| [8] | CAUDA F, COSTA T, TORTA D M, et al. Meta-analytic clustering of the insula cortex:characterizing the meta-analytic connectivity of the insula when involved in active tasks[J]. Neuroimage, 2012, 62(1): 343–355. DOI:10.1016/j.neuroimage.2012.04.012 |
| [9] | NORMI J S, FARRANT K, DAMARAJU E, et al. Dynamic functional network connectivity reveals unique and overlapping profiles of insula subdivisions[J]. Human Brain Mapping, 2016, 37(5): 1770–1787. DOI:10.1002/hbm.23135 |
| [10] | SHEN X, PAPADEMETRIS X, CONSTABLE R T. Graph-theory based parcellation of functional subunits in the brain from resting-state fMRI data[J]. Neuroimage, 2010, 50(3): 1027–1035. DOI:10.1016/j.neuroimage.2009.12.119 |
| [11] | JANSSEN R J, JYLÄNKI P, KESSELS R P C, et al. Probabilistic model-based functional parcellation reveals a robust, fine-grained subdivision of the striatum[J]. Neuroimage, 2015, 119(10): 398–405. |
| [12] | GOLLAND P, GOLLAND Y, MALACH R. Detection of spatial activation patterns as unsupervised segmentation of fMRI data[C]//International Confer ence on Medical Image Computing and Computer-as-sisted Intervention. MICCAI. Brisbane:Springer, 2006:110-118. https://dl.acm.org/citation.cfm?id=1780218 |
| [13] |
林琳, 王树勋. 基于自适应小生境混合遗传算法的说话人识别[J].
电子学报, 2007, 35(1): 8–12.
LIN Lin, WANG Shu-xun. Speaker recognition based on adaptive niche hybrid genetic algorithms[J]. Chinese Journal of Electronics, 2007, 35(1): 8–12. |
| [14] | BEHESHTI Z, SHAMSUDDIN S M. A review of population-based metaheuristic algorithm[J]. International Journal of Advances in Soft Computing and Its Applications, 2013, 5(1): 1–35. |
| [15] | HAKTANIRTAR ULUTAS B, KULTUREL-KONAK S. A review of clonal selection algorithm and its applications[J]. Artificial Intelligence Review, 2011, 36(2): 117–138. DOI:10.1007/s10462-011-9206-1 |
| [16] | KOTANODA K, MATSUDA Y, SUGISHITA M. A spatio-temporal regression model for the analysis of functional MRI data[J]. Neuroimage, 2002, 17(3): 1415–1428. DOI:10.1006/nimg.2002.1209 |
| [17] | OIKONOMOU V P, BLEKAS K. An adaptive regression mixture model for fMRI cluster analysis[J]. IEEE Transactions on Medical Imaging, 2013, 32(4): 649–659. DOI:10.1109/TMI.2012.2221731 |
| [18] | ARI Ç, AKSOY S, ARIKAN O. Maximum likelihood estimation of Gaussian mixture models using stochastic search[J]. Pattern Recognition, 2012, 45(7): 2804–2816. DOI:10.1016/j.patcog.2011.12.023 |
| [19] | BURNET F M. The clonal selection theory of acquired immunity[M]. London: Cambridge University Press, 1959. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1522512/ |
| [20] | DE CASTRO L N, VON ZUBEN F J. An immun-ological approach to initialize centers of radial basis function neural networks[C]//In Proceeding of Brazilian Conference on Neural Networks. CBRN, Rio de Janeiro:[s.n.], 2001:79-84. http://abricom.org.br/eventos/cbrn_2001/5cbrn_018/ |
| [21] | PENG Y, LU B L. Hybrid learning clonal selectionalgorithm[J]. Information Sciences, 2015, 296(1): 128–146. |
| [22] | MEJIA A F, NEBEL M B, SHOU H, et al. Improving reliability of subject-level resting-state fMRI parcellation with shrinkage estimators[J]. Neuroimage, 2015, 112(5): 14–29. |
| [23] |
朱峰, 罗立民, 宋余庆, 等. 基于自适应空间邻域信息GMM的图像分割[J].
计算机研究与发展, 2011, 48(11): 2000–2007.
ZHU Feng, LUO Li-min, SONG Yu-qing, et al. Adaptive spatially neighborhood information gaussian mixture model image segmentation[J]. Journal of computer Research and Development, 2011, 48(11): 2000–2007. |
| [24] | ZHANG Y, CASPERS S, FAN L, et al. Robust brain parcellation using sparse representation on resting-state fMRI[J]. Brain Structure and Function, 2014, 220(6): 1–15. |
| [25] | HE Y. The HE LAB[EB/OL]. http://www.yonghelab.org/downloads/data. |
| [26] | YAN C G. Data processing assistant for resting-state fMRI[EB/OL]. http://rfmri.org/DPARSF. |
| [27] | FAN Y, NICKERSON L, LI H, et al. Functional connectivity-based parcellation of the thalamus:an unsupervised clustering method and its validity investigation[J]. Brain Connectivity, 2015, 5(10): 620–630. DOI:10.1089/brain.2015.0338 |
| [28] | KAHNT T, CHANG L J, PARK S Q, et al. Connectivity-based parcellation of the human orbitofrontal cortex[J]. Journal of the Society for Neuroscience, 2012, 32(18): 6240–6250. DOI:10.1523/JNEUROSCI.0257-12.2012 |
| [29] | MEIL M. Comparing clusterings:an information based distance[J]. Journal of Multivariate Analysis, 2007, 98(5): 873–895. DOI:10.1016/j.jmva.2006.11.013 |



