2. 天津财经大学 理工学院, 天津 300222
2. School of science and engineering, Tianjin University of Finance and Economics, Tianjin 300222, China
目前, 优化问题研究在科学、工程和金融等领域占有重要的地位.然而, 传统的优化算法(如:蚁群算法[1]、粒子群算法[2]、遗传算法[3]等)在计算复杂性、参数依赖性、全局优化能力等方面还存在许多问题.潘文超[4-5]于2011年提出果蝇优化算法(fruit fly optimization algorithm, FOA), 通过模拟果蝇觅食行为获得最优参数值.与传统算法相比, FOA算法不仅实现简单、耗时小, 而且所依赖的参数较少, 能够有效避免传统优化算法中参数选取困难及对结果影响较大的问题.
韩俊英等[6]提出了一种自适应果蝇优化算法, 该算法在收敛后使用混沌映射产生果蝇新位置, 提高了算法的全局优化能力, 但缺点在于无法优化负值参数.Pan等[7]对FOA算法进行改进, 使用果蝇位置向量直接计算适应度函数, 去掉了气味浓度判定值及距离2个参数, 实现了针对负值参数的优化.该算法通过动态调整搜索半径提高算法的全局优化能力, 并且每次更新果蝇位置时只选择对应向量中某一维度进行更新, 但不足之处在于所得结果对于搜索半径依赖较强.Wang等[8]通过计算果蝇适应值的大小决定向全局最优靠近还是执行全局搜索, 通过在全局最优值附近实施扰动以避免算法陷入局部最优.算法优化能力较强, 但全局搜索时果蝇位置随机性大, 影响了算法的收敛速度及稳定性.为了提高果蝇分布的随机性, Mitic等[9]在果蝇位置更新时引入了由不同混沌映射函数产生的随机因子, 并通过实验验证了在优化过程中使用混沌映射能够有效提高算法的收敛速度.
现有的针对FOA的改进算法普遍面临以下问题:1)在全局最优值附近的特定范围内产生果蝇的新位置, 因此优化结果受搜索半径的影响较大;2)在进行全局搜索时随机在整个空间范围内产生果蝇新位置, 易获得不稳定的优化结果;3)未充分考虑种群收敛状态对优化结果的影响, 难以有效协调算法的局部搜索强度和全局搜索强度.为此, 本文引入群体聚集度的概念, 实现了一种基于双子群和分区采样的果蝇优化新算法(DDFOA).
1 果蝇优化算法受到果蝇在觅食过程中凭借敏锐的嗅觉和视觉发现食物最佳位置的启发, 潘文超[4-5]提出了果蝇优化算法, 具体步骤如下[10]:
1.初始化参数.具体包括:果蝇数量N、最大迭代次数T、果蝇最优位置(x_axis, y_axis)、果蝇最优气味浓度Smellgb(Smellgb=-∞)等;
2.随机生成每只果蝇Xi的位置(xi, yi);
3.按照式(1)更新果蝇Xi的位置:
| $ {x_i} = {x_{\_{\rm{axis}}}} + {\rm{Rand}}\left( \; \right),\;\;\;\;{y_i} = {y_{\_{\rm{axis}}}} + {\rm{Rand}}\left( \; \right). $ | (1) |
式中:Rand()产生一个(0, 1)区间内的随机数.
4.求Xi对应的气味浓度判定值si, 如式(2)所示:
| $ {d_i} = \sqrt {x_i^2 + y_i^2} ,{s_i} = \frac{1}{{{d_i}}}. $ | (2) |
| $ {\rm{Smel}}{{\rm{l}}_i} = F\left( {{s_i}} \right). $ | (3) |
5.根据适应度函数F求得果蝇Xi的气味浓度Smelli:
6.将气味浓度最大的果蝇对应的位置及气味浓度值分别记为(xb, yb)、Smellb;
7.若Smellb >Smellgb, 则将位置(xb, yb)作为果蝇最优位置(x_axis, y_axis);
8.循环执行3~7步骤直到达到最大迭代次数T.
2 本文算法为了提高算法的全局搜索能力, 人工蜂群算法(artificial bee colony, ABC)引入了“雇佣蜂”的概念[11-12].但是, “雇佣蜂”在每次迭代中只在自己当前的位置附近搜索, 因此所得结果对初始位置依赖性较强;ABC算法虽使用“侦察蜂”作为弥补, 但是“侦察蜂”产生的新位置随机性较大, 易影响算法的收敛稳定性.为此, 本文综合考虑了传统果蝇算法及ABC算法的优势和不足, 将整个果蝇种群均分成2个子群:搜索果蝇子群和跟随果蝇子群.其中, 搜索果蝇负责在整个搜索区间内搜索, 跟随果蝇负责在全局最优值附近进行精细化搜索.为提高全局搜索的稳定性, 本文提出了一种基于分区采样的搜索果蝇位置更新策略, 如图 1所示.
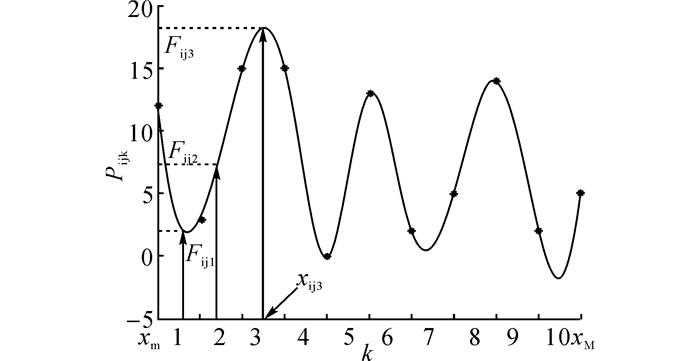
|
图 1 分区采样过程示意 Fig. 1 Schematic of partition sampling process |
图 1给出了针对搜索果蝇位置向量的某一维度进行分区采样的过程.该策略首先将搜索果蝇xi位置向量第j维上的搜索区间[xm, xM]平均分成g(本文取g=10)个分区;然后, 令搜索果蝇xi在每个分区内进行随机采样, 并按照式(4)计算第k(k≤g)次采样值xijk对应位置向量的适应值Fijk;最后, 根据贪心算法确定搜索果蝇的最终位置.
| $ {F_{ijk}} = \mathop F\limits_{{x_i} \triangleleft {x_{ijk}}} \left( {{x_i}} \right). $ | (4) |
式中:xi◁xijk表示使用xijk替换xi中第j维分量.具体地, 给出基于分区采样的搜索果蝇位置更新步骤如下:
1.令临时变量Fi=F(xi), l=(xM-xm)/g
2. for k=1:1:g
3.为保证算法的全局搜索能力, 将根据下面公式计算第k次采样结果对应的适应值Fijk:
| $ 4.\;\;{x_{ijk}} = {x_{\rm{m}}} + \left( {k - 1} \right)l + l \times {\rm{Rand}}\left( \; \right). $ | (5) |
| $ 5.\;\;{F_{ijk}} = \mathop F\limits_{{x_i} \triangleleft {x_{ijk}}} \left( {{x_i}} \right). $ | (6) |
6. if Fijk>Fi, then break; end if
7.令xi在维度j上的分量
| $ {x_{ij}} = {x_{\rm{m}}} + \left( {{x_{\rm{M}}} - {x_{\rm{m}}}} \right) \times {\rm{Rand}}\left( \; \right). $ | (7) |
end for
在果蝇算法执行过程中, 果蝇进行全局搜索的次数越多, 算法陷入局部最优的可能性越小, 但达到收敛状态所需的迭代次数则越大.为此, 本文引入了群体聚集度的概念, 用其描述搜索果蝇种群的收敛程度, 通过将每次迭代过程对应的群体聚集度与特定阈值α比较来决定是否执行全局搜索, 以此协调算法的优化精度与收敛速度.给定果蝇种群X(数量为N)、搜索果蝇子群U={x1, x2, …, xN/2}、跟随果蝇子群V={xN/2+1, xN/2+2, …, xN}及果蝇位置向量维数D, 群体聚集度W可通过公式(8)获得
| $ W = \sqrt {\frac{2}{{ND}}\sum\limits_{j = 0}^{D - 1} {\sum\limits_{i = 1}^{N/2} {{{\left| {{x_{ij}} - \overline {{x_j}} } \right|}^2}} } } . $ | (8) |
式中:
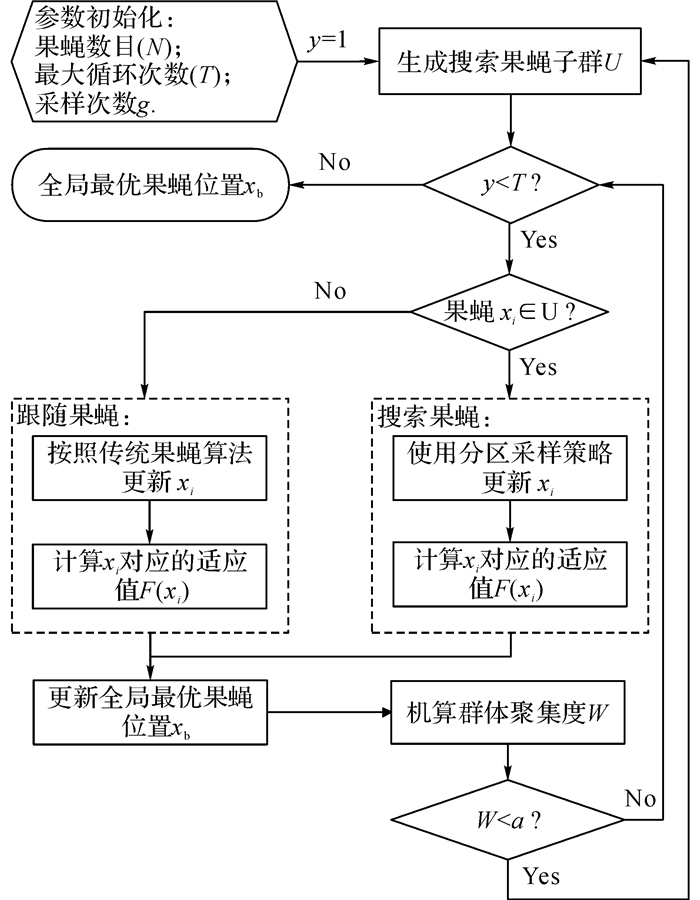
|
图 2 DDFOA算法流程图 Fig. 2 Flow chart of DDFOA |
由图 2可知, 与ACFOA[6]、IFOA[8]、cFOA[9]等算法不同, 本文通过对果蝇搜索范围进行分区采样来避免直接使用Rand函数、混沌映射函数等可能造成的收敛结果不稳定问题.具体地, 以最小值优化问题为例阐述本文算法执行步骤如下:
1.设置迭代次数y=1, 最优适应值Fb=+∞
2.for xi∈X, 按照式(9)随机生成xi的位置
| $ {x_{ij}} = {x_{\rm{m}}} + \left( {{x_{\rm{M}}} - {x_{\rm{m}}}} \right) \times {\rm{Rand}}\left( \; \right),\;\;\;\;\;0 \le j < D. $ | (9) |
3. end for
4.获得全局最优果蝇并将其记为xb
5. while(y < T)
6. for each xi∈U
7.针对xi的每个维度分量xij, 按照分区采样策略更新xij值
8. if F(xi) < Fb then xb=xi end if
9. end for
10. for each xi∈V
11.按照式(10)计算跟随果蝇每个维度分量xij值:
| $ {x_{ij}} = {x_{{\rm{b}}j}} + {\rm{Rand}}\left( \; \right) \times {\left( { - 1} \right)^{\left\lfloor {{\rm{Rand}}\left( \; \right) \times 10\;000} \right\rfloor }}. $ | (10) |
式中:xbj为xb的第j维分量.
12. if F(xi) < Fb then xb=xi end if
13. end for
更新全局最优果蝇xb, y++
14.按照式(8)计算群体聚集度W
15. if W < α then
16.令搜索果蝇子群U进行全局搜索, 即执行步骤6-9
18. end if
19. end while
3 实验结果与分析 3.1 实验设置分别选取3个单峰基准函数(F1-F3)、3个多峰基准函数(F4-F6)进行测试.不同函数的公式表示、目标值及目标值对应的位置向量如表 1所示[8, 12].公平起见, 设置不同算法对应的果蝇数量N=50, 最大迭代次数T=2 000.
| 表 1 不同函数公式表示、目标值及目标位置向量 Table 1 Formulas, target values and target position vectors of different functions |
为准确获得α值, 通过统计算法在测试函数F1-F6上的表现确定最优α.给定函数Fi对应的目标位置向量Xbi=[xb0, xb1, .., xbj, …, xbD-1]以及维度j上的搜索范围[xm, xM], 设置除F5外其他函数的维度D分别取2、4、6、8、10.针对每个优化函数执行100次, 并按式(11)计算群体聚集度的最大值αM值:
| $ {\alpha _{\rm{M}}} = \frac{1}{{100}}\sum\limits_{i = 1}^{100} {{W_i}} . $ | (11) |
式中:Wi为在第i次实验中果蝇位置初始化状态对应的群体聚集度.接着, 分别当α∈[0, αM]并以步长β=0.05递增时统计不同函数对应的目标值绝对值均值Fa以及达到收敛状态所需的迭代次数均值Nca, 结果如图 3所示.由图可知, 当α逐渐增加时, 算法的收敛速度变慢, 原因在于算法因强调全局搜索性能而弱化了精细化搜索过程.观察Fa值可知, 当α < 0.2时, Fa呈现逐渐减小的趋势;当α∈[0.2, 0.4]时, Fa值近似为0, 说明此时算法能够较好地协调全局搜索及局部搜索强度;随着α继续增加, 算法将过度强调全局搜索的作用, 导致收敛精度不高.因此, 为在保证收敛精度的同时尽可能提高算法的收敛速度, 本文取α=0.2并将其应用于后续实验中.

|
图 3 群体聚集度阈值α的选择 Fig. 3 Selection of population aggregation degree threshold α |
实验选用较复杂的多极值函数F4-F6, 分别使用Rand函数[6]、Logistic函数[9]、Circle函数[9]及本文进行100次全局搜索实验.随着迭代次数y逐渐增加, 计算果蝇对应的适应值均值Fga的变化情况, 结果如图 4所示.由图可知, 本文方法对应结果呈现稳定下降的趋势, 且在20次迭代左右探索到全局最优位置;其他方法所得结果波动明显, 虽然在某些情况下对应的适应值均值较小, 但随着迭代次数增加并未获得最优结果.可见, Rand函数、Logistic函数、Circle函数等方法全局搜索能力不强, 而本文基于分区采样的搜索策略能更好地保证全局优化效果, 提高算法的稳定性.
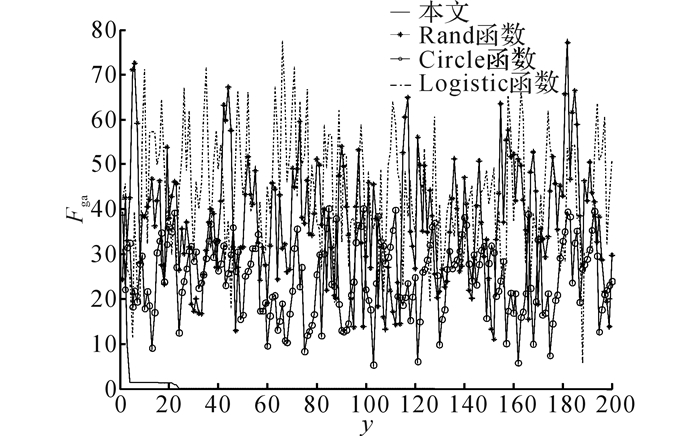
|
图 4 全局搜索能力比较 Fig. 4 Comparison of global searching abilities |
果蝇位置初始化过程对应本文算法中步骤1-4, 其时间复杂度为
| $ {T_1} = O\left( {DN} \right). $ | (12) |
果蝇位置更新过程对应本文算法中步骤6-14.由于基于分区采样的搜索果蝇位置更新策略使得搜索果蝇在每次迭代过程中至少进行1次、至多进行g次采样.因此, 该过程时间复杂度T2满足:
| $ O\left( {TDN/2} \right) \le {T_2} \le O\left( {TDNg/2} \right). $ | (13) |
由于g为固定值, 可得
| $ {T_2} = O\left( {TND} \right). $ | (14) |
群体聚集度计算过程对应本文算法中步骤15, 其时间复杂度为:T3=O(TND).
于是, 得到本文算法时间复杂度为
| $ T = {T_1} + {T_2} + {T_3} = O\left( {TND} \right). $ | (15) |
如表 2所示将几种典型优化算法对应的时间复杂度进行了对比.由表中可知, DDFOA算法时间复杂度虽比IFFO、ABC算法高, 但与FOA、IFOA、cFOA算法相等, 这说明本文方法在保证良好的全局搜索效果基础上并未带来显著的计算开销.
| 表 2 不同优化算法时间复杂度对比 Table 2 Time complexity comparison of different optimization algorithms |
设置除F5外其他函数的维度D分别取2、4、6、8、10.分别针对每个D值进行100次实验, 计算100次实验所得函数最优值均值μ和最优值标准差ε, 结果如表 3所示.由表中可知, 在处理最优位置向量分量为负数的函数F1时, FOA及IFOA算法对应μ值最低, 原因在于它们直接使用味道浓度作为选择全局最优果蝇的判定标准, 因此无法实现针对负值参数的优化.在处理多极值函数F4-F6时, FOA算法表现最差, IFOA及ABC所得结果明显优于IFFO及cFOA;ABC算法所得精度与DDFOA算法近似, 但对应ε值普遍偏大, 说明前者优化结果具有较大的不稳定性.总体来看, 相对于其他算法而言, DDFOA算法在优化精度及收敛稳定性方面均具有一定优势, 说明基于双子群及分区采样的果蝇搜索策略在提高全局搜索稳定性、协调算法局部搜索及全局搜索强度方面起到一定作用.
| 表 3 最优值均值及最优值标准差比较 Table 3 Comparison of average optimal values and standard deviations of optimal values |
设置除F5外其他函数的维度D分别取2、4、6、8、10.分别针对每个D值进行100次实验, 统计每种优化算法对应的平均适应值Fa随迭代次数y的变化情况, 结果如图 5所示.由图可知, FOA及IFOA收敛最慢, 达到收敛状态时对应的迭代次数均大于1 600;cFOA算法收敛最快, 但由于该算法在收敛后并未进行全局搜索, 因此极易陷入局部极值.进一步发现, DDFOA算法及ABC算法在达到收敛状态时对应的Fa值相近, 但DDFOA算法却早于ABC算法收敛, 这说明基于维度分区采样的搜索果蝇搜索策略能较好地减少果蝇进行全局搜索的盲目性, 在保证收敛精度的同时提高了算法的收敛速度.
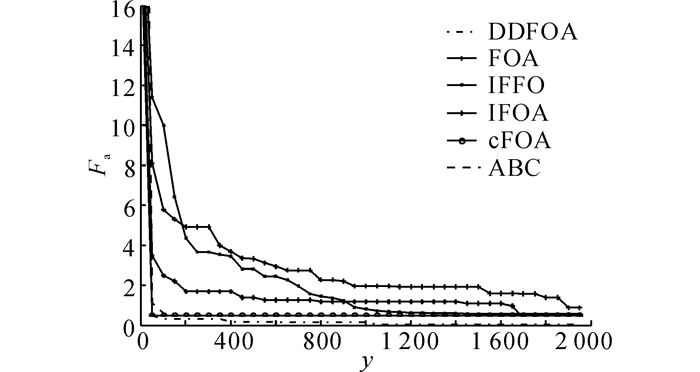
|
图 5 不同算法收敛速度比较 Fig. 5 Comparison of convergence speeds of different algorithms |
比例-积分-微分(proportion integration differentiation, PID)控制器是一个在工业控制应用中常见的反馈回路部件[13].给定被控对象M, 如图 6所示为PID控制器执行过程.图中:t为测量时间, rin (t)为给定信号, yout (t)为系统实际输出信号, e(t)为系统误差.由图 6可知, PID控制器以e(t)为输入, 将经过由比例单元P、积分单元I和微分单元D线性组合后的输出信号u(t)作为被控对象的输入.PID控制器传递函数表示如下[14]:
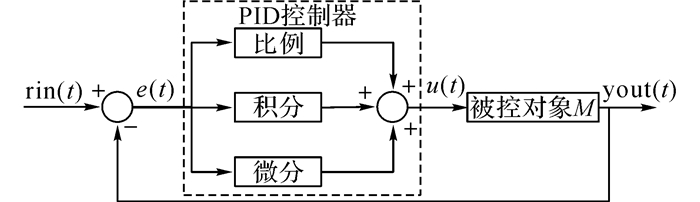
|
图 6 PID控制器原理 Fig. 6 Principle of PID controller |
| $ u\left( t \right) = {K_{\rm{p}}} \times e\left( t \right) + {K_{\rm{i}}}\int_0^t {e\left( t \right)} + 9 + {K_{\rm{d}}} \times \frac{{{\rm{d}}\left( {e\left( t \right)} \right)}}{{{\rm{d}}t}}. $ | (16) |
式中:u(t)为输出信号, Kp为比例系数, Ki为积分系数, Kd为微分系数.研究证明, Kp、Ki及Kd的取值对PID性能影响较大, 合理的参数取值能使控制信号朝着误差减小的方向变化.为此, 将使用DDFOA算法对PID控制参数向量x=[Kd, Ki, Kp]进行优化, 并将其结果与相同条件下其他算法对应结果进行比较.使用误差绝对值积分(ITAE)作为目标函数, 公式如下[14]:
| $ F\left( x \right) = \int_0^t {t\left| {e\left( t \right)} \right|} . $ | (17) |
进一步地, 给出被控对象的数学模型如下:
| $ G\left( s \right) = \frac{{523\;407}}{{{s^3} + 86.65{s^2} + 10\;465s}}. $ | (18) |
式中:采样时间为1 ms, 输入信号为阶跃信号.为了避免参数选取的范围过大而可能造成的盲目性搜索, 根据经验指定搜索边界为Xmin=0、Xmax=5.在此基础上, 设置最大迭代次数T=50, 并将不同算法各运行100次, 统计目标函数均值Fpa随迭代次数y的变化情况, 如图 7所示.由图可知, DDFOA及ABC收敛精度近似且明显高于其他算法;cFOA收敛速度最快, 但对应的目标函数均值却明显高于除IFOA以外的其他算法, 说明该算法极易陷入局部最优状态;与ABC、IFFO、FOA等算法相比, DDFOA算法达到收敛状态所需迭代次数明显偏少, 说明DDFOA算法能在保证收敛精度的同时有效提高算法收敛速度.由此可见, 使用DDFOA算法优化的PID控制器控制精度较高, 稳定性好, 针对仿真被控对象具有较强的控制性能.
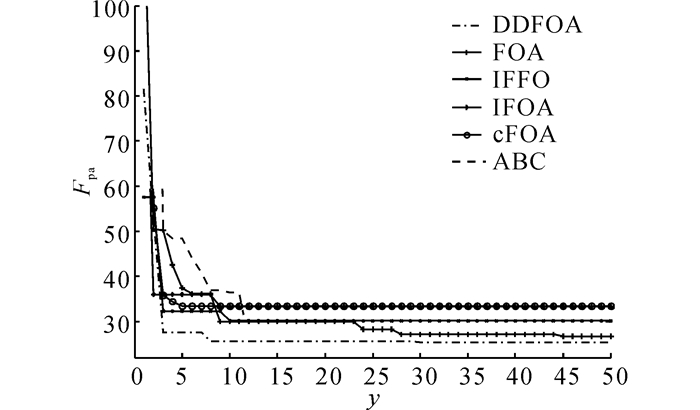
|
图 7 同算法对应的ITAE值比较 Fig. 7 Comparison of ITAE values of differentalgorithms |
提出了一种基于双子群和分区采样的果蝇优化新算法, 主要特点如下:
(1) 为降低算法对搜索半径的依赖, 将果蝇种群分为2类不同的子群;
(2) 为提高收敛稳定性, 提出了基于分区采样的搜索果蝇位置更新策略;
(3) 为准确判定算法何时执行全局搜索, 引入群体聚集度的概念并以此作为是否进行全局搜索的标准.针对6种典型函数的优化结果表明, 算法在收敛精度、稳定性、收敛速度等方面表现优于传统优化算法;针对PID控制系统的仿真结果表明, 使用本文算法优化后PID控制器调节精度高、稳定性好, 对于仿真被控系统表现出良好的控制性能.
进一步工作包括:1)研究群体聚集度阈值对算法表现的影响, 探索该阈值的自动化判定方法;2)研究多粒子并行处理技术, 提高算法计算效率.
| [1] | YU Q, CHEN L, LI B. Ant colony optimization applied to web service compositions in cloud computing[J]. Computers & Electrical Engineering, 2015, 41(1): 18–27. |
| [2] | GHAMISI P, BENEDIKTSSON J A. Feature selection based on hybridization of genetic algorithm and particle swarm optimization[J]. IEEE Geoscience & Remote Sensing Letters, 2015, 12(2): 309–313. |
| [3] | LI Z, LIU J. A multi-agent genetic algorithm for community detection in complex networks[J]. Physica A Statistical Mechanics & Its Applications, 2016, 449(5): 336–347. |
| [4] |
潘文超. 应用果蝇优化算法优化广义回归神经网络进行企业经营绩效评估[J].
太原理工大学学报:社会科学版, 2011, 29(4): 1–5.
PAN Wen-chao. Using fruit fly optimization algorithm optimized general regression neural network to construct the operating performance of enterprises model[J]. Journal of Taiyuan University of Technology:Social Sciences Edition, 2011, 29(4): 1–5. |
| [5] | PAN W T. A new fruit fly optimization algorithm:taking the financial distress model as an example[J]. Knowledge-Based Systems, 2012, 26: 69–74. DOI:10.1016/j.knosys.2011.07.001 |
| [6] |
韩俊英, 刘成忠. 自适应混沌果蝇优化算法[J].
计算机应用, 2013, 33(5): 1313–1316.
HAN Jun-ying, LIU Cheng-zhong. Adaptive chaos fruit fly optimization algorithm[J]. Journal of Computer Applications, 2013, 33(5): 1313–1316. |
| [7] | PAN Q K, SANG H Y, DUAN J H, et al. An improved fruit fly optimization algorithm for continuous function optimization problems[J]. Knowledge-Based Systems, 2014, 62(5): 69–83. |
| [8] | WANG Lin, SHI Yuan-long, LIU Shan. An improved fruit fly optimization algorithm and its application to joint replenishment problems[J]. Expert Systems with Applications, 2015, 42(9): 4310–4323. DOI:10.1016/j.eswa.2015.01.048 |
| [9] | MITIC M, VUKOVIC N, PETROVIC M, et al. Chaotic fruit fly optimization algorithm[J]. Knowledge-Based Systems, 2015, 89(C): 446–458. |
| [10] | CHEN Peng-wen, LIN Wei-yuan, HUANG Tsui-hua, et al. Using fruit fly optimization algorithm optimized grey model neural network to perform satisfaction analysis for e-business service[J]. Applied Mathematics & Information Sciences, 2013, 7(2L): 459–465. |
| [11] | KARABOGA D, AKAY B. A comparative study of artificial bee colony algorithm[J]. Applied Mathematics and Computation, 2009, 214(1): 108–132. DOI:10.1016/j.amc.2009.03.090 |
| [12] | KARABOGA D, BASTURK B. On the performance of artificial bee colony (ABC) algorithm[J]. Applied Soft Computing, 2008, 8(1): 687–697. DOI:10.1016/j.asoc.2007.05.007 |
| [13] | YANG Y. PID Parameter setting and optimization for the walking beam hydraulic control system[J]. Cancer Epidemiology Biomarkers & Prevention, 2015, 10(11): 1193–1199. |
| [14] |
宋娟. 一种用于PID控制参数优化的混合果蝇算法[J].
传感器与微系统, 2015(6): 137–140.
SONG Juan. A hybrid fly fruit algorithm for PID control parameters optimization[J]. Transducer and Microsystem Technologies, 2015(6): 137–140. |


